Impact of data distribution on the parallel performance of iterative linear solvers with emphasis on CFD of incompressible flows

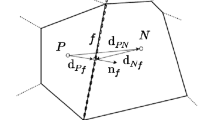
Abstract

A parallel data structure that gives optimized memory layout for problems involving iterative solution of sparse linear systems is developed, and its efficient implementation is presented. The proposed method assigns a processor to a problem subdomain, and sorts data based on the shared entries with the adjacent subdomains. Matrix–vector-product communication overhead is reduced and parallel scalability is improved by overlapping inter-processor communications and local computations. The proposed method simplifies the implementation of parallel iterative linear equation solver algorithms and reduces the computational cost of vector inner products and matrix–vector products. Numerical results demonstrate very good performance of the proposed technique.

Appendix

The performance of the present method is compared with that of PETSc, a widely adopted linear algebra library of routines [1]. A Cray PETSc 3.2.00 release, equivalent to a 3.2-p5 release by the Argonne National Laboratory, is used for comparison. Since there may be significant differences in the implementation of iterative linear algebra algorithms, only matrix-vector product operation is considered in this comparison study. Our choices for the PETSc matrix type, its initialization and assembly, and also the matrix-vector product operation are included here for completeness:

In the above pseudo-code $\tilde{\varvec{x}}$ and $\tilde{\varvec{A}}$ are the memory locations of the vector $\varvec{x}$ and matrix $\varvec{A}$, $\varvec{t}$ is a temporary array, and $I^i$ and $J^i$ are the C-compatible integer arrays with 0 as the first entry.

Computations associated with Fig. 5 are repeated using PETSc. One hundred matrix-vector products are computed and $t_\mathrm{cpu}$ is measured. To compare the methods in terms of minimal time to completion of a matrix-vector product operation, the cases of $n_\mathrm{p}=$8, 16, and 64 are considered for the small, medium, and large model, respectively (see Table 1). These correspond to near-peak performance of both techniques (see Fig. 5). The results show that by increasing the problem size the difference between the peak performance of the present method and PETSc becomes more apparent: The higher the number of partitions, the better the present method performs relative to PETSc. The improvement for the small, medium, and large model is 65, 177, and 516 %, respectively. Repeating the computations on a different machine and using a different version of PETSc had minimal effect on the results. Note that, among the several options available, we used a basic PETSc matrix type in this comparison. PETSc results may depend on the matrix type, however, this was not investigated here.