Modeling lipid accumulation in oleaginous fungi in chemostat cultures: I. Development and validation of a chemostat model for Umbelopsis isabellina

Abstract

Lipid-accumulating fungi may be able to produce biodiesel precursors from agricultural wastes. As a first step in understanding and evaluating their potential, a mathematical model was developed to describe growth, lipid accumulation and substrate consumption of the oleaginous fungus Umbelopsis isabellina (also known as Mortierella isabellina) in submerged chemostat cultures. Key points of the model are: (1) if the C-source supply rate is limited, maintenance has a higher priority than growth, which has a higher priority than lipid production; (2) the maximum specific lipid production rate of the fungus is independent of the actual specific growth rate. Model parameters were obtained from chemostat cultures of U. isabellina grown on mineral media with glucose and NH₄ ⁺. The model describes the results of chemostat cultures well for D > 0.04 h⁻¹, but it has not been validated for lower dilution rates because of practical problems with the filamentous fungus. Further validation using literature data for oleaginous yeasts is described in part II of this paper. Our model shows that not only the C/N-ratio of the feed, but also the dilution rate highly influences the lipid yield in chemostat cultures.

Introduction

As the need to replace fossil fuels increases, lipids accumulated in oleaginous organisms come into view for the production of biodiesel. Besides oleaginous microalgae, oleaginous yeasts and fungi may be a promising option, provided that these heterotrophs use biomass residues as a C-source [1–3]. We study the potential of oleaginous fungi to convert biomass residues to biodiesel precursors.

Previously, lipid accumulation in oleaginous yeasts and especially oleaginous fungi has been studied mainly with the aim to produce high-value poly-unsaturated fatty acids (PUFAs), such as arachidonic acid and γ-linolenic acid [4], in submerged fermentation with glucose as C-source. If the aim is biodiesel production, the use of other substrates such as agricultural or industrial waste streams becomes of interest, as well as the use of cheaper production systems, such as solid-state fermentation. Lipid production on waste streams has been studied in submerged fermentation [5–8] as well as in solid-state fermentation [9–12]. Theses studies mainly focused on maximum lipid fractions reached and less on production rates or yield on substrate. Especially in solid-state fermentation, only low yields were reached. Obviously, the product yield and formation rates are of primary importance for biodiesel production. To allow development of bioprocesses with higher yields and production rates, insight in the kinetics of lipid production has to be improved.

As a starting point to study kinetics, we chose a chemostat system. In chemostat, the supply of all substrates and the growth rate can be controlled by setting the dilution rate and the concentrations of the substrates in the feed. This makes chemostat culture a suitable tool to study lipid accumulation under different circumstances. This paper describes kinetic modeling of lipid production in submerged chemostat cultures. In part I of this paper, we develop a chemostat model and validate it with chemostat cultures of U. isabellina, a filamentous fungus that proved to be the most promising strain for solid-state fermentation among a large group of oleaginous fungi tested (results not published). In part II of this paper, we will compare our model to literature data for chemostat cultures of oleaginous yeasts, and to a previously described model for continuous culture published by Ykema et al. [13].

Model

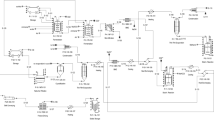
Figure 1 shows a simplified scheme of the metabolism of an oleaginous organism. The organism uses a C-source, an N-source and oxygen to produce lipid-free cell material (X), lipids (L), carbon dioxide and water. The compositions of lipid-free cell material and lipids given in Fig. 1 are based on the average composition of cells and lipids in our experiments (see “Results”). Symbols used in the model are listed in abbreviation.

Fig. 1

Schematic representation of the carbon and nitrogen metabolism in the oleaginous fungus U. isabellina. The production or uptake rates of the carbon source (glucose, r _S), lipid-free biomass (r _X), lipids (r _L) and CO₂ (r _C) are expressed in Cmol m⁻³ h⁻¹, the rate of nitrogen source (NH₃, r _N) is expressed in Nmol m⁻³ h⁻¹ and the rates of oxygen (r _O) and water (r _W) are expressed in mol m⁻³ h⁻¹. Compositions of lipid-free biomass and lipids are based on experimental results

The model is based on the Scheme in Fig. 1 and several assumptions:

• The C-source and/or the N-source is limiting for the production of lipid-free biomass and lipids; oxygen and other nutrients are supplied in abundance.

• No other carbon or nitrogen-containing products are produced besides lipid-free biomass, lipids and CO₂. This means that the element balances for C and N read:

  $$ r_{\text{S}} + r_{\text{X}} + r_{\text{L}} + r_{\text{C}} = 0\,\left( {\text{for carbon}} \right){\text{ and}}\;r_{\text{N}} + {\frac{{r_{\text{X}} }}{{Y_{\text{XN}} }}} = 0\,\left( {\text{for nitrogen}} \right) $$

  (1)

• The first priority of the fungus is to use the supplied C-source to satisfy its maintenance requirements, then to produce lipid-free biomass, and finally, only if there is C-source left, to accumulate lipids.

• The fungus always produces a basal amount of lipids for its cell membranes; the basal specific lipid production rate is proportional to the specific growth rate:

  $$ q_{\text{L,min}} = {\frac{{f_{\text{L0}} }}{{1 - f_{\text{L0}} }}}\mu $$

  (2)

• If sufficient C-source is available, the specific lipid production rate increases up to a maximum value $q_{\text{L,max}}$. This maximum specific lipid production rate is independent of the specific growth rate, as has been shown before in literature [14, 15].

• Low C-source and N-source concentrations do not affect the conversion rates of these components (zero-order kinetics with respect to reactants).

• Physiological or regulatory mechanisms do not impose a maximum on the lipid content of the cells. Such a maximum has been found in batch cultures [16], but it is not included in the model because high lipid contents were not reached in the experiments used for validation.

The model predicts the concentrations of lipid-free biomass ($C_{\text{X}}$), lipids ($C_{\text{L}}$), non-consumed C-source ($C_{\text{S}}$) and non-consumed N-source ($C_{\text{N}}$) in the culture during steady state at any combination of the dilution rate ($D$) and the concentrations of C-source ($C_{\text{Sin}}$) and N-source ($C_{\text{Nin}}$) in the feed. Component mass balances over the culture combined with Pirt’s linear growth law, read:

$$ {\text{Lipid}}{\text{-}} {\text{free biomass}}{:}\;0 = - D\,C_{\text{X}} + \mu \,C_{\text{X}} $$

(3)

$$ {\text{Lipids}}{:}\;0 = - D\,C_{\text{L}} + q_{\text{L}} \,C_{\text{X}} $$

(4)

$$ {\text{C}} {\text{-}} {\text{source}}{:}\;0 = D\,\left( {C_{\text{Sin}} - C_{\text{S}} } \right) - \left( {m_{\text{S}} + {\frac{\mu }{{Y_{\text{XS}} }}} + {\frac{{q_{\text{L}} }}{{Y_{\text{LS}} }}}} \right)\,C_{\text{X}} $$

(5)

$$ {\text{N}} {\text{-}} {\text{source}}{:}\,0 = D\,\left( {C_{\text{Nin}} - C_{\text{N}} } \right) - {\frac{\mu }{{Y_{\text{XN}} }}}\,C_{\text{X}}. $$

(6)

When we combine these balances, the assumptions above and the boundary conditions (all concentrations must be ≥0), we get the following set of equations:

$$ C_{\text{S}} = C_{\text{Sin}} - {\frac{{C_{\text{X}} }}{D}}\left( {m_{\text{S}} + {\frac{D}{{Y_{\text{XS}} }}} + {\frac{{q_{\text{L}} }}{{Y_{\text{LS}} }}}} \right) \ge 0 $$

(7)

$$ C_{\text{N}} = C_{\text{Nin}} - {\frac{{C_{\text{X}} }}{{Y_{\text{XN}} }}} \ge 0 $$

(8)

$$ C_{\text{L}} = {\frac{{q_{\text{L}} }}{D}}C_{\text{X}} \wedge \;q_{\text{L,min}} \le q_{\text{L}} \le q_{\text{L,max}} . $$

(9)

Three different regimes can be distinguished, depending on the concentrations of C-source ($C_{\text{Sin}}$) and N-source in the feed ($C_{\text{Nin}}$) and the dilution rate ($D$): single nitrogen limitation ($C_{\text{N}} = 0$), dual limitation ($C_{\text{N}} = 0$ and $C_{\text{S}} = 0$), and single carbon limitation ($C_{\text{S}} = 0$). The equations used in these regimes, all derived from Eqs. 7–9, are summarized in Table 1. Figure 2 shows the three regimes in a chemostat culture with a constant C/N-ratio of the feed and a variable dilution rate. All regimes are explained below.

Table 1 Equations used to calculate concentrations of glucose, ammonium, lipid-free biomass and lipids, and the specific lipid production rate for U. isabellina in a chemostat

Fig. 2

Concentrations of N-source (C _N), C-source (C _S), lipid-free biomass (C _X), lipids (C _L) and total biomass (C _X + C _L) for a variable dilution rate (D) predicted by the model (arbitrary units). Limitation regimes are indicated as described in the text. In cultures with a high C/N-ratio, the single carbon limitation area and the dual limitation area are usually very small, but are shown prominently here to give an overview of all limitation regimes possible

Single nitrogen limitation

Single nitrogen limitation implies that the nitrogen source is the only limiting substrate. Therefore, the concentration of the N-source in the culture ($C_{\text{N}}$) is 0 according to the model, and Eq. 8 gives the lipid-free biomass concentration ($C_{\text{X}}$).The concentration of C-source in the culture ($C_{\text{S}}$) is higher than 0. Therefore, the specific lipid production rate ($q_{\text{L}}$) has its maximum value ($q_{\text{L,max}}$), and the lipid concentration ($C_{\text{L}}$) can be calculated from Eq. 9. Equation 7 can be used to calculate the concentration of C-source in the culture ($C_{\text{S}}$). Single nitrogen limitation occurs when the C/N-ratio of the feed is high and a high enough dilution rate ($D$) is applied (see Fig. 2).

Dual limitation

Dual limitation implies that $C_{\text{N}} = 0$ and $C_{\text{S}} = 0$ in the model. Equation 8 gives the lipid-free biomass concentration ($C_{\text{X}}$), while Eq. 7 gives the specific lipid production rate ($q_{\text{L}}$). The N-source is limiting for lipid-free biomass production, and the C-source is limiting for lipid production because the cell will give priority to maintenance and growth. This dual limitation is known as heterologous dual limitation [17].

Single carbon limitation

Single carbon limitation occurs when $C_{\text{S}} = 0$ but $C_{\text{N}} > 0$ in the model. As the cells give priority to growth and maintenance above lipid production, only membrane lipids will be produced and the specific lipid production rate ($q_{\text{L}}$) will have its minimum value ($q_{\text{L,min}}$). The lipid-free biomass concentration ($C_{\text{X}}$) can be determined using Eq. 7, the remaining N-source concentration with Eq. 8. Single carbon limitation occurs when the C/N-ratio in the feed is lower than the C/N-ratio required for growth, but can also occur at higher C/N ratios in the feed when the dilution rate is very low (see Fig. 2), i.e. when maintenance plays an important role.

Respiration

The CO₂-production rate and the O₂-consumption rate are calculated using mass balances. From the carbon balance in Eq. 1 the CO₂-production rate is calculated. The O₂-production rate is calculated in a similar way using the oxygen and hydrogen balances, which can be calculated from the composition of all substrates and products involved. The equations for both rates are also shown in Table 1.

Materials and methods

Inoculum

Umbelopsis isabellina CBS 194.28 was cultured on potato dextrose agar (Oxoid CM139) for 14 days at 25 °C. The spores were harvested by adding 10 mL PFS-Tween (containing 1 g neutral bacterial peptone (Oxoid L34), 8.5 g NaCl and 0.5 g Tween-80 per l water) per plate and scraping with a glass spatula. The obtained spore solution was filtered through sterile glass wool to remove mycelium. Glycerol was added up to 23% v/v and the suspension was frozen at −80 °C in aliquots of 1 mL. Spore counts were done on plate count agar (Oxoid CM325) after thawing and dilution of the spore suspension. The vials contained 3 × 10⁷ CFU/mL.

Medium

Liquid medium for all cultures contained per liter: 0.5 g KCl, 0.5 g MgSO₄·7H₂O, 1.5 g Na₂HPO₄·2H₂O, 1 mL trace metal solution as described by Vishniac and Santer [18], glucose as C-source and (NH₄)₂SO₄ as N-source. Chemostat cultures were started as a batch culture with medium containing 50 mM glucose and 25 mM NH₄ ⁺. The different concentrations of glucose and ammonium in the feed during continuous operation are shown in Table 2. Pre-culture medium contained 100 mM glucose and 100 mM NH₄ ⁺. The pH of all media was adjusted to 6.0 with H₂SO₄. Glucose was autoclaved separately. To all media, except for the preculture, 1 mL of antifoam (Polypropylene glycol (Sigma), 50% v/v in ethanol) was added per liter.

Table 2 Results from chemostat experiments with U. isabellina in a 1 L bioreactor

Pre-culture

The pre-culture was carried out in 250 mL shake flasks with 100 mL pre-culture medium. The flasks were inoculated with 1 mL spore suspension and incubated at 25 °C in a shaking incubator at 225 rpm for 3 days.

Culture

The cultivation was carried out in a baffled glass bioreactor with a volume of 2.5 L and a working volume of 1 L (Applikon, The Netherlands), placed in a temperature-controlled cabinet to keep the culture at 28 °C. The reactor was stirred with one 6-blade disc turbine impeller (Applikon, The Netherlands) at 700 rpm. To reduce attachment of mycelium clumps behind the baffles, the stirring direction was reversed every 30 s as was done before by Song et al. [19]. The baffles were not removed because this would decrease oxygen transfer up to a factor three, according to calculations. The pH of the medium was kept at 6.0 with a pH electrode and a control system (biocontroller ADI 1030, Applikon, The Netherlands) by addition of NaOH (1 M). Air was blown into the culture at a rate of 1 L/min through a PTFE-filter (0.2 μm Whatman Polyvent 16), just below the stirrer. Off-gas was cooled to 4 °C in a condenser, before the O₂ and CO₂ concentrations were measured with a paramagnetic O₂ analyzer (Servomex 4100, The Netherlands) and an infrared CO₂ analyzer (Servomex 1440, The Netherlands); these measurements were logged using Labview 5.1 (National Instruments, US). Calculations showed that the CO₂ and O₂ dissolved in the outgoing medium could be neglected as compared to the CO₂ and O₂ in the off-gas. The O₂ concentration in the liquid was not controlled because the fungus grows on the membrane of an O₂ electrode, influencing the measurements. Calculations and measurements of the oxygen transfer rate at the start of a culture showed that at the used mixing rate and air flow rate, approximately 10 mol m⁻³ h⁻¹ of oxygen could be transferred from the gas phase to the liquid phase. Low substrate concentrations in the feed were used to keep the biomass concentration in the bioreactor low and therefore keep the O₂-consumption rate below 10 mol m⁻³ h⁻¹.

The cultivation was started as a batch culture by adding 50 mL preculture to 950 mL start medium. After 1 day, the feed was started at a fixed dilution rate using a peristaltic pump with the medium as indicated in Table 2. The weight of the fresh medium vessel was registered to calculate the dilution rate. Culture broth was removed every 12 min via an overflow tube, using a peristaltic pump operated at high rate. The removed culture broth was collected and stored in a fraction collector kept at 5 °C for a maximum of 18 h, before separation of biomass and medium. During this storage, no significant changes in the samples were observed. After a change in the dilution rate, samples were taken after at least three hydraulic residence times and when the CO₂-concentration in the off-gas remained stable for at least 12 h. Samples were taken during at least 12 h when a steady state was reached.

Dry weight measurement

Samples taken from the reactor were centrifuged (10 min, 4,000 g), and the supernatant was frozen until further analysis. The pellet was washed with water once and freeze-dried to determine the dry weight. The ash content of the cell material was determined after incubation in an oven at 500 °C. Elemental analysis (CHNS) of the samples was carried out with an EA1110 elemental analyzer (Thermoquest, CE Instruments, UK). All mass that was not determined as being ash, carbon, hydrogen, nitrogen or sulfur was assumed to be oxygen.

Lipid determination

Freeze dried mycelium was pulverized with a mortar and pestle and suspended in chloroform containing a known concentration of nonadecanoic acid (Fluka) as internal standard. The samples were incubated overnight in a head-over-tail-mixer. The chloroform was filtered through a paper filter (Whatman 595, Germany) to remove remains of the mycelium. The extracted lipids in the chloroform were transesterified by adding a small amount of trimethylsulfonium hydroxide solution (TMSH, 0.25 M in methanol, Fluka) and the methyl esters formed were measured on a GC (Hewlett Packard 6890 series) with column: Supelco 25357, 30 m × 530 μm, 1 μm nominal. The temperature of the column was raised from 90 °C to 200 °C with 10 °C/min, at which it stayed for 18 min. Both the injector and the detector (FID) had a temperature of 250 °C. The carrier gas was helium with a flow rate of 16.1 ml/min. We used nonadecanoic acid as an internal standard. Only C16:0, C18:0, C18:1 and C18:2 were measured, as these four fatty acids comprised more than 98% of the fatty acids present.

Medium analysis

The glucose concentration in the medium was determined using the glucose GOD-PAP test (Roche, Germany). The NH₄ ⁺ concentration was estimated using Merckoquant ammonium test strips (Merck). Total organic carbon (TOC) was measured using the Dr. Lange TOC test (LCK 386, Hach Lange, Germany).

Results and discussion

Results of chemostat cultures

Table 2 shows the results of the chemostat cultures of U. isabellina with glucose as C-source and NH₄ ⁺ as N-source. For all data points with a feed C/N-ratio of 16 or 20 Cmol/Nmol, the NH₄ ⁺ concentration in the effluent was ≤1 mol m⁻³. In the experiment with a feed C/N-ratio of 6 Cmol Nmol⁻¹, approximately 6 mol m⁻³ NH₄ ⁺ was found in the effluent.

The lipid fractions found in the experiments do not exceed 25% w/w, while U. isabellina is known to be capable of producing up to 55% w/w [20]. Reaching higher lipid fractions required lower dilution rates than we could use because of practical problems; this will be explained later. The fatty acid composition of the lipids depended on the lipid content of the cells (Fig. 3): 46% w/w of the lipids were C18:1 at the basal lipid fraction of 5% w/w, and this increased to 55% w/w at lipid fractions of 15% w/w or higher. All other measured fatty acids decreased with increasing lipid fraction. The lipid fraction was in most cases proportional to the average residence time (=1/D) and therefore to cell age. Fakas et al. [21] have shown before that similar changes in lipid composition of U. isabellina occur during the aging of mycelia. The composition of the lipids (CH_1.95O_0.11, MW = 15.7 g Cmol⁻¹) used in the model is based on the average of the compositions shown in Fig. 3. Although U. isabellina is a known producer of γ-linolenic acid [19], we did not detect this fatty acid in the strain we used.

Fig. 3

Composition of lipids produced by U. isabellina in a chemostat as a function of the fraction of lipids in the biomass. The shown fatty acids comprised more than 98% of the total lipids. Error bars indicate standard deviation. The lines emphasize the trend that can be observed

The elemental composition of lipid-free biomass was CH_1.77O_0.55N_0.17; the molecular mass was 28.7 ± 0.5 g Cmol⁻¹ including ash. These values were the same for all samples and independent of the dilution rate, feed C/N-ratio or lipid content of the cells.

The recovery of carbon in the culture (produced lipid-free biomass plus lipids and CO₂ divided by consumed glucose) was 88% on average (Table 2). Total organic carbon (TOC) measurements in supernatant samples showed that only a small part of the missing carbon was present in solution or as a dispersion of particles that were too small to separate during centrifuging. The largest part of the missing carbon was not found in the medium and we assume that this was present in cell aggregates attached to the baffles and stirrer.

Determination of parameter values

Data obtained with a feed C/N-ratio of 6 Cmol Nmol⁻¹ were used to determine the basal lipid fraction in the cells ($f_{\text{LO}}$). Biomass, lipid and glucose concentrations obtained with feed C/N-ratios of 16 and 20 Cmol Nmol⁻¹ were used to find the other model parameters $Y_{\text{XN}}$, $Y_{\text{XS}}$, $Y_{\text{LS}}$, $m_{\text{S}}$ and $q_{\text{L,max}}$. The determination of parameter values is explained below; parameter values are shown in Table 3a.

Table 3 Parameter values used in the model, obtained as described in the text. a Summary of all parameter values. b Y _XS, Y _LS and m _S obtained by linear regression analysis

Basal lipid fraction

At a feed C/N-ratio of 6 Cmol Nmol⁻¹, approximately 6 mol m⁻³ NH₄ ⁺ was found in the culture, while the glucose concentration in the culture was low. Therefore, we assume that all measured lipids are membrane lipids. The basal lipid fraction of the cells is then 4.5% w/w, which gives $f_{\text{L0}}\,=\,0.079$ Cmol Cmol⁻¹.

Yield of lipid-free biomass on N-source

The yield of lipid-free biomass on N-source ($Y_{\text{XN}}$) was determined using:

$$ Y_{\text{XN}} = \left\langle {{\frac{{C_{\text{X}} }}{{C_{\text{Nin}} - C_{\text{N}} }}}} \right\rangle $$

(22)

The average value found for the 12 data points is $Y_{\text{XN}}$ = 6.1 ± 0.7 Cmol Nmol⁻¹. The value of ${1 \mathord{\left/ {\vphantom {1 {Y_{\text{XN}} }}} \right. \kern-\nulldelimiterspace} {Y_{\text{XN}} }}$ = 0.16 ± 0.02 Nmol Cmol⁻¹ agrees well with the 0.17 Nmol Cmol⁻¹ found in the element analysis of the lipid-free biomass.

Maximum specific lipid production rate

The model uses a maximum specific lipid production rate ($q_{\text{L,max}}$) when there is an excess of glucose in the medium. We took the average of the specific lipid production rates calculated with Eq. 15 for all data points in the single N-limited regime ($C_{\text{N}} = 0$ and $C_{\text{S}} > 0$). First we omitted the data points with a low residual glucose concentration (<15 Cmol m⁻³); this gave $q_{\text{L,max}}$ = 0.022 ± 0.006 Cmol Cmol⁻¹ h⁻¹ (n = 7). Using this value, the model predicts that some of the data points with a low glucose concentration also fall in the single N-limitation regime. Inclusion of these data points in the calculation gave $q_{\text{L,max}}$ = 0.023 ± 0.005 Cmol Cmol⁻¹ h⁻¹ (n = 10); this value was used in the model and will be discussed and compared to other lipid producers in part II of this article. Figure 4 shows that this constant maximum specific lipid production rate gives an adequate description of the measurements in the single N-limitation regime.

Fig. 4

Measured and modeled specific lipid production rate for U. isabellina in a chemostat. Symbols indicate measured values, lines indicate the model, error bars indicate standard deviation

Yields of lipid-free biomass and lipids on C-source and maintenance coefficient

In a chemostat, lipid-free biomass production, lipid production and maintenance occur simultaneously, and glucose is used for all of these processes. The specific glucose consumption rate can be described by re-arranging Eq. 5:

$$ q_{\text{S}} = {\frac{{D\left( {C_{\text{Sin}} - C_{\text{S}} } \right)}}{{C_{\text{X}} }}} = {\frac{D}{{Y_{\text{XS}} }}} + {\frac{{q_{\text{L}} }}{{Y_{\text{LS}} }}} + m_{\text{S}} \, $$

(23)

Multiple linear regression analysis with $q_{\text{S}}$ as dependent variable and $D$ and $q_{\text{L}}$ as independent variables gave $Y_{\text{XS}}$ = 0.93 ± 0.09 Cmol Cmol⁻¹, $Y_{\text{LS}}$ = 4 ± 16 Cmol Cmol⁻¹ and $m_{\text{S}}$ = 0.09 ± 0.02 Cmol Cmol⁻¹ h⁻¹ (Table 3b). The value for $Y_{\text{LS}}$ is unreliable, which is due to the low correlation coefficient of $q_{\text{S}}$ and $q_{\text{L}}$ (−0.046). Therefore, we repeated the regression analysis using $Y_{\text{LS}}$ = 0.59 (the theoretical maximum according to Ratledge [22]). This gave $Y_{\text{XS}}$ = 0.92 ± 0.09 Cmol Cmol⁻¹ and $m_{\text{S}}$ = 0.05 ± 0.01 Cmol Cmol⁻¹ h⁻¹ (Table 3b). The 3-parameter fit gave a smaller sum of squares of residuals (SSE), but the F test showed that this is insignificant (F = 2.86, p = 0.125). Therefore, we used the results of the 2-parameter fit together with the assumed value $Y_{\text{LS}}$ = 0.59 in the rest of this paper (see Table 3a).

The regression analysis gave high values for $Y_{\text{XS}}$ and $m_{\text{S}}$. For $Y_{\text{XS}}$, the value of 0.67 Cmol Cmol⁻¹ was expected, as this is the theoretical yield of the conversion of glucose to acetylCoA, the precursor for most biomass components. For $m_{\text{S}}$, values around 0.02 Cmol Cmol⁻¹ h⁻¹ were found before for different fungal species [23] on glucose. A reason for our high values could be the incomplete carbon recovery (Table 2). If we assume that all the missing carbon is present as attached cells with the same lipid content and specific growth rate as the suspended cells found in the medium, we find a lower specific glucose uptake rate ($q_{\text{S}}$) while the dilution rate and specific lipid production rate remain unchanged. As a result, the regression analysis gives lower values for $Y_{\text{XS}}$ (0.88 ± 0.07 Cmol Cmol⁻¹) and $m_{\text{S}}$ (0.026 ± 0.009 Cmol Cmol⁻¹ h⁻¹). This value for the maintenance coefficient is reasonable, which means that cells attached to the baffles and stirrer can probably explain the high maintenance coefficient found in the regression analysis of uncorrected data. The cell yield, however, is still high after correcting the data for the carbon loss. In principle the cell yield can be high if the cells use anaplerotic pathways to bind CO₂. According to Wynn et al. [24], the enzyme pyruvate decarboxylase combines CO₂ and pyruvate to oxalo-acetate in the transhydrogenase cycle in oleaginous fungi. Therefore, we can assume that this enzyme is present and active in our fungus, and that it could have contributed to a higher than normal value of $Y_{\text{XS}}$. However, the use of the anaplerotic route decreases the ATP production, which makes a high value for $Y_{\text{XS}}$ still hard to explain. We have no conclusive explanation for the high value of $Y_{\text{XS}}$, but the parameters from Table 3a allow accurate simulation of the chemostat data as shown below.

Fit of the model to the data

Figure 5 shows the fitted model together with the measured concentrations of total biomass, lipids and glucose in the culture and the O₂ consumption rates and CO₂ production rates. The measured concentrations of NH₄ ⁺ are not shown because they were very low. The same parameter values (Table 3a) were used for all graphs. Figure 5a, b show that the model describes the decrease in lipids and the increase in residual glucose with increasing dilution rate very well. Furthermore, the fit for both C/N-ratios in the feed is equally good, which indicates that the model can predict the results of a change in C/N-ratio in the feed.

Fig. 5

Comparison of model predictions with results from chemostat culture of U. isabellina on glucose and NH₄. Symbols indicate measured values, lines indicate the model. Error bars indicate standard deviation a C/N-ratio of the feed = 20 Cmol Nmol⁻¹, b C/N-ratio of the feed is 16 Cmol Nmol⁻¹. Vertical dashed lines indicate boundaries between C-limited regime (left), dual limited regime (middle) and N-limited regime (right) c CO₂-production rate, d O₂-consumption rate

Figure 5c, d show that the measured CO₂ production and O₂ consumption rates—which were not used to determine the model parameters—are not predicted accurately. The C-balance attributes the missing carbon (12% on average) to CO₂, leading to an overestimation of the CO₂-production rate. However, this error does not affect the predictions for lipid-free biomass, lipids and glucose; these are predicted well for the tested dilution rates and C/N-ratios.

In Fig. 5a, b, the three limitation regimes described in the model section are shown: single C-limitation, dual limitation and single N-limitation. Most of the measurements fall in the single N-limitation regime, where the lipid concentration decreases with increasing dilution rate because the specific lipid production rate is constant while the specific growth rate increases. The lipid-free biomass concentration is not shown in the graph, but has an average value of 2.7 ± 0.3 g L⁻¹ for all data points in the N-limitation regime, which is close to the model value of 2.6 g L⁻¹. Glucose was detected at all data points in this regime, meaning that it was not limiting.

There are only two data points in the dual limitation regime and no data points in the single C-limitation regime. For the used C/N-ratios in the feed, a very low dilution rate was required to have dual limitation or single C-limitation. Cultures at dilution rates lower than 0.04 h⁻¹ were attempted, but no steady state could be reached and no reliable data could be obtained. This was due to problems associated with the filamentous form of U. isabellina. At high dilution rates (D > 0.1 h⁻¹), the fungus grew in small pellets (≪1 mm), but at lower dilution rates free mycelium was present, which caused formation of large aggregates adhering to the baffles and stirrer. Reversing the rotation direction of the stirrer every 30 s reduced formation of aggregates on the baffles, but still aggregates were formed and re-suspended periodically, leading to fluctuations in the biomass concentration and therefore to large error bars in Fig. 5. Furthermore, at lipid fractions of the cells above 10% w/w, the mycelium tended to float and clot together irreversibly at the surface of the culture, making it impossible to take representative samples. These problems make any submerged fermentation with U. isabellina an instable system, in which the chance of failure increases with time. As the time to reach steady state increases with decreasing dilution rate, it was not possible to get reliable results at very low dilution rates. Using other C/N-ratios than the tested ones would not have added extra information to validate the model, because for higher C/N-ratios an even lower dilution rate is required to reach high lipid concentrations, and for lower C/N-ratios the reached lipid concentration will be so low that it cannot be distinguished from the basal lipid concentration for membranes.

To validate our model also for the dual limitation regime and the single C-limitation regime, we used literature data for oleaginous yeasts, which do not have the problems that we experienced with our fungus at low dilution rates. Results of the validation with literature data can be found in part II of this paper.

Prediction of the maximum lipid content and production rate

Figure 6 shows a prediction of the lipid fraction in the cells for several C/N-ratios in the feed and a range of dilution rates. For D < 0.04 h⁻¹ this is an extrapolation, but we believe the shown pattern is correct. For a given feed C/N-ratio, the lipid fraction increases with decreasing dilution rate until it peaks. The peak occurs at the transition from single N-limitation to dual C and N-limitation; the dilution rate at the peak can be found with Eq. 10 using $C_{\text{S}} = 0$:

$$ D_{\text{opt}} = {\frac{{{\frac{{q_{\text{L,max}} }}{{Y_{\text{LS}} }}} + m_{\text{S}} }}{{\frac{1}{{Y_{\text{XN} }}}{\frac{{C_{\text{Sin}} }}{{C_{\text{Nin}} }}} - {\frac{1}{{Y_{\text{XS}} }}}}}}.$$

(24)

Fig. 6

Predicted lipid fraction in the cells as a function of the dilution rate. Numbers in the graph indicate C/N-ratio in the feed (Cmol Nmol⁻¹, C_Nin = constant)

Similarly, one can find the dilution rate at which no extra lipids are accumulated, by substituting $C_{\text{N}} = 0$ in Eq. 11:

$$ D_{\min } = {\frac{{m_{\text{S}} }}{{\frac{1}{{Y_{\text{XN}} }}{\frac{{C_{\text{Sin}} }}{{C_{\text{Nin}} }}} - {\frac{1}{{Y_{\text{XS}} }}} - {\frac{{f_{\text{L0}} }}{{1 - f_{\text{L0}} }}}\frac{1}{{Y_{\text{LS}} }}}}}. $$

(25)

The lipid production rate in the three regions is given by:

$$ {r}_{\text{L}} = \left\{ \begin{gathered} q_{\text{L,max}} \,Y_{\text{XN}} \,C_{\text{Nin}}\quad{\text{ if}}\;D \geq D_{\text{opt}} \hfill \\ Y_{\text{LS}} Y_{\text{XN}} C_{\text{Nin}} \left(\frac{C_{{\text{Sin}}}}{C_{{\text{Nin}}}} \frac{D}{Y_{{\text{XN}}}} - \frac{D}{Y_{{\text{XS}}}} - m_{{\text{S}}} \right)\quad{\text{if}}\;D_{ \min } < D < D_{\text{opt}} \hfill \\ {\frac{{{\frac{{f_{\text{L0}} }}{{1 - f_{\text{L0}} }}}\;C_{\text{Sin}} D}}{{{\frac{{m_{\text{s}} }}{D}} + {\frac{1}{{Y_{\text{XS}} }}} + {\frac{{f_{\text{L0}} }}{{1 - f_{\text{L0}} }}}\frac{1}{{Y_{\text{LS}} }}}}}\quad{\text{if}}\;D < D_{ \min }. \hfill \\ \end{gathered} \right. $$

(26)

In the single N-limited region ($D > D_{\text{opt}}$), the lipid production rate in the bioreactor is constant because the specific lipid production rate and the lipid-free biomass concentration are both constant (Eq. 15). In the dual C and N-limited region ($D_{ \min } < D < D_{\text{opt}}$) the lipid production rate in the bioreactor is proportional to $D$ because the specific lipid production rate increases with increasing glucose supply rate and the lipid-free biomass concentration is constant (Eqs. 16, 17). The lipid production rate in the single C-limited region ($D < D_{ \min }$) is proportional to $D$ but too low to be of interest (Eqs. 13, 19).

Operating the bioreactor at $D_{\text{opt}}$ gives the highest possible lipid production rate in the bioreactor, combined with the highest possible lipid content of the cells and the highest possible lipid yield on glucose. The lipid content of the cells can be increased by increasing the C/N-ratio of the feed and decreasing the dilution rate accordingly. Theoretically, it should be possible to reach much higher lipid fractions than we have measured, but in practice this will be difficult for two reasons: (1) The problems with cells adhering to the bioreactor and floating on the surface described above, and (2) At higher C/N-ratio and lower $D$ the lines in Fig. 6 are very steep, which means that a small deviation in the dilution rate has a large influence on the lipid fraction. So although the model predicts that very high lipid fractions can be reached at high C/N-ratios in the feed and low dilution rates, in practice it will not be easy to reach these high lipid fractions in a chemostat culture. The highest lipid fraction in the cells reached in our experiments was 25% w/w, at a C/N-ratio of 20 Cmol Nmol⁻¹ and a dilution rate of 0.04 h⁻¹. This is probably the highest lipid fraction that can be reached with U. isabellina in chemostat cultures.

Implications of the model

The most important insight in kinetics of lipid accumulation of U. isabellina is that the fungus only accumulates lipids when it has fully satisfied its carbon requirements for maintenance and growth. This can also have large implications for lipid production in other systems, such as solid-state fermentation. In solid-state fermentation, the substrate monomers are released from the solid substrate and diffuse to the fungal cells, at a certain supply rate. When this supply rate is low, for example because of diffusion limitation or low enzyme activity, we can compare the situation with a chemostat in the single-carbon limitation or dual limitation regime. As a result, even if the C/N-ratio of the ‘feed’ is high enough to allow for lipid production, the lipid yield on converted substrate can be very low (see Fig. 2). This may explain the low lipid yields reported in literature [9–12].

Most production systems reported in the literature are batch reactors. In a chemostat, the cells grow, but in batch culture, growth stops when the nitrogen source is exhausted, and this may give other lipid production kinetics. In future work, we will extend our work to submerged batch cultivation.