Modified couple stress-based free vibration and dynamic response of rotating FG multilayer composite microplates reinforced with graphene platelets

Abstract

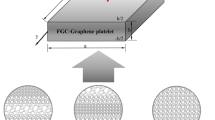
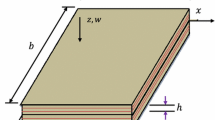
A centrifugally stiffened size-dependent model is developed for dynamic analysis of rotating functionally graded (FG) multilayer composite microplates reinforced with graphene platelets (GPLs) based on the modified couple stress theory and the first-order shear deformation theory. The effective elastic modulus of the graphene platelet-reinforced composite (GPLRC) is calculated on the basis of the modified Halpin–Tsai model, while a rule of mixture is adopted to predict the effective mass density and Poisson’s ratio. The second-kind Lagrange’s equations are employed to derive the governing equations of motion, in which the mode functions for displacements are constructed by Chebyshev polynomials multiplied by the boundary functions. The free vibration problem is determined by a complex modal analysis based on the state space method, and the dynamic responses under prescribed rotational motions are calculated by the fourth-order Runge–Kutta–Merson’s method. The convergence and comparative examples are carried out to validate the effectiveness and accuracy of the proposed model. A parametric study is conducted to investigate the effects of material length scale parameter, hub radius ratio, angular velocity, GPL weight fraction, distribution pattern and geometry property on the dynamic behaviors of the rotating FG GPLRC simply supported and cantilevered microplates. Numerical results show that the rotational motion and size dependency significantly affect the reinforcement effect of GPL. Results also indicate that the dispersion of the square GPLs with fewer graphene layers and larger contact surface area near the bottom and top positions can reinforce the stiffness more effectively.

Appendix

The details of all elements in matrices ${\overline{\mathbf{M}}}$, ${\overline{\mathbf{K}}}$, ${\overline{\mathbf{C}}}$ and ${\overline{\mathbf{Q}}}$ in Eq. (37) are given by

$$\begin{aligned} \overline{M}_{ij}^{uu} = & \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} \overline{U}_{j} } {\text{d}}\xi {\text{d}}\eta } ,\;\overline{M}_{ij}^{{u\varphi_{x} }} = \overline{I}_{1} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } ,\;\overline{M}_{ij}^{vv} = \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{i} \overline{V}_{j} } {\text{d}}\xi {\text{d}}\eta } \\ \overline{M}_{ij}^{{v\varphi_{y} }} = & \overline{I}_{1} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{i} \overline{\varphi }_{yj} } {\text{d}}\xi {\text{d}}\eta } ,\;\overline{M}_{ij}^{ww} = \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{i} \overline{W}_{j} } {\text{d}}\xi {\text{d}}\eta } \\ \overline{M}_{ij}^{{\varphi_{x} \varphi_{x} }} = & \overline{I}_{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } ,\;\overline{M}_{ij}^{{\varphi_{y} \varphi_{y} }} = \overline{I}_{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{yi} \overline{\varphi }_{yj} } {\text{d}}\xi {\text{d}}\eta } \\ \end{aligned}$$

(A.1a–g)

$$\begin{aligned} \overline{C}_{ij}^{uw} = & 2\gamma \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} \overline{W}_{j} } {\text{d}}\xi {\text{d}}\eta } ,\;\overline{C}_{ij}^{wu} = - 2\gamma \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{i} \overline{U}_{j} } {\text{d}}\xi {\text{d}}\eta } \\ \overline{C}_{ij}^{{w\varphi_{x} }} = & - 2\overline{I}_{1} \gamma \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{i} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } ,\;\overline{C}_{ij}^{{\varphi_{x} w}} = 2\overline{I}_{1} \gamma \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} \overline{W}_{j} } {\text{d}}\xi {\text{d}}\eta } \\ \end{aligned}$$

(A.2a–d)

$$\begin{gathered} \overline{K}_{ij}^{uu} = h_{0}^{2} a_{11} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi }} \overline{U}_{{j{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + h_{0}^{2} \alpha^{2} a_{66} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta }} \overline{U}_{{j{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } - \gamma^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} \overline{U}_{j} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \;\; + \frac{1}{4}a_{66} \beta^{2} h_{0}^{4} \alpha^{2} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi \eta }} \overline{U}_{{j{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta \eta }} \overline{U}_{{j{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.3)

$$\begin{gathered} \overline{K}_{ij}^{uv} = a_{12} h_{0}^{2} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi }} \overline{V}_{{j{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + a_{66} h_{0}^{2} \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta }} \overline{V}_{{j{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \; - \frac{1}{4}a_{66} \beta^{2} h_{0}^{4} \alpha \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi \eta }} \overline{V}_{{j{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta \eta }} \overline{V}_{{j{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.4)

$$\overline{K}_{ij}^{uw} = \dot{\gamma }\int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} \overline{W}_{j} } {\text{d}}\xi {\text{d}}\eta }$$

(A.5)

$$\begin{gathered} \overline{K}_{ij}^{{u\varphi_{x} }} = - \overline{I}_{1} \gamma^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } + b_{11} h_{0} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi }} \overline{\varphi }_{{xj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + b_{66} h_{0} \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta }} \overline{\varphi }_{{xj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad + \frac{1}{4}b_{66} \beta^{2} h_{0}^{3} \alpha^{2} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi \eta }} \overline{\varphi }_{{xj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta \eta }} \overline{\varphi }_{{xj{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.6)

$$\begin{gathered} \overline{K}_{ij}^{{u\varphi_{y} }} = b_{12} h_{0} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + b_{66} h_{0} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad - \frac{1}{4}b_{66} \beta^{2} h_{0}^{3} \alpha \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\xi \eta }} \overline{\varphi }_{{yj{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{U}_{{i{,}\eta \eta }} \overline{\varphi }_{{yj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.7)

$$\overline{K}_{ij}^{vu} = \overline{K}_{ji}^{uv}$$

(A.8)

$$\begin{gathered} \overline{K}_{ij}^{vv} = a_{11} h_{0}^{2} \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\eta }} \overline{V}_{{j{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + a_{66} h_{0}^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi }} \overline{V}_{{j{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \;\; + \frac{1}{4}a_{66} \beta^{2} h_{0}^{4} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi \xi }} \overline{V}_{{j{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi \eta }} \overline{V}_{{j{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.9)

$$\begin{gathered} \overline{K}_{ij}^{{v\varphi_{x} }} = b_{12} h_{0} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\eta }} \overline{\varphi }_{{xj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + b_{66} h_{0} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi }} \overline{\varphi }_{{xj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad - \frac{1}{4}b_{66} \beta^{2} h_{0}^{3} \alpha \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi \xi }} \overline{\varphi }_{{xj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi \eta }} \overline{\varphi }_{{xj{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.10)

$$\begin{gathered} \overline{K}_{ij}^{{v\varphi_{y} }} = b_{11} h_{0} \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\eta }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + b_{66} h_{0} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad + \frac{1}{4}b_{66} \beta^{2} h_{0}^{3} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi \xi }} \overline{\varphi }_{{yj{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{V}_{{i{,}\xi \eta }} \overline{\varphi }_{{yj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.11)

$$\overline{K}_{ij}^{wu} = - \overline{K}_{ji}^{uw}$$

(A.12)

$$\begin{gathered} \overline{K}_{ij}^{ww} = a_{44} h_{0}^{2} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi }} \overline{W}_{{j{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\eta }} \overline{W}_{{j{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) + \gamma^{2} \left( {\int_{0}^{1} {\int_{0}^{1} {T{(}\xi {)}\overline{W}_{{i{,}\xi }} \overline{W}_{{j{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } } \right. \hfill \\ \quad \quad \;\;\left. { - \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{i} \overline{W}_{j} } {\text{d}}\xi {\text{d}}\eta } } \right) + \frac{1}{4}a_{66} \beta^{2} h_{0}^{4} \left( {4\alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \eta }} \overline{W}_{{j{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{4} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\eta \eta }} \overline{W}_{{j{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right. \hfill \\ \quad \quad \;\;\left. { + \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \xi }} \overline{W}_{{j{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } - \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\eta \eta }} \overline{W}_{{j{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } - \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \xi }} \overline{W}_{{j{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.13)

$$\begin{gathered} \overline{K}_{ij}^{{w\varphi_{x} }} = - \overline{I}_{1} \dot{\gamma }\int_{0}^{1} {\int_{0}^{1} {\overline{W}_{i} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } + a_{44} h_{0} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi }} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad - \frac{1}{4}a_{66} \beta^{2} h_{0}^{3} \left( {2\alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \eta }} \overline{\varphi }_{{xj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } - \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\eta \eta }} \overline{\varphi }_{{xj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \xi }} \overline{\varphi }_{{xj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.14)

$$\begin{gathered} \overline{K}_{ij}^{{w\varphi_{y} }} = a_{44} h_{0} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\eta }} \overline{\varphi }_{yj} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad - \frac{1}{4}a_{66} \beta^{2} h_{0}^{3} \alpha \left( {2\int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \eta }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\eta \eta }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } - \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{{i{,}\xi \xi }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.15)

$$\overline{K}_{ij}^{{\varphi_{x} u}} = \overline{K}_{ji}^{{u\varphi_{x} }} ,\;\overline{K}_{ij}^{{\varphi_{x} v}} = \overline{K}_{ji}^{{v\varphi_{x} }}$$

(A.16a, b)

$$\begin{gathered} \overline{K}_{ij}^{{\varphi_{x} w}} = \overline{I}_{1} \dot{\gamma }\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} \overline{W}_{j} } {\text{d}}\xi {\text{d}}\eta } + a_{44} h_{0} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} \overline{W}_{{j{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \quad - \frac{1}{4}a_{66} \beta^{2} h_{0}^{3} \left( {2\alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta }} \overline{W}_{{j{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } - \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi }} \overline{W}_{{j{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } + \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi }} \overline{W}_{{j{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.17)

$$\begin{gathered} \overline{K}_{ij}^{{\varphi_{x} \varphi_{x} }} = - \overline{I}_{2} \gamma^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } + a_{44} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} \overline{\varphi }_{xj} } {\text{d}}\xi {\text{d}}\eta } + d_{11} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi }} \overline{\varphi }_{{xj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \;\quad + d_{66} \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta }} \overline{\varphi }_{{xj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + \frac{1}{4}a_{66} \beta^{2} h_{0}^{2} \left( {4\alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta }} \overline{\varphi }_{{xj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi }} \overline{\varphi }_{{xj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \quad \quad \quad \; + \frac{1}{4}d_{66} \beta^{2} h_{0}^{2} \alpha^{2} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi \eta }} \overline{\varphi }_{{xj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta \eta }} \overline{\varphi }_{{xj{,}\eta \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.18)

$$\begin{gathered} \overline{K}_{ij}^{{\varphi_{x} \varphi_{y} }} = d_{12} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } + d_{66} \alpha \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \;\quad - \frac{1}{4}a_{66} \beta^{2} h_{0}^{2} \alpha \left( {2\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \quad \quad \quad \; - \frac{1}{4}d_{66} \beta^{2} h_{0}^{2} \alpha \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\xi \eta }} \overline{\varphi }_{{yj{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{xi{,}\eta \eta }} \overline{\varphi }_{{yj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.19)

$$\overline{K}_{ij}^{{\varphi_{y} u}} = \overline{K}_{ji}^{{u\varphi_{y} }} ,\;\overline{K}_{ij}^{{\varphi_{y} v}} = \overline{K}_{ji}^{{v\varphi_{y} }} ,\;\overline{K}_{ij}^{{\varphi_{y} w}} = \overline{K}_{ji}^{{w\varphi_{y} }} ,\;\overline{K}_{ij}^{{\varphi_{y} \varphi_{x} }} = \overline{K}_{ji}^{{\varphi_{x} \varphi_{y} }}$$

(A.20a–d)

$$\begin{gathered} \overline{K}_{ij}^{{\varphi_{y} \varphi_{y} }} = a_{44} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{yi} \overline{\varphi }_{yj} } {\text{d}}\xi {\text{d}}\eta } + d_{11} \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{yi{,}\eta }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } \hfill \\ \quad \quad \;\quad + d_{66} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{yi{,}\xi }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + \frac{1}{4}a_{66} \beta^{2} h_{0}^{2} \left( {4\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{yi{,}\xi }} \overline{\varphi }_{{yj{,}\xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{yi{,}\eta }} \overline{\varphi }_{{yj{,}\eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \quad \quad \quad \; + \frac{1}{4}d_{66} \beta^{2} h_{0}^{2} \left( {\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{yi{,}\xi \xi }} \overline{\varphi }_{{yj{,}\xi \xi }} } {\text{d}}\xi {\text{d}}\eta } + \alpha^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{{yi{,}\xi \eta }} \overline{\varphi }_{{yj{,}\xi \eta }} } {\text{d}}\xi {\text{d}}\eta } } \right) \hfill \\ \end{gathered}$$

(A.21)

$$\overline{Q}_{i}^{u} = \frac{{\gamma^{2} }}{{h_{0} }}\int_{0}^{1} {\int_{0}^{1} {{(}\delta { + }\xi {)}\overline{U}_{i} } {\text{d}}\xi {\text{d}}\eta } - \overline{I}_{1} \dot{\gamma }\int_{0}^{1} {\int_{0}^{1} {\overline{U}_{i} } {\text{d}}\xi {\text{d}}\eta }$$

(A.22)

$$\overline{Q}_{i}^{w} = \frac{{\dot{\gamma }}}{{h_{0} }}\int_{0}^{1} {\int_{0}^{1} {{(}\delta { + }\xi {)}\overline{W}_{i} } {\text{d}}\xi {\text{d}}\eta } + \overline{I}_{1} \gamma^{2} \int_{0}^{1} {\int_{0}^{1} {\overline{W}_{i} } {\text{d}}\xi {\text{d}}\eta }$$

(A.23)

$$\overline{Q}_{i}^{{\varphi_{x} }} = \frac{{\overline{I}_{1} \gamma^{2} }}{{h_{0} }}\int_{0}^{1} {\int_{0}^{1} {{(}\delta { + }\xi {)}\overline{\varphi }_{xi} } {\text{d}}\xi {\text{d}}\eta } - \overline{I}_{2} \dot{\gamma }\int_{0}^{1} {\int_{0}^{1} {\overline{\varphi }_{xi} } {\text{d}}\xi {\text{d}}\eta }$$

(A.24)

in which, the dimensionless coefficients shown in Eqs. (A.1)–(A.24) are given by

$$\left( {\overline{I}_{1} {,}\;\overline{I}_{2} } \right) = \left( {\frac{{I_{1} }}{{I_{0} h}}{,}\;\frac{{I_{2} }}{{I_{0} h^{2} }}} \right)$$

(A.25)

$$\left( {a_{11} ,\;a_{12} ,\;a_{44} ,\;a_{66} } \right) = \left( {A_{11} ,\;A_{12} ,\;A_{44} ,\;A_{66} } \right)\frac{{T^{*2} }}{{I_{0} h^{2} }}$$

(A.26)

$$\left( {b_{11} {,}\;b_{12} {,}\;b_{66} } \right) = \left( {B_{11} {,}\;B_{12} {,}\;B_{66} } \right)\frac{{T^{*2} }}{{I_{0} h^{2} a}}$$

(A.27)

$$\left( {d_{11} ,\;d_{12} ,\;d_{66} } \right) = \left( {D_{11} ,\;D_{12} ,\;D_{66} } \right)\frac{{T^{*2} }}{{I_{0} h^{2} a^{2} }}$$

(A.28)