Introduction

Tamponade agents act by displacing both pre-retinal and sub-retinal fluid away from the site of retinal breaks and apposing the retina to the underlying retinal pigment epithelium [1]. The ability of any fluid to act as a tamponade therefore relies on it being immiscible with water and forming an interface with it. The efficiency of a tamponade largely depends on the shape of the bubble inside an eye [2, 3]. An intraocular bubble is acted upon both by buoyancy and its own weight. The shape of a large-volume bubble is determined primarily by the net force exerted on it (i.e., the "floatation force", being the difference between the buoyancy and the weight) [4]. Air (or gas) bubbles have a low specific gravity (about 0.001 g/ml). The buoyancy of 1 ml of air in water (or aqueous) is 1 g. Therefore, the floatation force is relatively high (1 g – 0.001 g = 0.999 g). Thus, a 1-ml intraocular bubble of air inside an eye tends to assume the shape of a spherical cap (a dome shape with flat bottom). Conventional silicone oil has a high specific gravity (0.97 g/ml). Therefore, the floatation force of 1 ml of oil is relatively low (1 g – 0.97 g = 0.03 g). Thus, 1 ml of silicone oil in the vitreous cavity assumes a spherical shape. The same applies to Densiron® (specific gravity 1.06 g/ml). This so-called "heavy silicone oil" is only just heavier than water. Consequently, it has a negative floatation force of a similar value to that of normal silicone oil, and its shape is also spherical [5].

When a tamponade bubble comes in contact with the retina, the contact angle is dependent on the interfacial tensions of three phases in contact with each other, namely between tamponade and water, between water and retina, and between retina and tamponade [2]. The interfacial energy controls the shape of the bubble at the point of contact, resulting in the shape of the meniscus, but will have little influence on the overall shape of large-volume bubbles. In the past, we have demonstrated that we can derive information about bubble shapes and thus tamponade efficiencies by using model eye chambers. We mimicked the surface properties of the retina by surface-modifying PMMA to make it hydrophilic. By using digital photography and measuring the geometry of bubbles, we could derive relationships between the fill and the arc of retinal contact between the tamponade and the inner surface of the chamber [2]. Efficient bubbles are those in which all the volume contributes to making contact with the retina (tamponade). Gas bubbles are efficient by virtue of their domed shape and flat bottom. Still, the shape of gas bubbles is not exactly that of a spherical cap. The interfacial energy at the point of contact means that some of the volume contributes to making the meniscus. Silicone oil, because of its rounded shape, makes little contact with the retina until the cavity is virtually full [6]. It is for this reason that a 100% fill is always advised.

Besides interfacial tensions and floatation forces, there may be a third factor which could determine the arc of retinal contact of an intraocular bubble and therefore affect its efficiency as a tamponade. We refer to the size and shape of the eye cavity. In the past, we have shown that silicone oil does not fit into small recesses, such as those adjacent to indentation caused by scleral buckling [7], but what about large or small eyes? For a given volume of tamponade, a bubble should theoretically subtend an arc of retinal contact with the surface of the retina that is larger in a small eye than a big eye. For an equivalent percentage fill, the volume of tamponade in a smaller eye would be less than that in a larger eye. In which case, more of the tamponade agent might contribute towards forming the meniscus than making contact with the retina. Secondly, for a given percentage fill, a larger eye cavity would contain a larger bubble. The larger the bubble, the greater the floatation force. Thus, this bubble might also have a flatter shape.

The aim of this study was therefore to investigate whether ocular axial length has an influence on the efficacy of the three commonly used retinal tamponade agents: gas, silicone oil, and heavy silicone oil. Our hypothesis was that a tamponade bubble of a smaller volume would take on a more spherical (and therefore less clinically useful) shape in an eye with short axial length compared to a larger volume bubble achieving an equivalent percentage fill in an eye with long axial length.

We believe that it is opportune to investigate this aspect of the tamponade effect at a time when new tamponade agents such as Densiron® are being more widely adopted. Additionally, there is currently a trend towards non-posturing or non-buckling surgery in the management of some retinal breaks. These include macular holes and retinal tears in the inferior fundus. These surgical techniques rely more critically on the fill of the eye in the early postoperative period. A better understanding of tamponade efficiencies may help inform the debate on the choice of tamponade and the need for posture.

Materials and methods

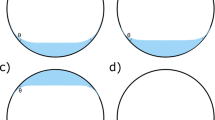
Three tamponade agents were used in this study: air, silicone oil (500 mPas), and heavy silicone oil (Densiron®). The surface-modified model eye chamber has been validated as tool to simulate the vitreous cavity [2, 4, 5, 7]. Two spherical polymethylmethacrylate (PMMA) model eye chambers of 19 mm and 25 mm diameter were constructed. A description of the spherical model eye chamber’s structure has previously been published [2, 4]. Prior to each experiment, the internal surface of the model eye chambers was rendered hydrophilic by coating it in protein to mimic the surface properties of the human retina. This technique has also been described previously [2, 4, 5, 7]. As an aqueous substitute, 0.5% bovine albumin in phosphate buffered saline was used. One drop of methylene blue was added to each 100 ml batch of aqueous substitute to aid visualization of the tamponade–aqueous interface (Fig. 1). We believe that this dye has a negligible influence on the physical properties of the agents under investigation. The experiments were carried out at room temperature. A series of filling experiments was conducted using the 19-mm and 25-mm model eye chambers, mounted in front of a digital camera. For silicone oil and heavy silicone oil, the tamponade agents were introduced into the chamber via a 1-mm-diameter port at the inferior pole of the chamber. A watertight cannula was secured to the port with silicone adhesive to facilitate manual introduction of the tamponade agent via silicone tubing and a graduated syringe. Excess aqueous substitute escaped passively via a cannula secured to a 1-mm-diameter port at the superior pole of the chamber. For air, aqueous substitute was instead withdrawn from the inferior port, allowing air tamponade to be recruited via the superior port. Each tamponade agent was introduced in 0.5-ml increments until no more could be introduced. Following each incremental addition of tamponade agent, a high-resolution photograph was obtained using a mounted digital camera.

Fig. 1
figure 1

A model eye chamber (aqueous substitute plus methylene blue in situ)

Full size image

Using simple digital image analysis software (Adobe Photoshop®), two measurements were taken as a means of quantifying the behavior of the tamponade agents:

  1. (1).

    The maximum height of tamponade bubble (mm) (Fig. 2a)

    Fig. 2
    figure 2

    a The maximum height of tamponade bubble (mm). b The height of the tamponade bubble at level of the meniscus (mm) (h)

    Full size image
  2. (2).

    The height of the tamponade bubble at level of the meniscus (mm) (Fig. 2b). This second measurement was used to calculate the arc of retinal contact subtended by the tamponade bubble (degrees) (Fig. 3)

    Fig. 3
    figure 3

    The arc of retinal contact subtended by the tamponade agent was calculated using a derivation of the standard polar cap formula:\( \begin{array}{*{20}{c}} {Volume = \pi {r^3}\left( {2 - 3\cos \phi /2 + \cos^3 \phi /2} \right)/3} \\{\phi = 2{{\cos }^{{ - 1}}}\left( {1 - h/r} \right)} \\\end{array} \)Where r = radius of sphere, h = height of tamponade and ϕ = arc of retinal contact subtended at the center of the sphere (degrees)

    Full size image

Each measurement was calibrated against fixed reference points to compensate for subtle differences in distance or magnification. Each experiment was run three times, and the data points were averaged.

Results

For each tamponade agent, the maximum height of the tamponade bubble (presented as a percentage of the maximum chamber height) and the arc of retinal contact subtended by the tamponade bubble (in degrees) were plotted against percentage fill (Figs. 4, 5, 6).

Fig. 4
figure 4

a, b Air (data are presented as the mean and 95% confidence interval at each point). Missing data points are due to impaired visualization of the tamponade–aqueous interface at the equatorial seal of the model eye

Full size image
Fig. 5
figure 5

a, b Silicone oil (data are presented as the mean and 95% confidence interval at each point)

Full size image
Fig. 6
figure 6

a, b Heavy silicone oil (data are presented as the mean and 95% confidence interval at each point). Missing data points are due to impaired visualisation of the tamponade/aqueous interface at the equatorial seal of the model eye

Full size image

A quadratic regression model was fitted to each data set between 20 and 90% fill. Polynomial regression analysis found no statistically significant difference between the regression models for the 19- and 25-mm model eye chambers for bubble height or arc of retinal contact subtended for any of the tamponade agents under investigation (p value range 0.128–0.835). If we regard the plotted data for silicone oil and heavy silicone oil (Figs. 5, 6), we observe a trend towards better retinal coverage for any particular percentage fill in the 25-mm versus the 19-mm model eye chamber. However, this was not statistically significant (p value range 0.221-0.835).

Discussion

In 1978, Parver and Lincoff showed that the bottom edge of an intraocular gas bubble was flat using a glass model [8]. They went on to explore the tamponade effect for equal volumes of air in different-sized cavities using mathematical modeling. They famously pointed out that for a cavity of 21 mm in diameter, a gas bubble of 0.28 ml would provide 90° arc of support to the retina. Clinically, however, we observe that when a small bubble (for example 0.3 ml) is injected into the vitreous cavity (as in pneumatic retinopexy), the bubble remains rounded. It is only after the bubble has expanded that it takes on its typical shape with a flat bottom.

The reason that air bubbles have a rounded shape when very small and a flat-bottomed shape when large is that interfacial energy will have a measurable influence on small bubbles, but is overtaken by floatation forces for larger bubbles. It is therefore important to consider this relationship between the interfacial energetics and floatation forces and their relative influence on the tamponade effect in eyeballs of different axial lengths.

To answer these questions, we used eye models similar to those we have used several times in the past to study the shape and the behavior of intraocular bubbles. For the purpose of this study, the human vitreous cavity was assumed to be a sphere. Essentially, we use a spherical chamber constructed of PMMA and rendered the surface hydrophilic by coating with albumin. We have previously shown that this is a good model for the hydrophilic properties of the retina [2]. The glass model used in the Parver and Lincoff study will have been more hydrophobic, which might explain the difference between their predictions and the clinical experience. It will be more energetically favorable for an air bubble to spread on a glass surface than the hydrophilic retinal surface.

For our experiment, we chose a range of chamber dimensions to mimic the range of sizes that we encounter in patients. Tamponade efficiency was reflected by measuring the maximum height, the height at the level of the meniscus, and calculation of the arc of contact made between the tamponade bubble and the internal surface of the model. We used three tamponade agents: air, silicone oil, and Densiron®. One reason for choosing gaseous and liquid tamponade was the large difference between their floatation forces, thus highlighting the influence of this on the resultant tamponade efficiency and its relation to the size of the eye cavity. That is, one might expect the shape to change more so with an air bubble than with an oil bubble (or vice versa).

Our results showed that the tamponade efficiencies as reflected by the measured dimensions of the bubbles were not significantly different. The tamponade efficiency does not seem to vary, at least in the range of size cavities that we have tested. This applies for air and silicone oil. In the case of air, the bubble is round at the very small volumes that we inject in pneumatic retinopexy. However, the shape quickly changes as the air bubble gets bigger, such that at the volumes that we were testing (0.5-8 ml), the bubbles have similar flat-bottomed shapes.

It remains true that for a given percentage fill, the relative volume involved in the meniscus may be larger in smaller eye cavities. However, in this study, it was not possible to measure any difference in the arc of retinal contact subtended for gas or oils, irrespective of the size of the cavity.

In practice, the findings highlight the fact that whether we use gas or oil, we should try to achieve the greatest percentage fill if we wish to obtain the maximal tamponade effect. This means that a complete vitrectomy is desirable, because any remaining vitreous gel might become compressed by the tamponade agents (gas or oil)[9, 10], giving rise to an increased capacity or an under-fill, leaving large parts of the retina unsupported [2]. This applies irrespective of the size of the globe that we are treating.