A new fractional derivative model for linearly viscoelastic materials and parameter identification via genetic algorithms

Abstract

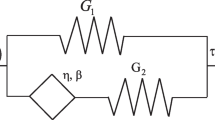
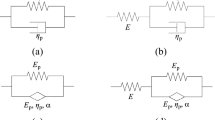
In this study, a new nested model consisting of springs and “spring pots” is proposed to better simulate the viscoelastic behavior of polymeric damping materials in the frequency domain. First, the one-dimensional constitutive equation that consists of ten parameters is derived. The dynamical mechanical properties, which are the storage modulus, the loss modulus, and the loss factor, are obtained from this equation. Then, the low- and high-frequency behavior of this model is investigated. Moreover, a new methodology to identify the unknown parameters that appear in the fractional derivative model, from the experimental data for the Wicket plot, by using genetic algorithms (GAs) is presented. This approach does not require shifting of the experimental data; therefore, possible errors that may arise are eliminated. The new model is fitted to experimental data for several polymeric damping materials that exist in the literature, in order to verify its success. The results are presented in a graphical form with comparison to the already existing models.

Appendix

The open form of the loss factor relation of ten-parameter model is as follows:

$$\begin{array}{@{}rcl@{}} && {\tan \delta = \left\langle {E_{0} \Omega \omega_{n}^{\alpha +\beta } \left[ {\sin \left( {\frac{\pi \left( {\alpha +\beta } \right)}{2}} \right)+\lambda_{3} \sin \left( {\frac{\pi \beta }{2}} \right)\omega_{n}^{\alpha} } \right]\left\{ {1+\lambda_{2} \omega_{n}^{\gamma} \left[ {2\cos \left( {\frac{\pi \gamma }{2}} \right)+\lambda_{2} \omega_{n}^{\gamma} } \right]} \right\}} \right.} \\ && {+\lambda_{1} \omega_{n}^{\gamma +\varphi } \left[ {\sin \left( {\frac{\pi \left( {\gamma +\varphi } \right)}{2}} \right)+\lambda_{2} \sin \left( {\frac{\pi \varphi }{2}} \right)\omega_{n}^{\gamma} } \right]\left\{ {1+\omega_{n}^{\alpha} \left[ {2\lambda_{3} \cos \left( {\frac{\pi \alpha }{2}} \right)+2\cos \left( {\frac{\pi \left( {\alpha +\beta } \right)}{2}} \right)\omega_{n}^{\beta} } \right]} \right.} \\ && {\left. {\left. {+\omega_{n}^{2\alpha } \left[ {\lambda_{3}^{2} +2\lambda_{3} \cos \left( {\frac{\pi \beta }{2}} \right)\omega_{n}^{\beta} +\omega_{n}^{2\beta } } \right]} \right\} } \right\rangle }\\ &&{\left\langle {E_{0} \left\{ {1+\lambda_{2} \omega_{n}^{\gamma} \left[ {2\cos \left( {\frac{\pi \gamma }{2}} \right)+\lambda_{2} \omega_{n}^{\gamma} } \right]} \right\}} \right.} \\ && {\times \left\{ {1+\left( {1+\Omega } \right)\omega_{n}^{2\alpha +2\beta } +\lambda_{3} \omega_{n}^{\alpha} \left[ {2\cos \left( {\frac{\pi \alpha }{2}} \right)+\lambda_{3} \omega_{n}^{\alpha} } \right]+\left( {2+\Omega } \right)\omega_{n}^{\alpha +\beta } \left[ {\cos \left( {\frac{\pi \left( {\alpha +\beta } \right)}{2}} \right)+\lambda_{3} \cos \left( {\frac{\pi \beta }{2}} \right)\omega_{n}^{\alpha} } \right]} \right\}} \\ && {+\lambda_{1} \omega_{n}^{\gamma +\varphi } \left\{ {\cos \left[ {\frac{\pi \left( {\gamma +\varphi } \right)}{2}} \right]+\lambda_{2} \cos \left( {\frac{\pi \varphi }{2}} \right)\omega_{n}^{\gamma} } \right\}\left\{ {1+2\lambda_{3} \cos \left( {\frac{\pi \alpha }{2}} \right)\omega_{n}^{\alpha} +2\cos \left[ {\frac{\pi \left( {\alpha +\beta } \right)}{2}} \right]\omega_{n}^{\alpha +\beta } } \right.} \\ && {\left. {\left. {+\omega_{n}^{2\alpha } \left[ {\lambda_{3}^{2} +2\lambda_{3} \cos \left( {\frac{\pi \beta }{2}} \right)\omega_{n}^{\beta} +\omega_{n}^{2\beta } } \right]} \right\} } \right\rangle } \end{array} $$

(A1)

The one-dimensional constitutive equation of the ten-parameter model, which can be derived from inverse Fourier transform of Eq. (19), is as follows:

$$\begin{array}{rcl} && {\sigma (t)+\lambda_{3} \tau^{\alpha} D^{\alpha} \sigma (t)+\tau^{\alpha +\beta }D^{\alpha +\beta }\sigma (t)+\lambda_{2} \tau^{\gamma} D^{\gamma} \sigma (t)+\lambda_{2} \lambda_{3} \tau^{\alpha +\gamma }D^{\alpha +\gamma }\sigma (t)+\lambda_{2} \tau^{\alpha +\beta +\gamma }D^{\alpha +\beta +\gamma }\sigma (t)} \\ && {=E_{0} \left[ {\varepsilon (t)+\lambda_{3} \tau^{\gamma} D^{\gamma} \varepsilon (t)+({\Omega +1})\tau^{\alpha +\beta }D^{\alpha +\beta }\varepsilon (t)+\lambda_{2} \tau^{\gamma} D^{\gamma} \varepsilon (t)} \right.+\lambda_{2} \lambda_{3} \tau^{\alpha +\gamma }D^{\alpha +\gamma }\varepsilon (t)} \\ && {\left. {+\lambda_{2} ({\Omega +1})\tau^{\alpha +\beta +\gamma }D^{\alpha +\beta +\gamma }\varepsilon (t)} \right]+\lambda_{1} \left[ {\tau^{\gamma +\varphi }D^{\gamma +\varphi }\varepsilon (t)+\lambda_{3} \tau^{\alpha +\gamma +\varphi }D^{\alpha +\gamma +\varphi }\varepsilon (t) +\tau^{\alpha +\beta +\gamma +\varphi }D^{\alpha +\beta +\gamma +\varphi }\varepsilon (t)} \right]} \end{array}$$

(A2)

where D is the fractional differentiation operator in Caputo sense, which can be expressed mathematically as follows:

$$D^{\alpha} \sigma (t) = \frac{1}{\Gamma ({1-\alpha })}\int\limits_{0}^{t} {\frac{\sigma^{\prime} (s)}{({t-s})^{\alpha} }ds} , 0 < \alpha \le 1.$$

(A3)