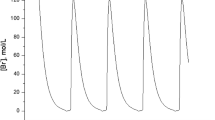
Abstract
We consider the dynamics of small networks of coupled cells. We usually assume asymmetric inputs and no global or local symmetries in the network and consider equivalence of networks in this setting; that is, when two networks with different architectures give rise to the same set of possible dynamics. Focussing on transitive (strongly connected) networks that have only one type of cell (identical cell networks) we address three questions relating the network structure to dynamics. The first question is how the structure of the network may force the existence of invariant subspaces (synchrony subspaces). The second question is how these invariant subspaces can support robust heteroclinic attractors. Finally, we investigate how the dynamics of coupled cell networks with different structures and numbers of cells can be related; in particular we consider the sets of possible “inflations” of a coupled cell network that are obtained by replacing one cell by many of the same type, in such a way that the original network dynamics is still present within a synchrony subspace. We illustrate the results with a number of examples of networks of up to six cells.
Similar content being viewed by others
References
Abeles, M., Bergman, H., Gat, I., Meilijson, I., Seidmann, E., Tishby, M.: Cortical activity flips among quasi-stationary states. Proc. Natl. Acad. Sci. 92, 8616–8620 (1995)
Afraimovich, V.S., Bunimovich, L.A.: Dynamical networks: interplay of topology, interactions and local dynamics. Nonlinearity 20, 1761–1771 (2007)
Afraimovich, V.S., Zhigulin, V.P., Rabinovich, M.I.: On the origin of reproducible sequential activity in neural circuits. Chaos 14(4), 1123–1129 (2004)
Agarwal, N.: Inflation of strongly connected networks. Math. Proc. Camb. Philos. Soc. (2010, accepted for publication)
Agarwal, N., Field, M.: Dynamical equivalence of networks of coupled dynamical systems I: asymmetric inputs. Nonlinearity 23, 1245–1268 (2010a)
Agarwal, N., Field, M.: Dynamical equivalence of networks of coupled dynamical systems II: general case. Nonlinearity 23, 1269–1289 (2010b)
Aguiar, M.A.D., Dias, A.P.S.: Minimal coupled cell networks. Nonlinearity 20, 193–219 (2007)
Aguiar, M.A.D., Dias, A.P.S.: Synchrony subspaces of coupled cell networks (2010, in preparation)
Aguiar, M.A.D., Castro, S.B.S.D., Labouriau, I.S.: Dynamics near a heteroclinic network. Nonlinearity 18(1), 391–414 (2005)
Aguiar, M.A.D., Dias, A.P.S., Golubitsky, M., Leite, M.C.A.: Bifurcations from regular quotient networks: a first insight. Physica D 238, 137–155 (2009)
Antoneli, F., Dias, A.P.S., Paiva, R.C.: Hopf bifurcation in coupled cell networks with interior symmetries. SIAM J. Appl. Math. 7, 220–248 (2008)
Ashwin, P., Borresen, J.: Discrete computation using a perturbed heteroclinic network. Phys. Rev. E 70, 026203 (2004)
Ashwin, P., Field, M.: Heteroclinic networks in coupled cell systems. Arch. Ration. Mech. Anal. 148, 107–143 (1999)
Ashwin, P., Field, M.: Product dynamics for homoclinic attractors. Proc. R. Soc., Ser. A 461, 155–177 (2005)
Ashwin, P., Swift, J.: The dynamics of n weakly coupled identical oscillators. J. Nonlinear Sci. 2, 69–108 (1992)
Ashwin, P., Orosz, G., Wordsworth, J., Townley, S.: Reliable switching between cluster states for globally coupled phase oscillators. SIAM J. Appl. Dyn. Syst. 6, 728–758 (2007)
Dias, A.P.S., Lamb, J.: Local bifurcation in symmetric coupled cell networks: linear theory. Physica D 223, 93–108 (2006)
Dias, A.P.S., Stewart, I.: Linear equivalence and ODE-equivalence for coupled cell networks. Nonlinearity 18, 1003–1020 (2005)
Dionne, B., Golubitsky, M., Stewart, I.: Coupled cells with internal symmetry: I. Wreath products. Nonlinearity 9, 559–574 (1996)
dos Reis, G.L.: Structural stability of equivariant vector fields on two manifolds. Trans. Am. Math. Soc. 283, 633–643 (1984)
Ermentrout, G.B.: xppaut (dynamical systems software). Available from http://www.math.pitt.edu/~bard/bardware/ (2000)
Field, M.J.: Dynamics, Bifurcation and Symmetry. Pitman Research Notes in Mathematics, vol. 356 (1996)
Field, M.J.: Combinatorial dynamics. Dyn. Syst. 19, 217–243 (2004)
Field, M.J.: Dynamics and Symmetry. Imperial College Press Advanced Texts in Mathematics, vol. 3 (2007)
Field, M.J., Richardson, R.W.: Symmetry breaking and branching patterns in equivariant bifurcation theory II. Arch. Ration. Mech. Anal. 120, 147–190 (1992)
Golubitsky, M., Stewart, I.: Nonlinear dynamics of networks: the groupoid formalism. Bull. Am. Math. Soc. 43, 305–364 (2006)
Golubitsky, M., Schaeffer, D.G., Stewart, I.N.: Singularities and Groups in Bifurcation Theory, vol. II. Appl. Math. Sci., vol. 69. Springer, New York (1988)
Golubitsky, M., Stewart, I., Buono, P.L., Collins, J.J.: Symmetry in locomotor central pattern generators and animal gaits. Nature 401, 693–695 (1999)
Golubitsky, M., Pivato, M., Stewart, I.: Interior symmetry and local bifurcation in coupled cell networks. Dyn. Syst. 19, 389–407 (2004)
Golubitsky, M., Stewart, I., Török, A.: Patterns of synchrony in coupled cell networks with multiple arrows. SIAM J. Appl. Dyn. Syst. 4(1), 78–100 (2005)
Guckenheimer, J., Holmes, P.: Structurally stable heteroclinic cycles. Math. Proc. Camb. Philos. Soc. 103, 189–192 (1988)
Hansel, D., Mato, G., Meunier, C.: Phase dynamics for weakly coupled Hodgkin-Huxley neurons. Europhys. Lett. 23, 367–372 (1993)
Hofbauer, J.: Heteroclinic cycles on the simplex. In: Proc. Int. Conf. Nonlinear Oscillations. Janos Bolyai Math. Soc., Budapest (1987)
Hofbauer, J.: Heteroclinic cycles in ecological differential equations. Tatra Mt. Math. Publ. 4, 105–116 (1994)
Hofbauer, J., Sigmund, K.: The Theory of Evolution and Dynamical Systems. Cambridge University Press, Cambridge (1988)
Hofbauer, J., Sigmund, K.: Evolutionary Games and Replicator Dynamics. Cambridge University Press, Cambridge (1998)
Homburg, A.J., Knobloch, J.: Switching homoclinic networks. Dyn. Syst. 25(3), 443 (2010). doi:10.1080/14689367.2010.499294
Karabacak, O., Ashwin, P.: Heteroclinic ratchets in a system of four coupled oscillators. J. Nonlinear Sci. 20, 105–129 (2010)
Kashtan, N., Alon, U.: Spontaneous evolution of modularity and network motifs. Proc. Natl. Acad. Sci. 102(39), 13773–13778 (2005)
Kirk, V., Silber, M.: A competition between heteroclinic cycles. Nonlinearity 7(6), 1605–1622 (1994)
Kiss, I., Rusin, C., Kori, H., Hudson, J.: Engineering complex dynamical structures: sequential patterns and desynchronization. Science 316, 1886–1889 (2007)
Kitchens, B.P.: Symbolic Dynamics. Universitext. Springer, Berlin (1998)
Krupa, M.: Robust heteroclinic cycles. J. Nonlinear Sci. 7, 129–176 (1997)
Krupa, M., Melbourne, I.: Asymptotic stability of heteroclinic cycles in systems with symmetry. Ergod. Theory Dyn. Syst. 15, 121–147 (1995)
Krupa, M., Melbourne, I.: Asymptotic stability of heteroclinic cycles in systems with symmetry, II. Proc. R. Soc. Edinb. A 134A, 1177–1197 (2004)
Leite, M.C.A., Golubitsky, M.: Homogeneous three-cell networks. Nonlinearity 19, 2313–2363 (2006)
May, R.M., Leonard, W.J.: Nonlinear aspects of competition between three species. SIAM J. Appl. Math. 29, 243–253 (1975)
Melbourne, I., Chossat, P., Golubitsky, M.: Heteroclinic cycles involving periodic solutions in mode interactions with O(2) symmetry. Proc. R. Soc. Edinb. 113A, 315–345 (1989)
Memmesheimer, R.-M., Timme, M.: Designing the dynamics of spiking neural networks. Phys. Rev. Lett. 97, 188101 (2006)
Nowotny, T., Rabinovich, M.: Dynamical origin of independent spiking and bursting activity in neural microcircuits. Phys. Rev. Lett. 98, 128106 (2007)
Pikovsky, A., Rosenblum, M., Kurths, J.: Synchronization; A Universal Concept in Nonlinear Sciences. Cambridge University Press, Cambridge (2001)
Rabinovich, M., Huerta, R., Laurent, G.: Transient dynamics for neural processing. Science 321, 48–50 (2008)
Restrepo, J.G., Ott, E., Hunt, B.R.: Emergence of synchronization in complex networks of interacting dynamical systems. Physica D 224, 114–122 (2006)
Scheel, A., Chossat, P.: Bifurcation d’orbites périodiques à partit d’un cycle homoclinic symétrique. C. R. Acad. Sci. Paris Sér. I 314, 49–54 (1992)
Stewart, I.: The lattice of balanced equivalence relations of a coupled cell network. Math. Proc. Camb. Philos. Soc. 143(1), 165–183 (2007)
Stewart, I., Golubitsky, M., Pivato, M.: Symmetry groupoids and patterns of synchrony in coupled cell networks. SIAM J. Appl. Dyn. Syst. 2(4), 606–646 (2003)
Strogatz, S.: From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Physica D 143, 1–20 (2000)
Zhigulin, V.: Dynamical motifs: building blocks of complex dynamics in sparsely connected random networks. Phys. Rev. Lett. 92, 238701 (2004)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by E. Knobloch.
Research of M.F. supported in part by NSF Grants DMS-0600927 & DMS-0806321 and of P.A. by EPSRC Grant EP/C510771. Research of M.A. and A.D. supported in part by CMUP financed by FCT through the programmes POCTI and POSI, with Portuguese and European Community structural funds.
Rights and permissions
About this article
Cite this article
Aguiar, M., Ashwin, P., Dias, A. et al. Dynamics of Coupled Cell Networks: Synchrony, Heteroclinic Cycles and Inflation. J Nonlinear Sci 21, 271–323 (2011). https://doi.org/10.1007/s00332-010-9083-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-010-9083-9