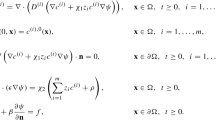Entropy and convergence analysis for two finite volume schemes for a Nernst–Planck–Poisson system with ion volume constraints

Abstract

In this paper, we consider a drift-diffusion system with cross-coupling through the chemical potentials comprising a model for the motion of finite size ions in liquid electrolytes. The drift term is due to the self-consistent electric field maintained by the ions and described by a Poisson equation. We design two finite volume schemes based on different formulations of the fluxes. We also provide a stability analysis of these schemes and an existence result for the corresponding discrete solutions. A convergence proof is proposed for non-degenerate solutions. Numerical experiments show the behavior of these schemes.

1 Introduction

Proper modeling of the motion of ions in electrolytes—mixtures of a solvent and N ionic species which can be described by their concentrations $c_i$—and associated simulations are crucial for the development of efficient batteries, fuel cells, and many other applications commonly considered as key technologies for the twenty first century as well as for the understanding of ion channels and other features of biological systems. The classical Nernst–Planck equation is a linear system which for given electrostatic potential $\Phi$, charge number $z_i$ and diffusion coefficient $D_i$ describes the evolution of the ion concentration $c_i$ via

$$\begin{aligned} \partial _t c_i -{{\,\mathrm{div}\,}}(D_iN_i)=0,\qquad N_i=\nabla c_i+z_ic_i\nabla \Phi =c_i\nabla \left( \log (c_i)+z_i\Phi \right) . \end{aligned}$$

The self-consistent electrostatic potential is described by the Poisson equation

$$\begin{aligned} -\nabla \cdot \lambda ^2\nabla \Phi = \sum _{i=1}^N z_i c_i. \end{aligned}$$

This model assumes that ions are infinitely small and that the ions of a given species i interact neither with the solvent nor with other ionic species. However, in reality, ion sizes are finite, and ion motion is only possible with a simultaneous displacement of solvent molecules. Moreover, the effective size of ions is increased by the fact that in a polar solvent like water, they are surrounded by a solvation shell consisting of a certain number of solvent molecules. The inclusion of these effects into the model is particularly important for concentrated electrolytes and in electrode boundary layers with high ion concentrations.

Historically, there have been many, often independent attempts to fix this situation, see e.g. the review in [3], the discussion in [30] or [40]. A comprehensive model of ideal mixtures of solvated ions has been derived in [21, 22]. In [30, 31], a two point flux finite volume discretization approach for these problems has been derived. Various variants of ionic flux approximations have been investigated for the unipolar case, where only one ionic species is considered, in [9], with the result that the flux approximation approach introduced in [30] has several more accurate alternatives. For two of them, we have been able to find appropriate generalizations to the case of several ionic species. One of these generalizations has been independently introduced in [41]. They are analyzed in the present paper using a similar analysis framework. Focus will be set on the cross-diffusion effects arising in the multi-species case, relying on [9] for the coupling with the potential and partial treatment the non-linearity.

In the sequel of Sect. 1, the continuous problem is formulated, and several key properties of the continuous system are discussed. Among these is the decay of an entropy functional for positive solutions.

1.1 The Nernst–Planck–Poisson system with finite ionic volumes

Consider a bounded connected polytopal domain $\text{\O}mega \subset \mathbb R^d$, and finite simulation horizon $T>0$. We model the evolution of the concentration $c_0$ of a solvent and N dissolved species: $c_i$, $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$. The mixture satisfies a volume filling constraint

$$\begin{aligned} \sum _{i=0}^{N} v_i c_i=1, \end{aligned}$$

where $v_i$ are the molar volumes of the species. We will use this constraint using ratios of molar volumes $k_i=\frac{v_i}{v_0}$:

$$\begin{aligned} \sum _{i=0}^N k_i c_i =\frac{1}{v_0}. \end{aligned}$$

(1.1)

The coefficients $(k_1,\dots ,k_N)$ are parameters of the problem and $k_0$ is by definition equal to 1. As the molar volumes are not the same, the total concentration

$$\begin{aligned} \overline{c}:=\sum _{i=0}^N c_i \end{aligned}$$

(1.2)

is not uniform. The set of positive concentrations $c_i, i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ such that $c_0$ is positive is denoted by

$$\begin{aligned}\mathcal {A}=\left\{ (c_1,...,c_N)\in (0,+\infty )^N | c_0:=\frac{1}{v_0}-\sum _{i=1}^{N}k_ic_i>0\right\} .\end{aligned}$$

We also introduce the topological adherence of $\mathcal {A}$:

$$\begin{aligned}\bar{\mathcal {A}}=\left\{ (c_1,...,c_N)\in [0,+\infty )^N | c_0:=\frac{1}{v_0}-\sum _{i=1}^{N}k_ic_i\ge 0\right\} .\end{aligned}$$

For the sake of clarity, we will let $C=(c_1,...,c_N)\in \mathcal {A}$ and often consider $c_0$ and $\overline{c}$ as functions of C thanks to (1.1) and (1.2) without clearly expressing the dependency. The dissolved species follow a conservation equation:

$$\begin{aligned} \partial _t c_i-{{\,\mathrm{div}\,}}D_i \mathcal {N}_i =0,\qquad \mathcal {N}_i=c_i\nabla \left( h_i(C)+{\widetilde{z_i}}\Phi \right) \qquad \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(1.3)

where ${\widetilde{z_i}}=z_i-k_iz_0$ the reduced charge number and $D_i>0$ the diffusion coefficient are parameters of the problem, while $h_i(C)$ the chemical potential depends on all the concentrations through:

$$\begin{aligned} h_i(C)=\log \frac{c_i}{\overline{c}}-k_i\log \frac{c_0}{\overline{c}} \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(1.4)

This system is supplemented with Poisson equation for the potential:

$$\begin{aligned} -\lambda ^2{{\,\mathrm{\Delta }\,}}\Phi =c^\text {dop}+\sum _{i=0}^N z_i c_i, \end{aligned}$$

(1.5)

where $c^\text {dop}:\text{\O}mega \rightarrow \mathbb R$ is a constant in time doping profile. To simplify the computations, we let $c^\text {dop}=\frac{z_0}{v_0}+{\widetilde{c}}^\text {dop}$. Using ${\widetilde{z_0}}=0$, we have:

$$\begin{aligned} c^\text {dop}+\sum _{i=0}^N z_i c_i={\widetilde{c}}^\text {dop}+\sum _{i=1}^N {\widetilde{z_i}} c_i. \end{aligned}$$

To avoid unnecessary complications of the notations, we will drop the tildas for the reduced molar charges as the real molar charges do not appear anymore. Moreover, to simplify the proofs, we will assume that the solvent carries no charge, hence $z_0=0$ and ${\widetilde{c}}^\text {dop}=0$. Treatment of nonzero ${\widetilde{c}}^\text {dop}$ can be found in [9].

As in [9], we consider a Dirichlet boundary condition for the potential on a non-negligible part of the boundary $\Gamma _\text {D}\subset \partial \text{\O}mega$ and homogeneous Neumann boundary condition on $\Gamma _\text {N}=\partial \text{\O}mega \setminus \Gamma _\text {D}$:

$$\begin{aligned} \Phi =\Phi ^D\qquad \text {on}\quad (0,T)\times \Gamma _\text {D},\qquad \qquad \nabla \Phi \cdot n=0\qquad \text {on}\quad (0,T)\times \Gamma _\text {N}, \end{aligned}$$

(1.6)

where $\Phi ^D$ is assumed to be constant in time and in $H^1(\text{\O}mega )\cap L^\infty (\text{\O}mega )$.

The system is supplemented with the following no flux boundary conditions for the concentrations:

$$\begin{aligned} c_i\nabla \left( h_i(C)+z_i\Phi \right) \cdot n=0 \qquad \text {on}\quad (0,T)\times \partial \text{\O}mega ,\quad \hbox {for all}\quad i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, \end{aligned}$$

(1.7)

and with an initial condition $C^0$ satisfying:

$$\begin{aligned} C^0\in L^\infty (\text{\O}mega ,\bar{\mathcal {A}})\qquad \qquad \text {and}\qquad \qquad \int _\text{\O}mega c_i^0(x)\mathrm{d}x>0\qquad \forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(1.8)

1.2 Key properties of the continuous system

In this section, we attempt to exhibit the properties of a smooth enough solution $(C,\Phi )$ to the system (1.3)–(1.8) so that calculations are justified. The first property is the conservation of mass. In other words, thanks to (1.3) and (1.7), C satisfies for any $t\in [0,T], i \in \mathbf{[}\mathbf{[}1, N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \int _\text{\O}mega c_i(0,x)\mathrm{d}x=\int _\text{\O}mega c_i(t,x)\mathrm{d}x. \end{aligned}$$

Moreover, we need the concentrations to be positive for (1.4) to have a sense. In the discrete setting, we will show that the concentrations belong to $\mathcal {A}$. In the continuous setting, it will be assumed. We hint that it might be possible to do it using the entropy method [38], the flux formulation proposed in [30] and [35,  Annex A]. Indeed, another key property of the system is the dissipation of a free energy. In this case, the chemical free energy density H(C) is defined as follows:

$$\begin{aligned} H(C):= \sum _{i=0}^N c_i\log \left( \frac{c_i}{\overline{c}}\right) =\sum _{i=0}^N c_i\log c_i -\overline{c}\log \overline{c}. \end{aligned}$$

This function is convex, however, the addition of the term $-\overline{c}\log \overline{c}$ makes the proof quite intricate. This point is detailed in “Appendix A” along with the proof of the following equations:

$$\begin{aligned}&\partial _{c_i} H(c_1,...,c_N)=h_i(C), \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]},\; C=(c_1,...,c_N)\in \mathcal {A}, \end{aligned}$$

(1.9)

$$\begin{aligned}&\frac{-\log (N+1)}{v_0\min k_i} \le H(C)\le 0 \qquad \forall C\in \mathcal {A}. \end{aligned}$$

(1.10)

The total free energy is formed by the integral of the chemical free energy density and electrical terms:

$$\begin{aligned} E(C,\Phi )=\int _\text{\O}mega H(C)+\lambda ^2 \frac{|\nabla \Phi |^2}{2}\mathrm{d}x-\lambda ^2\int _{\Gamma _\text {D}}\Phi _D\nabla \Phi \cdot n \mathrm{d}\gamma . \end{aligned}$$

Proposition 1.1

Let $(C,\Phi )$ be smooth solutions of (1.3)–(1.8) such that $C(t,x)\in \mathcal {A}$. For such solutions, E is a convex Lyapunov functional. Moreover, we have:

$$\begin{aligned} \partial _t E +\int _\text{\O}mega \sum _{i=1}^n D_i c_i |\nabla h_i(C)+z_i\Phi |^2\mathrm{d}x=0. \end{aligned}$$

(1.11)

Proof

We have using chain rules and (1.9):

$$\begin{aligned} \partial _t \int _\text{\O}mega H(c_1,...,c_N) \mathrm{d}x= \int _\text{\O}mega \sum _{i=1}^{N} h_i(C) \partial _t c_i \mathrm{d}x. \end{aligned}$$

(1.12)

We also have using chain rules and integrating by part:

$$\begin{aligned} \partial _t \int _\text{\O}mega \frac{|\nabla \Phi |^2}{2}\mathrm{d}x =\int _{\partial \text{\O}mega }\Phi \partial _t\left( \nabla \Phi \cdot n\right) \mathrm{d}\gamma -\int _\text{\O}mega \Phi \partial _t {{\,\mathrm{\Delta }\,}}\Phi \mathrm{d}x. \end{aligned}$$

Notice that we have $\nabla \Phi \cdot n=0$ on $\Gamma _\text {N}$ and $\Phi =\Phi _D$ on $\Gamma _\text {D}$. Using Eq. (1.5), we have:

$$\begin{aligned} \partial _t \lambda ^2 \left( \int _\text{\O}mega \frac{|\nabla \Phi |^2}{2}\mathrm{d}x -\int _{\Gamma _\text {D}}\Phi _D\nabla \Phi \cdot n\mathrm{d}\gamma \right) =\int _\text{\O}mega \Phi \sum _{i=1}^{N} z_i \partial _t c_i \mathrm{d}x. \end{aligned}$$

Using this equation and (1.12), we have:

$$\begin{aligned} \partial _t E=\sum _{i=1}^{N}\int _\text{\O}mega (h_i(C)+z_i\Phi ) \partial _t c_i \mathrm{d}x. \end{aligned}$$

Using now Eq. (1.3) and integration by parts, we have the desired Eq. (1.11). Due to the non-negativity of $D_ic_i$, E is a Lyapunov functional. Its convexity follows from the assumption $C\in \mathcal {A}$ (see Lemma A.1).$\square$

Finally, we introduce a notion of weak solution that relies on a reformulation of the fluxes:

$$\begin{aligned} \mathcal {N}_i=\nabla c_i-k_i c_i\nabla \log c_0+(k_i-1)c_i\nabla \log \overline{c}+z_ic_i\nabla \Phi , \end{aligned}$$

and the space of $H^1$ functions satisfying the Dirichlet boundary conditions for the potential:

$$\begin{aligned} \mathcal {H}_{\Gamma _\text {D}}=\lbrace f\in H^1(\text{\O}mega ), f_{|_{\Gamma _\text {D}}}=0\rbrace \qquad \text {and} \qquad Q_T= (0,T)\times \text{\O}mega .\end{aligned}$$

More precisely:

Definition 1

A couple $(C,\Phi )$ is a weak solution of (1.3)–(1.8) if

• $C \in L^\infty (Q_T,\overline{\mathcal {A}})$ with $\log (c_0) \in L^2((0,T),H^1(\text{\O}mega ))$,

• $\Phi$ such that $\Phi - \Phi ^D \in L^\infty ((0,T),\mathcal {H}_{\Gamma _\text {D}})$;

• for all $\varphi \in C^\infty _c([0,T)\times \overline{\text{\O}mega })^N$, $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$

  $$\begin{aligned}&\iint _{Q_T} c_i \partial _t \varphi _i \mathrm{d}x\mathrm{d}t + \int _\text{\O}mega c^0_i \varphi _i(0,x) \mathrm{d}x\nonumber \\&\quad - D_i\iint _{Q_T}\left( \nabla c_i+c_i\nabla \bigl (-k_i\log c_0+(k_i-1)\log \overline{c}+z_i \Phi \bigr ) \right) \cdot \nabla \varphi _i \mathrm{d}x\mathrm{d}t = 0;\nonumber \\ \end{aligned}$$

  (1.13)

• for all $\psi \in \mathcal {H}_{\Gamma _\text {D}}$ and almost all $t\in (0,T)$,

  $$\begin{aligned} \lambda ^2 \int _\text{\O}mega \nabla \Phi (t, x) \cdot \nabla \psi ( x) \mathrm{d}x = \int _\text{\O}mega \psi ( x)\sum _{i=1}^N z_i c_i(t, x) \mathrm{d}x. \end{aligned}$$

  (1.14)

1.3 Positioning and outline

The structure of cross-diffusion systems challenges the maximum principle-based methods. In this paper we aim to discretize the system (1.3)–(1.8). For $N=1$ this system is a nonlinear drift-diffusion problem and several discretizations have been proposed in [9]. We focus on the extension of these schemes to the more general setting with $N>1$ while adapting the proofs to tackle the challenges introduced by cross-diffusion.

More precisely, in Sect. 2, the two point flux based finite volume discretization with two variants of the flux approximation is introduced. The main theorems about the existence of discrete solutions and the convergence of approximate solutions are stated. Existence, free energy decay, and positivity of concentrations are proven in Sect. 3, whereas the convergence is proven in Sect. 4. Several 1D and 2D numerical examples showcasing the proven properties of the discretization scheme are discussed in Sect. 5.

2 Discretization and main theorems

In this section, we propose two discretizations of (1.3)–(1.8) and discrete counterparts of the continuous properties. First, in Sect. 2.1, we state the requirements on the mesh and fix some notations. Then in Sect. 2.2, we describe the common setting for the two schemes to be studied in this paper. These schemes, presented in Sect. 2.3, rely on so-called two-point flux approximations of different formulations of $\mathcal {N}_i$. Then in Sect. 2.4, we state our two main results. The first one, namely Theorem 2.1, focuses on the existence of a solution to the nonlinear system corresponding to the schemes for a given mesh, and the dissipation of the energy at the discrete level. More precisely, one establishes that all the studied schemes satisfy a discrete counterpart to Proposition 1.1. Our second main result, namely Theorem 2.2, is devoted to the convergence of the schemes as the time step and the mesh size tend to 0.

2.1 Discretization of $(0,T) \times \text{\O}mega$

In this paper, we perform a parallel study of two numerical schemes based on two-point flux approximation (TPFA) finite volume schemes. As explained in [23, 28], this approach appears to be very efficient for isotropic continuous problems when one has the freedom to choose a suitable mesh fulfilling the so-called orthogonality condition [29, 37]. We recall here the definition of such a mesh, which is illustrated in Fig. 1.

Definition 2

An admissible mesh of $\text{\O}mega$ is a triplet $\left( \mathcal {T}, \mathcal {E}, {(x_K)}_{K\in \mathcal {T}}\right)$ such that the following conditions are fulfilled.

• (i) The set $\mathcal {T}$ is finite and each control volume (or cell) $K\in \mathcal {T}$ is non-empty, open, polyhedral, and convex. We assume that

  $$\begin{aligned} K \cap L = \emptyset \quad \text {if}\; K, L \in \mathcal {T}\; \text {with}\; K \ne L, \qquad \text {while}\quad \bigcup _{K\in \mathcal {T}}\overline{K} = \overline{\text{\O}mega }. \end{aligned}$$

• (ii) Each face $\sigma \in \mathcal {E}$ is closed and is contained in a hyperplane of $\mathbb {R}^d$, with positive $(d-1)$-dimensional Hausdorff (or Lebesgue) measure denoted by $m_\sigma = \mathcal {H}^{d-1}(\sigma ) >0$. We assume that $\mathcal {H}^{d-1}(\sigma \cap \sigma ') = 0$ for $\sigma , \sigma ' \in \mathcal {E}$ unless $\sigma ' = \sigma$. For all $K \in \mathcal {T}$, we assume that there exists a subset $\mathcal {E}_K$ of $\mathcal {E}$ such that $\partial K = \bigcup _{\sigma \in \mathcal {E}_K} \sigma$. Moreover, we suppose that $\bigcup _{K\in \mathcal {T}} \mathcal {E}_K = \mathcal {E}$. Given two distinct control volumes $K, L\in \mathcal {T}$, the intersection $\overline{K} \cap \overline{L}$ either reduces to a single face $\sigma \in \mathcal {E}$ denoted by K|L, or its $(d-1)$-dimensional Hausdorff measure is 0.

• (iii) The cell centers $(x_K)_{K\in \mathcal {T}}$ belong to their cell: $x_K \in K$, and are such that, if $K, L \in \mathcal {T}$ share a face K|L, then the vector $x_L-x_K$ is orthogonal to K|L.

• (iv) For the boundary faces $\sigma \subset \partial \text{\O}mega$, we assume that either $\sigma \subset \overline{\Gamma }_\text {D}$ or $\sigma \subset \overline{\Gamma }_\text {N}$. For $\sigma \subset \partial \text{\O}mega$ with $\sigma \in \mathcal {E}_K$ for some $K\in \mathcal {T}$, we assume additionally that there exists $x_\sigma \in \sigma$ such that $x_\sigma - x_K$ is orthogonal to $\sigma$.

Fig. 1

Illustration of an admissible mesh as in Definition 2

We denote by $m_K$ the d-dimensional Lebesgue measure of the control volume K. The set of the faces is partitioned into two subsets: the set $\mathcal {E}_\text {int}$ of the interior faces defined by $\mathcal {E}_\text {int}= \left\{ \sigma \in \mathcal {E}\; | \; \sigma = K|L\; \text {for some}\; K, L \in \mathcal {T}\right\} ,$ and the set $\mathcal {E}_\text {ext}$ of the exterior faces defined by $\mathcal {E}_\text {ext}= \left\{ \sigma \in \mathcal {E}\; | \; \sigma \subset \partial \text{\O}mega \right\} ,$ which can also be partitioned into $\mathcal {E}^\text {D} = \{ \sigma \subset \overline{\Gamma }_\text {D}\}$ and $\mathcal {E}^\text {N} = \{\sigma \subset \overline{\Gamma }_\text {N}\}$.

Notice that for any $\sigma \in \mathcal {E}_\text {ext}$, the edge center $x_\sigma$ satisfying (2) is unique. Given $\sigma \in \mathcal {E}$, we let

$$\begin{aligned} d_\sigma = {\left\{ \begin{array}{ll} |x_K - x_L| &{} \text {if}\; \sigma = K|L \in \mathcal {E}_\text {int}, \\ |x_K - x_\sigma | &{} \text {if}\; \sigma \in \mathcal {E}_\text {ext}. \end{array}\right. } \qquad \text {and}\quad \tau _\sigma = \frac{m_\sigma }{d_\sigma } . \end{aligned}$$

Thanks to (2) and (2), we have $d_\sigma >0$, thus $\tau _\sigma$ is well defined. We finally introduce the size $h_\mathcal {T}$ and the regularity $\zeta _\mathcal {T}$ (which is assumed to be positive) of a discretization $(\mathcal {T}, \mathcal {E}, (x_K)_{K\in \mathcal {T}})$ of $\text{\O}mega$ by setting

$$\begin{aligned} h_\mathcal {T}= \max _{K \in \mathcal {T}}\;{\text {diam}}(K), \qquad \zeta _\mathcal {T}= \min _{K\in \mathcal {T}}\min _{\sigma \in \mathcal {E}_K} \frac{{\text {d}}(x_K,\sigma )}{d_\sigma }. \end{aligned}$$

Concerning the time discretization of (0, T), we consider an increasing finite family of times $0 = t_0< t_1< \dots , < t_{N_T} = T$. We denote by ${\Delta t}_n = t_{n}-t_{n-1}$ for $1\le n\le {N_T}$, by $\varvec{\Delta t} = \left( {\Delta t}_n\right) _{1\le n \le {N_T}}$, and by $h_{{\varvec{\Delta t}}} = \max _{1 \le n \le {N_T}} {\Delta t}_n$. We will use boldface notations for vectors whose number of components is dependent on the mesh while keeping the uppercase notation ${\varvec{C}}$ when we also consider different species.

2.2 A common setting for the Finite Volume schemes

The initial data $C^0$ which belongs to $L^\infty (\text{\O}mega ,\bar{\mathcal {A}})$ thanks to (1.8) is discretized into $\left( C^0_K\right) _{K\in \mathcal {T}} \in \bar{\mathcal {A}}^\mathcal {T}$ by setting

$$\begin{aligned} c_{K,i}^0=\frac{1}{|K|}\int _K c_i^0(x) \mathrm{d}x \qquad \forall K\in \mathcal {T}, i \in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(2.1)

Notice that previous equation also holds for $i=0$ and that this discretization satisfies:

$$\begin{aligned} \sum _{K\in \mathcal {T}} m_K c_{K,i}^0=\int _\text{\O}mega c_i^0(x) \mathrm{d}x>0, \quad \forall i \in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}\qquad \text {and}\qquad C_K^0\in \bar{\mathcal {A}}, \quad \forall K\in \mathcal {T}. \end{aligned}$$

(2.2)

Assume that ${\varvec{C}}^{n-1}=\left( c_{K,i}^{n-1}\right) _{K\in \mathcal {T},i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}}$ is given for some $n > 0$, then we have to define how to compute $({\varvec{C}}^n,{\varvec{\Phi }}^n)=\left( C_{K}^{n}, \Phi _K^n\right) _{K\in \mathcal {T}}$. First, we introduce some notations. For all $K\in \mathcal {T}$ and all $\sigma \in \mathcal {E}_K$, we define the mirror values $C_{K\sigma }^n$ and $\Phi _{K\sigma }^n$ of $C_K^n$ and $\Phi _K^n$ respectively across $\sigma$ by setting

$$\begin{aligned} C_{K\sigma }^n = {\left\{ \begin{array}{ll} C_L^n &{}\text {if}\; \sigma = K|L \in \mathcal {E}_\text {int},\\ C_K^n &{} \text {if}\; \sigma \in \mathcal {E}_\text {ext}, \end{array}\right. } \quad \Phi _{K\sigma }^n = {\left\{ \begin{array}{ll} \Phi _L^n &{} \text {if}\; \sigma = K|L \in \mathcal {E}_\text {int}, \\ \Phi _K^n &{} \text {if}\; \sigma \in \mathcal {E}^N,\\ \Phi _\sigma ^D = \frac{1}{|\sigma |}\int _\sigma \Phi ^D \mathrm{d}\gamma &{} \text {if}\; \sigma \in \mathcal {E}^D. \end{array}\right. } \end{aligned}$$

(2.3)

Given ${\varvec{u}}=\left( u_K\right) _{K\in \mathcal {T}} \in \mathbb {R}^\mathcal {T}$, we define the oriented and absolute jumps of ${\varvec{u}}$ across any edge by

$$\begin{aligned} D_{K\sigma }{\varvec{u}}= u_{K\sigma } - u_K, \quad D_\sigma {\varvec{u}}= |D_{K\sigma } {\varvec{u}}|, \qquad \forall K \in \mathcal {T}, \; \forall \sigma \in \mathcal {E}_K. \end{aligned}$$

We may now use these operators to describe our scheme. The potential is approximated using the classic TPFA scheme for the Poisson equation:

$$\begin{aligned} -\lambda ^2\sum _{\sigma \in \mathcal {E}_K}\tau _\sigma D_{K\sigma }{\varvec{\Phi }}^n = m_K \sum _{i=1}^N z_i c_{K,i}^n, \qquad \forall K \in \mathcal {T}. \end{aligned}$$

(2.4a)

The conservation equation is approximated using a backward-Euler scheme in time:

$$\begin{aligned} m_K\frac{c_{K,i}^n - c_{K,i}^{n-1}}{{\Delta t}_n} + \sum _{\sigma \in \mathcal {E}_K}F_{K\sigma ,i}^n = 0, \qquad \forall K \in \mathcal {T}, i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, \end{aligned}$$

(2.4b)

where $F_{K\sigma ,i}^n$ should be a conservative and consistent approximation of $-\frac{D_i}{{\Delta t}_n}\int _{t_{n-1}}^{t_n}\int _\sigma \mathcal {N}_i\cdot n_{K\sigma }$ ($n_{K\sigma }$ denotes the normal to $\sigma$ outward K). Finally, the concentration of the solvent is computed using a discrete version of the volume filling constraint:

$$\begin{aligned} c_{K,0}^n=\frac{1}{v_0}-\sum _{i=1}^{N}k_i c_{K,i}^n,\qquad \forall K \in \mathcal {T}. \end{aligned}$$

(2.4c)

It remains to define the numerical fluxes $F_{K\sigma ,i}^n$. Two possible choices are given in the next section.

2.3 Numerical fluxes for the conservation equations

To close the system (2.4), we have to define the numerical fluxes $F_{K\sigma ,i}^n$. As we intend to use two point flux approximations, they should be of the form:

$$\begin{aligned} F_{K\sigma ,i}^n = {\left\{ \begin{array}{ll} 0&{}\text {if }\sigma \in \mathcal {E}_\text {ext}\\ \tau _\sigma D_i \mathcal {F}_i(C_K,C_{L},\Phi _K,\Phi _{L})&{}\text {if } \sigma =K|L\in \mathcal {E}_\text {int} \end{array}\right. } \end{aligned}$$

(2.5)

For the sake of readability, we have chosen to define the flux functions $\mathcal {F}_i$ for unitary $D_i$. Thus this constant should rarely appear in the functional inequalities of the following sections. To preserve the conservation of mass, all the flux functions $\mathcal {F}_i$ defined afterward satisfy an anti-symmetry property:

$$\begin{aligned} \mathcal {F}_i(C_K,C_{L},\Phi _K,\Phi _{L})=-\mathcal {F}_i(C_L,C_K,\Phi _L,\Phi _K)\qquad \forall C_K,C_L\in \mathcal {A}, \Phi _K,\Phi _L \in \mathbb R, \end{aligned}$$

(2.6)

so that the fluxes are locally conservative, i.e.:

$$\begin{aligned} F_{K,\sigma }+F_{L,\sigma }=0 \qquad \forall \sigma =K|L\in \mathcal {E}_\text {int}. \end{aligned}$$

2.3.1 The centered flux

The first numerical flux we consider is based on the original expression of the flux (1.3):

$$\begin{aligned} \mathcal {N}_i=D_i c_i\nabla \Bigl (h_i(c) + z_i\Phi \Bigr ). \end{aligned}$$

The gradient and edge concentration are independently discretized:

$$\begin{aligned} \mathcal {F}_i(C_K,C_{L},\Phi _K,\Phi _{L})= \frac{c_{K,i}+c_{L,i}}{2} \left( h_i(C_K)-h_i(C_L))+z_i(\Phi _K-\Phi _L)\right) . \end{aligned}$$

(C)

This flux is a straightforward generalization of the eponymous flux presented in [9]. As such it is also similar to the fluxes introduced in [7, 11, 12, 15, 16].

2.3.2 The “Sedan” flux

The other flux under study is also a generalization of the Sedan flux presented in [9]. It originates from and is named after the SEDAN III semiconductor device simulation code [47] and is used to handle the case of degenerated semiconductors in semiconductor device simulators, see [45, 46]. In [41], this approach was applied to ion transport in electrolytes, resulting in a scheme almost identical with the one presented here. The scheme relies on the introduction of the excess chemical potential

$$\begin{aligned} \nu _i(C):=h_i(C)-\log (c_i)=-\log (\bar{c})-k_i \log \frac{c_0}{\bar{c}}. \end{aligned}$$

This excess potential characterizes the non-ideality of the electrolyte leading to the following equivalent continuous flux formulation:

$$\begin{aligned} \mathcal {N}_i=D_i \Biggl [\nabla c_i +c_i \nabla \left( z_i\Phi +\nu _i(C)\right) \Biggr ]. \end{aligned}$$

The Scharfetter–Gummel-inspired discretization [44] of this expression of the flux leads to the so-called Sedan flux:

where $B(x)=\frac{x}{e^x-1}$ for all $x\ne 0$ is the Bernoulli function. Notice that B can be extended by $B(0)=1$ and is in $C^\infty (\mathbb R)$.

Remark 1 In [9] we studied two other schemes. One was based on the diffusion enhancement and discretization ideas originating from [4]. The extension of this so-called Bessemoulin–Chatard scheme to the multi-species case appears to be not feasible due to the intrinsic use of one-dimensional chain rules. The other scheme based on activity variables and the averaging of the inverse activity coefficient was introduced for the multi-species case in [30]. Numerical analysis of such a scheme is more intricate and would likely not be satisfactory as we were not able to prove convergence in [9]. Moreover, unless more sophisticated inverse activity coefficient averaging strategies are available, this scheme is considerably less accurate compared to all the others discussed in [9].

2.4 Main theorems

We have proposed two schemes (2.4), (2.5) supplemented with either (C) or (S). Both schemes are nonlinear systems. Solutions to this nonlinear system should satisfy discrete equivalents of the properties listed in Sect. 1.2, namely conservation of mass and energy-dissipation. For the latter, we introduce the discrete energy functional $E_\mathcal {T}$ as a discrete counterpart of the continuous energy functional E. It is defined by:

$$\begin{aligned} E_\mathcal {T}({\varvec{C}}^n,{\varvec{\Phi }}^n) = \sum _{K\in \mathcal {T}}m_K H(C_K^n) + \frac{\lambda ^2}{2} \sum _{\sigma \in \mathcal {E}} \tau _\sigma \left( D_{\sigma } {\varvec{\Phi }}^n\right) ^2 - \lambda ^2\sum _{K\in \mathcal {T}}\sum _{\sigma \in \mathcal {E}^D\cap \mathcal {E}_K} \tau _\sigma \Phi _{\sigma }^D D_{K\sigma } {\varvec{\Phi }}^n. \end{aligned}$$

(2.7)

The first theorem proven in this paper focuses on the existence of discrete solutions for a given mesh, and the preservation of the physical bounds: positive concentrations, and the properties of Sect. 1.2.

Theorem 2.1

Let $(\mathcal {T},\mathcal {E},\left( x_K\right) _{K\in \mathcal {T}})$ be an admissible mesh and let ${\varvec{C}}^0$ be defined by (2.1). Then, for all $1\le n\le N_T$, the nonlinear system of equations (2.4), (2.5) supplemented with either (C) or (S) has a solution

$$\begin{aligned} ({\varvec{C}}^{n}, {\varvec{\Phi }}^{n})\in \mathcal {A}^{\mathcal {T}} \times \mathbb {R}^{\mathcal {T}}. \end{aligned}$$

Moreover, the solution to the scheme satisfies, for all $1\le n\le N_T$,

$$\begin{aligned} E_\mathcal {T}({\varvec{C}}^{n},{\varvec{\Phi }}^{n}) - E_\mathcal {T}({\varvec{C}}^{n-1},{\varvec{\Phi }}^{n-1})\le {\Delta t}_n \sum _{i=1}^N \sum _{\sigma \in \mathcal {E}}F_{K\sigma ,i}^n D_{K\sigma }(h_i({\varvec{C}}^n)+z_i{\varvec{\Phi }}^n), \end{aligned}$$

(2.8)

and

$$\begin{aligned} \sum _{K\in \mathcal {T}} c_{K,i}m_K=\int _{\text{\O}mega }c^0_i(x)\mathrm{d}x\qquad \forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(2.9)

The proof of this theorem is the purpose of Sect. 3. Knowing a discrete solution to the scheme, $({\varvec{C}}^{n}, {\varvec{\Phi }}^{n})_{1\le n\le N}$, we can define an approximate solution $(C_{\mathcal {T},{\varvec{\Delta t}}}, \Phi _{\mathcal {T},{\varvec{\Delta t}}})$. It is the piecewise constant function defined almost everywhere by

$$\begin{aligned} C_{\mathcal {T}, \varvec{\Delta t}}(t,x) = C_K^{n}, \quad \Phi _{\mathcal {T}, \varvec{\Delta t}}(t,x) = \Phi _K^{n} \quad \text {if}\;(t,x) \in (t_{n-1},t_n]\times K. \end{aligned}$$

This definition will be developed in Sect. 4 and supplemented by other reconstruction operators.

Using this existence result, we let $\left( \mathcal {T}_m, \mathcal {E}_m,(x_K)_{K\in \mathcal {T}_m}\right) _{m\ge 1}$, $({\varvec{C}}^{n}_m, {\varvec{\Phi }}^{n}_m)\in \mathcal {A}^{\mathcal {T}} \times \mathbb {R}^{\mathcal {T}}$, be a sequence of admissible meshes in the sense of Definition 2 and associated approximate solution. We assume that $h_{\mathcal {T}_m},h_{{\varvec{\Delta t}}_m} \underset{m\rightarrow \infty }{\longrightarrow }0$ while the mesh regularity remains bounded, i.e., $\zeta _{\mathcal {T}_m} \ge \zeta ^\star$ for some $\zeta ^\star >0$ not depending on m. A natural question is the convergence of $(C_{\mathcal {T}_m, \varvec{\Delta t}_m}, \Phi _{\mathcal {T}_m, \varvec{\Delta t}_m})$ towards a weak solution to the continuous problem. The convergence result is stated in Theorem 2.2 which will be proved in Sect. 4.

Theorem 2.2

For the two schemes under study, a sequence of approximate solutions $({\varvec{C}}_{\mathcal {T}_m,{\varvec{\Delta t}}_m}, {\varvec{\Phi }}_{\mathcal {T}_m,{\varvec{\Delta t}}_m})_{m\ge 1}$ satisfies, up to a subsequence:

$$\begin{aligned} C_{\mathcal {T}_m, {\varvec{\Delta t}}_m} \underset{m\rightarrow \infty }{\longrightarrow }C \quad \text {in} \; L^2(Q_T)^{N+1}, \qquad \Phi _{\mathcal {T}_m, {\varvec{\Delta t}}_m} \underset{m\rightarrow \infty }{\longrightarrow }\Phi \quad \text {in}\; L^2(Q_T). \end{aligned}$$

(2.10)

Moreover if $\inf _{\begin{array}{c} \text {mesh }m\\ n\in \mathbf{[}\mathbf{[}1,N_{T,m}\mathbf{]}\mathbf{]}\\ K\in \mathcal {T}_m \end{array}} c_{m,K,0}^n>0$, $(C, \Phi )$ is a weak solution of (1.3)–(1.8) in the sense of Definition 1.

3 Fixed Mesh analysis

In this section, we intend to prove Theorem 2.1. To this end, we will use a topological degree argument in Sect. 3.3. This topological degree relies on properties of the fluxes and a priori estimates detailed respectively in the following section and in Sect. 3.2. The methodology of this proof is very similar to the one done in [9]. The key changes and improvements are concentrated in Proposition 3.2, Lemmas 3.2 and 3.5.

3.1 Analysis of numerical flux based functions

In this section, we introduce several functions derived from $\mathcal {F}_i$. As in [9], the first functions of interest models the free energy dissipation for each species $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \mathcal {D}_i(C_K,C_{L}, \Phi _K,\Phi _{L}):=\mathcal {F}_i (C_K,C_L,\Phi _K,\Phi _L)\left( h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}\right) . \end{aligned}$$

We also introduce the local free energy dissipation $\mathcal {D}:= \sum _{i=1}^{N}\mathcal {D}_i$. In addition to this function, we can define a reconstruction of the concentration at the interfaces. This is the purpose of the following lemma:

Lemma 3.1

For a flux $\mathcal {F}_i$ defined either by (C) or (S), the corresponding face concentration functions defined by

$$\begin{aligned} \mathcal {C}_i(C_K,C_{L}, \Phi _K,\Phi _{L})= \frac{\mathcal {F}_i (C_K,C_L,\Phi _K,\Phi _L)}{ h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}} \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}\end{aligned}$$

(3.1)

if $h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}\ne 0$ can be extended by continuity on $\mathcal {A}\times \mathcal {A}\times \mathbb {R}\times \mathbb {R}$. Moreover, for all $(C_K,C_{L},\Phi _K,\Phi _{L}) \in \mathcal {A}\times \mathcal {A}\times \mathbb {R}\times \mathbb {R}$, and for all $i\in \mathbf{[}\mathbf{[}1, N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \min (c_{K,i},c_{L,i})\le \mathcal {C}_i(C_K,C_L,\Phi _K,\Phi _L)\le \max (c_{K,i},c_{L,i}). \end{aligned}$$

(3.2)

Proof

The proof of the extension by continuity and the average property (3.2) is highly similar to [9,  Lemma 3.1]. For the centered scheme defined by (C), we have by definition:

$$\begin{aligned} \mathcal {C}_i(C_K,C_{L}, \Phi _K,\Phi _{L})=\frac{c_{K,i}+c_{L,i}}{2}, \end{aligned}$$

hence the extension by continuity and Eq. (3.2).

For the Sedan scheme, defined by (S), we introduce $x_i=\log (c_{K,i}/c_{L,i})$ and $y_i= z_i\Phi _{L} + \nu _i(C_{L}) - z_i\Phi _{K} - \nu _i(C_{K})$ and notice that:

$$\begin{aligned} h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}=x_i-y_i,\nonumber \\ \mathcal {F}_i (C_K,C_L,\Phi _K,\Phi _L)=B(y_i)c_{K,i}-B(-y_i)c_{L,i}. \end{aligned}$$

(3.3)

Using the following property of the Bernoulli function:

$$\begin{aligned} B(\log (a) - \log (b)) a - B(\log (b) - \log (a))b =0, \qquad \forall (a,b) \in (0,+\infty )^2, \end{aligned}$$

we have:

$$\begin{aligned} \mathcal {F}_i (C_K,C_L,\Phi _K,\Phi _L)=(B(y_i)-B(x_i))c_{K,i}-(B(-y_i)-B(-x_i))c_{L,i}. \end{aligned}$$

(3.4)

Finally using (3.3) and the differentiability of B, we have the desired extension on $\mathcal {A}\times \mathcal {A}\times \mathbb {R}\times \mathbb {R}$. We also have Eq. (3.2) thanks to the monotony of B and the relation $B(x) - B(-x) = -x$ for all $x\in \mathbb {R}$.$\square$

Thanks to this lemma, $\mathcal {D}_i$ rewrites:

$$\begin{aligned} \mathcal {D}_i(C_K,C_{L}, \Phi _K,\Phi _{L})=\mathcal {C}_i(C_K,C_{L}, \Phi _K,\Phi _{L})\Bigl (h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}\Bigr )^2. \end{aligned}$$

(3.5)

This new formulation along with (3.2) grants the non-negativity of $\mathcal {D}_i$ and $\mathcal {D}$. The following coercivity lemma gives more detailed information on the behavior of $\mathcal {D}$:

Lemma 3.2

Let for $\delta ,\epsilon ,M,c>0$, $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \begin{aligned} {\Psi }_{\delta ,\epsilon ,M,i}(c)&:=\inf _{\begin{array}{c} (C_K,C_L)\in \mathcal {A}^2,\;(\Phi _K,\Phi _L) \in [-M,M]^2\\ c_{K,0},c_{L,0}>\epsilon ,\; c_{K,i}\ge \min (\delta ,\frac{0.5}{k_iv_0}),\; c_{L,i}<c \end{array}} \mathcal {D}_i(C_K,C_L, \Phi _K, \Phi _L),\\ {\Upsilon }_{\delta ,M}(c)&:=\inf _{\begin{array}{c} (C_K,C_L)\in \mathcal {A}^2,\;(\Phi _K,\Phi _L) \in [-M,M]^2\\ c_{K,0}\ge \min (\delta ,\frac{0.5}{v_0}) ,\; c_{L,0}<c \end{array}} \mathcal {D}(C_K,C_L, \Phi _K, \Phi _L). \end{aligned} \end{aligned}$$

(3.6)

We have, for all $\delta ,\epsilon ,M>0$:

$$\begin{aligned} \lim _{c\rightarrow 0^+} {\Upsilon }_{\delta ,M}(c)= + \infty \qquad \text {and}\qquad \lim _{c\rightarrow 0^+} {\Psi }_{\delta ,\epsilon ,M,i}(c)= + \infty \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

As the proof of this lemma is purely technical it has been relegated to Appendix B.

3.2 A priori estimates

In this section, we intend to establish uniform a priori estimates on the concentration and the potential, in order to prove the existence of solutions that satisfies the properties of Theorem 2.1.

We assume that we dispose of $({\varvec{C}}^n,{\varvec{\Phi }}^n)_{n\in \mathbf{[}\mathbf{[}0,N_\text {max}\mathbf{]}\mathbf{]}}$ solution of (2.1), (2.4), (2.5) supplemented with either (C) or (S) in $\overline{\mathcal {A}}^\mathcal {T}\times \mathbb R^\mathcal {T}$. Where $\overline{\mathcal {A}}$, the adherence of $\mathcal {A}$ is the set of non-negative concentrations $c_0,...c_N$ satisfying the volume filling constraint. The first a priori estimate is the conservation of mass (2.9):

Lemma 3.3

For all n in $\mathbf{[}\mathbf{[}0,N_\text {max}\mathbf{]}\mathbf{]}$, i in $\mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}$ we have:

$$\begin{aligned} \sum _{K\in \mathcal {T}} m_K c_{K,i}^n=\int _{\text{\O}mega }c_i^0(x)\mathrm{d}x. \end{aligned}$$

The proof is straightforward and classical thanks to the local conservativity of the fluxes, the no flux boundary conditions, and the discretization choice for ${\varvec{C}}^0$.

We can also build a discrete equivalent to Theorem 1.1 using $E_\mathcal {T}$ defined in (2.7) and the dissipation function $\mathcal {D}_i$. This is the purpose of the following proposition:

Proposition 3.1

For all n in $\mathbf{[}\mathbf{[}0,N_\text {max}\mathbf{]}\mathbf{]}$, we have

$$\begin{aligned} E_\mathcal {T}({\varvec{C}}^{n},{\varvec{\Phi }}^{n}) - E_\mathcal {T}({\varvec{C}}^{n-1},{\varvec{\Phi }}^{n-1})\le -{\Delta t}_n\sum _i D_i\sum _{\sigma =K|L \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {D}_i(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n). \end{aligned}$$

(3.7)

Remark 3.1

Thanks to (2.5) and the definition of $\mathcal {D}_i$, (3.7) and (2.8) are equivalents.

Proof

The proof is fairly classical once noticed that thanks to Lemma A.1, H is convex (thus $E_\mathcal {T}$ too). The inequality $f(a)-f(b)\le f'(a)(a-b)$ yields:

$$\begin{aligned}&E_\mathcal {T}({\varvec{C}}^{n},{\varvec{\Phi }}^{n}) - E_\mathcal {T}({\varvec{C}}^{n-1},{\varvec{\Phi }}^{n-1})\le \sum _{K\in \mathcal {T}}\sum _{i=1}^N m_K (c_{K,i}^n - c_{K,i}^{n-1})h_i(C_K^n)\nonumber \\&\quad +\lambda ^2\sum _{\sigma \in \mathcal {E}}\tau _\sigma D_{K\sigma } {\varvec{\Phi }}^nD_{K\sigma } ({\varvec{\Phi }}^n-{\varvec{\Phi }}^{n-1})-\lambda ^2\sum _{K\in \mathcal {T}}\sum _{\sigma \in \mathcal {E}^D\cap \mathcal {E}_K}\tau _\sigma \Phi _\sigma ^D D_{K\sigma }( {\varvec{\Phi }}^n- {\varvec{\Phi }}^{n-1}).\nonumber \\ \end{aligned}$$

(3.8)

Notice that the left-hand side is the term of interest, we will then focus on the reformulation of the right-hand side. We multiply Eq. (2.4b) by $h_i(C_K)+z_i\Phi _K$ and we sum over the cells and species in order to get the following three-terms formula:

$$\begin{aligned}&\underbrace{\sum _{K\in \mathcal {T}}\sum _{i=1}^N m_K \frac{c_{K,i}^n - c_{K,i}^{n-1}}{{\Delta t}_n}h_i(C_K^n)}_{T_\mathrm{chem}} +\underbrace{\sum _{K\in \mathcal {T}} \Phi _K\sum _{i=1}^N m_K z_i\frac{c_{K,i}^n - c_{K,i}^{n-1}}{{\Delta t}_n}}_{T_\mathrm{el}}\nonumber \\&\quad \qquad +\underbrace{\sum _{K\in \mathcal {T}} \sum _{i=1}^N \Biggl (\sum _{\sigma \in \mathcal {E}_K}F_{K\sigma ,i}^n\Biggr )(h_i(C_K)+z_i\Phi _K)}_{T_\mathrm{diss}}=0. \end{aligned}$$

(3.9)

The term concerning the chemical energy, ${\Delta t}_n T_\mathrm{chem}$, appears directly in (3.8), thus we focus on $T_\mathrm{el}$. Using Eq. (2.4a), we have:

$$\begin{aligned} {\Delta t}_n T_\mathrm{el} =\lambda ^2\sum _{\sigma \in \mathcal {E}}\tau _\sigma D_{K\sigma } {\varvec{\Phi }}^nD_{K\sigma } ({\varvec{\Phi }}^n-{\varvec{\Phi }}^{n-1})-\lambda ^2\sum _{K\in \mathcal {T}}\sum _{\sigma \in \mathcal {E}^D\cap \mathcal {E}_K}\tau _\sigma \Phi _\sigma ^D D_{K\sigma }( {\varvec{\Phi }}^n- {\varvec{\Phi }}^{n-1}), \end{aligned}$$

(3.10)

which is the second line of Eq. (3.8). For $T_\mathrm{diss}$, a discrete integration by parts (summation by parts) yields:

$$\begin{aligned} T_\mathrm{diss}=-\sum _{i=1}^N \sum _{\sigma \in \mathcal {E}}F_{K\sigma ,i}^n D_{K\sigma }(h_i({\varvec{C}})+z_i{\varvec{\Phi }}). \end{aligned}$$

Using this equation and equations (3.10), (3.9) in (3.8), we have (2.8):

$$\begin{aligned} E_\mathcal {T}({\varvec{C}}^{n},{\varvec{\Phi }}^{n}) - E_\mathcal {T}({\varvec{C}}^{n-1},{\varvec{\Phi }}^{n-1})\le {\Delta t}_n \sum _{i=1}^N \sum _{\sigma \in \mathcal {E}}F_{K\sigma ,i}^n D_{K\sigma }(h_i({\varvec{C}}^n)+z_i{\varvec{\Phi }}^n), \end{aligned}$$

which concludes the proof thanks to the preliminary remark.$\square$

In the following lemma, we will show several bounds on the potential ${\varvec{\Phi }}$ and then take advantage of them to get a bound on the free energy dissipation:

Lemma 3.4

There exist $M_\Phi$ depending only on $\lambda ,\Phi ^D, \text{\O}mega , \frac{1}{v_0}, (k_1,\dots ,k_N), (z_1,\dots ,z_N)$, and another constant $M_*$ depending also on $\zeta _\mathcal {T}$ such that:

$$\begin{aligned}&\Vert {\varvec{\Phi }}^n\Vert _\infty \le M_\Phi , \qquad \forall 1\le n \le N_\text {max}, \end{aligned}$$

(3.11)

$$\begin{aligned}&\sum _{\sigma \in \mathcal {E}} \tau _\sigma |D_\sigma {\varvec{\Phi }}^n|^2 \le M_*, \qquad \forall 1\le n \le N_\text {max}, \end{aligned}$$

(3.12)

$$\begin{aligned}&\left| \sum _{K\in \mathcal {T}}\sum _{\sigma \in \mathcal {E}^D\cap \mathcal {E}_K} \tau _\sigma \Phi _{\sigma }^D D_{K\sigma } {\varvec{\Phi }}^n\right| \le M_*, \qquad \forall 1\le n \le N_\text {max}, \end{aligned}$$

(3.13)

$$\begin{aligned}&\sum _{n=1}^{N_\text {max}}{\Delta t}_n\sum _{i=1}^N D_i\sum _{\sigma =K|L \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {D}_i(C_K^n,C_L^n,\Phi _{K}^n,\Phi _L^n) \le M_*. \end{aligned}$$

(3.14)

Proof

The proof of (3.11) is a straightforward application of [9,  Proposition A.1]. As the proof of (3.12) is detailed in [9,  Lemma 3.6], we focus on the proof of (3.13), assuming (3.12).

Multiplying Eq. (2.4a) by $\Phi _{K}^n$ and summing over $K\in \mathcal {T}$ yields, using (2.3):

$$\begin{aligned} \sum _{\sigma \in \mathcal {E}}\tau _\sigma \left( D_{\sigma }{\varvec{\Phi }}^n\right) ^2 -\sum _{\sigma \in \mathcal {E}^D}\tau _\sigma \Phi _{\sigma }^D D_{K\sigma }{\varvec{\Phi }}^n = \sum _{K\in \mathcal {T}}\Phi _{K}^n m_K \sum _{i=1}^N z_i c_{K,i}^n. \end{aligned}$$

Using Eq. (3.12), (3.11), and ${\varvec{C}}^n\in \overline{\mathcal {A}}^\mathcal {T}$, we have the desired result. The last result is based on (3.7). Summing that equation, we have:

$$\begin{aligned} \sum _{n=1}^{N_\text {max}}{\Delta t}_n\sum _{i=1}^N D_i\sum _{\sigma =K|L \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {D}_i(C_K^n,C_L^n,\Phi _{K}^n,\Phi _L^n)\le E_\mathcal {T}({\varvec{C}}^{0},{\varvec{\Phi }}^{0}) - E_\mathcal {T}({\varvec{C}}^{N_\text {max}},{\varvec{\Phi }}^{N_\text {max}}) \end{aligned}$$

(3.15)

We have thanks to Eqs. (1.10), (3.12), and (3.13):

$$\begin{aligned} E_\mathcal {T}({\varvec{C}}^{N_\text {max}},{\varvec{\Phi }}^{N_\text {max}})\ge -|\text{\O}mega |\frac{\log (N+1)}{v_0\min k_i}-\lambda ^2 M_*\qquad \text {and}\qquad E_\mathcal {T}({\varvec{C}}^{0},{\varvec{\Phi }}^{0})\le \frac{3}{2}\lambda ^2 M_*, \end{aligned}$$

so that (3.15) becomes:

$$\begin{aligned} \sum _{n=1}^{N_\text {max}}{\Delta t}_n\sum _{i=1}^N D_i\sum _{\sigma =K|L \in \mathcal {E}_\text {int}}-\tau _\sigma \mathcal {D}_i(C_K^n,C_L^n,\Phi _{K}^n,\Phi _L^n)\le \frac{5}{2}\lambda ^2 M_*+|\text{\O}mega |\frac{\log (N+1)}{v_0\min k_i}. \end{aligned}$$

Hence the desired result, up to the choice of a bigger constant $M_*$.$\square$

Finally, we use the free energy dissipation result (3.14), and the estimates on the free energy dissipation functional to improve the assumption ${\varvec{C}}^n\in \overline{\mathcal {A}}^\mathcal {T}$.

Lemma 3.5

There exist $\epsilon _0,\epsilon _1,...,\epsilon _N$ positive, depending on, among other things, $C^0$ and decreasing with $\min {\varvec{\Delta t}}$ and $\min _{\sigma \in \mathcal {E}}\tau _{\sigma }$ such that:

$$\begin{aligned} c_{K,i}^n\ge \epsilon _ i \qquad \forall K\in \mathcal {T},n\in \mathbf{[}\mathbf{[}1,N_\text {max}\mathbf{]}\mathbf{]},i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}\end{aligned}$$

Proof

The proof follows the idea of [14,  Lemma 3.10] (see also [15,  Lemma 3.7], [9,  Lemma 3.7]). We start with the proof for $i=0$ and a fixed time step n using $\Upsilon _{\delta ,M_\Phi }$, then treat the case of $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ using $\Psi _{\delta ,\epsilon _0,M_\Phi ,i}$ and finally notice that no assumptions were made on n.

Thanks to assumption (1.8) on the initial concentrations, and Lemma 3.3, we dispose of $K\in \mathcal {T}$ such that:

$$\begin{aligned} c_{K,0}^n\ge \frac{1}{|\text{\O}mega |}\int _\text{\O}mega c_0^0 \mathrm{d}x =:\delta _0 > 0 \end{aligned}$$

We let $\delta _1=\Upsilon _{\delta _0,M_\Phi }^{-1}(\frac{M_*}{\min {\varvec{\Delta t}}\min _{i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}}D_i\min _{\sigma \in \mathcal {E}}\tau _{\sigma }})$ where $M_*$ is as in Lemma 3.4. It is well defined thanks to the monotony of $\Upsilon$ and Lemma 3.2. Moreover, we have for every cell L sharing an edge with K:

$$\begin{aligned} c_{L,0}^n\ge \delta _1 > 0, \end{aligned}$$

thanks to the positivity of $\mathcal {D}_i$ and Eq. (3.14). Similarly we recursively define:

$$\begin{aligned} \delta _{l+1}=\Upsilon _{\delta _l,M_\Phi }^{-1}\left( \frac{M_*}{\min {\varvec{\Delta t}}\min _{i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}}D_i\min _{\sigma \in \mathcal {E}}\tau _{\sigma }}\right) \qquad \forall l\in \mathbb N^*, \end{aligned}$$

(3.16)

and notice that thanks to the connectivity of $\text{\O}mega$ there exist $l\le {\text {card}}(\mathcal {T})$ such that, for all $L \in \mathcal {T}$:

$$\begin{aligned} c_{L,0}^n\ge \delta _{l}. \end{aligned}$$

Hence a possible choice for $\epsilon _0$. As explained above, the proof is exactly the same for $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$, with the use of $\Psi _{\delta ,\epsilon _0,M_\Phi ,i}$ instead of $\Upsilon _{\delta ,M_\Phi }$ in Eq. (3.16) and again does not depend on the time step $n\ge 1$.$\square$

3.3 Existence of solutions

Using the estimates of the previous section we can establish the existence of a solution to our numerical scheme. Thanks to Proposition 3.1 and Lemmas 3.3 and 3.5, this will conclude the proof of Theorem 2.1.

Proposition 3.2

Let ${\varvec{C}}^0$ be defined by (2.1). Then, for all $1\le n\le N_T$, the nonlinear system of equations (2.4), (2.5) supplemented with either (C) or (S) has a solution $({\varvec{C}}^{n}, {\varvec{\Phi }}^{n})\in \mathcal {A}^{\mathcal {T}} \times \mathbb {R}^{\mathcal {T}}$.

Proof

As in [9,  Proposition 3.8], we use induction and a topological degree argument to transform continuously the non-linear system (2.4), (2.5) to a linear one. However, the path presented in [9] is no longer valid as we do not have a monotony property on $h_i$. The homotopy follows 3 steps. The first one is sketched in “Appendix C”, the second one changes the discretization while maintaining $k_i,D_i$ to 1 and the potential to zero. The last step corresponds to the activation of the potential and the remaining nonlinearities.

Following these ideas, we follow the zeros of a homotopy $\mathcal {H}^\alpha$ for $\alpha \in [0,3]$:

$$\begin{aligned} \mathcal {H}^\alpha : {\left\{ \begin{array}{ll} \mathcal {A}^\mathcal {T}\times \mathbb {R}^\mathcal {T}\rightarrow (\mathbb {R}^{N})^\mathcal {T}\times \mathbb {R}^\mathcal {T}\\ ({\varvec{C}}, {\varvec{\Phi }}) \mapsto \mathcal {H}^\alpha ({\varvec{C}},{\varvec{\Phi }}), \end{array}\right. } \end{aligned}$$

which is a standard finite volume scheme for the heat equation for $\alpha =0$, and our scheme for $\alpha =3$. Thanks to (2.4c), for every $\alpha$, ${\varvec{c}}_0$ is eliminated, and proving ${\varvec{c}}_0\dots {\varvec{c}}_N >0$ allows to conclude that uniformly in $\alpha$, ${\varvec{c}}_i<\frac{1}{v_i}$.$\square$

Step 1: implementation of the solvent effects using an ad hoc scheme. For $\alpha \in [0,1]$, $\mathcal {H}^\alpha =0$ means that for all $K\in \mathcal {T}$, $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$:

$$\begin{aligned}&\frac{c_{K,i}-c_{K,i}^{n-1}}{{\Delta t}_n}m_K+\sum _{\sigma =K|L\in \mathcal {E}_\text {int}}\tau _{\sigma }\frac{c_{K,i}-c_{L,i}}{\log (c_{K,i}/c_{L,i})}\Bigl ( \log (c_{L,i}/c_{K,i})+\alpha \bigl (\log (c_{K,0}/c_{L,0})\bigr )\Bigr )=0,\\&\quad -\lambda ^2\sum _{\sigma \in \mathcal {E}_K}\tau _\sigma D_{K\sigma }{\varvec{\Phi }}=0, \end{aligned}$$

where $\Phi ^D_\alpha$ is set to zero. As expressed in Lemma C.1 we dispose of $\epsilon _1$ such that the zeros of $\mathcal {H}^\alpha$ have a concentration that is bounded away from zero by $\epsilon _1$.

Step 2: change of scheme without potential and for identical species. We change the discretization of $c_i\nabla \log (c_i/c_0)$. For $\alpha \in [1,2]$, $\mathcal {H}^\alpha =0$ writes:

$$\begin{aligned}&\frac{c_{K,i}-c_{K,i}^{n-1}}{{\Delta t}_n}m_K+(2-\alpha )\sum _{\sigma =K|L\in \mathcal {E}_{K,\text {int}}}\tau _{\sigma }\frac{c_{K,i}-c_{L,i}}{\log (c_{K,i}/c_{L,i})}\\&\quad \Bigl ( \log (c_{L,i})-\log (c_{K,i})+\bigl (\log (c_{K,0})-\log (c_{L,0})\bigr )\Bigr )\\&\quad +(\alpha -1)\sum _{\sigma =K|L\in \mathcal {E}_{K,\text {int}}}\tau _{\sigma }\mathcal {F}_i(C_K,C_L,0,0)=0,\\&\quad -\lambda ^2\sum _{\sigma \in \mathcal {E}_K}\tau _\sigma D_{K\sigma }{\varvec{\Phi }}=0 \end{aligned}$$

where $k_{i,\alpha }$ is set to 1 and $\Phi ^D_\alpha$ is again set to zero. Here again we dispose of $\epsilon _2$ such that the zeros of $\mathcal {H}^\alpha$ have a concentration that is bounded away from zero by $\epsilon _2$.

Step 3: activation of the potential and the difference between the species. For $\alpha \in [2,3]$, $\mathcal {H}^\alpha =0$ means:

$$\begin{aligned}&\frac{c_{K,i}-c_{K,i}^{n-1}}{{\Delta t}_n}m_K+\bigl (3-\alpha +(\alpha -2)D_i \bigr )\\&\quad \sum _{\sigma =K|L\in \mathcal {E}_{K,\text {int}}}\tau _{\sigma }\mathcal {F}_i(C_K,C_L,(\alpha -2)\Phi _{K},(\alpha -2)\Phi _{L})=0\\&\quad -\lambda ^2\sum _{\sigma \in \mathcal {E}_K}\tau _\sigma D_{K\sigma }{\varvec{\Phi }}=m_K\sum _{i=1}^N (\alpha -2)z_ic_i, \end{aligned}$$

where $\Phi ^D_\alpha$ is set to $(\alpha -2)\Phi _D$ and $k_{i,\alpha }$ to $3-\alpha +(\alpha -2)k_i$. Thanks to Lemma 3.5, we dispose of $\epsilon _3$ such that the zeros of $\mathcal {H}^\alpha$ have a concentration that is bounded away from zero by $\epsilon _3$.

Conclusion. Using a topological degree argument [20, 39], we can derive the existence of a solution for $\mathcal {H}^\alpha =0$ for $\alpha =3$. A detailed development of this argument applied to a finite volume scheme for a scalar nonlinear convection-diffusion problem can be found in [26], proof of Lemma 4.1. It is straightforward to state the existence of a solution for $\mathcal {H}^0=0$—the classical finite volume scheme for the heat equation. This leads to a nonzero toplogical degree of $\mathcal {H}^0$. We have shown uniform bounds on the concentrations from below by $\min (\epsilon _1,\epsilon _2,\epsilon _3)$ and above by $\frac{1}{v_i}$ and the potential: $\pm M_\Phi$. Continuity of $\mathcal {H}^\alpha$ and the homotopy invariance of the topological degree yield a nonzero topologial degree of $\mathcal {H}^3$ and thus the existence of a solution for $\mathcal {H}^3=0$.

Remark 3.2

Concerning uniqueness of solutions, we think that, given the corresponding results for semiconductors found e.g. in [34, 36], it is worth to investigate uniqueness for the thermodynamic equilibrium, and for small times/applied voltages around thermodynamic equilibrium.

4 Convergence

In this section we prove Theorem 2.2, which states the convergence of our schemes towards a weak solution. We consider a sequence $\left( \mathcal {T}_m, \mathcal {E}_m, \left( x_K\right) _{K\in \mathcal {T}_m}\right) _{m\ge 1}$ of admissible meshes with $h_{\mathcal {T}_m}, h_{{\varvec{\Delta t}}_m}$ tending to 0 as m tends to $+\infty$, while the regularity $\zeta _{\mathcal {T}_m}$ remains uniformly bounded from below by a positive constant $\zeta ^\star$.

Thanks to Theorem 2.1, we have a family of discrete solutions $\left( {\varvec{C}}_m, {\varvec{\Phi }}_m\right) _m$. We will first propose different reconstructions of approximate solutions in Sect. 4.1, then we show several compactness properties in Sect. 4.2 in order to obtain the convergence of a subsequence of approximated solutions. Section 4.3 is then devoted to the identification of the limit as a weak solution.

To enlighten the notations, we will remove the subscript m as soon as it is not necessary for understanding.

4.1 Reconstruction operators

In order to carry out the analysis of convergence, we introduce some reconstruction operators following the methodology proposed in [25].

The operators $\pi _\mathcal {T}: \mathbb {R}^\mathcal {T}\rightarrow L^\infty (\text{\O}mega )$ and $\pi _{\mathcal {T},{\varvec{\Delta t}}}:\mathbb {R}^{\mathcal {T}\times N_T}\rightarrow L^\infty ((0,T)\times \text{\O}mega )$ are defined respectively by

$$\begin{aligned} \pi _\mathcal {T}{\varvec{u}}(x) = u_K \quad \text {if}\; x \in K, \qquad \forall {\varvec{u}}= \left( u_K\right) _{K\in \mathcal {T}}, \end{aligned}$$

and

$$\begin{aligned} \pi _{\mathcal {T},{\varvec{\Delta t}}}{\varvec{u}}(t,x) = u_K^n \quad \text {if}\; (t,x) \in (t_{n-1},t_n] \times K, \qquad \forall {\varvec{u}}= \left( u_K^n\right) _{K\in \mathcal {T}, 1 \le n \le N_T}. \end{aligned}$$

These operators allow passing from the discrete solution ${({\varvec{C}}^n, {\varvec{\Phi }}^n)}_{1 \le n \le N_T}$ to the approximate solution since

$$\begin{aligned} \Phi _{\mathcal {T},{\varvec{\Delta t}}} = \pi _{\mathcal {T},{\varvec{\Delta t}}} \left( {\varvec{\Phi }}\right) ,\qquad c_{i,\mathcal {T},{\varvec{\Delta t}}} = \pi _{\mathcal {T},{\varvec{\Delta t}}} \left( {\varvec{c}}_i\right) ,\qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

To carry out the analysis, we further need to introduce an approximate gradient reconstruction. Since the boundary conditions play a crucial role in the definition of the gradient, we need to enrich the discrete solution by face values $\left( C_\sigma ^n\right) _{\sigma \in \mathcal {E}_\text {ext}, 1\le n \le N}$ and $\left( \Phi _\sigma ^n\right) _{\sigma \in \mathcal {E}_\text {ext}, 1\le n \le N}$ defined by $C_\sigma ^n = C_{K\sigma }^n$ and $\Phi _\sigma ^n = \Phi _{K\sigma }^n$ for $\sigma \in \mathcal {E}_\text {ext}\cap \mathcal {E}_{K}$. With a slight abuse of notations, we still denote by ${\varvec{C}}^n = \left( (C_K^n)_{K\in \mathcal {T}},(C_\sigma ^n)_{\sigma \in \mathcal {E}_\text {ext}}\right)$ and ${\varvec{\Phi }}^n = \left( (\Phi _K^n)_{K\in \mathcal {T}},(\Phi _\sigma ^n)_{\sigma \in \mathcal {E}_\text {ext}}\right)$ the elements of $\mathcal {A}^{\mathcal {T}\cup \mathcal {E}_\text {ext}}$ and $\mathbb {R}^{\mathcal {T}\cup \mathcal {E}_\text {ext}}$ containing both the cell values and the exterior faces values of the concentration and the potential respectively.

For $\sigma = K|L \in \mathcal {E}_\text {int}$, we denote by $\Delta _\sigma$ the diamond cell corresponding to $\sigma$, that is the interior of the convex hull of $\sigma \cup \{x_K, x_L\}$. For $\sigma \in \mathcal {E}_\text {ext}$, the diamond cell $\Delta _\sigma$ is defined as the interior of the convex hull of $\sigma \cup \{x_K\}$. The approximate gradient $\nabla _{\mathcal {T}}: \mathbb {R}^{\mathcal {T}\cup \mathcal {E}_\text {ext}} \rightarrow L^2(\text{\O}mega )^d$ is piecewise constant on the diamond cells $\Delta _\sigma$, and it is defined as follows:

$$\begin{aligned} \nabla _{\mathcal {T}} {\varvec{u}}(x) = d \frac{D_{K\sigma } {\varvec{u}}}{d_\sigma } \varvec{n}_{K\sigma } \quad \text {if}\; x \in \Delta _\sigma , \qquad \forall {\varvec{u}}\in \mathbb {R}^{\mathcal {T}\cup \mathcal {E}_\text {ext}}. \end{aligned}$$

We also define $\nabla _{\mathcal {T},{\varvec{\Delta t}}}: \mathbb {R}^{(\mathcal {T}\cup \mathcal {E}_\text {ext})\times N_T} \rightarrow L^2(Q_T)^d$ by setting

$$\begin{aligned} \nabla _{\mathcal {T},{\varvec{\Delta t}}}{\varvec{u}}(t,\cdot ) = \nabla _\mathcal {T}{\varvec{u}}^n \quad \text {if}\; t\in (t_{n-1},t_n], \qquad \forall {\varvec{u}}= \left( {\varvec{u}}^n\right) _{1\le n\le N_T} \in \mathbb {R}^{(\mathcal {T}\cup \mathcal {E}_\text {ext})\times N_T}. \end{aligned}$$

This reconstruction is merely weakly consistent (unless $d=1$) and takes its source in [17, 27]. More consistent reconstruction operators will be introduced in Sect. 4.3. Let us recall now some key properties to be used in the analysis. First, for all ${\varvec{u}}, {\varvec{v}}\in \mathbb {R}^{\mathcal {T}\cup \mathcal {E}_\text {ext}}$,

$$\begin{aligned} \sum _{\sigma \in \mathcal {E}}\tau _\sigma D_{K\sigma } {\varvec{u}}D_{K\sigma } {\varvec{v}}= \frac{1}{d} \int _\text{\O}mega \nabla _{\mathcal {T}} {\varvec{u}}\cdot \nabla _{\mathcal {T}} {\varvec{v}}\mathrm{d}x. \end{aligned}$$

This implies in particular that

$$\begin{aligned} \sum _{\sigma \in \mathcal {E}}\tau _\sigma |D_\sigma {\varvec{u}}|^2 = \frac{1}{d}\int _{\text{\O}mega } |\nabla _{\mathcal {T}} {\varvec{u}}|^2 \mathrm{d}x, \qquad \forall {\varvec{u}}\in \mathbb {R}^{\mathcal {T}\cup \mathcal {E}_\text {ext}}. \end{aligned}$$

(4.1)

With slight abuse of notations, we extend the reconstructions operator presented above to the vectors of concentrations in $\mathcal {A}^\mathcal {T},\mathcal {A}^{\mathcal {T}\times N_T}$, etc.

4.2 Compactness

In this section we intend to prove a discrete $H^1$ estimate on the concentrations using the bound on the free-energy dissipation (3.14). To that extend we will introduce a chemical dissipation $\mathcal {D}_\text {chem}$ as a discrete equivalent to $\sum c_i|\nabla h_i(c)|^2$ and compare it both with the usual distance and the total dissipation $\mathcal {D}$.

As the identification of the limit is only possible for

$$\begin{aligned}\inf _{\begin{array}{c} \text {mesh }m\\ n\in \mathbf{[}\mathbf{[}1,N_{T,m}\mathbf{]}\mathbf{]}\\ K\in \mathcal {T}_m \end{array}} c_{m,K,0}^n>\epsilon >0,\end{aligned}$$

the results of this section are proved under this assumption and complemented with remarks indicating whether the hypothesis is necessary or not. In order to apply chain rules for the convergence, we need to change the face concentration $\mathcal {C}$ from the one defined by the numerical scheme through Lemma 3.1 to the logarithmic average:

$$\begin{aligned} {\widetilde{\mathcal {C}}}_i(C_K,C_{L})= \frac{c_{K,i}-c_{L,i}}{\log (c_{K,i})-\log (c_{L,i})} \qquad \forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(4.2)

This choice of edge concentration will also be used in the definition of $\mathcal {D}_\text {chem}$ to avoid a dependency on the potential. The following lemma provides an estimate the numerical-flux based averages using this logarithmic average.

Lemma 4.1

For all $\epsilon >0$ there exists $\alpha _\epsilon >0$ depending only on $\epsilon ,M_\Phi$ such that, for all $(C_K,C_{L},\Phi _K,\Phi _{L}) \in \mathcal {A}\times \mathcal {A}\times [-M_\Phi ,M_\Phi ] \times [-M_\Phi ,M_\Phi ]$, and for all $i\in \mathbf{[}\mathbf{[}1, N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} c_{K,0},c_{L,0}>\epsilon \implies \alpha _\epsilon {\widetilde{\mathcal {C}}}_i(C_K,C_{L})\le \mathcal {C}_i(C_K,C_L,\Phi _K,\Phi _L). \end{aligned}$$

(4.3)

Proof

For the centered scheme, this inequality is known with $\alpha _\epsilon =1$ without assumption on $c_0$ [42]. For the Sedan scheme the proof is more intricate and uses the hypothesis on $c_0$. Equation (4.3) is equivalent to the boundedness of

$$\begin{aligned} R_i(C_K,C_{L},\Phi _K,\Phi _{L}):=\frac{{\widetilde{\mathcal {C}_i}}(C_K,C_{L})}{\mathcal {C}_i(C_K,C_{L},\Phi _K,\Phi _{L})}, \end{aligned}$$

for $c_{K,0},c_{L,0}>\epsilon$.

Introduce $x_i=\log \frac{c_{K,i}}{c_{L,i}}$, and $y_i= z_i\Phi _{L} + \nu _i(C_{L}) - z_i\Phi _{K} - \nu _i(C_{K})$ as in the proof of lemma 3.1. By symmetry, one can assume $x_i\ge 0$ and thanks to our assumption on the solvent and the potential, $y_i$ is bounded by some K. Moreover, we notice that by definition of $x_i$, (3.4) yields:

$$\begin{aligned} \mathcal {F}_i (C_K,C_L,\Phi _K,\Phi _L)=c_{L,i}\bigl (B(y_i)e^{x_i}-B(-y_i)\bigr ), \end{aligned}$$

so that we have:

$$\begin{aligned} R_i(C_K,C_{L},\Phi _K,\Phi _{L})=\frac{e^{x_i}-1}{x_i}\frac{x_i-y_i}{B(y_i)e^{x_i}-B(-y_i)}. \end{aligned}$$

The right-hand side can be seen as a continuous function of $x_i,y_i$. It is bounded on the boundary of its definition domain $[0,+\infty )\times [-K,K]$ and admits a finite limit $\frac{1}{B(\mu )}$ for $x_i\rightarrow \infty , y_i\rightarrow \mu$, thus $R_i$ is bounded.$\square$

Remark 2 This result does not hold for $\epsilon =0$. In that case, we have to introduce:

$$\begin{aligned} \widehat{\mathcal {C}}_i(C_K,C_L)=\inf _{(\Phi _{K},\Phi _{L})\in [-M_\Phi ,M_\Phi ]^2}\mathcal {C}_i(C_K,C_L,\Phi _{K},\Phi _{L}), \end{aligned}$$

for which this lemma is trivially true with $\alpha =1$. That third edge reconstruction should be used in the following definition.

Then we try to take advantage of Proposition 3.1. As Lemma 3.4 already provides satisfying estimates on ${\varvec{\Phi }}$, we introduce

$$\begin{aligned} \mathcal {D}_\mathrm{chem,i}(C_K,C_L):\begin{array}{lcl} \mathcal {A}^2&{}\rightarrow &{}\mathbb R\\ (C_K,C_L)&{}\mapsto &{}\displaystyle {\widetilde{\mathcal {C}}}_i(C_K,C_{L}) (h_i(C_K)-h_i(C_L))^2, \end{array} \end{aligned}$$

and

$$\begin{aligned} \mathcal {D}_\mathrm{chem}=\sum _{i=1}^{N}\mathcal {D}_\mathrm{chem,i}. \end{aligned}$$

A first interesting result is that $\mathcal {D}_\mathrm{chem}$ is a semimetric on $\mathcal {A}$. The non-negativity and symmetry properties are trivially satisfied, the last property is the subject of the following lemma.

Lemma 4.2

We have $\mathcal {D}_\mathrm{chem}(C_K,C_L)=0$ if and only if $C_K=C_L$

Proof

If $C_K=C_L$, we obviously have $\mathcal {D}_\mathrm{chem}(C_K,C_L)=0$, we will then focus on the other implication. Assume that we dispose of $C_K, C_L$ in $\mathcal {A}$ such that $\mathcal {D}_\mathrm{chem}(C_K,C_L)=0$. We let for $i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} a_{K,i}=\log \frac{c_{K,i}}{\overline{c}_K}\qquad a_{L,i}=\log \frac{c_{L,i}}{\overline{c}_L}, \end{aligned}$$

(4.4)

such that $h_i(C_K)=a_{K,i}-k_ia_{K,0}$. We have ${\widetilde{\mathcal {C}}}_i(C_K,C_{L})\ge \min (c_{K,i},c_{L,i})>0$, thus $\mathcal {D}_\mathrm{chem}$ is the sum of non-negative terms. As we have $\mathcal {D}_\mathrm{chem}(C_K,C_L)=0$, we have:

$$\begin{aligned} a_{K,i}-k_ia_{K,0}=a_{L,i}-k_ia_{L,0} \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

Assume that $a_{K,0}=a_{L,0}$, then $A_K=A_L$, where $A=(a_0,...,a_N)$. Using $\sum _{i=0}^{N}k_i e^{a_i}=\frac{1}{v_0\overline{c}}$, $A_K=A_L$ implies $C_K=C_L$.

The other case is absurd: using the symmetry of $\mathcal {D}_\mathrm{chem}$, one can freely assume that $a_{K,0}>a_{L,0}$. Using $k_i>0$, we have $a_{K,i}>a_{L,i} \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ hence:

$$\begin{aligned} 1=\sum _{i=0}^{N}e^{a_{K,i}}>\sum _{i=0}^{N}e^{a_{L,i}}=1. \end{aligned}$$

$\square$

The function $\mathcal {D}_\mathrm{chem}$ cannot be extended by continuity onto $\overline{\mathcal {A}}^2$. Some information for near zero concentrations can be inferred from lemma 3.2. The following sequential result means that the semi-metric property is preserved near the boundary $\partial \mathcal {A}^2$.

Lemma 4.3

Let $(C_K^l,C_L^l)$ be a sequence of $\mathcal {A}^2$. If $\mathcal {D}_\mathrm{chem}(C_K^l,C_L^l)\rightarrow 0$ then $C_K^l-C_L^l\rightarrow 0$.

Proof

For the sake of simplicity, as this result will only be used with a lower bound on $c_0$, we keep the proof to this simpler case and assume that $\inf (c_{K,0}^l,c_{L,0}^l)>0$. To prove the limit, we will show that from any sub-sequence, we can extract a sub-sub-sequence such that $C_K^l-C_L^l\rightarrow 0$. Considering any sub-sequence, thanks to the boundedness of $\mathcal {A}$ we can extract a sub-sub-sequence such that $C_K^l$ and $C_L^l$ converge. If we dispose of $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ such that $c_{K,i}^l\rightarrow c^*>0$ while $c_{L,i}^l\rightarrow 0$ (or the symmetric situation), then we have:

(4.5)

so that , which is absurd. Necessary, we have $c_{L,i}^l\rightarrow 0$ if and only of $c_{K,i}^l\rightarrow 0$. If $\lbrace i\vert \inf _l(c_{L,i}^l)>0\rbrace$ is empty we have the desired result. Else, we use $\mathcal {D}_\mathrm{chem,i}(C_K^l,C_L^l)\rightarrow 0$, to get:

$$\begin{aligned} a_{K,i}^l-k_ia_{K,0}^l=a_{L,i}^l-k_ia_{L,0}^l+o(1) \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, \inf _l(c_{L,i}^l)>0, \end{aligned}$$

where $a_{K,i},a_{L,i}$ are defined by (4.4). As both $c_{K,i}^l$ and $c_{L,i}^l$ are bounded away from zero, $a_{K,i}^l$ and $a_{L,i}^l$ are convergent up to a subsequence. Using our assumption on $c_0$, we have the convergence of $a_{K,0}^l$ and $a_{L,0}^l$ up to yet another subsequence. Then we conclude using the proof of previous lemma.$\square$

Remark 3 The main simplification brought by the restriction to the setting $c_0>\epsilon$ is the use of ${\widetilde{\mathcal {C}}}_i$ in (4.5). The end of the proof can be adapted by considering the behaviour of $a_{K,0}^l-a_{L,0}^l$.

This semi-metric is however not commonly used and the following lemma intends to compare it with the usual distance.

Proposition 4.1

For all $i \in \mathbf{[}\mathbf{[}0, N\mathbf{]}\mathbf{]}$, there exist M such that:

$$\begin{aligned} \frac{\left( c_{K,i}-c_{L,i}\right) ^2}{\mathcal {D}_\mathrm{chem}(C_K,C_L)}\le M, \qquad \forall \;C_K,C_L \in \mathcal {A}^2. \end{aligned}$$

(4.6)

Proof

We will prove the result for $i \in \mathbf{[}\mathbf{[}1, N\mathbf{]}\mathbf{]}$ using reductio ad absurdum and case exhaustion.

Let $(C_K^n,C_L^n)\in (\mathcal {A}^2)^\mathbb N$ be such that $\frac{\left( c_{K,i}^n-c_{L,i}^n\right) ^2}{\mathcal {D}_\mathrm{chem}(C_K^n,C_L^n)}\rightarrow \infty$ . We let $\epsilon ^n:=C_L^n-C_K^n$ and use the boundedness of $\mathcal {A}$ to extract a convergent sub-sequence of $(C_K^n,\epsilon ^n)$ and denote $(C^*, \epsilon ^*)$ its limit. As $c_i$ is bounded, we have $\mathcal {D}_\mathrm{chem}(C_K^n,C_L^n)\rightarrow 0$. Thanks to Lemma 4.3, we have $\epsilon ^*=0$ so that we will consider first order development in $\epsilon ^n$. We notice that the blow-up of the ratio implies that:

$$\begin{aligned} \mathcal {D}_\mathrm{chem,j}(C_K^n,C_L^n)=o(|\epsilon ^n|^2) \qquad \forall j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(4.7)

For the sake of readability, we will drop from now on the superscript $^n$. We have to consider three cases:

• (1) $c^*_j=0$ implies $\epsilon _j=o(|\epsilon |)$;

• (2) we dispose of species such that $\epsilon _j\ne o(|\epsilon |)$ and $c^*_j=0$, but for all of them $\log \frac{\epsilon _j+c_j}{c_j}$ remains bounded;

• (3) we dispose of a specie such that $\epsilon _j\ne o(|\epsilon |)$, $c^*_j=0$, and up to a subsection, $\log \frac{\epsilon _j+c_j}{c_j}$ blows-up.

$\square$

Preliminary remark about the solvent We consider $j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ such that $c^*_j>0$ and let $\overline{\epsilon }_j=\sum _{i=0}^{N}\epsilon _i$. If such a j cannot be found, then $c_0\rightarrow \frac{1}{v_0}$ and the conclusion (4.8) holds. Else we have, thanks to (4.7):

$$\begin{aligned}&\log \frac{c_j+\epsilon _j}{c_j}=O(|\epsilon |) \qquad \text {and}\qquad \log \frac{\overline{c}_j+\overline{\epsilon }_j}{\overline{c}_j}=O(|\epsilon |) \qquad \text {and}\qquad \\&h_j(C_K)-h_j(C_L)=O(|\epsilon |), \end{aligned}$$

so that:

$$\begin{aligned} \log \frac{c_0+\epsilon _0}{c_0}=O(|\epsilon |), \end{aligned}$$

thus:

$$\begin{aligned} \frac{\epsilon _0}{c_0}=O(|\epsilon |) \qquad \text {and}\qquad \log \frac{c_0+\epsilon _0}{c_0}=\frac{\epsilon _0}{c_0}+o(|\epsilon |). \end{aligned}$$

(4.8)

Conclusion of the proof in case 4.2 The proof of this first case is by far the most intricate of the three. It is done in two step: first we use our hypothesis on $\mathcal {D}_\text {chem}$, c, and $\epsilon$ to obtain a estimate where the species are coupled through an ersatz of $\overline{\epsilon }$ and $\overline{c}$. Then we show an improved version of the Cauchy-Schwarz inequality to improve the estimate into decoupled estimates which are incompatible with our hypothesis 4.2.

First order development of $h_j$ gives:

$$\begin{aligned}&h_j(C_K)-h_j(C_L)=\frac{\epsilon _j}{c_j}-k_j\frac{\epsilon _0}{c_0}+(k_j-1)\frac{\overline{\epsilon }}{\overline{c}}+o(\epsilon ),\\&\qquad \forall j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, c_j^*>0. \end{aligned}$$

Thanks to (4.7) we have the estimation:

$$\begin{aligned}&\frac{\epsilon _j}{c_j}-k_j\frac{\epsilon _0}{c_0}+(k_j-1)\frac{\overline{\epsilon }}{\overline{c}}=o(|\epsilon |),\nonumber \\&\qquad \forall j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, c_j^*>0. \end{aligned}$$

(4.9)

To correct the effect of the species with negligible concentrations, we let:

$$\begin{aligned} {\widetilde{\epsilon _0}}=-\sum _{\begin{array}{c} c_j^*>0\\ j\ne 0 \end{array}}k_j\epsilon _j\qquad {\widetilde{\epsilon }}={\widetilde{\epsilon _0}}+\sum _{\begin{array}{c} c_j^*>0\\ j\ne 0 \end{array}}\epsilon _j \qquad \text {and}\qquad {\widetilde{c}}=\sum _{c_j^*>0}c_j \end{aligned}$$

By construction, we have ${\widetilde{c}}=\overline{c}+o(1)$. Using the hypothesis (4.2) we have ${\widetilde{\epsilon }}=\overline{\epsilon }+o(|\epsilon |)$ and ${\widetilde{\epsilon _0}}=\epsilon _0+o(|\epsilon |)$. These three results and Eq. (4.9) yield:

$$\begin{aligned} \frac{\epsilon _j}{c_j}-k_j\frac{{\widetilde{\epsilon _0}}}{c_0}+(k_j-1)\frac{{\widetilde{\epsilon }}}{{\widetilde{c}}}=o(|\epsilon |),\qquad \forall j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, c_j^*>0. \end{aligned}$$

We let $\xi _j=\frac{\epsilon _j}{c_j}-\frac{{\widetilde{\epsilon }}}{{\widetilde{c}}}$ for $j\ne 0$ and $\xi _0=\frac{{\widetilde{\epsilon _0}}}{c_0}-\frac{{\widetilde{\epsilon }}}{{\widetilde{c}}}$. Previous equation yields:

$$\begin{aligned} \xi _j=k_j\xi _0+o(|\epsilon |), \qquad \forall j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, c_j^*>0. \end{aligned}$$

Considering $\sum _{c_j^*>0}c_j\xi _j$, we have:

$$\begin{aligned} 0={\widetilde{\epsilon }}-{\widetilde{\epsilon }}=\sum _{c_j^*>0}c_j\xi _j=\sum _{c_j^*>0} c_jk_j\xi _0 +o(|\epsilon |)= \xi _0 \left( \frac{1}{v_0}+o(1)\right) +o(|\epsilon |), \end{aligned}$$

so that:

$$\begin{aligned}\xi _0=o(|\epsilon |).\end{aligned}$$

We conclude the first part of the proof with the following estimate that follows from (4.7):

$$\begin{aligned} \sum _{c_j^*>0 \cup \lbrace 0\rbrace }c_j\xi _j^2=o(|\epsilon |^2). \end{aligned}$$

(4.10)

For the sake of readability, we will drop the $\;{\widetilde{ }}\;$ over $\epsilon _0$ in the second part of the proof, introduce $S=\lbrace j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}\vert c_j^*>0\rbrace \cup \lbrace 0\rbrace$, and assume by symmetry that ${\widetilde{\epsilon }}\ge 0$. We have:

$$\begin{aligned} \sum _{j\in S}c_j\xi _j^2=\sum _{j\in S}\frac{\epsilon _j^2}{c_j}-\frac{{\widetilde{\epsilon }}^2}{{\widetilde{c}}}. \end{aligned}$$

(4.11)

Let $x_j=\sqrt{c_j}$, $y_j=\frac{\epsilon _j}{\sqrt{c_j}}$, $X=(x_j)_{j\in S}$ and $Y=(y_j)_{j\in S}$. We have:

$$\begin{aligned} {\widetilde{\epsilon }}=\sum _{j\in S} x_jy_j=\langle X,Y \rangle , \qquad |X|^2={\widetilde{c}}, \qquad |Y|^2=\sum _{j\in S}\frac{\epsilon _j^2}{c_j}, \end{aligned}$$

so that (4.10) becomes:

$$\begin{aligned} |X|^2|Y|^2-\langle X,Y \rangle ^2=o(|\epsilon |^2). \end{aligned}$$

The Cauchy-Schwarz inequality yields

$$\begin{aligned}{\widetilde{\epsilon }}^2\le {\widetilde{c}}\sum _{c_j^*>0}\frac{\epsilon _j^2}{c_j}.\end{aligned}$$

We intend to use ideas presented in [2] to improve the estimation of ${\widetilde{\epsilon }}$. More precisely, the stability version of the Cauchy–Schwarz presented in [1] gives:

$$\begin{aligned} {\widetilde{\epsilon }}=|X||Y|\left( 1-\frac{1}{2}\left| \frac{X}{|X|}-\frac{Y}{|Y|}\right| ^2\right) . \end{aligned}$$

We intend to show that $\left| \frac{X}{|X|}-\frac{Y}{|Y|}\right|$ is bounded away from zero. To show this bound we let:

$$\begin{aligned} K:\begin{array}{ccc} \mathbb R^S\times \mathbb R^S&{}\rightarrow &{}\mathbb R\\ (C,\epsilon )&{}\mapsto &{}\left| \frac{X}{|X|}-\frac{Y}{|Y|}\right| \end{array} \end{aligned}$$

and consider a minimizing sequence of K under the conditions

$$\begin{aligned}c_j>0,\qquad \epsilon _0=-\sum _{\begin{array}{c} j\in S\\ j\ne 0 \end{array}}k_j\epsilon _j.\end{aligned}$$

As K is invariant by scaling, we can assume that we have a convergent minimizing sequence $C_\text {inf}^l,\epsilon _\text {inf}^l$ of limit $C_\text {inf}^*,\epsilon _\text {inf}^*$ and of norm equal to 1. Note that we do not assume $C\in \mathcal {A}$, nor $C_\text {inf}^*>0$ thus we consider broader options than necessary for use in (4.11) to ensure existence of the minimum. Finally, we notice that K is non-negative, thus its infimum is either zero or positive. We will prove the positivity by contradiction.

Assume that the limit of $K(C_\text {inf}^l,\epsilon _\text {inf}^l)$ is zero, we show that $|Y^l_\text {inf}|$ is convergent up to a subsequence. We consider j such that, up to a subsequence, $\frac{|y^l_{\text {inf},j}|}{|Y^l_\text {inf}|}$ is bounded away from zero. If $c_{\text {inf},j}^*\ne 0$, $|y^l_{\text {inf},j}|$ is bounded thus $|Y^l_\text {inf}|$ is too, and up to another subsequence, the latter is convergent. If $c_{\text {inf},j}^*= 0$ we notice that $x_{\text {inf},j}^l \rightarrow 0$ and $|X^l_\text {inf}|$ is bounded away from zero, so that $\frac{|y^l_{\text {inf},j}|}{|Y^l_\text {inf}|} \rightarrow 0$, which is absurd. We let $\gamma$ be the limit of $|Y^l_\text {inf}|^2$.

As we have assumed the infimum to be zero, we have:

$$\begin{aligned} \epsilon _{\text {inf},j}^*=c_{\text {inf},j}^*\frac{\gamma }{{\widetilde{c_\text {inf}^*}}}, \qquad \forall j \in S. \end{aligned}$$

This would imply that $\epsilon _{\text {inf}}^*$ is non-negative, however, we have $\epsilon _{\text {inf},0}^*=-\sum _{j\in S\setminus \lbrace 0\rbrace } k_j\epsilon _{\text {inf},j}^*$ and $\epsilon _\text {inf}^*$ is of norm 1. This is absurd, hence the infimum cannot be zero. Thus we dispose of $0<\alpha$ depending only on $k_1,\dots k_N$ and S such that:

$$\begin{aligned} {\widetilde{\epsilon }}\le |X||Y|\left( 1-\alpha \right) . \end{aligned}$$

As we have assumed (using symmetry) ${\widetilde{\epsilon }}\ge 0$, we also have $\alpha \le 1$. So that we have:

$$\begin{aligned} \sum _{j\in S}\frac{\epsilon _j^2}{c_j}-\frac{{\widetilde{\epsilon }}^2}{{\widetilde{c}}}=|Y|^2-\frac{{\widetilde{\epsilon }}^2}{|X|^2}\ge |Y|^2(1-(1-\alpha )^2)=\sum _{j\in S}\frac{\epsilon _j^2}{c_j}(1-(1-\alpha )^2). \end{aligned}$$

Thanks to Eqs. (4.10) and (4.11), we have:

$$\begin{aligned} \sum _{j\in S}\frac{\epsilon _j^2}{c_j}=o(|\epsilon |^2), \end{aligned}$$

thus, thanks to (4.2), $\epsilon _j=o(|\epsilon |)$ for all $j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$, which is absurd.

Conclusion of the proof in case 4.2 We dispose of j such that $c_j\rightarrow 0$ and $\epsilon _j\ne o(|\epsilon |)$, thus have up to a sub-sequence:

$$\begin{aligned} |\epsilon |=O(\epsilon _j)\qquad \text {and}\qquad \mathcal {D}_\mathrm{chem,j}= {\widetilde{\mathcal {C}}}_{j}\left( \log \frac{c_j+\epsilon _j}{c_j}+O(|\epsilon |)\right) ^2. \end{aligned}$$

The assumed boundedness of $\log \frac{c_j+\epsilon _j}{c_j}$ implies that $\epsilon _j=O(c_j)$ thus, $c_j\ne o(|\epsilon |)$. Moreover, we also dispose of $\alpha =\min (1,\inf _n\frac{c_j^n+\epsilon _j^n}{c_j^n})>0$ such that:

$$\begin{aligned} {\widetilde{\mathcal {C}}}_{j}\ge \alpha c_j \end{aligned}$$

Necessary, we have $\log \frac{c_j+\epsilon _j}{c_j}\rightarrow 0$ thus:

$$\begin{aligned} \mathcal {D}_\mathrm{chem,j} \ge \alpha \frac{\epsilon _j^2}{c_j}+o(\frac{\epsilon _j^2}{c_j}), \end{aligned}$$

which is bigger than $|\epsilon |^2$ and thus contradicts (4.7).

Conclusion of the proof in case 4.2 Let j be such that $\epsilon _j\ne o(|\epsilon |)$, $c^*_j=0$, and $\log \frac{\epsilon _j+c_j}{c_j}$ blows-up.

We have:

$$\begin{aligned} h_j(C+\epsilon )-h_j(C)=\log \frac{\epsilon _j+c_j}{c_j}+o(1), \end{aligned}$$

and:

$$\begin{aligned} {\widetilde{\mathcal {C}}}_{j}(C+\epsilon ,C)=\frac{\epsilon _j}{\log \frac{\epsilon _j+c_j}{c_j}}, \end{aligned}$$

so that:

$$\begin{aligned} \mathcal {D}_\mathrm{chem,j}\sim \epsilon _j \log \frac{\epsilon _j+c_j}{c_j}, \end{aligned}$$

which contradicts (4.7) since $\epsilon _j\ne o(|\epsilon |)$.

4.2.1 Global conclusion

As each of the cases lead to a contradiction, we have the desired inequality for $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$. For the solvent, we see that:

$$\begin{aligned}c_{K,0}-c_{L,0}=-\sum _{i=1}^{N}k_i(c_{K,i}-c_{L,i}),\end{aligned}$$

thus the announced result up to the choice of a bigger constant M.$\square$

Remark 4 Even though this lemma is proved without the assumption on $c_0$, its adaptation to $\widehat{\mathcal {C}}$ is the most difficult. The shortest sketch of proof we obtained relied on the splitting of case (4.2) in more than 15 sub-cases.

Using these tools, we may now prove the following necessary compactness inequality:

Proposition 4.2

For all $\epsilon >0$, there exist M such that:

$$\begin{aligned} \inf _{\begin{array}{c} \text {mesh }m\\ n\in \mathbf{[}\mathbf{[}1,N_{T,m}\mathbf{]}\mathbf{]}\\ K\in \mathcal {T}_m \end{array}} c_{m,K,0}^n>\epsilon \implies \left\| \nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{c}}_i\right\| _{L^2(Q_T)}^2\le M, \;\forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}, \forall m. \end{aligned}$$

Proof

We will show the result for $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ and use the definition of $\mathcal {A}$ to extend it the solvent. For improved readability, we will drop the subscript m, and for $\sigma =K|L\in \mathcal {E}_\text {int}, i\in \mathbf{[}\mathbf{[}1,N \mathbf{]}\mathbf{]}$ let $\mathcal {C}_{\sigma ,i}=\mathcal {C}_i(C_K,C_L,\Phi _{K},\Phi _{L})$. By definition, we have:

$$\begin{aligned} \left| \nabla _{\mathcal {T},{\varvec{\Delta t}}}{\varvec{c}}_i\right| _{L^2(Q_T)}^2=\sum _{n=1}^{N_{T}}{\Delta t}_n\sum _{\sigma \in \mathcal {E}_\text {int}} \tau _\sigma (D_\sigma {\varvec{c}}_i^n)^2. \end{aligned}$$

Thanks to Proposition 4.1 and Lemma 4.1, we have:

$$\begin{aligned} \sum _{\sigma \in \mathcal {E}_\text {int}}\tau _\sigma (D_\sigma {\varvec{c}}_i^n)^2\le M\sum _{\sigma =K|L\in \mathcal {E}_{K,\text {int}}}\tau _\sigma \mathcal {D}_\mathrm{chem}(C_K^n,C_L^n)\le \frac{M}{\alpha _\epsilon }\sum _{\sigma \in \mathcal {E}_\text {int}}\sum _{j=1}^{N}\tau _\sigma \mathcal {C}_{\sigma ,j}^n(D_\sigma h_j({\varvec{C}}^n))^2. \end{aligned}$$

It is sufficient to bound $\sum _{n=1}^{N_{T}}{\Delta t}_n\sum _{\sigma \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {C}_{\sigma ,j}^n(D_\sigma h_j({\varvec{C}}^n))^2$, for all $j\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ to get the desired result. We have:

$$\begin{aligned} (D_\sigma h_j({\varvec{C}}^n))^2\le 2 (D_\sigma (h_j({\varvec{C}}^n)-z_j{\varvec{\Phi }}^n))^2+2 (z_jD_\sigma {\varvec{\Phi }}^n)^2. \end{aligned}$$

Thanks to Eq. (3.14) of Lemma 3.4, we dispose of M such that:

$$\begin{aligned} \sum _{n=1}^{N_{T}}{\Delta t}_n \sum _{\sigma \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {C}_{\sigma ,j}^n(D_\sigma (h_j({\varvec{C}}^n)-z_j{\varvec{\Phi }}^n))^2<M. \end{aligned}$$

Moreover, $\sum _{\sigma \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {C}_{\sigma ,j}^n(z_jD_\sigma {\varvec{\Phi }}^n)^2$ is also bounded thanks to (3.12) and the $L^\infty$ bound on $\mathcal {C}_i$ and $z_i$. Thus we have:

$$\begin{aligned} \sum _{n=1}^{N_{T}}{\Delta t}_n\sum _{\sigma \in \mathcal {E}_\text {int}}\tau _\sigma \mathcal {C}_{\sigma ,j}^n(D_\sigma h_j({\varvec{C}}^n))^2\le M, \end{aligned}$$

(4.12)

which in turn yields the desired result.

For the solvent we notice that:

$$\begin{aligned} \nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{c}}_0=-\sum _{i=1}^{N}k_i\nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{c}}_i, \end{aligned}$$

so that the bound on all $\nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{c}}_i$ transfers into a bound on $\nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{c}}_0$.$\square$

Using this discrete $L^2(H^1)$ estimate, we use a discrete Aubin–Lions lemma to get the compactness of the sequence of solutions, as stated in following proposition:

Proposition 4.3

Let $({\varvec{C}}_m,{\varvec{\Phi }}_m)$ be the family of discrete solutions defined either by the centered scheme or by the Sedan scheme. In both cases, there exists $\Phi \in L^\infty (Q_T; \mathbb R) \cap L^2((0,T);H^1(\text{\O}mega ))$, $C \in L^\infty (Q_T; \overline{\mathcal {A}})$ such that, up to a subsequence,

$$\begin{aligned}&\pi _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{C}}_m \underset{m\rightarrow \infty }{\longrightarrow }C \quad \text {strongly in } L^2(Q_T)^{N+1}, \end{aligned}$$

(4.13)

$$\begin{aligned}&\nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{C}}_m \underset{m\rightarrow \infty }{\longrightarrow }\nabla C \quad \text {weakly in } L^2(Q_T), \end{aligned}$$

(4.14)

$$\begin{aligned}&\pi _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{\Phi }}_m \underset{m\rightarrow \infty }{\longrightarrow }\Phi \quad \text {in the}\quad L^\infty (Q_T)\quad \hbox {weak-}\star \quad \hbox {sense}, \end{aligned}$$

(4.15)

$$\begin{aligned}&\nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{\Phi }}_m \underset{m\rightarrow \infty }{\longrightarrow }\nabla \Phi \quad \text {in the}\quad L^\infty ([0,T],L^2(\text{\O}mega )^d)\quad \hbox {weak-}\star \quad \hbox {sense}.\quad \end{aligned}$$

(4.16)

Proof

For improved readability we drop again the subscripts m. The proof of the first two result relies on a discrete Aubin–Lions lemma [33,  Lemma 3.4]. We intend to use it in the setting described in [10,  Lemma 9]. Proposition 4.2 provides a first property, but we still have to prove that there exist C independent of the mesh such that $\sum _n \Vert {\varvec{c}}_i^n-{\varvec{c}}_i^{n-1}\Vert _{\mathcal {T},-1}\le C$, where $\Vert \cdot \Vert _{\mathcal {T},-1}$ is defined by duality:

$$\begin{aligned} \Vert {\varvec{c}}\Vert _{\mathcal {T},-1}=\sup _{\varvec{\varphi }}\left( \int _\text{\O}mega \pi _{\mathcal {T}} {\varvec{c}}\pi _{\mathcal {T}} \varvec{\varphi }\mathrm{d}x,\; \Vert \pi _{\mathcal {T}}\varvec{\varphi }\Vert _{L^2}^2+ \Vert \nabla _{\mathcal {T}}\varvec{\varphi }\Vert _{L^2}^2=1\right) . \end{aligned}$$

Let $\varvec{\varphi }\in \mathbb R^\mathcal {T}$. Tanks to (2.4b), we have:

$$\begin{aligned} \int _\text{\O}mega \pi _{\mathcal {T}} ({\varvec{c}}_i^{n}-{\varvec{c}}_i^{n-1})\pi _{\mathcal {T}} \varvec{\varphi }\mathrm{d}x=-{\Delta t}_n\sum _{K\in \mathcal {T}}\varphi _K\sum _{\sigma \in \mathcal {E}_K} F_{K\sigma ,i}^n. \end{aligned}$$

Using the definition of $F_{K\sigma ,i}^n$ along with the definition of $\mathcal {C}_{i}$ respectively Eqs. (2.5) and (3.1), we have:

$$\begin{aligned}&\int _\text{\O}mega \pi _{\mathcal {T}} ({\varvec{c}}_i^{n}-{\varvec{c}}_i^{n-1})\pi _{\mathcal {T}} \varvec{\varphi }\mathrm{d}x\\&\quad ={\Delta t}_n\sum _{\sigma =K|L\in \mathcal {E}_{K,\text {int}}}D_i\tau _\sigma \mathcal {C}_{i}(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n) D_{K\sigma }\left( h_i({\varvec{C}}^n)+z_i{\varvec{\Phi }}^n\right) D_{K\sigma }\varvec{\varphi }. \end{aligned}$$

Thanks to the Cauchy-Schwarz inequality, we have:

$$\begin{aligned}&\int _\text{\O}mega \pi _{\mathcal {T}} ({\varvec{c}}_i^{n}-{\varvec{c}}_i^{n-1})\pi _{\mathcal {T}} \varvec{\varphi }\mathrm{d}x\\&\quad \le {\Delta t}_nD_i\left( \sum _{\sigma =K|L \in \mathcal {E}^\text {int}}\tau _\sigma \mathcal {C}_{i}(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n) \left( D_{K\sigma }h_i({\varvec{C}}^n)+z_i{\varvec{\Phi }}^n\right) ^2\right) ^\frac{1}{2} \\&\quad \left( \sum _{\sigma =K|L \in \mathcal {E}^\text {int}}\tau _\sigma \mathcal {C}_{i}(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n) \left( D_{K\sigma }\varvec{\varphi }\right) ^2\right) ^\frac{1}{2}. \end{aligned}$$

Using $\mathcal {C}_{i}\le \frac{1}{k_iv_0}$, the definition of $\mathcal {D}_{i}$ and $\Vert \nabla _{\mathcal {T}}\varvec{\varphi }\Vert _{L^2}^2\le 1$, we have:

$$\begin{aligned} \Vert {\varvec{c}}_i^{n}-{\varvec{c}}_i^{n-1}\Vert _{\mathcal {T},-1}\le \frac{{\Delta t}_nD_i}{k_iv_0}\left( \sum _{\sigma =K|L \in \mathcal {E}^\text {int}}\tau _\sigma \mathcal {D}_{i}(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n) \right) ^\frac{1}{2}. \end{aligned}$$

Using the Cauchy-Schwarz inequality and the Eq. (3.14) of Lemma 3.4, we have:

$$\begin{aligned}\sum _n \Vert {\varvec{c}}_i^n-{\varvec{c}}_i^{n-1}\Vert _{\mathcal {T},-1}\le \left( \sum _n \frac{{\Delta t}_nD_i^2}{k_i^2v_0^2}\right) ^\frac{1}{2}\left( \sum _n {\Delta t}_n\sum _{\sigma =K|L\in \mathcal {E}_{K,\text {int}}}\tau _\sigma \mathcal {D}_{i}(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n)\right) ^\frac{1}{2}\le C. \end{aligned}$$

This concludes the proof of Eqs. (4.13) and (4.14).

We may now focus on the convergence of the potential. The existence of $\Phi$ satisfying (4.15) is a straightforward consequence of (3.11). Similarly, (3.12) implies the existence of a vector field u such that $\nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{\Phi }}_m \underset{m\rightarrow \infty }{\longrightarrow }u$ in the $L^\infty ([0,T],L^2(\text{\O}mega )^d)$ weak-$\star$ sense.

We have to identify u with $\nabla \Phi$. We let $w\in C^\infty _c(Q_T,R^d)$ and define:

$$\begin{aligned} {\varvec{w}}_\sigma ^n=\frac{1}{|\sigma |}\int _\sigma w(t_n,x)\mathrm{d}x \qquad \forall \sigma \in \mathcal {E},n\in \mathbf{[}\mathbf{[}1,N_T\mathbf{]}\mathbf{]}, \end{aligned}$$

and the associated diamond-cell reconstruction:

$$\begin{aligned} w_{\mathcal {E},{\varvec{\Delta t}}}(t,x)={\varvec{w}}_\sigma ^n \qquad \text {if } x\in \Delta _\sigma \text { and } t\in (t_{n-1},t_n]. \end{aligned}$$

Thanks to the smoothness of w, we have convergence of $w_{\mathcal {E},{\varvec{\Delta t}}}$ toward w and:

$$\begin{aligned} \iint _{Q_T} w_{\mathcal {E},{\varvec{\Delta t}}}\cdot \nabla _{\mathcal {T}, {\varvec{\Delta t}}} {\varvec{\Phi }}\mathrm{d}x\mathrm{d}t \rightarrow \iint _{Q_T} w\cdot u\mathrm{d}x\mathrm{d}t. \end{aligned}$$

Using the geometric relation $d_\sigma m_\sigma =dm_{\Delta _\sigma }$ and the definition of ${\varvec{w}}_\sigma ^n$, we have:

$$\begin{aligned} \iint _{Q_T} w_{\mathcal {E},{\varvec{\Delta t}}}\cdot \nabla _{\mathcal {T}, {\varvec{\Delta t}}} {\varvec{\Phi }}\mathrm{d}x\mathrm{d}t=-\sum _{i=1}^{N_T} {\Delta t}_n\sum _{K\in \mathcal {T}}\Phi _{K}^n\int _K {{\,\mathrm{div}\,}}\bigl (w(t_n,x)\bigr )\mathrm{d}x. \end{aligned}$$

Thanks to the smoothness of w and the convergence of ${\varvec{\Phi }}$, we have:

$$\begin{aligned} \iint _{Q_T} w_{\mathcal {E},{\varvec{\Delta t}}}\cdot \nabla _{\mathcal {T}, {\varvec{\Delta t}}} {\varvec{\Phi }}\mathrm{d}x\mathrm{d}t\rightarrow -\iint _{Q_T}\Phi {{\,\mathrm{div}\,}}(w)\mathrm{d}x\mathrm{d}t=\iint _{Q_T}\nabla \Phi \cdot w\mathrm{d}x\mathrm{d}t \end{aligned}$$

This concludes the identification of u and the proof of (4.16).$\square$

These convergence topologies are sub-optimal and will be improved in Lemma 4.4. First, we notice that for the concentrations, we also dispose of edge averages $\mathcal {C}$ and ${\widetilde{\mathcal {C}}}$ defined in Eqs. (3.1) and (4.2). Using these edge values, we introduce two other reconstructions. For i in $\mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$, we let:

$$\begin{aligned} c_{\mathcal {E},{\varvec{\Delta t}},i}(x,t)={\left\{ \begin{array}{ll} \mathcal {C}_{i}(C_K^n,C_L^n,\Phi _{K}^n,\Phi _{L}^n)\qquad &{}\text { if } x\in \Delta _{K|L} \text { and } t\in (t_{n-1},t_n],\\ c_K^n&{}\text { if } x\in \Delta _\sigma , \sigma \in \mathcal {E}_{K}\cap \mathcal {E}^\text {ext} \text { and } t\in (t_{n-1},t_n]. \end{array}\right. } \end{aligned}$$

Similarly, we introduce ${\widetilde{c}}_{\mathcal {E},{\varvec{\Delta t}},i}$. As we expect, these reconstructions are convergent and share their limit with $\pi _{\mathcal {T},{\varvec{\Delta t}}}{\varvec{c}}_i$. This is the main purpose of the following lemma.

Lemma 4.4

Let C be as in Proposition 4.3. We have:

$$\begin{aligned} \pi _{\mathcal {T}_m, {\varvec{\Delta t}}_m}{\varvec{c}}_{m,i}\rightarrow c_i&\text {strongly in } L^p, p\in [1,\infty )&\forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}, \end{aligned}$$

(4.17)

$$\begin{aligned} \pi _{\mathcal {T}_m, {\varvec{\Delta t}}_m}{\varvec{\Phi }}\rightarrow \Phi&\text {strongly in } L^p, p\in [1,\infty ), \end{aligned}$$

(4.18)

$$\begin{aligned} c_{\mathcal {E}_m,{\varvec{\Delta t}}_m,i}\rightarrow c_i&\text {strongly in } L^p, p\in [1,\infty )&\forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}, \end{aligned}$$

(4.19)

$$\begin{aligned} {\widetilde{c}}_{\mathcal {E}_m,{\varvec{\Delta t}}_m,i}\rightarrow c_i&\text {strongly in } L^p, p\in [1,\infty )&\forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}. \end{aligned}$$

(4.20)

Proof

Equation (4.17) is a straightforward consequence of (4.13) and the boundedness of $\mathcal {A}$. The proof of (4.19) and (4.20) rely on the Lemma D.2. Thanks to Proposition 4.2, the hypothesis is satisfied with $p,{\widetilde{p}}=2$, using (4.17), we have the $L^1$ convergence of the diamond reconstructions. Thanks to the $L^\infty$ bound on the edge concentrations, this result translate in the desired equations. The enhanced convergence of the potential relies on the same ideas as the ones given in the previous proof ([33,  Lemma 3.4] and [10,  Lemma 9]) to get strong $L^2$ convergence. This is done following the lines of [9,  Proposition 4.5].$\square$

Finally, we show a weak-convergence property on the gradients of the logarithms:

Lemma 4.5

Let C be as in Proposition 4.3. We have:

$$\begin{aligned} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} \log (\overline{{\varvec{c}}}) \rightarrow \nabla \log (\overline{c}_m)\qquad \text {weakly in } L^2(Q_T)^d. \end{aligned}$$

(4.21)

Moreover, assuming $\inf _{\begin{array}{c} \text {mesh }m\\ n\in \mathbf{[}\mathbf{[}1,N_{T,m}\mathbf{]}\mathbf{]}\\ K\in \mathcal {T}_m \end{array}} c_{m,K,0}^n >0$, we have:

$$\begin{aligned} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} \log ({\varvec{c}}_{m,0}) \rightarrow \nabla \log (c_0)\qquad \text {weakly in } L^2(Q_T)^d. \end{aligned}$$

(4.22)

Proof

Let us start with the proof on Eq. (4.22). By definition (4.2), we have:

$$\begin{aligned} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} \log ({\varvec{c}}_{m,0})=\frac{1}{{\widetilde{c}}_{\mathcal {E}_m,{\varvec{\Delta t}}_m,0}}\nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{c}}_{m,0}, \end{aligned}$$

so that, using (4.20), (4.14), and the assumed bound on $c_0$ we have:

$$\begin{aligned} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} \log ({\varvec{c}}_{m,0})\rightarrow \frac{1}{c_0}\nabla c_0. \end{aligned}$$

We notice that the limit $c_0$ is also bounded away from 0 and conclude using the continuous chain-rule.

For (4.21), we proceed similarly. Notice that since $\overline{c}\ge \frac{1}{v_0\max k_i}>0$ the bound does not need to be assumed. We only need the strong $L^2$ convergence of the reconstruction using the logarithmic average on the diamond cells. This is an application of Lemma D.2, as in the proof of Lemma 4.4.$\square$

4.3 Identification

In this section we will identify the limits obtained in Proposition 4.3 as weak solutions in the sense of Definition 1. First we improve the convergence topology on the potential and identify it as a weak solution of the Poisson equation.

Proposition 4.4

The function $\Phi \in L^\infty ((0,T),H^1(\text{\O}mega ))$ defined in Proposition 4.3 satisfies: $\Phi - \Phi ^D \in L^\infty ((0,T),H_{\Gamma _\text {D}})$ and for all $\psi \in \mathcal {H}_{\Gamma _\text {D}}$ and almost all $t\in (0,T)$ Eq. (1.14) holds:

$$\begin{aligned} \lambda ^2 \int _\text{\O}mega \nabla \Phi (t,x) \cdot \nabla \psi (x) \mathrm{d}x = \int _\text{\O}mega \psi (x)\sum _{i=1}^N z_i c_i(t,x) \mathrm{d}x. \end{aligned}$$

Proof

Let $\psi \in C^\infty _c([0,T]\times \left\{ \text{\O}mega \cup \Gamma _\text {N}\right\} )$, then define $\psi _K^n=\psi (x_K,t_n)$ and $\psi _\sigma ^n = \psi (x_\sigma ,t_n)$ for $1\le n\le N_T$, $K\in \mathcal {T}$ and $\sigma \in \mathcal {E}_\text {ext}$. As for [9,  Proposition 4.5], we introduce an other reconstruction of the gradient following [24] (see [18] for a practical example). Let $\widehat{\nabla }_{\mathcal {T}}: \mathbb {R}^\mathcal {T}\rightarrow L^\infty (\text{\O}mega )^d$ be strongly consistent i.e.

$$\begin{aligned} \widehat{\nabla }_\mathcal {T}\varvec{\psi }^n \underset{h_\mathcal {T}\rightarrow 0}{\longrightarrow }\nabla \psi (\cdot , t_n)\;\;\text {uniformly in}\; \overline{\text{\O}mega }, \quad \forall n \in \{1,\dots , N_T\}, \end{aligned}$$

(4.23)

thanks to the smoothness of $\psi$. The operator $\widehat{\nabla }$ is also such that

$$\begin{aligned} \int _{\text{\O}mega }\nabla _\mathcal {T}{\varvec{u}}\cdot \widehat{\nabla }_\mathcal {T}{\varvec{v}}\mathrm{d}x = \sum _{\sigma \in \mathcal {E}} \tau _\sigma D_{K\sigma } {\varvec{u}}D_{K\sigma } {\varvec{v}}, \qquad \forall {\varvec{u}}, {\varvec{v}}\in \mathbb {R}^\mathcal {T}. \end{aligned}$$

The scheme (2.4a) then reduces to

$$\begin{aligned}&\lambda ^2\int _\text{\O}mega \nabla _\mathcal {T}{\varvec{\Phi }}^n \cdot \widehat{\nabla }_\mathcal {T}\varvec{\psi }^n \mathrm{d}x\\&\quad = \int _\text{\O}mega \pi _\mathcal {T}\varvec{\psi }^n \sum _{i=1}^{N}z_i\pi _\mathcal {T}{\varvec{c}}_i^n \mathrm{d}x, \quad \forall n \in \{1,\dots , N_T\}, \; \forall \varvec{\psi }\in \mathbb {R}^{(\mathcal {T}\cup \mathcal {E}_\text {ext})\times N_T}. \end{aligned}$$

Integrating with respect to time over (0, T) and passing to the limit $h_\mathcal {T}, h_{\varvec{\Delta t}}\rightarrow 0$ thanks to Proposition 4.3 Eqs. (4.13) and (4.16) and Eq. (4.23) we have:

$$\begin{aligned} \lambda ^2\iint _{Q_T} \nabla \Phi \cdot \nabla \psi \mathrm{d}x\mathrm{d}t = \iint _{Q_T} \psi \sum _{i=1}^{N}z_i c_i \mathrm{d}x\mathrm{d}t, \qquad \forall \psi \in C^\infty _c([0,T]\times \text{\O}mega \cup \Gamma _\text {N}). \end{aligned}$$

By density of $C^\infty _c([0,T]\times \text{\O}mega \cup \Gamma _\text {N})$ in $L^\infty ([0,T],H_{\Gamma _\text {D}})$ and continuity of the linear application, we have:

$$\begin{aligned} \lambda ^2\iint _{Q_T} \nabla \Phi \cdot \nabla \psi \mathrm{d}x\mathrm{d}t = \iint _{Q_T} \psi \sum _{i=1}^{N}z_ic_i \mathrm{d}x\mathrm{d}t, \qquad \forall \psi \in L^\infty ([0,T],H_{\Gamma _\text {D}}). \end{aligned}$$

In particular, (1.14) holds for almost every $t\in (0,T)$.

Concerning the boundary conditions for $\Phi$, the fact that $\Phi = \Phi ^D$ on $(0,T) \times \Gamma _\text {D}$ can be proved for instance following the lines of [6,  Section 4].$\square$

The following theorem focuses on the identification of C as a weak solution satisfying (1.13). As announced in Theorem 2.2 this can only be done with an assumption on the solvent. Remark 1.1 is a first clue of the validity of this assumption. For positive initial condition, this assumption is valid in all the numerical test. In the 1D setting and under a CFL condition, it might be possible to prove it through improvements of Lemmas 3.2 and 3.5. This could be the topic of further research.

Theorem 4.1

Let C and $\Phi$ be as in Propositions 4.3. If one has $\inf _{\begin{array}{c} \text {mesh }m\\ n\in \mathbf{[}\mathbf{[}1,N_{T,m}\mathbf{]}\mathbf{]}\\ K\in \mathcal {T}_m \end{array}} c_{m,K,0}^n c_0>0$, they are weak solutions of (1.3)–(1.8) in the sense of Definition 1.

Proof

Let $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$, $\varphi \in C^\infty _c([0,T)\times \overline{\text{\O}mega })$, then define $\varphi _K^n = \varphi ( x_K,t_n)$ for all $n \in \{0,\dots , N_T\}$ and $K \in \mathcal {T}$. Multiplying (2.4b) by ${\Delta t}_n\varphi _K^{n-1}$, then summing over $K\in \mathcal {T}$ and $n\in \{1,\dots , N_T\}$ leads to

$$\begin{aligned} T_1 + D_iT_2 + D_iz_iT_3 = 0, \end{aligned}$$

(4.24)

where we have set

$$\begin{aligned} T_1 =&\sum _{n=1}^{N_T}\sum _{K\in \mathcal {T}}m_K(c_{K,i}^n - c_{K,i}^{n-1}) \varphi _K^{n-1},\\ T_2 =&\sum _{n=1}^{N_T}{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma \mathcal {C}_{\sigma ,i}^n D_{K\sigma }h_ i({\varvec{c}}^n)D_{K\sigma }\varvec{\varphi }^{n-1},\\ T_3 =&\sum _{n=1}^{N_T}{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma \mathcal {C}_{\sigma _i}^n D_{K\sigma }{\varvec{\Phi }}^nD_{K\sigma }\varvec{\varphi }^{n-1}, \end{aligned}$$

where $\varphi _{K\sigma }^{n-1}=0$ for $\sigma \in \mathcal {E}_\text {ext}$ and $\mathcal {C}_{\sigma }$ is defined by Lemma 3.1. The treatment of terms $T_1$ and $T_3$ follows the lines of [9,  Proposition 4.7].

More precisely, for $T_1$ we use the discrete integration by part

$$\begin{aligned} \sum _{n=1}^{N_T}(c^n-c^{n-1})\varphi ^{n-1}=-c^0\varphi ^0+\sum _{n=1}^{N_T-1}c^n(\varphi ^{n-1}-\varphi ^n)+c^{N_T}\varphi ^{N_T-1}, \end{aligned}$$

and notice that $\varphi ^{N_T}=0$ to pass the time derivative on $\varphi$. Thanks to the smoothness of $\varphi$ and the convergence of $\pi _{\mathcal {T},{\varvec{\Delta t}}}c_i$ and $\pi _{\mathcal {T}}c_i^0$, we have:

$$\begin{aligned} T_1 \underset{m\rightarrow \infty }{\longrightarrow }-\iint _{Q_T} c_i \partial _t \varphi \mathrm{d}x\mathrm{d}t - \int _\text{\O}mega c_i^0 \varphi (0,\cdot )\mathrm{d}x. \end{aligned}$$

(4.25)

For $T_3$, we extend in time the reconstruction introduced in the proof of Proposition 4.4 and notice that:

$$\begin{aligned} T_3 = \iint _{Q_T} c_{\mathcal {E},{\varvec{\Delta t}},i} \nabla _{\mathcal {T},{\varvec{\Delta t}}} {\varvec{\Phi }}\cdot \widehat{\nabla }_{\mathcal {T},{\varvec{\Delta t}}} \varvec{\varphi }\mathrm{d}x\mathrm{d}t,\end{aligned}$$

so that

$$\begin{aligned} T_3 \underset{m \rightarrow \infty }{\longrightarrow }\iint _{Q_T} c_i \nabla \Phi \cdot \nabla \varphi \mathrm{d}x\mathrm{d}t. \end{aligned}$$

(4.26)

The treatment of the term $T_2$ is more intricate. First we let ${\widetilde{T_2}}$ be the same term with a different edge concentration:

$$\begin{aligned} {\widetilde{T}}_2 = \sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma {\widetilde{\mathcal {C}}}_{\sigma ,i}^n D_{K\sigma }h_ i({\varvec{c}}^n)D_{K\sigma }\varvec{\varphi }^{n-1}, \end{aligned}$$

where ${\widetilde{\mathcal {C}}}_{\sigma ,i}^n={\widetilde{\mathcal {C}}}_i(C_K^n,C_{K\sigma }^n)$ is the logarithmic mean introduced in (4.2). We will first prove the convergence of ${\widetilde{T_2}}$ then identify its limit. To this end, we set:

$$\begin{aligned} {\widetilde{T}}_{2,1} =&\sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma {\widetilde{\mathcal {C}}}_{\sigma ,i}^n D_{K\sigma }\log ({\varvec{c}}_ i^n)D_{K\sigma }\varvec{\varphi }^{n-1},\\ {\widetilde{T}}_{2,2} =&-k_i\sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma {\widetilde{\mathcal {C}}}_{\sigma ,i}^n D_{K\sigma }\log ({\varvec{c}}_ 0^n)D_{K\sigma }\varvec{\varphi }^{n-1},\\ {\widetilde{T}}_{2,3} =&(k_i-1)\sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma {\widetilde{\mathcal {C}}}_{\sigma ,i}^n D_{K\sigma }\log (\overline{{\varvec{c}}}^n)D_{K\sigma }\varvec{\varphi }^{n-1}. \end{aligned}$$

For term ${\widetilde{T}}_{2,1}$ we use the chain rule ${\widetilde{\mathcal {C}}}_{\sigma ,i}^n D_{K\sigma }\log ({\varvec{c}}_ i^n)=D_{K\sigma }{\varvec{c}}_ i^n$ and get:

$$\begin{aligned} {\widetilde{T}}_{2,1}=\sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma D_{K\sigma }{\varvec{c}}_ i^nD_{K\sigma }\varvec{\varphi }^{n-1}=\iint _{Q_T} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m}\cdot {\varvec{c}}_i\widehat{\nabla }_{\mathcal {T}_m, {\varvec{\Delta t}}_m} \varvec{\varphi }\mathrm{d}x\mathrm{d}t. \end{aligned}$$

Thanks to the weak convergence of $\nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m} {\varvec{c}}_i$ and the strong convergence of $\widehat{\nabla }_{\mathcal {T}_m, {\varvec{\Delta t}}_m} \varvec{\varphi }$, we have:

$$\begin{aligned} {\widetilde{T}}_{2,1}\rightarrow \iint _{Q_T}\nabla c_i\cdot \nabla \varphi \mathrm{d}x\mathrm{d}t. \end{aligned}$$

For the other terms, we need the enhanced convergence of gradients provided by Lemma 4.5. So that the terms ${\widetilde{T}}_{2,2}$ and ${\widetilde{T}}_{2,3}$ have the following limits:

$$\begin{aligned} {\widetilde{T}}_{2,2} =\,&-k_i\iint _{Q_T} {\widetilde{c}}_{\mathcal {E}_m,{\varvec{\Delta t}}_m,i} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m}\log ({\varvec{c}}_0)\widehat{\nabla }_{\mathcal {T}_m, {\varvec{\Delta t}}_m} \varvec{\varphi }\mathrm{d}x\mathrm{d}t\\&\quad \rightarrow -k_i\iint _{Q_T} c_i \nabla \log (c_ 0)\nabla \varphi \mathrm{d}x\mathrm{d}t,\\ {\widetilde{T}}_{2,3} = \,&(k_i-1)\iint _{Q_T} {\widetilde{c}}_{\mathcal {E}_m,{\varvec{\Delta t}}_m,i} \nabla _{\mathcal {T}_m, {\varvec{\Delta t}}_m}\log (\overline{{\varvec{c}}})\widehat{\nabla }_{\mathcal {T}_m, {\varvec{\Delta t}}_m} \mathrm{d}x\mathrm{d}t\varvec{\varphi }\\&\quad \rightarrow (k_i-1)\iint _{Q_T} c_i \nabla \log (\overline{c})\nabla \varphi \mathrm{d}x\mathrm{d}t.\\ \end{aligned}$$

Let us now establish that $T_2$ and ${\widetilde{T_2}}$ share the same limit.

Thanks to the triangle and Cauchy–Schwarz inequalities, one has

$$\begin{aligned} |T_2 - {\widetilde{T}}_2| \le&\; \sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma \left| \mathcal {C}_{\sigma ,i}^n-{\widetilde{\mathcal {C}}}_{\sigma ,i}^n\right| \left| D_{\sigma }h_i({\varvec{c}}^n)\right| \left| D_{\sigma }\varvec{\varphi }^{n-1}\right| \\ \le&\; \left( \sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma \mathcal {C}_{\sigma ,i}^n |D_\sigma h({\varvec{c}}^n)|^2\right) ^{1/2} \left( \sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma \frac{(\mathcal {C}_{\sigma ,i}^n - {\widetilde{\mathcal {C}}}_{\sigma ,i}^n)^2}{\mathcal {C}_{\sigma ,i}^n} |D_\sigma \varvec{\varphi }^{n-1}|^2\right) ^{1/2}. \end{aligned}$$

The first term in the right-hand side is uniformly bounded thanks to (4.12). Thus our problem amounts to show that

$$\begin{aligned} \mathcal {R}:=\sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma \frac{(\mathcal {C}_{\sigma ,i}^n - {\widetilde{\mathcal {C}}}_{\sigma ,i}^n)^2}{\mathcal {C}_{\sigma ,i}^n} |D_\sigma \varvec{\varphi }^{n-1}|^2 \underset{m\rightarrow \infty }{\longrightarrow }0. \end{aligned}$$

(4.27)

Let us reformulate $\mathcal {R}$ as

$$\begin{aligned} \mathcal {R}=\sum _{n=1}^N{\Delta t}_n\sum _{\sigma \in \mathcal {E}}\tau _\sigma |\mathcal {C}_{\sigma ,i}^n - {\widetilde{\mathcal {C}}}_{\sigma ,i}^n| \left| 1 - \frac{{\widetilde{\mathcal {C}}}_{\sigma ,i}^n}{\mathcal {C}_{\sigma ,i}^n}\right| |D_\sigma \varvec{\varphi }^{n-1}|^2. \end{aligned}$$

Thanks to Lemma 4.1, the quantity $\left| 1 - \frac{{\widetilde{\mathcal {C}}}_{\sigma ,i}^n}{\mathcal {C}_{\sigma ,i}^n}\right|$ is uniformly bounded, whereas the regularity of $\varphi$ implies that $D_\sigma \varvec{\varphi }^{n-1} \le \Vert \nabla \varphi \Vert _\infty d_\sigma$. Putting this in the above expression of $\mathcal R$, we obtain that

$$\begin{aligned} 0\le \mathcal {R} \le C \Vert c_{\mathcal {E}_m,{\varvec{\Delta t}}_m,i} - {\widetilde{c}}_{\mathcal {E}_m,{\varvec{\Delta t}}_m,i}\Vert _{L^1(Q_T)} \underset{m\rightarrow \infty }{\longrightarrow }0, \end{aligned}$$

thanks to Lemma 4.4. Thus $T_2$ and ${\widetilde{T}}_2$ share the same limit, which gives the announced result.$\square$

Remark 4.1

As the proof is based on compactness we cannot extract convergence rates for our solutions. The numerous non-linearities involved would render a proof of a convergence rate difficult. The best rate one could hope for given the reconstruction introduced is 1.

To get the second order "super convergence" shown in Fig. 6, we have used a $P_1$ reconstruction. To use this technique we need to use Voronoï meshes with cell centers on the boundary of our domain so that the dual Delaunay mesh covers the whole domain. Due to the specific treatment of boundary conditions in such meshes (formally, $\tau _{\sigma }=+\infty$) they are not covered by our analysis.

In meshes simply satisfying Definition 2, the key idea is to project the reference solution to the space of constant by cells function, i.e. to consider only the discretization errors. The projection to this $P_0$ space could be done either using $L^2$ projections (as for the discretiation of the initial condition) or by taking the value at the cell-centers (to acknowledge the degree of freedom in their choice for orthogonal meshes or simplify the code).

5 Numerical examples

The numerical examples have been implemented in the Julia language [5] based on the package VoronoiFVM.jl [32] which realizes the implicit Euler Voronoi finite volume method for nonlinear systems of diffusion-convection-reaction equations on simplicial grids. The two two schemes (2.4), (2.5) supplemented with either (C) or (S) require the solution of a nonlinear system of equations for each time step. For this purpose we use Newton’s method with analytical Jacobians with optional homotopy embedding. An advantage of the implementation in Julia is the availability of ForwardDiff.jl [43], a forward mode automatic differentiation package based on dual number arithmetic. This package allows the assembly of the analytical Jacobians based on the implementation of functions calculating two point fluxes and charges, without the need to write source code for derivatives. For the one- and two dimensional examples in this paper, the resulting linear systems are solved using UMFPACK [19] as Julia’s built-in sparse direct solver.

5.1 Species redistribution in a one-dimensional cell filled with binary electrolyte

Let $\text{\O}mega =(0,L)$ with $L=20$. As an initial state, assume a binary electrolyte with two ionic species with opposite charges and a solvent. At moment $t=0$, we assume a spatially constant, electroneutral distribution of the ions. We apply a potential difference via Dirichlet boundary conditions $\Phi |_{x=0}=-10$ and $\Phi _{x=L}=10$ and solve the Poisson equation with these data as initial value. We set homogeneous Neumann boundary conditions for both ionic species. With starting time step size $\Delta t=10^{-3}$ we start the evolution until the species distribution reaches its equilibrium under the applied potential difference. As discussed in [8], the time step sizes are controlled such that the energy dissipation per time step is limited: $E(t_{i})-E(t_{i+1})\le 10^{-1}$.

Fig. 2

Evolution of electrostatic potential $\Phi$, solvent concentration $c_0$, anion concentration $c^-$ and cation concentration $c^+$ for a symmetric binary electrolyte with equal sizes of solvent molecules, anions and cations

Figure 2 shows the evolution in the case $v_0=v_1=v_2 =1$, $z_0=0, z_1=1, z_2=-1$. At the end of the time evolution, most of the ions are accumulated in their respective polarization boundary layers, almost completely displacing the solvent. As predicted, the ion concentration is bounded by 1. The computation used the flux (S).

Fig. 3

Evolution of electrostatic potential $\Phi$, solvent concentration $c_0$, anion concentration $c^-$ and cation concentration $c^+$ for an asymmetric binary electrolyte with equal sizes of solvent molecules, cations and anions

Figure 3 shows the evolution in the case $v_0=v_1=v_2=1$ and $z_0=0, z_1=2, z_2=-1$. Once again, at the end of the evolution, anions and cations pile up in the corresponding boundary layers. Ion concentrations are bounded by 1, but due to the larger charge of the cation, the corresponding boundary layer becomes smaller.

Figure 4 shows the evolution in the case $v_0=v_2=1$, $v_1=2$ and $z_0=0, z_1=1, z_2=-1$. Once again, at the end of the evolution, anions and cations pile up in the corresponding boundary layers but now, the cation concentration is bounded by $\frac{1}{2}$. The corresponding evolution of the relative free energy $E(t) - E_\infty$ is shown in Fig. 5. We observe an exponential decay and almost equal behavior for both variants of the flux approximation (S) and (C). Moreover, the time step control algorithm keeps the dissipation per timestep below the intended limit. On the grid of 100 nodes the whole computation took 700ms on an Intel(R) Core(TM) i7-9850H CPU with 2.60GHz. The Newton method used 14 iterations for the first timestep, and at most 4 iterations for the remaining time steps.

Fig. 4

Evolution of electrostatic potential $\Phi$, solvent concentration $c_0$, anion concentration $c^-$ and cation concentration $c^+$ for a symmetric binary electrolyte with equal sizes of solvent molecules and anions, but larger cations

Fig. 5

Evolution of relative free energy and energy dissipation per time step for symmetric binary electrolyte with equal sizes of solvent molecules and anions, but larger cations

Fig. 6

Left: stationary solution of Dirichlet problem. Center and right: results of numerical convergence test

5.2 1D stationary convergence test

In the same domain as above, we set $v_0=1, v_1=2, v_2=1$, and $z_1=1,z_2=-1$. This time, we look for the stationary solution with homogeneous Dirichlet boundary conditions for $\Phi$, and Dirichlet boundary conditions for the concentrations. These boundary conditions are for $x=0$, $c_1v_1=1.0-3\epsilon , c_2v_2=\epsilon$ and for $x=L$, $c_1v_1=\epsilon , c_2v_2=1-3\epsilon$, where $\epsilon =10^{-2}$. Implicitely, this sets $c_0=2\epsilon$ at both boundaries. As shown in Fig 6, the result of the numerical convergence tests (comparison to fine grid solution with 40960 grid points) for both types of fluxes suggest $O(h^2)$ convergence in the $L^2$ norm and O(h) convergence in the $H^1$ seminorm.

Fig. 7

Electrostatic potential $\Phi$, solvent concentration $c_0$, anion concentration $c^-$ and cation concentration $c^+$ in an electrolytic diode filled with a symmetric binary electrolyte with equal sizes of solvent molecules at reverse bias $\Phi _{bias}=-10$ (top), zero bias $\Phi _{bias}=0$ (center) and forward bias $\Phi _{bias}=10$ (bottom)

Fig. 8

Left: Current-voltage curve for electrolytic diode, calculated using the scheme (S). Right: Convergence of calculated IV curve

5.3 An electrolytic diode

The second example regards a domain $\text{\O}mega =(0,W)\times (0,L)$ with $W=2$ and $L=10$. We assume $z_0=0, z_1=1, z_2=-1$ and $v_0=1, v_1=4, v_2=4$. At $y=0$ and $y=L$ we fix concentrations to a value $c_1=c_2=0.01$ We set $\Phi |_{y=0}=0$ and apply a changing value $\Phi _{bias}$ at $y=L$. At $x=0$ we apply symmetry (homogeneous Neumann) boundary conditions for $\Phi , c_1, c_2$. Homogeneous Neumann boundary conditions are also applied for $c_1,c_2$ at $x=W$. We set Neumann boundary conditions $\lambda \nabla \Phi \cdot n= q(y)$ at $x=W$, where

$$\begin{aligned} q(y)= {\left\{ \begin{array}{ll} \sigma , &{} y\in (\frac{1}{2}L,\frac{3}{4}L) \\ -\sigma , &{} y\in (\frac{1}{4}L,\frac{1}{2}L) \\ 0, &{} \text {else} \end{array}\right. } \end{aligned}$$

with $\sigma =5$.

Figure 7 shows three different states of the electrolytic diode. Figure 8 (left) shows the corresponding current-voltage curve. We see a well developed rectification effect: At reverse bias, ion concentrations under the charged surface are rather low, resulting in low conductance and low ionic current. Whereas at forward bias, larger ion concentrations lead to a larger ionic current. On the 2D grid with 1681 nodes, the whole computation for the IV curve took 19 seconds on the aforementioned system.

Figure 8 (right) shows the estimated error of the IV curve in dependence of the grid refinement. Reference was a calculation on a grid with the quarter of the stepsize of the finest grid result shown. From this experiment, we postulate a convergence rate for the ionic current calculation of $O(h^2)$.

Appendices

Appendix A: Chemical free energy density and chemical potentials

In this “Appendix”, we aim to prove (1.9), (1.10), and some convexity of:

$$\begin{aligned}H(c_1,...c_N)=-\overline{c}\log (\overline{c})+\sum _{i=0}^{N}c_i\log (c_i),\end{aligned}$$

where $c_0$ and $\overline{c}$ are functions of $c_1,...,c_N$. This is summarized in the following lemma:

Lemma A.1

The N-variables function H is convex, moreover we have:

$$\begin{aligned}&\partial _{c_i} H(c_1,...,c_N)=h_i(C), \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]},\; C=(c_1,...,c_N)\in \mathcal {A}, \end{aligned}$$

(1.9)

$$\begin{aligned}&\frac{-\log (N+1)}{v_0\min k_i} \le H(C)\le 0 \qquad \forall C\in \mathcal {A}. \end{aligned}$$

(1.10)

Elementary computation shows that:

$$\begin{aligned} \partial _{c_i}H(C)=\log \frac{c_i}{\overline{c}}-k_i\log \frac{c_0}{\overline{c}} \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

Hence the announced relation (1.9).

We now focus on the proof of the convexity of H over $\mathcal {A}$. Let $C,C^* \in \mathcal {A}$, we have:

$$\begin{aligned} (\nabla _{\mathbb {R}^N} H(C)-\nabla _{\mathbb {R}^N} H(C^*) |C-C^*) =&\sum _{i=0}^N\left( \log \frac{c_i}{\bar{c}}-\log \frac{c_i^*}{\bar{c}^*}\right) (c_i-c_i^*). \end{aligned}$$

(A.1)

To prove the convexity of H, it is sufficient to show that this quantity is non-negative. To that extend, we introduce $\mathcal {A}_{N+1}$ the natural extension of $\mathcal {A}$ in $\mathbb R^{N+1}$ and consider the right-hand side of (A.1) as a function of $C_{N+1}=(c_0(c_1,...c_N),c_1...,c_N)\in \mathcal {A}_{N+1}$ parameterized by $C^*$:

$$\begin{aligned} G_{C^*}(c_0,\dots ,c_N)=\sum _{i=0}^N\left( \log \frac{c_i}{\bar{c}}-\log \frac{c_i^*}{\bar{c}^*}\right) (c_i-c_i^*), \end{aligned}$$

and show that $\min _{C_{N+1}\in \mathcal {A}_{N+1}}(G_{C^*}(C))=0$. To do so we compute the derivatives of $G_{C^*}$ as a function of $\mathbb R^{N+1}$ and use the Lagrange multiplier theorem. After some simplifications, we have for all $i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \partial _{c_i} G_{C^*}(c_0,...c_N)&=\frac{\overline{c}^*}{c_i}\left( \frac{c_i}{\bar{c}}-\frac{c_i^*}{\bar{c}^*}\right) +\left( \log \frac{c_i}{\bar{c}}-\log \frac{c_i^*}{\bar{c}^*}\right) \end{aligned}$$

Notice that both terms have the sign of $\frac{c_i}{\bar{c}}-\frac{c_i^*}{\bar{c}^*}$. The Lagrange multiplier theorem states that any extremum satisfies:

$$\begin{aligned} \exists \alpha \in \mathbb R, \forall i\in \mathbf{[}\mathbf{[}0,N\mathbf{]}\mathbf{]}, \qquad \partial _{c_i} G_{C^*}=\alpha k_i \end{aligned}$$

Hence, all the partial derivatives of $G_{C^*}$ should have the same sign. Moreover, we notice that the sum of $\frac{c_i}{\bar{c}}-\frac{c_i^*}{\bar{c}^*}$ is zero. This is only possible the sign of the derivatives is constantly zero, i.e. : $\frac{c_i}{\bar{c}}=\frac{c_i^*}{\bar{c}^*}$. At such a point, we have $G_{C^*}=0$. As the coercitivity and continuity of $G_{C^*}$ grants the existence of a minimum, we have the desired result:

$$\begin{aligned} 0\le (\nabla _{\mathbb {R}^N} H(C)-\nabla _{\mathbb {R}^N} H(C^*) | C-C^*), \end{aligned}$$

which yields the convexity of H.

We still have to establish the bounds (1.10). To that end, we notice that:

$$\begin{aligned} H(C)=\overline{c}\sum _{i=0}^{N}\frac{c_i}{\overline{c}}\log \frac{c_i}{\overline{c}}\qquad \forall C\in \mathcal {A}. \end{aligned}$$

As $\overline{c}$ is positive and $0\le \frac{c_i}{\overline{c}}\le 1$, we have $H(C)\le 0$. For the lower bound, we notice that $-\sum _{i=0}^{N}\frac{c_i}{\overline{c}}\log \frac{c_i}{\overline{c}}$ can be interpreted as the entropy of a random variable over a set of $N+1$ elements. It is common knowledge that it is maximal for $\frac{c_i}{\overline{c}}=\frac{1}{N+1}$ thus:

$$\begin{aligned} -\overline{c}\log (N+1)\le H(C) \end{aligned}$$

Finally, notice that $\frac{1}{v_0\max k_i}\le \overline{c}\le \frac{1}{v_0\min k_i}$ yields

$$\begin{aligned} \frac{-\log (N+1)}{v_0\min k_i}\le H(C), \end{aligned}$$

which is the desired bound.

Appendix B: Proof of Lemma 3.2

This “Appendix” is devoted to the proof of Lemma 3.2 stating the blow-up of the diffusion for extreme concentrations. More precisely, we recall:

Lemma B.1

Let for $\delta ,\epsilon ,M,c>0$, $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \begin{aligned} {\Psi }_{\delta ,\epsilon ,M,i}(c)&:=\inf _{\begin{array}{c} (C_K,C_L)\in \mathcal {A}^2,\;(\Phi _K,\Phi _L) \in [-M,M]^2\\ c_{K,0},c_{L,0}>\epsilon ,\; c_{K,i}\ge \min (\delta ,\frac{0.5}{k_iv_0}),\; c_{L,i}<c \end{array}} \mathcal {D}_i(C_K,C_L, \Phi _K, \Phi _L),\\ {\Upsilon }_{\delta ,M}(c)&:=\inf _{\begin{array}{c} (C_K,C_L)\in \mathcal {A}^2,\;(\Phi _K,\Phi _L) \in [-M,M]^2\\ c_{K,0}\ge \min (\delta ,\frac{0.5}{v_0}) ,\; c_{L,0}<c \end{array}} \mathcal {D}(C_K,C_L, \Phi _K, \Phi _L). \end{aligned} \end{aligned}$$

We have, for all $\delta ,\epsilon ,M>0$:

$$\begin{aligned} \lim _{c\rightarrow 0^+} {\Upsilon }_{\delta ,M}(c)= + \infty \qquad \qquad \lim _{c\rightarrow 0^+} {\Psi }_{\delta ,\epsilon ,M,i}(c)= + \infty \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}. \end{aligned}$$

We will prove the result for ${\Psi }_{\delta ,\epsilon ,M,i}$ first, then use this property to show the bound on the solvent.

1.1 Limit of ${\Psi }_{\delta ,\epsilon ,M,i}$

In this section we intend to prove the limit:

$$\begin{aligned} \lim _{\begin{array}{c} c\rightarrow 0\\ c>0 \end{array}} {\Psi }_{\delta ,\epsilon ,M,i}(c)= + \infty \qquad \forall i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]},\;\delta ,\epsilon ,M>0. \end{aligned}$$

The proof for the centered scheme relies on expression (3.5):

$$\begin{aligned} \mathcal {D}_i(C_K,C_{L}, \Phi _K,\Phi _{L})=\mathcal {C}_i(C_K,C_{L}, \Phi _K,\Phi _{L})\left( h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}\right) ^2. \end{aligned}$$

We notice that $h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}$ blows up and that $\mathcal {C}_i\ge \frac{c_{K,i}}{2}$, hence the blow-up of the limit.

For the Sedan scheme, it is more intricate and try to bound $\mathcal {F}_i(C_K,C_{L}, \Phi _K,\Phi _{L})$ away from zero to take advantage of the blow-up of $\Big (h_i(C_K)+z_i\Phi _K-h_i(C_{L})-z_i\Phi _{L}\Big )$. The positivity of the product, ensures that the limit will have the right sign. Let $\delta ,\epsilon ,M>0$, $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$. We denote by $O_c$ the set:

$$\begin{aligned} O_c=\left\{ (C_K,C_L)\in \mathcal {A}^2,\;(\Phi _K,\Phi _L) \in [-M,M]^2 \mid c_{K,0},c_{L,0}>\epsilon ,\; c_{K,i}\in [\delta ,1),\; c_{L,i}<c\right\} . \end{aligned}$$

We notice that the hypothesis $c_0>\epsilon$ yields a bound on $\nu _i$. Moreover, this bound is uniform in c. We intend to use this bound to prove that the flux function defined by (S) is bounded away from zero. We let:

$$\begin{aligned} M'=\sup _{c\in \mathbb R_{+,*}}\left( \sup _{(C_K,C_L,\Phi _K,\Phi _L)\in O_c} z_i\Phi _L+\nu (C_{L,i})-z_i\Phi _K-\nu (C_{K,i})\right) <\infty . \end{aligned}$$

We have, for all $(C_K,C_L,\Phi _K,\Phi _L)\in O_c$:

$$\begin{aligned} \mathcal {F}_i(C_K,C_{L},\Phi _K,\Phi _{L})\ge B(M')\delta -B(-M')c, \end{aligned}$$

hence $\mathcal {F}_i$ is bounded away from zero for c small enough and the desired result.

1.2 Limit of $\Upsilon _{\delta ,M}$

In this section, we prove the remaining limit:

$$\begin{aligned} \lim _{c\rightarrow 0} {\Upsilon }_{\delta ,M}(c)= + \infty \qquad \forall \delta ,M>0 \end{aligned}$$

To reuse the ideas of previous section, we would like to dispose of a specie i such that $c_{L,i}>\epsilon$. We start by building one artificially. Let $\delta ,M>0$, and:

$$\begin{aligned} O(c)=\left\{ (C_K,C_L)\in \mathcal {A}^2,\;(\Phi _K,\Phi _L) \in [-M,M]^2\mid c_{K,0}\in [\delta ,1) ,\; c_{L,0}<c\right\} . \end{aligned}$$

Notice that for all $(C_K,C_L,\Phi _K,\Phi _L)\in O_c$, we dispose of $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$ such that $c_{L,i}\ge \frac{1-v_0c}{Nk_iv_0}$. Notice also that $\Upsilon _{\delta ,M}$ is increasing, it is then sufficient to prove the limit for a given sequence. Let $c^n$ be sequence that steadily decreases to zero such that for all $n\in \mathcal {N}$, $c^n\le \frac{1}{2v_0}$ and there exist $i\in \mathbf{[}\mathbf{[}1,N\mathbf{]}\mathbf{]}$, $(C_K^n,C_L^n,\Phi _K^n,\Phi _L^n)\in O_{c^n}$ satisfying:

$$\begin{aligned} \mathcal {D}(C_K^n,C_L^n,\Phi _K^n,\Phi _L^n)\le {\Upsilon }_{\delta ,M}(c^n)+\frac{1}{n} \qquad \text {and}\qquad c_{L,i}^n\ge \frac{1}{2Nk_iv_0}. \end{aligned}$$

We have, using $c_{L,0}^n\le c^n$, $c_{K,i}^n\le \frac{1}{k_iv_0}$, $\frac{1}{v_0\max k_j}\le \overline{c}\le \frac{1}{v_0\min k_j}$, $c_{K,0}^n\ge \delta$, the bounds on $\Phi$, and $c_{L,i}^n\ge \frac{1}{2Nk_iv_0}$:

$$\begin{aligned} h_i(C_K^n)+z_i\Phi _K^n-h_i(C_{L}^n)-z_i\Phi _{L}^n \le k_i\log \frac{c^n}{\delta } + |k_i-1|\log \frac{\max k_j}{\min k_j} +\log (2N) +2M|z_i|. \end{aligned}$$

As all the terms are bounded except $\log (c^n)$ which goes to $-\infty$, we have blow-up of $h_i(C_K^n)+z_i\Phi _K^n-h_i(C_{L}^n)-z_i\Phi _{L}^n$.

For the centered scheme, we use $\mathcal {C}_i(C_K^n,C_L^n,\Phi _K^n,\Phi _L^n)\ge \frac{1}{4Nv_i}$, and we have:

$$\begin{aligned} \Upsilon _{\delta ,M}(c^n)\ge & {} \mathcal {D}_i(C_K^n,C_L^n,\Phi _K^n,\Phi _L^n)-\frac{1}{n}\\\ge & {} \frac{1}{4Nv_i}\bigl ( h_i(C_K^n)+z_i\Phi _K^n-h_i(C_{L}^n)-z_i\Phi _{L}^n\bigr )^2 -\frac{1}{n}, \end{aligned}$$

hence the desired result.

For the Sedan scheme, we will also only consider $\mathcal {D}_i$, but we need a more precise approach: as in previous section, we bound the flux away from zero. We let:

$$\begin{aligned} M'=\sup _{c\in (0,\frac{1}{2v_0}]}\left( \sup _{(C_K,C_L,\Phi _K,\Phi _L)\in O_{c^0}, c_{L,i}\ge \frac{1}{2Nv_i}} z_i\Phi _L+(k_i-1)\log \overline{c_L}-z_i\Phi _K-\nu (C_{K,i})\right) . \end{aligned}$$

We have:

$$\begin{aligned} \mathcal {F}_i(C_K^n,C_{L}^n,\Phi _K^n,\Phi _{L}^n) \le B\left( -k_i\log c^n-M'\right) \frac{1}{v_i} -B\left( k_i\log c^n+M'\right) \frac{1}{2Nv_i}. \end{aligned}$$

As the right-hand side tends to $-\infty$, the left-hand side is bounded away from zero. Using the previously detailed arguments, we have the desired limit.

Appendix C: Study of a numerical scheme for $h_i=\log (c_i)-\alpha \log (c_0)$

To prove the existence of solutions to the Sedan and centered scheme, we introduce this simplified cross diffusion system where the coupling occurs only through the solvent using the chemical potential defined above. This system is discretized using the ideas of the centered scheme and [13]. In detail, we use equations (2.4b), (2.4c) with $k_i,D_i=1$, $z_i=0$, and:

$$\begin{aligned}&\mathcal {F}_i(C_K,C_L,\Phi _{K},\Phi _{L})={\widetilde{C}}_{j}(C_K,C_L)\left( h_i(C_K)-h_i(C_L)\right) , \\&{\widetilde{C}}_j(C_K,C_L)=\frac{c_{K,i}-c_{L,i}}{\log (c_{K,i})-\log (c_{L,i})} \end{aligned}$$

where $h_i(C)$ is: $\log (c_i)-\alpha \log (c_0)$. We want to bound the concentrations away from zero uniformly in $\alpha$. This is the meaning of the following lemma, which is highly inspired by Lemma 3.5.

Lemma C.1

There exist $\epsilon =\min (\epsilon _0,\epsilon _1,\dots ,\epsilon _N)>0$ depending on, among other things, $C^0$ and decreasing with $h_{{\varvec{\Delta t}}}$ and $\min _{\sigma \in \mathcal {E}}\tau _{\sigma }$ such that for all ${\varvec{C}}^{n-1}\in \mathcal {A}^\mathcal {T}$ satisfying Lemma 3.3, $\alpha \in [0,1]$, we have:

$$\begin{aligned} c_{K,i}^n\ge \epsilon _ i \qquad \forall K,i \end{aligned}$$

The proof follows the same reasoning as for the full system and is only sketched here. Using (2.4c) we have:

$$\begin{aligned} \frac{c_{K,0}^n-c_{K,0}^{n-1}}{{\Delta t}_n}m_K&= -\sum _{\sigma =K|L\in \mathcal {E}_\text {int}}\tau _{\sigma } \left( c_{K,0}^n-c_{L,0}^n\right) \nonumber \\&\quad -\alpha \sum _{\sigma =K|L\in \mathcal {E}_\text {int}}\tau _{\sigma }\mathcal {R}(C_K^n,C_L^n)\left( \log (c_{K,0}^n)-\log (c_{L,0}^n)\right) \end{aligned}$$

(C.1)

where we have set:

$$\begin{aligned} \mathcal {R}(C_K,C_L)=\sum _{i=1}^{N}\frac{c_{K,i}-c_{L,i}}{\log (c_{K,i})-\log (c_{L,i})}. \end{aligned}$$

Remark 1.1

Noticing that $\mathcal {R}(C_K,C_L)\ge 0$ yields a maximum principle on $c^0$. As we did not assume that $c_0^0$ is uniformly positive, we have to compute further.

Multiplying (C.1) by $\log (c_{K,0}^n)$ and summing over $K\in \mathcal {T}$ yields:

$$\begin{aligned}&\sum _{K\in \mathcal {T}}\frac{c_{K,0}^n-c_{K,0}^{n-1}}{{\Delta t}_n}m_K\log (c_{K,0}^n)+\sum _{\sigma =K|L\in \mathcal {E}_{K}}\tau _{\sigma }D_{KL}{\varvec{c}}_0^n D_{KL}\log {\varvec{c}}_0^n\\&\quad +\alpha \sum _{\sigma =K|L\in \mathcal {E}_{K}}\tau _{\sigma }\mathcal {R}(C_K,C_L)\left( D_{KL}\log {\varvec{c}}_0^n\right) ^2=0 \end{aligned}$$

using the convexity of $u\log u$, we have:

$$\begin{aligned} \sum _{K\in \mathcal {T}}\frac{m_k}{{\Delta t}_n}(c_{K,0}^n\log (c_{K,0}^n)-c_{K,0}^{n-1}\log (c_{K,0}^{n-1}))\le & {} -\sum _{\sigma =K|L\in \mathcal {E}_{K}}\tau _{\sigma }D_{KL}{\varvec{c}}_0^n D_{KL}\log {\varvec{c}}_0^n\\&-\alpha \sum _{\sigma =K|L\in \mathcal {E}_{K}}\mathcal {R}(C_K,C_L)\left( D_{KL}\log {\varvec{c}}_0^n\right) ^2. \end{aligned}$$

We may now use the decay of this entropy to prove the desired result for $i=0$. To that extent we proceed as in Lemma 3.5 and see that $D_{KL}{\varvec{c}}_0^n D_{KL}\log {\varvec{c}}_0^n$ is clearly coercive in the sense of lemma 3.2 while the part in $\alpha$ has the right sign. This yields the uniform bound for ${\varvec{c}}_0$.

The bound for ${\varvec{c}}_i$ relies on the entropy ${\widetilde{H}}=\sum _{j=1}^{N}c_j\log (c_j)+\alpha c_0\log (c_0)$. As for Lemma A.1, this entropy restricted to $\mathcal {A}$ is convex and its derivatives as a function of $\mathbb R^N$ are the chemical potentials, Thus multiplying the conservation equation by h yields:

$$\begin{aligned} \sum _{K\in \mathcal {T}}m_K\left( {\widetilde{H}}(C_K^n)-{\widetilde{H}}(C_K^{n-1})\right) \le \sum _{\sigma \in \mathcal {E}_\text {int}}\sum _{j=1}^{N} {\widetilde{C}}_{\sigma ,j} \left( D_\sigma h_j({\varvec{C}}^n)\right) ^2. \end{aligned}$$

This new dissipation is also coercive in the sense of Lemma 3.2, thus we can proceed as in Lemma 3.5 to get the announced bounds.

Appendix D: A simple convergence lemma

In this section, we express the results of [9] lemma 4.2 and [13,  lemma 4.2] in a more generic fashion. We let $\mathcal {T}_m$ be a sequence of admissible meshes of $\text{\O}mega$ such that $h_{\mathcal {T}_m}\rightarrow 0$, ${\varvec{u}}_m \in \mathbb R^{\mathcal {T}_m}$, and ${\widetilde{{\varvec{u}}}}_{m}\in \mathbb R^{\mathcal {E}^{\text {int}}_m}$ such that for all $\sigma =K|L\in \mathcal {E}^{\text {int}}_m$:

$$\begin{aligned} \min (u_K,u_L)\le {\widetilde{u}}_{\sigma ,m}\le \max (u_K,u_L). \end{aligned}$$

Lemma D.1

If we dispose of $p\in [1,\infty )$ such that

$$\begin{aligned} h_{\mathcal {T}_m}\Vert \nabla _{\mathcal {T}_m}{\varvec{u}}_{m}\Vert _{L^p(\text{\O}mega )}\rightarrow 0 \end{aligned}$$

The $L^1$ convergence of the natural and diamond reconstructions are equivalent, moreover if one of them is convergent, they share the same limit.

Proof

This result is equivalent to:

$$\begin{aligned} \Vert \pi _{\mathcal {T}_m}{\varvec{u}}_m-{\widetilde{{\varvec{u}}}}_{m,\mathcal {E}_m}\Vert _{L^1(\text{\O}mega )}\rightarrow 0. \end{aligned}$$

For the sake of simplicity, we drop the subscript m for the rest of the proof. We let $\Delta _{K\sigma }$ be the half diamond cell $\Delta _\sigma \cap K$, and notice that $m(\Delta _{K\sigma })=\frac{1}{d} m_\sigma d(x_K,\sigma )\le \frac{h_{\mathcal {T}}m_\sigma }{d}$. Elementary calculations yield:

$$\begin{aligned} \Vert \pi _{\mathcal {T}}{\varvec{u}}-{\widetilde{{\varvec{u}}}}_{\mathcal {E}}\Vert _{L^1(\text{\O}mega )}\le \frac{h_\mathcal {T}}{d}\sum _{K\in \mathcal {T}}\sum _{\sigma \in \mathcal {E}_K}m_\sigma |u_K-u_\sigma |. \end{aligned}$$

Thanks to our average assumption, we have $|u_K-u_\sigma |\le D_\sigma {\varvec{u}}$ thus:

$$\begin{aligned} \Vert \pi _{\mathcal {T}}{\varvec{u}}-{\widetilde{{\varvec{u}}}}_{\mathcal {E}}\Vert _{L^1(\text{\O}mega )}\le \frac{2h_\mathcal {T}}{d}\sum _{\sigma \in \mathcal {E}^{\text {int}}}m_\sigma D_\sigma {\varvec{u}}. \end{aligned}$$

Let p be as in the lemma and q its Hölder conjugate. We have:

$$\begin{aligned} \sum _{\sigma \in \mathcal {E}^{\text {int}}}m_\sigma D_\sigma {\varvec{u}}\le \left( \sum _{\sigma \in \mathcal {E}^{\text {int}}}m_\sigma d_\sigma \left( \frac{D_\sigma {\varvec{u}}}{d_\sigma }\right) ^p\right) ^\frac{1}{p}\left( \sum _{\sigma \in \mathcal {E}^{\text {int}}}m_\sigma d_\sigma \right) ^\frac{1}{q}\le d m(\text{\O}mega )^\frac{1}{q}\Vert \nabla _{\mathcal {T}}{\varvec{u}}\Vert _{L^p(\text{\O}mega )}, \end{aligned}$$

hence:

$$\begin{aligned} \Vert \pi _{\mathcal {T}}{\varvec{u}}-{\widetilde{{\varvec{u}}}}_{\mathcal {E}}\Vert _{L^1(\text{\O}mega )}\le 2m(\text{\O}mega )^\frac{1}{q} h_\mathcal {T}\Vert \nabla _{\mathcal {T}}{\varvec{u}}\Vert _{L^p(\text{\O}mega )}\rightarrow 0. \end{aligned}$$

(D.1)

This concludes the proof of the lemma.$\square$

For reconstructions in $\text{\O}mega \times [0,T]$, we consider ${\varvec{u}}_{m}\in \mathbb R^{\mathcal {T}_m\times {\varvec{\Delta t}}_m}$, ${\widetilde{{\varvec{u}}}}_{m}\in \mathbb R^{\mathcal {E}^{\text {int}}_m\times {\varvec{\Delta t}}_m}$ satisfying the same average property, and we have the same result.

Lemma D.2

If we dispose of $p\in [1,\infty )$, ${\widetilde{p}}\in [1,\infty )$ such that

$$\begin{aligned} h_{\mathcal {T}_m}\Vert \nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{u}}_{m}\Vert _{L^{\widetilde{p}}([0,T],L^p(\text{\O}mega ))}\rightarrow 0 \end{aligned}$$

The $L^1(\text{\O}mega \times [0,T])$ convergence of the natural and diamond reconstructions are equivalent, moreover if one of them is convergent, they share the same limit.

Proof

This result is equivalent to:

$$\begin{aligned} \Vert \pi _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{u}}_m-{\widetilde{{\varvec{u}}}}_{m,\mathcal {E}_m,{\varvec{\Delta t}}_m}\Vert _{L^1(\text{\O}mega \times [0,T])}\rightarrow 0. \end{aligned}$$

We make use of the computations for the previous lemma, namely (D.1) yields for all $n \in \mathbf{[}\mathbf{[}1,N_{T,m}\mathbf{]}\mathbf{]}$:

$$\begin{aligned} \Vert \pi _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{u}}_m^n-{\widetilde{{\varvec{u}}}}_{m,\mathcal {E}_m,{\varvec{\Delta t}}_m}^n\Vert _{L^1(\text{\O}mega )}\le 2m(\text{\O}mega )^\frac{1}{q} h_{\mathcal {T}_m}\Vert \nabla _{\mathcal {T}_m}{\varvec{u}}^n\Vert _{L^p(\text{\O}mega )}. \end{aligned}$$

Thus:

$$\begin{aligned} \Vert \pi _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{u}}_m-{\widetilde{{\varvec{u}}}}_{m,\mathcal {E}_m,{\varvec{\Delta t}}_m}\Vert _{L^1(\text{\O}mega \times [0,T])}\le 2 m(\text{\O}mega )^\frac{1}{q}h_{\mathcal {T}_m}\sum _{n=1}^{N_{T,m}}{\Delta t}_n\Vert \nabla _{\mathcal {T}_m}{\varvec{u}}^n\Vert _{L^p(\text{\O}mega )}. \end{aligned}$$

Hölder’s inequality yields:

$$\begin{aligned} \Vert \pi _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{u}}_m-{\widetilde{{\varvec{u}}}}_{m,\mathcal {E}_m,{\varvec{\Delta t}}_m}\Vert _{L^1(\text{\O}mega \times [0,T])}\le 2 m(\text{\O}mega )^\frac{1}{q}T^\frac{1}{{\widetilde{q}}} h_{\mathcal {T}_m} \Vert \nabla _{\mathcal {T}_m,{\varvec{\Delta t}}_m}{\varvec{u}}\Vert _{L^{\widetilde{p}}([0,T],L^p(\text{\O}mega ))}, \end{aligned}$$

where ${\widetilde{q}}$ is the Hölder conjugate of ${\widetilde{p}}$. Using the assumed estimation of the gradient, we have the announced result.$\square$