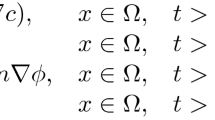Abstract
This paper deals with an initial-boundary value problem for the chemotaxis-(Navier–)Stokes system
in a bounded convex domain \(\Omega \subset \mathbb {R}^2\) with smooth boundary, with \(\kappa \in \mathbb {R}\) and a given smooth potential \(\phi :\Omega \rightarrow \mathbb {R}\). It is known that for each \(\kappa \in \mathbb {R}\) and all sufficiently smooth initial data this problem possesses a unique global classical solution \((n^{(\kappa )},c^{(\kappa )},u^{(\kappa }))\). The present work asserts that these solutions stabilize to \((n^{(0)},c^{(0)},u^{(0)})\) uniformly with respect to the time variable. More precisely, it is shown that there exist \(\mu >0\) and \(C>0\) such that whenever \(\kappa \in (-1,1)\),
for all \(t>0\). This result thereby provides an example for a rigorous quantification of stability properties in the Stokes limit process, as frequently considered in the literature on chemotaxis-fluid systems in application contexts involving low Reynolds numbers.
Similar content being viewed by others
References
Amann, H.: Compact embeddings of vector-valued Sobolev and Besov spaces. Glasnik Mat. 35(55), 161–177 (2000)
Bellomo, N., Bellouquid, A., Tao, Y., Winkler, M.: Toward a mathematical theory of Keller–Segel models of pattern formation in biological tissues. Math. Models Methods Appl. Sci. 25, 1663–1763 (2015)
Biler, P., Hebisch, W., Nadzieja, T.: The Debye system: existence and large time behavior of solutions. Nonlinear Anal. TMA 23(9), 1189–1209 (1994)
Cao, X., Lankeit, J.: Global classical small-data solutions for a three-dimensional chemotaxis Navier–Stokes system involving matrix-valued sensitivities. Calc. Var. 55, 107 (2016)
Chae, M., Kang, K., Lee, J.: Global existence and temporal decay in Keller–Segel models coupled to fluid equations. Commun. Partial Differ. Equ. 39, 1205–1235 (2014)
Difrancesco, M., Lorz, A., Markowich, P.A.: Chemotaxis-fluid coupled model for swimming bacteria with nonlinear diffusion: global existence and asymptotic behavior. Discrete Contin. Dyn. Syst. A 28, 1437–1453 (2010)
Duan, R., Lorz, A., Markowich, P.A.: Global solutions to the coupled chemotaxis-fluid equations. Commun. Partial Differ. Equ. 35, 1635–1673 (2010)
Duan, R., Xiang, Z.: A note on global existence for the chemotaxis—Stokes model with nonlinear diffusion. Int. Math. Res. Notices IMRN 2014, 1833–1852 (2014)
Espejo, E.E., Winkler, M.: Global classical solvability and stabilization in a two-dimensional chemotaxis-Navier–Stokes system modeling coral fertilization (preprint)
Friedman, A.: Partial Differential Equations. Holt, Rinehart and Winston, New York (1969)
Fujie, K., Ito, A., Winkler, M., Yokota, T.: Stabilization in a chemotaxis model for tumor invasion. Discrete Contin. Dyn. Syst. 36, 151–169 (2016)
Fujita, H., Kato, T.: On the Navier–Stokes initial value problem. I. Arch. Ration. Mech. Anal. 16, 269–315 (1964)
Fujiwara, D., Morimoto, H.: An \(L^r\)-theorem of the Helmholtz decomposition of vector fields. J. Fac. Sci. Univ. Tokyo 24, 685–700 (1977)
Giga, Y.: Solutions for semilinear parabolic equations in \(L_p\) and regularity of weak solutions of the Navier–Stokes system. J. Differ. Equ. 61, 186–212 (1986)
Giga, Y., Sohr, H.: Abstract \(L^p\) estimates for the Cauchy problem with applications to the Navier–Stokes equations in exterior domains. J. Funct. Anal. 102, 72–94 (1991)
Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Springer, Berlin (1981)
Herschlag, G., Miller, M.: Reynolds number limits for jet propulsion: a numerical study of simplified jellyfish. J. Theor. Biol. 285, 84–95 (2011)
Kozono, H., Miura, M., Sugiyama, Y.: Existence and uniqueness theorem on mild solutions to the Keller–Segel system coupled with the Navier–Stokes fluid. J. Funct. Anal. 2(70), 1663–1683 (2016)
Leray, J.: Sur le mouvement d’un liquide visqueus amplissant l’espace. Acta Math. 63, 193–248 (1934)
Ladyzenskaja, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasi-Linear Equations of Parabolic Type. In: Translations of Mathematical Monographs, vol. 23, American Mathematical Society, Providence, R.I. (1968)
Liu, J., Lorz, A.: A coupled chemotaxis-fluid model: global existence. Ann. I. H. Poincaré-AN 28, 643–652 (2011)
Lieberman, G.: Hölder continuity of the gradient of solutions of uniformly parabolic equations with conormal boundary conditions. Ann. Mat. Pura Appl. 148, 77–99 (1987)
Lions, P.L.: Résolution de problèmes elliptiques quasilinéaires. Arch. Ration. Mech. Anal. 74, 335–353 (1980)
Porzio, M.M., Vespri, V.: Hölder estimates for local solutions of some doubly nonlinear degenerate parabolic equations. J. Differ. Equ. 103(1), 146–178 (1993)
Sohr, H.: The Navier–Stokes Equations. An Elementary Functional Analytic Approach. Birkhäuser, Basel (2001)
Tan, Z., Zhang, X.: Decay estimates of the coupled chemotaxis-fluid equations in \({\mathbb{R}}^3\). J. Math. Anal. Appl. 410(1), 27–38 (2014)
Tao, Y.: Boundedness in a chemotaxis model with oxygen consumption by bacteria. J. Math. Anal. Appl. 381, 521–529 (2011)
Tao, Y., Winkler, M.: Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J. Differ. Equ. 252, 2520–2543 (2012)
Tao, Y., Winkler, M.: Global existence and boundedness in a Keller–Segel–Stokes model with arbitrary porous medium diffusion. Discrete Contin. Dyn. Syst. A 32(5), 1901–1914 (2012)
Tao, Y., Winkler, M.: Locally bounded global solutions in a three-dimensional chemotaxis-Stokes system with nonlinear diffusion. Ann. I. H. Poincaré-AN 30, 157–178 (2013)
Tao, Y., Winkler, M.: Energy-type estimates and global solvability in a two-dimensional chemotaxis-haptotaxis model with remodeling of non-diffusible attractant. J. Differ. Equ. 257, 784–815 (2014)
Tuval, I., Cisneros, L., Dombrowski, C., Kessler, J.O., Goldstein, R.E.: Bacterial swimming and oxygen transport near contact lines. Proc. Natl. Acad. Sci. 102, 2277–2282 (2005)
Vorotnikov, D.: Weak solutions for a bioconvection model related to Bacillus subtilis. Commun. Math. Sci. 12, 545–563 (2014)
Wang, Y., Cao, X.: Global classical solutions of a 3D chemotaxis-Stokes system with rotation. Discrete Contin. Dyn. Syst. B 20, 3235–3254 (2015)
Wang, Y., Xiang, Z.: Global existence and boundedness in a Keller–Segel–Stokes system involving a tensor-valued sensitivity with saturation. J. Differ. Equ. 259, 7578–7609 (2015)
Winkler, M.: Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 248, 2889–2905 (2010)
Winkler, M.: Global large-data solutions in a chemotaxis-(Navier–)Stokes system modeling cellular swimming in fluid drops. Commun. Partial Differ. Equ. 37, 319–351 (2012)
Winkler, M.: Stabilization in a two-dimensional chemotaxis-Navier–Stokes system. Arch. Ration. Mech. Anal. 211(2), 455–487 (2014)
Winkler, M.: Boundedness and large time behavior in a three-dimensional chemotaxis-Stokes system with nonlinear diffusion and general sensitivity. Calc. Variat. 54, 3789–3828 (2015)
Winkler, M.: Global weak solutions in a three-dimensional chemotaxis-Navier–Stokes system. Ann. I. H. Poincaré-AN 33, 1329–1352 (2016)
Winkler, M.: How far do chemotaxis-driven forces influence regularity in the Navier–Stokes system? Trans. Am. Math. Soc. 369, 3067–3125 (2017)
Ye, X.: Existence and decay of global smooth solutions to the coupled chemotaxis-fluid model. J. Math. Anal. Appl. 427, 60–73 (2015)
Zhang, Q., Li, Y.: Convergence rates of solutions for a two-dimensional chemotaxis-Navier–Stokes system. Discrete Contin. Dyn. Syst. Ser. B 20, 2751–2759 (2015)
Zhang, Q., Li, Y.: Global weak solutions for the three-dimensional chemotaxis-Navier–Stokes system with nonlinear diffusion. J. Differ. Equ. 259, 3730–3754 (2015)
Zhang, Q., Zheng, X.: Global well-posedness for the two-dimensional incompressible chemotaxis-Navier–Stokes equations. SIAM J. Math. Anal. 46, 3078–3105 (2014)
Acknowledgements
This work was initiated while the second author visited Xihua University and the University of Electronic Science and Technology of China in Chengdu in January 2016. He is very grateful for the warm hospitality. Y. Wang was supported by the NNSF of China (no. 11501457). Z. Xiang was supported by the NNSF of China (no. 11571063, 11501086).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, Y., Winkler, M. & Xiang, Z. The small-convection limit in a two-dimensional chemotaxis-Navier–Stokes system. Math. Z. 289, 71–108 (2018). https://doi.org/10.1007/s00209-017-1944-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-017-1944-6