Abstract
We prove a Faber-Krahn inequality for the first eigenvalue of the Laplacian with Robin boundary conditions, asserting that amongst all Lipschitz domains of fixed volume, the ball has the smallest first eigenvalue. We prove the result in all space dimensions using ideas from [M.-H. Bossel, C. R. Acad. Sci. Paris Sér. I Math. 302 (1986), 47–50], where a proof for smooth domains in the plane was given. The method does not involve the use of symmetrisation arguments. The results also imply variants of the Cheeger inequality for the first eigenvalue.
Similar content being viewed by others
References
Agmon, S.: On the eigenfunctions and on the eigenvalues of general elliptic boundary value problems. Comm. Pure Appl. Math. 15, 119–147 (1962)
Ahlfors, L.V.: Conformal invariants: topics in geometric function theory. McGraw-Hill Book Co., New York (1973)
Arendt, W., Warma, M.: The Laplacian with Robin boundary conditions on arbitrary domains. Potential Anal. 19(4), 341–363 (2003). DOI 10.1023/A:1024181608863
Bandle, C.: Isoperimetric inequalities and applications, Monographs and Studies in Mathematics, vol. 7. Pitman, Boston, Mass. (1980)
Bossel, M.H.: Longueurs extrémales et fonctionnelles de domaine. Complex Variables Theory Appl. 6(2–4), 203–234 (1986)
Bossel, M.H.: Membranes élastiquement liées: extension du théorème de Rayleigh-Faber-Krahn et de l'inégalité de Cheeger. C. R. Acad. Sci. Paris Sér. I Math. 302(1), 47–50 (1986)
Bossel, M.H.: Membranes élastiquement liées inhomogènes ou sur une surface: une nouvelle extension du théorème isopérimétrique de Rayleigh-Faber-Krahn. Z. Angew. Math. Phys. 39(5), 733–742 (1988)
Burago, Y.D., Zalgaller, V.A.: Geometric inequalities, Grundlehren der Mathematischen Wissenschaften, vol. 285. Springer-Verlag, Berlin (1988)
Dancer, E.N., Daners, D.: Domain perturbation for elliptic equations subject to Robin boundary conditions. J. Differential Equations 138(1), 86–132 (1997). DOI 10.1006/jdeq.1997.3256
Daners, D.: Robin boundary value problems on arbitrary domains. Trans. Amer. Math. Soc. 352(9), 4207–4236 (2000). DOI 10.1090/S0002-9947-00-02444-2
Daners, D.: Dirichlet problems on varying domains. J. Differential Equations 188(2), 591–624 (2003).
Doktor, P.: Approximation of domains with Lipschitzian boundary. Časopis Pěst. Mat. 101(3), 237–255 (1976)
Evans, L.C., Gariepy, R.F.: Measure theory and fine properties of functions. Studies in Advanced Mathematics. CRC Press, Boca Raton, FL (1992)
Faber, G.: Beweis dass unter allen homogenen Membranen von gleicher Fläche und gleicher Spannung die kreisförmige den tiefsten Grundton gibt. Sitzungsbericht der bayrischen Akademie der Wissenschaften pp. 169–172 (1923)
Federer, H.: Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, vol. 153. Springer-Verlag New York Inc., New York (1969)
Fraenkel, L.E.: An introduction to maximum principles and symmetry in elliptic problems, Cambridge Tracts in Mathematics, vol. 128. Cambridge University Press, Cambridge (2000)
Gilbarg, D., Trudinger, N.S.: Elliptic partial differential equations of second order, Grundlehren der Mathematischen Wissenschaften, vol. 224, second edn. Springer-Verlag, Berlin (1983)
Henrot, A.: Minimization problems for eigenvalues of the Laplacian. J. Evol. Equ. 3(3), 443–461 (2003).
Hersch, J.: Sur la fréquence fondamentale d'une membrane vibrante: évaluations par défaut et principe de maximum. Z. Angew. Math. Phys. 11, 387–413 (1960)
Hirsch, M.W.: Differential topology, Graduate Texts in Mathematics, vol. 33. Springer-Verlag, New York (1976)
Kawohl, B.: Rearrangements and convexity of level sets in PDE, Lecture Notes in Mathematics, vol. 1150. Springer-Verlag, Berlin (1985)
Krahn, E.: Über eine von Rayleigh formulierte Minimaleigenschaft des Kreises. Math. Ann. 94, 97–100 (1924)
Lax, P.D., Phillips, R.S.: On the scattering frequencies of the Laplace operator for exterior domains. Comm. Pure Appl. Math. 25, 85–101 (1972)
Maz'ja, V.G.: Sobolev spaces. Springer Series in Soviet Mathematics. Springer-Verlag, Berlin (1985). Translated from the Russian by T. O. Shaposhnikova
Nečas, J.: On domains of type
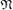 . Czechoslovak Math. J. 12(87), 274–287 (1962)
. Czechoslovak Math. J. 12(87), 274–287 (1962)Nečas, J.: Les méthodes directes en théorie des équations elliptiques. Academia, Prague (1967)
Osserman, R.: The isoperimetric inequality. Bull. Amer. Math. Soc. 84(6), 1182–1238 (1978)
Payne, L.E.: Isoperimetric inequalities and their applications. SIAM Rev. 9, 453–488 (1967)
Payne, L.E., Weinberger, H.F.: Lower bounds for vibration frequencies of elastically supported membranes and plates. SIAM J. 5, 171–182 (1957)
Pólya, G., Szegö, G.: Isoperimetric Inequalities in Mathematical Physics. Annals of Mathematics Studies, no. 27. Princeton University Press, Princeton, N. J. (1951)
Rudin, W.: Real and Complex Analysis, 2nd edn. McGraw-Hill Inc., New York (1974)
Sperb, R.: Bounds for the first eigenvalue of the elastically supported membrane on convex domains. Z. Angew. Math. Phys. 54(5), 879–903 (2003)
Sperb, R.P.: Untere und obere Schranken für den tiefsten Eigenwert der elastisch gestützten Membran. Z. Angew. Math. Phys. 23, 231–244 (1972)
Sperb, R.P.: An isoperimetric inequality for the first eigenvalue of the Laplacian under Robin boundary conditions. In: W. Walter (ed.) General Inequalities 6, International Series of Numerical Mathematics, vol. 103, pp. 361–367. Birkhäuser, Basel (1992)
Watson, G.N.: A Treatise on the Theory of Bessel Functions, 2nd edn. Cambridge University Press, Cambridge, England (1944)
Whitney, H.: A function not constant on a connected set of critical points. Duke Math. J. 1, 514–517 (1935)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Daners, D. A Faber-Krahn inequality for Robin problems in any space dimension. Math. Ann. 335, 767–785 (2006). https://doi.org/10.1007/s00208-006-0753-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-006-0753-8





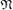 . Czechoslovak Math. J. 12(87), 274–287 (1962)
. Czechoslovak Math. J. 12(87), 274–287 (1962)