Skip to main content
SpringerLink
Log in

Darcy’s Flow with Prescribed Contact Angle: Well-Posedness and Lubrication Approximation

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

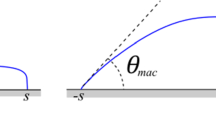
We consider the spreading of a thin two-dimensional droplet on a solid substrate. We use a model for viscous fluids where the evolution is governed by Darcy’s law. At the contact point where air and liquid meet the solid substrate, a constant, non-zero contact angle (partial wetting) is assumed. We show local and global well-posedness of this free boundary problem in the presence of the moving contact point. Our estimates are uniform in the contact angle assumed by the liquid at the contact point. In the so-called lubrication approximation (long-wave limit) we show that the solutions converge to the solution of a one-dimensional degenerate parabolic fourth order equation which belongs to a family of thin-film equations. The main technical difficulty is to describe the evolution of the non-smooth domain and to identify suitable spaces that capture the transition to the asymptotic model uniformly in the small parameter \({\varepsilon}\) .

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ambrose, D.M.: Well-posedness of two-phase Hele-Shaw flow without surface tension. Eur. J. Appl. Math. 15(5), 597–607 (2004). y:10.1017/S0956792504005662

  2. Ambrose D.M., Masmoudi N.: The zero surface tension limit of two-dimensional water waves. Commun. Pure Appl. Math. 58(10), 1287–1315 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  3. Angenent S.: Analyticity of the interface of the porous media equation after the waiting time. Proc. Am. Math. Soc. 102(2), 329–336 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bazaliy B.V., Friedman A.: The Hele-Shaw problem with surface tension in a half-plane. J. Differ. Equ. 216(2), 439–469 (2005)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  5. Bazaliy B.V., Friedman A.: The Hele-Shaw problem with surface tension in a half-plane: a model problem. J. Differ. Equ. 216(2), 387–438 (2005)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  6. Bear, J.: Dynamics of Fluids in Porous Media. Dover Publications, New York, 1972

  7. Beretta, E., Bertsch, M., Dal Passo, R.: Nonnegative solutions of a fourth-order nonlinear degenerate parabolic equation. Arch. Ration. Mech. Anal. 129(2), 175–200 (1995)

  8. Bertozzi A.L., Pugh M.: The lubrication approximation for thin viscous films: regularity and long-time behavior of weak solutions. Commun. Pure Appl. Math. 49(2), 85–123 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bertsch M., Giacomelli L., Karali G.: Thin-film equations with “partial wetting” energy: existence of weak solutions. Phys. D 209(1–4), 17–27 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  10. Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Lopez-Fernandez, M.: Rayleigh–Taylor breakdown for the Muskat problem with applications to water waves. Ann. Math. (2) 175(2), 909–948 (2012). doi:10.4007/annals.2011.173.1.10

  11. Constantin P., Pugh M.: Global solutions for small data to the Hele-Shaw problem. Nonlinearity 6(3), 393–415 (1993)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  12. Córdoba, A., Córdoba, D., Gancedo, F.: Interface evolution: the Hele-Shaw and Muskat problems. Ann. Math. (2) 173(1), 477–542 (2011). doi:10.4007/annals.2011.173.1.10

  13. Coutand, D., Shkoller, S.: Well-posedness of the free-surface incompressible Euler equations with or without surface tension. J. Am. Math. Soc. 20(3), 829–930 (2007). doi:10.1090/S0894-0347-07-00556-5

  14. Daskalopoulos P., Hamilton R.: Regularity of the free boundary for the porous medium equation. J. Am. Math. Soc. 11(4), 899–965 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  15. Duchon, J., Robert, R.: Évolution d’une interface par capillarité et diffusion de volume. I. Existence locale en temps. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(5), 361–378 (1984)

  16. Eidelman, S.D.: Parabolic Systems. Translated from the Russian by Scripta Technica, London. North-Holland Publishing Co., Amsterdam, 1969

  17. Escher J., Simonett G.: Classical solutions for Hele-Shaw models with surface tension. Adv. Differ. Equ. 2(4), 619–642 (1997)

    MathSciNet  MATH  Google Scholar 

  18. Escher, J., Simonett, G.: Classical solutions for the quasi-stationary Stefan problem with surface tension. Differential Equations, Asymptotic Analysis, and Mathematical Physics (Potsdam, 1996), Math. Res., Vol. 100. Akademie, Berlin, 98–104, 1997

  19. Germain, P., Masmoudi, N., Shatah, J.: Global solutions for the gravity water waves equation in dimension 3. Ann. Math. (2) 175(2), 691–754 (2012)

  20. Giacomelli, L., Gnann, M.V., Knüpfer, H., Otto, F.: Well-posedness for the Navier-slip thin-film equation in the case of complete wetting. J. Differ. Equ. 257(1), 15–81 (2014). doi:10.1016/j.jde.2014.03.010

  21. Giacomelli, L., Knüpfer, H.: A free boundary problem of fourth order: classical solutions in weighted Hölder spaces. Comm. Partial Differ. Equ. 35(11), 2059–2091 (2010). doi:10.1080/03605302.2010.494262

  22. Giacomelli L., Knüpfer H., Otto F.: Smooth zero-contact-angle solutions to a thin-film equation around the steady state. J. Differ. Equ. 245(6), 1454–1506 (2008)

    Article  ADS  MATH  Google Scholar 

  23. Giacomelli L., Otto F.: Variational formulation for the lubrication approximation of the Hele-Shaw flow. Calc. Var. Partial Differ. Equ. 13(3), 377–403 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  24. Giacomelli L., Otto F.: Rigorous lubrication approximation. Interfaces Free Bound. 5(4), 483–529 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  25. Kawarada H., Koshigoe H.: Unsteady flow in porous media with a free surface. Jpn. J. Ind. Appl. Math. 8(1), 41–84 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  26. Knüpfer H.: Navier slip thin-film equation for partial wetting. Commun. Pure Appl. Math. 64(9), 1263–1296 (2011)

    Article  MATH  Google Scholar 

  27. Knüpfer, H., Masmoudi, N.: Well-posedness and uniform bounds for a nonlocal third order evolution operator on an infinite wedge. Comm. Math. Phys. 320(2), 395–424 (2013). doi:10.1007/s00220-013-1708-z

  28. Koch, H.: Non-euclidean singular integrals and the porous medium equation. Ph.D. thesis, Dortmund (1999)

  29. Kozlov, V.A., Mazya, V.G., Rossmann, J.: Elliptic boundary value problems in domains with point singularities. Mathematical Surveys and Monographs, Vol. 52. Am. Math. Soc., Providence, 1997

  30. Krylov, N.V.: Lectures on elliptic and parabolic equations in Sobolev spaces. Graduate Studies in Mathematics, Vol. 96. American Mathematical Society, Providence, 2008

  31. Lannes D.: Well-posedness of the water-waves equations. J. Am. Math. Soc. 18(3), 605–654 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lindblad, H.: Well-posedness for the motion of an incompressible liquid with free surface boundary. Ann. Math. (2) 162(1), 109–194 (2005)

  33. Masmoudi, N., Rousset, F.: Uniform regularity and vanishing viscosity limit for the free surface Navier–Stokes equations (2012). arXiv:1202.0657

  34. McGeough J., Rasmussen H.: On the derivation of the quasi-steady model in electrochemical machining. J. Inst. Math. Appl. 13(1), 13–21 (1974)

    Article  Google Scholar 

  35. Otto F.: Lubrication approximation with prescribed nonzero contact angle. Commun. Partial Differ. Equ. 23(11–12), 2077–2164 (1998)

    MATH  Google Scholar 

  36. Prokert G.: Existence results for Hele-Shaw flow driven by surface tension. Eur. J. Appl. Math. 9(2), 195–221 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  37. Ren, W., Hu, D., Weinan, E.: Continuum models for the contact line problem. Phys. Fluids 22(10), 102103 (2010)

  38. Reynolds O.: On the theory of lubrication and its application to mr. beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Proc. R. Soc. Lond. 40, 191–203 (1886)

    Article  Google Scholar 

  39. Rubenstein, L.I.: The Stefan problem. Translated from the Russian by A. D. Solomon. Translations of Mathematical Monographs, Vol. 27. American Mathematical Society, Providence, 1971

  40. Shatah, J., Zeng, C.: Geometry and a priori estimates for free boundary problems of the Euler equation. Commun. Pure Appl. Math. 61(5), 698–744 (2008). doi:10.1002/cpa.20213

  41. Siegel, M., Caflisch, R.E., Howison, S.: Global existence, singular solutions, and ill-posedness for the Muskat problem. Commun. Pure Appl. Math. 57(10), 1374–1411 (2004). doi:10.1002/cpa.20040

  42. Simon, J.: Compact sets in the space L p(0, T; B). Ann. Math. Pura Appl. 146(4), 65–96 (1987). doi:10.1007/BF01762360

  43. Tabeling, P.: Growth and Form: Nonlinear Aspe. Springer, New York, 1991

  44. Wu, S.: Global wellposedness of the 3-D full water wave problem. Invent. Math. 184(1), 125–220 (2011). doi:10.1007/s00222-010-0288-1

  45. Young, T.: An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 95, 65–87 (1805). http://www.jstor.org/stable/107159

  46. Zhang, P., Zhang, Z.: On the free boundary problem of three-dimensional incompressible Euler equations. Commun. Pure Appl. Math. 61(7), 877–940 (2008). doi:10.1002/cpa.20226

Download references

Author information

Authors and Affiliations

  1. University of Heidelberg, Im Neuenheimer Feld 294, 69120, Heidelberg, Germany

    Hans Knüpfer

  2. Courant Institute of Mathematical Sciences, 251 Mercer Street, New York, NY, 10012, USA

    Nader Masmoudi

Authors
  1. Hans Knüpfer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nader Masmoudi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hans Knüpfer.

Additional information

Communicated by Felix Otto

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Knüpfer, H., Masmoudi, N. Darcy’s Flow with Prescribed Contact Angle: Well-Posedness and Lubrication Approximation. Arch Rational Mech Anal 218, 589–646 (2015). https://doi.org/10.1007/s00205-015-0868-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-015-0868-8

Keywords

Search

Navigation