Abstract
In the regime of lubrication approximation, we look at spreading phenomena under the action of singular potentials of the form \(P(h)\approx h^{1-m}\) as \(h\rightarrow 0^+\) with \(m>1\), modeling repulsion between the liquid–gas interface and the substrate. We assume zero slippage at the contact line. Based on formal analysis arguments, we report that for any \(m>1\) and any value of the speed (both positive and negative) there exists a three-parameter, hence generic, family of fronts (i.e., traveling-wave solutions with a contact line). A two-parameter family of advancing “linear-log” fronts also exists, having a logarithmically corrected linear behavior in the liquid bulk. All these fronts have finite rate of dissipation, indicating that singular potentials stand as an alternative solution to the contact-line paradox. In agreement with steady states, fronts have microscopic contact angle equal to \(\pi /2\) for all \(m>1\) and finite energy for all \(m<3\). We also propose a selection criterion for the fronts, based on thermodynamically consistent contact-line conditions modeling friction at the contact line. So as contact-angle conditions do in the case of slippage models, this criterion selects a unique (up to translation) linear-log front for each positive speed. Numerical evidence suggests that, fixed the speed and the frictional coefficient, its shape depends on the spreading coefficient, with steeper fronts in partial wetting and a more prominent precursor region in dry complete wetting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is about half a century since the no-slip paradox was discovered by Huh and Scriven (1971) and Dussan and Davis (1974). The paradox may be summarized as follows: take a liquid droplet which is sliding over a solid dry substrate, as modeled by Stokes equations; if the no-slip condition were adopted, that is, if a null liquid’s horizontal velocity were prescribed at the liquid–solid interface, then an infinite force would be required to move the contact line, i.e., the triple junction where solid, liquid and gas meet. In the words of Huh and Scriven (1971), “not even Herakles could sink a solid”. The paradox may be discussed already in the framework of lubrication approximation: this is an asymptotic limit of the full Navier–Stokes system under a suitable scaling, which in words requires a small ratio of vertical vs horizontal length-scale, a relatively small velocity, and a relatively large surface tension. It is a simplified model which, however, retains the essential physics at such scales: a dissipative evolution driven by surface tension and limited by both viscous and interfacial friction (see, for example, (1.7), (3.4), and (3.13)). In fact, generic contact lines, at leading order around one of their points, are locally straight: therefore the essential features of the contact-line paradox are already captured by a one-dimensional setting, which we therefore adopt in the sequel.
1.1 The Model
In lubrication theory, the evolution of a thin liquid film, or a droplet, of viscous incompressible liquid over a horizontal solid substrate is described by the thin-film equation (Greenspan 1978; Hocking 1983; Oron et al. 1997; Giacomelli and Otto 2003; Knüpfer and Masmoudi 2015), which in its basic one-dimensional form reads as:

Here the solid substrate corresponds to the x-axis, t is time, h(t, x) is the liquid’s height over the solid, \(\mu \) is the liquid’s viscosity, and \(\gamma \) is the liquid–gas surface tension. The mobility function  depends on the condition at the liquid–solid interface: when the no-slip condition is assumed, then
depends on the condition at the liquid–solid interface: when the no-slip condition is assumed, then

The potential Q usually combines the effects of intermolecular, surface, and gravitational forces (de Gennes 1985); here, we shall ignore the latter ones for simplicity:
The constant S (assumed to be relatively small in lubrication theory, cf. Remark 1.2) is the non-dimensional spreading coefficient:
where \(\gamma _{SL}\), and \(\gamma _{SG}\) are the solid–liquid and solid-gas tensions, respectively. There is, however, a caveat to be made at this point. In thermodynamic equilibrium of the solid with the surrounding vapor phase (the so-called moist case, which concerns, for instance, a surface which has been pre-exposed to vapor), \(\gamma _{SG}\) is usually denoted by \(\gamma _{SV}\), and its value can never exceed \(\gamma _{SL}+\gamma \). Indeed, otherwise the free energy of a solid/vapor interface could be lowered by inserting a liquid film in between: the equilibrium solid/vapor interface would then comprise such film, leading to \(\gamma _{SV}=\gamma _{SL}+\gamma \). Therefore, \(S\le 0\) in the “moist” case. On the other hand, when the solid and the gaseous phases are not in thermodynamical equilibrium (the so-called dry case), there is no constraint on the sign of S.
The function P is an intermolecular potential. Generally speaking, P is singular as \(h\rightarrow 0^+\) and decays to zero as \(h\rightarrow +\infty \), with \(\Pi =-P'\) usually referred to as the disjoining pressure. We consider the case in which P is short-range repulsive, in the sense that it penalizes short distances between the liquid–gas interface and the solidFootnote 1:
(the critical case \(P(h)\sim -A\log h\) will be briefly discussed in Remark 2.2). The standard choice for P yields \(m=3\):
which corresponds to an integration of Lifshitz–van der Waals interactions between molecules (Israelachvili 2011; Craster and Matar 2009) and which we shall hereafter refer to as van der Waals potentials. There are, however, reasons to examine different values of m. The first one is that the form of the disjoining pressure is highly dependent on the nature of the dominant intermolecular force (molecular, electrostatic, structural) and on the scales under consideration: for instance, the electrostatic and structural contributions for water on glass or silica surfaces yield \(P(h)\sim -A\log h\) or \(P(h)\sim A/h\), depending on thickness (Pashley 1980; Teletzke et al. 1988); we refer to the lucid discussion in Dallaston et al. (2018). A second reason will be introduced in Sect. 1.3.
1.2 The Contact-Line Paradox
In order to introduce the contact-line paradox, it is convenient to describe the basic energetic structure of (1.1). The free energy of the system is given by:
In lubrication theory, the term \(\gamma (1+\tfrac{1}{2} h_x^2)\) is the leading-order approximation of the liquid–gas surface energy density \(\gamma \sqrt{1+h_x^2}\). The summand 1 is incorporated in the potential Q. Smooth, positive and, say, periodic solutions to (1.1) (e.g., modeling a liquid film) satisfy the energy balance

When nonnegative solutions are considered (e.g., modeling a droplet), then contributions at the contact line appear (cf. e.g. (3.10)), but the rate of bulk dissipation remains the same: it encodes both viscous friction within the liquid and, through  , interfacial friction at the liquid–solid interface.
, interfacial friction at the liquid–solid interface.
In the framework of (1.1), the contact-line paradox manifests itself as follows. Assume the no-slip condition, i.e., (1.2), and consider a traveling-wave solutions to (1.1):
where \(V\ne 0\) is a constant velocity (here we have assumed w.l.o.g. that the contact line is initially located at \(x=0\)). If \(P\equiv 0\), then advancing (\(V>0\)) traveling-wave solutions to (1.1) of the form (1.8) do not exist, whereas receding ones (\(V<0\)) have a non-integrable rate of dissipation density (see (2.31)). Therefore, for  and \(P\equiv 0\), traveling waves with finite dissipation do not exist at all: this is the manifestation of the contact-line paradox in lubrication theory (see Bernis and Ferreira (1997); Bernis et al. (1992) for the non-existence of source-type solutions).
and \(P\equiv 0\), traveling waves with finite dissipation do not exist at all: this is the manifestation of the contact-line paradox in lubrication theory (see Bernis and Ferreira (1997); Bernis et al. (1992) for the non-existence of source-type solutions).
Since the contact-line paradox was discovered, quite a few enrichments of the basic model have being put forward to relieve it: we refer to the reviews by Oron et al. (1997); de Gennes (1985); Bonn et al. (2009) and Snoeijer and Andreotti (2013). The standard method, which was first investigated by Huh and Mason (1977); Hocking (1976, 1977), and Greenspan (1978), is to allow for fluid slip over the solid (at least in a neighborhood of the contact line), which amounts to prescribing a relation between horizontal velocity and shear stress at the liquid–solid interface. In lubrication theory, these relations modify the mobility function to  (\(n=2\) for the classical Navier (1823) slip condition); \(\lambda \) is a length-scale whose inverse is proportional to liquid–solid friction. A second one, introduced to our knowledge by Weidner and Schwartz (1994), is to assume a shear-thinning rheology, with a vanishing liquid’s viscosity as the shear stress blows up: this introduces a nonlinear dependence of V on \(h_{xxx}\) [see, e.g. Flitton and King (2004); King (2001); Ansini and Giacomelli (2002, 2004)]. More recently, it has been observed by Rednikov and Colinet (2013, 2019) and Janecek et al. (2013, 2015) that the Kelvin effect, i.e., a curvature-induced variation of saturation conditions, may also be employed to resolve contact-line paradox: in this case, (1.1) is complemented with a singular term in non-divergence form.
(\(n=2\) for the classical Navier (1823) slip condition); \(\lambda \) is a length-scale whose inverse is proportional to liquid–solid friction. A second one, introduced to our knowledge by Weidner and Schwartz (1994), is to assume a shear-thinning rheology, with a vanishing liquid’s viscosity as the shear stress blows up: this introduces a nonlinear dependence of V on \(h_{xxx}\) [see, e.g. Flitton and King (2004); King (2001); Ansini and Giacomelli (2002, 2004)]. More recently, it has been observed by Rednikov and Colinet (2013, 2019) and Janecek et al. (2013, 2015) that the Kelvin effect, i.e., a curvature-induced variation of saturation conditions, may also be employed to resolve contact-line paradox: in this case, (1.1) is complemented with a singular term in non-divergence form.
Another way to resolve the paradox was first discussed by Starov (1983), de Gennes (1984) and Hervet and de Gennes (1984): it consists in taking the effect of intermolecular potentials P into account. The goal of this note is to revisit this phenomenon in a systematic way for generic potentials. To this aim, it is convenient to review the statics first.
1.3 Statics
Consider absolute minimizers \(h_{min}\) of E, as given by (1.6), under the constraint of given mass M.
When \(P\equiv 0\) and \(S<0\), \(h_{min}\) is an arc of parabola characterized by its mass M and |S|; in particular, its slope at the contact line \(\partial \{h>0\}\) is determined by |S|:
When \(P\equiv 0\) and \(S\ge 0\), \(h_{min}\) instead does not exist, and minimizing sequences converge to an unbounded film with zero thickness. Therefore, it is common to define the static (or equilibrium) microscopic contact angle \(\theta _S\), and to name the two regimes, as follows:
Let us now take P into account. Consider steady states \(h_{\textsc {ss}}\) with connected positivity set, that is, solutions to the Euler–Lagrange equation
where \(\Lambda \in {\mathbb {R}}\) is a Lagrange multiplier coming from the mass constraint. The properties of \(h_{\textsc {ss}}\) have been formally discussed by Joanny and de Gennes (1984); de Gennes (1985), and Leger and Joanny (1992). Their macroscopic shape (here encoded by looking at the regime \(M\gg 1\)) may be droplet-like or pancake-like. When \(R(h)=Q(h)/h\) has a unique absolute minimum point \(e_*\), then \(e_*\) is characterized by
and \(h_{\textsc {ss}}\) is pancake-shaped:
Since \(S>0\) implies \(e_*<+\infty \), this configuration is generic in dry complete wetting. Thus, it is the wetting coefficient which drives the system toward a “pancake” equilibrium. If on the other hand R has no absolute minimum, then necessarily \(S\le 0\); steady states are droplet-shaped if \(S<0\),
where \(\theta _{mac}\) denotes the macroscopic contact angle (see Fig. 1). When \(S=0\) and \(e_*=+\infty \) the shape is still droplet-like, but constants depend on the large-h behavior of P. Finally, a simple asymptotic expansion of (1.10) using (1.4) shows that
implying that the microscopic contact angle equals \(\pi /2\) for any \(m>1\) (Fig. 1).
If the model is assumed to hold down to \(h=0\), the above characterization suffers from a limitation if \(m\ge 3\). Indeed, it follows from (1.14) that both summands in the energy, \(h_x^2\) and Q(h), are not integrable for \(m\ge 3\). Therefore, steady states have unbounded energy if \(m\ge 3\):
The dual of this phenomenon is the following:
This yields the variational counterpart of (1.15):
On the other hand, if the singularity is milder, that is if \(1<m<3\), it was recently observed in Durastanti and Giacomelli (2022) that compactly supported minimizers \(h_{min}\) do exist, and coincide with steady states with connected positivity set. In particular, \(h_{min}\) satisfies (1.12) and (1.13) with \(e_*\) defined by (1.11). In summary:
When \(m\ge 3\), as for the van der Waals potential \(P_0\), the limitation in (1.15)–(1.17) is usually handled by arguing that, at scales below a few molecules’ radii (say, about ten Ångström for water), a continuum description of molecular interaction through \(P_0\) may not be valid any more, since it is based on integration of binary molecular interactions. Hence, the validity of a continuum description such as (1.1) is taken only up to a molecular threshold length-scale \(\epsilon \) (\(\epsilon ^2=a^2=A/6\pi \gamma \) in de Gennes (1985); Gennes et al. (1990), and Leger and Joanny (1992)).
On the other hand, (1.15)–(1.17) cannot be ignored when one assumes \(m\ge 3\) and seeks for a continuum model which consistently describes the liquid’s profile all the way down to \(h=0\), capturing “pancake” shapes in dry complete wetting (\(S>0\)). Unfortunately, simple fixes do not work. Indeed, either setting a virtual “zero height” at \(\epsilon \) by the translation \({\hat{h}} =h-\epsilon \), or introducing a naive cut-off of the potential, such as \(P(h)=\min \{P_0(h),P_{0}(\epsilon )\}\), make (1.1) non-singular; hence, the final spreading equilibrium will not be a pancake either (mass-constrained minimizing sequences tend to zero: in more suggestive terms, the equilibrium is an unbounded layer of zero thickness). A much more ingenious fix dates back to the work of Bertozzi and Pugh (1994) and consists in introducing a less singular “molecular cut-off”, such as
where \(P_0\) is as in (1.5) and \(\epsilon \) is a molecular-sized threshold length-scale. Based on (1.18), we expect that (1.19) may provide an equally effective description of droplets’ profiles in the framework of van der Waals potentials, without the disadvantage of an infinite energy.
The goal of this manuscript is to explore, in the dynamical framework, a parallel between \(m\ge 3\) and \(m<3\) analogous to the one in (1.18). The preliminary matter in dynamical studies is of course that of traveling-wave solutions, which will be discussed in Sect. 2. In Sect. 3, we will identify a class of thermodynamically consistent contact-line conditions modeling contact-line friction, in the spirit of Ren and E (2007); Ren et al. (2010); Ren and E (2011). Finally, in Sect. 4 we will draw our conclusions and present quite a few open questions. All of our observations will be supported by numerical examples.
Remark 1.1
An alternative approach to the contact-line paradox, which is quite common in the applied math community, is to take advantage of (1.16): when their validity down to \(h=0^+\) is assumed, potentials that are sufficiently repulsive at \(h=0^+\) and attractive at \(\infty \), e.g., of the form
yield periodic steady states, which consist of arrays of droplets over a microscopic film of thickness \(O(h_*)\) fully covering the substrate. Thus, (1.20) circumvents, rather than solving, the paradox. However, (1.20) has proved to be particularly fruitful in numerical simulations and asymptotic studies, mainly in relation to dewetting phenomena: (in)stability of the flat film, bifurcation, concentration, and asymptotic scaling laws with respect to the potential’s parameters,; see Bertozzi et al. (2001); Laugesen and Pugh (2002); Becker et al. (2003); Otto et al. (2006); Liu and Witelski (2020); Dallaston et al. (2021), the references therein, and Witelski (2020) for a recent overview. Potentials of the form (1.20) have also been successfully employed in the analysis of the macroscopic dynamics of wetting, see, e.g. Eggers (2005a); Pismen and Eggers (2008); Savva and Kalliadasis (2011), and the references therein. However, this approach obviously cannot capture pancake-shaped equilibria in dry complete wetting.
Remark 1.2
One may question whether a microscopic contact angle equal to \(\pi /2\) is consistent with the small ratio of vertical vs horizontal length-scale required by lubrication approximation. In this respect, we should mention that the rigorous derivation of the thin-film equation in Giacomelli and Otto (2003) only requires a global smallness conditions on such ratio, in form of relations between mass, energy, and second moments. (The result is proved for Darcy’s flow in complete wetting, but it is plausible that similar conclusions may be drawn as well for Stokes flow and partial wetting.) In fact, the validity of lubrication theory under global (hence weak) assumptions is most evident when looking at the statics: for instance, in partial wetting (\(S<0\)) with \(P\equiv 0\) and one space dimension, it has been shown that
under the sole assumptions that \(h\ge 0\) has finite energy, mass, and second moment, cf. (Giacomelli and Otto (2001), (3) in Proposition 1). Note, however, that the finite-energy requirement is violated when \(m\ge 3\). This is another indication of the necessity for a cut-off at a molecular-size length-scale \(\epsilon \) when van der Waals forces dominate as \(h\rightarrow 0\).
2 Traveling Waves
As we mentioned, the idea that a film can spread because of a gradient of the disjoining pressure \(\Pi =-P'\) is not new (Starov 1983; de Gennes 1984; Hervet and de Gennes 1984). In Section IV.C.3 of his review, de Gennes (1985) presents a heuristic analysis of advancing traveling waves for (1.1) in the case of van der Waals potentials. We will now revisit part of his discussion in a more general way, i.e. assuming that
(see Remark 2.2 for the critical case \(m=1\)) and that
The cases \(B>0\), resp. \(B<0\), correspond to long-range repulsive, resp. attractive, potentials. Once again, for \(m<3\) (2.1) may also be thought of as a cut-off of van der Waals potentials at molecular scales, such as in (1.19). Since our focus is on the contact-line paradox, we adopt the no-slip condition, i.e.  (in this respect, see also Remark 2.1 in Sect. 2.3).
(in this respect, see also Remark 2.1 in Sect. 2.3).
We look for traveling-wave solutions to (1.1) with a constant speed V:
We require H to display a contact line; capitalizing on translation invariance, we assume without losing generality that the contact line is located at \(y=0\):
In addition, we ask that H connects to a bulk profile as \(y\rightarrow +\infty \):
Plugging the Ansatz (2.3) into (1.1) and using (1.3) yields, in case of (1.2),
Assuming null mass flux through the contact line gives, after an integration,
Note that |U| coincides, up to a factor three, with the capillary number. Finally, we ask H to have finite rate of bulk dissipation near the contact line, in the sense that (cf. (1.7))

For brevity, we will call front a solution to (2.5)–(2.4) satisfying (2.6). Of course, as in the static case, it will be important to highlight which fronts have finite energy near the contact line, in the sense that
We will argue that singular potentials generically solve the contact-line paradox, in the following sense:
- (Q):
-
Quadratic fronts. Assume (1.3), (1.2), (2.1), and (2.2). For any \(U\in {\mathbb {R}}\setminus \{0\}\) there exists a two parameter (\(a>0\), \(b\in {\mathbb {R}}\)), hence generic, family of fronts. They have quadratic growth as \(y\rightarrow +\infty \),
$$\begin{aligned} H(y)= ay^2+by + O(1) \quad \text{ as }\, y\rightarrow +\infty , \end{aligned}$$(2.8)and satisfy
$$\begin{aligned} \tfrac{1}{2} (H_y(y(H)))^2= P(H)\left( 1 + c_1 H^{m-1} + o(H^{m-1})\right) \quad \text{ as }\, H\rightarrow 0, \end{aligned}$$(2.9)where O(1), \(o(H^{m-1})\) and \(c_1\in {\mathbb {R}}\) are determined by m, U, P, a, and b. These fronts have finite energy if and only if \(m<3\).
This shows that, even if a no-slip condition is adopted at the contact-line, i.e.,  , singular potentials allow the existence of generic fronts (both advancing and receding) for any value of the normalized speed U. Since fronts have finite rate of dissipation, this means that singular potentials stand as an alternative solution to the contact-line paradox. In terms of H, (2.9) translates into
, singular potentials allow the existence of generic fronts (both advancing and receding) for any value of the normalized speed U. Since fronts have finite rate of dissipation, this means that singular potentials stand as an alternative solution to the contact-line paradox. In terms of H, (2.9) translates into
which coincides with (1.14). Therefore, as in the static case, fronts are compatible with a fully consistent continuum theory down to \(h=0\) if \(m<3\), whereas if \(m\ge 3\) the energy is unbounded, and one must cut-off the fronts at a molecular length-scale \(\epsilon \). In this respect, (Q) parallels the static summary (1.18).
Starting from the work of Voinov (1976), various formal asymptotic arguments have been developed for spreading droplets [see, e.g. Greenspan (1978); Hocking (1983); Cox (1986); Ehrhard and Davis (1991); Haley and Miksis (1991); Hocking (1992); Bertsch et al. (2000); Eggers and Stone (2004); Eggers (2005a); Pismen and Eggers (2008); Chiricotto and Giacomelli (2013)]. In this framework, advancing fronts (\(U>0\)) are usually matched to a macroscopic profile. Such matching (parts of which were made rigourous in Giacomelli and Otto (2002); Giacomelli et al. (2016); Delgadino and Mellet (2021)) requires to select those fronts which, instead of a quadratic one, display a linear (though logarithmically corrected) growth for \(y\gg 1\); they are identified by
We will argue that, even if a no-slip condition is assumed at the contact-line, i.e.,  , such linear-log fronts also exist when singular potentials are adopted, for any positive speed:
, such linear-log fronts also exist when singular potentials are adopted, for any positive speed:
- (L):
-
Linear-log fronts. Assume (1.3), (1.2), (2.1), and (2.2). For any \(U>0\) there exists a one-parameter (\(a\in {\mathbb {R}}\)) family of fronts \(H_L\) such that (2.11) holds. They have linear-log growth in the sense that
$$\begin{aligned} H_{y}^3(y(H)) = 3U\left( \log H -\tfrac{1}{3}\log \log H +a + O(\tfrac{\log \log H}{\log H})\right) \quad \text{ as }\, H\rightarrow +\infty \nonumber \\ \end{aligned}$$(2.12)and satisfy (2.9). These fronts have finite energy if and only if \(m<3\).
Note that (2.12) does imply linear-log behavior as \(y\rightarrow +\infty \):
As quadratic ones, also linear-log fronts are compatible with a fully consistent continuum theory down to \(h=0\) only if \(m<3\), whereas a molecular-sized cut-off is necessary if \(m\ge 3\).
Remark 2.1
Since our focus is on the contact-line paradox, we have only discussed the mobility  , corresponding to the no-slip condition. However, analogous arguments yield (Q) and (L) also for mobilities of the form
, corresponding to the no-slip condition. However, analogous arguments yield (Q) and (L) also for mobilities of the form  with \(n<3\).
with \(n<3\).
In slippage models with \(P\equiv 0\), a single linear-log front (and a one-parameter family of quadratic fronts) can be identified by imposing a condition on the value of the microscopic contact angle \(H_y(0)\): in other words, the microscopic contact angle \(H_y(0)\) may be taken as one of the parameters spanning the fronts. This additional condition on the contact angle is also necessary for uniqueness of generic solutions to (1.1) (Giacomelli et al. 2008, 2014; Knüpfer 2011, 2015; Knüpfer and Masmoudi 2013, 2015; Gnann 2015; Gnann and Petrache 2018). In (Q) and (L) above, the microscopic contact angle can not be a selection criterion, since all fronts have \(H_y(0)=+\infty \). This points to the necessity of a different criterion which, for instance, singles out a unique linear-log front.
One possible selection criterion is the so-called maximal film, an advancing traveling wave supported in \({\mathbb {R}}\) (i.e., without a contact line). For van der Waals potentials, the maximal film has been successfully employed as a first approximation of droplets’ advancing fronts for large positive spreading coefficient, where a prominent precursor region is supposed to form ahead of the macroscopic contact line. For instance, it is used by Hervet and de Gennes (1984) and de Gennes (1985) to infer the Voinov–Cox–Hocking logarithmic correction to Tanner’s law (Voinov 1976; Tanner 1979; Cox 1986; Hocking 1983, 1992), see, e.g., the discussion in Eggers and Stone (2004). We will argue that such maximal film exists for any \(m\ge 2\):
- (M):
-
Maximal film. Assume (1.3), (1.2), (2.1), and (2.2). For any \(U>0\) and \(m\ge 2\), there exists a unique (up to translations) solution \(H_M\) to (2.5) in \({\mathbb {R}}\) such that \(H_M(y)\rightarrow 0^+\) as \(y\rightarrow -\infty \) and (2.11) holds. They satisfy (2.13) and
$$\begin{aligned} \begin{array}{ll} H_{M}(y)\sim \left( -\tfrac{(m-2)U}{A m}y\right) ^{\frac{1}{2-m}} &{} \text{ if }\, m>2 \\ H_{M}(y)\sim e^{\frac{U}{2A}y} &{} \text{ if }\, m=2 \end{array} \quad \text{ as }\, y\rightarrow -\infty , \ \ U>0. \end{aligned}$$(2.14)
In Sect. 2.1–2.3, we provide the formal asymptotic arguments which motivate (Q), (L) and (M); in Sect. 2.4, we give numerical examples supporting them; finally, in Sect. 2.5 we compare them with analogous results for the slippage model.
2.1 Asymptotics Near the Contact Line
Note that (2.5) is autonomous: as customary, it is convenient to get rid of translation invariance by exchanging dependent and independent variable, thus reducing the order of the ODE. Therefore, we let
For \(H_y>0\) in a neighborhood of \(H=0\), (2.5) reads as
At leading order as \(H\rightarrow 0\), a simple asymptotic expansion using (2.1) shows that two cases occur:
Case (a), resp. (b), may be read off from (2.16) by neglecting the first term on the right-hand side, resp. the left-hand side.
We anticipate that the solutions in (a) are generic and have finite rate of dissipation, whereas those in (b) are non-generic and have unbounded rate of dissipation. However, the solutions in (b) will capture the maximal film identified in (M). We thus distinguish the two cases.
2.1.1 Case (a)
We linearize (2.16) around P(H): define the function v(H) as
It follows from (2.16) that
where
The linearization of (2.18) around \(v=0\) is given by:
The left-hand side is a Cauchy–Euler equation, whereas the terms under braces on the right-hand side are o(1) as \(H\rightarrow 0^+\) in view of (2.1). Therefore, the equation has a two-parameter family of solutions of the form
Generically, \(v_p(H)=o(H^{m-1})\) as \(H\rightarrow 0^+\) (if \(c_1=0\), its regularity improves) is a function determined by U, P, m, \(c_1\), and \(c_2\). In terms of H, this translates into (2.9). Returning to the y variable, the additional degree of freedom coming from invariance under translation \(y\mapsto y-y_0\) is spent to match the condition \(H(0)=0\). Therefore, (2.9) translates into
Since \(\frac{2}{m+1}<1\) for \(m>1\), these solutions have finite rate of dissipation; in addition, they have finite energy if and only if \(m<3\):
In summary,
- (TW\(_0\)):
-
Assume (1.3), (1.2), and (2.1). Locally for \(y\ll 1\), for any \(U\in {\mathbb {R}}\setminus \{0\}\) there exists a two-parameter family of generic solutions H to (2.5)–(2.4a) satisfying (2.9) and (2.10). Their rate of bulk dissipation is finite, in the sense that (2.6) holds; if \(m<3\) their energy is also finite, in the sense that (2.7) holds.
We note for further reference that the traveling waves in (TW\(_0\)) satisfy
Remark 2.2
In the critical case \(P(h) \sim -A\log {h}\) as \(h\rightarrow 0^+\) (\(A>0\)), which corresponds to \(m=1\) in (2.1), analogous arguments show that a two-parameter family of generic solutions H to (2.5)–(2.4a) still exists. However, they are such that \(\frac{1}{2} H_y^2(y(H))\sim P(H)\) as \(H\rightarrow 0^+\), i.e. \(H(y)\sim y\sqrt{-2A\log y}\) as \(y\rightarrow 0^+\): hence the rate of bulk dissipation (cf. (2.6)) is unbounded.
2.1.2 Case (b)
We recall that \(U>0\) in this case. We linearize (2.16) around \(\psi _0(H)= \frac{1}{2} \left( \frac{U}{H^2P''(H)}\right) ^2\). In fact, it is convenient to write the linearization in terms of \(\psi \) itself, writing \(\psi =\psi _0\left( 1+\left( \frac{\psi }{\psi _0}-1\right) \right) \):
In view of the asymptotic of P in (2.1), this means that
At leading order as \(H\rightarrow 0^+\), the change of variables
leads to a non-homogeneous modified Bessel equation,
The homogeneous solutions are spanned by modified Bessel functions (Abramowitz and Stegun 1992): \({\hat{\psi }}(\eta )= c_1 K(\eta ) + c_2 I(\eta )\), where \(K=K_{(2|\beta |)^{-1}}\) and \(I=I_{(2|\beta |)^{-1}}\). Since I is unbounded as \(\eta \rightarrow +\infty \), the condition \(\psi (0)=0\) implies that \(c_2=0\). Simple computations thus show that \({\hat{\psi }}(\eta )= c_1 K(\eta ) + {\hat{\psi _p}}(\eta )\) with \(c_1\in {\mathbb {R}}\), where the particular solution \({\hat{\psi _p}}\) is given by:
(here we used that the Wronskian \(KI'-IK'=\eta ^{-1}\)). A simple asymptotic expansion, using \(I(\eta )\sim \frac{1}{\sqrt{2\pi }}\eta ^{-1/2}e^\eta \) and \(K(\eta )\sim \frac{\sqrt{\pi }}{\sqrt{2}}\eta ^{-1/2}e^{-\eta }\) as \(\eta \rightarrow +\infty \), shows that
Returning to \(\psi (H)=\frac{1}{2} H_y^2(y(H))\), this means that
where \(\psi _o\) and \(\psi _p\) are functions depending on m, U, and P; they satisfy
In terms of H(y) as \(y\rightarrow 0^+\), for \(U>0\) and \(m<2\) (2.21) translates into a one-parameter, hence non-generic, family of solutions to (2.5)–(2.4a), which had already been identified by Bertozzi and Pugh (1994): they all behave as
Note the constraint \(m<2\): if \(m\ge 2\), H diverges as \(y\rightarrow 0^+\), hence it is not admissible. It is clear that these solutions have unbounded rate of dissipation, since \(\frac{1}{2-m}>1\) for \(m\in (1,2)\) (cf. (2.6)).
For \(m\ge 2\), the above argument also reveals a two-parameter (including translation, whence non-generic) family of separatrices, which may be identified by requiring that \(H(y)\rightarrow 0^+\) as \(y\rightarrow -\infty \). Therefore,
- (TW\(_{-\infty }\)):
-
Assume (1.3), (1.2), and (2.1). For \(U>0\) and \(m\ge 2\), there exists a two-parameter (including translation) family of solutions \(H_{\mathrm{{sep}}}\) to (2.5) satisfying (2.14).
2.2 Asymptotics in the Liquid Bulk
We now look at the behavior of solutions to (2.5) such that \(H(y)\rightarrow +\infty \) as \(y\rightarrow +\infty \). We will argue that:
-
(TW\(_\infty \)) Consider (2.5) with (2.4b). Assume (1.3), (1.2), and (2.2).
-
(TW\(_\infty \)-Q) For any \(U\in {\mathbb {R}}\setminus \{0\}\) there exists a generic, three-parameter (including translation) family of quadratically growing solutions:
$$\begin{aligned} H(y)= & {} a(y-y_0)^2+b(y-y_0) + O(y^{-\gamma }) \quad \text{ as }\, y\rightarrow +\infty ,\nonumber \\ \quad \gamma= & {} \min \{1,2p-2\}, \end{aligned}$$(2.22)with \(a>0\) and \(b,y_0\in {\mathbb {R}}\).
-
(TW\(_\infty \)-L) For any \(U>0\) there exists a non-generic, two-parameter (including translation) family of linear-log solutions satisfying (2.12) with \(a\in {\mathbb {R}}\).
-
To motivate (TW\(_\infty \)), in view of (2.2) we rewrite (2.5) as
The asymptotic expansion yielding (TW\(_\infty \)-Q) is straightforward. For (TW\(_\infty \)-L), let \(U>0\). The equation for
is
Following Giacomelli et al. (2016), we exploit the homogeneity of the \((B=0)\)-part of the equation letting \(s=\log H\), which yields
This equation has been analyzed in (Giacomelli et al. (2016), Sects. 4 and 5) with a slippage-type perturbation (namely, \(f(s,u)= (1+e^{(3-n)s})^{-1}\)) whose specific form is, however, immaterial as long as \(f(s)=O(s^{-2}\log s)\). Their analysis shows that (2.24) with \(f=0\) has a one-parameter family of solutions such that \(u(s)/s\rightarrow 1\) and \(u'(s)\rightarrow 1\) as \(s\rightarrow +\infty \), with an asymptotic expansion of the form
Since \(f(s,u)\approx e^{s(1-p)}u^{1/3}\) and \(p>1\), it is apparent that f produces only an exponentially small perturbation: thus solutions to (2.24) have the same behavior, which in terms of \(H=e^s\) yields (2.12).
2.3 Global Behavior
For the global picture, one has to make sure that local solutions are global. This is not always the case, in the sense that (2.5) also has generic solutions with compact support, a feature which is common to the slippage model. However, we have strong numerical evidence that generic members of both (TW\(_\infty \)-Q) and (TW\(_\infty \)-L) touch down to \(H=0\) at some point \(y_0\in {\mathbb {R}}\) (see Sect. 2.4). Capitalizing on translation invariance, one of the three parameters in (TW\(_\infty \)-Q) may be used to match \(H(0)=0\), yielding a two-parameter family of fronts satisfying (TW\(_0\)): this yields (Q). Analogously, one of the two parameters in (TW\(_\infty \)-L) may be used to match \(H(0)=0\), yielding a one-parameter family of fronts satisfying (TW\(_0\)): this yields (L). Finally, up to a translation, there exists a one parameter family of separatrices \(H_{\textrm{sep}}\) emanating from \(-\infty \) as well as a one-parameter family of linear-log fronts emanating from \(+\infty \). Since (2.5) is of third order but autonomous, this entails a unique (up to translation) maximal film \(H_M\) which satisfies (2.5) and is such that both (TW\(_{-\infty }\)) and (TW\(_\infty \)-L) hold: this yields (M).
2.4 Numerical Observations
In order to provide numerical evidence of (Q), (L), and (M), we take as prototype example
The reason for considering such simple model instead of, for instance, (1.19) or (1.20), is twofold. Firstly, this choice is sufficient for a first numerical check on (Q), (L) and (M), since they quantitatively depend only on the behavior of P as \(h \rightarrow 0^+\) (its sign and decay at infinity matters only qualitatively, independently of the power-law exponent p). Secondly, we can capitalize on the homogeneity of P to normalize the dimensionless speed U to \(\pm 1\): indeed, letting
we may rewrite (2.5) with (2.25) as
Of course, a quantitative investigation of the fronts’ behavior in the intermediate regions and/or in terms of the parameters will require both a more careful choice of P and a more extensive numerical study, both outside the scope of this contribution. Note that a change in sign of U is equivalent, in (2.27), to a change of sign of \({\hat{y}}\) and that the left-hand side of (3.16) is unaffected by the latter change: hence, removing hats, in place of (2.27), we will equivalently consider
with the understanding that
-
advancing fronts (\(U>0\)) correspond to solutions to (2.28) with \(H(0)=0\), \(\mathop {\textrm{supp}}\limits H=[0,+\infty )\) and \(H(+\infty )=+\infty \);
-
receding fronts (\(U<0\)) correspond to solutions to (2.28) with \(H(0)=0\), \(\mathop {\textrm{supp}}\limits H=(-\infty ,0]\) and \(H(-\infty )=+\infty \).
Generic solutions to (2.27) can be obtained by noting that H is concave near \(H=0\) (see (2.19)) and convex near \(H=+\infty \) (see (2.22) and (2.13)). Therefore, there exists a point y such that \(H_{yy}=0\). By translation invariance, we may fix that point to be \(y=1\). Shooting from \(y=1\) with the two parameters H(1) and \(H_{y}(1)\) produces a two-parameter family of solutions, which can then be translated in y to match \(H(0)=0\). Consider therefore
For a fixed \(\alpha \), the generic picture is the following (cf. Figs. 2, 3):
-
advancing, quadratic fronts for \(\beta >\beta _0(\alpha )\);
-
an advancing, linear-log front \(H_L\) for \(\beta =\beta _0(\alpha )\);
-
compactly supported solutions for \(\beta \in (\beta _1(\alpha ),\beta _0(\alpha ))\);
-
a separatrix \(H_{\mathrm{{sep}}}\) for \(\beta =\beta _1(\alpha )\);
-
receding (quadratic) fronts for \(\beta <\beta _1(\alpha )\).
The picture confirms the existence of both a two-parameter family of quadratic fronts (both advancing and receding, see (Q)) and two one-parameter families of advancing linear-log fronts (see (L)), resp. separatrices (see (TW\(_{-\infty }\))). In this case, the two parameters which span the fronts are taken to be \(\alpha =H|_{H_{yy}=0}\) and \(\beta =H_y|_{H_{yy}=0}\).
Solutions to (2.29) with \(m=2\), \(\alpha =1/4\) (top) and \(\alpha =1\) (bottom), at two different scales. For \(\alpha =1/4\) (top), the separatrix \(H_{\mathrm{{sep}}}\) and the black receding front are indistinguishable for small heights, as well as the gray compactly supported solution and the linear-log front
Solutions to (2.29) with \(m=3\), \(\alpha =1/4\) (top) and \(\alpha =1\) (bottom), at two different scales. For \(\alpha =1/4\) (top) quadratic fronts, linear-log front, and compactly supported solutions are indistinguishable for small heights, as well as the separatrix and the black receding front
It is interesting to compare the shapes of the linear-log fronts \(H_L\) for varying values of \(\alpha =H_L|_{(H_L)_{yy}=0}\). The shapes reported in Fig. 4 show that \(H_L\) increase as \(\alpha \) increases. It also shows that a prominent precursor region forms ahead of the “macroscopic contact line” for small values of \(\alpha \).
Linear-log solutions to (2.29) with \(m=2\) for \(\alpha =H_L|_{(H_L)_{yy}=0}=e^k\), with k ranging from \(-3\) (bottom) to 3 (top), at two different scales. For \(k=-3\), on the right, the “macroscopic contact line” Y
Figure 5 shows the maximal film \(H_M\) (see (M)), which is obtained observing that \((H_M)_{yy}(y)\rightarrow 0\) as \(y\rightarrow \pm \infty \); hence, there exists \(y_0\in {\mathbb {R}}\) such that \((H_M)_{yyy}(y_0)=0\), which implies that \(m(H_M)_y(y_0)=H_M^{m-1}(y_0)\). Then, \(H_M\) is identified by shooting from \(y_0\), using \(H_M(y_0)\) and \((H_M)_{yy}(y_0)\) as parameters.
2.5 Comparison with Slippage Models
It is useful to compare the features in (Q), (L) and (M) with parallel ones for the case \(P\equiv 0\) under slip conditions. In this case, traveling-wave solutions (if they exist) solve
with the same boundary conditions.
First of all, (Q) and (L) obviously contrasts (2.30) in the no-slip case \(\lambda =0\). Indeed, solutions to (2.30) with \(\lambda =0\) exist only if \(U<0\) (receding), but their rate of bulk dissipation density is not integrable near \(y=0\); indeed,

as \(y\rightarrow 0^+\). Therefore, fronts of (2.30) do not exist at all if \(\lambda =0\).
On the other hand, if \(\lambda >0\) (positive slippage), computations analogous to the ones above show that the picture is very much the same as in (Q) and (L): for any \(U\in {\mathbb {R}}\) (\(U>0\) if \(H_y(0)=0\) and \(n>\frac{3}{2}\)) there exists a two-parameter family of quadratic fronts satisfying (2.22) (though with a different remainder); in addition, for any \(U>0\) there exists a one-parameter family of linear-log fronts satisfying (2.12)–(2.13) (Boatto et al. 1993; Buckingham et al. 2002; Chiricotto and Giacomelli 2011; Giacomelli et al. 2016). A prototype case is given in Fig. 6: the only notable qualitative difference is that \(H_{\mathrm{{sep}}}\) are compactly supported; in fact, the unique separatrix with zero microscopic contact-angle coincides with the unique linear-log front in complete wetting; thus, it is the counterpart of the maximal film \(H_M\) in (M).
Fronts for the thin-film equation with slippage (2.30) with \(n=2\), \(\lambda =1\), and \(\alpha =H(1)=1/4\), at two different scales
3 Thermodynamically Consistent Contact-Line Conditions
For exact, compactly supported solutions to the full evolution equation (1.1), the maximal film can obviously not be taken as a selection criterion for the fronts. In this section, we will therefore identify a different criterion, which replaces contact-angle conditions in slippage models: it consists in a class of thermodynamically consistent contact-line conditions modeling friction at the contact line. The class will be identified by requiring dissipativity of the energy along the flow, in the spirit of the proposal by Ren and E (2007) (see also Ren et al. (2010); Ren and E (2011)).
We assume for simplicity that \(\{h>0\}\) is and remains connected for all times (i.e., we exclude coalescence or splitting of droplets):
\(s_\pm (t)\) denoting the contact lines. Since \(s_\pm (t)\) are unknown and (1.1) is of fourth order, three conditions are needed for well-posedness. Two of them are obvious:
The first one defines the contact lines \(s_\pm (t)\), while the second one is a kinematic condition guaranteeing no mass flux through \(s_\pm (t)\). The third condition, the so-called contact-line condition, is yet debated (to a certain extent inevitably, due to the variety of material properties and configurations, which may involve surface roughness and hysteretic effects; see, e.g., Feldman and Kim (2018); Alberti and DeSimone (2005, 2011), as well as the above-mentioned reviews). The most common one amounts to prescribing a constant microscopic contact angle equal to the static one, as defined by (1.9):
Of particular interest to us is a relatively recent proposal by Ren and E (2007) (see also Ren et al. (2010); Ren and E (2011)), based on consistency with the second law of thermodynamics, which also gives a robust motivation to older models by Greenspan (1978) and Ehrhard and Davis (1991). In lubrication approximation (Chiricotto and Giacomelli 2011, 2013), when \(P\equiv 0\) and \(S=-\frac{1}{2}\tan ^2\theta _S\) (the moist case, cf. (1.9)), the simplest form of the Ren-E model reads as followsFootnote 2:
with \(\mu _{\textsc {cl}}>0\) a coefficient measuring friction at the contact line. Indeed, under (3.3), the energy balance reads as

(see Chiricotto and Giacomelli (2017)), which shows that (3.3) is consistent with the second law and accounts for frictional forces at the contact line, with \(\mu _{\textsc {cl}}\ge 0\) a friction coefficient. When \(\mu _{\textsc {cl}}=0\) (null contact-line friction), (3.3) coincides with (3.2).
We will now revisit the argument for (3.3) in the case of a singular potential P. We base our computations on the expectation that the behavior of generic solutions coincides with that of the fronts near the contact line: letting

we assume that
Let \(\varepsilon >0\). Locally around \(x=s_\pm (t)\), we may define \(s_\pm ^\varepsilon (t)\) by:
Using the convention \(\pm a_\pm |_{x=s^\varepsilon _\pm }:=a_+|_{x=s^\varepsilon _+}-a_-|_{x=s^\varepsilon _-}\) for the boundary terms, we compute:
We now notice three facts. Firstly, and crucially, the first boundary term remains bounded as \(\varepsilon \rightarrow 0\): indeed,
In addition, the second boundary term vanishes as \(\varepsilon \rightarrow 0\):
Finally, the integral on the right-hand side of (3.7) is finite; indeed,

which is integrable at \(x=s_\pm (t)\) since \(\frac{2}{m+1}<1\). Passing to the limit as \(\varepsilon \rightarrow 0\), we obtain from (3.6)–(3.9) that

Remark 3.1
This formal computation is fully consistent if \(m<3\). If \(m\ge 3\), instead, the limit \(\varepsilon \rightarrow 0\) on the left-hand side of (3.10) does not make sense since \(E[h]\equiv +\infty \) in that case. However, (3.7) does make sense for any positive \(\varepsilon \), and the limit as \(\varepsilon \rightarrow 0\) on its right-hand side makes sense for any \(m>1\).
In order to be thermodynamically consistent, the contact-line condition has to be such that the free energy is dissipated along the flow, i.e., that the r.h.s. of (3.10) is non-positive: this leads to the following class of contact-line conditions:
The term \(f(\dot{s})\) is a contribution to the dissipation which is concentrated at the contact line: in the description of Bonn et al. (2009), it corresponds to the term \(W_m(U)\) in formula (75). Recalling that \(Q(h)=P(h)-S\), we see that the spreading coefficient S enters the contact-line conditions (3.11)–(3.12) in an essential way, in analogy with the contact-line conditions (3.2)–(3.3) for the slippage model.
The simplest choice of f is a linear relation \(f(\dot{s})=\mu _{\textsc {cl}}\dot{s}\) (\(\mu _{\textsc {cl}}\ge 0\)), in analogy with (3.3); it leads to
Substituting (3.12) into (3.10), we obtain an energy balance analogous to the one in (3.4):

which encodes a quadratic dissipation of kinetic energy through frictional forces acting at the contact line. Note that (3.13) coincides with (1.7) if \(\mu _{\textsc {cl}}=0\).
Let us comment on the contact-line condition (3.12). Its left-hand side is zero for the global minimizers \(h_{min}\) discussed in Sect. 1.3 (see Durastanti and Giacomelli (2022), Theorem 4.5). Also, its left-hand side is well defined on the fronts. Indeed, though both summands are unbounded as \(x\rightarrow s_{\pm }(t)\), their difference is not:
For traveling waves with constant speed \(V= \frac{\gamma }{3\mu }U\), \(s_-(t)=-Vt\) and the contact-line condition (3.12) reads as
In view of (3.14)–(3.15), we expect that:
To support the choices of both (3.12) as free boundary condition and \(\Theta [H]\) as selection parameter, we report numerical values of \(\Theta [H_L]\) as computed for the rescaled equation (2.28): under (2.26), the rescaled version of (3.15) is, after removing hats,
It is apparent from Fig. 7A that \(\Theta [H_L]\) monotonically covers the whole real line as linear-log solutions are spanned: in particular, a unique linear-log front can be selected such that the contact-line condition (3.16) holds. This confirms the expectation in (S2). For completeness, in Fig. 7B we also report numerical values of the separatrix \(H_{\mathrm{{sep}}}\) which discriminates between receding and compactly supported solutions. It is apparent that \(\Theta [H_{\mathrm{{sep}}}]\) increases with \(\alpha \) and diverges to \(-\infty \) as \(\alpha \rightarrow 0^+\).
For (2.28) with \(m=2\): A On the left, the values of \(\Theta [H_L]\) versus \(k=\log ({H_L}|_{(H_L)_{yy}=0})\). B On the right, the values of \(\Theta [H_{\mathrm{{sep}}}]\) versus \(k=\log ({H_{\mathrm{{sep}}}}|_{(H_{\mathrm{{sep}}})_{yy}=0})\)
Combining Fig. 7A with Fig. 4, it is also apparent that, as \(\Theta [H_L]\) decreases, a more prominent precursor region forms ahead of the macroscopic contact line (Fig. 8). Thus, if (3.16) is assumed as a contact-line condition, we expect that \(H_L\) matches the following intuitive properties:
-
for fixed \(\mu _{\textsc {cl}}\) and S, a greater speed U yields steeper profiles of \(H_L\);
-
for fixed U and S, a greater contact-line friction \(\mu _{\textsc {cl}}\) yields steeper profiles of \(H_L\);
-
for fixed \(\mu _{\textsc {cl}}\) and U, a larger positive spreading coefficient S yields gentler profiles of \(H_L\).
In particular, under the contact-line condition (3.16), numerics suggest that larger positive spreading coefficients S yield more prominent precursor regions ahead of the macroscopic contact line (Fig. 8). This agrees with the discussion in de Gennes (1985) for \(m=3\), which is instead based on perturbations of the maximal film.
Typical linear-log fronts \(H_L\) depending on \(\Theta [H_L]\). Under the contact-line condition (3.15), for given speed \(U>0\) and contact-line frictional coefficient \(\mu _{\textsc {cl}}>0\), these are typical fronts for large and positive (left), resp. large and negative (right), values of the spreading coefficient S (“dry” complete wetting, resp. partial wetting)
When \(H_{y}|_{H_{yy}=0}>(H_L)_{y}|_{(H_L)_{yy}=0}\), resp. \(H_{y}|_{H_{yy}=0}<(H_{\mathrm{{sep}}})_{y}|_{(H_{\mathrm{{sep}}})_{yy}=0}\), fronts are advancing, resp. receding, and have a quadratic profile for large y. In Fig. 9, we report numerical values of \(\Theta [H]\) for such solutions. There, it is apparent that, for each value of \(\alpha =H|_{H_{yy}=0}\), \(\Theta [H]\) diverges to \(+\infty \) as \(|H_{y}||_{H_{yy}=0}\) does. Since \(\Theta [H_L]\), resp. \(\Theta [H_{\mathrm{{sep}}}]\), diverge to \(-\infty \) as \(H|_{H_{yy}=0}\rightarrow 0\), (Fig. 7), \(\Theta [H]\) covers the whole real line as advancing, resp. receding, traveling waves are spanned, thus confirming (S1). There is, however, a difference between advancing and receding fronts, since receding ones may be non-monotonic (Figs. 2 and 3); note that the same happens for slippage models (Fig. 6). This reflects into a lack of monotonicity of \(\Theta [H]\) for fixed \(\alpha \) on receding waves. Note that the minimum of \(\Theta [H]\) appears to be on the left half-plane; hence, the corresponding waves have negative derivative at their inflection point, and thus, they are monotonic. Therefore, the branch of receding fronts emanating from \(\Theta [H]=+\infty \) consists of monotone ones. This phenomenon might be related to the existence of a “limiting speed” of receding fronts calculated by Eggers (2004, 2005b) in the slippage case.
For \(m=2\): On the left, the value of \(\Theta [H]\) versus \({H_{y}}|_{H_{yy}=0}\) for receding fronts. On the right, the value of \(\Theta [H]\) versus \({H_{y}}|_{H_{yy}=0}-(H_L)_{y}|_{(H_L)_{yy}=0}\) for advancing fronts. In both cases, \(k=\log H|_{H_{yy}=0}\) ranges from \(-3\) (bottom) to 3 (top)
4 Conclusions and Open Questions
We have discussed thin-film models under singular potentials:
with
Based on formal arguments supported by numerical evidence, we have argued that singular potentials generically solve the contact-line paradox, in the sense that (4.1) admits for any value of \(m>1\):
- (Q):
-
a two-parameter family of both advancing and receding traveling-waves with finite rate of dissipation at the contact line;
- (L):
-
a one-parameter family of advancing “linear-log” traveling waves displaying a logarithmically corrected linear behavior in the bulk, also with finite rate of dissipation at the contact line.
In agreement with mass-constrained steady states, traveling waves have finite energy if and only if \(m<3\), whereas for \(m\ge 3\) a cut-off at a molecular-size length-scale is necessary (cf. e.g. (1.19)). However, the qualitative properties of the waves are the same for any \(m>1\). Our formal arguments also suggest that for \(m\ge 2\) and any positive speed there exists:
- (M):
-
a unique maximal film, i.e., an advancing linear-log traveling wave H(y) which decays to zero as \(y\rightarrow -\infty \) instead of touching down to zero at a finite point.
Intermolecular potentials thus stand as a possible solution to the contact-line paradox, alternative to the most common one, given by slippage models:
For equation (4.3), the classification of traveling waves is analogous to (Q) and (L) (cf. Sect. 2.5); however, the microscopic contact angle \(h_x|_{\{h=0\}}\) may be used as a parameter to span them, thus selecting a unique advancing linear-log front. This is impossible for (4.1)–(4.2), since in that case the microscopic contact angle is always \(\pi /2\). Here, we have also proposed a class of thermodynamically consistent contact-line conditions, which replaces contact-angle ones and is expected to single out a unique advancing linear-log front with a contact line. The simplest among such conditions reads as:
where \(\{h(t)>0\}=(s_-(t),s_+(t))\), \(\mu _{\textsc {cl}}\ge 0\) is a contact-line frictional coefficient, and S is the non-dimensional spreading coefficient. We expect that:
- (S):
-
for any value of the speed, (4.4) selects a one-parameter family of fronts in (Q) and a unique linear-log front in (L).
Numerical evidence also suggests that linear-log fronts are steep for \(\Theta [h]\gg 1\), whereas they display a precursor region ahead of the macroscopic contact line for \(\Theta [h]\ll -1\). Therefore, we expect that (4.4) yields precursor regions for large positive values of the spreading coefficient.
The above four observations issue quite a few challenges.
-
The rigorous validation of (Q), (L) and (M) is highly desirable. Once the asymptotics in (Q) and (L) have been proved, we expect that (S) will follow as a byproduct.
-
For relatively large values of S, it would be interesting to quantify height and length of the precursor region, which appears to exist ahead of the “macroscopic” contact line, in relation to the contact-line condition (4.4).
-
It would be very useful to have numerical simulations and/or matched asymptotic studies available for generic solutions to (4.1) with the contact-line condition (4.4), for potentials P of the general form (4.2). Of particular interest would be the (in)stability of advancing/receding traveling waves, the detection of scaling laws (such as the Voinov–Cox–Hocking logarithmic correction to Tanner’s law), an estimate of the rate of convergence to equilibria, and an insight on the evolution of the precursor region for relatively large values of S.
-
Based on (S), for potentials P of the form (4.2), we conjecture that for any non-negative \(h_0\in H^1({\mathbb {R}})\) such that \(E[h_0]<+\infty \) there exists a unique solution to (4.1) with the contact-line conditions (3.1) and (4.4). A difficult but extremely interesting task would be to develop a well-posedness theory at least when \(h_0\) is a perturbation of a traveling wave, in the spirit of (Giacomelli et al. 2008, 2014; Knüpfer 2011, 2015; Knüpfer and Masmoudi 2013, 2015; Gnann 2015; Gnann and Petrache 2018).
-
De Silva and Savin (2022) recently analyzed the \(\Gamma \)-convergence of the energy E in the limit \(m\rightarrow 3^-\) and vanishing A (\(A=A_m\approx (3-m)^2\rightarrow 0\) as \(m\rightarrow 3\)). It would be interesting to understand how this scaling limit extends to the dynamic framework.
-
In relation to the issue of infinite energy for \(m\ge 3\), it would be interesting to explore the effect of taking the full curvature operator into account, i.e., replacing \(1+\frac{1}{2} h_x^2\) with \(\sqrt{1+h_x^2}\). We are aware of only a few studies (Novick-Cohen 1992, 1993; Minkov and Novick-Cohen 2001, 2006), dealing with the statics under convex potentials.
-
Interesting, though of seemingly lesser impact, would also be to face the above challenges for more general mobilities, e.g., of the form
 (cf. alos Remark 2.1).
(cf. alos Remark 2.1).
Data Availability
All data generated or analyzed during this study are included in this published article.
Notes
As \(h\rightarrow h_0\), we write: \(f(h)\sim g(h)\) when \(f(h)/g(h)\rightarrow 1\); \(f(h)\approx g(h)\) when \(C>0\) exists such that \(f(h)/g(h)\rightarrow C\); \(f(h)=O(g(h))\) when f(h)/g(h) remains bounded; \(f(h)=o(g(h))\) when \(f(h)/g(h)\rightarrow 0\). Also, we write \(a\ll b\) if a universal constant \(C\ge 1\) exists such that \(a\le Cb\).
More precisely, one should write \((h_x^2-2h h_{xx})\) in place of \(h_x^2\) in the left-hand side of (3.3), but it is expected that the second summand always vanishes at \(x=s_\pm (t)\).
References
Abramowitz, M., Stegun, I.A.: editors. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications, Inc., New York (1992). Reprint of the 1972 edition
Alberti, G., DeSimone, A.: Wetting of rough surfaces: a homogenization approach. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 461(2053), 79–97 (2005)
Alberti, G., DeSimone, A.: Quasistatic evolution of sessile drops and contact angle hysteresis. Arch. Ration. Mech. Anal. 202(1), 295–348 (2011)
Alt, H.W., Phillips, D.: A free boundary problem for semilinear elliptic equations. J. Reine Angew. Math. 368, 63–107 (1986)
Ansini, L., Giacomelli, L.: Shear-thinning liquid films: Macroscopic and asymptotic behaviour by quasi-self-similar solutions. Nonlinearity 15(6), 2147–2164 (2002)
Ansini, L., Giacomelli, L.: Doubly nonlinear thin-film equations in one space dimension. Arch. Ration. Mech. Anal. 173(1), 89–131 (2004)
Becker, J., Grün, G., Seemann, R., Mantz, H., Jacobs, K., Mecke, K., Blossey, R.: Complex dewetting scenarios captured by thin-film models. Nat. Mater. 2(1), 59–63 (2003)
Bernis, F., Ferreira, R.: Source-type solutions to thin-film equations in higher dimensions. European J. Appl. Math. 8(5), 507–524 (1997)
Bernis, F., Peletier, L.A., Williams, S.M.: Source type solutions of a fourth order nonlinear degenerate parabolic equation. Nonlinear Anal. 18(3), 217–234 (1992)
Bertozzi, A.L., Pugh, M.: The lubrication approximation for thin viscous films: the moving contact line with a “porous media’’ cut-off of van der Waals interactions. Nonlinearity 7(6), 1535–1564 (1994)
Bertozzi, A.L., Grün, G., Witelski, T.P.: Dewetting films: bifurcations and concentrations. Nonlinearity 14(6), 1569–1592 (2001)
Bertsch, M., Dal Passo, R., Davis, S.H., Giacomelli, L.: Effective and microscopic contact angles in thin film dynamics. Eur. J. Appl. Math. 11(2), 181–201 (2000)
Boatto, S., Kadanoff, L., Olla, P.: Traveling-wave solutions to thin-film equations. Phys. Rev. E 48(6), 4423–4431 (1993)
Bonn, D., Eggers, J., Indekeu, J., Meunier, J.: Wetting and spreading. Rev. Mod. Phys. 81(2), 739–805 (2009)
Buckingham, R., Shearer, M., Bertozzi, A.: Thin film traveling waves and the Navier slip condition. SIAM J. Appl. Math. 63(2), 722–744 (2002)
Chiricotto, M., Giacomelli, L.: Droplets spreading with contact-line friction: lubrication approximation and traveling wave solutions. Commun. Appl. Ind. Math. 2(2): e–388, 16 (2011)
Chiricotto, M., Giacomelli, L.: Scaling laws for droplets spreading under contact-line friction. Commun. Math. Sci. 11(2), 361–383 (2013)
Chiricotto, M., Giacomelli, L.: Weak solutions to thin-film equations with contact-line friction. Interfaces Free Bound. 19(2), 243–271 (2017)
Cox, R.: The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194 (1986)
Craster, R., Matar, O.: Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81(3), 1131–1198 (2009)
Dallaston, M., Fontelos, M., Herrada, M., Lopez-Herrera, J., Eggers, J.: Regular and complex singularities of the generalized thin film equation in two dimensions. J. Fluid Mech. 917, A20 (2021)
Dallaston, M.C., Fontelos, M.A., Tseluiko, D., Kalliadasis, S.: Discrete self-similarity in interfacial hydrodynamics and the formation of iterated structures. Phys. Rev. Lett. 120, 034505 (2018)
de Gennes, P.-G.: Dynamique d’étalement d’une goutte. C. R. Acad. Sc. Paris II 298(4), 111–115 (1984)
de Gennes, P.G.: Wetting: statics and dynamics. Rev. Mod. Phys. 57(3, part 1), 827–863 (1985)
De Silva, D., Savin, O.: Uniform density estimates and \(\gamma \)-convergence for the alt-phillips functional of negative powers. Math. Eng. 5(5), 1–27 (2023)
Delgadino, M.G., Mellet, A.: On the relationship between the thin film equation and Tanner’s law. Commun. Pure Appl. Math. 74(3), 507–543 (2021)
Durastanti, R., Giacomelli, L.: Spreading equilibria under mildly singular potentials: pancakes versus droplets. J. Nonlinear Sci., 32(5) (2022)
Dussan, V.E., Davis, S.: On the motion of a fluid-fluid interface along a solid surface. J. Fluid Mech., 65(1), 71–95 (1974)
Eggers, J.: Hydrodynamic theory of forced dewetting. Phys. Rev. Lett. 93, 094502 (2004)
Eggers, J.: Contact line motion for partially wetting fluids. Phys. Rev. E - Stat. Nonlinear Soft Matter Phys., 72(6) (2005a)
Eggers, J.: Existence of receding and advancing contact lines. Phys. Fluids 17(8), 1–10 (2005)
Eggers, J., Stone, H.: Characteristic lengths at moving contact lines for a perfectly wetting fluid: the influence of speed on the dynamic contact angle. J. Fluid Mech. 505, 309–321 (2004)
Ehrhard, P., Davis, S.: Non-isothermal spreading of liquid drops on horizontal plates. J. Fluid Mech. 229, 365–388 (1991)
Feldman, W.M., Kim, I.C.: Liquid drops on a rough surface. Commun. Pure Appl. Math. 71(12), 2429–2499 (2018)
Flitton, J.C., King, J.R.: Surface-tension-driven dewetting of Newtonian and power-law fluids. J. Eng. Math. 50(2–3), 241–266 (2004)
Gennes, P.G.D., Hua, X., Levinson, P.: Dynamics of wetting: local contact angles. J. Fluid Mech. 212, 55–63 (1990)
Giacomelli, L., Otto, F.: Variational formulation for the lubrication approximation of the Hele–Shaw flow. Calc. Var. Partial Differ. Equ. 13(3), 377–403 (2001)
Giacomelli, L., Otto, F.: Droplet spreading: intermediate scaling law by PDE methods. Commun. Pure Appl. Math. 55(2), 217–254 (2002)
Giacomelli, L., Otto, F.: Rigorous lubrication approximation. Interfaces Free Bound. 5(4), 483–529 (2003)
Giacomelli, L., Knüpfer, H., Otto, F.: Smooth zero-contact-angle solutions to a thin-film equation around the steady state. J. Differ. Equ. 245(6), 1454–1506 (2008)
Giacomelli, L., Gnann, M.V., Knüpfer, H., Otto, F.: Well-posedness for the Navier-slip thin-film equation in the case of complete wetting. J. Differ. Equ. 257(1), 15–81 (2014)
Giacomelli, L., Gnann, M.V., Otto, F.: Rigorous asymptotics of traveling-wave solutions to the thin-film equation and Tanner’s law. Nonlinearity 29(9), 2497–2536 (2016)
Gnann, M.V.: Well-posedness and self-similar asymptotics for a thin-film equation. SIAM J. Math. Anal. 47(4), 2868–2902 (2015)
Gnann, M.V., Petrache, M.: The Navier-slip thin-film equation for 3D fluid films: existence and uniqueness. J. Differ. Equ. 265(11), 5832–5958 (2018)
Greenspan, H.: On the motion of a small viscous droplet that wets a surface. J. Fluid Mech. 84(1), 125–143 (1978)
Haley, P., Miksis, M.: The effect of the contact line on droplet spreading. J. Fluid Mech. 223, 57–81 (1991)
Hervet, H., de Gennes, P.-G.: Dynamique du mouillage: films précurseurs sur solide “sec’’. C. R. Acad. Sc. Paris II 299(9), 499–503 (1984)
Hocking, L.: The spreading of a thin drop by gravity and capillarity. Q. J. Mech. Appl. Mech. 36(1), 55–69 (1983)
Hocking, L.: Rival contact-angle models and the spreading of drops. J. Fluid Mech. 239, 671–681 (1992)
Hocking, L.M.: A moving fluid interface on a rough surface. J. Fluid Mech. 76(4), 801–817 (1976)
Hocking, L.M.: A moving fluid interface. Part 2. The removal of the force singularity by a slip flow. J. Fluid Mech. 79(2), 209–229 (1977)
Huh, C., Mason, S.: The steady movement of a liquid meniscus in a capillary tube. J. Fluid Mech. 81(3), 401–419 (1977)
Huh, C., Scriven, L.: Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35(1), 85–101 (1971)
Israelachvili, J.: Intermolecular and Surface Forces: Third Edition (2011)
Janecek, V., Andreotti, B., Pražák, D., Bárta, T., Nikolayev, V.S.: Moving contact line of a volatile fluid. Phys. Rev. E 88, 060404 (2013)
Janecek, V., Doumenc, F., Guerrier, B., Nikolayev, V.: Can hydrodynamic contact line paradox be solved by evaporation-condensation? J. Colloid Interface Sci. 460, 329–338 (2015)
Joanny, J.F., de Gennes, P.-G.: Structure statique des films de mouillage et des lignes de contact. C. R. Acad. Sc. Paris II 299(7), 279–283 (1984)
King, J.R.: Two generalisations of the thin film equation. Math. Comput. Model. 34(7–8), 737–756 (2001)
Knüpfer, H.: Well-posedness for the Navier slip thin-film equation in the case of partial wetting. Commun. Pure Appl. Math. 64(9), 1263–1296 (2011)
Knüpfer, H.: Well-posedness for a class of thin-film equations with general mobility in the regime of partial wetting. Arch. Ration. Mech. Anal. 218(2), 1083–1130 (2015)
Knüpfer, H., Masmoudi, N.: Well-posedness and uniform bounds for a nonlocal third order evolution operator on an infinite wedge. Commun. Math. Phys. 320(2), 395–424 (2013)
Knüpfer, H., Masmoudi, N.: Darcy’s flow with prescribed contact angle: well-posedness and lubrication approximation. Arch. Ration. Mech. Anal. 218(2), 589–646 (2015)
Laugesen, R.S., Pugh, M.C.: Energy levels of steady states for thin-film-type equations. J. Differ. Equ. 182(2), 377–415 (2002)
Lazer, A.C., McKenna, P.J.: On a singular nonlinear elliptic boundary-value problem. Proc. Am. Math. Soc. 111(3), 721–730 (1991)
Leger, L., Joanny, J.F.: Liquid spreading. Rep. Prog. Phys. 55(4), 431–486 (1992)
Liu, W., Witelski, T.P.: Steady states of thin film droplets on chemically heterogeneous substrates. IMA J. Appl. Math. 85(6), 980–1020 (2020)
Minkov, E., Novick-Cohen, A.: Droplet profiles under the influence of van der Waals forces. Eur. J. Appl. Math. 12(3), 367–393 (2001)
Minkov, E., Novick-Cohen, A.: Errata: “Droplet profiles under the influence of van der Waals forces” [European J. Appl. Math 12 (2001), no. 3, 367–393; mr1936203]. Eur. J. Appl. Math., 17(1), 128 (2006)
Navier, C.: Memoire sur les lois du mouvement des fluides. Memoires de l ’Acad. Royale des Sci. de l’nstitut de France 6, 389–440 (1823)
Novick-Cohen, A.: On a minimization problem arising in wetting. SIAM J. Appl. Math. 52(3), 593–613 (1992)
Novick-Cohen, A.: A singular minimization problem for droplet profiles. Eur. J. Appl. Math. 4(4), 399–418 (1993)
Oron, A., Davis, S., Bankoff, S.: Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69(3), 931–980 (1997)
Otto, F., Rump, T., Slepčev, D.: Coarsening rates for a droplet model: rigorous upper bounds. SIAM J. Math. Anal. 38(2), 503–529 (2006)
Pashley, R.: Multilayer adsorption of water on silica: an analysis of experimental results. J. Colloid Interface Sci. 78(1), 246–248 (1980)
Pismen, L.M., Eggers, J.: Solvability condition for the moving contact line. Phys. Rev. E - Stat. Nonlinear Soft Matter Phys. 78(5) (2008)
Rednikov, A., Colinet, P.: Singularity-free description of moving contact lines for volatile liquids. Phys. Rev. E 87, 010401 (2013)
Rednikov, A.Y., Colinet, P.: Contact-line singularities resolved exclusively by the kelvin effect: volatile liquids in air. J. Fluid Mech. 858, 881–916 (2019)
Ren, W.: Boundary conditions for the moving contact line problem. Phys. Fluids, 19(2), 022101 (2007)
Ren, W., Weinan, E.: Derivation of continuum models for the moving contact line problem based on thermodynamic principles. Commun. Math. Sci., 9(2), 597–606 (2011)
Ren, W., Hu, D: Continuum models for the contact line problem. Phys. Fluids, 22(10), 102103 (2010)
Savva, N., Kalliadasis, S.: Dynamics of moving contact lines: a comparison between slip and precursor film models. EPL, 94(6) (2011)
Snoeijer, J., Andreotti, B.: Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292 (2013)
Starov, R.: Spreading of droplets of nonvolatile liquids over a flat solid surface. Colloid J. USSR 45(6), 1009–1015 (1983)
Tanner, L.: The spreading of silicone oil drops on horizontal surfaces. J. Phys. D Appl. Phys. 12(9), 1473–1484 (1979)
Teletzke, G., Davis, H., Scriven, L.: Wetting hydrodynamics. Rev. Phys. Appl. (Paris) 23(6), 989–1007 (1988)
Voinov, O.: Hydrodynamics of wetting. Fluid Dyn. 11(5), 714–721 (1976)
Weidner, D.E., Schwartz, L.W.: Contact-line motion of shear-thinning liquids. Phys. Fluids 6(11), 3535–3538 (1994)
Witelski, T.P.: Nonlinear dynamics of dewetting thin films. AIMS Math. 5(5), 4229–4259 (2020)
Acknowledgements
Authors have been partially supported by GNAMPA, INdAM (Project “Analisi di fenomeni di wetting in presenza di potenziali singolari”). The first author has also been supported by PON Ricerca e Innovazione D.M. 1062/21.
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alain Goriely.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The limitation (1.16) of the energy in (1.6) is well known, though with slightly different formulations, see, e.g., (Durastanti and Giacomelli (2022), Lemma 2.10) in \({\mathbb {R}}\) and (Lazer and McKenna (1991), Theorem 2) on bounded domains. For completeness, here we provide a comprehensive statement in \({\mathbb {R}}\). Note that E is a singular version of the Alt and Phillips (1986) functional.
Lemma 1
Let E as in (1.6) and let \(Q:[0,+\infty )\rightarrow {\mathbb {R}}\) be such that \(Q\in C((0,+\infty ))\), \(Q(0)=0\) and \(Q(h)\gtrsim h^{-2}\) as \(h\rightarrow 0^+\). Let \(h\in H^1_{\text {loc}}({\mathbb {R}})\) such that \(h\ge 0\) and \(\int _{{\mathbb {R}}} h\in (0,+\infty ]\). If E[h] is finite, then \(h>0\) in \({\mathbb {R}}\) and \(h\not \rightarrow 0\) as \(|x|\rightarrow +\infty \).
Proof
Since the mass is positive, \(h\not \equiv 0\). For the first statement, assume by contradiction that \(h^{-1}(\{0\})\ne \emptyset \). Since \(h\not \equiv 0\), \(x_0\in {\mathbb {R}}\) exists such that \(h(x_0)=0\) and a left or right neighborhood \({{\mathcal {U}}}\) of \(x_0\) exist such that \(h>0\) in \({{\mathcal {U}}}\). Now, \(h\in H^1({{\mathcal {U}}})\) implies that \(h(x)\lesssim |x-x_0|^{1/2}\) in \({{\mathcal {U}}}\); therefore, \(Q(h(x))\ge h(x)^{-2}\gtrsim |x-x_0|^{-1}\) in \({{\mathcal {U}}}\), whence a contradiction:
The second statement is straightforward: if by contradiction \(h\rightarrow 0\) as, say, \(x\rightarrow +\infty \), then we would have \(0<h\ll 1\) for \(x\gg 1\), hence \(Q(h)\gg 1\) for all \(x\gg 1\), which obviously contradicts the finiteness of the energy. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Durastanti, R., Giacomelli, L. Thin-Film Equations with Singular Potentials: An Alternative Solution to the Contact-Line Paradox. J Nonlinear Sci 34, 11 (2024). https://doi.org/10.1007/s00332-023-09982-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-023-09982-2
Keywords
- Asymptotic expansions
- Traveling-wave solutions
- Thin-film equations
- Drops
- Contact lines
- Thin liquid films
- Wetting
- Lubrication theory
- Precursor
- Intermolecular potential


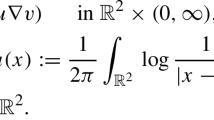










 (cf. alos Remark
(cf. alos Remark