1 Introduction

The precise knowledge of Earth’s gravity field is crucial for a multitude of geosciences as it can be used to deploy vertical reference frames and to give insights into the distribution of masses in the system Earth. As an example, a precise high-resolution gravity model is fundamental for a global height unification (e.g. Gruber et al. 2012; Ihde et al. 2017) or a consistent sea level analysis (e.g. Woodworth et al. 2012). In oceanographic applications, for instance, the gravity field can be used as a physical reference surface to derive the mean dynamic topography (MDT, e.g. Siegismund 2013). In geophysics, gravity field information is used for lithospheric modelling where it serves as a constraining boundary value (e.g. McKenzie et al. 2014).

Since the emergence of satellite gravity field missions, especially the Gravity Recovery And Climate Experiment (GRACE, Tapley et al. 2004) and the Gravity field and steady-state Ocean Circulation Explorer (GOCE, Drinkwater et al. 2003), the quality of global gravity field models has significantly improved. For instance, GRACE data augmented with a comprehensive collection of ground gravity observations contributed to the widely used high-resolution combined global gravity field model EGM2008 (Pavlis et al. 2012). Other subsequent high-resolution models like EIGEN6-C4 (Förste et al. 2014) or GECO (Gilardoni et al. 2016) extended EGM2008 later on by additionally including GOCE data, which resulted in a further improvement in the longer wavelengths.

With the introduction of the release 6 series of GOCE gravity field models, new improved combined satellite-only models such as GOCO06s (Kvas et al. 2019b) have emerged. Consequently, this allows the calculation of new high-resolution combined gravity field models, with the intention to optimally merge satellite-only models with terrestrial, altimetric and topographic gravity information, such that each data source keeps its high-quality information without using information from pre-existing high-resolution models. This triggered the development of the high-resolution combined gravity field model XGM2019e.

At the time of writing, only three models next to EGM2008 with maximum d/o larger than 2000 were published at the International Centre for Global Earth Models (ICGEM, Ince et al. 2019). All these models are using EGM2008 as data source above the resolution of satellite models and consequently are highly dependent on that model. With XGM2019e, we present a new model that is independent of EGM2008: as ground gravity data, it solely includes a primary 15′ gravity anomaly grid augmented with topographic information over land and gravity anomalies derived from altimetry over sea (cf. Sect. 2). The inclusion of these augmentation datasets allows the calculation of XGM2019e up to the remarkable resolution of 2′ resp. d/o 5400 (cf. Sect. 3).

In comparison with the precursor model XGM2016 (Pail et al. 2018), some new techniques regarding the combination strategy are introduced with XGM2019e. These include the new and improved empirical weighting approach for the ground gravity observations and a newly developed spectral filter technique in the spatial domain (cf. Sect. 3). Other changes are the application of spheroidal harmonics instead of spherical harmonics and the complete reimplementation of the associated Legendre function routines, which eventually enable the calculation of spherical/spheroidal harmonics up to very high d/o (remark: the term spheroid is used to denote ellipsoids of revolution and to differentiate from arbitrary 3-axis ellipsoids).

2 Data sources

XGM2019e is composed of three main data sources: the combined satellite-only model GOCO06s, the 15′ ground gravity anomaly dataset provided by NGA, and the 1′ min augmentation dataset consisting of gravity anomalies derived from altimetry over the oceans and topography over the continents. All three datasets are briefly presented in the following.

2.1 The GOCO06s satellite-only gravity field model

GOCO06s is a combined satellite-only model consisting mainly of data from the GOCE (TIM6, Brockmann et al. 2019) and GRACE (ITSG-Grace2018s, Kvas et al. 2019a) missions. For the lower-degree coefficients also, satellite laser ranging (SLR) and satellite-to-satellite tracking (SST) observations (using the Global Positioning Satellite (GPS) system) of several other satellite missions were included. For the combination in XGM2019e, the unconstrained normal equation (NEQ) system of GOCO06s up to d/o 300 is used. Since in the original GOCO06s also temporal gravity variations are parameterized, all non-static parameters have been pre-eliminated. The correctness of this procedure is confirmed by comparing the original GOCO06s static coefficients with the recomputed solution by adding back the Kaula regularization to the NEQ system. As expected, the resulting coefficient differences are in the magnitude of numerical precision.

2.2 The 15′ ground gravity dataset

As the primary source for the ground gravity observations (land and oceans), a pre-compiled 15′ (\( \sim30 \) km at the equator) global geographic grid provided by the US National Geospatial-Intelligence Agency (NGA) is used. The dataset has already been spectrally limited beforehand to d/o 719 (in the spheroidal harmonic domain) and reduced to the spheroid’s surface. This ground gravity dataset is identical to the dataset used in XGM2016 and is mainly based on observed gravity anomalies over land and DTU13 (Andersen et al. 2013) gravity anomalies derived from altimetry over sea (Fig. 1).

Fig. 1
figure 1

Data composition of NGA’s primary 15′ dataset (see Pail et al. 2018). Dark blue: airborne gravity datasets over Antarctica (Scheinert et al. 2016). Orange: contributed pre-compiled dataset covering parts of Siberia (Pavlis et al. 2012). Dark grey: areas processed (collocated) by the NGA (Pail et al. 2018). Light grey: areas with sparse/inaccurate data coverage where topographic information is filled in (EARTH2014, Rexer et al. 2017). Red: GRAV-D airborne data over North America from the US National Geodetic Survey (e.g. Li et al. 2016). Light blue: altimetric gravity anomalies derived from DTU13 (Andersen et al. 2013). Green: Combination of DTU13 and other datasets (Pail et al. 2018)

Full size image

2.3 The 1′ augmentation dataset

To further extend the spatial resolution, a 1′ (\( \sim2 \) km at the equator) global geographic grid of gravity anomalies is compiled in a preliminary step, containing forward-modelled gravity anomalies from topography over land, and gravity anomalies derived from altimetry over sea.

For the topography-derived gravity, the EARTH2014 (Rexer et al. 2017) spherical harmonic model is used up to d/o 5480, and gravity anomalies are synthesized on the 1′ target grid. An in-depth evaluation of the performance of EARTH2014 can be found in Rexer et al. 2016 and Hirt et al. 2017. To reduce the largest uncertainties in the longer wavelengths which are induced by the hypothetical density assumptions in the course of the numerical forward modelling, EARTH2014 is combined with GOCO06s in the spectral domain beforehand. For more details regarding the applied combination strategy used for the combined model (SATOP1), the reader is referred to Zingerle et al. 2019b. The combination with the satellite model is necessary to minimize the (long wavelength) gravity anomaly differences to the altimetry dataset in the coastal areas because they would hamper the subsequent merging of both datasets.

To be consistent with the altimetric data of the primary 15′ dataset, the same DTU13 gravity anomalies are used within the augmentation dataset, but now using the full resolution (1′). Both the altimetric and topographic datasets are combined using a land–ocean mask derived from the GSHHS database (Wessel and Smith 1996). In order to avoid discontinuities at the coastline (i.e. to smoothen the land–ocean transition), a distance-dependent tapering function is applied, which linearly decreases until 30 km into the ocean. The distance of 30 km is chosen because it roughly corresponds to the resolution of the primary 15′ dataset. The tapering is necessary not only to avoid high-frequency artefacts induced by such discontinuities but also to account for the decreasing quality of altimetric observations towards the coasts.

3 Combination strategy and results

The calculation of the XGM2019e model can conceptually be split into two steps: Firstly, the combination of the GOCO06s with the primary 15′ ground gravity dataset leading to a d/o 719 model is referred to as XGM2019, as it logically succeeds the XGM series of gravity field models. Secondly, and independently of XGM2019, the higher-resolution part of the model in the spectral band between d/o 720 and 5480 can be derived through the augmentation dataset.

3.1 Calculation of XGM2019 (up to d/o 719)

The calculation of the XGM2019 spheroidal harmonic model coefficients up to d/o 719 consists of a weighted least squares adjustment of GOCO06s with the primary 15′ NGA ground gravity dataset. Introducing individual point weights into the least squares adjustment (LSA) approach leads to the loss of the orthogonality of spheroidal harmonics and therefore results in a dense normal equation system with more than 500.000 unknowns (cf. Pail et al. 2018).

One of the challenges of this combination method is the realistic choice of ground gravity observation error variances \( {\text{evar}}_{\text{gr}} \) relative to the satellite component. In the previous model GOCO05c (Fecher et al. 2017), variance component estimation was used for a relative weighting of different regional data sets of the world. In XGM2016, the regionally varying relative weights were empirically derived from differences of the ground gravity dataset with the global satellite-only model GOCO05s up to d/o 200. The main drawback of latter method is that only their “commission error” was considered, but the gravity signal and corresponding errors beyond this cut-off degree were not taken into account. Therefore, for XGM2019 the computation strategy has been improved in order to include also errors of the higher-frequency signals: the comparison to the 15′ ground observations \( \delta g_{\text{ground}} \) is now performed using a preliminary solution of XGM2019 up to d/o 719, called XGM19a in the following. XGM19a is obtained by using the same LSA approach as for XGM2019 by combining GOCO06s and \( \delta g_{\text{ground}} \), but assigning an equal error of 2 mGal to all observations of the ground gravity grid. Based on gravity anomalies \( \delta g_{\text{XGM19a}} \), that are synthesized from XGM19a, local error variances \( {\text{evar}}_{0} \left( {\theta ,\lambda } \right) \) are estimated applying a Gaussian kernel function \( W_{G} \) with a filter strength of 50 km half-width at half-maximum (HWHM, empirically derived):

$$ {\text{evar}}_{0} \left( {\theta ,\lambda } \right) \approx \left( {W_{G} *\left( {\delta g_{\text{XGM19a}} - \delta g_{\text{ground}} } \right)^{2} } \right)\left( {\theta ,\lambda } \right) $$
(1)

Since the solution of XGM19a converges strongly towards \( \delta g_{\text{ground}} \) above the resolution of the satellite model, \( \delta g_{\text{XGM19a}} \) differs from \( \delta g_{\text{ground}} \) mainly in the spectral band of the satellite model (up to about d/o 200). Correspondingly, also the thereby derived error variances \( {\text{evar}}_{0} \) only differ in this spectral band (similar to XGM2016). Therefore, they are not fully representative for the ground observations which contain the full spectral content up to d/o 719. To account for this and to restore the missing spectral content within the local error variances, an omission/commission (signal) variance ratio \( f_{\text{o/c}} \) is additionally estimated and applied to the uncorrected error variances \( {\text{evar}}_{0} \), such that:

$$ {\text{evar}}_{\text{gr}} \left( {\theta ,\lambda } \right) = f_{\text{o/c}} \left( {\theta ,\lambda } \right) {\text{evar}}_{0} \left( {\theta ,\lambda } \right) $$
(2)

The location-dependent factor \( f_{\text{o/c}} \left( {\theta ,\lambda } \right) \) is determined by the ratio of signal variances:

$$\begin{aligned} & f_{\text{o/c}} \left( {\theta ,\lambda } \right) = \frac{{{\text{var}}\;{\text{up}}\;{\text{to}}\;{\text{model}}\;{\text{res}}.}}{{{\text{var}}\;{\text{in}}\;{\text{satellite}}\;{\text{band}}}} = \\ & \quad\quad\quad = \frac{{\text{var}_{\text{XGM19a}} \left( {\theta ,\lambda } \right)}}{{\text{var}_{\text{sat}} \left( {\theta ,\lambda } \right)}} \approx \frac{{\left( {W_{G} *\delta g_{\text{XGM19a}}^{2} } \right)\left( {\theta ,\lambda } \right)}}{{\left( {W_{G} *\delta g_{\text{rsat}}^{2} } \right)\left( {\theta ,\lambda } \right)}}.\end{aligned} $$
(3)

Like the local error variances \( {\text{evar}}_{0} \), also the local signal variances \( \text{var}_{\text{XGM19a}} \) and \( \text{var}_{\text{sat}} \) are derived using the same Gaussian filter (cf. Eqs. 1, 3). For the estimation of \( \text{var}_{\text{sat}} \), the satellite-influenced spectral part of the XGM19a solution is needed. In the scope of LSA theory, this part is described by the redundancy component of the satellite system (GOCO06s) within XGM19a. Applying this satellite redundancy component to the solution of XGM19a (through multiplication) leads to the gravity anomalies \( \delta g_{\text{rsat}} \) which are assumed to contain the same spectral content as the error variances \( {\text{evar}}_{0} \). The basic assumption of this scaling approach is that the error variances of the ground observations have no spectral correlations and therefore scale identically to the signal variances in the spatial domain. Figure 2 shows the resulting ground gravity error estimates \( \sigma_{\text{gr}} = \sqrt {{\text{evar}}_{\text{gr}} } \).

Fig. 2
figure 2

Standard deviations assumed for the NGA ground gravity dataset in the LSA. As the dataset itself, the deviations are provided in terms of gravity anomalies. Colours are scaled logarithmically

Full size image

Finally, we note that the LSA for XGM2019 is performed in the spheroidal harmonic domain, implying that the whole GOCO06s normal equation system has been transformed to the spheroidal harmonic domain beforehand (Jekeli 1988). After the LSA, the entire variance–covariance matrix is transformed back to spherical harmonics to provide the final formal errors.

3.2 Calculation of the coefficients above d/o 719

The higher d/o coefficients for XGM2019e are calculated solely from the augmentation dataset, using the rigorous block-diagonal technique (Sneeuw 1994). As this high-resolution dataset is primarily created in the spatial domain (cf. Sect. 2.3), it cannot be assumed that it is spectrally limited to a certain d/o. Thus, trying to perform a spheroidal harmonic analysis will inevitably introduce aliasing as well as spectral leakage effects (even when using the block-diagonal technique, as the 2:1 relation of observations to estimated coefficients is inevitable on geographic grids).

To avoid this, we introduce a three-step filter strategy, called the SLASH approach (Spatial Low pass—Analysis—Spectral High pass): in the first step, a Gaussian filter is applied to the combined grid with the aim to remove most of the grid’s content beyond the Nyquist wavelength (< 1′ in this case). In the second step, the resulting low-pass filtered 1′ grid can be safely analysed up to d/o 10700 (cf. Fig. 3, green line). Due to the existence of an analytical correspondence of the Gaussian filter in the spatial and spectral domain (Jekeli 1981), the influence of the filter on the analysed signal can be reverted in the spectral domain (step three). This is done by multiplying the appropriate spectral Gaussian filter factors (one per degree, cf. Fig. 3, orange line) to the analysed coefficients, forming the restored signal (cf. Fig. 3, blue line). This signal represents an optimally low-pass filtered result in the sense that the obtained coefficients (1) exactly match the unfiltered coefficients in the case when the grid is spectrally limited beforehand and (2) are minimally influenced by aliasing and spectral leakage effects from signals beyond the Nyquist frequency otherwise. Figure 3 visualizes this spectral limitation procedure for the 1′ augmentation dataset in the spheroidal harmonic domain (the findings of Jekeli (1981) are also valid for spheroidal harmonics). Please note the increase in the signal degree variances of the result above d/o ~ 3000 is attributed to the increasing divergence of the spheroidal harmonic series expansion (cf. Sect. 3.3) and not related to the SLASH procedure.

Fig. 3
figure 3

Illustration of the applied spectral limitation procedure in the spheroidal harmonic domain. Orange: the degree-dependent factor of a Gaussian filter with \( \sigma = 1^{{\prime }} \). Green: signal degree variances in terms of height anomalies after the analysis (up to d/o 10700) of the spatially filtered grid (\( \sigma = 1^{{\prime }} \)). As the attenuation of the filtered signal at d/o 10700 is very high, aliasing and spectral leakage effects are minimized. Blue: final signal degree variances after rescaling using the inverse Gaussian filter factors. In the case of the augmentation dataset, degree variances above d/o 5400 are very small (\( < 0.01\;{\text{mm}} \)) for filtered and restored signal degree variances

Full size image

3.3 Compilation of XGM2019e

Since the topographic data (EARTH2014) are limited to d/o 5480, the high-degree coefficients (that were calculated to d/o 10700) are also only used up to this d/o, resulting in the target resolution of XGM2019e. Theoretically, a model up to d/o 10700 would be feasible, but due to the limited resolution of EARTH2014 and the fact that DTU13 gravity anomalies do not show any geophysical signal content beyond d/o 5400 (as DTU13 is filtered to 6.5 km HWHM, see Andersen et al. 2013), it has been decided to cut the final model at d/o 5480.

In the last step, XGM2019e is created by merging the coefficients of XGM2019 up to d/o 719 and the high-resolution coefficients starting at d/o 720. No tapering function is applied. This is possible due to the use of spheroidal harmonics, since the reference surface of the expansion (spheroid) coincides with the surface where the ground data are located, and thus, cut-off effects as experienced with spherical harmonics are avoided. Additionally, to avoid further artefacts, the 1′ augmentation dataset was compiled with the requirement to be most compatible with the primary NGA dataset. Therefore, the same altimetric gravity anomalies DTU13GRA were used, a wide tapering function towards the land was chosen, and a similar replacement of the longest wavelengths took place, cf. Sect. 2.3. Finally, the whole spectrum of XGM2019e is transformed into the spherical harmonic domain (Jekeli 1988).

The error degree variances of XGM2019e beyond d/o 719 are derived by comparing the high-resolution coefficients \( c_{\text{lm}}^{\text{AUG}} \) (from the augmented dataset, cf. Sect. 3.2) to the XGM2019(e) coefficients \( c_{\text{lm}}^{\text{XGM2019}} \) in the lower band (up to d/o 719, cf. Sect. 3.1) and applying an extrapolation function. The extrapolation is performed through a first-order polynomial fit (of parameters \( a_{0} , a_{1} \)) in the double logarithmic domain:

$$ {\text{evar}}_{l}^{\text{AUG}} \sim\mathop \sum \limits_{m = - l}^{l} \frac{{\left( {c_{\text{lm}}^{\text{AUG}} - c_{\text{lm}}^{\text{XGM2019}} } \right)^{2} }}{2l + 1}, \quad \text{var}_{l}^{\text{AUG}} \text{ := }\mathop \sum \limits_{m = - l}^{l} \frac{{\left( {c_{\text{lm}}^{\text{AUG}} } \right)^{2} }}{2l + 1} $$
$$ {\text{Fit}} \left( {a_{0} , a_{1} } \right) {\text{with}}\; l \le 719\; {\text{in}}: \log \left( {\frac{{{\text{evar}}_{l}^{\text{AUG}} }}{{\text{var}_{l}^{\text{AUG}} }}} \right) = a_{0} + a_{1} \log \left( l \right) $$
$$ {\text{Extrapolate}}\;l > 719:{\text{evar}}_{l}^{\text{XGM2019e}} = \log^{ - 1} \left( {a_{0} + a_{1} \log \left( l \right)} \right)\text{var}_{l}^{\text{AUG}} $$
(4)

where \( c_{\text{lm}} \) denotes a spheroidal harmonic coefficient of degree \( l \) and order \( m \). The estimated error degree variances \( {\text{evar}}_{l} \) are then transformed to the spherical domain and merged with the XGM2019 error degree variances, forming the final error degree variances of XGM2019e. The results in terms of degree signals and errors in the spherical harmonic domain are depicted in Fig. 4. Important to note here is:

Fig. 4
figure 4

Spherical harmonic degree signals and errors in terms of height anomalies. Dark blue: signal XGM2019e. Light red: formal error XGM2019e. Green: signal difference GOCO06s-XGM2019e. Dashed violet: formal error GOCO06s. Yellow: signal difference of a ground-only solution versus XGM2019e. The ground-only solution is obtained using the unweighted block-diagonal analysis technique. Dark red: signal difference XGM2016-XGM2019e. Light blue: signal difference EGM2008-XGM2019e. Magenta: signal difference EIGEN6C4-XGM2019e

Full size image
  1. (1)

    The good agreement of the coefficient differences with the formal errors of GOCO06s in the spectral band of the transition (above d/o 100), which proves the correctness of the LSA approach.

  2. (2)

    The convergence of XGM2019 solution towards a (block-diagonal) ground-only solution with increasing d/o (especially above d/o 500).

  3. (3)

    The jump in the formal error at d/o 720 that is inevitable due to the change of the data source.

  4. (4)

    The slowed convergence (commencing divergence) of the harmonic series in the highest degrees as the Earth’s surface exceeds the Brillouin sphere (in the spherical case) resp. spheroid (in the spheroidal case) due to high elevations in the topography. The manifestation of this effect is stronger in terms of spheroidal harmonics as the reference spheroid is on average further below Earth’s surface than the reference sphere (since its radius is per definition the semi-major axis). This is discernible by comparing the blue line of Fig. 3 (spheroidal case, already diverging) with the blue line of Fig. 4 (spherical case, still converging).

  5. (5)

    The increase in the formal error in the highest degrees which is an effect of the spherical harmonic transformation, as it is not visible in the spheroidal harmonic domain. Eventually, this is also related to the spheroidal harmonic series divergence.

4 Validation and discussion

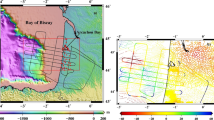
The fact that XGM2019e only contains forward-modelled topographic gravity anomalies over land beyond d/o 719 likely shifts the primary use of the model more towards oceanographic applications. With its 2′ resolution, it covers all the signal present in the DTU13 gravity anomaly dataset (cf. Sect. 3.3). Together with the weighted LSA combination strategy (cf. Sect. 3), this leads to an improved oceanic geoid which allows the derivation of a higher-quality MDT (Fig. 5b). The MDT itself is a central parameter of the maritime system and inherently connected to dynamic processes like ocean currents (Fig. 5d–f), heat transport and sea level rise. Hence, it is of major importance for Earth system sciences like oceanography or climatology and may ultimately lead to a deeper comprehension of the Earth system as a whole, thus also allowing for better predictions in the future.

Fig. 5
figure 5

Unfiltered geodetic MDT solutions from the CNES/CLS 2015 means sea surface and the EGM2008 (a) resp. XGM2019e (b) ocean geoid (shown for the Western Pacific). c reference MDT obtained from the drifter-optimized DTU17MDT (Knudsen et al. 2018). Geostrophic current velocities for the Agulhas current derived from (identically) Gaussian-filtered EGM2008 MDT (d) resp. XGM2019e MDT (e). f reference geostrophic current velocities from DTU17MDT

Full size image

4.1 MDT comparisons

To demonstrate the model’s performance over the ocean, geostrophic currents are derived by comparing the XGM2019e geoid to the independent CNES/CLS 2015 mean sea surface (Schaeffer et al. 2016, see Fig. 5) and thereby generating an MDT: it is clearly discernible that the unfiltered MDT derived from XGM2019e (Fig. 5b) shows fewer artefacts and delivers a smoother result than the MDT derived from EGM2008 (Fig. 5a, the most comparable model in terms of performance, all other high-resolution models show even larger artefacts). Consequently, the improved MDT allows one to derive improved geostrophic currents, as is shown in the comparison of the Agulhas current (Fig. 5d, e). This visual evidence is proved by comparing both MDTs to the drifter-optimized DTU17MDT (Fig. 5c, Knudsen et al. 2018). Within the open ocean (up to 60° northern/southern latitude and 30 km away from coasts), the XGM2019e-derived MDT shows a global standard deviation to DTU17MDT of 2.02 cm, while the MDTs derived from EGM2008 and EIGEN6-C4 have standard deviations of 3.34 cm and 4.25 cm, respectively. This means that the performance in the ocean has improved by \( \sim \) 40% in comparison with EGM2008 (\( \sim \) 52% to EIGEN6-C4) when validating against DTU17MDT. A statistically complete evaluation of the comparisons to DTU17MDT is found in Fig. 6a in terms of empirically derived probability density functions (PDFs).

Fig. 6
figure 6

a Empirically derived probability density functions (PDFs) for deviations of unfiltered geoid derived MDTs (using CNES/CLS 2015 MSS) from the reference DTU17MDT. Mean values of MDT deviations were eliminated beforehand. Blue: deviation of the XGM2019e derived MDT. Red: deviation of the EGM2008 derived MDT. Violet: deviation of the EIGEN6-C4 derived MDT. b Empirically derived PDFs for deviations from the XGM2019e geoid calculated from the roughest 10% of the ocean’s geoid surface. Red: deviation of the EGM2008 derived geoid. Violet: deviation of the EIGEN6-C4 derived geoid. Green: deviation of the XGM2019e (up to d/o 2159) derived geoid. Yellow: deviation of the XGM2019 (up to d/o 719) derived geoid

Full size image

Please be aware that due to the use of the altimetric gravity anomalies (DTU13A) in the ground observations (cf. Fig. 1), the XGM2019e model may be biased to a certain degree to the a priori MDT used within DTU13GRA. In the course of the processing of DTU13A, an a priori MDT is removed from the mean sea surface up to d/o 100 (cf. Andersen et al. 2013). Since up to d/o 100 XGM2019e is dominated by the satellite model (cf. Fig. 4), the bias towards this a priori MDT is completely removed. Nevertheless, there is still a bias to expect, as removing an MDT up to d/o 100 implies to neglect all MDT signal present above d/o 100. Through the inclusion of GOCO06s data in the XGM2019e model, it is possible to restore the MDT signal up to the satellite resolution of d/o \( \sim \) 200 (cf. Figs. 4, 5b), meaning that all actual MDT signal above this resolution remains as bias within XGM2019e. As the actual MDT has in general a long-wavelength character (cf. Fig. 5c), the magnitude of this bias can be considered as small (cf. differences to DTU17MDT), but one may expect that an MDT derived from XGM2019e is still somewhat too smooth compared to the actual MDT.

Even though the ocean’s geoid can be considered smooth compared to the land geoid (since the signal of the seabed gets attenuated due to upward continuation of the gravity field onto the ocean’s surface), there is still significant signal left above d/o 2159. This can be observed in XGM2019e especially over rough seabed structures (e.g. oceanic trenches or ridges) where deviations in the ocean’s geoid can reach up to about 2 cm when neglecting gravity field signal above d/o 2159 (cf. Fig. 7). In the proximity of such rough structures, one can expect a global standard deviation of about 5 mm induced by the residual signal above d/o 2159 (cf. Fig. 6b, green line). This standard deviation increases strongly to about 10 cm when further reducing the maximal spectral resolution of XGM2019e to d/o 719 (cf. Fig. 6b, yellow line).

Fig. 7
figure 7

Residual signal of XGM2019e above d/o 2159 over the ocean in terms of maximum absolute height anomalies (i.e. geoid heights) on a 5′ raster

Full size image

4.2 GNSS/levelling performance

GNSS/levelling-derived geoid comparisons pose a good way to evaluate the performance of global models over land. For this, we apply the procedure described in Gruber and Willberg 2019 and compare four models with some regional GNSS/levelling geoid heights. It is noted that the XGM2019e model has only been used up to a spectral resolution of d/o 2190 (see also below) in order to be comparable with the resolution of EGM2008 and EIGEN6-C4. From Fig. 8, which shows the RMS differences between a regional GNSS/levelling-derived geoid data set and geoid heights computed from the models, the following observations can be made:

Fig. 8
figure 8

GNSS-levelling performance of XGM2019e, XGM2016, EGM2008 and EIGEN6-C4 for different spectral resolutions up to d/o 2190 (lower RMS values of geoid differences mean better performance, for details see Gruber and Willberg 2019). RMS of geoid differences a in Germany, b in Japan, c in the US, d in Australia, e in Brazil, f in Mexico. GNSS/levelling comparisons in other regions are also performed. As they support the drawn conclusions and thus give no further insights, they are not shown within this work

Full size image
  1. (1)

    In case of XGM2019e, the RMS of geoid height differences to the GNSS/levelling values is always constant for all model truncation degrees because this model was also used for estimating the omission error above this degree and order. In case the RMS of geoid differences for other gravity models is below this line, a model performs better than XGM2019e and vice versa.

  2. (2)

    In areas where one can assume high-quality ground observations (Fig. 8a–d), the XGM2019e model up to d/o 719 performs better than all other tested models in most cases. This is rather obvious for the EGM2008 model, for which the RMS of geoid height differences is significantly higher than for XGM2019e in all areas. As this is observed already for low truncation degrees (e.g. between d/o 50 and 200), one can assume that the largest impact stems from the inclusion of GOCE data, which was not yet available at the time of EGM2008. In these areas, XGM2019e also performs slightly better than XGM2016 indicating some improved modelling as for both models used an identical land data set. For EIGEN6-C4, one can identify that for 3 areas XGM2019e outperforms this model as well, which is mainly due to the use of the latest GOCE solution (release 6 instead of release 5) and probably also due to an improved modelling approach. Only for Australia (Fig. 8d) EIGEN6-C4 provides slightly better results.

  3. (3)

    When looking to the RMS of geoid differences in well-observed areas for degrees above 719, it becomes obvious that EGM2008 and EIGEN6-C4 outperform XGM2019e. This is visible in Fig. 8a–d as the reduced RMS for both models between degree 720 and their full resolution. This clearly shows the impact of using observed instead of topography-derived gravity anomalies in the range between d/o 719 and d/o 2190 in EGM2008 and EIGEN6-C4.

  4. (4)

    In less well-surveyed areas one can identify from the geoid differences RMS that the XGM2019e model outperforms all other models (Fig. 8e, f). This shows on the one hand again the impact of the GOCE satellite data (up to d/o 200) and on the other hand that topography-derived gravity anomalies can provide better information than less accurate ground gravity data. For example, in Brazil the RMS reduction from the EGM2008 model to the XGM2019e model is at a remarkable level of 7 cm. The major part of this (about 80% of the total reduction) can be attributed to the GOCE data, which is nicely shown by the EIGEN6-C4 performance in the lower degrees and the remaining reduction results from improved gravity data in the area including the topography-derived gravity anomalies for the very high frequencies.

In summary, one can conclude from the GNSS/levelling comparisons that despite the use of topographic information, XGM2019e shows a solid performance even over land. For the longer wavelengths up to d/o 719, XGM2019e exhibits a slightly better performance as compared to previous models. Above d/o 719 and in well-surveyed areas, XGM2019e cannot fully compete with EGM2008 and EIGEN6-C4 due to the lack of gravity measurements with a higher resolution than 15′. In areas with poor data coverage/quality, the performance of XGM2019e might be considered as identical, or even better than that of other models. Thus, it can be stated that XGM2019e performs globally more consistently than other models (i.e. accuracies within XGM2019e vary less than accuracies within EGM2008 or EIGEN6-C4, cf. Fig. 8). This seems reasonable since the topographic information used within XGM2019e is available globally with nearly constant quality while the availability (and quality) of direct gravity field measurements is strongly location dependent. This better consistency and the fact that gravity field information provided within XGM2019e is globally available up to \( \sim4 \) km can be important, e.g. for a more consistent gravity field reduction in the frame of a compute–remove–restore process of regional gravity field modelling (especially in areas where the terrestrial data quality is low or data access is restricted). In the scope of regional gravity field modelling, it is also noteworthy that for XGM2019e full variance–covariance information is available up to d/o 719 which can be used for more realistic error propagations into the spatial domain to improve regional modelling approaches (see e.g. Willberg et al. 2019).

4.3 Provision of XGM2019e

To comply with the existing standard, XGM2019e is published as spherical harmonic model. As a matter of fact, it is problematic to truncate the spherical harmonic series expansion at a certain degree when evaluating functionals on a spheroid since artefacts are introduced (cf. Pavlis et al. 2012). In order to avoid these problems, spectral truncations must be performed in the spheroidal harmonic domain. The resulting procedure is considered problematic for most end-users, as they may not be familiar with the theory of spheroidal harmonics and/or the spectral transformation formulas involved. It is therefore decided to provide the model pre-calculated at three different spectral resolutions: d/o 5540, 2190 and 760. All three resolutions are available on ICGEM (Zingerle et al. 2019a).

5 Outlook

It is planned to continue the series of high-resolution XGM models in the future. On the processing branch, improvements can still be made by increasing the maximum d/o of the densely modelled part (soon up to d/o 2159, as new supercomputing resources at the Leibniz Supercomputing Center are available). One point to focus within the preparation of future models will be the task of data acquisition resp. compilation. As of now (January 2020), access to gravity field information is still restricted in many regions of the world, so the outcome of this endeavour is open. The situation over land might improve after the public release of EGM2020. In the oceanic regions, we are confident to achieve further enhancements in the future by switching to updated altimetric products and changing the processing strategy. As an example, it is planned to directly use mean sea surface heights and individual MDT products to derive the gravity field instead of using pre-calculated gravity anomalies.