1 Introduction

During the past thirty years, the geodetic space techniques of satellite altimetry, positioning using the Global Navigation Satellite Systems (GNSS), and satellite gravimetry have enriched the possibilities and scope of geodesy fundamentally. Geoid models with centimeter precision up to medium wavelength scales (including temporal geoid changes) became available, point positioning by GNSS reaches the sub-centimeter level, and since about thirty years, altimetry delivers time-series of the global sea surface (and ice covers) with centimeter precision and great consistency. The method of GNSS-leveling gives physical heights H, i.e., heights above an adopted geoid surface, by combining ellipsoidal heights h from GNSS and geoid heights N from a high-resolution geoid model according to

$$\begin{aligned} H\;=\;h \,-\,N, \end{aligned}$$
(1)

again with centimeter precision.

The method will supersede classical geodetic leveling soon (Sánchez et al. 2021). Currently, over short to medium distances (say up to 100 km), its precision, in many cases, is still inferior to that of leveling, mainly due to still existing limitations of regional gravity data and geoid models.

Nevertheless, for many practical cases, the precision of GNSS-leveling seems adequate, while the method is much more convenient and economic than traditional geodetic leveling. In the same setup and with little additional effort, temporal height changes are monitored as well. At tide gauges, i.e., along the coastlines, GNSS-leveling can be crosschecked using the methods of altimetric and ocean leveling.

The intention of this article is to reflect on the role of classical geodetic leveling in times of GNSS and altimetric leveling. Of course, classical leveling will keep its importance in most engineering applications. Furthermore, also the many official governmental height registers, derived from decades of geodetic leveling, will keep their relevance and value. Our question is, however, whether there remains a relevant role for the existing classical geodetic levelings in science applications despite the great efficiency of GNSS-leveling and altimetric leveling. This is also reflected in Featherstone et al. (2012) where the pros and cons of adopting a leveling or geoid-based vertical datum are discussed. From the perspective of consistency of the vertical reference frame with related observations or models (heights from GNSS, leveled potential differences and the adopted geoid model) the proposed combination methods may be a viable way for vertical reference frame realization.

In Sect. 2, we will give a historic summary of classical geodetic first-order levelings. We will address their error characteristics and how their comparisons with mean sea level (MSL) evolved with time. In recent times, GNSS-leveling and altimetric as well as oceanic leveling offer new means of an independent comparison with classical geodetic leveling. In Sect. 3, we propose two theoretical concepts for a combination of geodetic leveling with the new method of GNSS-leveling. Numerical studies are carried out in Sect. 4 to illustrate main characteristics of these methods. Approach 1, a classical network adjustment, is analyzed with synthetic data resembling the Unified European Leveling Network (UELN). This approach is similar to the combination of UELN heights with height differences between tide gauges determined by hydrodynamic leveling as proposed in Afrasteh et al. (2021). In approach 2, potential differences from classical geodetic leveling are used as an independent gravity field functional. Thus they are used for regional gravity field modeling in combination with terrestrial gravity anomalies. Here we use synthetic data for simulating a combined geoid computation covering the area of Switzerland. This second concept, which to our knowledge has not been implemented before, can of course be modified in the sense of locally updating the fine structure of an already existing geoid model, and it can also handle geopotential differences from alternative observation techniques like, e.g., chronometric leveling. Finally, in Sect. 5, we summarize the results and draw some conclusions.

2 Historical remarks on leveling

Geodetic leveling, i.e., the combination of spirit leveling with gravimetry, corresponds to the measurement of gravity potential differences. The measured differences \(\Delta W_{AB}\) between two points A and B tell us unambiguously, which one of the two is higher or lower and by what amount:

$$\begin{aligned} \Delta W_{AB}\;=\;\int _{A}^{B}\,\text{ d }W \;=\; -\sum _A^B\,g_i\,\text{ d }n_i, \end{aligned}$$
(2)

with \(g_i\) gravity and \(\text{ d }n_i\) the leveled height increment along the leveling line. As mentioned already, it is well established that classical geodetic leveling is very precise over short distances, say below 100 km. The error standard deviation \(\sigma \) of the observed height difference is being proportional to the square root of the length of the leveling line, i.e.,

$$\begin{aligned} \sigma \;=\;\sigma _0\,\sqrt{L}, \end{aligned}$$
(3)

where L is the length of the line in kilometer and \(\sigma _0\) is the standard deviation for a line of 1 km length. For precision leveling, \(\sigma _0\) is about 1 mm. The equation describes the propagation of random errors and shows that even for very long lines, random errors do hardly accumulate to more than around 10 cm. However, for longer distances, such as the size of a state, systematic errors tend to dominate the error budget. In order to limit distortions from systematic errors, national leveling networks were often fixed to several tide gauges because already in the early days of national leveling networks, one was aware of the fact that MSL had to be close to an equipotential surface of the gravity field. This way, effects of systematic errors could be controlled and limited to the magnitude of coastal mean dynamic ocean topography.

When there was no alternative method available, in particular during the pioneering years of geodesy, greatest care was taken to minimize random and systematic leveling errors. In addition, many detailed studies were carried out about the effects that influence the error behavior of leveling and about the proper mathematical representation of this error behavior. There exist early discussions on the nature of leveling errors and their detectability, such as Kneissl (1955), Edge (1959), Entin (1959), Lucht (1972), Borre and Meissl (1974) or Bomford (1983) or also Pelzer (1984), Niemeier (1984) and Kok (1984) who have discussed among other issues the question of reliability in connection with the size of the leveling loops. In particular, the origin, characteristics and detectability of systematic errors remained controversial. A convincing account is given by Bomford (1983). He starts pointing out that the propagation of random leveling errors of fore and back leveling is following \(\sigma _0\sqrt{2\,L}\) with typical numbers of \(\sigma _0\) in the sub-mm and mm-range depending on whether it is first-, second-, or third-order leveling. Thereby, \(\sqrt{L}\) is expressing the proportionality with the length of the leveling line and \(\sqrt{2}\) is resulting from fore and back leveling. However, according to Bomford (ibid.) there are systematic leveling errors as well. Their accumulated effect can be represented by proportionality to L rather than \(\sqrt{L}\). He points out that the proportionality to L is not necessarily directly related to the length L of the leveling line but indirectly via the number of setups n or the time t spent on the work. Error accumulation with topographic height H and with latitude difference \(\Delta \,\varphi \) requires separate consideration. The errors related to L, n and t may be expected to show up in the closing errors of leveling loops and are minimized during the adjustment. The errors related to H and \(\Delta \,\varphi \), if constant, will not. Errors accumulating with height may be related to the subdivision of the staff, non-verticality of the staff, or unequal refraction. Error accumulation with latitude could be caused by sunlight influences on the staff, sun exposure of the invar stripe or neglected tidal effects. Errors depending on H or \(\Delta \,\varphi \) do not show up as a difference between fore and back leveling or in the closure of a circuit. It is today not feasible to reconstruct the exact procedures that have been applied to the first- and second-order leveling in various countries in the past and even at present. Bomford (ibid.) gives values for the standard error \(\sigma _0\) in western European level nets in 1959 as between 0.6 and 2.5 mm \(\sqrt{L}\), depending on location and age of the data. These numbers comprise both, random and systematic effects. The study of the size of systematic errors, their behavior and possible causes required methods of control independent from geodetic leveling. The quest for such methods evolved in parallel with geodetic leveling and culminated in GNSS-leveling, and along coastlines, in ocean and altimetric leveling.

From the very beginning, geodetic leveling and sea-level monitoring were intimately related. Mean sea level is close to an equipotential (or level) surface of the gravity field, and geodetic leveling is able to measure the local deviations of MSL from the one chosen reference equipotential surface. This mutual control of measured MSL, e.g., at tide gauges, and measured potential differences plays a particular role in lowland countries such as the Netherlands. There, sophisticated systems of water management are employed. The reference system Amsterdamse Peil was established in the late seventeenth century for the purpose of water management (Waalewijn 1986a). In 1864, at the General Assembly of the "Mitteleuropäische Gradmessung" a resolution was passed to establish first-order height systems in all member countries and to connect them at tide gauges with the MSL of the adjacent seas at as many locations as possible for defining the absolute height level (Börsch and Kühnen 1891). As height reference the Normaal Amsterdamse Peil (NAP) was chosen, a reconstruction of the much older Amsterdamse Peil (Waalewijn 1986b). It took another 20 to 25 years before the methods applied to the national first-order leveling and to the mean sea-level determination were developed far enough to be able to materialize the resolution of 1864 (Börsch and Kühnen 1891).

The deviation of MSL from one global level surface, i.e., the geoid, is denoted mean dynamic topography (MDT). It was expected that MDT is small, typically less than one meter. Bruns (1878) discusses several causes for the deviation of MSL from the geoid such as air pressure variations, tides, steady-state ocean circulation and wind stress. However, one was not sure whether MDT could be identified at tide gauges in the presence of leveling and reduction uncertainties. We refer to Börsch and Kühnen (1891), Helmert (1884, ch. 7, sec. 18) and in more detail to Bruns (1878, paragraph 1). Börsch and Kühnen (ibid.), who performed adjustments of selected leveling lines for comparing the sea levels of the waters adjacent to Western Europe, conclude in 1891 that their error budget, in particular possible systematic errors, does not yet allow a reliable comparison; see also their note on the preliminary work of Lallemand (Börsch and Kühnen (1891), paragraph 1, page 2) who comes to the same conclusion.

Bowie (1927) looked into the comparison of MSL at various locations in North America and Europe. His article starts with the statement: "An adjustment of the level net of the United States,..., indicates that the tidal planes determined by observations of the waters of the oceans and their tributaries do not lie in the same level surface." He discusses the differences in MSL between tide gauges, as recovered by national levelings, at various locations of North America and Europe. William Bowie suggests, similar to Bruns, these tilts being caused by meteorological conditions, prevailing winds, barometric pressure as well as water salinity and density. At this time, no accurate oceanographic methods of sea surface determination were available. This changed in the sixties and seventies of the last century and lead to a famous and fierce dispute among geodesists and oceanographers concerning the sea level along the Atlantic and Pacific coast of North America (Sturges 1967; Montgomery 1969; Sturges 1974; Fischer 1975, 1977; Forrester 1978). Finally, the oceanographers were right and the geodesists wrong.

In the 1960s, based on a request of IAG’s REUN CommissionFootnote 1 to investigate the slope of sea level along the European coastline, sea-level variations in Europe were analyzed, see Rossiter (1967). Sturges could show that ocean leveling is a valid and accurate method of MSL determination independent from geodetic leveling and useful for mutual control (Sturges 1974). The author distinguishes two methods. The determination of a geopotential anomaly of the sea surface relative to a deep pressure surface is called steric leveling and is based on the probing of temperature and salinity down to a chosen reference depth. Geostrophic leveling (using current measurements) is based on the geostrophic balance, which leads in good approximation to

$$\begin{aligned} f\,v\;=\;g\,i, \end{aligned}$$
(4)

with Coriolis parameter \(f=2\,\omega \,\sin \varphi \) (\(\omega \) being the angular velocity of the Earth and \(\varphi \) geographical latitude), velocity v of the geostrophic ocean current, gravity g and the slope i of the sea surface in direction orthogonal to the current’s flow direction. The challenge of steric leveling is the transfer from a reference equipotential surface at depth to the coastline, in particular in the presence of Eastern boundary currents. Sturges (1974) demonstrates a good agreement between the two available methods of ocean leveling, steric and geostrophic leveling. He points at significant discrepancies between the ocean and geodetic leveling in some areas and suggests the presence of systematic errors in geodetic leveling as their cause. A recent discussion of the tilt of mean sea level along the coast of North America is given in Higginson et al. (2015) along with new estimates derived from altimetric and oceanographic leveling. For sea-level variations as determined by the Australian leveling, we refer to Hamon and Greig (1972) and Featherstone and Filmer (2012).

Presently, several alternatives exist for detecting and studying systematic errors of classical geodetic leveling nets, in particular the method of GNSS-leveling, see Colombo (1980), Rummel and Teunissen (1988), Rapp and Balasubramania (1992), Xu (1992) and many others. The geometric part of GNSS-leveling is the determination of ellipsoidal heights using GNSS. This approach reached the required cm-accuracy level in the nineties of the last century. The application to the determination of potential differences or physical heights requires the availability of gravity or geoid models of corresponding accuracy. This step was taken one to two decades later with the data of the dedicated satellite gravimetry missions CHAMP (2000–2010), GRACE (2002–2017), GOCE (2009–2013) and GRACE-FO (2018-present), see Pail (2020). A new generation of gravity models became available. The models are commonly expressed as a series of spherical harmonic coefficients. They are available as pure satellite models with coefficients up to degree and order 280 (Brockmann et al. 2014) or 300 (Bruinsma et al. 2014). For height determination with GNSS, one typically uses a grid of regional geoid heights in which the global models are complemented at short spatial scales by regional gravity data. Alternatively, satellite and terrestrial data are combined into high-resolution global gravity field models such as EGM2008 (Pavlis et al. 2008) or EIGEN-6C4 (Förste et al. 2014). These models combine satellite gravimetry with terrestrial and altimetric gravity anomalies and topographic models. The maximum degree of the spherical harmonic series of such models is currently 2190. Alternatively, at tide gauges, there are as well-improved oceanic and geodetic methods of MSL determination. As mentioned already, ocean leveling was understood as either steric or geostrophic leveling (Bowden 1960; Doodson 1960; Rossiter 1967; Sturges 1974; Rummel and Ilk 1995). Modern ocean leveling is based on advanced numerical ocean circulation models (Woodworth et al. 2012; Higginson et al. 2015; Woodworth et al. 2015; Filmer et al. 2018). The geodetic method uses satellite altimetry or GNSS positioning at tide gauges combined with accurate geoid modeling.

The new techniques of height determination—GNSS-leveling, and along coastlines altimetric leveling and ocean leveling—clearly show the existence and character of systematic distortions of existing classical national and continental height systems and reveal off-sets between them. In several studies the systematic errors of level nets have been analyzed, such as in Europe, Australia, and North and South America. For the European case, Duquenne et al. (2007) report a systematic latitude error of about 34 mm/degree for the traverse from Marseille to Dunkirk; Penna et al. (2013) finds a slope of 20–25 mm/degree latitude of leveled heights with respect to both, mean sea level at British tide gauges and the EGM2008 geoid model; Rülke et al. (2012) determine slopes of European national leveling networks with respect to a combination of the global potential model GOCO03S (Mayer-Gürr et al. 2012) and the regional quasigeoid model EGG2008 (Denker 2013) and find values of several centimeters up to the decimeter (per 100 km) for the tilt in latitude and longitude direction. It is still an open question, where the systematic errors exactly come from. Maps of errors of national networks as provided in Wang et al. (2012) for the continental USA, do neither show a clear latitude nor elevation dependence but a mixture of the two. The order of magnitude of these distortions, however, agrees well with the tilts found in European countries, i.e., around 30 mm/100 km. In some countries the size of the systematic errors has been tried to be kept within reasonable limits by constraining the leveling net to several datum points at tide gauges; examples are North America and Australia. This, however, must be done with caution, i.e., spatial variability of ocean topography would have to be known and taken into account. Otherwise an additional systematic distortion of the leveling network is introduced, see, e.g., Featherstone and Filmer (2012) who show that the tilt of the Australian leveling net was almost completely caused by MDT because the network was constrained to zero height at several tide gauges around the continent. Similarly, other systematics, like inconsistencies in permanent tide systems, would cause a systematic north–south tilt, possibly increasing the tilt from systematic leveling errors.

All this does not take away the fact that over short distances classical leveled height differences remain a very valuable data source all over the world. Therefore, our question is: assuming that in the future global and regional height systems will be based on GNSS-leveling (Ihde et al. 2017), how to make still use of this precious geodetic data treasure? The objective of the paper is to make use of potential differences either directly for the realization of geoid-based vertical reference frames or indirectly by installing potential differences as additional gravity functional. This will add a large and highly precise additional database to global and regional gravity modeling (GGM and RGM) and thus also to the Global Geodetic Observing System, GGOS.

3 Methodology

The International Terrestrial Reference Frame (ITRF) is in its essence a list of precise three-dimensional Cartesian coordinates (or equivalently provided as geodetic latitude, geodetic longitude, ellipsoidal height) of a global set of carefully selected terrestrial stations (Altamimi et al. 2011). It is given in a well-defined geocentric coordinate system, and it is referring to an epoch. In an international effort, the coordinates are derived from the geodetic space techniques VLBI, SLR, DORIS and GNSS. The ITRF resembles the geometric figure of the Earth by a global set of terrestrial points. Following the idea of a Bruns’ polyhedron, the realization of a future global height system could be the addition of potential numbers to the set of ITRF stations, as proposed by Rummel and Beutler (2019) or described by Sánchez et al. (2021). It would add to the geometric 3-D coordinates of the points their physical height value (their geopotential number). Simply expressed, the realization of this idea would tell us the direction and strength of the flow of water between any two points of the global polyhedron. The potential numbers could be calculated from the best available combined high-resolution gravity field model, including regional refinements. Such a model is expected to be free of systematic errors due to the high quality of modern satellite gravimetry. It will be accurate to a few centimeters or decimeters (translating potential numbers to corresponding physical height values). Variations in accuracy will mainly depend on the state of the art of terrestrial gravimetry in various parts of the world. The approach corresponds to a global implementation of the method of GNSS-leveling. It is in line with current efforts to define and realize a global vertical reference frame. Strategies for the realization of such a frame are discussed in Sánchez et al. (2021). Thereby, height differences (or geopotential differences) from geodetic leveling are either used to define the vertical datum (leveling-based datum) or used as independent data for validation purposes only (geoid-based datum).

Reflecting on a geoid-based datum, we pose the question how such a global height system could benefit from the first- and second-order leveling data, still available in many countries. Specifically, whether the incorporation of leveled potential (or height) differences could improve on short scales the accuracy of the International Height Reference Frame (IHRF)?

In this study, two approaches are chosen to test the effect of classical geodetic leveling (1) on a network of geopotential numbers (or physical heights) and (2) on high-resolution gravity field modeling. The tests are based on the following three data sets:

  • Differences in geopotential numbers \(C_{PQ}\) between two stations P and Q (or equivalently, differences of physical heights \(H_{PQ}\)) from geodetic leveling.

  • Geometric heights \(h_P\) above the adopted reference ellipsoid derived from geodetic space techniques, most notably GNSS.

  • Geopotential numbers \(C_P\) (or geoid heights \(N_P\) above the adopted reference ellipsoid) taken from a conventional high-resolution gravity field model.

3.1 Approach 1

Assume the IHRF is realized at a set of 3-D points by geopotential numbers derived from an adopted gravity field model. The points may correspond to the stations of the ITRF or its densification. This set of (absolute) geopotential numbers could be combined with the leveled geopotential differences between the stations in the frame of least-squares network adjustment.

The corresponding vector of observations \(\varvec{b}\) is given by

$$\begin{aligned} \varvec{b} \;=\;\left( \begin{array}{c} C_P = W_0\,-\,(T_P + U_P)\\ C_{PQ} \end{array} \right) \end{aligned}$$
(5)

with geopotential numbers \(C_P\) at GNSS-leveling stations and leveled geopotential differences \(C_{PQ}\) between the stations. \(C_P\) is derived from the disturbing potential \(T_P\) of the adopted gravity field model, the normal potential \(U_P\), e.g., from GRS80, and it refers to the \(W_0\) value of the vertical datum. Because \(U_P=U(h_P, \varphi _P)\), the normal potential is directly affected by GNSS errors especially by errors in the vertical component \(h_P\).

The stochastic model comprises the error variance–covariance matrices \(\varvec{\Sigma _{TT}}\) of the adopted gravity field model, \(\varvec{\Sigma _{hh}}\) of the geometric heights, and \(\varvec{\Sigma _{CC}}\) of the leveled geopotential differences. Equation (5) shows that the first observable combines the error contributions from the adopted gravity field model and GNSS at the GNSS-leveling stations, while the second observable contains only the leveling errors between the stations.

3.2 Approach 2

An alternative and completely different approach would be to introduce leveled geopotential differences \(C_{PQ}\) from geodetic leveling between adjacent GNSS points P and Q as additional gravity functional in regional or global gravity field modeling (or refinement). Because modeling is done in terms of anomalous or disturbing quantities, the disturbance \(\delta C_{PQ}\) of leveled potential differences would be used along with other functionals like gravity anomalies \(\Delta g_i\) (or disturbances \(\delta g_i\)), deflections of the vertical \((\xi _i, \eta _i)\) or even disturbing potential values \(T_i\) from an already existing gravity field model. The corresponding vector of observations \(\varvec{b}\) is given by

$$\begin{aligned} \varvec{b} \;=\;\left( \begin{array}{c} \Delta g_i\\ T_i\\ \ldots \\ \delta C_{PQ} = C_{PQ}-U_{PQ} \end{array} \right) \end{aligned}$$
(6)

The error budget comprises the error variance–covariance matrices of all observables as in approach 1. This time, however, errors in GNSS-heights add up with the leveling errors in \(\delta C_{PQ}\), while in Eq. (5) they belong to the error budget of \(C_P\).

3.3 Double use of geodetic leveling?

As a critical side remark, one may argue that the approaches imply a double use of geodetic leveling. Obviously it is used to construct the geopotential differences \(C_{PQ}\). In addition, height information from leveling may also have been used for the computation of terrestrial gravity anomalies which enter the adopted gravity field model (approach 1) or are used as observables (approach 2).

The critics are based on the fact that we already make use of physical height values H taken from a leveling-based vertical reference frame when computing gravity anomalies according to

$$\begin{aligned} \Delta g \;=\; g_P-\gamma _{P_0}+\frac{\partial \gamma }{\partial h}\,H_P \end{aligned}$$
(7)

with \(g_P\) gravity measured at surface point P, \(\gamma _{P_0}\) normal gravity at the corresponding point on the surface of the ellipsoid, the free-air gradient \(\frac{\partial \gamma }{\partial h}\approx 0.3\) mGal/m and \(H_P\) the height above sea level of point P. Therefore, we may not be allowed to make use of \(H_P\) (more explicitly, leveled potential differences \(C_{PQ}\)) once more.

However, we argue that we are still allowed to use observations \(C_{PQ}\) as an independent observable when considering the error budget of gravity anomalies \(\Delta g\). The error budget contains measurement errors of gravity and height (i.e., errors of the leveling network), but also errors in reductions and the representation error. The latter is unavoidable in the transition from discrete observations to a continuous representation of the gravity field and is an inherent component of gravity field modeling. It may also be identified with an interpolation or prediction error.

Considering the pure measurement errors, a reasonable assumption for the error standard deviation \(\sigma _g\) of gravity observations may be 0.01 mGal. Errors \(\sigma _H\) for height values derived from precision leveling over short to medium distances (say up to 100 km or so) may accumulate to around 0.01 m (large-scale distortions are not relevant here because they can be effectively filtered out during gravity field modeling, see Gerlach and Rummel (2012)). The height error maps into the gravity anomaly via the free-air gradient providing an error contribution of around 0.3 mGal/m \(\cdot \) 0.01 m \(\approx \) 0.003 mGal. The representation error requires a description of the short-scale signal properties of the gravity field. Such a description is provided by the signal degree variance model by Flury (Flury 2006). Using this model the prediction error from relatively dense (point spacing of 1–2 km) sets of point gravity data is estimated to be in the range of 0.3–0.6 mGal, see Fig. 13 of Flury (ibid.).

The above numbers show that the height error maps into the gravity anomaly by a factor of 3 below the gravity measurement error and is at least a factor of 100 below the representation error. Thus, we do not need to worry about a double use of leveled heights. It is also worth mentioning that the discussion is obsolete if gravity disturbances are used instead of gravity anomalies, because the former are based on GNSS-heights and leveled heights do not enter at all.

4 Numerical experiments

4.1 Approach 1

Here we want to test the benefit of using leveled potential differences in order to improve the short-scale quality of a vertical reference frame realized by geopotential numbers from an adopted gravity field model at GNSS-leveling stations. We use stations of the Unified European Leveling Network (UELN) and connect them to form synthetic leveling lines (not corresponding to the real lines of the UELN and not covering its whole area). The resulting network is shown in Fig. 1.

Fig. 1
figure 1

Synthetic leveling network based on UELN stations

Full size image

We assume a high-resolution gravity field model from which geopotential numbers \(C_P\) at all stations of our network are derived by means of GNSS-leveling (as indicated in Eq. (5)). For Europe, such a model might be the European Gravimetric Quasigeoid model EGG2015 (Denker 2015) or one of its future realizations. We use least-squares adjustment to combine these geopotential numbers with leveled geopotential differences \(C_{PQ}\). Thereby, the geopotential numbers from GNSS-leveling define the absolute level of the combined network and are introduced into the adjustment as pseudo observations. This way, all GNSS stations are used to constrain the absolute level of the leveling network. Then the design matrix \(\varvec{A}\) can be separated into two sections

$$\begin{aligned} \varvec{A}\;=\;\left[ \begin{array}{c} A_l\\ A_c \end{array} \right] \end{aligned}$$
(8)

where index l indicates the section related to leveling observations and c indicates the section related to the constraints, i.e., to the GNSS reference points. Accordingly, the error covariance matrix of the observations \(\varvec{Q}_{bb}=\varvec{P}_{bb}^{-1}\) comprises two uncorrelated blocks

$$\begin{aligned} \varvec{Q}_{bb}\;=\;\left[ \begin{array}{cc} \varvec{Q}_{ll} &{} \varvec{0}\\ \varvec{0} &{} \varvec{Q}_{cc} \end{array} \right] . \end{aligned}$$
(9)

Thereby, \(\varvec{Q}_{cc}\) contains error contributions of the adopted gravity field model and of GNSS heights, while \(\varvec{Q}_{ll}\) contains the errors of geodetic leveling. The combination of leveled geopotential differences and (absolute) geopotential numbers from GNSS-leveling is then performed in the least-squares sense according to

$$\begin{aligned} \hat{\varvec{x}}\;=\;\left( \varvec{A}^T\varvec{P}_{bb}\varvec{A}\right) ^{-1}\varvec{A}^T\varvec{P}_{bb}\tilde{\varvec{b}}, \end{aligned}$$
(10)

with

$$\begin{aligned} \varvec{Q}_{\hat{x}\hat{x}} \;=\; \left( \varvec{A}^T\varvec{P}_{bb}\varvec{A}\right) ^{-1} \end{aligned}$$
(11)

being the error variance–covariance matrix of the adjusted geopotential numbers \(\hat{\varvec{x}}\). The adjusted values \(\hat{\varvec{x}}\) will deviate from the error-free synthetic values \(\varvec{x}\) which we have chosen in our simulation world and from which the observations are created. The difference between the two quantities will be termed the empirical error

$$\begin{aligned} \varvec{\epsilon }_x\;=\; \varvec{x}\,-\, \hat{\varvec{x}}, \end{aligned}$$
(12)

while the formal errors are described by matrix \(\varvec{Q}_{\hat{x}\hat{x}} \).

For our numerical experiment we have defined the error level of all observations as described below. According to this error level, the observations

$$\begin{aligned} \tilde{\varvec{b}} \;=\; \varvec{b} \,+\, \varvec{\epsilon }_b \end{aligned}$$
(13)

consist of error-free synthetic observations \(\varvec{b}\) and a synthetic noise component \(\varvec{\epsilon }_b\). The GNSS-leveling observations, related to sub-matrix \(\varvec{A}_c\), correspond to the absolute point values as defined in our simulation world, i.e., \(\varvec{b}_c=\varvec{x}\), while observations related to geodetic leveling (sub-matrix \(\varvec{A}_l\)) correspond to differences between the end points i and j of the leveling lines, i.e., \(\varvec{b}_l=\varvec{\Delta x}_{ij}\).

The error description is typically provided in metric units. Since the transformation from metric units to geopotential numbers has no relevance for our synthetic examples, all subsequent descriptions are given in units of metric heights.

Denker has provided an error covariance model for the EGG08 gravimetric quasigeoid (Denker (2013), Fig. 5.15) which we adopt here to generate a realistic description for \(\varvec{Q}_{cc}\). Denker’s model is based on error degree variances of the underlying geopotential model and 1 mGal correlated errors of terrestrial gravity anomalies. These error correlations are defined using the exponential model given in Weber (1984) and have a correlation length of around 20 km. The final error covariance model for geoid heights shows error correlations of around 60 km and an error standard deviation of 2.5 cm. This order of magnitude seems to be realistic compared to the standard deviations of differences between the European quasigeoid model and GNSS-leveling as reported in Denker (2013). The error model does not contain any contributions from GNSS, so we add a 1 cm white noise component, which increases the error standard deviation from 2.5 to 2.7 cm.

Due to the combination of different sources of systematic errors (as described in Sect. 2 above) it turns out that the systematic errors also follow some random behavior. Thus they are described along with the random errors by the error covariance matrix of leveled potential differences \(\varvec{Q}_{ll}\). In chapter 3.07 of Bomford (1983), two different error descriptions for leveled height differences are discussed, namely the models presented in Lallemand (1912) and Vignal (1936). In the present study we follow Lallemand’s formula which can be written as

$$\begin{aligned} \sigma ^2_{l}\;=\; \sigma _0^2\,L\;+\;\mu _0^2\,L^2, \end{aligned}$$
(14)

with L being the length of the leveling line in units of kilometer and \(\sigma _0\) and \(\mu _0\) representing the average magnitude of random and systematic errors, respectively. We have chosen the model by Lallemand instead of Vignal’s model due to its simplicity. In Vignal’s model, the magnitude of the systematic errors typically varies after intervals of some tens to hundreds of kilometers and after a certain distance they even become random, i.e., the systematic errors are bounded, which is not the case for Lallemand’s formula. Vignal’s model might therefore be considered more realistic, especially over larger distances. Our numerical example, however, does not contain very long leveling lines, and the focus of our study is to take advantage of the high quality of geodetic leveling over short distances, while the longer distances are based on GNSS-leveling. Therefore, we have chosen the simpler Lallemand model—the only requirement for our simulation being that synthetic errors and stochastic model are consistent.

In our numerical study we have chosen values of \(\sigma _0=1\) mm and \(\mu _0=0.1\) mm. These values describe the typical magnitude of random errors of first- or second-order levelings over short distances as well as of systematic latitude-dependent errors of around 1 cm per degree of latitude difference. For our numerical experiment, we have generated synthetic random errors with 1 mm standard deviation and a systematic trend of 10 mm per degree in latitude direction. The trend is depicted in Fig. 2.

Fig. 2
figure 2

Synthetic North–South tilt of the vertical reference frame representing a systematic (latitude-dependent) error contribution from geodetic leveling. Numbers in mm

Full size image

Figures 3 and 4 show formal and empirical errors of geopotential numbers (expressed in units of height) after the adjustment. The formal errors at the UELN stations are between 6 and 13 mm, thus showing a clear improvement over the formal errors of the pure GNSS-leveling-based reference frame with its formal error standard deviation of 27 mm (constant value for all stations). Errors tend to be smallest in areas of high point density (shorter leveling lines) and tend to be larger in areas of lower point density and at the edges of the network. On average, the formal error amounts to 8.3 mm which corresponds to an improvement of 69%. Minimum and maximum improvements are 51% and 78%, respectively.

Fig. 3
figure 3

Formal height errors after adjustment using synthetic data. Numbers in mm

Full size image
Fig. 4
figure 4

Empirical height errors after adjustment using synthetic data. Numbers in mm

Full size image

The empirical errors of the adjusted heights give a less good agreement and are between \(-46\) mm and \(+43\) mm. Their standard deviation is 14.1 mm which corresponds to an improvement of 48% compared to the 27 mm standard deviation of the empirical observation errors from GNSS-leveling. But it is also a factor of 1.7 worse than the average formal error after the adjustment. From Fig. 4 it also seems that part of the systematic trend of the leveling data is still present in the combined solution. This indicates that the combined adjustment was not able to fully correct the systematic trend—this however cannot be expected, because the ability to correct systematics in the leveling data is limited by the accuracy of the GNSS-leveling points. Thereby, it should be recalled that in our example reduction of systematics is only driven by the stochastic modeling without introducing any parametric models (plane, spline, etc.) as part of the functional model. Additional estimation of such a corrector surface may improve the ability to reduce systematics of the leveling network. Further reduction of systematic distortions especially along the coast lines, i.e., at the border of the network, may be expected in reality by combination with results from ocean leveling, as proposed by Afrasteh et al. (2021).

Besides quantifying errors of (absolute) height values or geopotential numbers of the adjusted network, we may also check height differences along leveling lines. Figure 5 shows errors of height differences as a function of the length of a leveling line or the spherical distance between benchmarks (which is the same in our simulation). The errors represent either empirical (\(\epsilon \)) or formal errors (\(\sigma \)). The empirical errors are RMS values of observed or adjusted height differences using synthetic data. The formal errors are standard deviations either taken from an a priori error model (Denker’s error covariance function or Lallemand’s formula) or from the error variance–covariance matrix \(\varvec{Q}_{\hat{x}\hat{x}} \) of the adjustment process. Thereby, three different realizations of heights/height differences are used, namely (i) heights from GNSS-leveling (termed “geoid+GNSS,” blue colors), (ii) height differences from geodetic leveling (“leveling,” green) and (iii) the combination of these two (“combination,” red).

Fig. 5
figure 5

Errors of height differences from different realizations of the vertical reference frame as functions of the point distance (=length of leveling line). Different realizations are GNSS-leveling (bluish colors), geodetic leveling (green) and their combination (reddish colors)

Full size image

The formal errors of GNSS-leveling (light and dark blue curves) are shown in two different versions to illustrate the effect of random components (in our simulation from GNSS-heights). The lighter blue curve is only based on the correlated error description of geoid heights (Denker’s model), while the darker blue curve also takes into account the additional 1 cm white noise component from GNSS. In both cases, the standard deviation of a height difference \(\Delta {H_{ij}}\) between stations i and j is derived from

$$\begin{aligned} \sigma ^2(\Delta {H_{ij}})\;=\;\sigma ^2(H_i) \,+\, \sigma ^2(H_j)\,-\,2\,\text{ cov }(H_i,H_j). \end{aligned}$$
(15)

Thereby the first two terms on the right-hand side represent the combined effect of GNSS and geoid errors, while the third term only represents error correlations of the geoid model (GNSS errors are assumed uncorrelated).

If the random component from GNSS is not considered ("geoid"-case, light blue), the error of the height difference goes toward zero for short distances, while it approaches \(\sqrt{2}\,\cdot \sigma (\text{ GNSS})\) when considering the GNSS error ("geoid+GNSS"-case, dark blue). This illustrates that any white noise component in the GNSS heights is the limiting factor for GNSS-leveling over short distances. The geoid model does not contribute to the error budget over short distances because in this case its errors are strongly correlated. For distances much larger than the correlation length of geoid errors, the third term in Eq. (15) goes toward zero and the error of height differences approaches \(\sqrt{2}\,\cdot \sigma (H)\).

In our simulation, the error standard deviation is set to 1.0 cm for GNSS-heights and 2.5 cm for geoid heights. Accordingly the error of height differences approaches 1.4 cm over short distances and 3.8 cm over large distances. In all cases, the RMS values of the empirical errors nicely follow the structure of the formal error description. We also see that the combination case strongly benefits from leveled height differences and reflects the same error behavior for short distances up to, say, 20 km. For large distances the combination stays below the pure leveling case, indicating that combination with GNSS-leveling helps to reduce systematic errors.

Finally, it may be worth considering that the RMS values shown in Fig. 5 are computed from synthetic errors for certain distance classes. There are hardly leveling lines for distances longer than 120 km. Therefore, the corresponding distance classes contain very few samples and the computation of RMS values becomes very uncertain (statistically insignificant)—thus Fig. 5 is limited to distances up to 120 km.

4.2 Approach 2

Potential differences as observables In this approach, geopotential differences \(C_{PQ}\) from geodetic leveling are used as observables in gravity field modeling along with other data types like, e.g., gravity anomalies \(\Delta g\) or disturbing potential values T from an already existing gravity field model. Modeling is performed on the level of anomalous or disturbing quantities. Therefore we separate the gravity potential \(W_P\) at leveling station P into disturbing potential \(T_P\) and normal potential \(U_P\) and write the geopotential number \(C_{P}\) as

$$\begin{aligned} C_P = W_0 - W_P = W_0 - (T_P + U_P). \end{aligned}$$
(16)

The leveled geopotential difference \(C_{PQ}\) can then be written as

$$\begin{aligned} C_{PQ}= & {} W_P-W_Q = T_P-T_Q\,+\,(U_P-U_Q)\nonumber \\= & {} W_{PQ} = T_{PQ}+U_{PQ} \end{aligned}$$
(17)

The disturbing quantity used for gravity field modeling is then given by the disturbing potential difference

$$\begin{aligned} \delta C_{PQ}\;=\;T_{PQ} \;=\;C_{PQ} - U_{PQ} \end{aligned}$$
(18)

which is formed by subtracting the normal potential difference \(U_{PQ}\) from the leveled geopotential difference \(C_{PQ}\).

Evaluation of \(U=U(\varphi _P, h_P)\) requires knowledge of ellipsoidal coordinates latitude \(\varphi _P\) and height \(h_P\). If the stations P and Q have not been observed with GNSS, one only knows their heights above sea level (e.g., orthometric or normal heights). Then, U is evaluated at the approximate point \(P'\) and we may rewrite Eq. (16) as

$$\begin{aligned} C_P = W_0 \;-\; \left( T_P + U_{P'} + \frac{\partial U}{\partial z}\Delta z_P\right) . \end{aligned}$$
(19)

Thereby, \(\Delta z_P\) is the vertical displacement between P and \(P'\), thus corresponding to either height anomalies (when working with Molodensky’s theory) or geoid heights (in case of Stokes theory). Accordingly, the disturbing quantity in Eq. (18) is given by

$$\begin{aligned} \delta C_{PQ}\;=\;T_{PQ} \;=\;C_{PQ} - U_{P'Q'} - \gamma \Delta z_{PQ}, \end{aligned}$$
(20)

where we have replaced the vertical derivative \(\partial U/\partial z\) by normal gravity \(\gamma \).

Gravity field modeling using spherical radial basis functions Global gravity field modeling is typically performed in terms of spherical harmonic basis functions, while regional modeling is often based on either Stokes integration, least-squares collocation or a representation in spherical radial basis functions. Being equivalent in theory (Ophaug and Gerlach 2017) all methods have their pros and cons regarding, e.g., spatial coverage and numerical effort, data availability and combination of different observables, the need for regularization or error propagation. In the present study, we make use of spherical radial basis functions, because they easily allow combining different gravity field functionals and implementing potential differences as observable.

Any gravity field quantity f given at point P can be represented as linear combination

$$\begin{aligned} f(P)\;=\;\sum _{k=1}^K\,d_k B^{f}(\psi _{Pk}) \end{aligned}$$
(21)

of spherical radial basis functions (SRBFs) \(B^f(\psi _{Pk})\), which are functions of the spherical distance \(\psi _{Pk}\) between computation point P and the location k of the respective SRBF. Each SRBF is weighted with its own location-dependent coefficient \(d_k\). In matrix form, this may be written as

$$\begin{aligned} \varvec{f}(P)\;=\;\varvec{A}^{f}\varvec{d}, \end{aligned}$$
(22)

where matrix \(\varvec{A}^f\) contains the different SRBFs and the upper index f indicates the functional under consideration. The coefficients \(d_k\) can be determined by least-squares adjustment (Schmidt et al. 2006) according to the functional model

$$\begin{aligned} \varvec{f}+\varvec{v}\;=\;\varvec{A}^f \varvec{d}. \end{aligned}$$
(23)

The regularized solution may be written as

$$\begin{aligned} \varvec{d}\;=\;\left( \left[ \varvec{A}^f\right] ^T\!\!\!\varvec{P\!}_{f\!f}\varvec{A}^f\,+\,\alpha \varvec{I}\right) ^{-1}\left[ \varvec{A}^f\right] ^T\!\!\!\varvec{P\!}_{f\!f}\varvec{f} \end{aligned}$$
(24)

with regularization parameter \(\alpha \) and the inverse error variance–covariance matrix of the observations \(\varvec{P\!}_{f\!f}=\varvec{Q\!}_{f\!f}^{\,-1}\).

A general expression for SRBF in the spectral band between spherical harmonic degrees \(l_1\) and \(l_2\) is given by

$$\begin{aligned} B^{f}(\psi _{Pk}) \;=\; \sum _{l=l_1}^{l_2} \,\frac{2l+1}{4\pi R^2}\,\lambda _l^f\,B_l\,P_l(\cos \psi _{Pk}). \end{aligned}$$
(25)

The shape of the SRBF is determined by the kernel function \(B_l\) for which various options have been proposed, like the Shannon, Blackman, cubic polynomial or Abel-Poisson kernel (Bentel et al. 2013). Here we have chosen the spherical spline kernel (Jekeli 2005; Ophaug and Gerlach 2017) which is based on the (dimensionless) signal degree variances \(c_l\) of the gravity field and are given by

$$\begin{aligned} B_l\;=\; \sqrt{\frac{c_l}{2l+1}}. \end{aligned}$$
(26)

The spectral coefficients \(\lambda _l^f\) of Eq. (25) reflect the spectral characteristics of the functional under consideration and provide the proper units. Spectral coefficients for the functionals used in the present study are listed in Table 1.

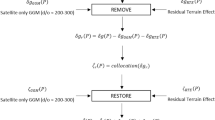
A typical example for regional gravity field modeling is the transformation from an areal distribution of gravity anomalies to geoid heights. Using SRBF the transformation consists of an analysis step, followed by a synthesis step. In the analysis step, coefficients \(d_k\) are estimated using Eq. (24) with observations \(\varvec{f}\) being given by the set of gravity anomalies \(\Delta \varvec{g}\). In the following synthesis step, geoid heights can be derived from the estimated \(d_k\) according to (22) employing the spectral coefficients for geoid heights \(\lambda _l^N\).

Table 1 Spectral factors of gravity field quantities used in the present study
Full size table

In the present study, we propose to use leveled geopotential differences as additional observable in the analysis step. Using, according to Eq. (20), as observable the disturbing potential differences \(T_{PQ}\) between the end points P and Q of a leveling line, the synthesis step can be formulated as

$$\begin{aligned} T_{PQ} \;=\; T_P-T_Q= & {} \sum _{k=1}^K d_k\left( B^T(\psi _{Pk})\,-\,B^T(\psi _{Qk})\right) \nonumber \\= & {} \varvec{A}^T_{PQ}\varvec{d}. \end{aligned}$$
(27)

Obviously, the design matrix \(\varvec{A}^T_{PQ}\) contains differences between SRBFs related to the two end points of the leveling line.

Setup of the numerical experiment High-resolution gravity field modeling using SRBFs is a numerically demanding task if performed on an ordinary PC for the entire area of the European leveling network as used in the numerical example of approach 1; using 5 arcmin spacing between the SRBFs, the normal equation matrix, which needs to be inverted, would require storage space of around 165 GB. Therefore, we have selected for the numerical example of approach 2 a smaller area with relatively rough gravity field signal. We have chosen the area of Switzerland and created a regular grid of synthetic leveling lines as shown in Fig. 6. The residual gravity field signal is shown in the background in terms of geoid heights. They are derived from the coefficients of the EGM2008 geopotential model (Pavlis et al. 2008) above spherical harmonic degree 250, implying that a long wavelength satellite-only gravity field model has been removed before (gravity field modeling according to the classical remove-restore procedure).

The white circles in Fig. 6 represent leveling benchmarks. Potential differences between neighboring benchmarks (in longitude and latitude direction) are used as one set of observables. The other set is given by a \(5'\times 5'\) grid of gravity anomalies (also created from EGM2008 above degree 250). The grid of residual geoid heights (background of Fig. 6) is used as validation data set for evaluating the quality of our modeling exercise.

Fig. 6
figure 6

Synthetic leveling network used for gravity field modeling in approach 2. Background represents the residual gravity field signal of the area in terms of geoid heights in units of meter

Full size image

The error model of the leveled potential differences \(C_{PQ}\) corresponds to the error model applied in approach 1 (see Sect. 4.1). However, our observable is the disturbing potential difference \(T_{PQ}\) and includes an additional error contribution reflecting the errors of GNSS-heights used for evaluating the normal potential difference \(U_{PQ}\) (see Eq. 18). In correspondence to approach 1, the individual sections of the leveling network are treated as uncorrelated. The error of gravity anomalies is set to 1 mGal, which is also the basis for the error model of geoid heights used in approach 1. The anomalies are assumed uncorrelated. The GNSS-height error is set to 5 mm, which is less than the 1 cm level used in approach 1. However, Denker’s error model for geoid heights used in approach 1 assumes geoid errors at the level of 2.5 cm, while in approach 2 formal geoid errors come out on the level of 5 mm (see Fig. 7); therefore, we decided to set the GNSS error level similar to the geoid quality. Since we do not intend to compare the absolute error level of both approaches, but to draw general conclusions from them, slight variations of the error level seem acceptable.

Fig. 7
figure 7

Formal errors of geoid heights derived from synthetic gravity anomalies only (upper panel) and from a combination of gravity anomalies and leveled potential differences (lower panel). Units: mm

Full size image

SRBF modeling and spherical harmonic synthesis of the input and validation data grids were limited to an inner cap of \(1^{\circ }\) spherical radius. This roughly corresponds to the spatial resolution of the lower end of the spherical harmonic degree band of the residual gravity field, i.e., spherical harmonic degree 250. In order to avoid edge effects, the actual target area of Switzerland (where synthetic leveling lines are defined, see Fig. 6) was padded by a margin zone of width \(1^{\circ }\). The extended area (target area + margin) comprises the data area for which synthetic gravity anomalies were created as input data. An additional margin of \(0.33^{\circ }\) was used for placing the SRBFs, following the empirical rule of Bentel (2013).

The regularized solution requires to set an optimized value for the regularization parameter \(\alpha \), see Eq. 24. There exist different approaches to find the best \(\alpha \) value, e.g., the L-curve method, variance component estimation or generalized cross-validation (see, e.g., Liu et al. (2020) for a recent study on regularization applied to gravity field modeling using SRBFs). In our synthetic simulation scenario, however, we did not apply any of these methods because the exact solution is known. Therefore, we selected the best \(\alpha \) value following Ophaug and Gerlach (2020) by comparing solutions based on a broad range of \(\alpha \) values to the validation data set. The \(\alpha \)-value producing the solution with the best fit (in terms of RMS of geoid height differences) to the validation data set was chosen as the final one.

Solution quality: (a) formal errors Figure 7 shows the quality of the modeled geoid heights in terms of formal errors. The upper panel shows a scenario based on synthetic gravity anomalies only (\(\Delta g\)-only case); the lower panel shows the combination of gravity anomalies and potential differences between leveling benchmarks. The comparison of both solutions shows the improvement brought by incorporating leveled potential differences as new or additional gravity field observable.

The formal error of the \(\Delta g\)-only case is quite homogeneous over the whole target area, with a slight degradation toward the edges (from 4.7 mm in the center to 5.6 mm at the corner points). When considering leveled potential differences in addition, this pattern of formal errors is overlaid by the structure of the leveling network (compare the error pattern in the lower panel of Fig. 7 to the structure of the synthetic leveling lines in Fig. 6). Along the leveling lines the formal errors are significantly reduced from 4.7 mm (\(\Delta g\)-only case) to 3.7 mm at benchmarks, i.e., the formal errors are reduced for up to 21%. Averaging the formal error over the entire target area, i.e., also over locations where there are no leveling data, we see only a slight reduction from 4.8 to 4.5 mm, which corresponds to a reduction of 6%.

Solution quality: (b) true errors Besides formal errors, we also analyze the true errors of our solution represented by the differences of the SRBF solutions to the validation data set. This is done in terms of relative geoid heights, i.e., geoid height differences between two points, which are the quantity of interest in GNSS-leveling. This also allows for a direct comparison of the corresponding errors to the quality of geodetic and GNSS-leveling over various distances.

Fig. 8
figure 8

Square root of error covariance functions of geoid height differences from SRBF solutions (blue and red) along with the error budget of geodetic and GNSS-leveling. Top: functions derived from all grid points in the target area. Bottom: functions based on leveling benchmarks only. Units: mm

Full size image

The results are shown in Fig. 8. The top panel shows the empirical (red/blue dots) and analytical (thick red/blue lines) covariance functions \(E^{\Delta N}(\psi )\) of the true errors of geoid height differences between two points separated by spherical distance \(\psi \); they represent the average relative error characteristics over the entire geoid grid in the target area. The bottom panel shows the same empirical errors, but instead of analyzing the complete geoid grid in the target area, the functions are based on leveling benchmarks only, i.e., the analysis is restricted to those points where leveled potential differences \(T_{PQ}\) were provided as input data and where we expect \(T_{PQ}\) to contribute most to the SRBF-solution.

In order to study the improvement of geoid height differences brought by the inclusion of leveled potential differences \(T_{PQ}\), the panels show covariance functions for the \(\Delta g\)-only case (blue color), as well as for the combination of \(\Delta g\) and \(T_{PQ}\) (red color). For comparison, the error characteristics of height differences from geodetic leveling are added to the plots: the solid black line represents Lallemand’s error model (Eq. (14)); the dashed line is the same model restricted to the random term. Finally, the dashed red and blue lines provide the expected error level of GNSS-leveling. Thereby, geoid height differences and GNSS-height differences are combined; accordingly, the error level of geoid-height differences (thick red/blue lines) is increased for the contribution of the GNSS height error. The error level for geodetic and GNSS-leveling corresponds to the values used in our numerical experiment, i.e., \(\sigma _0=1\) mm and \(\mu _0=0.1\) mm for Lallemand’s model and \(\sigma _h=5\) mm for the white noise error of GNSS heights.

Before discussing the error covariance functions of Fig. 8 in detail, let us take a look at how they were derived. In a preliminary step (not shown), true geoid errors at all grid points in the target area were used to derive empirical geoid error covariance functions \(E^N(\psi )\) (for the \(\Delta g\)-only and the combined case). To both of these empirical covariance functions, we visually fitted analytical covariance functions following the simple exponential model

$$\begin{aligned} E^{N}(\psi )= & {} E_0^N \, e^{A\,\psi }, \end{aligned}$$
(28)

with \(E_0^N\) the geoid error variance, \(A=-\ln 2/\xi \) and \(\xi \) the correlation length of the function. The empirical and analytical error covariance functions \(E^{\Delta N}(\psi )\) of geoid height differences \(\Delta N\) in Fig. 8 were then derived by error propagation from \(E^N(\psi )\) using the relation

$$\begin{aligned} E^{\Delta N}(\psi )= & {} 2\,\left( E_0^N \,-\, E^N(\psi ) \right) . \end{aligned}$$
(29)

Inserting Eq. (28) into (29) gives the analytical error model for geoid height differences

$$\begin{aligned} E^{\Delta N}(\psi )= & {} 2\,E_0^N \, \left( 1\,-\,e^{A \,\psi }\right) . \end{aligned}$$
(30)

For spherical distances significantly larger than the correlation length, the exponential term goes to zero and the function approaches twice the error variance \(E_0^N\). For very small distances (approaching \(\psi =0\)) the exponential term goes to 1 and the error covariance function approaches zero. This is illustrated in Fig. 8. The error standard deviation of the true geoid errors in the entire target area amounts to 5.2 mm in the \(\Delta g\)-only and 4.6 mm in the combined case. Accordingly, the two error functions (top panel) converge for larger distances to 7.3 mm and 6.5 mm, respectively. This indicates an improvement of 11% by including \(T_{PQ}\). The improvement is even larger along the leveling lines (bottom panel): the empirical error function for the \(\Delta g\)-only case (blue line) is at the level of 7.4 mm (almost identical to the upper panel), while the function of the combined case (red line) stays well below 6 mm (max. 5.8 mm). The improvement brought by including \(T_{PQ}\) as observable increases, accordingly, from 11% (entire target area) to 20% (between benchmarks). This number nicely fits to the 21% improvement of formal errors found further above (section (a): formal errors).

It is also interesting to compare the gravimetric geoid height differences (from SRBF modeling) with the quality of geodetic and GNSS-leveling. The errors of geoid height differences and geodetic leveling go to zero for short distances, the latter because measurement errors are very small indeed, the former, because the errors are strongly correlated (independent of the actual error level of the absolute geoid heights). In contrast, the error of GNSS-leveling never goes to zero, because the error budget of gravimetric geoid height differences is increased for the error of GNSS-heights. Since these are considered uncorrelated, the total error budget is increased by \(\sqrt{2}\,\sigma _h\), in our numerical example by 7.1 mm (which corresponds to the error of GNSS-leveling for very short distances). Further quantitative comparison of geoid height differences and geodetic leveling is not considered meaningful, because this means comparing two different quantities (geoid height differences and physical height differences).

It is more relevant to compare the error level of geodetic and GNSS-leveling, represented by the black (geodetic leveling) and dashed red/blue lines in Fig. 8. The intersection points of the functions tell us at which distance the errors from geodetic leveling and GNSS-leveling are equal. For shorter distances geodetic leveling provides more accurate results, for longer distances GNSS-leveling does. Table 2 lists the intersection points for all different cases: random-only (dashed black line in Fig. 8) or random and systematic (solid black) leveling errors; \(\Delta g\)-only (blue) or \(\Delta g+T_{PQ}\) (red) geoid modeling; entire target area (top panel) or leveling benchmarks only (bottom panel). The numerical values of the intersection points are of course dependent on the specific stochastic model of our numerical example and must be expected to change for other cases.

Table 2 Distances at which errors from geodetic leveling and GNSS-leveling are equal. Distances are provided as spherical distance and in metric units
Full size table

5 Summary and conclusions

Since the realization of the first national and continent-wide height networks, geodetic leveling in combination with gravimetry was the observational method of choice. Geodetic leveling allows to measure height differences with high accuracy over short to medium distances but is prone to systematic distortions over long distances, this also in connection to a generally low redundancy of the leveling networks. Classically, the networks are connected to tide gauges, which allows, on the one hand, to define the absolute level of the network (datum choice), and on the other hand, to keep systematic distortions under control if several datum points are chosen (below the level of 1–2 m, depending on the magnitude of mean dynamic ocean topography along the coast line). Ambiguities in the datum choice led to a patchwork of local and regional vertical datums on slightly different absolute levels and each affected by specific systematic distortions (often correlated to larger height differences or the North–South extent of the networks), see, e.g., Bomford (1983), Rülke et al. (2012), Wang et al. (2012) or Penna et al. (2013).

Today modern geodetic space techniques open up the possibility for realizing a unified global height datum free of large-scale systematics, see, e.g., Ihde et al. (2017), Sánchez and Sideris (2017) or Sánchez et al. (2021). Based on high-resolution global or regional gravity field modeling, the application of GNSS-leveling as efficient alternative to the classical combination of spirit leveling and gravimetry becomes feasible. A prominent example for a modernized vertical reference frame is Canada, where since 2015 the vertical reference frame is realized by a regional geoid model, currently the Canadian Gravimetric Geoid model of 2013 (CGG2013a), see Véronneau and Huang (2016).

If, in the future, vertical datums will be realized by satellite-based high-resolution gravimetric gravity field models, the question arises if or how to use existing geodetic leveling data. These data of geopotential differences between benchmarks are a rich source of gravity field information with high quality, especially over short scales. If geodetic leveling is not completely abolished for the realization of vertical reference frames, one may use it as independent control data allowing for validation of gravimetric gravity field models (this is extensively done for validation of global satellite models, see, e.g., Huang et al. 2015) or one can try to combine potential differences from geodetic leveling with absolute potential values derived from a gravimetric geoid model. Undoubtedly, spirit leveling will be used in the future for local applications because of its high quality and efficiency and its simplicity of use. In addition, future chronometric leveling will allow to derive geopotential differences from the frequency shift of atomic clocks, see, e.g., Wu et al. (2019). In the light of the envisaged realization of modern, unified vertical reference frames, which take into account satellite and terrestrial data with their corresponding sensitivities, a combination strategy is required for the incorporation of potential differences from existing and future geodetic and chronometric leveling.

We have presented two approaches to sketch such a combination using synthetic simulations. Thereby, the focus is on the combination of geodetic and GNSS-leveling data with their typical error characteristics. The first approach corresponds to a combined least-squares network adjustment, where potential differences between benchmarks of a leveling network are constrained by absolute potential values derived from a gravimetric geoid model and GNSS coordinates of the benchmarks (GNSS-leveling). Our numerical example for this approach resembles the structure of the Unified European Leveling Network.

In the second approach, geopotential differences are used as observables for combined gravity field modeling. In our numerical example, potential differences between benchmarks of a synthetic grid are used along with a grid of gravity anomalies for modeling a regional geoid. Modeling is performed in terms of spherical radial basis functions, because this allows implementing potential differences as observable and combining them with gravity anomalies in a straight forward manner.

In both approaches, we employ Lallemand’s stochastic model for geodetic leveling which comprises the classical random error component as a function of the square root of the length of the leveling line and an additional distance-dependent component which describes systematic distortions.

In the first approach, geoid and GNSS errors add up thus reducing the high accuracy of geoid height differences over short distances, while height differences from geodetic leveling enter the solution with their full accuracy. In the second approach, the high neighborhood accuracy of geodetic leveling is deteriorated by GNSS errors because observed geopotential differences need to be transformed to disturbing potential differences by subtracting the corresponding difference in normal potential values.

Over medium to large distances, systematic distortions of geodetic leveling may enter the combined solution. In the first approach, the error budget of GNSS-leveling (combination of geoid and GNSS errors) determines the ability of the combined adjustment to correct the systematics in geodetic leveling. In our numerical example, incorporation of leveled potential differences reduces the standard deviation of empirical errors from GNSS-leveling for 48% and a synthetic North–South tilt of 20 cm is reduced to 8 cm; thereby, the systematics are only incorporated in the stochastic part (by using Lallemand’s error model) and no additional corrector surface is estimated or reduced beforehand. Both options could further decrease residual systematic components in the combined solution. In the second approach, gravity field modeling is based on spherical radial basis functions which allow modification of the kernel function. As has been shown by Gerlach and Rummel (2012), suitable modification of the kernel function can effectively filter out long wavelength distortions of the input data, such that systematic errors of geodetic leveling over large distances do not affect the combined geoid model. In our numerical example, the geoid error is reduced for up to 10% over the entire target area and for around 20% at leveling benchmarks both in terms of formal errors of geoid heights and in terms of empirical errors of geoid height differences. Evaluation of the error characteristics also shows over which distances geodetic leveling is superior to GNSS-leveling—in our numerical example up to distances between around 60 and 100 km, depending on the stochastic model assumption.

Even though the exact numbers of our simulation scenarios depend on the specific choice of noise level and error characteristics, the results still show the general benefit of using potential differences from geodetic leveling for the realization of vertical reference frames even in the age of geoid-based datums. The advantage of combining the different data sets lays not only in the improved error budget of the vertical reference frame, but also in its consistency with all available observation types, namely geoid, GNSS-heights and leveled potential differences. This also means that such a frame is consistently accessible by both, GNSS-leveling and geodetic leveling. In this sense, we should not expect inconsistencies between height (or geopotential) values at the benchmarks of the reference frame and, e.g., new leveling observations—at least not within the error bounds of the frame and the observations. These conclusions hold not only for geodetic leveling, but also for future chronometric leveling.

Glossary The present paper describes several leveling techniques. For clarity we provide here short definitions of these techniques.

  • GNSS-leveling: Combines ellipsoidal heights h from GNSS with geoid heights N to derive physical heights H according to Eq. (1), see, e.g., Rülke et al. (2012).

  • Chronometric leveling: Determine potential differences between stations by clock comparisons exploiting the relativistic gravitational frequency redshift, see e.g., Grotti et al. (2018).

  • Ocean leveling: Methods comparable to GNSS-leveling applied to the ocean surface. Mean dynamic ocean topography (MDT) takes the role of physical heights H, see, e.g., Woodworth et al. (2012).

  • Altimetric leveling: An approach to ocean leveling where the ellipsoidal heights h of the ocean surface are represented by the mean sea surface (MSS) derived from satellite altimetry, see, e.g., Woodworth et al. (2012).

  • Steric leveling: An approach to ocean leveling where MDT differences are determined by probing of temperature and salinity down to a chosen reference depth, see, e.g., Sturges (1974).

  • Geostrophic leveling: An approach to ocean leveling where MDT differences are determined from measurements of ocean currents using the geostrophic equations Eq. (4), see, e.g., Sturges (1974).

  • Hydrodynamic leveling: Connects tide gauges by measuring mean water level (MWL) at the tide gauges and knowing MDT difference between them. The MDT differences are taken from a hydrodynamic model, see, e.g., Slobbe et al. (2018).