Hart–Mas-Colell consistency and the core in convex games

Abstract

This paper formally introduces Hart–Mas-Colell consistency for general (possibly multi-valued) solutions for cooperative games with transferable utility. This notion is used to axiomatically characterize the core on the domain of convex games. Moreover, we characterize all nonempty solutions satisfying individual rationality, anonymity, scale covariance, superadditivity, weak Hart–Mas-Colell consistency, and converse Hart–Mas-Colell consistency. This family consists of (a) the Shapley value, (b) all homothetic images of the core with the Shapley value as center of homothety and with positive ratios of homothety not larger than one, and (c) their relative interiors.

1 Introduction

Interactive situations where players are able to generate revenues in coalitions can be modeled as cooperative games with transferable utility. In this model, the worth of each coalition represents the monetary opportunities when these players join forces. Once the grand coalition is formed, the worths of subcoalitions serve as benchmarks for a fair allocation of the worth of the grand coalition. Solutions assign to each transferable utility game a set of recommended allocations for the cooperating players. These solutions are fundamentally distinguished on the basis of axioms, i.e., formal expressions of properties which may or may not be satisfied.

Already since the earlier development of cooperative game theory, the core has been one of the central solution concepts for transferable utility games. This solution recommends all allocations which are efficient and stable, i.e., which fully allocate the worth of the grand coalition in such a way that each subcoalition is allocated at least its worth. As the core of a game is closed, bounded, and convex, it consists of zero, one, or infinitely many allocations.

The core has been mainly studied on the basis of consistency and reduced game properties. Consistency of the core can be generally described as follows. Consider a transferable utility game and a corresponding core allocation. Suppose that some players leave with their allocated money and the remaining players reevaluate the allocation. For this, a reduced game for the remaining players is specified. If the core is consistent, then the initial allocation restricted to the remaining players is in the core of this reduced game.

The exact formulation of consistency axioms is determined by the specific definition of reduced games. The most appealing definition may depend on the context of the underlying collaborative situation, and alternative definitions may admit alternative interpretations. In fact, the core has been proven to be consistent for several definitions of reduced games.

Inspired by Davis and Maschler (1965), Peleg (1986) showed that the core is consistent when the worth of a coalition of remaining players in reduced games is defined as the maximal surplus to any subgroup of leaving players, and that this reduced game property characterizes the core in conjunction with individual rationality and superadditivity. Tadenuma (1992) showed that the core is consistent when the worth of a coalition of remaining players in reduced games is defined as the surplus to all leaving players, and that this reduced game property characterizes the core in conjunction with individual rationality. Funaki and Yamato (2001) showed that the core is consistent when the worth of a coalition of remaining players in reduced games is defined as its worth in the original game, and that this reduced game property characterizes the core in conjunction with individual rationality and a weak version of coalitional rationality.

In fact, the results of Peleg (1986), Tadenuma (1992) and Funaki and Yamato (2001) are derived on the domain of balanced games, i.e., transferable utility games with a nonempty core. Nevertheless, the core is consistent on other domains as well. Peleg (1989) and Sudhölter and Peleg (2002) characterized the core using Davis–Maschler consistency on the subdomain of totally balanced games, i.e., transferable utility games with a nonempty core for each subgame. Hwang and Sudhölter (2001) presented a characterization of the core based on Davis–Maschler consistency on the domain of all transferable utility games which is also valid on several subdomains, e.g., totally balanced games, balanced games, and superadditive games. Recently, Hokari et al. (2020) studied consistency characterizations of the core on the domain of convex games.

To our knowledge, the relation of the core with another well-known consistency axiom formulated by Hart and Mas-Colell (1989) has not been studied so far. This reduced game property was originally introduced for single-valued solutions and explored for the Shapley value (Shapley 1953). In the corresponding reduced game, the worth of a coalition of remaining players is defined as the monetary surplus to the leaving players when the solution is applied to the joint subgame. Dutta (1990) suggested an extension to multi-valued solutions in terms of selections, but explored it for Dutta–Ray’s single-valued egalitarian solution (Dutta and Ray 1989) on the domain of convex games, for which it boils down to the original definition.

In this paper, we formally define Hart–Mas-Colell consistency and its converse for multi-valued solutions for transferable utility games on the basis of allocation schemes. We show that the core is the unique inclusion-wise maximal solution satisfying individual rationality and a weak version of Hart–Mas-Colell consistency on the domain of convex games and we derive a pure axiomatic characterization. Moreover, we characterize all nonempty solutions satisfying individual rationality, anonymity, scale covariance, superadditivity, weak Hart–Mas-Colell consistency, and converse Hart–Mas-Colell consistency. This family consists of (a) the Shapley value, (b) all homothetic images of the core with the Shapley value as center of homothety and with positive ratios of homothety not larger than one, and (c) their relative interiors.

This paper is organized as follows. Section 2 provides preliminary notions and notations. Section 3 formally introduces Hart–Mas-Colell consistency and its converse. Section 4 studies the core and Sect. 5 provides a joint characterization. Section 6 concludes.

2 Preliminaries

Let U with $|U|\ge 3$ be a universe of players. A coalition is a nonempty and finite subset of U. Let N be a coalition and denote $2^N=\{S\mid S\subseteq N\}$. An order of N is a bijection $\pi :N\rightarrow \{1,\ldots ,|N|\}$. The set of all orders of N is denoted by $\Pi ^N$. An allocation for N is a vector $x\in \mathbb {R}^N$. An allocation scheme for N is a collection $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^S\in \mathbb {R}^S$ for all $S\in 2^N{\setminus }\{\emptyset \}$. For each $x\in \mathbb {R}^N$ and each $S\in 2^N$, $x_S\in \mathbb {R}^S$ denotes $x_S=(x_i)_{i\in S}$, and $x(S)\in \mathbb {R}$ denotes $x(S)=\sum _{i\in S}x_i$. For all $x,y\in \mathbb {R}^N$, $x\le y$ denotes $x_i\le y_i$ for all $i\in N$.

A transferable utility game is a pair (N, v), where $N\subseteq U$ is a nonempty and finite set of players and $v:2^N\rightarrow \mathbb {R}$ assigns to each subset $S\in 2^N$ its worth $v(S)\in \mathbb {R}$ with $v(\emptyset )=0$. The subgame $(T,v_T)$ of (N, v) on $T\in 2^N{\setminus }\{\emptyset \}$ is defined by $v_T(S)=v(S)$ for all $S\subseteq T$. Throughout this paper, $\Gamma$ denotes a set of games. A set $\Gamma$ is closed if $(T,v_T)\in \Gamma$ for all $(N,v)\in \Gamma$ and all $T\in 2^N{\setminus }\{\emptyset \}$. A game $(N,v)\in \Gamma$ is additive if $v(S)=\sum _{i\in S}v(\{i\})$ for all $S\in 2^N$. A game $(N,v)\in \Gamma$ is convex (Shapley 1971) if for all $i\in N$ and all $S\subseteq T\subseteq N{\setminus }\{i\}$,

$$\begin{aligned} v(S\cup \{i\})-v(S)\le v(T\cup \{i\})-v(T). \end{aligned}$$

Let $\Gamma _{vex}$ denote the set of convex games. Note that additive games are convex and that $\Gamma _{vex}$ is closed. Moreover, $(N,\alpha v+\beta )\in \Gamma _{vex}$ for¹ all $(N,v)\in \Gamma _{vex}$, all $\alpha >0$, and all $\beta \in \mathbb {R}^N$.

A solution $\sigma$ on $\Gamma$ assigns to each game $(N,v)\in \Gamma$ a set $\sigma (N,v)$ of feasible allocations for N, i.e., $\sigma (N,v)\subseteq \mathbb {R}^N$ satisfies $x(N)\le v(N)$ for all $x\in \sigma (N,v)$. A solution $\sigma$ on $\Gamma$ is nonempty if $|\sigma (N,v)|\ne 0$ for all $(N,v)\in \Gamma$, and single-valued if $|\sigma (N,v)|=1$ for all $(N,v)\in \Gamma$. For a single-valued solution $\sigma$ on $\Gamma$ and a game $(N,v)\in \Gamma$, $\sigma (N,v)$ is often identified with its unique element. A solution $\sigma$ on $\Gamma$ is a subsolution of $\sigma '$ on $\Gamma$ if $\sigma (N,v)\subseteq \sigma '(N,v)$ for all $(N,v)\in \Gamma$.

Let $(N,v)\in \Gamma$. The set of preimputations, denoted by X(N, v), is the set

$$\begin{aligned} X(N,v)=\left\{ x\in \mathbb {R}^N\ \Bigg |\ x(N)=v(N)\right\} . \end{aligned}$$

The set of imputations, i.e., individually rational preimputations, denoted by I(N, v), is the set

$$\begin{aligned} I(N,v)=\left\{ x\in X(N,v)\ \Bigg |\ x(\{i\})\ge v(\{i\})\ \text {for all}\ i\in N\right\} . \end{aligned}$$

The core, denoted by C(N, v), is the set

$$\begin{aligned} C(N,v)=\left\{ x\in X(N,v)\ \Bigg |\ x(S)\ge v(S)\ \text {for all}\ S\in 2^N\right\} \end{aligned}$$

Recall that the relative interior of a convex set is the interior of this set in its affine hull. We use “ri” for relative interior. The relative interior of a nonempty convex set is nonempty. It is known (see Orshan and Sudhölter (2010) for a generalization) that

$$\begin{aligned} {\hbox {ri}} C(N,v)=\left\{ x\in C(N,v)\ \Bigg |\ x(S)>v(S)\ \text {for all}\ S\in 2^N{\setminus }\mathcal {S}(N,v)\right\} , \end{aligned}$$

where

$$\begin{aligned} \mathcal {S}(N,v)=\left\{ S\in 2^N\ \Bigg |\ x(S)=v(S)\ \text {for all}\ x\in C(N,v)\right\} . \end{aligned}$$

The relative interior of the core is a subsolution of the core, the core is a subsolution of the imputation set, and the imputation set is a subsolution of the preimputation set, and all inclusions may be strict.

For each $\pi \in \Pi ^N$ and each $S\in 2^N{\setminus }\{\emptyset \}$, $a^{\pi ,S}(N,v)\in \mathbb {R}^S$ is for all $i\in S$ defined by

$$\begin{aligned} a_i^{\pi ,S}(N,v)=v(\{j\in S\mid \pi (j)\le \pi (i)\})-v(\{j\in S\mid \pi (j)<\pi (i)\}). \end{aligned}$$

If $(N,v)\in \Gamma _{vex}$, then $a^{\pi ,S}(N,v)\le a_S^{\pi ,T}(N,v)$ for all $\pi \in \Pi ^N$ and all $S,T\in 2^N{\setminus }\{\emptyset \}$ with $S\subseteq T$, and, by Shapley (1971),

$$\begin{aligned} C(N,v)=\left\{ \sum _{\pi \in \Pi ^N}\lambda _\pi a^{\pi ,N}(N,v)\ \Bigg |\ \lambda \in \mathbb {R}_+^{\Pi ^N},\sum _{\pi \in \Pi ^N}\lambda _\pi =1\right\} , \end{aligned}$$

and by Theorem 6.9 of Rockafellar (1970),

$$\begin{aligned} {\hbox {ri}} C(N,v)=\left\{ \sum _{\pi \in \Pi ^N}\lambda _\pi a^{\pi ,N}(N,v)\ \Bigg |\ \lambda \in \mathbb {R}_{++}^{\Pi ^N},\sum _{\pi \in \Pi ^N}\lambda _\pi =1\right\} . \end{aligned}$$

(1)

Moreover, if $(N,v)\in \Gamma _{vex}$, then $S\in 2^N{\setminus }\mathcal {S}(N,v)$ if and only if $v(S)+v(N{\setminus } S)<v(N)$, so that

$$\begin{aligned} {\hbox {ri}} C(N,v){=}\left\{ x\in C(N,v)\ \Bigg |\ x(S){>}v(S)\ \text {for all}\ S\in 2^N\ \text {with}\ v(S){+}v(N{\setminus } S){<}v(N)\right\} . \end{aligned}$$

The Shapley value (Shapley 1953), denoted by $\phi (N,v)$, is defined by

$$\begin{aligned} \phi (N,v)=\frac{1}{|N|!}\sum _{\pi \in \Pi ^N}a^{\pi ,N}(N,v). \end{aligned}$$

If $(N,v)\in \Gamma _{vex}$, the egalitarian solution (Dutta and Ray 1989), denoted by E(N, v), is defined by²

$$\begin{aligned} E(N,v)={{\mathop {\textrm{argmin}}\limits _{x\in C(N,v)}}}\sum _{i\in N}x_i^2. \end{aligned}$$

On the domain of convex games, both the Shapley value and the egalitarian solution are single-valued and subsolutions of the core.

A solution $\sigma$ on $\Gamma$ satisfies

• efficiency if $x(N)=v(N)$ for all $(N,v)\in \Gamma$ and all $x\in \sigma (N,v)$;

• individual rationality if $x(\{i\})\ge v(\{i\})$ for all $(N,v)\in \Gamma$, all $x\in \sigma (N,v)$, and all $i\in N$;

• anonymity if $\sigma (\rho (N),\rho v)=\rho (\sigma (N,v))$ for all $(N,v)\in \Gamma$ and all injections³$\rho :N\rightarrow U$ with $(\rho (N),\rho v)\in \Gamma$;

• scale covariance if $\sigma (N,\alpha v)=\alpha \sigma (N,v)$ for all $(N,v)\in \Gamma$ and all $\alpha >0$ with $(N,\alpha v)\in \Gamma$;

• translation covariance if $\sigma (N,v+\beta )=\sigma (N,v)+\beta$ for all $(N,v)\in \Gamma$ and all $\beta \in \mathbb {R}^N$ with $(N,v+\beta )\in \Gamma$;

• superadditivity if $\sigma (N,v)+\sigma (N,w)\subseteq \sigma (N,v+w)$ for⁴ all $(N,v),(N,w)\in \Gamma$ with $(N,v+w)\in \Gamma$.

The preimputation set satisfies efficiency, anonymity, scale covariance, translation covariance, and superadditivity, but does not satisfy individual rationality. The imputation set and the core satisfy efficiency, individual rationality, anonymity, scale covariance, translation covariance, and superadditivity. On the domain of convex games, the Shapley value satisfies efficiency, individual rationality, anonymity, scale covariance, translation covariance, and superadditivity, and the egalitarian solution satisfies efficiency, individual rationality, anonymity, and scale covariance, but does not satisfy translation covariance and superadditivity.

3 Hart–Mas-Colell consistency

Hart and Mas-Colell (1989) introduced a reduced game property for single-valued solutions for transferable utility games which can be described as follows. After the solution is applied to a game, some players leave with their allocated money. The remaining players reevaluate their allocation by applying the solution to the corresponding reduced game. The worth of a coalition of remaining players in this reduced game is defined as the monetary surplus to the leaving players when the solution is applied to the joint subgame. The solution is consistent if it assigns to each such reduced game the restricted allocation of the original game.

Since allocated money is ambiguous when multi-valued solutions are applied, Hart–Mas-Colell consistency cannot be straightforwardly defined for general solutions. Dutta (1990) suggested an approach based on selections of a solution. We interpret this suggestion in terms of allocation schemes as follows. For each game and each recommended allocation, there exists an allocation scheme corresponding to the solution such that the recommended allocation is consistently assigned to all reduced games where the worth of a coalition is defined as the monetary surplus according to this allocation scheme. Naturally, this definition requires that all subgames and reduced games belong to the underlying domain.

Definition 3.1

A solution $\sigma$ on a closed domain $\Gamma$ satisfies HM-consistency if, for all $(N,v)\in \Gamma$ and all $x\in \sigma (N,v)$, there exists $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$ such that $(T,v_T^{\varvec{x}})\in \Gamma$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N{\setminus }\{\emptyset \}$, where

$$\begin{aligned} v_T^{\varvec{x}}(S)=v(S\cup (N{\setminus } T))-x^{S\cup (N{\setminus } T)}(N{\setminus } T)\ \text {for all }S\in 2^T{\setminus }\{\emptyset \}. \end{aligned}$$

Hart and Mas-Colell (1989) and Dutta (1990) explored HM-consistency for the Shapley value and the egalitarian solution, respectively. According to Hokari (2002), on the domain of convex games, the egalitarian solution does not satisfy HM-consistency because his Example 1 shows that the corresponding reduced game is not necessarily convex, but the proof of Dutta (1990) shows that the egalitarian solution satisfies the weaker version of the property that only requires to consider reduced games with one or two players. According to Hokari and Van Gellekom (2003), there also exists a non-convex reduced game corresponding to the Shapley value, but also this solution satisfies the weak version of HM-consistency.⁵ For general multi-valued solutions, weak Hart–Mas-Colell consistency is defined as follows.

Definition 3.2

A solution $\sigma$ on a closed domain $\Gamma$ satisfies weak HM-consistency if, for all $(N,v)\in \Gamma$ and all $x\in \sigma (N,v)$, there exists $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$ such that $(T,v_T^{\varvec{x}})\in \Gamma$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N{\setminus }\{\emptyset \}$ with $|T|\le 2$.

Hart and Mas-Colell (1989) characterized the Shapley value on the domain of all games by efficiency, HM-consistency, and standardness. A solution $\sigma$ on $\Gamma$ satisfies standardness if, for all $(N,v)\in \Gamma$ with $|N|=2$,

$$\begin{aligned} \sigma _i(N,v)=v(\{i\})+\tfrac{1}{2}\left( v(N)-v(\{i\})-v(N{\setminus }\{i\})\right) \ \text {for all }i\in N. \end{aligned}$$

In fact, the corresponding proof provided by Peleg and Sudhölter (2007) shows that HM-consistency can be replaced by weak HM-consistency and that this stronger characterization is also valid on the domain of convex games. Hence, the Shapley value is the unique single-valued solution for convex games satisfying standardness and weak HM-consistency.

Dutta (1990) characterized the egalitarian solution on the domain of convex games by efficiency, weak HM-consistency, and constrained egalitarianism. A solution $\sigma$ on $\Gamma _{vex}$ satisfies constrained egalitarianism if, for all $(N,v)\in \Gamma _{vex}$ with $|N|=2$,

$$\begin{aligned} \sigma _i(N,v)= {\left\{ \begin{array}{ll} \max \{v(\{i\}),\frac{1}{2}v(N)\} &{} \text {if }v(\{i\})\ge v(N{\setminus }\{i\}); \\ v(N)-\sigma _{N{\setminus }\{i\}}(N,v) &{} \text {if }v(\{i\})\le v(N{\setminus }\{i\}). \end{array}\right. } \end{aligned}$$

Hence, the egalitarian solution is the unique single-valued solution for convex games satisfying constrained egalitarianism and weak HM-consistency.

Converse Hart–Mas-Colell consistency requires that if each two-player restriction of a preimputation belongs to the solution of the corresponding reduced game according to some particular allocation scheme, then the preimputation belongs to the solution of the original game. Chang and Hu (2007) formulated converse HM-consistency for single-valued solutions and their Lemma 13 implies that both the Shapley value and the egalitarian solution satisfy converse HM-consistency on the domain of convex games. We provide the definition for general, possibly multi-valued solutions.

Definition 3.3

A solution $\sigma$ on a closed domain $\Gamma$ satisfies converse HM-consistency if, for all $(N,v)\in \Gamma$ with $|N|\ge 3$, the following condition is satisfied for all $x\in X(N,v)$ and all $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$:

if $(T,v_T^{\varvec{x}})\in \Gamma$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$, then $x\in \sigma (N,v)$.

4 The core

Although the core is consistent for several definitions of reduced game properties, Hart–Mas-Colell consistency of the core has not been studied because this property was introduced for single-valued solutions. Being equipped with a general definition, the question whether the core satisfies HM-consistency now arises. The proof that no subsolution of the core satisfies HM-consistency on the domain of convex games (provided that $|U|\ge 7$) is available upon demand from each of the authors. We show that both the core and its relative interior do satisfy weak HM-consistency on the domain of convex games and converse consistency on each domain closed under subgames and reduced games.

Lemma 4.1

The core and its relative interior satisfy weak HM-consistency on the domain of convex games.

Proof

Let $(N,v)\in \Gamma _{vex}$ and let $x\in C(N,v)$. Let $\lambda \in \mathbb {R}_+^{\Pi ^N}$ with $\sum _{\pi \in \Pi ^N}\lambda _\pi =1$ be such that $x=\sum _{\pi \in \Pi ^N}\lambda _\pi a^{\pi ,N}(N,v)$. Define $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ by $x^S=\sum _{\pi \in \Pi ^N}\lambda _\pi a^{\pi ,S}(N,v)$ for all $S\in 2^N{\setminus }\{\emptyset \}$. Then $x^N=x$ and $x^S\in C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$. Let $T\in 2^N{\setminus }\{\emptyset \}$ with $|T|\le 2$. Then

$$\begin{aligned} v_T^{\varvec{x}}(T)=v(N)-x^N(N{\setminus } T)=x^N(T)=x(T). \end{aligned}$$

Hence, if $|T|=1$, then $(T,v_T^{\varvec{x}})\in \Gamma _{vex}$ and $x_T\in C(T,v_T^{\varvec{x}})$. Assume that $|T|=2$. For all $i\in T$,

$$\begin{aligned} v_T^{\varvec{x}}(\{i\})&= v(\{i\}\cup (N{\setminus } T))-x^{\{i\}\cup (N{\setminus } T)}(N{\setminus } T)=x^{\{i\}\cup (N{\setminus } T)}(\{i\})=x_i^{\{i\}\cup (N{\setminus } T)} \\&= \sum _{\pi \in \Pi ^N}\lambda _\pi a_i^{\pi ,\{i\}\cup (N{\setminus } T)}(N,v)\le \sum _{\pi \in \Pi ^N}\lambda _\pi a_i^{\pi ,N}(N,v)=x_i^N=x(\{i\}). \end{aligned}$$

Therefore, $(T,v_T^{\varvec{x}})\in \Gamma _{vex}$ and $x_T\in C(T,v_T^{\varvec{x}})$. Hence, the core satisfies weak HM-consistency on the domain of convex games.

Now, let $x\in {\hbox {ri}} C(N,v)$. Then we may assume that $\lambda \in \mathbb {R}_{++}^{\Pi ^N}$. Therefore, we also obtain $x^S\in {\hbox {ri}} C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$. If $|T|=1$, then $x_T\in {\hbox {ri}} C(T,v_T^{\varvec{x}})$. Assume that $|T|=2$. If $x(\{i\})>v_T^{\varvec{x}}(\{i\})$ for all $i\in T$, then $x_T\in {\hbox {ri}} C(T,v_T^{\varvec{x}})$. Assume that there exists $i\in T$ such that $x(\{i\})=v_T^{\varvec{x}}(\{i\})$. Denote $T=\{i,j\}$. Then $a_i^{\pi ,N{\setminus }\{j\}}(N,v)=a_i^{\pi ,N}(N,v)$ for all $\pi \in \Pi ^N$. For all $\pi \in \Pi ^N$ with $\pi (i)>\pi (j)$, we obtain $a_j^{\pi ,N{\setminus }\{i\}}(N,v)=a_j^{\pi ,N}(N,v)$ by definition. Let $\pi \in \Pi ^N$ with $\pi (i)<\pi (j)$ and let $\pi '\in \Pi ^N$ differ from $\pi$ only inasmuch as $\pi '(i)=\pi (j)$ and $\pi '(j)=\pi (i)$. For $S=\{k\in N{\setminus }\{i\}\mid \pi (k)<\pi (j)\}=\{k\in N{\setminus }\{j\}\mid \pi '(k)<\pi '(i)\}$, we deduce

$$\begin{aligned} v(S\cup \{i\})-v(S)=a_i^{\pi ',N{\setminus }\{j\}}(N,v)=a_i^{\pi ',N}(N,v)=v(S\cup T)-v(S\cup \{j\}), \end{aligned}$$

so that

$$\begin{aligned} a_j^{\pi ,N{\setminus }\{i\}}(N,v)=v(S\cup \{j\})-v(S)=v(S\cup T)-v(S\cup \{i\})=a_j^{\pi ,N}(N,v). \end{aligned}$$

Therefore,

$$\begin{aligned} v_T^{\varvec{x}}(\{j\})=\sum _{\pi \in \Pi ^N}\lambda _\pi a_j^{\pi ,N{\setminus }\{i\}}(N,v)=\sum _{\pi \in \Pi ^N}\lambda _\pi a_j^{\pi ,N}(N,v)=x(\{j\}), \end{aligned}$$

so that $C(T,v_T^{\varvec{x}})$ is single-valued, i.e., ${\hbox {ri}} C(T,v_T^{\varvec{x}})=C(T,v_T^{\varvec{x}})$. Hence, the relative interior of the core satisfies weak HM-consistency on the domain of convex games. $\square$

Lemma 4.2

The core and its relative interior satisfy converse HM-consistency.

Proof

Let $(N,v)\in \Gamma$ with $|N|\ge 3$ and $(S,v_S)\in \Gamma$ for all $S\in 2^N{\setminus }\{\emptyset \}$, let $x\in X(N,v)$, and let $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$ be such that $(T,v_T^{\varvec{x}})\in \Gamma$ and $x_T\in C(T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. Let $S\in 2^N{\setminus }\{\emptyset ,N\}$ and let $j\in N{\setminus } S$. For all $i\in S$,

$$\begin{aligned} x(\{i\})\ge v_{\{i,j\}}^{\varvec{x}}(\{i\})=v(N{\setminus }\{j\})-x^{N{\setminus }\{j\}}(N{\setminus }\{i,j\})=x^{N{\setminus }\{j\}}(\{i\}). \end{aligned}$$

Therefore,

$$\begin{aligned} x(S)\ge x^{N{\setminus }\{j\}}(S)\ge v(S). \end{aligned}$$

Hence, $x\in C(N,v)$ and the core satisfies converse HM-consistency.

Now, let $x^S\in {\hbox {ri}} C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$ be such that $x_T\in {\hbox {ri}} C(T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. Let $S\in 2^N{\setminus }\{\emptyset ,N\}$. Assume that $x(S)=v(S)$. Then $x(\{i\})=v_{\{i,j\}}^{\varvec{x}}(\{i\})=x^{N{\setminus }\{j\}}(\{i\})$ for all $i\in S$ and all $j\in N{\setminus } S$. As $x_{\{i,j\}}\in {\hbox {ri}} C(\{i,j\},v_{\{i,j\}}^{\varvec{x}})$, we conclude that $x(\{j\})=v_{\{i,j\}}^{\varvec{x}}(\{j\})=x^{N{\setminus }\{i\}}(\{j\})$ for all $i\in S$ and all $j\in N{\setminus } S$, so that $x(N{\setminus } S)=x^{N{\setminus }\{i\}}(N{\setminus } S)$. For all $i\in S$,

$$\begin{aligned} v(N)-v(S)&= x(N)-x(S)=x(N{\setminus } S)=x^{N{\setminus }\{i\}}(N{\setminus } S) \\&= x^{N{\setminus }\{i\}}(N{\setminus }\{i\})-x^{N{\setminus }\{i\}}(S{\setminus }\{i\}) \\&\le v(N{\setminus }\{i\})-v(S{\setminus }\{i\})\le v(N)-v(S), \end{aligned}$$

so that $x^{N{\setminus }\{i\}}(S{\setminus }\{i\})=v(S{\setminus }\{i\})$. As $x^{N{\setminus }\{i\}}\in {\hbox {ri}} C(N{\setminus }\{i\},v_{N{\setminus }\{i\}})$, we obtain $v(N{\setminus } S)+v(S{\setminus }\{i\})=v(N{\setminus }\{i\})$ for all $i\in S$, so that $x(N{\setminus } S)=x^{N{\setminus }\{i\}}(N{\setminus } S)=v(N{\setminus } S)$. Hence, $x\in {\hbox {ri}} C(N,v)$ and the relative interior of the core satisfies converse HM-consistency. $\square$

In line with the reduced game properties studied by Peleg (1986), Tadenuma (1992), and Funaki and Yamato (2001), each solution satisfying individual rationality and weak HM-consistency is necessarily a subsolution of the core. This result is valid on each closed domain of games. To prove it, we first show that each such solution satisfies efficiency.

Lemma 4.3

If a solution satisfies individual rationality and weak HM-consistency, then it satisfies efficiency.

Proof

Let $\sigma$ be a solution on $\Gamma$ satisfying individual rationality and weak HM-consistency. Suppose that $\sigma$ does not satisfy efficiency. Then there exist $(N,v)\in \Gamma$ and $x\in \sigma (N,v)$ such that $x(N)<v(N)$. Let $i\in N$. By weak HM-consistency, $(S,v_S)\in \Gamma$ for all $S\in 2^N{\setminus }\{\emptyset \}$ and there exists $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$ such that $(\{i\},v_{\{i\}}^{\varvec{x}})\in \Gamma$ and $x_i\in \sigma (\{i\},v_{\{i\}}^{\varvec{x}})$. By individual rationality,

$$\begin{aligned} x(\{i\})\ge v_{\{i\}}^{\varvec{x}}(\{i\})=v(N)-x^N(N{\setminus }\{i\})>x(N)-x(N{\setminus }\{i\})=x(\{i\}), \end{aligned}$$

which is a contradiction. Hence, $\sigma$ satisfies efficiency. $\square$

Lemma 4.4

If a solution satisfies individual rationality and weak HM-consistency, then it is a subsolution of the core.

Proof

Let $\sigma$ be a solution on $\Gamma$ satisfying individual rationality and weak HM-consistency. By Lemma 4.3, $\sigma$ satisfies efficiency. We show by induction on the number of players that $\sigma (N,v)\subseteq C(N,v)$ for all $(N,v)\in \Gamma$. By efficiency, $\sigma (N,v)\subseteq C(N,v)$ for all $(N,v)\in \Gamma$ with $|N|=1$. By efficiency and individual rationality, $\sigma (N,v)\subseteq C(N,v)$ for all $(N,v)\in \Gamma$ with $|N|=2$.

Let $k\in \mathbb {N}$ with $k\ge 3$ and assume that $\sigma (N,v)\subseteq C(N,v)$ for all $(N,v)\in \Gamma$ with $|N|<k$. Let $(N,v)\in \Gamma$ with $|N|=k$ and let $x\in \sigma (N,v)$. By efficiency, $x\in X(N,v)$. By weak HM-consistency, $(S,v_S)\in \Gamma$ for all $S\in 2^N{\setminus }\{\emptyset \}$ and there exists $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$ such that $(T,v_T^{\varvec{x}})\in \Gamma$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. By the induction hypothesis, $x^S\in C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$ and $x_T\in C(T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. Then Lemma 4.2 implies that $x\in C(N,v)$. Hence, $\sigma (N,v)\subseteq C(N,v)$ for all $(N,v)\in \Gamma$. $\square$

The following result follows directly from Lemmas 4.1 and  4.4.

Theorem 4.1

The core is the unique inclusion-wise maximal solution for convex games satisfying individual rationality and weak HM-consistency.

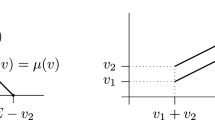
By means of examples, we show that each of the properties in Theorem 4.1 is logically independent of the remaining property. Let $\underline{\sigma }$ on $\Gamma _{vex}$ be, for all $(N,v)\in \Gamma _{vex}$, defined by

$$\begin{aligned} \underline{\sigma }(N,v)= {\left\{ \begin{array}{ll} \{x\in \mathbb {R}^N\mid x(N)\le v(N)\} &{} \text {if }|N|=1; \\ C(N,v) &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Then $\underline{\sigma }$ satisfies weak HM-consistency, but is not a subsolution of the core. The imputation set satisfies individual rationality, but is not a subsolution of the core. Thus, the claimed logical independence is shown.

In line with the characterizations of the Shapley value and the egalitarian solution, weak HM-consistency can be used to obtain a pure characterization of the core by fixing the solution for two-player games. There, the core coincides with the imputation set. The corresponding property with the name unanimity was introduced by Peleg (1986) and also exploited by Peleg (1989). A solution $\sigma$ on $\Gamma$ satisfies unanimity if, for all $(N,v)\in \Gamma$ with $|N|=2$,

$$\begin{aligned} \sigma (N,v)=\left\{ x\in X(N,v)\ \Bigg |\ x(\{i\})\ge v(\{i\})\ \text {for all}\ i\in N\right\} . \end{aligned}$$

We now show that the core on the domain of convex games is axiomatized by efficiency, unanimity, weak Hart–Mas-Colell consistency, and converse Hart–Mas-Colell consistency.

Theorem 4.2

The core is the unique solution for convex games satisfying efficiency, unanimity, weak HM-consistency, and converse HM-consistency.

Proof

The core satisfies efficiency and unanimity. By Lemmas 4.1 and  4.2, the core satisfies weak HM-consistency on the domain of convex games and converse HM-consistency. Let $\sigma$ be a solution for convex games satisfying efficiency, unanimity, weak HM-consistency, and converse HM-consistency. We show by induction on the number of players that $\sigma (N,v)=C(N,v)$ for all $(N,v)\in \Gamma _{vex}$. By unanimity, $\sigma (N,v)=C(N,v)$ for all $(N,v)\in \Gamma _{vex}$ with $|N|=2$. By efficiency, unanimity, and weak HM-consistency, $\sigma (N,v)=C(N,v)$ for all $(N,v)\in \Gamma _{vex}$ with $|N|=1$.

Let $k\in \mathbb {N}$ with $k\ge 3$ and assume that $\sigma (N,v)=C(N,v)$ for all $(N,v)\in \Gamma _{vex}$ with $|N|<k$. Let $(N,v)\in \Gamma _{vex}$ with $|N|=k$. By individual rationality and weak HM-consistency, Lemma 4.4 implies that $\sigma (N,v)\subseteq C(N,v)$. Let $x\in C(N,v)$. Then $x\in X(N,v)$. By Lemma 4.1, there exists $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$ such that $(T,v_T^{\varvec{x}})\in \Gamma _{vex}$ and $x_T\in C(T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. By the induction hypothesis, $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. By converse HM-consistency, $x\in \sigma (N,v)$. Therefore, $C(N,v)\subseteq \sigma (N,v)$. Hence, $\sigma (N,v)=C(N,v)$ for all $(N,v)\in \Gamma _{vex}$. $\square$

The following result follows directly from Lemma 4.3 and Theorem 4.2.

Theorem 4.3

The core is the unique solution for convex games satisfying individual rationality, unanimity, weak HM-consistency, and converse HM-consistency.

By means of examples, we show that each of the properties in Theorems 4.2 and  4.3 is logically independent of the remaining properties. The solution $\underline{\sigma }$ on $\Gamma _{vex}$ satisfies unanimity, weak HM-consistency, and converse HM-consistency, but does not satisfy efficiency. The Shapley value on $\Gamma _{vex}$ satisfies individual rationality, weak HM-consistency, and converse HM-consistency, but does not satisfy unanimity. The imputation set on $\Gamma _{vex}$ satisfies efficiency, individual rationality, unanimity, and converse HM-consistency, but does not satisfy weak HM-consistency. Let $\overline{\sigma }$ on $\Gamma _{vex}$ be, for all $(N,v)\in \Gamma _{vex}$, defined by

$$\begin{aligned} \overline{\sigma }(N,v)= {\left\{ \begin{array}{ll} \phi (N,v) &{} \text {if }|N|\ge 3; \\ C(N,v) &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Then $\overline{\sigma }$ on $\Gamma _{vex}$ satisfies individual rationality, unanimity, weak HM-consistency, but does not satisfy converse HM-consistency. Table 1 shows the relevant properties of the aforementioned solutions. Thus, the claimed logical independence is shown.

Table 1 Independence of properties in Theorems 4.2 and 4.3

5 A joint characterization

On the domain of convex games, both the core and the Shapley value, as well as their relative interiors, satisfy efficiency, individual rationality, anonymity, scale covariance, translation covariance, and superadditivity. Moreover, the Shapley value for convex games is a subsolution of the core, namely the barycenter of its vertices weighted by the numbers of orders that generate them. It turns out that a nonempty solution satisfies all the aforementioned properties if and only if it is (a) this aforementioned barycenter, (b) a polytope that is homothetic to the core with positive ratio of homethety not larger than one, centered at this barycenter, or (c) the relative interior of such a solution. Formally, for each $\delta \in [0,1]$, let $C^\delta$ on $\Gamma _{vex}$ be, for all $(N,v)\in \Gamma _{vex}$, defined by

$$\begin{aligned} C^\delta (N,v)=\delta C(N,v)+(1-\delta )\phi (N,v)=\left\{ \delta x+(1-\delta )\phi (N,v)\ \Bigg |\ x\in C(N,v)\right\} . \end{aligned}$$

Let $(N,v)\in \Gamma _{vex}$. As the relative interior is scale covariant and translation covariant,

$$\begin{aligned} {\hbox {ri}} C^\delta (N,v)=\delta {\hbox {ri}} C(N,v)+(1-\delta )\phi (N,v). \end{aligned}$$

For $0<\delta<\delta '<1$, we obtain

$$\begin{aligned} \phi (N,v)={\hbox {ri}} C^0(N,v)=C^0(N,v)&\subseteq {\hbox {ri}} C^\delta (N,v)\subseteq C^\delta (N,v) \\&\subseteq {\hbox {ri}} C^{\delta '}(N,v)\subseteq C^{\delta '}(N,v) \\&\subseteq {\hbox {ri}} C^1(N,v)\subseteq C^1(N,v)=C(N,v), \end{aligned}$$

where all inequalities are equalities if and only if the game is additive, and all inequalities are strict if and only if the game is not additive.

Theorem 5.1

A solution $\sigma$ on $\Gamma _{vex}$ satisfies nonemptiness, individual rationality, anonymity, scale covariance, superadditivity, weak HM-consistency, and converse HM-consistency if and only if there exists $\delta \in [0,1]$ such that $\sigma =C^\delta$ or $\sigma ={\hbox {ri}} C^\delta$.

Proof

On the domain of convex games, both the core and the Shapley value satisfy nonemptiness, individual rationality, anonymity, scale covariance, and superadditivity. Clearly, the relative interior of the core inherits nonemptiness, individual rationality, anonymity, and scale covariance from the core. By Lemma 1 of Hokari et al. (2020), it also satisfies superadditivity. The Shapley value satisfies weak HM-consistency and converse HM-consistency. By Lemmas 4.1 and  4.2, the core and its relative interior also satisfy these properties.

Let $\delta \in [0,1]$ and let $\sigma \in \{C^\delta ,{\hbox {ri}} C^\delta \}$. Then $\sigma$ satisfies nonemptiness, individual rationality, anonymity, scale covariance, and superadditivity because the core, its relative interior, and the Shapley value satisfy these properties.

In order to show weak HM-consistency, let $(N,v)\in \Gamma _{vex}$ and let $x\in \sigma (N,v)$. Then $x=\delta y+(1-\delta )z$, where $y\in C(N,v)$ or $y\in {\hbox {ri}} C(N,v)$, and $z=\phi (N,v)$. By weak HM-consistency of the core, its relative interior, and the Shapley value, there exist $\varvec{y}=(y^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ and $\varvec{z}=(z^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $y^N=y$, $z^N=z$, $y^S\in C(S,v_S)$ or $y^S\in {\hbox {ri}} C(S,v_S)$, and $z^S=\phi (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$, respectively, such that $(T,v_T^{\varvec{y}}),(T,v_T^{\varvec{z}})\in \Gamma _{vex}$, $y_T\in C(T,v_T^{\varvec{y}})$ or $y_T\in {\hbox {ri}} C(T,v_T^{\varvec{y}})$, and $z_T=\phi (T,v_T^{\varvec{z}})$ for all $T\in 2^N{\setminus }\{\emptyset \}$ with $|T|\le 2$, respectively. Let $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ be defined by $x^S=\delta y^S+(1-\delta )z^S$ for all $S\in 2^N{\setminus }\{\emptyset \}$. Then $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$. As $v_T^{\varvec{x}}=\delta v_T^{\varvec{y}}+(1-\delta )v_T^{\varvec{z}}$, we obtain $(T,v_T^{\varvec{x}})\in \Gamma _{vex}$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N{\setminus }\{\emptyset \}$ with $|T|\le 2$ by scale covariance of the core, its relative interior, and the Shapley value. Hence, $\sigma$ satisfies weak HM-consistency.

In order to show converse HM-consistency, let $(N,v)\in \Gamma _{vex}$ with $|N|\ge 3$, let $x\in X(N,v)$, and let $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$ be such that $(T,v_T^{\varvec{x}})\in \Gamma _{vex}$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. For all $S\in 2^N{\setminus }\{\emptyset \}$, respectively, there exists a unique $y^S\in C(S,v_S)$ or $y^S\in {\hbox {ri}} C(S,v_S)$, and $z^S=\phi (S,v_S)$, such that $x^S=\delta y^S+(1-\delta )z^S$. Let $\varvec{y}=(y^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ and $\varvec{z}=(z^S)_{S\in 2^N{\setminus }\{\emptyset \}}$. For all $T\in 2^N$ with $|T|=2$, respectively, $v_T^{\varvec{x}}=\delta v_T^{\varvec{y}}+(1-\delta )v_T^{\varvec{z}}$, $y_T\in C(T,v_T^{\varvec{y}})$ or $y_T\in {\hbox {ri}} C(T,v_T^{\varvec{y}})$, and $z_T=\phi (T,v_T^{\varvec{z}})$. Converse HM-consistency of the core, its relative interior, and the Shapley value, imply that $y\in C(N,v)$ or $y\in {\hbox {ri}} C(N,v)$, and $z=\phi (N,v)$. By scale covariance and translation covariance of the core, its relative interior, and the Shapley value, we conclude that $x\in \sigma (N,v)$. Hence, $\sigma$ satisfies converse HM-consistency.

In order to prove the uniqueness part, let $\sigma$ be a solution on the domain of convex games satisfying nonemptiness, individual rationality, anonymity, scale covariance, superadditivity, weak HM-consistency, and converse HM-consistency. By Lemma 3 of Hokari et al. (2020), $\sigma$ satisfies translation covariance. By Lemma 4.4, $\sigma$ is a subsolution of the core. Then $\sigma (N,v)=C(N,v)=\phi (N,v)$ for all additive games $(N,v)\in \Gamma _{vex}$ with $|N|\le 2$. Let $(N,v)\in \Gamma _{vex}$ with $|N|=2$ and $v(N)>\sum _{i\in N}v(\{i\})$. By translation covariance, we may assume without loss of generality that $v(\{i\})=0$ for all $i\in N$. By scale covariance, we may assume without loss of generality that $v(N)=1$. By anonymity, we may assume without loss of generality that $N=\{1,2\}$. We now show that $\sigma (N,v)$ is a convex set. Let $x,y\in \sigma (N,v)$ and let $\theta \in [0,1]$. By scale covariance, $\theta x\in \sigma (N,\theta v)$ and $(1-\theta )y\in \sigma (N,(1-\theta )v)$. By superadditivity, $\theta x+(1-\theta )y\in \sigma (N,v)$. Hence, $\sigma (N,v)$ is a convex set. By anonymity, $(1-t,t)\in \sigma (N,v)$ for all $t\in [0,1]$ with $(t,1-t)\in \sigma (N,v)$. For

$$\begin{aligned} \delta =1-2\inf \left\{ t\in [0,1]\ \Bigg |\ (t,1-t)\in \sigma (N,v)\right\} , \end{aligned}$$

we therefore obtain $\sigma (N,v)=C^\delta (N,v)$ or $\sigma (N,v)={\hbox {ri}} C^\delta (N,v)$. Hence, $\sigma (N,v)=C^\delta (N,v)$ or $\sigma (N,v)={\hbox {ri}} C^\delta (N,v)$ for all $(N,v)\in \Gamma _{vex}$ with $|N|\le 2$, respectively. We show by induction on the number of players that $\sigma (N,v)=C^\delta (N,v)$ or $\sigma (N,v)={\hbox {ri}} C^\delta (N,v)$, respectively, for all $(N,v)\in \Gamma _{vex}$. Let $k\in \mathbb {N}$ with $k\ge 3$ and assume that $\sigma (N,v)=C^\delta (N,v)$ or $\sigma (N,v)={\hbox {ri}} C^\delta (N,v)$ for all $(N,v)\in \Gamma _{vex}$ with $|N|<k$. Now, let $(N,v)\in \Gamma _{vex}$ with $|N|=k$ and let $x\in \sigma (N,v)$. Then $x\in X(N,v)$. By weak HM-consistency, there exists $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=x$ and $x^S\in \sigma (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$ such that $(T,v_T^{\varvec{x}})\in \Gamma _{vex}$ and $x_T\in \sigma (T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. By the induction hypothesis, $x^S\in C^\delta (S,v_S)$ or $x^S\in {\hbox {ri}} C^\delta (S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset ,N\}$, respectively, and $x_T\in C^\delta (T,v_T^{\varvec{x}})$ or $x_T\in {\hbox {ri}} C^\delta (T,v_T^{\varvec{x}})$ for all $T\in 2^N$ with $|T|=2$. By converse HM-consistency of $C^\delta$ and ${\hbox {ri}} C^\delta$, $x\in C^\delta (N,v)$ or $x\in {\hbox {ri}} C^\delta (N,v)$. Hence, $\sigma (N,v)\subseteq C^\delta (N,v)$ or $\sigma (N,v)\subseteq {\hbox {ri}} C^\delta (N,v)$ for all $(N,v)\in \Gamma _{vex}$, respectively. Similarly, by interchanging the roles of $\sigma$ and $C^\delta$ or ${\hbox {ri}} C^\delta$, we obtain $C^\delta (N,v)\subseteq \sigma (N,v)$ or ${\hbox {ri}} C^\delta (N,v)\subseteq \sigma (N,v)$ for all $(N,v)\in \Gamma _{vex}$, respectively. Hence, $\sigma =C^\delta$ or $\sigma ={\hbox {ri}} C^\delta$. $\square$

Note that all the above solutions, i.e., $C^\delta$ and $\text{ ri } C^\delta$, even satisfy additivity⁶ rather than superadditivity on the domain of convex games. Indeed, the Shapley value satisfies additivity on each domain of games, and it is known that the core satisfies additivity on the domain of convex games. Therefore, $C^\delta$ is additive. Moreover, a careful inspection of (1) shows the additivity of $\text{ ri } C$ so that $\text{ ri } C^\delta$ is additive for each $\delta \in [0,1]$ as well. However, in the foregoing theorem it is sufficient to employ superadditivity, a property that is satisfied by the core on each domain of games.

By means of examples, we show that each of the properties in Theorem 5.1 is logically independent of the remaining properties. Clearly, the solution $\varnothing$ on $\Gamma _{vex}$ that assigns to each convex game the empty set, exclusively violates nonemptiness. The solution $\underline{\sigma }$ on $\Gamma _{vex}$ exclusively violates individual rationality. For the following three examples, note that each solution on the domain of convex games with at most two players that satisfies weak HM-consistency admits a unique extension to the domain of all convex games that satisfies weak Hart–Mas-Colell consistency and converse Hart–Mas-Colell consistency. Let $i\in U$ and let $\sigma ^i$ on $\Gamma _{vex}$ be the unique subsolution of the core that satisfies weak HM-consistency and converse HM-consistency, and is, for all $(N,v)\in \Gamma _{vex}$ with $|N|\le 2$, defined by

$$\begin{aligned} \sigma ^i(N,v)= {\left\{ \begin{array}{ll} \phi (N,v) &{} \hbox { if}\ i\in N; \\ C(N,v) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Then $\sigma ^i$ on $\Gamma _{vex}$ exclusively violates anonymity. Let $\widetilde{\sigma }$ on $\Gamma _{vex}$ be the unique subsolution of the core that satisfies weak HM-consistency and converse HM-consistency, and is, for all $(N,v)\in \Gamma _{vex}$ with $|N|\le 2$, defined by

$$\begin{aligned} \widetilde{\sigma }(N,v)= {\left\{ \begin{array}{ll} \phi (N,v) &{} \hbox { if}\ v(N)-\sum _{i\in N}v(\{i\})\le 1; \\ C(N,v) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Then ${\widetilde{\sigma }}$ on $\Gamma _{vex}$ exclusively violates scale covariance. Let $\widehat{\sigma }$ on $\Gamma _{vex}$ be the unique subsolution of the core that satisfies weak HM-consistency and converse HM-consistency, and is, for all $(N,v)\in \Gamma _{vex}$ with $|N|\le 2$, defined by

$$\begin{aligned} \widehat{\sigma }(N,v)= {\left\{ \begin{array}{ll} \phi (N,v) &{}{} \text{ if }\, v(\{i\})=v(\{j\})\ \text{ for } \text{ all }\ i,j\in N; \\ C(N,v) &{}{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Then ${\widehat{\sigma }}$ on $\Gamma _{vex}$ exclusively violates superadditivity. The imputation set on $\Gamma _{vex}$ exclusively violates weak HM-consistency. The solution $\overline{\sigma }$ on $\Gamma _{vex}$ exclusively violates converse HM-consistency. Table 2 shows the relevant properties of the aforementioned solutions. Thus, the claimed logical independence is shown.

Table 2 Independence of properties in Theorem 5.1

6 Concluding remarks

This paper introduced Hart–Mas-Colell consistency for general solutions for cooperative games with transferable utility. We focused on weak Hart–Mas-Colell consistency and converse Hart–Mas-Colell consistency of the core on the domain of convex games. The question arises whether the results hold on a larger domain of games. Note that such domain should at least be closed under subgames, e.g., the domain of totally balanced games where the core of each subgame is nonempty. A significantly smaller closed domain that contains the set of convex games is the set of quasi-convex games⁷ introduced by Sprumont (1990), who showed, e.g., that the Shapley value of a quasi-convex game is still a member of the core. As the following example shows, the core does not satisfy weak Hart–Mas-Colell consistency even on the domain of quasi-convex games.

Example 6.1

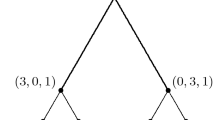
Let $(N,v)\in \Gamma$ with $N=\{1,2,3,4\}$ be given by

$$\begin{aligned} v(S)= {\left\{ \begin{array}{ll} 12 &{} \text {if }S=\{1,2,3,4\}; \\ 7 &{} \text {if }S\in \{\{1,2,3\},\{1,2,4\},\{1,3,4\}\}; \\ 4 &{} \text {if }S\in \{\{1,2\},\{1,3\},\{1,4\}\}; \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

The straightforward proof that (N, v) is quasi-convex is left to the reader. Consider $(0,4,4,4)\in C(N,v)$. For each $\varvec{x}=(x^S)_{S\in 2^N{\setminus }\{\emptyset \}}$ with $x^N=(0,4,4,4)$ and $x^S\in C(S,v_S)$ for all $S\in 2^N{\setminus }\{\emptyset \}$,

$$\begin{aligned} v_{\{1,2\}}^{\varvec{x}}(\{1\})=v(\{1,3,4\})-x^{\{1,3,4\}}(\{3,4\})=x^{\{1,3,4\}}(\{1\})\ge 1. \end{aligned}$$

Therefore $(0,4)\notin C(\{1,2\},v_{\{1,2\}}^{\varvec{x}})$. Hence, the core does not satisfy weak Hart–Mas-Colell consistency on the domain of quasi-convex games.