Skip to main content
SpringerLink
Log in

A fast active learning method in design of experiments: multipeak parallel adaptive infilling strategy based on expected improvement

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

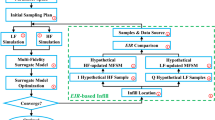
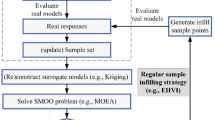
Surrogate models are widely used in simulation-based engineering design. The distribution of samples directly determines the quality and efficiency of surrogate models, which has a significant influence on follow-up work. This paper proposes a multipeak parallel adaptive infilling (MPEI) strategy based on expected improvement (EI), which can be divided into two stages: the construction of candidate peak areas and the selection of appropriate candidates at the candidate peak areas. In the first stage, the candidates are divided into the corresponding subspaces in sequence according to the value of EI and the position of each candidate to construct the candidate peak areas. In the second stage, the Gaussian function is used to extract the uncorrelated parent point and the corresponding offspring points in each candidate peak area. Based on these stages, the MPEI strategy selects multiple new samples in spaces with both local optima and areas of large uncertainty interest, which can fully balance global exploration and local exploitation. In addition, the samples selected in each candidate peak area are concise and locally uniform, which can effectively reduce the computational cost. Seven benchmark cases and one engineering problem are used to validate the performance of the MPEI strategy. The results show that the MPEI strategy can efficiently obtain the desired prediction accuracy of surrogate models at a small price of a few samples and confirm the feasibility and robustness of the presented methodology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

References

  • Boddy R, Smith G (2011) Effective experimentation: for scientists and technologists. John Wiley & Sons, Hoboken

    MATH  Google Scholar 

  • Cox DD, John S (1992) A statistical method for global optimization. Proc IEEE Int Conf Syst Man Cybern 2:1241–1246

    Google Scholar 

  • Forrester AIJ, Keane AJ (2009) Recent advances in surrogate-based optimization. Prog Aerosp Sci 45:50–79

    Article  Google Scholar 

  • Gao Y (2008) Optimization methods based on kriging surrogate model and their application in injection molding. Dissertation, Dalian University of Technology

  • Garud SS, Karimi IA, Kraft M (2017) Design of computer experiments: a review. Comput Chem Eng 106:71–95

    Article  Google Scholar 

  • Ginsbourger D, Le Riche R, Carraro L (2007) A multi-points criterion for deterministic parallel global optimization based on kriging, the International Conference on Nonconvex Programming: local and global approaches, Rouen, France

  • Ginsbourger D, Le Riche R, Carraro L (2008) A multi-points criterion for deterministic parallel global optimization based on Gaussian processes

  • Ginsbourger D, Le Riche R, Carraro L (2010) Kriging is well-suited to parallelize optimization. In: Computational intelligence in expensive optimization problems. Springer, Berlin, pp 131–162

    Chapter  Google Scholar 

  • Gunst RF, Mason RL (2009) Fractional factorial design. Wiley Interdiscip Rev Comput Stat 1(2):234–244

    Article  Google Scholar 

  • Guo Z, Song L, Park C, Li J, Haftka RT (2018) Analysis of dataset selection for multi-fidelity surrogates for a turbine problem. Struct Multidiscip Optim 57:2127–2142

    Article  Google Scholar 

  • Hao P, Feng S, Zhang K, Li Z, Wang B, Li G (2018) Adaptive gradient-enhanced kriging model for variable-stiffness composite panels using Isogeometric analysis. Struct Multidiscip Optim 58:1–16

    Article  MathSciNet  Google Scholar 

  • Hao P, Feng S, Li Y, Wang B, Chen H (2020) Adaptive infill sampling criterion for multi-fidelity gradient-enhanced kriging model. Struct Multidiscip Optim 62(1):353–373

  • Hlawka E (1961) Funktionen von beschränkter Variatiou in der Theorie der Gleichverteilung. Annali di Matematica 54:325–333

    Article  Google Scholar 

  • Iman RL, Conover WJ (1980) Small sample sensitivity analysis techniques for computer-models, with an application to risk assessment. Commun Stat-Theor M 9:1749–1842

    Article  MathSciNet  Google Scholar 

  • Janusevskis J, Le Riche R, Ginsbourger D (2011) Parallel expected improvements for global optimization: summary, bounds and speed-up. Technical report:1–21

  • Johnson ME, Moore LM, Ylvisaker D (1990) Minimax and maximin distance designs. J Stat Plan Infer 26:131–148

    Article  MathSciNet  Google Scholar 

  • Jones DR, Schonlau M, Welch WJ (1998) Efficient global optimization of expensive black-box functions. J Glob Optim 13:455–492

    Article  MathSciNet  Google Scholar 

  • Kushner HJ (1964) A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise. J Basic Eng 86:97–106

    Article  Google Scholar 

  • Liu H, Xu S, Ma Y, Chen X, Wang X (2016) An adaptive Bayesian sequential sampling approach for global metamodeling. J Mech Des 138(1):011404

    Article  Google Scholar 

  • Liu H, Cai J, Ong YS (2017a) An adaptive sampling approach for kriging metamodeling by maximizing expected prediction error. Comput Chem Eng 106:171–182

    Article  Google Scholar 

  • Liu J, Song WP, Han ZH, Zhang Y (2017b) Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models. Struct Multidiscip Optim 55:1–19

    Article  MathSciNet  Google Scholar 

  • Liu H, Ong Y-S, Cai J (2018) A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct Multidiscip Optim 57:393–416

    Article  Google Scholar 

  • Liu J, Yi J, Zhou Q, Cheng Y (2020) A sequential multi-fidelity surrogate model-assisted contour prediction method for engineering problems with expensive simulations. Eng Comput: 1–19

  • Loeppky JL, Sacks J, Welch WJ (2009) Choosing the sample size of a computer experiment: a practical guide. Technometrics 51:366–376

    Article  MathSciNet  Google Scholar 

  • Lophaven S, Nielsen H, Sondergaard J (2002a) Aspects of the Matlab toolbox DACE. Technical report, Informatics and Mathematical Modelling

  • Lophaven S, Nielsen HB, Sondergaard JJ (2002b) DACE—a Matlab Kriging toolbox; version 2; informatics and mathematical modelling. Technical University of Denmark, Copenhagen

    Google Scholar 

  • Lv L, Shi ML, Song XG, Sun W, Zhang J (2020) A fast-converging ensemble infilling approach balancing global exploration and local exploitation: the go-inspired hybrid infilling strategy. J Mech Des 142(2):021403

    Article  Google Scholar 

  • Morris MD, Mitchell T (1995) Exploratory designs for computational experiments. J Stat Plan Infer 43:381–402

    Article  Google Scholar 

  • Sasena MJ (2002) Flexibility and efficiency enhancements for constrained global design optimization with kriging approximations. Dissertation, University of Michigan, Ann Arbor, MI

  • Schonlau M (1997) Computer experiments and global optimization. Dissertation, University of Waterloo

  • Schonlau M, Welch WJ, Jones DR (1998) Global versus local search in constrained optimization of computer models. Lecture Notes-Monograph Series 34:11–25

    Article  MathSciNet  Google Scholar 

  • Sóbester A, Leary SJ, Keane AJ (2004) A parallel updating scheme for approximating and optimizing high fidelity computer simulations. Struct Multidiscip Optim 27:371–383

    Article  Google Scholar 

  • Sóbester A, Leary SJ, Keane A (2005) On the design of optimization strategies based on global response surface approximation models. J Glob Optim 33:31–59

    Article  MathSciNet  Google Scholar 

  • Song X, Sun G, Li G, Gao W, Li Q (2013) Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models. Struct Multidiscip Optim 47:221–231

    Article  MathSciNet  Google Scholar 

  • Turner CJ, Crawford RH, Campbell MI (2007) Multidimensional sequential sampling for NURBs-based metamodel development. Eng Comput 23:155–174

    Article  Google Scholar 

  • Williams CK, Rasmussen CE (2006) Gaussian processes for machine learning. MIT press, Cambridge

    MATH  Google Scholar 

  • Xu S, Liu H, Wang X, Jiang X (2014) A robust error-pursuing sequential sampling approach for global metamodeling based on voronoi diagram and cross validation. J Mech Des 136(7):071009

    Article  Google Scholar 

  • Zeng P (2008) Fundamentals of finite element analysis. Tsinghua University Press, Beijing

    Google Scholar 

  • Zhang Y, Kim N H, Haftka R T (2020) General-surrogate adaptive sampling using interquartile range for design space exploration. J Mech Des 142(5):051402

Download references

Funding

This research is financially supported by the National Key Research and Development Program of China (Grant No. 2018YFB1700704) and the National Natural Science Foundation of China (Grant No. 52075068).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Dalian University of Technology, Dalian, 116024, China

    Yang Zhang, Shuo Wang, Chang’an Zhou & Xueguan Song

  2. Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou, 310016, China

    Liye Lv

Authors
  1. Yang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuo Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chang’an Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liye Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xueguan Song
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xueguan Song.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Replication of results

The main codes and raw data are submitted as supplementary materials.

Additional information

Responsible Editor: Xiaoping Du

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

ESM 1

(ZIP 3.14 mb).

Appendix

Appendix

Table 10 The required AIIs when the performance of the surrogate model of BR case meets the specified requirements under different combinations of λ, Rp, and Rr
Full size table
Table 11 The required AIIs when the performance of the surrogate model of Camel3 case meets the specified requirements under different combinations of λ, Rp, and Rr
Full size table
Table 12 The required AINs when the performance of the surrogate model of BR case meets the specified requirements under different combinations of λ, Rp, and Rr
Full size table
Table 13 The required AINs when the performance of the surrogate model of Camel3 case meets the specified requirements under different combinations of λ, Rp, and Rr
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., Wang, S., Zhou, C. et al. A fast active learning method in design of experiments: multipeak parallel adaptive infilling strategy based on expected improvement. Struct Multidisc Optim 64, 1259–1284 (2021). https://doi.org/10.1007/s00158-021-02915-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-021-02915-1

Keywords

Search

Navigation