Topology optimization using a continuous-time high-cycle fatigue model

Abstract

We propose a topology optimization method that includes high-cycle fatigue as a constraint. The fatigue model is based on a continuous-time approach where the evolution of damage in each point of the design domain is governed by a system of ordinary differential equations, which employs the concept of a moving endurance surface being a function of the stress and back stress. Development of fatigue damage only occurs when the stress state lies outside the endurance surface. The fatigue damage is integrated for a general loading history that may include non-proportional loading. Thus, the model avoids the use of a cycle-counting algorithm. For the global high-cycle fatigue constraint, an aggregation function is implemented, which approximates the maximum damage. We employ gradient-based optimization, and the fatigue sensitivities are determined using adjoint sensitivity analysis. With the continuous-time fatigue model, the damage is load history dependent and thus the adjoint variables are obtained by solving a terminal value problem. The capabilities of the presented approach are tested on several numerical examples with both proportional and non-proportional loads. The optimization problems are to minimize mass subject to a high-cycle fatigue constraint and to maximize the structural stiffness subject to a high-cycle fatigue constraint and a limited mass.

1 Introduction

In mechanical components, fluctuating loads and stress concentrations lead to fatigue and possible failure. Thus, fatigue phenomena often govern the overall life of the component, quantified in terms of load cycles to failure. Concerning topology optimization (TO), fatigue constraints are either implemented as stress constraints (Holmberg et al. 2014) or with cycle-counting techniques like in Jeong et al. (2018), but these models are restricted to proportional loading histories. To incorporate a fatigue model in a TO problem that can handle a general loading history, we propose to use an evolution-based fatigue model.

Examples of other structural optimization formulations with fatigue constraints are found in Collet et al. (2017) and Oest et al. (2017b), where the fatigue prediction is done for a simplified damage model assuming a periodic load. Other examples can be found in Gerzen et al. (2017), where sizing optimization of shell structures is done with fatigue constraints at the welded joints using the commercial software SIMULIA Fe-safe, and Oest and Lund (2017a), where the TO is formulated with finite-life fatigue constraints. However, the fatigue is calculated using a cycle-counting algorithm, specifically rainflow counting (Amzallag et al. 1994), and this restricts the applicability to scalar stress measures, like signed von Mises. However, in many industrial applications, fatigue due to both proportional and non-proportional loads threaten the life of components. A recent contribution (Zhang et al. 2019) uses classical techniques, including rainflow counting, mean stress correction, and Palmgren-Miner’s rule, initially developed for unidirectionally loaded structures, to handle non-proportional loading. This is done by using a signed von Mises stress at each point of the structure as the single stress measure affecting fatigue. However, certain modes of stress reversal, including rotary stress states with constant principal stresses, give a constant signed von Mises stress, so that zero fatigue damage is predicted. This limitation of the validity of the model is a concern in TO, since the optimizer could exploit such weaknesses of the model. This motivated us to extend our previous contribution (Suresh et al. 2019), where we use a fatigue model that captures the fatigue damage from non-proportional loads as a constraint in TO problems.

The fatigue model follows a high-cycle (HC) evolution-based model developed in Ottosen et al. (2008). This model uses a continuous-time approach in the form of differential equations governing the time evolution of fatigue damage at each point in the design domain. Such evolution occurs when the stress state lies outside a so-called endurance surface, which moves in stress space depending on the current stress and a back stress tensor. The model states that the development of damage only occurs if the stress state lies outside the endurance surface while this surface evolves. The advantage of using such a model is that non-proportional loading histories can be considered in the prediction of fatigue damage. Further developments of the model can be found in (Brighenti et al. 2012), where the fatigue is assessed for complex multiaxial load histories, in Holopainen et al. (2016), where the model is extended to transversely isotropic materials, and in Ottosen et al. (2018), where the multiaxial fatigue criterion considers the stress gradient effects in critical regions like holes and notches.

Fatigue is here included in TO as a constraint on the maximum damage found in the design domain at the end of a given load history. The maximum damage is approximated by means of an aggregation function, namely the p-norm (Kennedy and Hicken 2015). The assumption of HC fatigue, in which the geometry and the material properties remain constant until failure, implies that the finite element (FE) stiffness matrix is constant throughout the load history for a given design. Therefore, the stress history required to evolve the damage can be computed at a reasonable cost. Once the stress history is obtained, we solve the spatially uncoupled ordinary differential equations for damage and back stress to get the total accumulated damage in selected points in the design domain (here the centroid of each FE) and compute the approximate maximum value.

The TO problem is solved using a gradient-based method with sensitivities of the approximated maximum fatigue determined by adjoint analysis (Haftka and Adelman 1989; Tortorelli and Michaleris 1994; van Keulen et al. 2005). Since the damage is governed by an evolution problem, computing these sensitivities requires the solution of a terminal value problem for the adjoint variables. The overall solution process is somewhat similar to that of e.g., Panagiotis et al. (1994) and Wang et al. (2017) for TO with plasticity.

2 Continuous-time approach

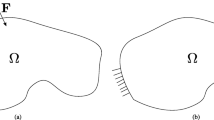
Consider a linearly elastic body B undergoing small deformations. The boundary is divided into two disjoint parts, Γ_t and Γ_u, having prescribed surface loads and displacements, respectively. The body is assumed to be in quasi-static equilibrium for given time-dependent surface loads t = t(t) and, thus, by the principle of virtual work, we have

$$ \begin{array}{@{}rcl@{}} &&{\int}_{B} \boldsymbol{\sigma}(\boldsymbol{u}):\boldsymbol{\varepsilon}(\boldsymbol{v})dV = {\int}_{{\varGamma}_{t}}\boldsymbol{t}^{\text{T}} \boldsymbol{v}ds \quad \forall \boldsymbol{v}\in {V} \\ &&\boldsymbol{u} = \boldsymbol{u}_{0} \quad \text{ on } {\varGamma}_{u} \end{array} $$

(1)

for all t ∈ [0,T]. Here, σ : 𝜖 = tr(σ𝜖), where tr(*) is the trace of a tensor. Using Hooke’s law, the stress tensor σ(u) = Eε(u), where E is the constitutive tensor and ε is the linearized strain tensor. The space V consists of suitably smooth test functions that vanish on Γ_u.

In general, damage can affect both the material (viaE) and the geometry (viaB). However, we are only concerned with high-cycle fatigue, where these properties are assumed to be unaffected by damage until failure. This means that we will first solve (1) for all t, and then determine the fatigue-development based on the computed stresses. Henceforth, we therefore consider the stress σ = σ(t) as given and then predict fatigue damage by the continuous-time approach following Ottosen et al. (2008, 2018).

For a given load history in terms of the associated stress history, we define an endurance surface {σ | β(σ,α) = 0}, where α is the back stress tensor, and β is the endurance function. It is assumed that damage development only occurs if the stress state lies outside this surface, and the endurance function β increases, i.e.,

$$ \text{damage development}\quad\text{i.f.f.}\quad\left\{\begin{array}{ll} \beta(\boldsymbol{\sigma}, \boldsymbol{\alpha}) > 0 \\ \dot{\beta}(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha}, \dot{\boldsymbol{\alpha}}) > 0 \end{array}\right., $$

where a superposed dot indicates time derivative. Later, it will be shown that the dependence of $\dot {\beta }$ on $\dot {\boldsymbol {\alpha }}$ is eliminated for a certain choice of back stress evolution equation.

The fatigue damage at a point is described by a real-valued state variable D = D(t) that increases monotonously with time from D = 0 (no damage) to D = 1 (critical failure). In general form, the damage model is represented by the evolution equations:

$$ \begin{array}{@{}rcl@{}} \dot{\boldsymbol{\alpha}} &= &J(\beta, \dot{\beta})\boldsymbol{G}_{\alpha}(\boldsymbol{\sigma}, \boldsymbol{\alpha})\dot{\beta}, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} \dot{D} &= &J(\beta, \dot{\beta})G_{D}(\beta, D)\dot{\beta}, \end{array} $$

(3)

where the functions G_α and G_D > 0 if β > 0 are instantiated later, and J is an indicator function defined as

$$ {J}(\beta,\dot{\beta}) = \left\{\begin{array}{lll} 1 \quad \text{if} \quad \beta > 0\quad \text{and}\quad \dot{\beta} > 0 \\ 0 \quad \text{otherwise}. \end{array}\right. $$

(4)

The fatigue damage is calculated by solving (2) and (3) using a numerical scheme. With this model, the evolution of back stress in (2) is independent of the damage. From (2), (3), and (4), the rates-of-change of the back stress tensor $\dot {\boldsymbol {\alpha }}$ and the damage $\dot {D}$ are governed by the indicator function $J(\beta ,\dot {\beta })$. During the loading state, β > 0 and $\dot {\beta } > 0$, the damage develops, i.e. $\dot {D} > 0$ (Fig. 1b). However, for the unloading state, β > 0 and $\dot {\beta } < 0$, there is no further development of damage, i.e. $\dot {D} = 0$ (Fig. 1c).

Fig. 1

Evolution of the endurance surface in a deviatoric plane: a initial state, b in loading state, $\dot {D} > 0$ and $\dot {\boldsymbol {\alpha }} \ne \boldsymbol {0}$ as β > 0 and $\dot {\beta } > 0$, and c in unloading state, and $\dot {D} = 0$ and $\dot {\boldsymbol {\alpha }} = \boldsymbol {0}$ as β > 0 and $\dot {\beta } < 0$

We use the endurance function from Ottosen et al. (2008), defined as

$$ {\beta}(\boldsymbol{\sigma}, \boldsymbol{\alpha}) = \frac{1}{S_{0}}\left[\bar{\sigma} + A\text{tr}(\boldsymbol{\sigma}) - S_{0}\right], $$

(5)

where S₀ > 0 is the endurance stress and A > 0 is a dimensionless parameter. The effective stress $\bar {\sigma }$ in (5) is defined as

$$ \bar{\sigma} = \left[\frac{3}{2}(\boldsymbol{s}-\boldsymbol{\alpha}):(\boldsymbol{s}-\boldsymbol{\alpha})\right]^{\frac{1}{2}}, $$

(6)

with s as the deviatoric stress tensor, i.e.,

$$ \boldsymbol{s} = \boldsymbol{\sigma} - \frac{1}{3}\text{tr}(\boldsymbol{\sigma})\boldsymbol{I}, $$

where I is the second-order identity tensor. The endurance surface defined in (5) evolves in different stress states, as illustrated in Fig. 1. At the initial time, i.e., for a pristine material before any loading is applied, we have a back stress α = 0. Here, the endurance surface lies at the center of the deviatoric plane (Fig. 1a). At the loading state, the back stress evolves, i.e., $\dot {\boldsymbol {\alpha }} \ne \boldsymbol {0}$. Because of this evolution, the surface also moves with α in its center (Fig. 1b). During unloading, we have $\dot {\boldsymbol {\alpha }} = \boldsymbol {0}$, which implies that the surface does not move (Fig. 1c).

The relation between the rates-of-change of the back stress $\dot {\boldsymbol {\alpha }}$ and the endurance function $\dot {\beta }$ is taken to be

$$ \dot{\boldsymbol{\alpha}} = J(\beta, \dot{\beta})C(\boldsymbol{s}-\boldsymbol{\alpha})\dot{\beta}, $$

(7)

meaning that G_α(σ,α) = C(s −α) in (2), where C > 0 is a dimensionless material parameter. Equation (7) ensures that α remains a deviatoric tensor (Ottosen et al. 2008) for all t. Substituting (6) into (5) and taking the derivative with respect to time gives

$$ \dot{\beta}(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha}, \dot{\boldsymbol{\alpha}}) = \frac{1}{S_{0}}\left[\frac{3}{2}\frac{(\boldsymbol{s} - \boldsymbol{\alpha}):(\dot{\boldsymbol{s}} - \dot{\boldsymbol{\alpha}})}{\bar{\sigma}} + A\text{tr}(\dot{\boldsymbol{\sigma}})\right]. $$

Using (7), this expression can be written as

$$ \dot{\beta}(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha}) = \frac{1}{S_{0} + J(\beta, \dot{\beta})C\bar{\sigma}}\left[\frac{3}{2}\frac{(\boldsymbol{s} - \boldsymbol{\alpha})}{\bar{\sigma}}:\dot{\boldsymbol{s}} + A\text{tr}(\dot{\boldsymbol{\sigma}})\right]. $$

(8)

Since $S_{0} + J(\beta , \dot {\beta })C\bar {\sigma } > 0$, the sign of $\dot {\beta }$ only depends on the factor in square parenthesis, where $\dot {\boldsymbol {\alpha }}$ does not occur. This implies that $J(\beta , \dot {\beta })$ from (4) can be written as $J(\boldsymbol {\sigma }, \dot {\boldsymbol {\sigma }}, \boldsymbol {\alpha })$. Thus, we conclude that $\dot {\beta }(\boldsymbol {\sigma }, \dot {\boldsymbol {\sigma }}, \boldsymbol {\alpha })$ is given in explicit form.

It remains to instantiate the damage evolution (3) by defining G_D(β,D). In previous publications, this has been done by selecting a particular expression for damage (Ottosen et al.2008, 2018; Holopainen et al. 2016). Here, we consider a whole family of functions on the form of G_D(β,D) = g(β)/f(D), with g(β) ≥ 0 and f(D) > 0 when β ≥ 0 and D ∈ [0,1), where the previous choices of G_D emerge as special cases. Now (3) takes the form

$$ f(D)\dot{D} = J(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha})g(\beta)\dot{\beta}. $$

(9)

Substituting $\hat {D} = F(D)$, where

$$F(D)={{\int}_{0}^{D}}f(D^{\prime})dD^{\prime},$$

into (9) gives

$$ \dot{\hat{D}} = J(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha})g(\beta)\dot{\beta}, $$

(10)

with $D = F^{-1}(\hat {D})$. The solution to the reformulated damage evolution in (10) also yields solutions to a range of evolution equations with different functions f(D). For instance, we consider the damage model from Holopainen et al. (2016), where $G_{D}(\beta ,D)={K}{(1-D)^{-\kappa }}\exp (L\beta )$ with K and L as material parameters and κ a model parameter, giving

$$ \dot{D} = J(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha})\frac{K}{(1-D)^{\kappa}}\exp(L\beta)\dot{\beta}. $$

This equation is rewritten into the form of (10) by setting f(D) = (1 − D)^κ and $g(\beta )=K\exp (L\beta )$, giving

$$ \dot{\hat{D}} = J(\boldsymbol{\sigma}, \dot{\boldsymbol{\sigma}}, \boldsymbol{\alpha})K\exp(L\beta)\dot{\beta}, $$

(11)

where $\hat {D} = F(D) =(\kappa + 1)^{-1}(1 - (1 - D)^{\kappa + 1})$. Critical failure thus occurs when $\hat {D} = F(D = 1) = (\kappa + 1)^{-1}$. The damage D is calculated by inverting the function F(D), i.e., $D = F^{-1}(\hat {D}) = 1 - (1 - (\kappa + 1)\hat {D})^{(1+\kappa )^{-1}}$. Understanding that there is seldom any reason to investigate more elaborate damage evolution equations than (10), we henceforth concentrate our investigation to the damage evolution (11). For simplicity, we use the notation $D = \hat {D}$ below.

The continuous-time fatigue problem is summarized in the box below.

3 Numerical implementation of the fatigue model

The fatigue problem is solved numerically by dividing the time domain [0,T] into a finite number of time steps of equal length Δt, i.e., t_i = iΔt with i = 0,1,2,...,N. The ordinary differential equations (ODEs) in (7) and (11) are approximated using a forward Euler scheme. The stresses at the time steps are σ_i = σ(iΔt), $\boldsymbol {s}\left |{~}_i\right . = \boldsymbol {s}(\boldsymbol {\sigma }_i)$ and α_i = α(iΔt), where $\left |{~}_i\right .$ represents function evaluation at time step i.

The increment of the endurance function in (8) during time step i is approximated as

$$ \begin{array}{@{}rcl@{}} {\Delta} \beta \left|{~}_i\right. & = &{\Delta} t \dot{\beta}\left( \boldsymbol{\sigma}_{i-1}, \frac{\boldsymbol{\sigma}_{i}-\boldsymbol{\sigma}_{i-1}}{\Delta t}, \boldsymbol{\alpha}_{i-1}\right)\\ &= &\frac{1}{S_0 + J\left|{~}_i\right.C\bar{\sigma}\left|{~}_{i-1}\right.}\left[\frac{3}{2}\frac{(\boldsymbol{s}\left|{~}_{i-1}\right. - \boldsymbol{\alpha}_{i-1})}{\bar{\sigma}\left|{~}_{i-1}\right.}:{\Delta}{\boldsymbol{s}}\left|{~}_i\right.\right.\\ &&\left.+\vphantom{\frac{(\boldsymbol{s}\left|{~}_{i-1}\right. - \boldsymbol{\alpha}_{i-1})}{\bar{\sigma}\left|{~}_{i-1}\right.}} A\boldsymbol{I}:{\Delta}{\boldsymbol{\sigma}}\left|{~}_i\right.\right], \end{array} $$

(12)

with stress increments ${\Delta } \boldsymbol {s}\left |{~}_i\right . = \boldsymbol {s}\left |{~}_i\right . - \boldsymbol {s}\left |{~}_{i-1}\right .$ and ${\Delta } \boldsymbol {\sigma }\left |{~}_i\right . = \boldsymbol {\sigma }_{i} - \boldsymbol {\sigma }_{i-1}$, indicator function $\ J\left |{~}_i\right . = J\left (\boldsymbol {\sigma }_{i-1}, \frac {\boldsymbol {\sigma }_{i}-\boldsymbol {\sigma }_{i-1}}{\Delta t}, \boldsymbol {\alpha }_{i-1}\right )$, and the effective stress $\bar {\sigma }\left |{~}_i\right . = \bar {\sigma }({\boldsymbol {\sigma }_{i}}, \boldsymbol {\alpha }_{i})$. The discrete versions of (7) and (11) become

$$ \boldsymbol{\alpha}_{i} - \boldsymbol{\alpha}_{i-1} = J\left|{~}_i\right.C(\boldsymbol{s}\left|{~}_{i-1}\right. - \boldsymbol{\alpha}_{i-1}){\Delta}{\beta}\left|{~}_i\right. $$

(13)

$$ D_{i} - {D}_{i-1} = J\left|{~}_i\right.{K}\exp(L\beta\left|{~}_{i-1}\right.){\Delta}{\beta}\left|{~}_i\right., $$

(14)

where $\beta \left |{~}_i\right . = \beta (\boldsymbol {\sigma }_i, \boldsymbol {\alpha }_i)$.

The numerical implementation of the model is summarized in the box below.

Note that in this time discretization, we have replaced the time derivatives of the stress tensor by an approximate finite difference expression. However, in many applications, even treated in this paper, such time derivatives will be explicitly known. The discretization could then be simplified, but to keep the method and presentation general, we have not explicitly treated this as a special case.

4 Optimization problem formulations

We obtain a spatially discretized model by using the FE method. The design variables collected in x are scale factors of elemental properties without any direct physical interpretation. Each design variable is associated with a single FE. In TO, one strives for the so-called black-and-white designs, where ideally the design variables only take the values 0 or 1. Such designs are promoted by introducing penalization of intermediate design variable values (Bendsoe and Sigmund 2004; Christensen and Klarbring 2009). A design variable filter (Bruns and Tortorelli 2001) is then applied to avoid mesh dependency and checkerboard patterns. This filter gives a relation between the design variables x and the variables $\boldsymbol {\rho } = [\rho _1, \rho _2, ..., \rho _{n_e}]^{\text {T}}$, with n_e as the total number of elements. The variables ρ = ρ(x) are called physical design variables as they are used to define the structural stiffness and the mass. The filtered variable for element e is given by

$$ \rho_e(\boldsymbol{x})=\frac{\overset{n_e}{\underset{k=1}{\sum}}w_{k,e}x_k}{\overset{n_e}{\underset{k=1}{\sum}}w_{k,e}}, $$

(15)

where the weight w_k,e is defined as

$$ w_{k,e} = \max\{0, r_0 - \|\boldsymbol{x}_k - \boldsymbol{x}_e\|\}, $$

where ∥x_k −x_e∥ is the Euclidean distance between the centroids of elements e and k, and r₀ is the filter radius. In order to avoid singular stiffness matrices, a small lower bound 𝜖 > 0 is used for the design variables, i.e., x_e ≥ 𝜖. It then follows from (15) that ρ_e(x) ≥ 𝜖.

Discretizing (1) in space using the FE method gives the equations:

$$ \boldsymbol{K}(\boldsymbol{\rho}(\boldsymbol{x}))\boldsymbol{u}(t) = \boldsymbol{F}(t), \quad \forall\ t\in[0,T], $$

with K(ρ(x)) as the global stiffness matrix, u(t) as the displacement vector, and $\boldsymbol {F}(t) = \overset {n_e}{\underset {e=1}{\boldsymbol {\bigwedge }}}\int \limits _{{\Gamma }_{e}\cap {\Gamma }_{t}}\boldsymbol {N}_e^{\text {T}}\boldsymbol {t}(t)ds$, in which $\boldsymbol {\bigwedge }$ is an assembly operator, N_e is the shape function matrix for element e, and Γ_e is the boundary of element e. Therefore, at each time step t_i = iΔt, we have

$$ \boldsymbol{K}(\boldsymbol{\rho}(\boldsymbol{x}))\boldsymbol{u}_i = \boldsymbol{F}_i, $$

(16)

where F_i = F(t_i), and the solution for a given i is denoted by u_i(x).

To promote black-and-white designs, the SIMP approach is used to penalize the global stiffness matrix, i.e.,

$$ \boldsymbol{K}(\boldsymbol{\rho}(\boldsymbol{x})) = \overset{n_e}{\underset{e=1}{\boldsymbol{\bigwedge}}}(\rho_e(\boldsymbol{x}))^q\boldsymbol{K}_e, $$

(17)

where K_e are elemental stiffness matrices and q > 1 is a penalization parameter.

For a given u_i(x), the stress vector at an integration point is calculated as

$$ \hat{\boldsymbol{\sigma}}_i(\boldsymbol{x}) = \hat{\boldsymbol{\sigma}}_i(\boldsymbol{x}, \boldsymbol{u}_i(\boldsymbol{x})) = \boldsymbol{E}\boldsymbol{B}\boldsymbol{u}_i(\boldsymbol{x}), $$

(18)

where E is the constitutive tensor in Voigt form and B is the strain displacement matrix. The stress used to compute the fatigue response is given by

$$ \boldsymbol{\sigma}_i(\boldsymbol{x}) = \left( \frac{\rho_e(\boldsymbol{x}) - \epsilon}{1 - \epsilon}\right)^{r}\hat{\boldsymbol{\sigma}}_i(\boldsymbol{x}), $$

(19)

where r < q is a parameter introduced to avoid the stress singularity phenomenon, (Bruggi 2008; Holmberg et al. 2013). The penalization factor gives exactly zero stress in voids, where ρ_e(x) = 𝜖. Hence, no artificial damage is developed in such regions. It also gives $\boldsymbol {\sigma }_i = \hat {\boldsymbol {\sigma }}_i$ when ρ_e(x) = 1 as desired. The discretized evolution (13) and (14) are solved by using these penalized stresses to estimate the fatigue damage.

We consider two optimization problem formulations: The first formulation is to minimize the mass of the structure, and the second formulation is to maximize structural stiffness. The stiffness at each time step is quantified inversely in the form of compliance, i.e., Fi Tu_i(x). A possible objective function or a constraint function in the TO problem would then be

$$ \max_{i = 1, 2, ..., N}\boldsymbol{F}_i^\text{T}\boldsymbol{u}_i(\boldsymbol{x}). $$

However, for simplicity, we only consider the compliance for one load F, which represents a static load case of interest. These objective functions are combined with a fatigue constraint. Assuming one integration point per element, for each element e we calculate the total accumulated damage D_N,e at the final time step T = t_N = NΔt for a given load history. The fatigue constraints can be defined as

$$ D_{N,e}(\boldsymbol{x}) \le \bar{{D}}_e,\quad e=1,2, ...,n_e, $$

(20)

where ${\bar {{D}}_e}$ is the maximum allowable damage for element e.

A key issue with (20) is that often a large number of fatigue constraints needs to be considered. Thus, the effort in solving this optimization problem is high. To minimize this effort, the n_e fatigue constraints are replaced by a single bound:

$$ \underset{e = 1, 2, ..., n_e}{\max}D_{N,e}(\boldsymbol{x}) \le \bar{D}, $$

(21)

with $\bar {D}$ as the maximum allowable damage. Since the max-function is non-differentiable, (21) is approximated using a smooth aggregation function (Kennedy and Hicken 2015), here the p-norm:

$$ D^{{PN}}(\boldsymbol{x}) = \left[\sum\limits_{e=1}^{n_e}(D_{N,e}(\boldsymbol{x}))^P \right]^{\frac{1}{P}} $$

(22)

with P > 1, where D^PN is the approximated maximum damage. It holds that $D^{PN}(\boldsymbol {x}) \to \max \limits _e D_{N,e}(\boldsymbol {x})$ when $P \to \infty$, but too large values for P can cause numerical problems.

The mass minimization problem is formulated using (22), as

$$ (\mathbb{P}_1) \left\{\begin{array}{ll} \underset{\boldsymbol{x}}{\min}\underset{e=1}{\overset{n_e}{\sum}}m_e\rho_e(\boldsymbol{x})\\ \text{s.t.}\left\{\begin{array}{ll} \boldsymbol{F}^\text{T}\boldsymbol{u}(\boldsymbol{x}) \le \bar{C}, \\ D^{PN}(\boldsymbol{x}) \le \bar{{D}} \\ \epsilon \leq x_e \leq 1,\ e=1,2, ...,n_e \end{array}\right. \end{array}\right. $$

where m_e is the elemental mass and $\bar {C}$ is the maximum structural compliance. The abbreviation s.t. stands for “subject to.” The compliance constraint is included to avoid all-void solutions, see remark below.

The stiffness-based TO problem is written as

$$ (\mathbb{P}_2) \left\{\begin{array}{ll} \underset{\boldsymbol{x}}{\min}\ \boldsymbol{F}^T\boldsymbol{u}(\boldsymbol{x})\\ \text{s.t.}\left\{\begin{array}{ll} \underset{e=1}{\overset{n_e}{\sum}}m_e\rho_e(\boldsymbol{x})\leq \bar{M}\\ D^{PN}(\boldsymbol{x}) \le \bar{{D}}, \\ \epsilon \leq x_e \leq 1,\ e=1,2, ...,n_e \end{array}\right. \end{array}\right. $$

where $\bar {M}$ is the maximum allowable mass.

Remark 1

The problem related to ($\mathbb {P}_1$) of minimizing mass subject to a fatigue (or stress) constraint, without a constraint on the compliance, has been previously considered in the literature (Holmberg et al. 2013, 2014; Jeong et al. 2018; Oest and Lund 2017a; Zhang et al. 2019). As shown in Appendix A, also for our fatigue model, gradient-based solution methods frequently show convergence to realistic structures without inclusion of a compliance constraint. However, note that the globally optimal solution to $(\mathbb {P}_1)$ without compliance constraint is actually x_e = 𝜖 for all e. This is seen by noting that x_e = 𝜖 for all e gives zero fatigue, because of the scaling in (19), while obviously minimizing the mass. Therefore, while the solution shown in Appendix looks plausible from an engineering point of view, it actually represents (at best) a local optimum. It makes intuitive sense that the optimal solution is a domain-spanning void; if one’s only desire is to minimize weight and avoid fatigue, then the best solution is to not create any structure in the first place. By including the compliance constraint in $(\mathbb {P}_1)$, the solution x_e = 𝜖 for all e is no longer feasible (provided $\overline {C}$ is small enough). By choosing $\bar {C}$ such that the compliance constraint is not active at the solution, we can solve the problem of minimizing mass subject to a fatigue constraint without running the risk of obtaining a solution which is degenerate from an engineering perspective.

5 Sensitivity analysis

Sensitivity analyses deal with finding derivatives of the objective function and constraints with respect to the design variables x. This forms the core of any gradient-based optimization method. We use adjoint sensitivity analysis for computational efficiency. Similar to elasto-plastic models, the predicted damage has history dependence, which is reflected in the sensitivity analysis (Panagiotis et al. 1994). The expression for the sensitivity of the compliance in both the TO problems is well known (Christensen and Klarbring 2009), while the sensitivity of the fatigue constraint is elaborated upon in the following.

5.1 Aggregation function sensitivity

The derivative of (22) with respect to the design variable x_j is

$$ \begin{array}{@{}rcl@{}} \frac{d D^{{PN}}(\boldsymbol{x})}{d {x}_j} &= &\frac{1}{P}\left[\sum\limits_{e=1}^{n_e}({D}_{N,e}(\boldsymbol{x}))^P\right]^{(\frac{1}{P}-1)} \cdot\\ &&\left[\sum\limits_{e=1}^{n_e}P({D}_{N,e}(\boldsymbol{x}))^{(P-1)}\frac{d{D}_{N,e}(\boldsymbol{x})}{d{x}_j}\right], \end{array} $$

(23)

where $\frac {d {D}_{N,e}(\boldsymbol {x})}{d {x}_j}$ is calculated using adjoint analysis as described below.

5.2 Adjoint sensitivity analysis

For brevity, a new state variable v_i that comprises the back stress and damage is introduced for each time step, i.e.,

$$ \begin{array}{@{}rcl@{}} &&\boldsymbol{v}_i = \left[\boldsymbol{v}_{i,1}, \boldsymbol{v}_{i,2}, ..., \boldsymbol{v}_{i,n_e}\right]^{\text{T}}, \quad i = 0, 1, 2, ..., N,\\ &&\boldsymbol{v}_{i,e} = \left[\begin{array}{c} \boldsymbol{\alpha}_{i,e} \\ D_{i,e} \end{array}\right]. \end{array} $$

(24)

A general system response, G_e, at the final time step t_N = NΔt can be expressed as a function of the design variables x and the field variables u_N and v_N, i.e.,

$$ G_e(\boldsymbol{x}) = G_e(\boldsymbol{x}, \boldsymbol{u}_N(\boldsymbol{x}), \boldsymbol{v}_N(\boldsymbol{x})). $$

(25)

The sensitivity of G_e(x) with respect to a design variable x_j is

$$ \frac{d G_e(\boldsymbol{x})}{d x_j} = \frac{\partial G_e}{\partial x_j} + \frac{\partial G_e}{\partial \boldsymbol{u}_N}^{\text{T}}\frac{d \boldsymbol{u}_N}{d x_j} + \frac{\partial G_e}{\partial \boldsymbol{v}_N}^{\text{T}}\frac{d \boldsymbol{v}_N}{d x_j}. $$

(26)

The residuals, $\boldsymbol {R}\left |{~}_i\right .$ of the equilibrium (16) and $\boldsymbol {H}\left |{~}_i\right .$ of the evolution (13) and (14) are expressed as

$$ \begin{array}{@{}rcl@{}} &&{\boldsymbol{R}}(\boldsymbol{x})\left|{~}_i\right. = \boldsymbol{R}(\boldsymbol{x},{\boldsymbol{u}_i}(\boldsymbol{x})) = \boldsymbol{0}, \end{array} $$

(27)

$$ \begin{array}{@{}rcl@{}} &&{\boldsymbol{H}}(\boldsymbol{x})\left|{~}_i\right. = \boldsymbol{H}\left( \boldsymbol{x},{\boldsymbol{u}_i}(\boldsymbol{x}), {\boldsymbol{u}_{i-1}}(\boldsymbol{x}), \boldsymbol{v}_i(\boldsymbol{x}), \boldsymbol{v}_{i-1}(\boldsymbol{x})\right) = \boldsymbol{0},\\ \end{array} $$

(28)

for i = 1,2,...,N. Taking the derivative of $\boldsymbol {R}(\boldsymbol {x})\left |{~}_i\right .$ with respect to design variable x_j, we get

$$ {\frac{d\boldsymbol{R}(\boldsymbol{x})}{d x_j}}\left|{~}_i\right. = \partial_1\boldsymbol{R}\left|{~}_i\right. + \partial_2\boldsymbol{R}\left|{~}_i\right.\frac{d\boldsymbol{u}_i}{dx_j}, $$

(29)

where, ∂_a denotes partial differentiation with respect to the a th argument. Similarly, the derivative of $\boldsymbol {H}(\boldsymbol {x})\left |{~}_i\right .$ with respect to design variable x_j is

$$ \begin{array}{@{}rcl@{}} \frac{d\boldsymbol{H}(\boldsymbol{x})}{d x_j}\left|{~}_i\right. = \partial_1\boldsymbol{H}\left|{~}_i\right. +\partial_2\boldsymbol{H}\left|{~}_i\right.\frac{d\boldsymbol{u}_i}{dx_j} + \partial_3\boldsymbol{H}\left|{~}_i\right.\frac{d\boldsymbol{u}_{i-1}}{dx_j}\\ + \partial_4\boldsymbol{H}\left|{~}_i\right.\frac{d\boldsymbol{v}_i}{dx_j} + \partial_5\boldsymbol{H}\left|{~}_i\right.\frac{d\boldsymbol{v}_{i-1}}{dx_j}. \end{array} $$

(30)

As any system response should preserve structural residuum, (27) and (28), we multiply these equations by Lagrange multipliers λ_i and γ_i, referred to as adjoint variables, to obtain the following augmented version of (25):

$$ G_e(\boldsymbol{x}) = G_e(\boldsymbol{x}) - \sum\limits_{i = 1}^{N}\boldsymbol{\lambda}_i\boldsymbol{R}(\boldsymbol{x})\left|{~}_i\right. - \sum\limits_{i = 1}^{N}\boldsymbol{\gamma}_i\boldsymbol{H}(\boldsymbol{x})\left|{~}_i\right.. $$

(31)

Substituting (26), (29), and (30) into the derivative of (31) with respect to design variable x_j, we get

$$ \begin{array}{@{}rcl@{}} \frac{d G_e(\boldsymbol{x})}{d x_j} &= &\frac{\partial G_e}{\partial x_j} + \frac{\partial G_e}{\partial \boldsymbol{u}_N}^{\text{T}}\frac{d \boldsymbol{u}_N}{d x_j} + \frac{\partial G_e}{\partial \boldsymbol{v}_N}^{\text{T}}\frac{d\boldsymbol{v}_N}{d x_j}\\ &- & \sum\limits_{i=1}^{N}\boldsymbol{\lambda}_i^{\text{T}}\left[\partial_1\boldsymbol{R}\left|{~}_i\right. + \partial_2\boldsymbol{R}\left|{~}_i\right.\frac{d\boldsymbol{u}_i}{d x_j}\right]\\ &&- \sum\limits_{i=1}^{N}\boldsymbol{\gamma}_i^{\text{T}} \left[\partial_1\boldsymbol{H}\left|{~}_i\right. + \partial_2\boldsymbol{H}\left|{~}_i\right.\frac{d\boldsymbol{u}_i}{d x_j} + \partial_3\boldsymbol{H}\left|{~}_i\right.\frac{d \boldsymbol{u}_{i-1}}{d x_j} \right.\\ &&+ \left.\partial_4\boldsymbol{H}\left|{~}_i\right.\frac{d \boldsymbol{v}_i}{d x_j} + \partial_5\boldsymbol{H}\left|{~}_i\right.\frac{d \boldsymbol{v}_{i-1}}{d x_j}\right]. \end{array} $$

Rearranging the terms, we get

$$ \begin{array}{@{}rcl@{}} \frac{d G_e(\boldsymbol{x})}{d x_j} &= &\frac{\partial G_e}{\partial x_j} - \sum\limits_{i=1}^{N}\boldsymbol{\lambda}_i^{\text{T}}\partial_1\boldsymbol{R}\left|{~}_i\right. - \sum\limits_{i=1}^{N}\boldsymbol{\gamma}_i^{\text{T}} \partial_1\boldsymbol{H}\left|{~}_i\right. \\ &&- \underset{=\boldsymbol{0}}{ \underbrace{\left[\boldsymbol{\lambda}_N^{\text{T}}\partial_2\boldsymbol{R}\left|{~}_{N}\right. + \boldsymbol{\gamma}_N^{\text{T}}\partial_2\boldsymbol{H}\left|{~}_{N}\right. - \frac{\partial G_e}{\partial \boldsymbol{u}_N}^{\text{T}}\right]}}\frac{d \boldsymbol{u}_N}{d x_j} \\ &&- \underset{=\boldsymbol{0}}{\underbrace{ \left[\boldsymbol{\gamma}_N^{\text{T}}\partial_4\boldsymbol{H}\left|{~}_{N}\right. - \frac{\partial G_e}{\partial \boldsymbol{v}_N}^{\text{T}}\right]}}\frac{d\boldsymbol{v}_N}{d x_j}\\ &&- {\sum}_{i = 2}^{N}\underset{=\boldsymbol{0}}{\underbrace{\left[\boldsymbol{\lambda}_{i-1}^{\text{T}}\partial_2\boldsymbol{R}\left|{~}_{i-1}\right. + \boldsymbol{\gamma}_{i-1}^{\text{T}}\partial_2\boldsymbol{H}\left|{~}_{i-1}\right. + \boldsymbol{\gamma}_{i}^{\text{T}}\partial_3\boldsymbol{H}\left|{~}_i\right.\right]}}\frac{d\boldsymbol{u}_{i-1}}{d x_j}\\ &&- \sum\limits_{i = 2}^{N}\underset{=\boldsymbol{0}}{\underbrace{\left[\boldsymbol{\gamma}_{i-1}^{\text{T}}\partial_4\boldsymbol{H}\left|{~}_{i-1}\right. + \boldsymbol{\gamma}_{i}^{\text{T}}\partial_5\boldsymbol{H}\left|{~}_i\right.\right]}}\frac{d\boldsymbol{v}_{i-1}}{d x_j} \\ &&- \underset{=\boldsymbol{0}}{\underbrace{\boldsymbol{\gamma}_{1}^{\text{T}}\partial_3\boldsymbol{H}\left|{~}_{1}\right.}}\frac{d\boldsymbol{u}_{0}}{d x_j} - \underset{=\boldsymbol{0}}{\underbrace{\boldsymbol{\gamma}_{1}^{\text{T}}\partial_5\boldsymbol{H}\left|{~}_{1}\right.}}\frac{d\boldsymbol{v}_{0}}{d x_j}, \end{array} $$

where the zero terms are obtained by requiring that the arbitrary adjoint variables satisfy the following discrete terminal value problems:

$$ \left[\begin{array}{cl} {\partial_2\boldsymbol{R}}\left|{~}_{N}\right. & {\partial_2\boldsymbol{H}}\left|{~}_{N}\right.^\text{T} \\ \\ \boldsymbol{0} & {\partial_4\boldsymbol{H}}\left|{~}_{N}\right.^\text{T} \end{array}\right] \left[\begin{array}{l} \boldsymbol{\lambda}_N\\ \\ \boldsymbol{\gamma}_N \end{array}\right] = \left[\begin{array}{ll} \frac{\partial G_e}{\partial \boldsymbol{u}_N} \\ \\ \frac{\partial G_e}{\partial \boldsymbol{v}_N} \end{array}\right], $$

(32)

$$ \left[\begin{array}{cll} {\partial_2\boldsymbol{R}}\left|{~}_{i-1}\right. & {\partial_2\boldsymbol{H}}\left|{~}_{i-1}\right.^\text{T} \\ \\ \boldsymbol{0} & {\partial_4\boldsymbol{H}}\left|{~}_{i-1}\right.^\text{T} \end{array}\right] \left[\begin{array}{ll} \boldsymbol{\lambda}_{i-1}\\ \\ \boldsymbol{\gamma}_{i-1} \end{array}\right] = - \left[\begin{array}{ll} {\partial_3\boldsymbol{H}}\left|{~}_i\right.^\text{T} \\ \\ {\partial_5\boldsymbol{H}}\left|{~}_i\right.^\text{T} \end{array}\right]\boldsymbol{\gamma}_i, $$

(33)

where i = N,N − 1,...,2.

The final sensitivity expression is

$$ \begin{array}{@{}rcl@{}} \frac{d{G}_e(\boldsymbol{x})}{d x_j} &= &\frac{\partial G_e}{\partial x_j} - \sum\limits_{i=1}^{N}\boldsymbol{\lambda}_i^{\text{T}}{\partial_1 \boldsymbol{R}}\left|{~}_i\right. - \sum\limits_{i=1}^{N}\boldsymbol{\gamma}_i^{\text{T}}{\partial_1 \boldsymbol{H}}\left|{~}_i\right. \end{array} $$

$$ \begin{array}{@{}rcl@{}} &= & \frac{\partial G_e}{\partial x_j} - \sum\limits_{i=1}^{N}\boldsymbol{\lambda}_i^{\text{T}}\frac{\partial \boldsymbol{R}}{\partial x_j}\left|{~}_i\right. - \sum\limits_{i=1}^{N}\boldsymbol{\gamma}_i^{\text{T}}\frac{\partial \boldsymbol{H}}{\partial x_j}\left|{~}_i\right.. \end{array} $$

(34)

5.3 Fatigue sensitivity

The general function G_e is now specialized to damage, i.e.,

$$ G_e(\boldsymbol{x}, \boldsymbol{u}_N(\boldsymbol{x}), \boldsymbol{v}_N(\boldsymbol{x})) = D_{N,e}(\boldsymbol{x}). $$

(35)

The partial terms in the sensitivity expression (26) is

$$ \begin{array}{@{}rcl@{}} &&\frac{\partial G_e}{\partial x_j} = 0,\ \frac{\partial G_e}{\partial \boldsymbol{u}_N} = \boldsymbol{0},\ \frac{\partial G_e}{\partial \boldsymbol{v}_N} = \left[\boldsymbol{0}, ..., \frac{\partial G_e}{\partial \boldsymbol{v}_{N,e}}, ..., \boldsymbol{0}\right]^{\text{T}},\\ &&\frac{\partial G_e}{\partial \boldsymbol{v}_{N,e}} = \left[\begin{array}{c} \boldsymbol{0} \\ 1 \end{array}\right]. \end{array} $$

(36)

The residual (27) is expressed as

$$ \boldsymbol{R}(\boldsymbol{x})\left|{~}_i\right. = \boldsymbol{R}(\boldsymbol{x}, \boldsymbol{u}_i(\boldsymbol{x})) = \boldsymbol{K}(\boldsymbol{\rho}(\boldsymbol{x}))\boldsymbol{u}_i(\boldsymbol{x}) - \boldsymbol{F}_i. $$

(37)

Recalling (13) and (14), we can write the residual in (28) as

$$ {\boldsymbol{H}}(\boldsymbol{x})\left|{~}_i\right. = \left[\boldsymbol{H}(\boldsymbol{x})\left|{~}_{i,1}\right., \boldsymbol{H}(\boldsymbol{x})\left|{~}_{i,2}\right., ..., \boldsymbol{H}(\boldsymbol{x})\left|{~}_{i,n_{e}}\right.\right]^{\text{T}}, $$

(38)

where $\boldsymbol {H}(\boldsymbol {x})\left |{~}_{i,e}\right .$ is the residual restricted to element e defined as

$$ \boldsymbol{H}(\boldsymbol{x})\left|{~}_{i,e}\right. \!\!{=}\! \left[\!\begin{array}{c} \boldsymbol{\alpha}_{i-1,e} {+} J\left|{~}_{i,e}\right.C(\boldsymbol{s}\left|{~}_{i{-}1,e}\right. {-} \boldsymbol{\alpha}_{i-1,e}){\Delta} \beta\left|{~}_{i,e}\right. {-} \boldsymbol{\alpha}_{i,e} \\ D_{i-1,e} {+} J\left|{~}_{i,e}\right.{K}\exp(L\beta\left|{~}_{i{-}1,e}\right.){\Delta} \beta\left|{~}_{i,e}\right. {-} D_{i,e} \end{array}\!\!\right]. $$

(39)

With help of (36), (37), (38), and (39), the adjoint variables, λ_i and γ_i are solved using (32) and (33).

The final sensitivity expression, (34), specialized for fatigue is

$$ \frac{d{D}_{N,e}(\boldsymbol{x})}{d x_j} = - \sum\limits_{i=1}^{N}\boldsymbol{\lambda}_i^{\text{T}}\frac{\partial \boldsymbol{R}}{\partial x_j}\left|{~}_i\right. - \sum\limits_{i=1}^{N}\boldsymbol{\gamma}_i^{\text{T}}\frac{\partial \boldsymbol{H}}{\partial x_j}\left|{~}_i\right.. $$

(40)

These fatigue sensitivities are verified against sensitivities calculated using forward finite difference for a plate with a hole geometry in Appendix A.

6 Numerical examples

The proposed method is implemented in the in-house finite element program TRINITAS (Torstenfelt 2012). We consider an isotropic material, namely AISI-SAE 4340 alloy steel with Young’s modulus 210 GPa and Poisson’s ratio 0.33. As mentioned in Section 2, the damage D increases from D = 0 to D = D_crit = F(1) and using these conditions, the fatigue model parameters are calibrated against the Wöhler curves for different mean stresses following the fitting procedure shown in Ottosen et al. (2008). The fitted material properties for AISI-SAE 4340 alloy steel are as follows: S₀ = 490 MPa, A = 0.225, C = 1.25, K = 2.65 ⋅ 10^− 5 and L = 14.5.

The optimization problems ($\mathbb {P}_{1}$) and ($\mathbb {P}_{2}$) are solved by the method of moving asymptotes (MMA) (Svanberg 1987) on a desktop computer with an Intel(R) Core(TM) i7-7500U CPU @ 2.70 GHz with 24 GB of RAM. Several examples are tested, all discretized by bi-linear quadrilateral plane stress elements having a thickness of 1 mm. We take the values of the penalization parameters as q = 3 in (17) and r = 0.5 in (19). The initial design variables are taken as x_e = 0.7 and the lower bound of the design variables as 𝜖 = 0.001. The problems are solved with the exponent of the p-norm as P = 12 along with the filter radius r₀ as 1.5 times the element size. The stopping criterion for the optimization is given by

$$ \left|\frac{f_{k+1}^{0} - {f_{k}^{0}}}{f_{k+1}^{0}}\right| < \text{tol}, $$

where ${f_{k}^{0}}$ is the objective value at the k th iteration. The tolerance is set to tol = 0.1E − 5.

6.1 L-shaped beam with periodic load history

For the first example, we consider an L-shaped beam with a proportional periodic load history. The dimensions used for this geometry are shown in Fig. 2, where L₁ = 100 mm. The design domain is discretized by 3600 elements with the top edge of the beam clamped. Two load cases are created: the first load case includes a static load Q₁ = 1500 N, distributed over 4 nodes, applied for compliance; the second load case consists of a periodic load of 10 cycles, i.e., $\boldsymbol {\sigma }(t) = \boldsymbol {\sigma }(Q_{1})\sin \limits (2\pi t)$ with t = 0,0.05,...,10, for fatigue estimation. The stress σ(Q₁) for the load Q₁ is calculated using (18) and (19).

Fig. 2

Geometry of the L-shaped beam

Since the applied load history has a constant amplitude with a zero mean stress, and also the estimated damage is a function of stresses, we expect a similar topology when solving the optimization problem with fatigue constraints as when solving with stress constraints. To demonstrate this, we compare the solution of the mass minimization TO problem with fatigue constraint $(\mathbb {P}_{1})$ to the solution of the stress-constrained TO problem, as treated in Holmberg et al. (2013).

For the problem $(\mathbb {P}_{1})$, we set the maximum fatigue damage $\bar {{D}} = 0.4$ along with compliance bound $\bar {C} = 0.4\text {E}-2$ Nmm. The maximum stress obtained after solving this problem is used as the stress limit in the stress-constrained problem.

After solving the fatigue-constrained problem $(\mathbb {P}_{1})$ and the stress-constrained problem, the optimized results are shown in Table 1. Here, the optimized designs of both problems are similar. The profiles obtained, particularly at the re-entrant corner, have a low stress concentration. However, there is a significant difference in the damage plots. In the stress-constrained TO problem, the maximum damage is localized at the re-entrant corner, whereas in the fatigue-constrained problem, we have a more uniform distribution of fatigue damage. The white line, which overlaps the damage plots, indicates the outline of the density plots.

Table 1 Fatigue constraint vs stress constraint: mass minimization problem with fatigue constraint $(\mathbb {P}_{1})$ and stress constraint

With the computed results from problem $(\mathbb {P}_{1})$, we set up the compliance problem $(\mathbb {P}_{2})$. The final mass that is obtained from $(\mathbb {P}_{1})$ is set as a mass constraint in $(\mathbb {P}_{2})$. The optimized results of these problems are shown in Table 2. The convergence behavior of the objective function and the fatigue constraint is seen in this table along with their final values after 586 and 474 iterations. The computation time required to solve these problems is around 6 h and 8 h, respectively. Most time is spent in the sensitivity analysis (approx. 80% of the total computation time), which depend, not only on the total number of elements but also on the size of the time steps. For problem $(\mathbb {P}_{1})$, we notice two peaks in the fatigue convergence plot. At these peaks, the compliance constraint becomes active. However, at the other regions, this constraint remains inactive and the convergence is eventually smooth.

Table 2 Optimization results of the L-shaped beam with periodic load history

6.2 L-shaped beam with non-periodic load history

For the next example, we again use the L-shaped beam shown in Fig. 2. However, for the second load case, a non-periodic load history, σ(t) = σ(Q₁)S_f(t), t = 0,0.1,...,100, is used for fatigue estimation. Here S_f(t) is a pseudorandom function depicted in Fig. 3.

For problem $(\mathbb {P}_{1})$, the fatigue and compliance bounds are set to $\bar {D} = 0.5$ and $\bar {C} = 0.40\text {E}-2$ Nmm, respectively. Similar to the previous example, the mass obtained from problem $(\mathbb {P}_{1})$ is set as a mass limit in problem $(\mathbb {P}_{2})$.

Fig. 3

Non-periodic load history

The optimized results are shown in Table 3. The evolution of the objective function and the fatigue constraint for both problems are also seen along with the final objective and constraint values after 700 iterations. The computation time to solve these problems are around 10 h and 13 h, respectively. We notice that the profiles of both the optimized models have a smooth radius at the re-entrant corner, thereby reducing high stress concentrations and thus prolonging life. A final damage plot of $(\mathbb {P}_{1})$ reveals that damage is distributed across the structure, and that no damage is accumulated in the voids (see Fig. 4).

Table 3 Optimization results of the L-shaped beam with non-periodic load history

Fig. 4

Damage D_N,e from $(\mathbb {P}_{1})$ with Mass = 21 × 10^− 3 kg and D^PN = 0.501. The white line represent the contour of the density plot in Table 3

6.3 MBB beam with out-of-phase load history

For this example, we take an MBB beam discretized by 4800 elements and subject to a out-of-phase biaxial loading. To account for such a load history, we create two load cases as shown in Fig. 5. The first load case consists of two static loads F_y = 1500N and F_x = 1500N, which are used for compliance calculation. The second load case is used for fatigue estimation and consists of load histories defined as $F_{y}(t) = F_{y}\sin \limits (2\pi t)$ and $F_{x}(t) = F_{x}\sin \limits (2\pi t - \phi )$ with t = 0,0.05,...,10 and phase angle ϕ.

Fig. 5

Loading conditions of MBB beam considering out of phase load history

Problem $(\mathbb {P}_{2})$ is solved for three different phase angles ϕ = 0^∘,45^∘, and 90^∘ and fatigue bounds $\bar {{D}} = 0.35, 0.35$, and 0.50, respectively. The reason for setting a higher fatigue bound for ϕ = 90^∘ is that, with out-of-phase loading history, the model predicts that the fatigue strength increases, i.e., fatigue damage decreases, with the phase difference; thereafter, a decrease of the fatigue limit is predicted, i.e., fatigue damage increases. This tendency is in accordance with experimental data (Liu and Zenner 2003).

Table 4 shows the optimized MBB beam for different phase angles along with the evolution of the objective function and fatigue constraint. Different compliance values are obtained for each of the optimized models and also different designs are obtained in trying to adapt for the phase change in the loading histories.

Table 4 Optimization results of MBB beam with different phase angles for the problem $(\mathbb {P}_{2})$

7 Conclusion and outlook

A new gradient-based TO formulation with fatigue constraint based on a continuous-time approach for fatigue calculation was proposed. As the fatigue damage is integrated for the whole stress history, cycle-counting techniques like rainflow counting were not used. The presented model can handle a general load history, that also includes non-proportional loads.

The fatigue sensitivities were derived using an adjoint method. Since this approach has history dependence, the adjoint variables are obtained by solving a discrete terminal value problem. The validity of the fatigue sensitivities derived by the adjoint method were verified by comparing against a finite difference calculation. The proposed method was tested on several numerical examples, namely, the L-shaped beam with periodic and non-periodic loads, and the MBB beam geometry with out-of-phase loading. Although we have numerically solved only 2-D models, the theoretical presentation is not restricted to these cases. However, the high computational cost we experience makes it presently difficult to treat 3-D models in practice. An important extension of the work is, therefore, to develop acceleration techniques that can improve the overall performance and shorten the computational time. One possibility is to discretize the time domain using a higher order scheme, which could enable us to use larger time steps. However the sensitivity analysis becomes more elaborate, increasing the number of floating-point operations needed for each time step. Thus, it is difficult to make an a priori prediction of the relative efficiency of different order implementations.

8 Replication of results

To reproduce the above optimized results, a first step is to implement the fatigue model following the box in Section 3. The optimization problems $(\mathbb {P}_{1})$ and $(\mathbb {P}_{2})$ can be solved using the MMA method from Svanberg (1987). The sensitivities are derived in Section 5 and the verification study is shown in Appendix . Relevant parameters are given in Section 6.

Appendices

Appendix A: Verification of fatigue sensitivities

We verify the fatigue sensitivities for a plate with hole geometry. The design variable of a single element is perturbed to get a perturbed damage value. Then, the sensitivities are calculated using a forward finite difference scheme, which are subsequently compared against the adjoint method.

We use AISI-SAE 4340 alloy steel with the fitted fatigue material parameters in Section 6. The plate with a hole, shown in Fig. 6, is used for verifying the fatigue sensitivities. The dimensions of the model are L = 1 m and R = 0.4L. Using symmetry, only a quarter of the geometry is modeled using 160 bi-linear quadrilateral plane stress elements with a thickness of 0.01 m. At the left and bottom edges, symmetry boundary conditions are applied, with a fatigue load. A uniformly distributed peak load Q = 160N is applied on the right edge, along with a sinusoidally varying factor that is applied for 10 cycles, give the stress variation $\boldsymbol {\sigma }(t) = \boldsymbol {\sigma }(Q)\sin \limits (2\pi t)$, t = 0, 0.05,..., 10. The stress tensor σ(Q) is calculated from the static load Q using (18) and (19).

Fig. 6

Model used for verifying sensitivities

Table 5 Sensitivity comparison with Δρ = 1E − 4

Figure 6 also shows the elements around the hole that are crucial for fatigue analysis as the highest stress concentrations are expected at these elements. We verify the fatigue sensitivities, i.e., ${d D^{{PN}}(\boldsymbol {x})}/{d {x}_{e}}$, for these elements by taking the initial design variables as 1. In addition, the exponent value of the p-norm function is set to P = 12.

The relative error 𝜖_e used for sensitivity verification is given by

$$ \epsilon_{e} = \frac{{S_{e}^{a}} - {S_{e}^{d}}}{{S_{e}^{d}}}, $$

where ${S_{e}^{a}}$ is the adjoint fatigue sensitivities and ${S_{e}^{d}}$ is the sensitivities calculated by finite difference for element e. Different design variable perturbation values Δρ ranging from 1E-02 to 1E-10, are considered |𝜖_e| decreases with decreasing Δρ and levels out at Δρ = 1E − 4. Using this value, ${S_{e}^{d}}$ is calculated for the elements around the hole shown in Fig. 6. It is found that sensitivities calculated by the adjoint method are almost same as those calculated by finite differences. For the considered numerical example, the maximum damage using p-norm D^PN = 5.045E − 4. Table 5 shows the sensitivity comparison for these elements along with the perturbed damage values $D^{PN}_{d}$, where the absolute of the relative error |𝜖_e| is less than 1%.

Appendix B: Mass minimization problem subjected to only a fatigue constraint

As indicated in the remark of Section 4, removing the stiffness constraint from ($\mathbb {P}_{1}$) results in a problem with an obvious global solution x_e = 𝜖. However, a gradient-based method, as developed in this paper, may still converge to a realistic structure, which if the stiffness constraint is non-active can be considered a solution to the full problem ($\mathbb {P}_{1}$).

As an example, we solve ($\mathbb {P}_{1}$) without the compliance constraint for the L-shaped beam in Fig. 2 with the non-periodic load history shown in Fig. 3. We use AISI-SAE 4340 alloy steel along with the fitted material and optimization parameters as defined in Section 6.

Fig. 7

Optimized model with mass = 24 ⋅ 10^− 3 kg

For the mass minimization problem, we set the maximum fatigue damage bound $\bar {{D}} = 0.40$. The optimized model after 400 iterations is shown in Fig. 7.