High-Order Propagation of Jet Noise on a Tetrahedral Mesh Using Large Eddy Simulation Sources

Abstract

Jet noise is an important area of research in commercial aviation due to its high contribution to the overall noise generated by an aircraft. Conventionally, CFD combined with surface integral methods is used to study jet noise because of its low cost. However, it is not always trivial to define integration surfaces around complex geometries. This study employs a different two-step approach that can handle complex geometries. It combines a large-eddy simulation (LES) to obtain the acoustic sources from the flow field, and an acoustic perturbation equations (APE) solver to propagate the sound to the far field. The LES is performed with an industrial 2nd-order finite volume solver. The APE code is a high-order discontinuous Galerkin (DG) spectral/hp solver of the Nektar+ + framework. The APE solver is validated on a canonical test case. A study on different polynomial expansion orders and meshes is further performed to estimate the mesh size for noise propagation in the high-order spectral/hp DG context. Finally, a three-dimensional jet noise case (Re = 10, 000 and Mach =  0.9) is simulated using unstructured tetrahedral mesh for the APE solver and improved noise results for high frequencies are obtained. The results demonstrate that the present approach is capable of predicting noise in complex geometry scenarios, such as installed jets under the aircraft wings.

1 Introduction

Due to the rapid expansion of the commercial aviation industry, authorities have been tightening the legislation for aircraft noise. For instance, the European Commission has set a 65% reduction goal of overall aircraft noise from the year 2000 to 2050 [1]. The noise generated by the jet exhaust is one of the main contributors to the overall aircraft noise, especially during take-off [2]. Moreover, in new generation ultra-high by-pass ratio turbofan engines the increased interaction between the engine jet and the high-lift devices can potentially affect the noise field [3]. Thus, our overall aim is to develop and investigate an accurate and efficient method for the prediction of far-field jet noise in installed jet configurations.

Rapid growth in computing power during the last decades has enabled the use of scale resolving numerical simulations for jet noise research at a reduced cost than most experimental campaigns. Conventionally, 2nd-order numerical schemes combined with surface integral techniques, particularly the Ffowcs Williams-Hawkings (FW-H) method [4] have been widely adopted for predicting the far-field noise, due to its simplicity and low cost. However, defining the envelope surface used in the FW-H method is not always trivial in complex configurations [5], for example, installed jets on aircraft wings. Also, the results may be overly sensitive to the size, shape and location of these surfaces. Now, directly resolving the Navier-Stokes (NS) equations for sufficiently accurate far-field jet noise results is prohibitively expensive [6]. LES using finite volume 2nd-order accurate schemes has proven to be reliable and robust for solving jets’ near field, but large numerical dispersion and dissipation error makes them less suitable for the propagation of the sound waves to the far field. High-order methods provide more accurate propagation due to their reduced numerical error but are insufficiently robust for simulating complex jet flows. Therefore, we have used a coupled approach in which a finite volume LES solver is used to obtain the acoustic sources, which are then transferred to a high-order acoustic solver that propagates noise to the far-field.

The spectral/hp DG method [7] is capable of providing high-order accuracy and handling mixed mesh elements types such as tetrahedra and hexahedra, thus providing a potential solution to geometrically complex acoustic problems. The solver based on this approach is AcousticSolver of the Nektar+ + framework [8, 9]. The LES code HYDRA and acoustic code AcousticSolver have been coupled and validated using hexahedral elements [10, 11]. A similar coupling strategy has been used previously for jet noise [12] and combustion noise on tetrahedral grids [9].

In this paper, our focus is on two aspects: (1) estimates of mesh design for the high-order solver using a canonical two-dimensional (2D) case and (2) comparison of three-dimensional (3D) turbulent isolated jet-noise results on a tetrahedral grid and a comparable hexahedral grid using the coupling approach. From the perspective of our near future work, the tetrahedral grid results provide motivation and parameters for the set-up of the coupled methodology for jet-flap interactions.

2 Numerical Methods and Solvers

In this section, the details of the high-order spectral/hp DG solver employed to solve the APE equations are provided followed by a brief description of the LES code that solves the filtered compressible NS equations. Finally, the coupling of the two is briefly mentioned.

2.1 APE Solver

Equations for Propagation

The acoustic perturbation equations (APE) solved here are the ones proposed by Ewert and Schröder [6] in the APE-4 form. These equations describe the transport of acoustic fluctuations in a linearized form, where the source terms can be non-linear, and can be written as:

$$\displaystyle \begin{aligned} \partial_tp^{\prime}+\overline{c}^2\nabla\cdot\left(\overline{\rho}\mathbf{u^{\prime}}+\overline{\mathbf{u}}\frac{p^{\prime}}{\overline{c}^2}\right)=\overline{c}^2q_c, {} \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \partial_t\mathbf{u^{\prime}}+\nabla\left(\overline{\mathbf{u}}\cdot\mathbf{u^{\prime}}\right)+\nabla\left(\frac{p^{\prime}}{\overline{\rho}}\right)={\mathbf{q}}_m, {} \end{aligned} $$

(2)

where p ^′, u are the acoustic pressure and acoustic velocity vector respectively and c is the speed of sound. The time-averaged quantities are denoted by the over-bar and acoustic fluctuations are primed. The left-hand side of (1) and (2) represents the advection of waves in the mean flow. The right-hand side describes different sources that may be present in a generic aeroacoustic problem.

Finally, the source terms, q _c and q _m are defined as:

$$\displaystyle \begin{aligned} q_c=-\nabla\cdot\left(\rho^{\prime}\mathbf{u^{\prime}}\right)^{\prime}+\frac{\overline{\rho}}{c_p}\frac{\overline{D}s^{\prime}}{Dt}, \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} {\mathbf{q}}_m=-\left(\boldsymbol{\omega}\times\mathbf{u}\right)^{\prime}+T^{\prime}\nabla\overline{s}-s^{\prime}\nabla\overline{T}-\left(\frac{\nabla\left({\mathbf{u}}^{\prime}\right)^2}{2}\right)^{\prime}+\left(\frac{\nabla\cdot\underline{\tau}}{\rho}\right)^{\prime}. \end{aligned} $$

(4)

These terms are classified into four categories:

• 1. the non-linear terms: $-\nabla \cdot \left (\rho ^{\prime }\mathbf {u^{\prime }}\right )^{\prime }$ and $-(\nabla \left ({\mathbf {u}}^{\prime }\right )^2/2)^{\prime }$,

• 2. the heat/entropy terms: $(\overline {\rho }/{c_p})\cdot (\overline {D}s^{\prime }/{Dt})$ and $T^{\prime }\nabla \overline {s}-s^{\prime }\nabla \overline {T}$,

• 3. the viscous term: $(\nabla \cdot \underline {\tau }/{\rho })^{\prime }$ and

• 4. the vortical term, known as the Lamb vector, L ^′ = −(ω ×u)^′.

In this paper, only the Lamb vector L ^′ is considered as a source term because it is the dominant contributor for isothermal applications with strong vortical motions (shear layers and wakes), as demonstrated in [12, 13].

Numerical Solver

The solver used for the above APE equations is called AcousticSolver, which is part of the open-source Nektar+ + framework [8]. The solver employs a high-order, spectral/hp element method with a DG formulation [7]. In short (for details see [9]), the present DG method works as follows:

• 1. The computational domain is divided into non-overlapping elements.

• 2. The governing equations are discretised in each element by a weighted sum of basis functions where the coefficients of the expansion are the unknowns. In case of tetrahedral elements, the basis functions are modified hierarchical Jacobi basis [8].

• 3. The discretised equation is then multiplied by a test function (same as the basis function) followed by integration over each element in order to obtain the variational form of the governing equations.

• 4. The flux terms in the variational equation are responsible for communicating the information across the elements. The interface fluxes are calculated using the immediate left- and right-side values with a Riemann solver.

The scheme used here to solve the Riemann problem is a local Lax-Friederichs scheme as defined in [9]. The temporal discretisation is performed using a 4^th-order Runge-Kutta scheme. A numerical sponge layer [14] is set up using source terms to dampen out the outgoing acoustic waves smoothly, thus minimising reflections from the boundaries of the domain.

2.2 LES Solver

The LES is performed using the in-house code of Rolls-Royce plc., HYDRA [15] that solves Favre-filtered unsteady compressible Navier-Stokes equations [10]. It is a density-based, spatially 2nd-order accurate finite volume cell-vertex code used for propulsion and turbomachinery applications. More details on the set-up of the spatial scheme used can be found in [10]. For the temporal discretisation, a 2nd-order, four-stage Runge-Kutta explicit algorithm is employed. The size of the time step is chosen to keep the Courant number less than unity. The code is capable of solving arbitrary mesh topologies which is beneficial for complex geometries. The sub-grid scale model is chosen as σ-model [16] with model constant C _σ = 1.35 [17].

2.3 Coupling of Solvers

The 3D data from LES mesh is transferred and interpolated onto the APE mesh in real time. The interpolation is necessary because two solvers have different meshes designed specifically to capture flow and acoustics. The transfer-interpolation process takes place in parallel. This is achieved using an MPI based coupling strategy with the open-source library CWIPI [18]. More details on the coupling mechanism are provided in Lackhove et al. [9] and Moratilla-Vega et al. [10]. Note that larger time steps can be used for AcousticSolver since it is not restricted to resolve the small flow structures.

3 Test Cases

Two cases are presented here. First, a canonical noise propagation case due to a well-defined vortex-pair source run on AcousticSolver alone. A study of numerical error by changing the mesh and polynomial expansion order (P) is performed. The second case uses the mesh parameters from the first to propagate noise generated by an isolated jet in an LES simulation. This case provides validation of the coupling for a 3D turbulent jet noise case on a fully tetrahedral mesh. The results are then compared to the ones obtained with the FW-H technique.

3.1 Spinning Vortex Pair

The case is an acoustic wave propagation problem in two dimensions where the source is mathematically well-defined, as in the original work on APE [6]. The case is run with standalone AcousticSolver. The source is in the form of two-point vortices at a distance of r ₀ from the origin, rotating with a circulation Γ. An analytical solution of the induced acoustic field was found by Müller and Obermeier [19] as:

$$\displaystyle \begin{aligned} \tilde{p}^{\prime}=\frac{\rho_\infty\Gamma^4}{64\pi^3r_0^4c_\infty^2}H_2^{(2)}(kr), {} \end{aligned} $$

(5)

where, $H_2^{(2)}$ is the Hankel function of 2nd-order and second kind, the rotation period is defined as $T=8\pi ^2r_0^2/\Gamma$; the angular velocity as $\omega =\Gamma /4\pi r_0^2$ and the Mach number as M _r =  Γ∕4πr ₀ c _∞. The real part of Eq. (5) gives the pressure fluctuations. Ewert and Schröder [6] found the source-term based on the Lamb vector that represents the acoustic field for this case as:

$$\displaystyle \begin{aligned} \boldsymbol{q}_m=-\frac{\Gamma^2\boldsymbol{e}_r(t)}{8\pi^2\sigma^2r_0}\sum_{i=1}^{2}(-1)^i\exp\left(-\frac{\mid{\boldsymbol{r}+(-1)^i\boldsymbol{r}_0(5)}\mid^2}{2\sigma^2}\right), \quad \sigma\approx r_0, \end{aligned} $$

(6)

where, r = (x, y)^T, r ₀ = r ₀ e _r, $\boldsymbol {e}_r=(\cos \theta ,\sin \theta )^T$ and θ = ωt.

The computational domain considered is circular and extends to 250r ₀. The source parameters are set as in [6] i.e. Γ∕(c _∞ r ₀) = 1.6 and M _r = 0.1273. Simulations are run until the pressure fluctuations reach r = 200r ₀ in order to minimise the boundary effects. All the elemental meshes consist of triangles and a modified hierarchical Jacobi polynomial basis [8].

Fig. 1

(a) Pressure field along x = y line, (b) solution points, and contours of the source term in the source region and the pressure field in the propagation region

First, a reference simulation with polynomial order 4 (P4) is run on a fine uniform mesh. The resulting acoustic pressure field is plotted along a diagonal line in Fig. 1a. The result from this simulation matches its analytical counterpart well. Further comparisons are made with respect to this well-resolved P4 numerical result, henceforth called as “P4 reference”. For the test cases, elemental meshes are coarsened radially and the polynomial order is elevated in the propagation region, such that, the solution points-per-wavelength (referred as “ppw”) distribution is similar in the radial direction. The radial growth rate is kept ∼1.023 with geometric distribution in all the cases. In the source region, the mesh is kept the same with P1 expansion for all cases. This allows having a smooth transition of solution points distribution when crossing from one region to the other. A sample P2 mesh and contours are shown in Fig. 1b. Table 1 summarises the test runs.

Table 1 Details of the test cases run

Fig. 2

Acoustic pressure and relative error comparison of the test cases. (a) Pressure along x=y line. (b) Relative error (as moving average)

Figure 2a compares the pressure fields in different test cases with the P4 reference. As expected, the P1 simulation shows a considerable reduction in the amplitude. P2 and P4 preserve this quantity more accurately. For simplification, we unify the dissipation and dispersion error by calculating the overall relative error as a moving average (M.A.) over bins of ∼30r ₀. This is plotted in Fig. 2b. For P1 and P2 simulations, a 2% error limit is reached around 50r ₀ (ppw ∼ 9) and 85r ₀ respectively (ppw ∼ 6.4). P4 simulations remain below this limit under the present conditions (note ppw ∼ 5 at 150r ₀). The values of ppw for different P agree with those suggested in [20] and provide an estimate for mesh design in different polynomial order setting.

Note that for the given ppw, mesh expansion rate and Riemann solver, we did not observe reflections of the acoustic signals on the inter-element boundaries. A caveat of the present study is that we calculate total numerical error here for brevity, however dissipation and dispersion error could be studied separately as done in [20] on a one-dimensional advection study.

Fig. 3

Cross-section view through the centre of the jet nozzle. (a) LES mesh elements. (b) AcousticSolver meshes

3.2 3D Turbulent Isolated Jet Noise

As a step forward towards noise prediction of installed jets, an isolated jet is simulated using a tetrahedral mesh for AcousticSolver to verify the capabilities of the present methodology for complex 3D cases. Note that the coupling is already validated on a cylinder in cross flow and a cylinder-airfoil interaction case in [11].

Jet Flow

The LES performed is described here briefly since the same is detailed in [10]. An isothermal turbulent jet issuing from a circular cross-section nozzle at Mach 0.9 and Reynolds number Re = 10, 000 (based on jet bulk velocity U _j and jet diameter D _j) is considered. Following Shur et al. [21], the present LES domain is cylindrical in shape and extends as x∕D _j = [−5, 100] and r∕D _j = [0, 50]. The mesh has 190 × 75 × 49 nodes in the axial, radial and azimuthal directions respectively. It is refined in the shear layer development area and coarsened towards the outer boundaries. Figure 3a shows a central cross-section of the LES mesh. The inlet boundary condition is a total pressure profile.

Jet Acoustics

The acoustics domain is cubical to facilitate control on mesh growth. It extends as [−5, 40]D _j in streamwise direction and [−25, 25]D _j in transverse directions. Noise propagation on two different grids is compared: fully hexahedral (“hexa”) and fully tetrahedral (“tetra”). The former mesh consists of 107 × 69 × 69 elements in the streamwise and transverse directions respectively [10]. The tetra grid is generated to give a similar distribution as the hexa mesh in the vicinity of the jet, providing 300,000 elements in total. Figure 3b shows the two meshes where it is seen that the nominal element size in the tetra mesh is slightly larger away from the jet nozzle. Results on the hexa grid (P4) are available from [10] and calculations are performed on the tetra grid in this study. The expansion type utilised is a P4 modified Jacobi basis [8]. A numerical sponge layer [14] of thickness 3D _j is applied at the outer boundaries to avoid reflections of the outgoing waves. A factor of 3 in time step size is used as compared to the compressible LES. In line with Sect. 3.1 and [20], a value of ppw ∼ 5 is chosen for accurately resolving frequencies up to a Strouhal number St = 0.9.

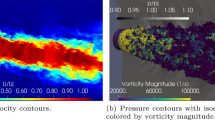
It is already demonstrated in [10] that the LES flow quantities are in acceptable agreement with the high-order LES study of Shur et al. [21]. The noise propagation is calculated using the FW-H method [4] in addition to the present coupled approach. The nominal cut-off St for the integral surface defined is ∼0.3 based on the 22 ppw criterion [6]. Figure 4 shows a visual comparison between the acoustic pressure field computed by LES alone and coupled LES-APE (on two meshes). Figure 4a, b qualitatively show that the coupled LES-APE has retained more acoustic content (especially at higher frequencies) due to lower numerical error. This difference is more pronounced in the direction perpendicular to the jet centre-line. Qualitatively comparable results are obtained on the tetra mesh as depicted in Fig. 4c.

Fig. 4

Acoustic pressure field at the same time instant (in grayscale [−30, 30] Pa). (a) LES. (b) LES-APE (hexa). (c) LES-APE (tetra)

Fig. 5

PSD at 120D _j at two observer locations with respect to the jet centre-line. (a) 30^∘. (b) 90^∘

Figure 5 shows a quantitative comparison in terms of power-spectral-density (PSD) at two observer locations at a distance of 120D _j. The PSD for FW-H is calculated over the surface indicated by the dashed line in Fig. 4a (details in [10]). Comparison is done with the LES of Shur et al. [21] and the experiment of Tanna [22] (Re = 10⁶, Mach = 0.9). As previously observed in Fig. 4, the difference between FW-H and the present coupled approach is significant at higher frequencies. For the 30^∘ location, the tetra mesh results match the hexa results well. At 90^∘ location, there is an improvement of cut-off St from 0.3 to 0.8. A small discrepancy is seen at 90^∘ for St > 0.8 (close to the cut-off St = 0.9). This may be improved by using a finer mesh in the far-field. Overall, the APE results are an improvement over the present FW-H prediction in the high frequency domain. Moreover, the results from the tetra mesh are comparable to ones from the hexa mesh. This implies that the present methodology using tetra grids can be extended to more complex cases (such as installed jets).

4 Conclusions

A spectral/hp code AcousticSolver (under Nektar+ + framework) has been employed for acoustic waves propagation. The favourable properties of this solver are high-order accuracy and capability to handle unstructured mesh elements. A study on a canonical test case with an analytical solution provided estimates for designing the mesh for the jet application. For polynomial order expansion P4, 5 solution points-per-wavelength is found to provide a low overall error. This value is close to the one reported in a related study [20]. These estimates are used to design a tetrahedral mesh for prediction of noise from an isolated jet (Re = 10⁴, Mach = 0.9). The noise sources are calculated from a 2nd-order accurate finite volume LES solver and interpolated onto AcousticSolver mesh on-the-fly for noise propagation. The noise results thus obtained offer an improvement over the traditional FW-H method due to high-order accuracy. The power-spectral-density (PSD) results of the noise signal at two different locations relative to the jet nozzle show that the PSDs obtained on the tetrahedral mesh agree with the ones obtained on a slightly finer hexahedral mesh. Further improvements may be achieved by refining the former mesh in the radial direction. These results are encouraging for noise-prediction of more complex industrially relevant geometries such as installed jets.