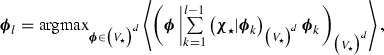Geometry-dependent reduced-order models for the computation of homogenized transfer properties in porous media

Abstract

This article investigates reduced-order models (ROMs) based on proper orthogonal decomposition for efficient computation of the homogenized diffusion properties of saturated porous media. The homogenized tensor, whose classical expression may be obtained from periodic homogenization techniques, is computed by solving a local problem on an elementary cell that includes one or several circular solid inclusions. The cost of the repeated resolution of this problem by the finite element method for different inclusions radii may be important, and classical model order reduction methods based on the computation of a spatial basis cannot be applied directly. The method proposed in this work to cope with the variability of circular inclusions relies on the introduction of a transformation from a reference domain to the physical domain that admits an exact affine decomposition in the three-dimensional cases, allowing to split the problem into an offline learning phase and an online evaluation phase which does not depend on the number of degrees of freedom of the original full-order solution. Approximate affine decomposition for two-dimensional cases is also provided with an explicit estimation of the truncation error. The efficiency of the proposed algorithm in terms of accuracy and of computing time is evaluated first for 2D and 3D isotropic and anisotropic elementary cells with a single inclusion, and second for a 2D anisotropic cell with multiple inclusions. Furthermore the ROM is used to estimate in quasi-real time the homogenized diffusion tensor for a given probability distribution of the geometry parameters.

Appendices

Recalls on the proper orthogonal decomposition (POD)

Reduced-order models consist in approximating the solution ${\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho )$ of a given problem parametrized by $\rho$ on a spatial basis $\left( {\varvec{\phi }}_i\right) _{i=1}^{N_{\mathrm {rom}}}$ of small size $N_{\mathrm {rom}}$:

$$\begin{aligned} {\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ) \simeq {\widehat{{\varvec{\chi }}}}_{\mathrm {\star }}({\varvec{\xi }}; \rho ) = \sum _{i=1}^{n_{\varvec{\chi }}}a_i(\rho )\,{\varvec{\phi }}_i({\varvec{\xi }}), \end{aligned}$$

where ${\varvec{\xi }}$ is the space variable. There exist numerous methods to build this spatial basis, but the most used stays the proper orthogonal decomposition that combines accuracy and optimality. The space-dependent functions ${\varvec{\phi }}_i$ obtained by the POD, lying in the Hilbert space $\big (V_{\mathrm {\star }}\big )^d$, satisfy the two conditions:

• (i) Orthogonality: $({\varvec{\phi }}_i)_i$ is orthogonal,

• (ii) Optimality of $({\varvec{\phi }}_i)_i$:

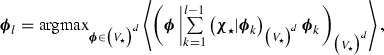
where $(\bullet \vert \bullet )_{\big (V_{\mathrm {\star }}\big )^d}$ denotes the scalar product of $\big (V_{\mathrm {\star }}\big )^d$ and $\langle \bullet \rangle$ denotes the mean over the variable $\rho$. The latter condition ensures that the space engendered by the $\{{\varvec{\phi }}_i\}_{i=1}^l$ gives the best approximation of the functions ${\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho )$, among the subspaces of $\big (V_{\mathrm {\star }}\big )^d$ with rank l.

The method of snapshots introduced in [33] is used in this article. It consists in computing by the FEM a set of vector fields ${\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ^j)$ (called the snapshots) for a finite set of parameter values $\{\rho ^j\}_{j=1}^{N_{\mathrm {snap}}}$. Then, POD modes ${\varvec{\phi }}_i$ are sought inside the functional space $[{\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ^j)]_{j=1}^{N_{\mathrm {snap}}}$. The snapshots ${\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ^j)$ are expected to be linearly independent in practical cases so that, by exploiting the orthogonality and optimality conditions, the POD modes can be determined by the formula

$$\begin{aligned} {\varvec{\phi }}_i=\frac{1}{\sqrt{\lambda _i}}\sum \limits _{j=1}^{N_{\mathrm {snap}}}[{\varvec{v}}_i]_j{\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ^j)\text {,} \end{aligned}$$

where $\lambda _i$ are the eigenvalues and ${\varvec{v}}_i$ are the unit eigenvectors of the symmetric positive definite correlation matrix ${\varvec{C}}$ whose coefficients are given by

$$\begin{aligned} {\varvec{C}}_{jk}=\dfrac{1}{N_{\mathrm {snap}}}\displaystyle \int \limits _{\varOmega } {\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ^k)\cdot {\varvec{\chi }}_{\mathrm {\star }}({\varvec{\xi }}; \rho ^j)\text {d}{\mathbf {y}}\text {.} \end{aligned}$$

The POD basis is then truncated to a number of $N_{\mathrm {rom}}$ modes which is selected to ensure that the error on the relative content of information due to the projection on the retained POD modes is below a given threshold $\nu$:

$$\begin{aligned} N_{\mathrm {rom}}=\min \left\{ N\in 1\dots N_{\mathrm {snap}}; \;\frac{\sum \nolimits _{i=1}^N\lambda _i}{\sum \nolimits _{i=1}^{N_{\mathrm {snap}}}\lambda _i} >1-\nu \right\} \cdot \end{aligned}$$

(69)

Formulas and proofs associated with the parametrized transformation

Let us recall the definition of the transformation ${\varvec{\tau }}_\rho$, for each ${\varvec{\xi }}$ in the reference fluid domain:

$$\begin{aligned} {\varvec{\tau }}_\rho ({\varvec{\xi }}) = \left\{ \begin{array}{ll} \alpha _{\rho }{\varvec{u}}({\varvec{\xi }})+\beta _{\rho }{\varvec{\xi }}, &{}\quad \text{ if }\;\rho _{\mathrm {\star }}\le \parallel {\varvec{\xi }} \parallel < q, \\ {\varvec{\xi }},&{}\quad \text{ if }\; q\le \parallel {\varvec{\xi }} \parallel , \end{array} \right. \end{aligned}$$

where $\rho _{\mathrm {\star }}$ and $q$ are the internal and external radii of the crown ${\varOmega ^{\mathrm {\star }}_{\mathrm {c}}}$, ${\varvec{u}}({\varvec{\xi }})=\dfrac{{\varvec{\xi }}}{\parallel {\varvec{\xi }} \parallel }$ denotes the radial unit vector and

$$\begin{aligned} \alpha _{\rho }=q\dfrac{\rho -\rho _{\mathrm {\star }}}{q-\rho _{\mathrm {\star }}}, \quad \beta _{\rho }=\dfrac{q-\rho }{q-\rho _{\mathrm {\star }}}. \end{aligned}$$

The following formulas related to the Jacobian matrix of the transformation ${\varvec{\tau }}_\rho$ are the core of the affine dependence to the geometry of the proposed POD-ROM.

Lemma 1

For all $\rho$ such that $\rho < q$:

$$\begin{aligned} {\varvec{J}}_{\rho }({\varvec{\xi }})= & {} \beta _{\rho }{\varvec{I}}+\alpha _{\rho }\nabla _{\!{\varvec{\xi }}}{\varvec{u}}({\varvec{\xi }}), \end{aligned}$$

(70)

$$\begin{aligned} {\varvec{J}}_{\rho }^{-1}({\varvec{\xi }})= & {} \frac{1}{\beta _{\rho }} {\varvec{I}}-\frac{\alpha _{\rho }}{\beta _{\rho }}\cdot \frac{1}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert +\alpha _{\rho }}{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}, \end{aligned}$$

(71)

$$\begin{aligned} j_{\rho }({\varvec{\xi }})= & {} \beta _{\rho }\sum \limits _{p=0}^{d-1}C_{d-1}^p\frac{\alpha _{\rho }^p}{\Vert {\varvec{\xi }}\Vert ^p}\beta _{\rho }^{d-1-p}, \end{aligned}$$

(72)

with the convention

$$\begin{aligned} {\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} : = {\varvec{I}}-\frac{1}{\Vert {\varvec{\xi }}\Vert ^2}{\varvec{\xi }}\cdot {\varvec{\xi }}^\intercal \cdot \end{aligned}$$

(73)

Proof

(70) is obvious, it follows from the definition of ${\varvec{\tau }}_\rho$ and the linearity of the gradient operator. To prove (71) we need an explicit formula for the inverse mapping ${{\varvec{\tau }}_\rho }^{-1}$. We first notice that, according to the geometrical characterization of ${\varvec{\tau }}_\rho$ at the beginning of Sect. 3, ${{\varvec{\tau }}_\rho }^{-1}$ is obtained by switching $\rho _{\mathrm {\star }}$ and $\rho$ in ${\varvec{\tau }}_\rho$. Then we have for ${\varvec{y}}={\varvec{\tau }}_\rho ({\varvec{\xi }})$:

$$\begin{aligned} {{\varvec{\tau }}_\rho }^{-1}({\varvec{y}}) = \left\{ \begin{array}{ll} \alpha _{\rho }'{\varvec{u}}({\varvec{y}})+\beta _{\rho }' {\varvec{y}}, &{} \text{ if }\;\rho _{\mathrm {\star }}\le \parallel {\varvec{y}} \parallel < q, \\ {\varvec{y}},&{} \text{ if }\; q\le \parallel {\varvec{y}} \parallel , \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} \alpha _{\rho }'=q\dfrac{\rho _{\mathrm {\star }}-\rho }{q-\rho }, \quad \beta _{\rho }'=\dfrac{q-\rho _{\mathrm {\star }}}{q-\rho }. \end{aligned}$$

Note that $\alpha _{\rho }' =-\frac{\alpha _{\rho }}{\beta _{\rho }}$ and $\beta _{\rho }'=\frac{1}{\beta _{\rho }}$. Now, differentiating ${{\varvec{\tau }}_\rho }^{-1}$ at ${\varvec{\tau }}_\rho ({\varvec{\xi }})$ to compute ${\varvec{J}}_{\rho }^{-1}({\varvec{\xi }})$ for each ${\varvec{\xi }}<q$ yields ${\varvec{J}}_{\rho }^{-1}({\varvec{\xi }})=\left( \nabla _{{\varvec{\tau }}_\rho ({\varvec{\xi }})}{{\varvec{\tau }}_\rho }^{-1}\right) ({\varvec{\tau }}_\rho ({\varvec{\xi }}))$, from which it follows by linearity that

$$\begin{aligned}{\varvec{J}}_{\rho }^{-1}({\varvec{\xi }})=\dfrac{1}{\beta _{\rho }}\left( {\varvec{I}}\,-\alpha _{\rho }\nabla _{{\varvec{\tau }}_\rho ({\varvec{\xi }})}{\varvec{u}}({\varvec{\tau }}_\rho ({\varvec{\xi }}))\right) .\end{aligned}$$

By definition of the unitary vector ${\varvec{u}}({\varvec{y}})=\dfrac{{\varvec{y}}}{\Vert {\varvec{y}}\Vert }$, we have $\nabla _{{\varvec{y}}}{\varvec{u}}({\varvec{y}})=\frac{1}{\Vert {\varvec{y}}\Vert }\left( {\varvec{I}}-\frac{1}{\Vert {\varvec{y}}\Vert ^2}{\varvec{y}}\cdot {{\varvec{y}}}^\intercal \right)$. To conclude, notice that ${\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} = {\varvec{G}}_{{\varvec{u}}({\varvec{y}})}$ since ${\varvec{\tau }}_\rho ({\varvec{\xi }})$ is always positively co-linear to ${\varvec{\xi }}$ so that

$$\begin{aligned}{\varvec{J}}_{\rho }^{-1}({\varvec{\xi }})=\dfrac{1}{\beta _{\rho }}\left( {\varvec{I}}\,-\alpha _{\rho }\dfrac{1}{\Vert {\varvec{\tau }}_\rho ({\varvec{\xi }})\Vert }\left( {\varvec{I}}-\frac{1}{\Vert {\varvec{\xi }}\Vert ^2}{\varvec{\xi }}\cdot {{\varvec{\xi }}}^\intercal \right) \right) ,\end{aligned}$$

which provides the expected result.

Thereafter, we provide the proof of latest statement (72) in the case $d=3$. Notice that the matrix ${\varvec{\xi }}\cdot {\varvec{\xi }}^\intercal$ is by construction of rank $1$ and symmetric so that it exists an orthogonal matrix ${\varvec{P}}$ for which

$$\begin{aligned} {\varvec{\xi }}\cdot {\varvec{\xi }}^\intercal = {\varvec{P}} \cdot \left( \begin{array}{ccc} {\text {Tr}} \ ({\varvec{\xi }}\cdot {\varvec{\xi }}^\intercal )&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0\\ \end{array} \right) \cdot {\varvec{P}}^\intercal . \end{aligned}$$

Moreover, we have ${\text {Tr}} ({\varvec{\xi }}\cdot {\varvec{\xi }}^\intercal )=\Vert {\varvec{\xi }}\Vert ^2$ for all ${\varvec{\xi }}$ so that

$$\begin{aligned} \nabla _{\!{\varvec{\xi }}}{\varvec{u}}({\varvec{\xi }}) = {\varvec{P}} \cdot \left( \begin{array}{ccc} 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \frac{1}{\Vert {\varvec{\xi }}\Vert }&{}\quad 0\\ 0&{}\quad 0&{}\quad \frac{1}{\Vert {\varvec{\xi }}\Vert }\\ \end{array} \right) \cdot {\varvec{P}}^\intercal , \end{aligned}$$

and

$$\begin{aligned} {\varvec{J}}_{\rho }({\varvec{\xi }}) = {\varvec{P}} \cdot \left( \begin{array}{ccc} \beta _{\rho }&{}\quad 0&{}\quad 0\\ 0&{}\quad \beta _{\rho }+\frac{\alpha _{\rho }}{\Vert {\varvec{\xi }}\Vert }&{}\quad 0\\ 0&{}\quad 0&{}\quad \beta _{\rho }+\frac{\alpha _{\rho }}{\Vert {\varvec{\xi }}\Vert }\\ \end{array} \right) \cdot {\varvec{P}}^\intercal . \end{aligned}$$

We deduce formula (72) by expending the expression $\beta _{\rho }\left( \beta _{\rho }+\frac{\alpha _{\rho }}{\Vert {\varvec{\xi }}\Vert }\right) ^{d-1}$ using the binomial theorem. $\square$ $\square$

Notice that this demonstration relies on the symmetry of ${\varvec{J}}_{\rho }({\varvec{\xi }})$ which stands from the spherical symmetry of the transformation ${\varvec{\tau }}_\rho$, so that it does not generalize directly to other kind of transformations. We are ready to establish the two main statements of this paragraph.

Theorem 1

$$\begin{aligned} {\varvec{J}}_{\rho }^{-1}\,j_{\rho }= {\left\{ \begin{array}{ll} \left( \beta _{\rho }+\alpha _{\rho }\frac{1}{\Vert {\varvec{\xi }}\Vert }\right) {\varvec{I}}-\alpha _{\rho }\frac{1}{\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}, &{}\text {if }d=2\, , \\ \left( \beta _{\rho }^2+2\alpha _{\rho }\beta _{\rho }\frac{1}{\Vert {\varvec{\xi }}\Vert }+\alpha _{\rho }^2\frac{1}{\Vert {\varvec{\xi }}\Vert ^2}\right) {\varvec{I}}- \alpha _{\rho }\left( \beta _{\rho }\frac{1}{\Vert {\varvec{\xi }}\Vert }+\alpha _{\rho }\frac{1}{\Vert {\varvec{\xi }}\Vert ^2}\right) {\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}, &{}\text {if }d=3\,. \end{array}\right. } \end{aligned}$$

Proof

From lemma 1 and the equality

$$\begin{aligned} j_{\rho }=\beta _{\rho }\left( \dfrac{\Vert {\varvec{\tau }}_\rho ({\varvec{\xi }})\Vert }{\Vert {\varvec{\xi }}\Vert }\right) ^{d-1} \end{aligned}$$

we have

$$\begin{aligned} {\varvec{J}}_{\rho }^{-1}\,j_{\rho }=\beta _{\rho }\left( \dfrac{\Vert {\varvec{\tau }}_\rho ({\varvec{\xi }})\Vert }{\Vert {\varvec{\xi }}\Vert }\right) ^{d-1}\, \left( \frac{1}{\beta _{\rho }} {\varvec{I}}- \frac{\alpha _{\rho }}{\beta _{\rho }}\cdot \frac{1}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert +\alpha _{\rho }}{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}\right) . \end{aligned}$$

The multiplication by $\Vert {\varvec{\tau }}_\rho ({\varvec{\xi }})\Vert ^{d-1}$ simplifies the denominator which is due to ${\varvec{J}}_{\rho }^{-1}$, whatever $d$ can be. This yields the expected formulas. $\square$ $\square$

Theorem 2

$$\begin{aligned} {\varvec{J}}_{\rho }^{-2}\,j_{\rho }= {\left\{ \begin{array}{ll} \left( 1 + \dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }\right) {\varvec{I}}\,- \left( 1+\beta _{\rho }^{n_{\mathrm {t}}+1}\,+ (1-\beta _{\rho })\left( \sum \limits _{l=1}^{n_{\mathrm {t}}}(-1)^{l}\left( \sum \limits _{m=l}^{n_{\mathrm {t}}}\beta _{\rho }^mC^{l}_m\right) \dfrac{\Vert {\varvec{\xi }}\Vert ^{l}}{q^{l}} +{\mathcal {R}}_{n_{\mathrm {t}}}\left( \rho , {\varvec{\xi }}\right) \right) \right) \dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} &{}\text {if }d=2\, , \\ \left( \beta _{\rho }+2\alpha _{\rho }\dfrac{1}{\Vert {\varvec{\xi }}\Vert }+\dfrac{\alpha _{\rho }^2}{\beta _{\rho }}\dfrac{1}{\Vert {\varvec{\xi }}\Vert ^2}\right) {\varvec{I}}- 2\alpha _{\rho }\dfrac{1}{\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}-\dfrac{\alpha _{\rho }^2}{\beta _{\rho }}\dfrac{1}{\Vert {\varvec{\xi }}\Vert ^2}{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}, &{}\text {if }d=3\, , \end{array}\right. } \end{aligned}$$

where the residual is given by ${\mathcal {R}}_{n_{\mathrm {t}}}\left( \rho , {\varvec{\xi }}\right) =\left( \frac{\beta _{\rho }}{q}(q-\Vert {\varvec{\xi }}\Vert )\right) ^{n_{\mathrm {t}}+1}\dfrac{1}{1-\beta _{\rho }\frac{q-\Vert {\varvec{\xi }}\Vert }{q}}$.

Proof

As well as in the proof of theorem 1 we have

$$\begin{aligned} \left( {\varvec{J}}_{\rho }^{-2}\right) j_{\rho }= \beta _{\rho }\left( \dfrac{\Vert {\varvec{\tau }}_\rho ({\varvec{\xi }})\Vert }{\Vert {\varvec{\xi }}\Vert }\right) ^{d-1}\, \left( \frac{1}{\beta _{\rho }}{\varvec{I}}-\frac{\alpha _{\rho }}{\beta _{\rho }}\left( \dfrac{1}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert +\alpha _{\rho }}{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}\right) \right) ^2. \end{aligned}$$

(74)

The result announced for $d=3$ follows easily, but the same reasoning fails when $d=2$: indeed, the multiplication by $\Vert {\varvec{\tau }}_\rho ({\varvec{\xi }})\Vert =\alpha _{\rho }+\beta _{\rho }\Vert {\varvec{\xi }}\Vert$ does not compensate the presence of $\left( \dfrac{1}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert +\alpha _{\rho }}\right) ^2$ in the latest expression. Unfortunately, the fraction $\dfrac{1}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert +\alpha _{\rho }}$ is an obstruction for the offline computation required for Algorithms 1, 2. We overcome this difficulty by approximating $\left( {\varvec{J}}_{\rho }^{-2}\right) j_{\rho }$: starting from (74) we get:

$$\begin{aligned} \left( {\varvec{J}}_{\rho }^{-2}\right) j_{\rho }= {\varvec{I}}+ \dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{I}}- 2\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} + \frac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }(1-\beta _{\rho })\cdot \dfrac{1}{1-\beta _{\rho }\frac{q-\Vert {\varvec{\xi }}\Vert }{q}}{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}. \end{aligned}$$

(75)

The key point is the following intermediate result:

Lemma 2

For every $\rho$ and $\rho _{\mathrm {\star }}\le \parallel {\varvec{\xi }} \parallel < q$, we have

$$\begin{aligned} \beta _{\rho }\frac{q-\Vert {\varvec{\xi }}\Vert }{q}\in \left[ 0, \dfrac{q-\rho }{q}\right] . \end{aligned}$$

(76)

Consequently and for all $0<\rho <q$, this ratio belongs to $]0,1[$.

Then the fraction $\dfrac{1}{1-\beta _{\rho }\frac{q-\Vert {\varvec{\xi }}\Vert }{q}}$ can be developed as a power series, which entails

$$\begin{aligned} \left( {\varvec{J}}_{\rho }^{-2}\right) j_{\rho }&= \left( 1 + \dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }\right) {\varvec{I}}- 2\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} \nonumber \\&\quad + \left( \sum \limits _{m=0}^{n_{\mathrm {t}}}\left( \frac{\beta _{\rho }}{q}\right) ^m\cdot \left( q-\Vert {\varvec{\xi }}\Vert \right) ^m\right) (1-\beta _{\rho })\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }\cdot {\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} + {\mathcal {R}}_{n_{\mathrm {t}}}\left( \rho , {\varvec{\xi }}\right) (1-\beta _{\rho })\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }\cdot {\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}, \nonumber \\ \end{aligned}$$

(77)

where ${\mathcal {R}}_{n_{\mathrm {t}}}\left( \rho , {\varvec{\xi }}\right)$ is the announced residual of order $n_{\mathrm {t}}$. The latter vanishes when $n_{\mathrm {t}}\rightarrow +\infty$ according to Lemma 2, and in practical cases the convergence is very fast (we use $n_{\mathrm {t}}\le 3$ for all numerical applications in this work). To fully establish the affine separation of ${\varvec{\xi }}$ and $\rho$ we write:

$$\begin{aligned} \sum \limits _{m=0}^{n_{\mathrm {t}}}\left( \frac{\beta _{\rho }}{q}\right) ^m\cdot \left( q-\Vert {\varvec{\xi }}\Vert \right) ^m= \sum \limits _{m=0}^{n_{\mathrm {t}}}\beta _{\rho }^m\left( 1-\frac{\Vert {\varvec{\xi }}\Vert }{q}\right) ^m= \sum \limits _{m=0}^{n_{\mathrm {t}}}\sum \limits _{l=0}^m\beta _{\rho }^m\,C_m^l(-1)^l\dfrac{\Vert {\varvec{\xi }}\Vert ^l}{q^l}= \sum \limits _{l=0}^{n_{\mathrm {t}}}\sum \limits _{m=l}^{n_{\mathrm {t}}}\beta _{\rho }^m\,C_m^l(-1)^l\dfrac{\Vert {\varvec{\xi }}\Vert ^l}{q^l}. \end{aligned}$$

(78)

For $l=0$, the sum $\sum \nolimits _{m=l}^{n_{\mathrm {t}}}\beta _{\rho }^m\,C_m^l(-1)^l\dfrac{\Vert {\varvec{\xi }}\Vert ^l}{q^l}$ is a geometric sum and equals $\dfrac{1-\beta _{\rho }^{n_{\mathrm {t}}+1}}{1-\beta _{\rho }}$, so that

$$\begin{aligned} - 2\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}+ \sum \limits _{m=l}^{n_{\mathrm {t}}}\beta _{\rho }^m\,C_m^l(-1)^l\dfrac{\Vert {\varvec{\xi }}\Vert ^l}{q^l}(1-\beta _{\rho })\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})} = -(1+\beta _{\rho }^{1+n_{\mathrm {t}}})\dfrac{\alpha _{\rho }}{\beta _{\rho }\Vert {\varvec{\xi }}\Vert }{\varvec{G}}_{{\varvec{u}}({\varvec{\xi }})}\,\text {for }l=0.\nonumber \\ \end{aligned}$$

(79)

Injecting (78) and (79) into (77) gives the announced statement. Provided a rank $n_{\mathrm {t}}$ for which the residual ${\mathcal {R}}_{n_{\mathrm {t}}}\left( \rho , {\varvec{\xi }}\right)$ can be neglected, we obtain an expression of $\left( {\varvec{J}}_{\rho }^{-2}\right) j_{\rho }$ where variables $\rho$ and ${\varvec{\xi }}$ are separated. $\square$ $\square$

Notice that since the inequality stated in Lemma 2 is normalized by $q$, the same $n_{\mathrm {t}}$ can be chosen for each inclusion in the multiparametric case, indifferently to the size of the inclusions. It is the case for the numerical applications of this work, although a unique $q$ has been used in this work.