Abstract
This chapter presents an overview of brain-inspired reservoir computing models for sensory-motor information processing in the brain. These models are based on the idea that the brain processes information using a large population of interconnected neurons, where the dynamics of the system can amplify, transform, and integrate incoming signals. We discuss the reservoir predictive coding model, which uses predictive coding to explain how the brain generates expectations regarding sensory input and processes incoming signals. This model incorporates a reservoir of randomly connected neurons that can amplify and transform sensory inputs. Moreover, we describe the reservoir reinforcement learning model, which explains how the brain learns to make decisions based on rewards or punishments received after performing a certain action. This model uses a reservoir of randomly connected neurons to represent various possible actions and their associated rewards. The reservoir dynamics allow the brain to learn which actions lead to the highest reward. We then present an integrated model that combines these two reservoir computing models based on predictive coding and reinforcement learning. This model demonstrates how the brain integrates sensory information with reward signals to learn the most effective actions for a given situation. It also explains how the brain uses predictive coding to generate expectations about future sensory inputs and accordingly adjusts its actions. Overall, brain-inspired reservoir computing models provide a theoretical framework for understanding how the brain processes information and learns to make decisions. These models have the potential to revolutionize fields such as artificial intelligence and neuroscience, by advancing our understanding of the brain and inspiring new technologies.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1 Introduction
The brain’s capacity to process sensory information and make decisions can be attributed to the intricate neural dynamics within a highly interconnected network of nonlinear elements known as neurons. However, the specific mechanisms underlying this framework are not yet fully understood. The primary objective of engineering and computer science researchers is to develop models that replicate the brain’s information processing capabilities. A promising approach in this regard is the brain-inspired reservoir computing model, which has demonstrated effectiveness in diverse applications.
Reservoir computing (RC) is a framework for constructing recurrent neural networks that can model time-varying complex sensory signals [1, 2]. In the RC framework, recurrent connections are randomly and sparsely configured and do not require training. The readout connections from the reservoir are trained to reproduce a given target time series, reducing the network’s computational cost. An important feature of RC is that it requires extremely low computational cost for learning because only the connections in the readout part are acquired through training. In addition, RC has many applications, including time-series generation and prediction, pattern recognition in time series, and robot control. The key requirement for RC is the presence of high-dimensional, that is, a large number of nodes or neurons that give rise to complex dynamics. Another important feature of the RC framework is the several possible physical implementations [3, 4], including electrical and optical systems, among other numerous possibilities. Provided that it has high dimensionality, nonlinearity, and echo state property, it can serve as a reservoir for computing. The framework of reservoir computing is being actively researched as an approach for modeling brain regions, such as the prefrontal cortex and cerebellum [5, 6].
Predictive coding is a theory of brain function, in which the brain processes sensory information by generating and updating internal models of the external world [7,8,9]. These models enable the brain to predict future sensory inputs. When the actual input deviates from the predicted input, prediction error signals are generated and sent back through the neural network to update the models. The iterative process of generating and updating predictions improves the accuracy of the model and reduces prediction error over time. Predictive coding is a widely accepted framework for understanding perception, attention, and learning in the brain and has been applied to various sensory modalities, including vision, audition, and touch. The predictive coding model is a key component of many neural network models of the brain and has been used to explain different neural phenomena, such as adaptation, attentional modulation, and perceptual illusions. Despite its success, however, the predictive coding model remains an active area of research with ongoing debates over the specific mechanisms and neural substrates underlying predictive coding in the brain [10].
The brain’s reward system and the process of reinforcement learning are essential components of decision-making and learning. The reward system is a collection of neural circuits that processes information related to motivation, pleasure, and rewards. It plays a critical role in shaping behavior, such as learning and motivation, by providing feedback on the outcomes of an action. The neurotransmitter dopamine, which is released in response to a reward or the anticipation of a reward, is a key mediator of the activity of the reward system. In reinforcement learning, an agent learns to select actions based on rewards or punishments [12]. This involves learning to maximize long-term cumulative rewards by taking actions in an environment. Reinforcement learning algorithms often use trial and error to learn the optimal behavior, explore the environment, and observe the consequences of different actions. The brain’s reward system and the process of reinforcement learning are closely related. The reward system provides feedback that drives the learning process, and reinforcement learning provides a framework for understanding how the brain learns to make decisions based on rewards. Computational models of reinforcement learning have been successful in explaining different behaviors, including goal-directed behavior, habit formation, and addiction [12].
In this chapter, we discuss brain-inspired reservoir computing models for sensory-motor information processing in the brain [13, 14]. First, we introduce the reservoir predictive coding model that corresponds to sensory information processing in the cerebral cortex [11]. Subsequently, we discuss the reservoir reinforcement learning model that corresponds to action learning based on rewards in the basal ganglia [14]. Finally, we present an integrated model that combines these two RC models based on predictive coding and reinforcement learning [14]. This integrated model has the potential to provide a more comprehensive understanding of the brain’s information processing mechanisms.
2 Reservoir-Based Predictive Coding Model
Predictive coding is a neuroscience theory explaining how the brain processes sensory information by constantly making predictions about the world and updating them based on incoming data [7,8,9]. This concept is particularly relevant to the hierarchical organization of the visual system in the brain, which consists of multiple processing stages, each of which is responsible for detecting specific features of the visual input. For example, lower-level neurons may detect simple features such as edges, whereas higher-level neurons may identify more complex patterns or objects. The same principle applies to the architecture of CNNs, which have multiple layers that learn to extract increasingly complex features from input images.
Predictive coding posits that the brain actively generates predictions regarding sensory input at each level of the hierarchy. These predictions are based on information gathered from higher hierarchical levels and on previously learned internal models. These internal models, also known as generative models, make predictions and propagate them to lower levels via a top-down pathway. The difference between the actual input and the prediction, known as the prediction error, then propagates up the hierarchy in a bottom-up manner. This error signal helps the brain update its internal models and refine future predictions.
In the field of neural networks, the predictive coding with reservoir computing (PCRC) model proposed by Katori et al. [11] is a novel approach for processing time-varying sensory signals. The PCRC model employs a reservoir as the generative model for predictive coding, wherein the reservoir generates multidimensional, time-varying sensory signals. The prediction error is subsequently transmitted back to the reservoir, allowing for the rectification of the network’s internal state. This model demonstrates the capability of reconstructing and predicting time-varying sensory signals.
The network architecture within each module comprises four key components: the prediction layer, input layer, prediction error layer, and reservoir (Fig. 1a). Within the module, the input signal located in the input layer is replicated in the prediction layer, which is facilitated by the complex motion of the reservoir. This prediction error is then fed back into the reservoir to minimize errors. During the training phase, the connection between the reservoir and the prediction layer is modulated using the first-order reduced and controlled error (FORCE) algorithm [15].
In the testing phase, the model operates in two distinct modes: error-driven and free-running. The error-driven mode involves feedback on the prediction error to the reservoir to further reduce the error. In contrast, the free-running mode does not involve the transmission of the prediction error to the reservoir, allowing for the autonomous operation of the reservoir. This dual-mode functionality highlights the versatility and adaptability of the PCRC model for processing time-varying sensory signals.
The PCRC module consists of a reservoir, prediction layer, input layer, and prediction error layer, which are mathematically described as follows: The membrane potential, or internal state, and the neuron activities within the reservoir are represented by \(\boldsymbol{m} \in \mathbb {R}^{N_x}\) and \(\boldsymbol{r} \in \mathbb {R}^{N_x}\), respectively, where \(N_x\) denotes the size of the reservoir. The states of the reservoir are updated according to the following equations:
where \(W_{\textrm{rec}} \in \mathbb {R}^{N_x \times N_x} \) represents the matrix for recurrent connections, and \(\tau \) is the time constant. The parameter \(\beta _m\) scales the neuron activities. The reservoir receives inputs from the prediction layer \(\boldsymbol{y}^{(i)} \in \mathbb {R}^{N_y}\) through the feedback connection \(W_{\textrm{back}}\in \mathbb {R}^{N_x \times N_y}\), the prediction error layer \(\boldsymbol{e} \in \mathbb {R}^{N_y}\) with a coefficient \(\alpha _e\) that determines the error feedback strength and model operation mode, and the top-down input from the higher area network \(\boldsymbol{b}^{(i)}(n)\). The states of the prediction and prediction error layers are given by
In the error-driven mode (\(\alpha _e=1\)), the reservoir is updated using the prediction error, and the state of the prediction layer follows the state of the input layer. In the free-running mode (\(\alpha _e=0\)), the reservoir states are updated based on the internal dynamics, independent of the sensory input.
The network’s configuration and learning process involve the following steps. The recurrent connections within the reservoir and the feedback connections from the prediction layer to the reservoir are configured in a random and sparse manner, with no need for training their connectivity. During the training phase, the network operates in error-driven mode, and the connections from the reservoir to the prediction layer are trained using the FORCE learning algorithm with a given time-series dataset. Recurrent connections \(W_{\textrm{rec}}\) are set up using the following procedure. First, create a matrix \(W_0\) filled with zeros. Then, assign the non-zero values of either \(-1\) or 1 to randomly chosen \(\beta _r \times N_x \times N_x\) elements. Then, compute the spectral radius of \(W_0\): \(|\rho _0|\). Define \(W_{\textrm{rec}} = \alpha _r W_0 / |\rho _0| \), where \(\alpha _r\) indicates the strength of recurrent connections. Feedback connections \(W_{\textrm{back}}\) and \(W_{\textrm{e}}\) are set up using the following procedure. Similar to \(W_{\textrm{rec}}\), generate a zero matrix \(W_0\) and assign non-zero values of \(-1\) or 1 to the randomly selected \(\beta _b \times N_x \times N_y\) elements, where \(\beta _b\) specifies connectivity of the recurrent connection. Define \(W_{\textrm{back}} = \alpha _b W_0\), with the strength of the feedback connections given by \(\alpha _b\). Use the same procedure to generate \(W_{\textrm{e}}\) with the coefficient \(\alpha _e\).
The readout connections from the reservoir \(W_{out}\) are updated using the FORCE learning algorithm [15] as follows:
The initial value of \(P(n) \in \mathbb {R}^{N_x \times N_x}\) is \(P(0) = \frac{\boldsymbol{I}}{\alpha _f}\), where matrix \(\boldsymbol{I}\) is an identity matrix and \(\alpha _f\) is a scaling parameter. Once the readout connection training is complete, the module can reconstruct the given input in error-driven mode and predict the input in free-running mode.
The PCRC-based hierarchical model for multimodal processing comprises three modules (Fig. 2b). Each module in the hierarchical model is distinguished by superscript (i), where \(i \in \{V, A, I\}\) denotes the visual, auditory, and integration modules, respectively.
The configuration and learning of this model were performed using the following steps: The recurrent and feedback connections were established in accordance with the previously described procedure. The connection matrices between the lower and higher levels, \(U_{(A)}\) and \(U_{(V)}\), are defined using the method below; their inverse matrices are used for dimensionality reduction.
Firstly, operate the lower area network (visual and auditory areas) in error-driven mode (\(\alpha _e^{(V)}=1\) and \(\alpha _e^{(A)}=1\)) without top-down signals (\(\alpha _{td}=0\)), and gather the time course of the reservoirs \(\boldsymbol{r}^{(V)}\) and \(\boldsymbol{r}^{(A)}\) in the state collecting matrices \(R^{(V)}\) and \(R^{(A)}\), respectively. Next, compute the dimension reduction matrices \(U_{(V)}\) and \(U_{(A)}\). Assuming that T timesteps of reservoir states are collected in \(R^{(i)}\) (\(i\in \{V,A\}\)), \(R^{(i)}\) can be decomposed by principal component analysis (PCA) as \(R^{(i)}=S^{(i)} U_{(i)}^T\). Here, \(S^{(i)}\) is a \(T \times 20\) matrix, and \(U_{(i)}\) is an \(N_x^{(i)} \times 20\) matrix. The dimension reduction matrix \(U_{(i)}^{-1}\) can be obtained as the pseudo-inverse matrix of \(U_{(i)}\). Finally, connect the sensory modules (visual and auditory modules) and the integration using the obtained \(U_{(i)}\), and operate the entire network in error-driven mode (\(\alpha _e^{(V)}=\alpha _e^{(A)}=1\)) with \(\alpha _{td}>0\). The matrices \(W_{\textrm{out}}^{(V)}\), \(W_{\textrm{out}}^{(A)}\), and \(W_{\textrm{out}}^{(I)}\) are acquired using FORCE learning.
Within the hierarchical PCRC model for visual and auditory processing, the integration reservoir is responsible for reconstructing and predicting the compressed and concatenated states of the sensory reservoirs. Consequently, the integration reservoir is expected to reconstruct information from one modality using information from another modality. Both the visual and auditory reservoirs are driven by the prediction error on each sensory module and the integration reservoir.
The multimodal model is assessed using time-series data, consisting of pairs of hand-written digit images and their corresponding spoken number utterances. Three hand-written digit images (“2,” “5,” and “9”) from the MNIST dataset are employed as visual signals [16]. Each image comprises \(28 \times 28\) (784) grayscale pixels. These images undergo preprocessing via non-negative matrix factorization (NMF) and are converted into a 20-dimensional signal. Assuming V is an \(L \times 784\) matrix with each row representing an individual image, and V is a collection of L images, NMF decomposes V into two matrices: \(V=H W\), where H is an \(L \times 20\) coefficient matrix and W is a \(20 \times 784\) feature matrix. The transformed 20-dimensional vector serves as the input to the visual area network. The coefficient vector reconstructed by the PCRC module can be converted back into images using W.
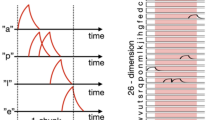
In addition, linguistic data containing spoken number utterances from the Ti46 dataset are utilized as auditory signals [17]. This dataset comprises uncompressed audio data. Each dataset is preprocessed using a cochlear filter model [18], an auditory model that simulates sound propagation within the inner ear, and the conversion of acoustic energy into neural representations. The auditory signals are transformed into 55-dimensional signals. Figure 2 displays samples of the dataset. In the auditory signal, the initiation of spoken number utterances exhibits jitter, starting anywhere from 60 to 90 timesteps. The corresponding visual signals are presented from 80 to 160 timesteps without jitter.
Evaluation of the PCRC-based multimodal model with auditory and visual signals. a Training phase: All modules are operated in error-driven mode. The model is trained with the datasets comprising time-series pairs of visual signals (hand-written digits) and auditory signals (spoken utterances of corresponding digits). Each signal is displayed for 100 timesteps. Visual signals undergo preprocessing using NMF, resulting in a 20-dimensional signal that serves as sensory input for the visual area network. Auditory signals are preprocessed with a cochlear filter and converted into 55-dimensional signals. These signals are then provided as sensory input to the auditory area network. b Cross-modal association from the auditory signal to the visual signal after the training phase: Auditory and the integration modules are operated in error-driven mode, whereas the auditory module is operated in free-running mode. The model is driven by an auditory signal, and the corresponding visual image appears in the prediction layer of the visual area
After training, the network is expected to reconstruct sensory information from one modality based on input signals originating from the other modality. In the subsequent analysis, the focus is on reconstructing visual information in the presence of corresponding auditory signals. In this case, the auditory and integration reservoirs operate in error-driven mode, whereas the visual reservoir functions in free-running mode.
In the association process, a given auditory signal is initially presented to the input layer of the auditory area. At this time, the reservoir maintains a silent state; as no signal is formed in the prediction layer, a significant prediction error occurs. This prediction error serves as a trigger, inducing the motion of the auditory reservoir and generating the auditory signal in the prediction layer. Subsequently, the prediction error gradually decreases. A spatial pattern reflecting the temporal pattern in the auditory signal is represented within the reservoir. This information is spatially compressed and conveyed to the integration reservoir, where only the auditory information is input. The prediction layer in the integration area initially remains silent, and the prediction error triggers the activity of the integration reservoir. As the integration reservoir begins to move, predictions are generated to compensate for the prediction error. At this time, both the auditory and corresponding visual signals are generated. Because there is no signal coming from the lower visual layer, the prediction error regarding the visual information is larger. This prediction error is then transmitted to the visual area, inducing activity in the visual reservoir. Based on the fluctuations in the visual reservoir, visual signal prediction is performed. In summary, a visual signal corresponding to the input auditory signal is generated in the prediction layer of the visual area.
During the processing of multidimensional complex time courses, the proposed hierarchical model combines the mechanisms of temporal structure accumulation and spatial pattern compression. The input signal is reconstructed using a reservoir that captures the temporal structure of the signal within its high-dimensional nonlinear dynamics. Subsequently, the high-dimensional state vector in the reservoir, which encompasses a short history of the signal, undergoes spatial compression and is transferred to the integration area network. This combination of accumulation and compression results in a higher-order abstraction of the intricate time course. In cross-modal association, the processes of compression and abstraction are reversed, allowing the generation of sensory information through expansion and instantiation.
3 Reservoir-Based Reinforcement Learning Model
Reinforcement learning is a type of learning in which an agent learns to choose actions based on rewards or punishments, with the goal of maximizing long-term cumulative rewards by taking actions in an environment. Reinforcement learning algorithms often employ trial and error to learn optimal behavior, explore the environment, and observe the consequences of various actions. The learning process is fueled by feedback from the environment, providing information on the outcomes of an agent’s actions. Among the various reinforcement learning approaches, TD-learning is a model-free technique that merges ideas from dynamic programming and Monte Carlo methods [12, 19]. It estimates the value function (expected future reward) by learning from the difference between consecutive predictions, which is known as the temporal difference error. This method enables agents to learn online and update their value estimates incrementally as new experiences are acquired, making it particularly suitable for learning in dynamic environments.
In recent years, RL has been combined with deep learning to create deep reinforcement learning (DRL), which has achieved remarkable success in solving complex control tasks with high-dimensional sensory inputs, such as images and sounds [20]. DRL algorithms, such as Deep Q-Networks (DQN) [20], proximal policy optimization (PPO) [21], and actor-critic methods [22, 23], have been successfully applied to various applications, such as video game playing, robotics, and autonomous driving.
The two important frameworks within RL are Markov decision processes (MDPs) [24] and partially observable Markov decision processes (POMDPs) [25]. MDPs are a mathematical framework used to model decision-making problems in reinforcement learning, where the environment’s state transitions and rewards are assumed to be Markovian; that is, the future state depends only on the current state and action taken and not on previous states or actions. Although MDPs have been successfully applied to various problems, they exhibit certain limitations, particularly in partially observable environments.
In real-world situations, an agent may not have full access to the environment’s state owing to noisy sensors, occlusions, or other factors. This lack of complete information about the environment’s state can lead to suboptimal decision-making, as the agent cannot accurately estimate the value of different actions. This is where POMDPs play a significant role, extending the MDP framework to handle environments with partial observability.
POMDPs are a generalization of MDPs that consider uncertainty in perceiving the environment’s state. Instead of using the environment’s true state, the agent maintains a belief state, which is a probability distribution over the possible environment states. The belief state is updated as the agent takes actions and receives observations, allowing it to make better-informed decisions even with incomplete information. However, solving POMDPs is generally more computationally demanding than MDPs owing to the increased complexity associated with maintaining and updating belief states.
One approach to address POMDP is the use of reservoirs. Reservoirs, which store not only the current state but also the history of sensory inputs reflecting the environmental state in high-dimensional state vectors, can be expected to function effectively in POMDP environments by compensating for information that cannot be directly observed. In the following, we introduce how the reservoir reinforcement learning model, which is a model that reads action values from the reservoir states where the history of sensory information is accumulated, can effectively function in POMDP environments.
Reservoir-based reinforcement learning and its evaluation. a Network structure of the reservoir-based reinforcement learning. b Environment of the autonomous robot: The robot (agent) is required to move from the start to the goal position. The agent receives a positive reward depending on the distance between the goal position and the robot and receives a negative reward (punishment) if the robot crashes into the wall. c The robot sequentially chooses from one of the possible three actions (move left, right, or forward)
The proposed model consists of a sensory layer, a dynamical reservoir, and an output layer (Fig. 3a). The reservoir receives sensory input from the environment through the sensory layer and generates action values in the output layer, which are then converted to action commands. The reservoir state, comprising \(N_x\) neurons, is denoted by \(\boldsymbol{x}(t) \in \mathbb {R}^{N_x}\). The dynamical reservoir state \(\boldsymbol{x}(t)\) evolves as follows:
where \(\tau _x\) is the time constant; \(W^{\text {in}}\) is the \(N_x \times N_u\) sensory matrix from the sensory layer to the dynamical reservoir, \(W^{\text {rec}}\) is the \(N_x \times N_x\) recurrent weight matrix in the dynamical reservoir, and \(W^{\text {back}}\) is the \(N_x \times N_y\) feedback matrix from the output layer to the dynamical reservoir. These weight matrices \(W^{\text {in}}\), \(W^{\text {rec}}\), and \(W^{\text {back}}\) are randomly and sparsely generated and remain fixed. The neuron firing rate in the dynamical reservoir, r(t), is defined as \(r(t) = f_r(\beta x(t))\), where \(\beta \) specifies the firing rate responses and \(f_r(x) = \tanh (x)\). The output layer state, denoted by \(\boldsymbol{q}(t) \in \mathbb {R}^{N_y}\), represents the \(N_y\) action values and is specified according to:
\(W^{\text {out}}\) is the \(N_y \times N_x\) output weight matrix from the dynamical reservoir to the output layer. Reservoir-based TD-learning is performed on the matrix \(W^{\text {out}}\) to minimize the temporal difference and approximate the action quality (Q-value). Exploration noise, \(s(t) \in \mathbb {R}^{N_y}\), is added to the output. The Q-value for the exploration noise is denoted by \(\tilde{\boldsymbol{q}}(t)\). The connection from the reservoir to the output layer, \(W^{\text {out}}\), is trained using the following equations in an online learning manner:
where a is the index of the action commands, and the action command at time t is given by \(a(t) = \arg \max _i(q_i(t))\). R(t) represents the reward received from the environment, and \(f_q(x) = \tanh (x)\). \(\gamma \) is the discount factor, and \(\eta (t)\) is the learning rate. The exploration noise is temporally correlated and changes according to the following equation:
where \(\tau _s\) is a time constant, and \(\sigma _s\) represents the noise strength. N(0, 1) is a random variable following a normal distribution with a mean of 0 and a standard deviation of 1.
The proposed reservoir reinforcement learning model was assessed within a simulation environment, in which the model was tasked with navigating a robot to a designated goal (Fig. 3b, c). The information received by the agent from the environment is the distance to the obstacles in eight directions around the robot. The sensory layer state is given by \(\boldsymbol{u}(t) = \exp \left( -\frac{\boldsymbol{d}(t)}{d_0}\right) \in \mathbb {R}^{N_u}\), where \(\boldsymbol{d}(t)\) is the sensory signal from \(N_u = 8\) distance sensors. Note that the position and direction information of the robot are not provided to the agent. The agent is required to continuously choose one of three possible actions (move left, right, or forward). The agent receives a positive reward depending on the distance between the robot and the given goal position and a negative reward if the robot crashes on the obstacle. In the simulations, we use the following parameter values: \(N_x = 500\), \(N_u = 8\), \(N_y = 3\), \(\varDelta t = 1\), \(\beta = 1\), \(\tau _x = 2\), \(\tau _s = 20\), \(\gamma = 0.9\), and \(d_0 = 100\).
Figure 4a illustrates the typical robot trajectories during training. Initially, the robot quickly collided with obstacles and failed to reach the goal. However, as training continued, the robot learned to avoid obstacles; after 300 episodes, it successfully circumvented most obstacles and reached the goal.
Robot navigation task a Trajectory of the robot during the learning process. At the beginning of the learning stage (episodes 51–100), the robot collides with obstacles shortly after starting and does not reach the goal. However, in the middle of the learning stage (episodes 151–200), the robot learns to avoid collisions with obstacles. At the end of the learning stage (episodes 251–300), the robot learns to reach the goal while avoiding obstacles. b Temporal changes of sensory input, reservoir, and action value after learning. (Top) Sensory signal reflecting changes in the distance to obstacles as the robot moves. (Middle) Internal state of the reservoir that fluctuates according to the sensory signal. (Bottom) Action-value functions corresponding to the three actions
Figure 4b shows a typical time course of the network state after 300 training episodes. The reservoir state fluctuated in response to the sensory signals, which varied based on the distance between the robot and the obstacles. In the output layer, the Q-values for the three potential actions were determined, reflecting reservoir fluctuations. The action corresponding to the highest Q-value was selected as the motor command. The Q-value for moving forward was lower than those for turning right or left. The maximum Q-value alternated between turning right and left, thereby restricting the robot’s motion to either turning right or left.
The proposed reservoir reinforcement learning model effectively learned the action sequence required to reach a given goal within the environment. The sequence of sensory signals induced substantial fluctuations in the reservoir state, and reward-based training resulted in an appropriate action sequence. Future studies should focus on refining the network model in several ways. From a neuroscience perspective, the function demonstrated in this study, specifically the transformation of sensory information into motor information, underlies the prefrontal cortex. Additional neuroscience-inspired functions should be incorporated, such as the amygdala, which offers a gating mechanism for sensory signals based on their importance, or hippocampal grid and place cells, which enable flexible representation of the agent’s position.
4 Integrated Model and Mental simulation
Mental simulation is a cognitive process in which an individual mentally enacts or imagines a scenario or action without physically performing it [29]. This mental rehearsal can be used for various purposes, such as problem-solving, planning, decision-making, and skill development [28]. Mental simulation allows individuals to predict the outcomes of various actions, assess risks, and evaluate potential solutions without committing to a specific course of action in the real world.
In the context of artificial intelligence and robotics, mental simulation refers to an agent’s ability to internally model and predict the consequences of its actions in a given environment [30]. One approach for implementing mental simulation in AI systems is to use world models, which is an internal representation of the agent’s environment, capturing relevant information regarding the relationships, objects, and dynamics within that environment. By simulating potential actions and their consequences within the world model, the agent can make better-informed decisions, adapt to new situations, and learn from hypothetical scenarios without requiring actual interaction or trial-and-error experiences. This approach can improve the learning efficiency and reduce the time and resources required for training.
Integrated reservoir model of predictive coding and reinforcement learning. a Overall network structure. b Network components operating in each phase and mode: pretraining phase (left), planning model in the test phase, and the execution mode of the test phase. c Optimization of the bias terms of the action value. Optimization of the bias terms is performed so that the state of the simulated environment is close to the desired state. The sequences of the action values generated by the reservoir (upper panel) and the bias term (lower panel). The case of the three possible actions is shown
Action planning task. The goal location is set at the position marked by a star. Robot trajectories (solid curves) are shown when operating in the environment using the action value bias obtained through optimizing the action sequence by mental simulation. Trajectories without action planning (no bias) are represented by dashed curves. When using the action value bias obtained through action planning, the robot reaches the vicinity of the goal location. The starting orientation of the robot is facing right (upper panel) and upward (lower panel)
A reservoir-based mental simulation model combining the predictive coding and reinforcement learning models described above (Fig. 5) has been proposed [27]. In this model, the reservoir generates predictions of the sensory input and action values as readouts. After a pretraining phase, the model operates in two distinct modes: execution and mental simulation. In execution mode, the agent and environment are connected, allowing the reservoir to receive information from the environment and output actions that influence the environment. In contrast, the mental simulation mode involves decoupling the agent’s actions from the environment, with the predictive error feedback disconnected. In this mode, the reservoir functions as a world model, simulating environmental changes within the agent’s internal network.
The process of action planning using mental simulation consists of two phases: pretraining and test. The pretraining phase involves collecting fundamental information about the environment and constructing a world model within the reservoir. In the test phase, the reservoir is detached from the environment, and action planning is conducted by simulating the constructed world model. This enables the optimization of action sequences required to achieve the desired state.
The overall network structure is illustrated in Fig. 5a. The agent receives sensory signals \(\boldsymbol{d}\) from the environment and generates sensory information predictions \(\boldsymbol{y}\) from the reservoir. The agent generates action values \(\boldsymbol{q}\) based on sensory information predictions and the state of the reservoir. This action value is modulated by the bias input \(\boldsymbol{b}\), which is determined by optimization. Actions a are determined based on the action values, and these actions are sent to the environment while simultaneously being fed back into the reservoir.
In the pretraining phase, the agent is connected to the environment and updates the connections from the reservoir to the layers representing sensory information predictions and action values (Fig. 5b left). In the planning mode of the test phase, the agent is disconnected from the environment, and environmental changes and action selection are simulated through the reservoir’s internal dynamics (Fig. 5b center). In the execution mode of the test phase, the agent reconnects to the environment and performs actions in the real environment using the bias determined in the planning mode (Fig. 5b right). During the planning mode of the test phase, the bias terms are optimized such that the state of the simulated environment is close to the desired state.
The model is evaluated in the context of a mobile robot environment. The robot receives the following sensory signals: the distance to obstacles in eight directions around the robot, the position of the robot with a place-cell representation, and the direction of the robot [31].
During the pretraining phase, the robot learns to move through the environment while avoiding collisions with the walls. This pretraining involves generating outputs for both the predictive layer and action value readouts, following predictive coding and temporal difference learning models. In this phase, no specific goal location is defined; however, a negative reward (penalty) is given upon collision with a wall.
During the test phase, action planning is conducted, with the task requiring the robot to navigate to a specific location within the environment. In the mental simulation of the planning mode, the robot generates and optimizes action sequences from the starting point to the desired position in the environment. Action values are augmented with the bias term to modify the actions.
The bias terms consist of three parameters corresponding to the possible number of actions: \(N_y = 3\). In addition to these three parameters, the start time and duration of the bias application must be optimized. In the case of \(N_y=3\), there are a total of five parameters to be optimized. Depending on the task, these bias terms can be combined into multiple sets of modifications to optimize actions. These parameters are optimized by minimizing the distance between the robot’s current position and target location. In the mental simulation, the robot’s position can be estimated from the states generated in the predictive layer, and the distance to the desired position can be measured. The Nelder-Mead method [32] is utilized for parameter optimization.
Figure 6 demonstrates that the action sequences planned through mental simulation can be successfully applied in a real environment, allowing the robot to effectively reach the target location. The solid line represents the trajectory of the robot’s actions. Without context-vector-based action modification, the robot cannot reach its destination (dashed line).
This example illustrates how the dynamic characteristics of reservoir computing can be effectively employed in action planning. Although the robot task presented herein involves only three possible actions and relatively simple planning, more complex environments require further evaluation in the future. In addition to action planning, mental simulation may help accelerate learning processes. Reinforcement learning typically requires trial-and-error learning, involving numerous interactions between the agent and the environment. However, this process can be replaced by mental simulation through internal dynamics.
5 Summary
The brain is an important organ that allows us to perceive the world around us, learn from our experiences, and make decisions based on this learning process. However, understanding the brain’s information processing mechanisms is challenging because of its complexity and dynamism. Brain-inspired reservoir computing models are one approach that seeks to elucidate these mechanisms. These models are based on the idea that the brain processes information using a large population of interconnected neurons, where the dynamics of the system can amplify, transform, and integrate incoming signals.
In this chapter, we discussed brain-inspired reservoir computing models for sensory-motor information processing in the brain. We began by introducing the reservoir predictive coding model based on the theory of predictive coding. Predictive coding posits that the brain constantly generates expectations regarding the sensory input it receives and uses these expectations to interpret and process incoming signals. The reservoir predictive coding model incorporates a reservoir of randomly connected neurons that amplify and transform sensory inputs and generates predictions regarding future sensory inputs. This model also highlights the role of feedback connections between different levels of processing in the brain, which can refine and update these predictions.
Subsequently, we discussed the reservoir reinforcement learning model, which corresponds to action learning based on rewards in the basal ganglia. This model explains how the brain learns to make decisions based on rewards or punishments received after performing a certain action. This model uses a reservoir of randomly connected neurons to represent various possible actions and their associated rewards. The reservoir dynamics allow the brain to learn which actions lead to the most rewards. The reservoir reinforcement learning model also highlights the role of neuromodulators, such as dopamine, in shaping the learning and decision-making processes of the brain.
Finally, we presented an integrated model that combines these two reservoir computing models based on predictive coding and reinforcement learning. This integrated model has the potential to provide a more comprehensive understanding of the brain’s information processing mechanisms. This model demonstrates how the brain integrates sensory information with reward signals to learn the most effective actions for a given situation. It also explains how the brain uses predictive coding to generate expectations about future sensory inputs and accordingly adjusts its actions.
Overall, these brain-inspired reservoir computing models offer a new perspective on the workings of the brain. They provide a theoretical framework for understanding how the brain processes information and learns to make decisions. By incorporating principles from both predictive coding and reinforcement learning, these models offer a more complete picture of the brain’s information processing mechanisms. This could have important implications in fields such as artificial intelligence and robotics, where researchers are trying to build machines that can learn and adapt similar to the human brain.
There are several directions for future research on brain-inspired reservoir computing models. First, it is important to understand the computational and neural mechanisms underlying these models. This could involve conducting simulations and experiments to validate the models and test their predictions. Second, it is interesting to explore how these models can be applied to real-world problems, such as robotic control or natural language processing. Finally, it is important to consider the ethical and societal implications of developing more intelligent machines based on these models.
In conclusion, brain-inspired reservoir computing models offer a promising approach for understanding the brain’s information processing mechanisms. They provide a theoretical framework for guiding future research and motivating new technologies. By advancing our understanding of the brain, these models have the potential to revolutionize fields such as artificial intelligence and neuroscience.
References
H. Jaeger, Tutorial on Training Recurrent Neural Networks, Covering BPPT, RTRL, EKF and the “Echo State Network” Approach, GMD Report, vol. 5 (2002)
W. Maass, T. Natschläger, H. Markram, Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14(11), 2531–2560 (2002). https://doi.org/10.1162/089976602760407955. (Nov.)
G. Tanaka, T. Yamane, J.B. Héroux, R. Nakane, N. Kanazawa, S. Takeda, H. Numata, D. Nakano, A. Hirose, Recent advances in physical reservoir computing: A review. Neural Netw. 115, 100–123 (2019). https://doi.org/10.1016/j.neunet.2019.03.005. (Jul.)
K. Nakajima, Physical reservoir computing—An introductory perspective, nlin.AO, 2005.00992 (2020). https://doi.org/10.35848/1347-4065/ab8d4f
T. Yamazaki, S. Tanaka, Computational models of timing mechanisms in the cerebellar granular layer. Cerebellum 8(4), 423–432 (2009). https://doi.org/10.1007/s12311-009-0115-7
K. Tokuda, N. Fujiwara, A. Sudo, Y. Katori, Chaos may enhance expressivity in cerebellar granular layer (2020). arXiv:2006.11532v1 [q-bio.NC]
R.L. Gregory, Perceptions as hypotheses. Philos. Trans. R. Soc. B Biol. Sci. 290(1038), 181–197 (1980). https://doi.org/10.2307/2395424
R. Rao, D. Ballard, Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87 (1999). https://doi.org/10.1038/4580
K. Friston, Hierarchical models in the brain. PLoS Comput. Biol. 4(11), e1000211 (2008). https://doi.org/10.1371/journal.pcbi.1000211
S. Shipp, Neural elements for predictive coding. Front. Psychol. 7, 1792 (2016). https://doi.org/10.3389/fpsyg.2016.01792
Y. Katori, Network model for dynamics of perception with reservoir computing and predictive coding, in Advances in Cognitive Neurodynamics (VI), eds. by J.M. Delgado-Garcia, X. Pan, R. Sanchez-Campusano, R. Wang (Springer Nature, Singapore, 2017), pp. pp. 89–95. https://doi.org/10.1007/978-981-10-8854-4_11
R.S. Sutton, A.G. Barto, Reinforcement Learning: An Introduction, 2nd edn. (MIT Press, 2018)
E.A. Antonelo, D. Stefan, S. Benjamin, Learning navigation attractors for mobile robots with reinforcement learning and reservoir computing, in Proceedings of the X Brazilian Congress on Computational Intelligence (CBIC) (Fortaleza, Brazil, 2011)
M. Inada, Y. Tanaka, H. Tamukoh, K. Tateno, T. Morie, Y. Katori, Prediction of sensory information and generation of motor commands for autonomous mobile robots using reservoir computing, in Proceedings 2019 International Symposium on Nonlinear Theory and its Applications (NOLTA2019) (2019), p. 333
D. Sussillo, L.F. Abbott, generating coherent patterns of activity from chaotic neural networks. Neuron 63(4), 544–557 (2009)
Y. LeCun, C. Corinna, C. Burges, MNIST Handwritten Digit Database (Florham Park, NJ, USA, 2010)
Texas Instruments Inc, The TI-46 Word Speech Corpus (1990). Visit https://catalog.ldc.upenn.edu/LDC93S9 Linguistic data consortium, TI 46-Word
R. Lyon, A computational model of filtering, detection, and compression in the cochlea. Proc. IEEE 86(11), 2278–2324 (1998); ICASSP ’82. IEEE International Conference on Acoustics, Speech, and Signal Processing, vol. 7 (1982), pp. 1282–1285. https://doi.org/10.1109/ICASSP.1982.1171644
R.S. Sutton, Learning to predict by the methods of temporal differences. Mach. Learn. 3(1), 9–44 (1988)
V. Mnih, K. Kavukcuoglu, D. Silver, A.A. Rusu, J. Veness, M.G. Bellemare, A. Graves et al., Human-level control through deep reinforcement learning. Nature 518(7540), 529–33 (2015)
J. Schulman, F. Wolski, P. Dhariwal, A. Radford, O. Klimov, Proximal Policy Optimization Algorithms, arXiv [cs.LG] (2017). arXiv. http://arxiv.org/abs/1707.06347
V. Konda, J. Tsitsiklis, Actor-critic algorithms, in Advances in Neural Information Processing Systems (2000), pp. 1008–1014
R.S. Sutton, D. McAllester, S. Singh, Y. Mansour. Policy gradient methods for reinforcement learning with function approximation, in Advances in Neural Information Processing Systems (2000), pp. 1057–1063
M.L. Puterman, Markov Decision Processes: Discrete Stochastic Dynamic Programming (Wiley, New York, 1994)
L.P. Kaelbling, M.L. Littman, A.R. Cassandra, Planning and acting in partially observable stochastic domains. Artif. Intell. 101(1–2), 99–134 (1998)
I. Szita, G. Viktor, L. András, Reinforcement learning with echo state networks, in International Conference on Artificial Neural Networks (Springer, Berlin, Heidelberg, 2006), pp.830–839
Y. Yonemura, Y. Katori, Mental simulation on reservoir computing as an efficient planning method for mobile robot navigation, in 2020 International Symposium on Nonlinear Theory and Its Applications (NOLTA2022) (2022), pp.83–86
X. Xiao, B. Liu, G. Warnell, P. Stone, Motion Planning and Control for Mobile Robot Navigation Using Machine Learning: a Survey. Auton. Robot. 1–29 (2022)
S.E. Taylor, L.B. Pham, I.D. Rivkin, D.A. Armor, Harnessing the imagination: mental simulation, selfregulation, and coping. Am. Psychol. 53(4), 429–439 (1998). (April)
J.B. Hamrick, Analogues of mental simulation and imagination in deep learning. Curr. Opin. Behav. Sci. 29, 8–16 (2019)
K. Zhang, I. Ginzburg, B.L. McNaughton, T.J. Sejnowski, Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. J. Neurophysiol. 79(2), 1017–1044 (1998)
F. Gao, L. Han, Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 51, 259–277 (2012)
Acknowledgements
This work was supported by JST CREST(JPMJCR18K2) and JSPS KAKENHI (21H05163, 20H04258, 20H00596, 21H03512) and was based on the results obtained from a project, JPNP16007, commissioned by the New Energy and Industrial Technology Development Organization (NEDO).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this chapter
Cite this chapter
Katori, Y. (2024). Brain-Inspired Reservoir Computing Models. In: Suzuki, H., Tanida, J., Hashimoto, M. (eds) Photonic Neural Networks with Spatiotemporal Dynamics. Springer, Singapore. https://doi.org/10.1007/978-981-99-5072-0_13
Download citation
DOI: https://doi.org/10.1007/978-981-99-5072-0_13
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-99-5071-3
Online ISBN: 978-981-99-5072-0
eBook Packages: Computer ScienceComputer Science (R0)