Keywords

1 Introduction

As the core component of a nuclear reactor, the nuclear reactor pressure vessel (RPV) contains the active zone of the core, holds the primary circuit coolant, supports all components of the reactor, and stabilizes the operating pressure in the reactor [1]. The RPV structural integrity affects the service life of nuclear power plants. Structural materials subjecte to high energy neutron irradiation during the service life in a nuclear power plant, resulting in irradiation aging and deterioration of the mechanical properties [2, 3]. The aging degree of structural materials affects the safety and economy of the reactor, which can be evaluated through the ductile-brittle transition temperature (DBTT) curve of the pre-placed irradiation surveillance specimen in the reactor [4,5,6,7].

In recent years, the early service nuclear power plants are facing the problem of life extension. Considering the conservative design of nuclear power plants, the service life is primarily based on the economic life of construction costs, rather than the aging degree of the structural materials. Therefore, many nuclear power plants approaching the end of the service life need to be evaluated for life-extending. Actually, due to the space limitation inside the reactor cores, the available irradiation surveillance specimens are limited for mechanical testing. The specimen reconstitution technique is considered the most promising solution to the problem of insufficient samples. As shown in Fig. 1, the Charpy specimen reconstitution technique [8,9,10,11] removes the plastic deformation zone of the broken specimen and welds the materials with similar properties at both ends of the retaining elastic zone. The reconstituted specimen is eventually processed into the standard specimen. The reconstitution technique enables the reuse of irradiation surveillance specimens to provide more material property data. With the development of the specimen reconstitution technique, many countries have established relevant technical specifications to guide the reconstituted specimen, such as the enhanced irradiation surveillance program in Belgium [12], the specimen reconstitution technique implementation standard ASTM E1253 in the United States [8], and the formulated technical specifications of JEAC 4201-2007 for irradiation surveillance specimens in Japan [13], etc.

Fig. 1.
figure 1

The specimen reconstitution technique.

Full size image

The central insertion section of the reconstituted specimen should avoid the plastic deformation zone to prevent affecting the results of the reconstituted specimen. Measurement of Stress distribution and the plastic zone for the broken specimen is a necessary step to determine the insertion size in the specimen reconstitution technique. In previous studies, the hardness test was often performed on impact fractures to determine the plastic deformation zone. The place where the hardness test value increases sharply is determined as the edge of the plastic zone. In recent years, finite element numerical simulation has been widely used in the field of engineering science due to the high agreement between the simulation results and the experimental results. The plastic zone can be determined by the simulation graph of the fracture model. Therefore, the hardness test results and simulation results are usually combined to determine the plastic deformation zone of the broken specimen. The reasonable insert length of the reconstituted specimen was determined.

The Ni-Cr-Mo-V steel is studied in this paper. The different temperature impact tests were selected to confirm the ductile-brittle transition temperature. The impact fracture at different temperatures was obtained. And the maximum plastic deformation zone of Ni-Cr-Mo-V steel through the hardness test was determined. In addition, the numerical model of the upper shelf temperature region of Ni-Cr-Mo-V steel was established based on the reverse finite element method. The simulation results were combined with the microhardness test results to accurately determine the reasonable size of the insertion section in the reconstituted specimen. The results provide a theoretical basis for establishing the insertion section sampling specification for the Charpy impact reconstitution technique of the Ni-Cr-Mo-V steel.

2 Experimental Procedure and Materials

2.1 Experiment

The material used in the test is the Ni-Cr-Mo-V steel for RPV. The Charpy impact test is carried out to obtain the DBTT curve of the Ni-Cr-Mo-V steel. And the impact fracture in the different temperature regions was obtained. The absorbed energies are recorded during the impact tests at different temperatures. The RPV steel taken from the base material was processed into a standard Charpy impact specimen, referring to the Russian GOST-9454-1978 standard. The size of the specimen is shown in Fig. 2. The Charpy impact test machine spans 40 mm at both ends of the anvil. The radius of the hammer tup is R = 2 mm. And the theoretical impact speed is 5.2 m/s. The test temperature range is from −120 °C to 100 °C with a temperature control accuracy of ± 1 °C.

Fig. 2.
figure 2

The size of Charpy impact specimens.

Full size image

Vickers hardness is used in the experiment to obtain the hardness distribution in the impact fracture because of its accurate and reliable measurement. The impact fractures that are not broken should be cut from the V-notch as shown in Fig. 3. Before the test started, the impact fracture was polished with sandpaper, 600#, 1000#, 1200# and 1500# respectively. Then polish the specimen with 0.9μm polishing liquid in the microcre polishing. Finally the polished specimens were washed with anhydrous ethanol. The treated specimens were tested by the FALCON-500 automatic micro-Vickers hardness tester. The hardness test was carried out at an interval of 2 mm at the same position from the broken end. Based on the results, the hardness distribution graph was drawn. And the average value of the distance from the same position of the broken end was obtained to draw the hardness trend graph.

Fig. 3.
figure 3

The impact fracture.

Full size image

2.2 Numerical Simulation

In the process of numerical simulation, an accurate and reasonable intrinsic constitutive relationship is the premise for the success of a numerical simulation. Damage to metallic materials is usually characterized by ductile damage, which is based on the nucleation, growth, and aggregation of micro-voids within the material [14,15,16]. In this case, Gurson [17] developed a set of damage constitutive equations based on introducing the void volume fraction in the mesoscopic damage mechanics. The Gurson model establishes the relationship between plastic deformation and the evolution of microcavities. Since then Tvergaard [18, 19] and Needleman [19, 20] further modified the Gurson model to obtain a more accurate Gurson-Tvergaard-Needleman model (GTN) [21,22,23].

The Charpy impact process was simulated using ABAQUS/Explicit based on the reverse finite element method. The model adopts the GTN intrinsic equation with element type C3D8R and local refinement of the mesh at the contact of the specimen. The mechanical property parameters of the Ni-Cr-Mo-V steel required for the simulations were obtained by tensile experiments. The tensile test was carried out on a ZWICK tester using the videoXtens2-120 HP video extensometer. The tensile test refers to GB/T 229.

3 Results and Discussion

3.1 Experiment

3.1.1 Charpy Impact Test

According to the Charpy impact results, the upper and lower shelf energy of the Ni-Cr-Mo-V steel was determined according to the experimental temperature and the absorbed energy. And the ductile-brittle transition temperature curves for Ni-Cr-Mo-V steel were obtained through the hyperbolic tangent function (1):

$$ {\rm{U}} = \frac{{\mathop E\nolimits_{p} + \mathop E\nolimits_{l} }}{2} + \frac{{\mathop E\nolimits_{p} - \mathop E\nolimits_{l} }}{2}\tanh \frac{T - D}{C} $$
(1)

where: Ep – the upper shelf energy, J;

El – the lower shelf energy, J;

T – Temperature, °C;

C, D – the fitted value.

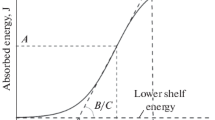
According to Eq. (1), the ductile-brittle transition temperature curves are fitted for Ni-Cr-Mo-V steel, which is shown in Fig. 4. It shows that the overall temperature curve presents an “S” shape. The absorbed energy is basically around the fitted curve. The Charpy impact data shows good stability. On the curve, the upper shelf energy (USE) of the steel is 238J and the lower shelf energy (LSE) is 2.7J. Figure 4 shows that when the temperature rises to 70 °C, the absorbed energy value of the Ni-Cr-Mo-V steel tends to 238J. When the specimen is cooled to −105 °C, the material also has a similar change trend. The absorbed energy in the energy transition temperature (ETT) is relatively discrete. The phenomenon is caused by unstable material properties in the ETT region. According to the PДЭO.0598–2004 specification, the temperature corresponding to the absorbed energy of 47J is used as the DBTT Tk = T47J ≈ −72 °C.

Fig. 4.
figure 4

The ductile-brittle transition temperature curves for Ni-Cr-Mo-V steel.

Full size image

3.1.2 Hardness Test

After the Charpy impact test, the impact fracture at different temperatures was obtained. Based on the hardness test results, the hardness distribution graph at different temperatures was drawn.

Figure 5 shows the hardness distribution along the length of the impact fracture at the lower shelf. It is found that the hardness of the specimen at the lower shelf does not change significantly. There is almost no plastic deformation in the lower shelf of the Ni-Cr-Mo-V steel. Figure 6 shows the hardness distribution of the impact fracture at −55 °C. There is an abrupt change near the broken end, especially at the location of the hammer tup impact where the hardness is highest. This is due to the high strain rate strengthening causing plastic deformation of the material during the impact. The conclusion is that the upper shelf fracture should have a similar deformation in Fig. 7. Comparing Fig. 6 with Fig. 7, it was found that the specimen has a larger hardness abrupt change region on the upper shelf. The width of the plastic deformation zone is the largest in the hardness distribution graph of the upper shelf fracture.

According to the hardness distribution of the material, the location where the hardness value steep increases would be the edge of the plastic deformation zone of the broken specimen. To accurately measure the size of the plastic deformation zone, the hardness trend graph is shown in Fig. 8. The hardness value of the lower shelf fracture remains largely unchanged at 232 HV0.3. The impact fracture of the ETT region shows that the hardness value is relatively stable in the elastic zone away from the fracture. And the hardness value has a large change in the plastic zone. The hardness of the specimen in the transformation zone changes from 232HV0.3 to 241 HV0.3 at 4.5 mm from the fracture. The upper shelf fracture has a similar phenomenon, except that the length of the plastic deformation zone changes from 4.5 mm to 7.0 mm. Figure 8 shows that the plastic deformation zone of the specimen becomes increases with the temperature increases. The largest plastic deformation zone at the upper shelf with a length of approximately 7 mm. The hardness test results match the prediction of the ductile-brittle transition temperature curve for Ni-Cr-Mo-V steel, which with the largest plastic deformation zone in the upper shelf region.

Fig. 5.
figure 5

The hardness distribution of the impact fracture at the lower shelf. a) impact fracture, b) The hardness distribution graph.

Full size image
Fig. 6.
figure 6

The hardness distribution of the impact fracture at −55 °C. a) impact fracture, b) The hardness distribution graph.

Full size image
Fig. 7.
figure 7

The hardness distribution of the impact fracture at the upper shelf. a) impact fracture, b) The hardness distribution graph.

Full size image
Fig. 8.
figure 8

The hardness trend of the impact fracture at different temperatures region.

Full size image

3.2 Numerical Simulation

The GTN model is widely used to simulate ductile damage fracture of metals, and it is one of the most classic models in damage dynamics. The complete GTN model with the following Eqs. (2):

$$ \Phi = \mathop {(\frac{{\mathop \sigma \nolimits_{eq} }}{{\mathop \sigma \nolimits_{m} }})}\nolimits^{2} + 2\mathop q\nolimits_{1} \mathop f\nolimits^{ * } \cosh (\mathop q\nolimits_{2} \frac{3}{2}\frac{{\mathop \sigma \nolimits_{h} }}{{\mathop \sigma \nolimits_{m} }}) - (1 + \mathop q\nolimits_{3} \mathop f\nolimits^{ * 2} ) = 0 $$
(2)

where q1, q2, q3, \({f}^{*}\) are the correction parameters. The void volume fraction \({f}^{*}\) affects the growth, nucleation and coalescence of the material. The functional relationship is as follows (3):

$$ \mathop f\nolimits^{ * } = \left\{ {\begin{array}{*{20}l} f \hfill & {f_{0} \le f \le \mathop f\nolimits_{c} } \hfill \\ {\mathop f\nolimits_{c} + \frac{{(\mathop f\nolimits_{u}^{ * } - \mathop f\nolimits_{c} )}}{{(\mathop f\nolimits_{F} - \mathop f\nolimits_{c} )}}(f - \mathop f\nolimits_{c} )} \hfill & {f_{c} {\rm{ < }}f \le \mathop f\nolimits_{F} } \hfill \\ \end{array} } \right. $$
(3)

where \({f}_{u}^{*}\) is the ultimate value of the damage parameter, \({f}_{0}\) is the initial void volume fraction, \({f}_{\mathrm{c}}\) is the critical void volume fraction, \({f}_{\mathrm{F}}\) is the final void volume fraction. The equation shows that the material has certain microvoids in the GTN model. With the increase of plastic deformation, the void volume fraction reaches the critical value \({f}_{\mathrm{c}}\), at which time the microvoids coalesce. When the void volume fraction further coalescence to \({f}_{\mathrm{F}}\), the material will fracture. At this time, the material appears a lost load-bearing capacity. The failure element will be deleted.

The damage evolution of the material in the GTN model exists mainly in two forms, the growth of the initial voids fg and the nucleation of new voids fnu. Therefore, the change of the void volume fraction of the material is also dominated by these two components, as shown in (4):

$$ df = \mathop {df}\nolimits_{g} + \mathop {df}\nolimits_{nu} $$
(4)
$$ \begin{gathered} \mathop {df}\nolimits_{g} = (1 - f)\mathop {d\varepsilon }\nolimits^{p} :I \hfill \\ \hfill \\ \end{gathered} $$
(5)
$$ \mathop {df}\nolimits_{nu} = \frac{{\mathop f\nolimits_{N} }}{{\mathop S\nolimits_{N} \sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}\mathop {(\frac{{\mathop \varepsilon \nolimits^{p} - \mathop \varepsilon \nolimits_{n} }}{{\mathop S\nolimits_{N} }})}\nolimits^{2} } \right]d\mathop \varepsilon \nolimits^{p} $$
(6)

where \({\varepsilon }^{p}\) is the equivalent plastic strain of the material, fN is the volume fraction of void nucleation, \({\upvarepsilon }_{\mathrm{n}}\) is the mean strain for void nucleation, SN is the corresponding standard deviation of void nucleation.

The requirements of the GTN model include the inherent material parameters. There are nine undetermined parameters to be determined which are q1, q2, q3, f0, fN, fc, fF, εn, SN. Considering the symmetry of the Charpy impact specimen structure and load, the model is established with 1/2 of the thickness direction of the Charpy impact specimen. The symmetry constraint boundary conditions were given at the cross-section. The impact results have shown that Ni-Cr-Mo-V steel has the largest absorbed energy and the greatest plastic deformation zone of the fracture in the upper shelf. To ensure that the size of the insertion section of the reconstituted specimen satisfies the reconstitution technique. The numerical simulations should be carried out for the upper shelf. The load-displacement curve obtained from the simulation was compared with the experimental curve. The two curves should be matched to accurately reproduce the impact process of the Ni-Cr-Mo-V steel. The GTN damage model parameters were finally determined, as shown in Table 1. The hammer tup and anvil of the model are set as rigid structures with a material density is 7.8 × 103 kg/m3, Young’s modulus is 210 GPa and the Poisson’s ratio is 0.3. The parameters obtained from the tensile test and the required for the impact model are shown in Table 2.

Fig. 9.
figure 9

The load-displacement graph of the Charpy impact and simulation results on the upper shelf.

Full size image
Fig. 10.
figure 10

The cloud diagram of the plastic deformation on the upper shelf.

Full size image

At the end of the simulation of the impact process, the load-displacement graph was obtained. Figure 9 shows that the simulation results are consistent with the overall trend of the impact test. The simulation model better reproduces the impact of the Ni-Cr-Mo-V steel on the upper shelf. The cloud diagram of the plastic deformation zone of the upper shelf fracture is shown in Fig. 10. The figure shows that the plastic deformation of the broken specimens on both sides of the notch is symmetrically distributed, which is consistent with the theoretical reasoning of fracture mechanics. The cloud has a similar deformation distribution to the hardness distribution shown in Fig. 7b. The graph shows that the greatest plastic deformation where the hammer tup touches. There is no plastic deformation in the region of the V-notch, which the stresses from the impact are released near the V-notch. The maximum plastic deformation size of the upper shelf fracture can be determined from the outermost contours of the plastic cloud in the numerical simulation. Figure 10 shows that the maximum length of the plastic deformation zone at the upper shelf is approximately 7 mm, which also corresponds to the hardness results.

Table 1. GTN model parameters.
Full size table
Table 2. The impact model parameters.
Full size table

3.3 Insert Length

To accurately measure the mechanical properties of the reconstituted specimen, the reconstituted specimen should reflect the properties of the virgin specimen, which requires that the central portion should avoid the plastic deformation zone. Finally, the broken specimen on the upper shelf was selected for the simulation. The hardness test results are consistent with the simulation results. The plastic deformation zone of the Ni-Cr-Mo-V steel in the upper shelf region is about 7.0 mm. Ultimately, the insert length of the Charpy reconstituted specimen of the Ni-Cr-Mo-V steel was determined to be 20 mm, which conforms to the technical specification for reconstituted specimens, as shown in Fig. 11.

Fig. 11.
figure 11

The insertion section sampling specification of the Charpy reconstituted specimen.

Full size image

4 Conclusions

The main purpose of the paper is the reconstituted specimens of Ni-Cr-Mo-V steel to obtain more specimen data in response to the scarcity of irradiation surveillance specimens. After obtaining the DBTT curve, the impact fractures at different temperatures are also obtained. The DBTT of the Ni-Cr-Mo-V steel is −72 °C. The conclusion shows that the Ni-Cr-Mo-V steel has better ductility. The hardness test is carried out on the impact fractures of the different temperature regions. The length of the plastic deformation zone in the ETT region is 4.5 mm. But the length of the plastic deformation zone in the USE region is 7.0 mm. The hardness test results show that the plastic deformation zone of the Ni-Cr-Mo-V steel becomes increases with the temperature increases. In addition, the finite element numerical simulation of the impact process in the upper shelf was carried out by ABAQUS. The GTN (Gurson-Tvergaard-Needleman) fine damage model was established based on the reverse finite element method. The numerical simulation results compared with Charpy impact results to determine the GTN model parameters. The maximum plastic deformation zone of the simulation results is approximately 7.0 mm, which is consistent with the hardness test results. The insertion section size of the Ni-Cr-Mo-V steel reconstituted specimen was determined to be 20 mm, which provided data basis for the insertion section sampling specification of the Charpy reconstituted specimen.