Keywords

1 Introduction

The lock capacity is an important technical and economic parameter to determine the scale of lock. It is an important research content in the planning and design of lock. The scientificity of its calculation results will directly affect the rationality of lock design scale. China's code for Master Design of shiplocks (2001) defines the lock capacity as the total deadweight tonnage of ships passing through the lock and the cargo volume passing through the lock in the design level year. Among them, the total deadweight tons of ships passing the lock refer to the sum of deadweight tons of all ships passing the lock in a year under the conditions of predicted ship type combination, ship passing efficiency and navigation days, which is the capacity under ideal conditions. The calculation of cargo volume passing through the gate should also consider non cargo factors, ship loading rate and operation imbalance, so as to obtain the sum of the actual cargo volume passing through the lock in one year. There are many factors affecting the lock capacity, including ship type scale and ship type combination, navigation speed of ships entering and leaving the lock, ship spacing, lock filling and emptying time, gate opening and closing time, plane scale of lock chamber and approach channel, navigation days, ship loading rate, traffic volume imbalance, daily working time, etc. so the calculation of lock capacity is a very complex work.

The simulation research of lock capacity refers to the method of analyzing the lock capacity by building a simulation model based on the system simulation theory and using the scheduling algorithm and optimization algorithm. In the simulation model, the random arrival of ships and the distribution proportion of ship types could be considered, so as to realize the random arrangement of ships passing through the lock and simulating the dispatching rules of ships passing through the lock. Compared with the methods of manual arrangement shifting and calculating the lock capacity according to the code for overall design of lock, it is more objective and scientific.

Many scholars have applied the research method of system simulation to the determination of the lock capacity, and the optimization problems such as the joint scheduling of multi-level and multi-line locks and upstream and downstream navigation buildings (Shang et al. 2018). Shang et al. (2011) constructed the simulation model of the joint scheduling of the four line lock of Changzhou hydro junction project, and analyzed the lock capacity and operation effect under different joint scheduling schemes. Zhang et al. (2015) constructed the shipping scheduling simulation model of multi lock and bottleneck reach of Yangzhou section of Yanshao line to simulate and optimize the shipping scheduling. Adhikari et al. (2014) used the research method of sensitivity analysis on demand change and waiting time to evaluate the Ohio Hanoi river shipping system composed of 9 ship locks.

When the system simulation method is applied to study the lock capacity and other related problems (Shang et al. 2018; Wu et al. 2013), and when the lock capacity is scientifically and reasonably determined in engineering practice, the parameters of the simulation model are generally taken as the average value. However, in reality, some data in the process of ship passing the lock change within a certain range and have a certain randomness. Therefore, whether the average value of the corresponding parameters in the simulation model, rather than the random value within a certain range, will have a significant impact on the results of lock capacity. So this needs further research. This paper analyzes and studies the rationality of taking the average value of parameters when using the system simulation method to study lock capacity.

2 Calculation and Simulation Model of Lock Capacity

2.1 Scope of Model Research

The whole process of ship passing through the lock is simulated by the lock capacity simulation model, which includes upstream and downstream anchorages, upstream and downstream approach channels, berthing structures and lock chambers.

2.2 Ship Passing Simulation Process

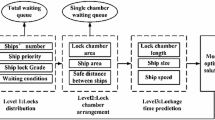
The simulation flow of ship passing through the lock (taking the downstream direction as an example) is shown in Fig. 1. The ship's passing arrangement algorithm is based on the two-dimensional packing algorithm (Shang et al. 2011).

Fig. 1.
figure 1

Simulation flow for ship passing the lock.

Full size image

2.3 Model Input Parameters

  • Lock dimensions. It mainly includes the dimensions of the lock chamber, approach channel and other dimensions related to the ship arrangement and navigation in and out of the lock.

  • Passing ship. It mainly includes the scale of the ship passing the lock, the composition of the ship and the relevant characteristics of the ship's entering and exiting operation.

  • Lock operation. It mainly includes the operation time of relevant facilities and equipment of the lock and the time when the lock can work normally.

Among the above parameters, the length and width of ship arrangement in the lock chamber, the water depth on sill and the operation distance entering and exiting the lock have been determined when designing the lock. The ship type combination and the distribution of ship arrival law are determined after economic analysis. The annual operation days and daily working hours are determined by considering the factors that may affect the operation in the design stage.

Generally, these parameters will not change in the simulation process. In the real scene, the speed of entering and leaving the lock and the start interval between the front and back ships are not only affected by the objective conditions such as the ship's operating performance, the weight and type of loaded goods, the layout of the lock and the water flow conditions, but also affected by the subjective factors such as the captain's experience and driving style. Therefore, there are great differences between ships. The opening and closing time of the gate is mainly determined by the mechanical equipment and water flow conditions. The filling and emptying time is mainly determined by the layout of the lock culvert and water flow conditions. Generally, there will be little change during normal operation.

Therefore, this paper mainly analyzes the rationality of average value for the ship entering and exiting speed and start interval in the simulation model.

2.4 Output Results

Through the simulation model, the utilization rate of lock chamber, the number of ships passing through the lock and the lock capacity can be obtained. Among them, the utilization rate of lock chamber is the average value of the ratio of the sum of the lock chamber area occupied by ships in lock chamber area during the operation period of the simulation model. The number of ships passing through the lock is the sum of the number of ships passing through the lock in the running time period of the simulation model; the lock capacity of the ship lock is the sum of the cargo tonnage of each ship passing through the lock in the running time period of the simulation model.

3 Selection of Probability Distribution

3.1 Typical Probability Distribution

Typical probability distributions include normal distribution, Irish distribution, exponential distribution and triangular distribution. Normal distribution is the most important distribution in probability theory and mathematical statistics. The central limit theorem has proved that many random variables, such as measurement error, product weight, human height and annual rainfall, can be described or approximately described by normal distribution. The distribution is also widely used in engineering field. Irish distribution and exponential distribution are widely used in queuing theory, including port service system. The analysis of a large number of port statistical data shows that the arrival law of ships and the time of ships occupying berths generally accord with the exponential distribution and Irish distribution. Triangular distribution is usually used to calculate reasonable common values according to the known minimum and maximum values in the absence of sampling data.

3.2 Random Values and Assumptions of Parameters

In conclusion, in the absence of statistical data, a simple probability distribution, namely triangular distribution, should be adopted as the probability distribution of random value of parameters. Normal distribution or Irish distribution can also be selected when there are certain statistical data.

In the simulation model of this study, the random values of ship entering and exiting speed and start interval are assumed as follows:

  1. i.

    The start intervals of each ship and its previous ship in a lock are different, and the starting intervals of the same ship when entering and exiting the lock are the same, which meets the triangular distribution;

  2. ii.

    The speed of each ship entering and exiting the lock is different, and the speed meets the triangular distribution, while the ratio of the speed of the same ship entering and leaving the lock to the corresponding average value is the same;

  3. iii.

    If the calculated speed of ship is greater than the front ship, in order to avoid the possibility of ship overtaking or collision in the model, set the speed of the ship behind to be the same as the front ship, so that the distance between the two ships remains unchanged.

4 Case Analysis

4.1 Test Parameters and Simulation Conditions

4.1.1 Dimension of Lock Chamber

In the simulation model, the length of the lock chamber is 280 m and the width is 34 m and 40 m respectively, without considering the influence of the water depth on sill when the ship passes the lock.

4.1.2 Ship Type Distribution Proportion

The statistical data of ship types passing through the lock in a certain year are selected as the distribution proportion of current ship types (see Table 1). Considering the improvement of the scale of the lock and the navigation conditions of the channel in the future, it is expected that the ship type passing the lock will continue to develop towards large-scale, and the proportion of large ships (ship width greater than 16.3 m) will gradually increase and become the main ship type. Therefore, it is predicted that the proportion of large ships is 50%, 60%, 70% and 80% respectively as combination 1–4 (see Table 2). Large ships of current ship types account for about 20.2%.

Table 1. Distribution proportion of current ship type
Full size table
Table 2. Predicted ship type distribution proportion
Full size table

4.1.3 Parameter Random Value

Take the average value of the ship's entering and exiting speed and the start interval between the front and back ships as the basic working condition. When the above parameters are taken at random, considering the range of probability distribution from small to large, the following three groups of triangular distribution forms are adopted: Form 1 - the minimum and maximum values of distribution are 90% and 110% of the average value respectively, form 2 - the minimum and maximum values of distribution are 80% and 120% of the average value respectively, and form 3 - the minimum and maximum values of distribution are 70% and 130% of the average value respectively. From taking the average value to taking the random value in the form of triangular distribution 1–3, the randomness of parameter value gradually increases.

4.1.4 Lock Operation

Considering the weather, maintenance, overhaul and other reasons, the annual operation days are taken as 335d. The daily operation hours are taken as 24 h.

4.1.5 Test Conditions

A total of 40 groups are selected according to different lock chamber dimensions and random parameters. See Table 3 for details.

Table 3. Test conditions
Full size table

4.2 Analysis of Simulation Results

4.2.1 Test Condition Analysis

The lock capacity is affected by many factors, such as the total number of ships passing through the lock, the distribution proportion of ship types and so on. For the 34 m wide lock, although with the increase of the proportion of large ships, the total number of ships passing through the lock decreases and the utilization rate of the lock chamber decreases, the lock capacity decreases first and then increases; For the 40 m wide ship lock, with the increase of the proportion of large ships, the total number of ships passing through the lock decreases, the utilization of the lock chamber first increases and then decreases, while the lock capacity first increases and then decreases; See Figs. 2, 3 and 4 for details. With the increase of the proportion of large ships, the complex change trend of lock capacity shows that different factors have successively become the main factors affecting the lock capacity. Therefore, it can be considered that the test condition can comprehensively reflect the combination of different influencing factors.

Fig. 2.
figure 2

Lock capacity.

Full size image
Fig. 3.
figure 3

Lock chamber utilization.

Full size image
Fig. 4.
figure 4

Numbers of ships passing the lock.

Full size image

4.2.2 Influence of Random Value of Entering and Exiting Speed on the Lock Capacity

Keeping the average start interval unchanged, the lock capacity under the condition of random entering and exiting speed are shown in Fig. 5 and Fig. 6. It can be seen that under the condition of the same lock chamber size and ship type distribution combination, the lock capacity decreases with the increase of the randomness of the entering and exiting speed. Under the same ship type distribution combination, compared with the average value method, the maximum reduction of the lock capacity is only 1.5%–1.7%, which can be considered as no effect on the lock capacity.

Fig. 5.
figure 5

The lock capacity under the different ship type combinations, when the entering and exiting speed is taken as different distribution (dimension of lock chamber, 280 m × 34 m).

Full size image
Fig. 6.
figure 6

The lock capacity under the different ship type combinations, when the entering and exiting speed is taken as different distribution (dimension of lock chamber, 280 m × 40 m).

Full size image

4.2.3 Influence of Random Value of Start Interval Between Front and Back Ships on the Lock Capacity

Keeping the average value of the entering and exiting speed unchanged, the lock capacity under the condition of random value of the start interval between the front and back ships are shown Fig. 7 and Fig. 8. It can be seen that under the same lock chamber scale and ship type distribution combination, with the increase of the randomness of the value of start interval, there is no obvious change law of ship lock capacity. Under the same ship type distribution combination, compared with the average value method, the maximum reduction of the lock capacity is only 0.1%, which has no effect.

Fig. 7.
figure 7

The lock capacity under the different ship type combinations, when the start interval of the ship is taken as different distribution (dimension of lock chamber, 280 m × 34 m).

Full size image
Fig. 8.
figure 8

The lock capacity under the different ship type combinations, when the start interval of the ship is taken as different distribution (dimension of lock chamber, 280 m × 40 m).

Full size image

5 Conclusions

  1. i.

    The parameters with certain randomness in the simulation study of lock capacity mainly include ship entering and exiting speed and start interval.

  2. ii.

    Under the condition of the same lock chamber scale, ship type distribution combination and start interval, with the increase of the randomness of the value of the entering and exiting speed, the lock capacity shows a decreasing trend, but it can be ignored.

  3. iii.

    Under the condition of the same lock chamber scale, ship type distribution combination and average entering and exiting speed, the lock capacity does not change significantly with the increase of the randomness of the starting interval.

  4. iv.

    It is reasonable and credible to take the average value of each parameter in the simulation model when carrying out the simulation research of lock capacity and applying the system simulation method to scientifically and reasonably determine the ship lock capacity in engineering practice.

  5. v.

    The random value of parameters in the simulation model will increase the difficulty of parameter acquisition and simulation modeling in the research process, and may reduce the operation efficiency of the model. Therefore, considering the above factors, it is suggested to take the average value of the parameters in the model when using the system simulation method to determine the lock capacity.