Skip to main content
SpringerLink
Log in

Impact of Forthcoming Price Increase for Maximum Fixed Lifetime Product with Preservation Technology Investment and Price-Sensitive Demand

  • Conference paper
  • First Online:
Recent Trends in Design, Materials and Manufacturing

Part of the book series: Lecture Notes in Mechanical Engineering ((LNME))

  • 349 Accesses

Abstract

Whenever a supplier proclaims a price rise, the effect is amplified at a predetermined point in the future. At that point, each retailer should decide whether to buy more stock or to purchase at a higher price to take benefit of the present lower price. The result of price changes on the retailer's daily replenishment strategy for deteriorating items with expiry dates is discussed in this model. Price-sensitive demand is addressed in this research and is appropriate for products whose demand falls rapidly as the price of the product rises. This article advocates two scenarios: (I) when the special-order time coincides with the retailer’s replenishment time; and (II) when the special-order time occurs during the retailer’s sales period. The crucial objective of this article is to determine the best ordering policies for the retailer in all cases that reduce the profit difference function between the regular order and the special order during the reduction time of the special-order quantity concerning cycle time, selling price, and investment for preservation technology. The scenarios are set up and demonstrated with numerical illustrations. Additionally, to investigate the impacts of key parameters on an optimum solution, a sensitivity analysis is carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 189.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 249.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Naddor E (1966) Inventory systems. Wiley, New York, NY

    MATH  Google Scholar 

  2. Lev B, Soyster AL (1979) An inventory model with finite horizon and price changes. J Oper Res Soc 30(1):43–53

    Article  Google Scholar 

  3. Goyal SK (1979) A note on the paper: an inventory model with the finite horizon and price changes. J Oper Res Soc 30(9):839–842

    Article  Google Scholar 

  4. Lev B, Weiss HJ (1990) Inventory models with cost changes. Oper Res 38(1):53–63

    Google Scholar 

  5. Goyal SK, Srinivasan GF, Arcelus F (1991) One-time only incentives and inventory policies. Eur J Oper Res 54(1):1–6

    Article  Google Scholar 

  6. Khouja M, Park S (2003) Optimal lot sizing under continuous price decrease. Omega 31(6):539–545

    Article  Google Scholar 

  7. Ouyang LY, Wu KS, Yang CT, Yen HF (2014) Optimal order policy in response to the announced price increase for deteriorating items with limited special-order quantity. Int J Syst Sci 47(3):718–729

    Article  MathSciNet  Google Scholar 

  8. Harris FW (1913) How many parts to make at once. Fact Mag Manag 10(2):135–136, 152

    Google Scholar 

  9. Hariga M (1996) Optimal EOQ models for deteriorating items with time-varying demand. J Oper Res Soc 47(10):1228–1246

    Article  Google Scholar 

  10. Panda S, Senapati S, Basu M (2008) Optimal replenishment policy for perishable seasonal products in a season with ramp-type time-dependent demand. Comput Ind Eng 54(2):301–314

    Google Scholar 

  11. Hossen MA, Hakim MdA, Ahmed SS, Uddin MS (2016) An inventory model with price and time-dependent demand with fuzzy valued inventory costs under inflation. Ann Pure Appl Math 11(2):21–32

    Google Scholar 

  12. Shah NH, Jani MY, Chaudhari B (2017) Retailer’s optimal policies for price-credit dependent trapezoidal demand under two-level trade credit. Int J Oper Quant Manag 23(02):115–130

    Google Scholar 

  13. Mashud A, Khan M, Uddin M, Islam M (2018) A non-instantaneous inventory model having different deterioration rates with stock and price dependent demand under partially backlogged shortages. Uncertain Supply Chain Manag 6(1):49–64

    Article  Google Scholar 

  14. Agi MAN, Soni HN (2020) Joint pricing and inventory decisions for perishable products with age-, stock-, and price-dependent demand rate. J Oper Res Soc 71(1):85–99

    Google Scholar 

  15. Ghare PM, Schrader GH (1963) A model for the exponentially decaying inventory system. J Ind Eng 14(5):238–243

    Google Scholar 

  16. Philip GC (1974) A generalized EOQ model for items with weibull distribution deterioration. AIIE Trans 6(2):159–162

    Google Scholar 

  17. Yang HL (2004) Two-warehouse inventory models for deteriorating items with shortages under inflation. Eur J Oper Res 157(2):344–356

    Article  MathSciNet  Google Scholar 

  18. Skouri K, Konstantaras I, Papachristos S, Ganas I (2009) Inventory models with ramp type demand rate, partial backlogging, and Weibull deterioration rate. Eur J Oper Res 192(1):79–92

    Article  MathSciNet  Google Scholar 

  19. Tripathi RP, Tomar SS (2015) Optimal order policy for deteriorating items with time-dependent demand in response to temporary price discounts linked to order quantity. Int J Math Anal 23(9):1095–1109

    Google Scholar 

  20. Shah NH, Jani MY, Chaudhari UB (2016) Impact of future price increase on ordering policies for deteriorating items under quadratic demand. Int J Ind Eng Comput 7(3):423–436

    Google Scholar 

  21. Jani MY, Shah NH, Chaudhari UB (2020) Inventory control policies for time-dependent deteriorating item with variable demand and two-level order linked trade credit. Optim Inven Manag 55–67

    Google Scholar 

  22. Hwang H, Kim D, Kim Y (1993) Multiproduct economic lot size models with investment costs for setup reduction and quality improvement. Int J Prod Res 31(3):691–703

    Article  Google Scholar 

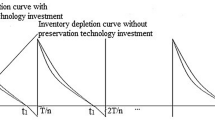
  23. Hsu PH, Wee HM, Teng HM (2010) Preservation technology investment for deteriorating inventory’. Int J Prod Econ 124(1):388–394

    Article  Google Scholar 

  24. Dye CY, Hsieh TP (2012) An optimal replenishment policy for deteriorating items with effective investment in preservation technology. Eur J Oper Res 218(1):106–112

    Article  MathSciNet  Google Scholar 

  25. Shah NH, Chaudhari UB, Jani MY (2017) Optimal policies for a time-varying deteriorating item with preservation technology under selling price and trade credit-dependent quadratic demand in a supply chain. Int J Appl Comput Math 3(2):363–379

    Article  MathSciNet  Google Scholar 

  26. Chaudhari UB, Shah N\H, Jani MY (2020) Inventory modelling of deteriorating item and preservation technology with advance payment scheme under quadratic demand. Optim Inven Manag 69–79

    Google Scholar 

  27. Cárdenas-Barrón LE, Sana SS (2015) Multi-item EOQ inventory model in a two-layer supply chain while demand varies with a promotional effort. Appl Math Model 39(21):6725–6737

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Sciences, Faculty of Engineering and Technology, Parul University, Vadodara, Gujarat, 391760, India

    Mrudul Y. Jani & Manish R. Betheja

  2. Government Polytechnic Dahod, Dahod, Gujarat, 389151, India

    Urmila Chaudhari

Authors
  1. Mrudul Y. Jani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manish R. Betheja
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Urmila Chaudhari
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Department of Mechanical Engineering, Amity School of Engineering and Technology, Amity University, Madhya Pradesh, India

    Manvandra Kumar Singh

  2. Department of Mechanical Engineering, IIT(BHU) Varanasi, Uttar Pradesh, India

    Rakesh Kumar Gautam

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Jani, M.Y., Betheja, M.R., Chaudhari, U. (2022). Impact of Forthcoming Price Increase for Maximum Fixed Lifetime Product with Preservation Technology Investment and Price-Sensitive Demand. In: Singh, M.K., Gautam, R.K. (eds) Recent Trends in Design, Materials and Manufacturing. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-16-4083-4_7

Download citation

  • DOI: https://doi.org/10.1007/978-981-16-4083-4_7

  • Published:

  • Publisher Name: Springer, Singapore

  • Print ISBN: 978-981-16-4082-7

  • Online ISBN: 978-981-16-4083-4

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics

Search

Navigation