Abstract
Motivated by the goal of constructing efficient hash functions, we investigate the possibility of hashing a long message by only making parallel, non-adaptive calls to a hash function on short messages. Our main result is a simple construction of a collision-resistant hash function \(h:\{0,1\}^n\rightarrow \{0,1\}^k\) that makes a polynomial number of parallel calls to a random function \(f:\{0,1\}^k\rightarrow \{0,1\}^k\), for any polynomial \(n=n(k)\). This should be compared with the traditional use of a Merkle hash tree, that requires at least \(\log (n/k)\) rounds of calls to f, and with a more complex construction of Maurer and Tessaro [26] (Crypto 2007) that requires two rounds of calls to f. We also show that our hash function h satisfies a relaxed form of the notion of indifferentiability of Maurer et al. [27] (TCC 2004) that suffices for implementing the Fiat-Shamir paradigm. As a corollary, we get sublinear-communication non-interactive arguments for NP that only make two rounds of calls to a small random oracle.
An attractive feature of our construction is that h can be implemented by Boolean circuits that only contain parity gates in addition to the parallel calls to f. Thus, we get the first domain-extension scheme which is degree-preserving in the sense that the algebraic degree of h over the binary field is equal to that of f.
Our construction makes use of list-recoverable codes, a generalization of list-decodable codes that is closely related to the notion of randomness condensers. We show that list-recoverable codes are necessary for any construction of this type.
The first author was supported by ISF grant 1076/11, I-CORE grant 4/11, BSF grant 2010196, and Check Point Institute for Information Security. The second author was supported by ERC starting grant 259426, ISF grant 1709/14, and BSF grant 2012378. The third author was supported by ERC starting grants 259426 and 279559, and by ISF grant 544/13. The fourth author was supported by ERC starting grant 279559, BSF grant 2010120, and ISF grant 864/11.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In this work we consider the problem of extending the domain of cryptographic hash functions. We start by discussing the case of collision-resistant hash functions, and later address extensions to other types of hash functions.
A family \(\left\{ g:{\{0,1\}}^v\rightarrow {\{0,1\}}^k\right\} \) of efficiently computable, length-decreasing functions is called collision resistant if given the description of a random g from the family, it is computationally infeasible to find a pair of distinct inputs \(s,s'\) such that \(g(s)=g(s')\).
Collision-resistant hashing is a fundamental primitive in cryptography that has been the subject of a large body of work. Its applications span many areas, ranging from the commonly used “hash and sign” paradigm for practical digital signatures [10, 29] to cryptographic protocols such as sublinear-communication commitments [9, 21], succinct and efficiently verifiable arguments for NP [23, 30], and protocols that bypass black-box simulation barriers [1].
The existence of collision-resistant hash functions can be based on a variety of standard number theoretic or algebraic cryptographic assumptions, including the conjectured intractability of factoring, discrete logarithms, and lattice problems [8, 13, 25, 33]. Yet, the task of heuristically constructing highly efficient hash functions that can also be conjectured to have near-optimal security is quite challenging. In particular, this task is arguably more challenging than a similar task for other “symmetric” cryptographic primitives such as one-way functions [41], pseudorandom generators [5, 41], and universal one-way hash functions [31]. This intuition is supported by theoretical results that rule out the possibility of obtaining collision-resistant hash functions from any of these other symmetric primitives via a black-box construction [19, 36]. Practical collision attacks on commonly used hash functions such as MD5 [40] may also be viewed as an indication for the subtle nature of hash function design. Despite the above, there are many practical constructions of cryptographic hash functions that are conjectured to satisfy collision resistance as well as other useful properties. See [4] for a description of SHA-3, the winner of the recent NIST hash function competition, as well as an overview of other work on practical hash function design.
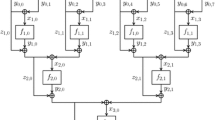
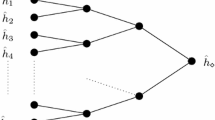
A common technique for building a hash function \(g:{\{0,1\}}^v\rightarrow {\{0,1\}}^k\) that compresses a long input into a short output is by combining multiple invocations of a smaller hash function \(f:{\{0,1\}}^{{k_{in}}} \rightarrow {\{0,1\}}^{{k_{out}}}\) in a way that supports a black-box reduction of the collision-resistance of g to that of f. This technique, known as domain-extension, is motivated by the possibility of carefully designing and analyzing an optimized implementation of f on some fixed input length, and then scaling up its efficiency and security advantages to apply to arbitrarily long inputs. It is sometimes the case that the collision-resistance of g relies on a stronger assumption on f than just collision-resistance. In fact, several domain-extension schemes assume f to be a completely random function (see e.g., [26, 34, 37, 38] and references therein, as well as [20] for discussion of the meaningfulness of such results). In the following we will use the term “domain-extension” in this broader sense. A simple domain-extension technique due to Merkle [28] extends the domain of a hash function \(f:{\{0,1\}}^{2k} \rightarrow {\{0,1\}}^{k}\) for short inputs into a hash function \(g:{\{0,1\}}^{nk} \rightarrow {\{0,1\}}^{k}\) for long inputs by applying a tree of invocations of f whose leaves are k-bit input blocks and whose root is the output.
In this work we consider the question of minimizing the parallel complexity of domain-extension schemes. A natural measure of this complexity is the number of rounds of parallel calls to f. Ideally, one could hope to compute g by only making a single round of calls to f, where the input for each call is computed directly from the input for g, and the outputs of the calls are used to compute the output of g. The hash tree construction falls short of this goal, requiring at least \(\lceil \log _2 n\rceil \) rounds. A more complex construction of [26] comes close to this goal, requiring only two rounds of calls to f.Footnote 1
Our main result is a simple construction of a fully parallel (single-round) domain-extension scheme that realizes a collision-resistant \(g:\{0,1\}^v\rightarrow \{0,1\}^k\) by making a polynomial number of parallel calls to a random function \(f:\{0,1\}^k\rightarrow \{0,1\}^k\), for any polynomial \(v=v(k)\). The construction achieves a near-optimal level of security, requiring an attacker to make roughly \(2^{k/2}\) calls to f in order to find a collision in g with high probability. However, this may come at the cost of a higher number of calls to f compared to traditional domain-extension schemes. See Sect. 7 for a more detailed discussion of the achievable parameters.
Our domain-extension scheme has the attractive feature that g can be implemented by Boolean circuits consisting only of parity gates in addition to the parallel calls to f. Thus, we get the first degree-preserving domain-extension scheme, in the sense that the algebraic degree of g over the binary field is equal to that of f. In contrast, in constructions that make two rounds of calls to f, the degree of g is at least quadratic in that of f. Low-degree hash functions are motivated by applications in the domain of secure computation, in which the cost of evaluating a function may depend on its algebraic degree. See [20] for further discussion.
Our construction makes use of list-recoverable codes, a generalization of list-decodable codes that is closely related to the notion of randomness condensers. We show that list-recoverable codes are necessary for any construction of this type. In the following we give a more detailed account of our results and the underlying techniques.
2 Parallel Domain-Extension
Recall that a domain-extension scheme for hash functions takes as input a fixed length hash function \(f:{\{0,1\}}^{{k_{in}}} \rightarrow {\{0,1\}}^{{k_{out}}}\) and outputs a new hash function for much larger inputs, namely a function \(g:{\{0,1\}}^v \rightarrow {\{0,1\}}^{{k_{out}}}\) for a given \(v > {k_{in}}\). (For the sake of simplicity, we assume that the output length of g is \({k_{out}}\), rather than an additional parameter.) We consider the standard model in which the function f is provided to the construction after being chosen by some randomized process, and the function g uses f as a black-box (i.e., it is oblivious to the concrete implementation of f). The focus of this work is on parallel domain-extension: upon receiving an input \(s \in {\{0,1\}}^v\), the function g first prepares n queries to the hash function f (which we will denote by \(C(s)=(x_1,\ldots ,x_n)\)), and then the final output of g is obtained by computing some function h on the input s and the answers \(f(x_1),\ldots ,f(x_n)\).
Definition 1
(Parallel Domain-Extension Scheme). Let \({k_{in}},{k_{out}},v,n\) be integers, let \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^{{k_{in}}} \right) ^n\) and let h be defined over \({\{0,1\}}^v \times \left( {\{0,1\}}^{{k_{out}}} \right) ^n\). The parallel domain-extension scheme (C, h) is the oracle-aided function \(g_{(C,h)}\) defined as follows. For \(f:{\{0,1\}}^{{k_{in}}} \rightarrow {\{0,1\}}^{{k_{out}}}\), let \(g^f_{(C,h)}:{\{0,1\}}^v \rightarrow {\{0,1\}}^{{k_{out}}}\) be defined by
If the value of (C, h) is clear from the context, we refer to \(g^f_{(C,h)}\) as \(g^f\) or g.
Such a construction should maintain the security of the underlying hash function (i.e., f). In particular, whenever f is chosen from a collision-resistant hash function family, the resulting function g should be collision-resistant as well. As a step towards this goal, it is common to consider the following intermediate goal: assume that f is a random function (which in particular is collision-resistant), and prove that the resulting function g is collision-resistant. In the following let \(\mathcal{{F}}_{{k_{in}},{k_{out}}}\) be the family of all functions mapping \({k_{in}}\)-bit strings to \({k_{out}}\)-bit strings.
Definition 2
(Collision-Resistance in the Random Oracle Model). Let g be an oracle-aided function (i.e., deterministic algorithm), with an oracle mapping \({k_{in}}\)-bit strings to \({k_{out}}\)-bit strings. The function g is \((\ell ,\varepsilon )\)-collision-resistant in the random oracle model, if for any \(\ell \)-query adversary \(\mathcal{A}\) (i.e., \(\mathcal{A}\) makes \(\ell \) oracle calls), it holds that \(\Pr _{f\leftarrow \mathcal{{F}}_{{k_{in}},{k_{out}}}}\left[ (s_1,s_2) \leftarrow \mathcal{A}^f :s_1 \ne s_2 \wedge g^f(s_1)=g^f(s_2)\right] \le ~\varepsilon \).
An important goal is to come up with an efficient collision-resistant parallel domain-extension scheme, according to Definition 2, where efficiency can be measured in terms of circuit size, depth, or algebraic degree. This motivates schemes in which n (the number of queries) is as small as possible, and the functions C and h are efficiently computable.
Our main result is that if we take C to be a list-recoverable code (defined below), then for making the resulting scheme collision-resistant in the random-oracle model, it suffices to take h to be simply the XOR function applied to the n outputs of f.
It turns out that when used with (short) random oracle, our parallel domain-extension scheme also maintains other useful properties of the random oracle. While we cannot show our parallel domain-extension scheme to be indifferentiable from a random function in the sense of Maurer et al. [27], we show that it enjoys a weaker form of indifferentiability, which neither implies nor is implied by collision-resistance. This property will turn out to be sufficient for converting interactive proof system into non-interactive ones using the Fiat-Shamir paradigm [12].
Definition 3
(Weak Indifferentiability). Let \(g:{\{0,1\}}^v \mapsto {\{0,1\}}^t\) be an oracle-aided function, taking an oracle mapping \({k_{in}}\)-bit strings to \({k_{out}}\)-bit strings. The function g is \((\ell ,R,r)\)-weak-indifferentiable from a random function, if for any two-oracle algorithm \(\mathsf {D}\) making \(\ell \) queries to the left-hand side oracle, and a single query to the right-hand side oracle, there exists a single-query algorithm \({\text {Sim}}\) such that \(\Pr _{{f_{{\text {Ideal}}}}\leftarrow \mathcal{{F}}_{{k_{in}},{k_{out}}}}\left[ \mathsf {D}^{{f_{{\text {Ideal}}}},g^{{f_{{\text {Ideal}}}}}} \in E\right] \le R \cdot \Pr _{{g_{{\text {Ideal}}}}\leftarrow \mathcal{{F}}_{v,t}}\left[ \mathsf {D}^{{\text {Sim}}^{{g_{{\text {Ideal}}}}},{g_{{\text {Ideal}}}}} \in E\right] \) for any event E. The simulator \({\text {Sim}}\) is of size r, i.e., it is implemented by a next message circuit of size r (i.e., a circuit that gets as input the past queries and the current one, and returns the answer to the current query).
The main difference between Definition 3 and the standard notion of indifferentiability from [27], is that the above definition only requires domination between the real and emulated pair of systems, whereas [27] require statistical closeness. We also provide \({\text {Sim}}\) the query parameter \(\ell \) as a parameter, which makes our relaxed definition easier to realize. For simplicity, we have fixed the number of queries to the right-hand side oracle to one (both for the distinguisher and the simulator). It turns out that this type of security is achieved by our parallel domain-extension scheme and is sufficient for applying the Fiat-Shamir paradigm as described below. Concretely, we show that by taking C and h to be as above, the resulting function is weakly indifferentiable from a random function, with small (i.e., polynomial) parameters.
We now give some brief intuition for why the above weak indifferentiability property suffices for applying the Fiat-Shamir paradigm to simulate the verifier’s challenge in 3-message public-coin interactive proofs. Let \(\mathsf {P}\) be a malicious prover that convinces the verifier \(\mathsf {V}\) with noticeable success probability. \(\mathsf {P}\) may make \(\ell \) queries to the real short-input oracle before sending his message to \(\mathsf {V}\). We can consider a distinguisher \(\mathsf {D}\) that simulates \(\mathsf {P}\) and then uses one query to the long-input oracle to see whether \(\mathsf {V}\) accepts. \(\mathsf {D}\) accepts iff \(\mathsf {V}\) accepts. Now consider the behavior of \(\mathsf {D}\) in the two experiments that appear in Definition 3. In the real experiment, the probability that \(\mathsf {D}\) accepts is the success probability of \(\mathsf {P}\). In the ideal experiment, \(\mathsf {V}\) uses an ideal (full length) oracle and so the success probability of \(\mathsf {D}\) is bounded by the success probability when applying the Fiat-Shamir paradigm with an ideal hash function.
3 List-Recoverable Codes
Definition 4
(List-Recoverable Code). Let \(\alpha \in [0, 1]\). A tuple \(x \in \left( {\{0,1\}}^k \right) ^n\) is
-
\(\alpha \)-consistent with a set \(T \subseteq {\{0,1\}}^k\), if \(\left| \left\{ i:x_i \in T\right\} \right| \ge \alpha \cdot n\).
-
\(\alpha \)-consistent with sets \(T_1,\ldots ,T_n \subseteq {\{0,1\}}^k\), if \(\left| \left\{ i:x_i \in T_i\right\} \right| \ge \alpha \cdot n\).
A function \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^k \right) ^n\) is \((\alpha ,\ell ,L)\)-list recoverable, if for every set \(T \subseteq {\{0,1\}}^k\) of size at most \(\ell \), there are at most L strings \(s \in {\{0,1\}}^v\) such that C(s) is \(\alpha \)-consistent with T. It is strongly \((\alpha ,\ell ,L)\)-list recoverable, if for every \(T_1,\ldots ,T_n \subseteq {\{0,1\}}^k\) each of size at most \(\ell \), there are at most L strings \(s \in {\{0,1\}}^v\) such that C(s) is \(\alpha \)-consistent with \(T_1,\ldots ,T_n\).
For \(\alpha =1\), we omit \(\alpha \) in the above notation. The strings in the image of C are referred to as codewords, and C has distance \(\beta \), if every two codewords differ on at least \(\beta \cdot n\) of the indices.
The function C has a size r list-recovering algorithm, if there exists a circuit of size r that given a set \(T\subseteq {\{0,1\}}^k\) of size at most \(\ell \) returns the full list of (at most L) strings that are \(\alpha \)-consistent with T.
The notion of strongly list-recoverable codes (explicitly defined in [15]) is a natural extension of the more standard uniquely decodable codes (captured by \(\ell =L=1\)) and list-decodable codes (captured by \(\ell =1\) and \(L>1\)). The reader is referred to [14] for a comprehensive treatment of list-decodable codes. In this paper we use the weaker notion of list-recoverable codes (with a single set T instead of a collection \(T_1,\ldots ,T_n\)), as it turns out to be more natural for the applications we consider.Footnote 2 List-recoverable codes show up naturally in coding theory when one considers list-decoding of concatenated codes.Footnote 3 Conveniently, many list-decoding algorithms (e.g., [16, 17, 32, 39]) solve the more general list-recovering problem, and list-decoding is achieved as a special case. The parameter regime that we consider is less standard in coding theory and is strongly related to unbalanced expanders and randomness condensers. We elaborate on this connection in [20].
In our construction we require codes that, in addition to having large distance and being list-recoverable, are also well ordered.
Definition 5
(Well-Ordered Codes). A function \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^k \right) ^n\) is well ordered, if for every \(s_1,s_2 \in {\{0,1\}}^v\) (not necessarily distinct) and for every \(i \ne j\), \(C(s_1)_i \ne C(s_2)_j\).
Constructions of list-recoverable codes in the literature typically have this property. Furthermore, a given function \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^k \right) ^n\) can be converted into a function \(\bar{C}:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^{k+\log n} \right) ^n\) that is well ordered by defining \(\bar{C}(s)_i=(C(s)_i,i)\). This transformation increases the alphabet of the code, but does not compromise the distance or list-recoverability. In our setting \(\log n\) is typically negligible compared to k and so the increase in alphabet size is immaterial. Hence, one can assume without loss of generality that a list-recoverable code is well ordered.
4 Parallel Domain-Extension via List-Recoverable Codes
We show that well-ordered, list-recoverable codes with large distance yield parallel domain-extension schemes that are collision-resistant in the random-oracle model, and furthermore are weak-indifferentiable from a random function. Specifically, this holds for any domain-extension scheme of the form \(g^f(s) = \bigoplus _{i=1}^{n}{f\left( C(s)_i \right) }\), where C is such a list-recoverable code. Hereafter, we refer to this scheme as the XOR parallel domain extension scheme.
Theorem 1
Let \({k_{in}},{k_{out}},v\) be integers, \(\alpha >0\), and let \(C:{\{0,1\}}^{v} \rightarrow \left( {\{0,1\}}^{{k_{in}}} \right) ^n\) be a well-ordered, \((\alpha ,\ell ,L)\)-list recoverable code of distance \(\alpha \). Define \(h:{\{0,1\}}^v \times \left( {\{0,1\}}^{{k_{out}}} \right) ^n \rightarrow {\{0,1\}}^{{k_{out}}}\) by \(h(s,a_1,\ldots ,a_n)=\bigoplus _{i=1}^n a_i\). Then \(g_{(C,h)}\) is \((\ell ,L^2/2^{{k_{out}}})\)-collision-resistant in the random-oracle model.
We remark that the collision-resistance of \(g_{(C,h)}\) holds even if we only require that the function f it gets as oracle be \(L^2\)-wise independent. Thus, using codes with small L allows us to require less of the oracle.
Theorem 2
Let \({k_{in}},{k_{out}},v\) be integers, and let \(C:{\{0,1\}}^{v} \rightarrow \left( {\{0,1\}}^{{k_{in}}} \right) ^n\) be a well-ordered, \((\ell ,L)\)-list recoverable code, with size r list-recovering algorithm, and let h be as in Theorem 1. Then \(g_{(C,h)}\) is \((\ell ,L,\hat{r})\)-weak-indifferentiable from random function (from v bits to \({k_{out}}\) bits), with \(\hat{r} = O(r + \ell \cdot \left( {k_{out}}+ {k_{in}} \right) )\).
Note that the weak-indifferentiablity of the scheme requires much less from the underlying code. In particular, it is not sensitive to the consistency parameter (allowing it to be 1) nor to the distance of the code, and hence does not imply collision-resistance. On the other hand, our application of this notion in the context of computationally sound arguments will require the list-recovering algorithm to be computationally efficient, a feature that is not needed for collision-resistance.
We prove Theorem 1 below. For the proof of Theorem 2, and proofs of the other theorems in this paper, see full version [20].
4.1 Proving Theorem 1
We show that an \(\ell \)-query adversary is unlikely to find a collision in the above construction (i.e., find two elements \(s_1\ne s_2\in {\{0,1\}}^v\), with \(g^f(s_1)=g^f(s_2)\)), when f is chosen at random from \(\mathcal{{F}}\) — the set all functions mapping \({k_{in}}\)-bit strings to \({k_{out}}\)-bit strings.
Fix a code C of the type considered in Theorem 1 and an \(\ell \)-query (without loss of generality, deterministic) adversary \(\mathcal{A}\), and let \(g = g_{(C,{\text {xor}})}\). The core of the argument is using the list-recoverability of C, and its distance, to bound the number of input pairs that \(\mathcal{A}\) is able to try out. We use the following definition.
Definition 6
(Dangerous Pairs). A pair \((s_1,s_2) \in \left( {\{0,1\}}^v \right) ^2\) of distinct elements is dangerous w.r.t. a (query) set Q of elements in \({\{0,1\}}^{{k_{in}}}\), if \(C(s_1)_i, C(s_2)_i\in Q\) for all \(1\le i\le n\) with \(C(s_1)_i \ne C(s_2)_i\).
We bound the number dangerous pairs w.r.t. an \(\ell \)-size query set Q using the bound on the number of codewords that are \(\alpha \)-consistent with Q.
Claim 3
Let \((s_1,s_2)\) be a dangerous pair w.r.t. a query set Q, then both \(C(s_1)\) and \(C(s_2)\) are \(\alpha \)-consistent with Q.
Proof
Assume that \((s_1,s_2)\) is a dangerous pair w.r.t. a query set Q. Let \(D=\left\{ i :C(s_1)_i\ne C(s_2)_i\right\} \). Since the distance of C is \(\alpha \), it holds that \(\left| D\right| \ge \alpha \cdot n\). Since \((s_1,s_2)\) is a dangerous pair, \(C(s_1)_i, C(s_2)_i\in Q\) for all \(i\in D\), and hence, both \(C(s_1)\) and \(C(s_2)\) are \(\alpha \)-consistent with Q.
Corollary 1
There are at most \({L \atopwithdelims ()2}\) dangerous pairs w.r.t. an \(\ell \)-size query set.
Proof
Since C is \((\alpha ,\ell ,L)\)-list recoverable, there are at most L strings \(s\in {\{0,1\}}^v\) such that C(s) is \(\alpha \)-consistent with an \(\ell \)-size query set Q. Hence, by Claim 3, there are at most \({L \atopwithdelims ()2}\) dangerous pairs w.r.t. Q.
For \(f\in \mathcal{{F}}\), let \(Q_{\mathcal{A},f}\) be the \(\ell \)-size query set asked by \(\mathcal{A}^f\). Corollary 1 yields that there are at most \({L \atopwithdelims ()2}\) dangerous pairs w.r.t. \(Q_{\mathcal{A},f}\). A straightforward union bound yields that a non-adaptive \(\mathcal{A}\) (i.e., one that “writes" all its queries in advance) is unlikely to find a collision within the dangerous pairs w.r.t. \(Q_{\mathcal{A},f}\). A slightly more involved argument yields the same bound also for adaptive adversaries. Specifically, we give the following bound (proof given below).
Claim 4
\(\Pr _{f\leftarrow \mathcal{{F}}}[(s_1,s_2) \leftarrow \mathcal{A}^f :(s_1,s_2) \text{ is } \text{ dangerous } \text{ w.r.t. } Q_{\mathcal{A},f} \wedge g^f(s_1) = g^f(s_2)] \le {L \atopwithdelims ()2} \cdot 2^{-{k_{out}}}\).
On the other hand, it is immediate that \(\mathcal{A}\) is unlikely to find a collision of a non-dangerous pair.
Claim 5
\(\Pr _{f \leftarrow \mathcal{{F}}}[(s_1,s_2) \leftarrow \mathcal{A}^f :s_1\ne s_2 \wedge (s_1,s_2) \text{ is } \text{ non-dangerous }\) w.r.t. \(Q_{\mathcal{A},f}\) \(\wedge g^f(s_1) = g^f(s_2)] = 2^{-{k_{out}}}\).
Proof
Since \((s_1,s_2)\) is non-dangerous, it follows that \(C(s_1)_i \ne C(s_2)_i\) for some \(i\in [v]\), and without loss of generality \(C(s_1)_i \notin Q_{\mathcal{A},f}\). Consider any fixing of all f queries but \(C(s_1)_i\) that is consistent with the actual answers of f on the queries in \(Q_{\mathcal{A},f}\). Since C is well ordered, this fixes \(C(s_t)_{j}\) for all \(t\in \left\{ 1,2\right\} \) and \(j\notin [n]\). The claim follows, since for each such fixing, it holds that
It follows that \(\mathcal{A}^f\) finds a collision with probability at most \(({L \atopwithdelims ()2} +1)\cdot 2^{-{k_{out}}} \le L^2/2^{{k_{out}}}\), proving the first part Theorem 1.
Proving Claim 4 . Recall that the \(\ell \)-query adversary \(\mathcal{A}\) in consideration may be adaptive, which means that it possibly selects its oracle queries based on the answers it received for previous queries. Our goal is to bound the probability that \(\mathcal{A}\) finds a pair of codewords that is both dangerous (with respect to \(Q_{\mathcal{A},f}\)) and forms a collision.
To this end, we first introduce the following notations. Let \(Q_{\mathcal{A},f}^{(j)}=\left\{ q_{\mathcal{A},f}^{(1)},\ldots ,q_{\mathcal{A},f}^{(j)}\right\} \) be the set of first j queries made by \(\mathcal{A}^f\). Let \(E_{\mathcal{A},f}^{(j)}\) be the event that there exists a pair \(\left( s_1,s_2 \right) \in \left( {\{0,1\}}^v \right) ^2\) of distinct elements that is dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j)}\) and \(g^f(s_1) = g^f(s_2)\). Finally, denote by \(d_{\mathcal{A},f}^{(j+1)}\) the number of pairs \(\left( \hat{s}_1,\hat{s}_2 \right) \) that are dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j+1)}\) and there exists \(1\le i\le n\) such that \(C(\hat{s}_1)_i = q_{\mathcal{A},f}^{(j+1)} \ne C(\hat{s}_2)_i\).
We next bound the probability that after making the \({j+1}\) query, the adversary finds – for the first time – a pair that is both dangerous and colliding.
Claim 6
For any \(1\le j < \ell \) and \(d\in {\mathbb {N}}\), it holds that \(\Pr _{f\leftarrow \mathcal{{F}}}\left[ E_{\mathcal{A},f}^{(j+1)} \wedge \lnot E_{\mathcal{A},f}^{(j)}\;|\;d_{\mathcal{A},f}^{(j+1)} = d\right] \le \frac{d}{2^{{k_{out}}}}\).
Proof
By simple rules of conditional probability, it suffices to prove \(\Pr _{f\leftarrow \mathcal{{F}}}\left[ E_{\mathcal{A},f}^{(j+1)} \;|\;\lnot E_{\mathcal{A},f}^{(j)}\wedge d_{\mathcal{A},f}^{(j+1)} = d\right] \le \frac{d}{2^{{k_{out}}}}\). For \(E_{\mathcal{A},f}^{(j+1)}\) to occur, there needs to be a pair \(\left( \hat{s}_1,\hat{s}_2 \right) \) that is dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j+1)}\) and \({g^f(\hat{s}_1) = g^f(\hat{s}_2})\). The condition that \(E_{\mathcal{A},f}^{(j)}\) does not occur yields that if \(\left( \hat{s}_1,\hat{s}_2 \right) \) is dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j)}\), then \({g^f(\hat{s}_1) \ne g^f(\hat{s}_2})\). Hence, for computing the probability that such a pair exists, one should only consider pairs that are dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j+1)}\) and are not dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j)}\).
Let \(\left( \hat{s}_1,\hat{s}_2 \right) \) be a pair that is dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j+1)}\) and not dangerous w.r.t. \(Q_{\mathcal{A},f}^{(j)}\). Note that there exists a (single) \(1\le i\le n\) with \(C(\hat{s}_1)_i = q_{\mathcal{A},f}^{(j+1)} \ne C(\hat{s}_2)_i\); the existences holds since otherwise, this pair is already a dangerous pair w.r.t. \(Q_{\mathcal{A},f}^{(j)}\), and the uniqueness follows since C is well-ordered. We next compute the probability that \({g^f(\hat{s}_1) = g^f(\hat{s}_2})\). Consider any fixing of all f queries but \(C(s_1)_i\) that is consistent with the actual answers of f on the queries in \(Q_{\mathcal{A},f}^{(j)}\) (specifically, \(E_{\mathcal{A},f}^{(j)}\) does not occur and \(d_{\mathcal{A},f}^{(j+1)}=d\) for such fixings). Since C is well ordered, this fixes \(C(s_t)_{j}\) for all \(t\in \left\{ 1,2\right\} \) and \(j\notin [n]\). For each such fixing, it holds that
By assumption, there are d such dangerous pairs. Hence, by a union bound, the claim follows.
Proof
(Proof of Claim 4 ). Since \(Q_{\mathcal{A},f}= Q_{\mathcal{A},f}^{(\ell )}\), it holds that \(E_{\mathcal{A},f} :=E_{\mathcal{A},f}^{(\ell )}\) is the event that there exists a pair \(\left( \hat{s}_1,\hat{s}_2 \right) \in \left( {\{0,1\}}^v \right) ^2\) of distinct elements that is dangerous w.r.t. \(Q_{\mathcal{A},f}\) and \(g^f(\hat{s}_1) = g^f(\hat{s}_2)\). Clearly, the probability of \(E_{\mathcal{A},f}\) upperbounds the probability that \(\mathcal{A}\) outputs such a pair.
Evidently, \(E_{\mathcal{A},f}^{(1)}\) can never occur, since no pair is dangerous w.r.t. a single query. Furthermore, \(E_{\mathcal{A},f}^{(j')}\) for any \(j'\le j\) implies \(E_{\mathcal{A},f}^{(j)}\). Hence, we have that
where the inequality follows from Claim 6. By linearity of expectation, it holds that
The last inequality follows since
for every \(f\in \mathcal{{F}}\). To see that Eq. (3) holds, note that each pair that is dangerous w.r.t. \({Q_{\mathcal{A},f}^{(j)}}\) is also dangerous w.r.t. \(Q_{\mathcal{A},f}^{(\ell )}\) (i.e., the set of all queries made by \(\mathcal{A}\)). Furthermore, each such dangerous pair \((s,s')\) is only counted by a single \({d_{\mathcal{A},f}^{(j)}}\), i.e., for the first j in which \(Q_j\) contains all the queries \(C(s)_i\ne C(s')_i\). Hence, Eq. (3) follows from Corollary 1.
5 Beyond Collision-Resistance
We suggest some applications of the XOR parallel domain-extension scheme described in [20] to parallel constructions of other cryptographic primitives in the random oracle model. These applications exploit both the collision-resistance and weak-indifferentiability properties of our construction. In this section we give a high level description of these applications and refer the reader to [20] for formal statements.
Fiat-Shamir Paradigm. We show that the XOR parallel domain-extension scheme can be used to implement the Fiat-Shamir paradigm for converting any three-message public-coin argument, which may possibly employ a random oracle, into a non-interactive (i.e., single-message) argument in the random oracle model.
We start by describing the Fiat-Shamir transformation when applied to three-message protocols. Let \(\left\langle \mathsf {P},\mathsf {V} \right\rangle \) be a public-coin three-message argument system for an \(\mathrm {NP}\) language. Such a protocol has the following high level structure: (1) \(\mathsf {P}\) send a v-bit message to \(\mathsf {V}\); (2) \(\mathsf {V}\) sends a random k-bit challenge to \(\mathsf {P}\); (3) \(\mathsf {P}\) responds to this challenge; (4) \(\mathsf {V}\) decides whether to accept by applying an efficient predicate to the input and the protocol’s transcript.
The Fiat-Shamir transformation makes \(\mathsf {P}\) generate all three messages by applying a hash function \(h:{\{0,1\}}^v\rightarrow {\{0,1\}}^k\) to the first message of \(\mathsf {P}\) to simulate the random challenge. This paradigm is provably secure in the random oracle model, but requires the random oracle input length to be as long as \(\mathsf {P}\)’s first message. We then use the weak-indifferentiability property, as discussed in Sect. 2, to show that the resulting scheme is also secure when h is the hash function obtained by applying the XOR parallel domain-extension scheme to a random oracle \(f:{\{0,1\}}^k\rightarrow {\{0,1\}}^k\). Namely, we create a Fiat-Shamir like transformation that uses parallel calls to a small random oracle.
Parallel Commitment with Local Decommitment. Next, we consider commitment schemes for strings \(s\in {\{0,1\}}^v\) that support a sublinear-communication local decommitment of any bit from s. Intuitively, in such schemes we require that the sender be bound to the string it committed to, but we do not explicitly require that it hide s. Instead, we require that the communication of both the commitment to s and the decommitment of each bit \(s_i\) be sublinear in v. We observe that such a commitment scheme can be obtained by dividing s into \(\sqrt{v}\) blocks of length \(\sqrt{v}\) each and applying the XOR parallel domain-extension separately to each block. To decommit \(s_i\), the sender reveals the entire block containing \(s_i\), and the receiver applies the hash function to ensure consistency. In this scheme, both the sender and the receiver only make parallel calls to a small random oracle.
Two-Adaptive Sublinear Non-interactive Arguments. Finally, we combine the above two applications to obtain sublinear-communication non-interactive arguments for NP in the random oracle model, which does not require the oracle input length to be large. To this end, we first apply the three-message protocol of [22], which combines a probabilistically checkable proof (PCP) with a commitment scheme as above. Then, following [30], we apply the Fiat-Shamir transformation to make this argument non-interactive.
By using efficient PCP constructions (e.g., those from [2]) and applying the XOR parallel domain-extension in both steps of the process, we get the following corollary: every \(\mathrm {NP}\) language that can be recognized by a non-deterministic Turing machine of running time T(n) has a non-interactive argument of length \(\tilde{O}(T^{1/2}(n))\) in the random oracle model, in which the prover and the verifier make only two rounds of calls to the oracle.
6 Necessity of List-Recoverability for Parallel Domain-Extension
It turns out that some form of list-recoverability is necessary for the collision-resistance of a parallel domain-extension. Let (C, h) be a domain-extension scheme, and assume that C is not \((1,\ell ,L)\)-list recoverable. Namely, there exists a set \(T \subseteq {\{0,1\}}^{{k_{in}}}\) of size at most \(\ell \), for which there are (at least) \(L+1\) distinct elements \(s_1,\ldots ,s_{L+1} \in {\{0,1\}}^v\) such that for every \(1 \le i \le L+1\): \(g^f(s_i)=h(s_i,f(x_{1}),\ldots ,f(x_{n}))\) for \(x_1,\ldots ,x_n \in T\). Hence, by querying f only on the \(\ell \) elements in T, an adversary obtains the required information for computing \(g^f(s_1),\ldots ,g^f(s_{L+1})\). This attack finds a collision in \(g^f\) if \(L \ge 2^{{k_{out}}}\). Thus, \((1,\ell ,L)\)-list-recoverability with \(L \le 2^{{k_{out}}}\), is necessary for the collision-resistance of g in the random-oracle model. This is formally stated below.
Theorem 7
Let \({k_{in}},{k_{out}},v,n\) be integers. For every \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^{{k_{in}}} \right) ^n\) and \(h:{\{0,1\}}^v \times \left( {\{0,1\}}^{{k_{out}}} \right) ^n \rightarrow {\{0,1\}}^{{k_{out}}}\) if C is not \((1,\ell ,2^{{k_{out}}})\)-list-recoverable then \(g_{(C,h)}\) is not \((\ell ,0.99)\)-collision-resistant in the random oracle model.
We note that there are codes of large minimal distance (such as the repetition code) for which the attack in the proof of Theorem 7 can be implemented in polynomial time, by using linear algebra.
Necessity of List-Recoverability with \(L \approx 2^{\frac{{k_{out}}}{2}}\). Note that Theorem 7 discusses \(L=2^{{k_{out}}}\) while in Theroem 1 we require \(L \le 2^{\frac{{k_{out}}}{2}}\) to get a meaningful result. Is it possible to show that \((\ell ,L)\) list-recoverability with \(L \approx 2^{\frac{{k_{out}}}{2}}\) is also necessary for security? We give a partial answer to this question below.
Observe that the above attack allows the adversary to use \(\ell \) queries into f and come up with \({{L+1} \atopwithdelims ()2} \approx 2^{{k_{out}}} \) pairs \(s \ne s'\), such that he can compute g(s) and \(g(s')\). In some natural settings, computing g on this number of pairs suffices to find a collision. For instance, this is the case if the function g is 4-wise independent.Footnote 4 There are codes C satisfying the properties requested in Theorem 1, with which the construction of Theorem 1 is 4-wise independent. This implies that Theorem 1 cannot be improved to imply security with \(L > 2^{\frac{k}{2}}\).
Necessity of List-Recoverability with \(\alpha <1\). Theorem 7 shows that it is necessary that C is list-recoverable with \(\alpha =1\) in any parallel domain-extension scheme. In our construction, however, we use stronger codes with \(\alpha <1\), and we also require that the codes have large distance. The next theorem shows that this assumption is necessary in case h is the XOR function (as we chose in Theorem 1).
Theorem 8
There exists \(c>0\) such that the following holds for every \(\alpha <1\), integers \({k_{in}}\ge c \cdot \log (\frac{v}{1-\alpha })\), \({k_{out}}\), \(v \ge c \cdot \max \left\{ {k_{in}},{k_{out}}\right\} \), \(c \cdot (\frac{v}{1-\alpha }) \le n \le 2^{{k_{in}}/2}\), \(c \cdot (\frac{n}{1-\alpha }) \le \ell \le 2^{{k_{in}}/4}\) and \(L \ge \ell \). There exists a function \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^{{k_{in}}} \right) ^n\) that is \((1,\ell ,L)\)-list recoverable, well ordered, and has distance \(\alpha \), and (yet) for \(h(s,a_1,\ldots ,a_n)=\bigoplus _{i=1}^n a_i\), the parallel domain-extension scheme \(g_{(C,h)}\) is not \((O(\frac{n}{1-\alpha }),0.99)\)-collision-resistant in the random-oracle model.
Theorem 8 shows that there exist codes C which satisfy all the requirements of Theorem 1 with the single exception being that the list-recoverability parameter is taken to be one (rather than the distance \(\alpha \) of the code). Yet, the resulting construction is insecure. In fact, there is a lot of slack in the counterexample, one can choose the parameters \(\ell ,L\) to be much more favorable than in Theorem 1, and still an adversary with only \(O(\frac{n}{1-\alpha })\) queries can break the scheme with probability arbitrarily close to one.
It should be noted that the previous construction of [26] extends the domain of a random function by relying on a notion of “input-restricting families”, which is equivalent to strongly list-recoverable codes with \(\alpha =1\).Footnote 5 Such input-restricting families were subsequently used in [11] for the purpose of extending the domain of MACs. The construction from [26] is not fully parallel, requiring two rounds of calls to the random oracle f. The example provided in Theorem 8 gives a formal explanation why the use of input-restricting families does not suffice for using a single round of calls, even if one is only interested in collision-resistance as in this work.
Intuitively, the issue is as follows. In order to break collision-resistance the adversary is only required to produce a distinct pair \((s,s')\) of inputs such that \(g(s)=g(s')\), and the adversary is not required to be able to compute g(s). Loosely speaking, parallel domain-extension schemes in which C is \((\alpha =1,\ell ,L)\)-list recoverable, have the property that after asking \(\ell \) queries the adversary cannot come up with \(t > L\) inputs \(s_1,\ldots ,s_t\) such that he can compute \(g(s_1),\ldots ,g(s_t)\). The example in Theorem 8 shows that there are \((1,\ell ,L)\)-list-recoverable codes, in which the adversary can a produce a collision \((s,s')\) even though he did not query f on all the inputs required to compute \(g(s),g(s')\) (and therefore is not controlled by list-recoverability with \(\alpha =1\)). In Theorem 1 we show how to bypass this limitation by using list-recoverable codes with \(\alpha <1\). We hope that the introduction of this stronger combinatorial object to the area of domain-extensions may help to improve and simplify other tasks in this area.
7 Using Known Explicit List-Recoverable Codes
In this section we plug in list-recoverable codes with specific parameters to obtain concrete results. We use the Parvaresh-Vardy code [32] in the range of parameters analyzed by Guruswami, Umans and Vadhan [18].
Theorem 9
([18]). For every \(\alpha \ge 1/2\), \(0< \beta < 1\), and \(k<v \in {\mathbb {N}}\), there exists a \({\text {poly}}(v)\)-time computable function \(C:{\{0,1\}}^v \rightarrow \left( {\{0,1\}}^{k} \right) ^n\) for \(n=O(v \cdot k )^{\frac{1}{1-\beta }}\), that is well ordered, has distance \(\alpha \), and for every \(L \le 2^{\beta \cdot (k-2\log n)}\), it is \((\alpha ,\ell ,L)\)-list recoverable with \(\ell =\varOmega (n \cdot L)\) and has a \({\text {poly}}(v,\ell )\)-size list-recovering algorithm. Furthermore, when viewed as a function \(C:\mathbb {F}_2^v \rightarrow \mathbb {F}_2^{k \cdot n}\), every output bit can be expressed as a degree one polynomial in the input bits.
We remark that [18] give a more general trade-off of parameters as well as a tighter connection between the parameters. More specifically, the theorem of [18] is stated as a condenser, and the statement given here is using the interpretation of condensers as list-recoverable codes (see [20] for more details). The facts that the construction of [18] is well-ordered and has large distance are not explicitly stated in [18], but are easily verified from the actual construction. The list-recovering algorithm is also not explicitly stated but follows directly from the proof of [18]. Finally, the fact that the mapping can be seen as a collection of degree one polynomials over \(\mathbb {F}_2\) also follows from the specific structure of the construction of [18], or more generally from the structure of the Parvaresh-Vardy code.Footnote 6
We now plug this code into Theorem 1 and obtain concrete results. For simplicity, we assume here that the input and output length of the oracle (i.e., f) are the same, and denote both lengths by k. We consider powerful adversaries with \(\ell =2^{(\frac{1}{2}-\gamma ) \cdot k}\) for a small constant \(\gamma >0\) and shoot for \(\varepsilon \) that is exponentially small in k. Plugging the code of [18] into the construction of Theorem 1, yields that for desired security \(\varepsilon \), it suffices to take \(L = c \cdot \varepsilon ^{\frac{1}{2}} \cdot 2^{\frac{k}{2}}\) for some constant c. By the construction of [18] we can achieve this with \(\ell =\varOmega (L \cdot n)= \varOmega (\varepsilon ^{\frac{1}{2}} \cdot 2^{\frac{k}{2}} \cdot n)\). Namely, we can achieve \(\varepsilon =2^{-2\gamma k}\) for \(\ell =2^{(\frac{1}{2}-\gamma ) \cdot k}\)-query adversaries. Furthermore, \(\ell \) can be taken to be \(\varOmega ( 2^{k/2} \cdot n)\) (that is larger than \(2^{k/2}\)) for any small constant \(\varepsilon >0\). This is best possible in the sense that with \(2^{\frac{k}{2}} \cdot n\) queries to f, one can simulate a birthday attack against g, and find a collision.
Comparing to the standard Merkle-tree based domain-extension, the resulting construction does make significantly more oracle calls to the underlying small domain function. Specifically, our construction makes \(n =O( v^2 \cdot k^2)\) calls, whereas the Merkle-tree construction makes O(v / k) calls. We remark that if we were to use a random code (rather than an explicit one), then the number of calls decreases to O(v / k) as is the case for Merkle trees. Furthermore, even when using explicit codes, if we settle for security against \(2^{\beta k}\)-query adversaries, the query complexity of our construction can be reduced to roughly \((v \cdot k)^{\frac{1}{1-\beta }}\), which roughly matches the Merkle-tree construction for v that is significantly larger than k (which is the interesting range of parameters). Parvaresh-Vardy codes allow for some other trade-offs between security and number of queries that we do not examine here.
The code C that we use can be evaluated by degree one polynomials over \(\mathbb {F}_2\). This immediately gives a very efficient parallel implementation in the standard model of Boolean circuits with parity gates of fan-in 2. Such circuits can compute the code C with depth \(\log _2 v\). Moreover, in this model, computing the final xor in our construction, can be done by circuits of depth \(\log _2 n\). Thus, overall our final hash function g can be implemented by circuits whose depth is bigger than the depth of f by \(\log _2 v + \log _2 n\). By our bounds on n, this quantity is roughly \(3\log _2 v\) for \(2^{(\frac{1}{2}-\gamma ) \cdot k}\)-query adversaries with small \(\gamma >0\), and roughly \((2+\beta ) \cdot \log _2 v\) for small \(\beta >0\) and \(2^{\beta k}\)-query adversaries. We remark that future developments in the area of list-recoverable codes or randomness condensers may reduce n to O(v / k). It is also natural to expect that random \(\mathbb {F}_2\)-linear codes (or even families of efficiently encodable LDPC codes that are used in practice) achieve this bound. However, this is not known at this point.
8 Additional Related Work
Extending the domain of collision-resistant hash functions is of great importance for many cryptographic applications that depend on collision-resistance. Classical construction paradigms for domain-extension are the Merkle hash tree [28] and the Merkle-Damgård paradigm [10, 29]. Both paradigms are iterative, namely, use sequential calls to the underlying hash-function. More specifically, in both paradigms \(n= O(v/k)\) calls are made to the primitive, where the former paradigm requires \(\log (n)\) rounds of calls, and the latter paradigm requires n rounds. Indeed, the Merkle-Damgård paradigm realizes the much stronger task of extending a fixed domain hash function to a full-fledged hash function, i.e., one that can deal with input of any length. The Merkle-Damgård paradigm is extensively used in practice and was the subject of much theoretical research and extensions (see, e.g., [3, 7, 24]). Lower bounds on the security of these domain-extension techniques were obtained, e.g., in [37, 38]. The construction of Shrimpton and Stam [35] was the first construction achieving optimal collision-resistance security in an inherently non-trivial way. Their construction only doubles the domain, and requires two rounds of calls.
Most relevant to our work is the work of Maurer and Tessaro [26], already discussed above. This work considers the more challenging problem of extending the domain of a random function. Specifically, given a random function f from k bits to k bits, they construct a function g from m(k) bits to \(\ell (k)\) bits, for arbitrary polynomials \(m,\ell \), such that g is indistinguishable from a random function. The latter is formalized by using the indifferentiability framework from [27], which implies collision-resistance as a special case. The main goal of [27] is to obtain near-optimal security, namely to guarantee security against attackers that make \(2^{(1-\varepsilon )k}\) oracle queries to f, improving over previous works.Footnote 7 However, their construction also achieves a high level of parallelism, requiring only two rounds of calls to f. Compared to the construction from [27], our construction is considerably simpler, it is fully parallel (i.e., requires only one round of calls to f), and it preserves the algebraic degree of f (whereas the construction from [27] more than squares the degree). As discussed in Sect. 6 (below Theorem 8), these disadvantages of [26] seem inherent given the type of combinatorial object on which they rely.
Building on and extending the techniques of [26], Dodies and Steinberger [11] construct a domain-extension scheme for MACs that has security beyond the “birthday barrier”. Finally, Canetti et al. [6] considered the related, but somewhat orthogonal, goal of amplifying the security of a collision-resistant hash function.
Notes
- 1.
Their construction actually realizes the stronger goal of constructing a function g that is indistinguishable from a random function. See Sect. 8 for further discussion.
- 2.
Note that it is immediate that a strongly list recoverable code is also (weakly) list-recoverable, and that a weakly list-recoverable code with \(L' = n \cdot L\) is strongly list recoverable. In our setting n is negligible compared to L and so the distinction between the two notions of list-recoverable code makes little difference.
- 3.
More precisely, if the inner code is list-decodable (rather than uniquely decodable) then to obtain a list-decodable code, the outer code needs to be list-recoverable (and not only list-decodable).
- 4.
g is 4-wise independent, if for every four distinct \(s_1,s_2,s_3,s_4 \in {\{0,1\}}^v\) the random variables \(g(s_1),g(s_2),g(s_3),g(s_4)\) are uniformly distributed and independent (over the random choice of the oracle f). For such g, the expectation of the random variable counting the number of pairs \(s \ne s'\) such that \(g(s)=g(s')\) is at least \({{L+1} \atopwithdelims ()2} /2^{{k_{out}}}\) (which is large if \(L \ge 2^{{k_{out}}/2}\)). Moreover, 4-wise indpendence implies that the variance of the random variable above is small, and therefore, the number of collisions is with high probability, close to the expectation. This implies that the adversary obtains a collision with high probability.
- 5.
This notion is also equivalent to certain unbalanced expander graphs, see discussion in [20].
- 6.
More precisely, the function C has the following form. It sets \(v=v_1 \cdot v_2\) for some integers \(v_1,v_2\). Given an input \(x \in {\{0,1\}}^v\) it is interpreted as a vector in \(\mathbb {F}_{2^{v_1}}^{v_2}\) which is in turn interpreted as the coefficients of a degree \(v_2\) univariate polynomial f(X) over \(\mathbb {F}_{2^{v_1}}\). For every \(i \in [n]\), \(C(x)_i=(i,f_0(\alpha _i),\ldots ,f_{m-1}(\alpha _i))\) where \(\alpha _i \in \mathbb {F}_{2^{v_1}}\) is a constant that depends only on i, and for every \(j \in [m]\), \(f_j(X)\) is a univariate polynomial defined by \(f_j=f^{h^j} \mod E\), where h is a parameter and E is some degree \(v_2+1\) irreducible polynomial. Thus, the code is immediately seen to be well-ordered and to inherit distance from the Reed-Solomon code (that corresponds to \(j=1\)). The analysis of [18] allows choosing h that is even. Note that for an even h, the identity \((x+y)^h = x^h+y^h\) holds in \(\mathbb {F}_{2^{v_1}}\). It is standard that this implies that for every fixed \(\alpha \in \mathbb {F}_{2^{v_1}}\), the map \(f \rightarrow (f^h \mod E)(\alpha )\) is \(\mathbb {F}_2\)-linear. This indeed implies that viewing the function C as a map from \(\mathbb {F}_2^v\) to \(\mathbb {F}_2^{k \cdot n}\), it is a degree one mapping.
- 7.
Note that in the context of collision-resistance, the birthday paradox implies that collisions can be found with high probability using \(2^{{k_{out}}/2}\) oracle calls.
References
Barak, B.: How to go beyond the black-box simulation barrier. In: Proceedings of the 42nd Annual Symposium on Foundations of Computer Science (FOCS), pp. 106–115 (2001)
Ben-Sasson, E., Sudan, M.: Short pcps with polylog query complexity. SIAM J. Comput. 38(2), 551–607 (2008)
Bertoni, G., Daemen, J., Peeters, M., Assche, G.V.: Sufficient conditions for sound tree and sequential hashing modes. Int. J. Inf. Sec. 13(4), 335–353 (2014a)
Bertoni, G., Daemen, J., Peeters, M., Assche, G.V.: The making of KECCAK. Cryptologia 38(1), 26–60 (2014b). doi:10.1080/01611194.2013.856818. http://dx.doi.org/10.1080/01611194.2013.856818
Blum, M., Micali, S.: How to generate cryptographically strong sequences of pseudo random bits. In: Proceedings of the 23th Annual Symposium on Foundations of Computer Science (FOCS), pp. 112–117 (1982)
Canetti, R., Rivest, R., Sudan, M., Trevisan, L., Vadhan, S.P., Wee, H.M.: Amplifying collision resistance: a complexity-theoretic treatment. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 264–283. Springer, Heidelberg (2007)
Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005)
Damgård, I.B.: Collision free hash functions and public key signature schemes. In: Price, W.L., Chaum, D. (eds.) EUROCRYPT 1987. LNCS, vol. 304, pp. 203–216. Springer, Heidelberg (1988)
Damgård, I., Pedersen, T.P., Pfitzmann, B.: On the existence of statistically hiding bit commitment schemes and fail-stop signatures. J. Cryptol. 10(3), 163–194 (1997)
Damgård, I.B.: A design principle for hash functions. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 416–427. Springer, Heidelberg (1990)
Dodis, Y., Steinberger, J.: Domain extension for MACs beyond the birthday barrier. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 323–342. Springer, Heidelberg (2011)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987)
Goldreich, O., Goldwasser, S., Halevi, S.: Public-key cryptosystems from lattice reduction problems. In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 112–131. Springer, Heidelberg (1997)
Guruswami, V.: List Decoding of Error-Correcting Codes. Ph.D. thesis, Massachusetts Institute of Technology (2005)
Guruswami, V., Indyk, P.: Expander-based constructions of efficiently decodable codes. In: 42nd Annual Symposium on Foundations of Computer Science, pp. 658–667 (2001)
Guruswami, V., Rudra, A.: Explicit codes achieving list decoding capacity: error-correction with optimal redundancy. IEEE Trans. Inf. Theory 54(1), 135–150 (2008)
Guruswami, V., Sudan, M.: Improved decoding of reed-solomon and algebraic-geometry codes. IEEE Trans. Inf. Theory 45(6), 1757–1767 (1999)
Guruswami, V., Umans, C., Vadhan, S.P.: Unbalanced expanders and randomness extractors from Parvaresh-Vardy codes. J. ACM 56(4), 20:1–20:34 (2009)
Haitner, I., Hoch, J.J., Reingold, O., Segev, G.: Finding collisions in interactive protocols - tight lower bounds on the round and communication complexities of statistically hiding commitments. SIAM J. Comput. 44(1), 193–242 (2015a). Preliminary version in STOC’07
Haitner, I., Ishai, Y., Omri, E., Shaltiel, R.: Parallel hashing via list recoverability (2015b). www.cs.tau.ac.il/~iftachh/papers/CRHDomainExtension/CRH.pdf. Full version of this paper
Halevi, S., Micali, S.: Practical and provably-secure commitment schemes from collision-free hashing. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 201–215. Springer, Heidelberg (1996)
Kilian, J.: A note on efficient zero-knowledge proofs and arguments (extended abstract).In: Proceedings of the 24th Annual ACM Symposium on Theory of Computing (STOC), pp. 723–732 (1992)
Kilian, J.: On the complexity of bounded-interaction and noninteractive zero-knowledge proofs. In: Proceedings of the 35th Annual Symposium on Foundations of Computer Science (FOCS), pp. 466–477 (1994)
Lucks, S.: Design principles for iterated hash functions. Technical report, Cryptology ePrint Archive (2004)
Lyubashevsky, V., Micciancio, D.: Generalized compact knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006)
Maurer, U.M., Tessaro, S.: Domain extension of public random functions: beyond the birthday barrier. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 187–204. Springer, Heidelberg (2007)
Maurer, U.M., Renner, R.S., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004)
Merkle, R.C.: A digital signature based on a conventional encryption function. In: Pomerance, C. (ed.) CRYPTO 1987. LNCS, vol. 293, pp. 369–378. Springer, Heidelberg (1988)
Merkle, R.C.: A certified digital signature. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 218–238. Springer, Heidelberg (1990)
Micali, S.: Computationally sound proofs. SIAM J. Comput. 30(4), 1253–1298 (2000). Preliminary version in FOCS 1994
Naor, M., Yung, M.: Universal one-way hash functions and their cryptographic applications. In: Proceedings of the 21st Annual ACM Symposium on Theory of Computing (STOC), pp. 33–43. ACM Press (1989)
Parvaresh, F., Vardy, A.: Correcting errors beyond the Guruswami-Sudan radius in polynomial time. In: 46th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2005, pp. 285–294 (2005)
Peikert, C., Rosen, A.: Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 145–166. Springer, Heidelberg (2006)
Rogaway, P., Steinberger, J.P.: Constructing cryptographic hash functions from fixed-key blockciphers. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 433–450. Springer, Heidelberg (2008)
Shrimpton, T., Stam, M.: Building a collision-resistant compression function from non-compressing primitives. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 643–654. Springer, Heidelberg (2008)
Simon, D.R.: Findings collisions on a one-way street: can secure hash functions be based on general assumptions? In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 334–345. Springer, Heidelberg (1998)
Stam, M.: Beyond uniformity: better security/efficiency tradeoffs for compression functions. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 397–412. Springer, Heidelberg (2008)
Steinberger, J., Sun, X., Yang, Z.: Stam’s conjecture and threshold phenomena in collision resistance. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 384–405. Springer, Heidelberg (2012)
Sudan, M.: Decoding of reed solomon codes beyond the error-correction bound. J. Complex. 13(1), 180–193 (1997)
Wang, X., Yu, H.: How to break MD5 and other hash functions. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 19–35. Springer, Heidelberg (2005)
Yao, A.C.: Theory and applications of trapdoor functions. In: Proceedings of the 23th Annual Symposium on Foundations of Computer Science (FOCS), pp. 80–91 (1982)
Acknowledgments
We thank Yevgeniy Dodis, Swastik Kopparty, Phil Rogaway, Atri Rudra and Stefano Tessaro for helpful discussions and pointers.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologic Research
About this paper
Cite this paper
Haitner, I., Ishai, Y., Omri, E., Shaltiel, R. (2015). Parallel Hashing via List Recoverability. In: Gennaro, R., Robshaw, M. (eds) Advances in Cryptology -- CRYPTO 2015. CRYPTO 2015. Lecture Notes in Computer Science(), vol 9216. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48000-7_9
Download citation
DOI: https://doi.org/10.1007/978-3-662-48000-7_9
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-47999-5
Online ISBN: 978-3-662-48000-7
eBook Packages: Computer ScienceComputer Science (R0)