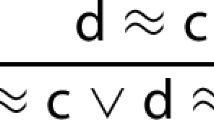Abstract
We make a new contribution to the field by providing a new method of using SMT solvers in saturation-based reasoning. We do this by introducing two new inference rules for reasoning with non-ground clauses. The first rule utilises theory constraint solving (an SMT solver) to perform reasoning within a clause to find an instance where we can remove one or more theory literals. This utilises the power of SMT solvers for theory reasoning with non-ground clauses, reasoning which is currently achieved by the addition of often prolific theory axioms. The second rule is unification with abstraction where the notion of unification is extended to introduce constraints where theory terms may not otherwise unify. This abstraction is performed lazily, as needed, to allow the superposition theorem prover to make as much progress as possible without the search space growing too quickly. Additionally, the first rule can be used to discharge the constraints introduced by the second. These rules were implemented within the Vampire theorem prover and experimental results show that they are useful for solving a considerable number of previously unsolved problems. The current implementation focuses on complete theories, in particular various versions of arithmetic.
This work was supported by EPSRC Grants EP/K032674/1 and EP/P03408X/1. Martin Suda and Andrei Voronkov were partially supported by ERC Starting Grant 2014 SYMCAR 639270. Martin Suda was also partially supported by the Austrian research projects FWF S11403-N23 and S11409-N23. Andrei Voronkov was also partially supported by the Wallenberg Academy Fellowship 2014 – TheProSE. Part of this work was done when Andrei Voronkov was part-time employed by Chalmers University of Technology.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Reasoning in quantifier-free first-order logic with theories, such as arithmetic, is hard. Reasoning with quantifiers and first-order theories is very hard. It is undecidable in general and \(\varPi _1^1\)-complete for many simple combinations, for example linear (real or integer) arithmetic and uninterpreted functions [16]. At the same time such reasoning is essential to the future success of certain application areas, such as program analysis and software verification, that rely on quantifiers to, for example, express properties of objects, inductively defined data structures, the heap and dynamic memory allocation. This paper presents a new approach to theory reasoning with quantifiers that (1) uses an SMT solver to do local theory reasoning within a clause, and (2) extends unification to avoid the need to explicitly separate theory and non-theory parts of clauses.
There are two directions of research in the area of reasoning with problems containing quantifiers and theories. The first is the extension of SMT solvers with instantiation heuristics such as E-matching [9, 12]. The second is the extension of first-order reasoning approaches with support for theory reasoning (note that the instantiation heuristics from SMT solvers are not appropriate in this context, as discussed in [26]). There have been a number of varied attempts in this second direction with some approaches extending various calculi [2, 3, 7, 8, 13, 16, 28] or using an SMT solver to deal with the ground part of the problem [20]. This second approach includes our previous work developing AVATAR modulo theories [21], which complements the approach presented in this paper as explained later. A surprisingly effective approach to theory reasoning with first-order theorem provers is to add theory axioms (i.e. axioms from the theory of interest). Whilst this has no hope of being complete, it can be used to prove a large number of problems of interest. However, theory axioms can be highly prolific in saturation-based proof search and often swamp the search space with irrelevant consequences of the theory [22]. This combinatorial explosion prevents theory axioms from being useful in cases where deep theory reasoning is required. This paper provides a solution that allows for a combination of these approaches i.e. the integration with an SMT solver, the use of theory axioms, and the heuristic extension of the underlying calculi.
Our paper contains two main ideas and we start with examples (which we revisit later) to motivate and explain these ideas. The first idea is motivated by the observation that the theory part of a first-order clause might already be restricting the interesting instances of a clause, sometimes uniquely, and we can use this to produce simpler instances that are useful for proof search. For example, the first-order clause
has a single solution for x which makes the first literal false with respect to the underlying theory of arithmetic, namely \(x = 7\). Therefore, every instance of this clause is a logical consequence of its single instance
in the underlying theory. If we apply standard superposition rules to the original clause and a sufficiently rich axiomatisation of arithmetic, we will most likely end up with a very large number of logical consequences and never generate p(7), or run out of space before generating it. For many clauses the solution will not be unique but can still provide useful instances, for example by taking the clause
and using its instance
we can derive the clause
This clause does not represent all solutions for \(7 \le x\), but it results in a clause with fewer literals. Moreover, this clause is ground and can be passed to an SMT solver (this is where this approach complements the work of AVATAR modulo theories).
Finally, there are very simple cases where this kind of approach can immediately find inconsistencies. For example, the clause
has instances making it false, for example via the substitution \(\{x \mapsto 1,y \mapsto 0\}\).
As explained in Sect. 3, these observations lead to an instantiation rule that considers clauses to be in the form \(T \rightarrow C\), where T is the theory part, and uses an SMT solver to find a substitution \(\theta \) under which T is valid in the given theory, thus producing the instance \(C\theta \). Which, in the case where \(C=\bot \), can find general inconsistencies.
The second rule is related to the use of abstraction. By an abstraction we mean (variants of) the rule obtaining from a clase C[t], where t is a non-variable term, a clause \(x \not \simeq t \vee C[x]\), where x is a new variable. Abstraction is implemented in several theorem provers, including the previous version of our theorem prover Vampire [18] used for experiments described in this paper.
Take, for example, the formula
which is ARI189=1 from the TPTP library [33]. When negated and clausified, this formula gives two unit clauses
from which we can derive nothing without abstracting at least one of the clauses.
If we abstract p(10) into \(p(y) \vee y\not \simeq 10\) then a resolution step would give us \(2x \not \simeq 10\) and simple evaluation would provide \(x \not \simeq 5\), which is refutable by equality resolution. However, the abstraction step is necessary. Some approaches rely on full abstraction where theory and non-theory symbols are fully separated. This is unattractive for a number of reasons which we enumerate here:
-
1.
A fully abstracted clause tends to be much longer, especially if the original clause contains deeply nested theory and non-theory symbols. Getting rid of long clauses was one of the motivations of our previous AVATAR work on clause splitting [34] (see this work for why long clauses are problematic for resolution-based approaches). However, the long clauses produced by abstraction will share variables, reducing the impact of AVATAR.
-
2.
The AVATAR modulo theories approach [21] ensures that the first-order solver is only exploring part of the search space that is theory-consistent in its ground part (using a SMT solver to achieve this). This is effective but relies on ground literals remaining ground, even those that mix theory and non-theory symbols. Full abstraction destroys such ground literals.
-
3.
As mentioned previously, the addition of theory axioms can be effective for problems requiring shallow theory reasoning. Working with fully abstracted clauses forces us to make first-order reasoning to treat the theory part of a clause differently. This makes it difficult to take full advantage of theory axiom reasoning.
The final reason we chose not to fully abstract clauses in our work is that the main advantage of full abstraction for us would be that it deals with the above problem, but we have a solution which we believe solves this issue in a more satisfactory way, as confirmed by our experiments described in Sect. 5.
The second idea is to perform this abstraction lazily, i.e., only where it is required to perform inference steps. As described in Sect. 4, this involves extending unifications to produce theory constraints under which two terms will unify. As we will see, these theory constraints are exactly the kind of terms that can be handled easily by the instantiation technique introduced in our first idea.
As explained above, the contributions of this paper are
-
1.
a new instantiation rule that uses an SMT solver to provide instances consistent with the underlying theory (Sect. 3),
-
2.
an extension of unification that provides a mechanism to perform lazy abstraction, i.e., only abstracting as much as is needed, which results in clauses with theory constraints that can be discharged by the previous instantiation technique (Sect. 4),
-
3.
an implementation of these techniques in the Vampire theorem prover (described in Sects. 3 and 4),
-
4.
an experimental evaluation that demonstrate the effectiveness of these techniques both individually and in combination with the rest of the powerful techniques implemented within Vampire (Sect. 5).
An extended version of this paper [32] contains further examples and discussion. We start our presentation by introducing the necessary background material.
2 Preliminaries and Related Work
First-Order Logic and Theories. We consider a many-sorted first-order logic with equality. A signature is a pair \(\varSigma = (\varXi ,\varOmega )\) where \(\varXi \) is a set of sorts and \(\varOmega \) a set of predicate and function symbols with associated argument and return sorts from \(\varXi \). Terms are of the form c, x, or \(f(t_1,\ldots ,t_n)\) where f is a function symbol of arity \(n \ge 1\), \(t_1,\ldots , t_n\) are terms, c is a zero arity function symbol (i.e. a constant) and x is a variable. We assume that all terms are well-sorted. Atoms are of the form \(p(t_1,\ldots ,t_n), q\) or \(t_1 \simeq _s t_2\) where p is a predicate symbol of arity n, \(t_1, \ldots , t_n\) are terms, q is a zero arity predicate symbol and for each sort \(s\in \varXi \), \(\simeq _s\) is the equality symbol for the sort s. We write simply \(\simeq \) when s is known from the context or irrelevant. A literal is either an atom A, in which case we call it positive, or a negation of an atom \(\lnot A\), in which case we call it negative. When L is a negative literal \(\lnot A\) and we write \(\lnot L\), we mean the positive literal A. We write negated equalities as \(t_1 \not \simeq t_2\). We write \(t[s]_p\) and \(L[s]_p\) to denote that a term s occurs in a term t (in a literal L) at a position p.
A clause is a disjunction of literals \(L_1 \vee \ldots \vee L_n\) for \(n \ge 0\). We disregard the order of literals and treat a clause as a multiset. When \(n=0\) we speak of the empty clause, which is always false. When \(n=1\) a clause is called a unit clause. Variables in clauses are considered to be universally quantified. Standard methods exist to transform an arbitrary first-order formula into clausal form (e.g. [19] and our recent work in [25]).
A substitution is any expression \(\theta \) of the form \(\{x_1 \mapsto t_1,\ldots ,x_n \mapsto t_n\}\), where \(n \ge 0\). \(E\theta \) is the expression obtained from E by the simultaneous replacement of each \(x_i\) by \(t_i\). By an expression we mean a term, an atom, a literal, or a clause. An expression is ground if it contains no variables. An instance of E is any expression \(E\theta \) and a ground instance of E is any instance of E that is ground. A unifier of two terms, atoms or literals \(E_1\) and \(E_2\) is a substitution \(\theta \) such that \(E_1\theta =E_2\theta \). It is known that if two expressions have a unifier, then they have a so-called most general unifier.
We assume a standard notion of a (first-order, many-sorted) interpretation \(\mathcal {I}\), which assigns a non-empty domain \(\mathcal {I}_s\) to every sort \(s\in \varXi \), and maps every function symbol f to a function \(\mathcal {I}_f\) and every predicate symbol p to a relation \(\mathcal {I}_p\) on these domains so that the mapping respects sorts. We call \(\mathcal {I}_f\) the interpretation of f in \(\mathcal {I}\), and similarly for \(\mathcal {I}_p\) and \(\mathcal {I}_s\). Interpretations are also sometimes called first-order structures. A sentence is a closed formula, i.e., with no free variables. We use the standard notions of validity and satisfiability of sentences in such interpretations. An interpretation is a model for a set of clauses if (the universal closure of) each of these clauses is true in the interpretation.
A theory \(\mathcal {T}\) is identified by a class of interpretations. A sentence is satisfiable in \(\mathcal {T}\) if it is true in at least one of these interpretations and valid if it is true in all of them. A function (or predicate) symbol f is called uninterpreted in \(\mathcal {T}\), if for every interpretation \(\mathcal {I}\) of \(\mathcal {T}\) and every interpretation \(\mathcal {I}'\) which agrees with \(\mathcal {I}\) on all symbols apart from f, \(\mathcal {I}'\) is also an interpretation of \(\mathcal {T}\). A theory is called complete if, for every sentence F of this theory, either F or \(\lnot F\) is valid in this theory. Evidently, every theory of a single interpretation is complete. We can define satisfiability and validity of arbitrary formulas in an interpretation in a standard way by treating free variables as new uninterpreted constants.
For example, the theory of integer arithmetic fixes the interpretation of a distinguished sort \(s_ int \in \varXi _ IA \) to the set of mathematical integers \(\mathbb {Z}\) and analogously assigns the usual meanings to \(\{ +, -, <, >, * \} \in \varOmega _ IA \). We will mostly deal with theories in which their restriction to interpreted symbols is a complete theory, for example, integer or real linear arithmetic. In the sequel we assume that \(\mathcal {T}\) is an arbitrary but fixed theory and give definitions relative to this theory.
Abstracted Clauses. Here we discuss how a clause can be separated into a theory and non-theory part. To this end we need to divide symbols into theory and non-theory symbols. When we deal with a combination of theories we consider as theory symbols those symbols interpreted in at least one of the theories and all other symbols as non-theory symbols. That is, non-theory symbols are uninterpreted in all theories.
A non-equality literal is a theory literal if its predicate symbol is a theory symbol. An equality literal \(t_1 \simeq _s t_2\) is a theory literal, if the sort s is a theory sort. A non-theory literal is any literal that is not a theory literal. A literal is pure if it contains only theory symbols or only non-theory symbols. A clause is fully abstracted, or simply abstracted, if it only contains pure literals. A clause is partially abstracted if non-theory symbols do not appear in theory literals. Note that in partially abstracted clauses theory symbols are allowed to appear in non-theory literals.
A non-variable term t is called a theory term (respectively non-theory term) if its top function symbol is a theory (respectively non-theory) symbol. When we say that a term is a theory or a non-theory term, we assume that this term is not a variable.
Given a non-abstracted clause \(L[t] \vee C\) where L is a theory literal and t a non-theory term (or the other way around), we can construct the equivalent clause \(L[x] \vee C \vee x\not \simeq t\) for a fresh variable x. Repeated application of this process will lead to an abstracted clause, and doing this only for theory literals will result in a partially abstracted clause. In both cases, the results are unique (up to variable renaming).
The above abstraction process will take \(a+a \simeq 1\), where a is a non-theory symbol, and produce \(x+y \simeq 1 \vee x \not \simeq a \vee y \not \simeq a\). There is a simpler equivalent fully abstracted clause \(x+x \simeq 1 \vee x \not \simeq a\), and we would like to avoid unnecessarily long clauses. For this reason, we will assume that abstraction will abstract syntactically equal subterms using the same fresh variable, as in the above example. If we abstract larger terms first, the result of abstractions will be unique up to variable renaming.
Superposition Calculus. Later we will show how our underlying calculus, the superposition and resolution calculus, can be updated to use an updated notion of unification. For space reasons we do not replicate this calculus here (but it is given in our previous work [15]). We do, however, draw attention to the following Equality Resolution rule

as, without modification, this rule will directly undo any abstractions. This rule will be used in Sect. 3 to justify ignoring certain literals when performing instantiation.
Saturation-Based Proof Search (and Theory Reasoning). We introduce our new approach within the context of saturation-based proof search. The general idea in saturation is to maintain two sets of Active and Passive clauses. A saturation-loop then selects a clause C from Passive, places C in Active, applies generating inferences between C and clauses in Active, and finally places newly derived clauses in Passive after applying some retention tests. The retention tests involve checking whether the new clause is itself redundant (i.e. a tautology) or redundant with respect to existing clauses.
To perform theory reasoning within this context it is common to do two things. Firstly, to evaluate new clauses to put them in a common form (e.g. rewrite all inequalities in terms of <) and evaluate ground theory terms and literals (e.g. \(1+2\) becomes 3 and \(1<2\) becomes \( false \)). Secondly, as previously mentioned, relevant theory axioms can be added to the initial search space. For example, if the input clauses use the \(+\) symbol one can add the axioms \(x+y \simeq y+x\) and \(x+0 \simeq x\), among others.
3 Generating Simpler Instances
In the introduction, we showed how useful instances can be generated by finding substitutions that make theory literals false. We provide further motivation for the need for instances and then describe a new inference rule capturing this approach.
There are some very simple problems that are difficult to solve by the addition of theory axioms. Consider, for example, the following conjecture valid in the theory of integer arithmetic:
which yields the following unit clause after being negated for refutation
It takes Vampire almost 15 s to refute this clause using theory axioms (and non-trivial search parameters) and involves the derivation of intermediate theory consequences such as \(x+1 \simeq y+1 \vee y+1 \le x \vee x+1 \le y\). In contrast, applying the substitution \(\{x \mapsto 1\}\) immediately leads to a refutation via evaluation.
The generation of instances in this way is not only useful where theory axiom reasoning explodes, it can also significantly shorten proofs where theory axiom reasoning succeeds. For example, there is a proof of the problem DAT101=1 from the TPTP library using theory axioms that involves generating just over 230 thousand clauses. In contrast, instantiating an intermediate clause
with \(\{ x \mapsto 4 \}\) solves the problem after generating just 171 clauses.
Theory Instantiation. From the above discussion it is clear that generating instances of theory literals may drastically improve performance of saturation-based theorem provers. The problem is that the set of all such instances can be infinite, so we should try to generate only those instances that are likely not to degrade the performance.
There is a special case of instantiation that allows us to derive from a clause C a clause with fewer literals than C. We can capture this in the following theory instantiation inference rule where the notion of trivial literal has not yet been defined.

such that
-
1.
P contains only pure theory literals;
-
2.
\(\lnot {P}\theta \) is valid in \(\mathcal {T}\) (equivalently, \(P\theta \) is unsatisfiable in \(\mathcal {T}\)).
-
3.
P contains no literals trivial in \(P \vee D\);
The second condition ensures that \(P\theta \) can be safely removed. This also avoids making a theory literal valid in the theory (a theory tautology) after instantiation. For example, if we had instantiated clause (1) with \(\{ x \mapsto 3\}\) then the clause would have been evaluated to \( true \) (because of \(3<4\)) and thrown away as a theory tautology.
The third condition avoids the potential problem of simply undoing abstraction. For example, consider the unit clause p(1, 5) which will be abstracted as
The substitution \(\theta = \{ x \mapsto 1, y \mapsto 5 \}\) makes the formula \(x \simeq 1 \wedge y \simeq 5\) valid. Its application, followed by evaluation produces \(p(x,y)\theta = p(1,5)\), i.e. the original clause.
More generally, a clause does not need to be abstracted to contain such literals. For example, the clause
might produce, after applying TheoryInst (without the third condition) and evaluation, the instance p(1, 0), but it can also be used to produce the more general clause \(p(y+1,y)\) using equality resolution.
Based on the above discussion we define literals that we do not want to use for applying TheoryInst since we can use a sequence of equality resolution steps to solve them. Let C be a clause. The set of trivial literals in C is defined recursively as follows. A literal L is trivial in C if
-
1.
L is of the form \(x \not \simeq t\) such that x does not occur in t;
-
2.
L is a pure theory literal;
-
3.
every occurrence of x in C apart from its occurrence in \(x \not \simeq t\) is either in a literal that is not a pure theory literal, or in a literal trivial in C.
We call such literals trivial as they can be removed by a sequence of equality resolution steps. For example, in clause (2) both \(x \not \simeq 1\) and \(y \not \simeq 5\) are trivial. Consider another example: the clause
The literal \(x \not \simeq y + 1\) is trivial, because, apart from this literal, x occurs only in the non-theory literal p(x, y, z). The literal \(y \not \simeq z \cdot z\) is also trivial, because y occurs only in non-theory literal p(x, y, z) and in a trivial literal \(x \not \simeq y + 1\).
It is easy to argue that all pure theory literals introduced by abstraction are trivial.
Implementation. To use \( TheoryInst \), we apply the following steps to each given clause C:
-
1.
abstract relevant literals;
-
2.
collect (all) non-trivial pure theory literals \(L_1,\ldots , L_n\);
-
3.
run an SMT solver on \(T = \lnot L_1 \wedge \ldots \wedge \lnot L_n\);
-
4.
if the SMT solver returns
-
a model, we turn it into a substitution \(\theta \) such that \(T\theta \) is valid in \(\mathcal {T}\);
-
unsatisfiable, then C is a theory tautology and can be removed.
-
Note that the abstraction step is not necessary for using \( TheoryInst \), since it will only introduce trivial literals. However, for each introduced theory literal \(x \not \simeq t\) the variable x occurs in a non-theory literal and inferences applied to this non-theory literal may instantiate x to a term s such that \(s \not \simeq t\) is non-trivial. Let us now discuss the implementation of each step in further detail.
Selecting Pure Theory Literals. In the definition of \( TheoryInst \) we did not specify that P contains all pure theory literals in the premise. The reason is that some pure theory literals may be unhelpful. For example, consider
Here the SMT solver could select any value for x, apart from 0. In general, positive equalities are less helpful than negative equalities or interpreted predicates as they restrict the instances less. We introduce three options to control this selection:
-
strong: Only select strong literals where a literal is strong if it is a negative equality or an interpreted literal.
-
overlap: Select all strong literals and additionally those theory literals whose variables overlap with a strong literal.
-
all: Select all non-trivial pure theory literals.
At this point there may not be any pure theory literals to select, in which case the inference will not be applied.
Interacting with the SMT solver. In this step, we replace variables in selected pure theory literals by new constants and negate the literals. Once this has been done, the translation of literals to the format understood by the SMT solver is straightforward (and outlined in [21]). We use Z3 [11] in this work.
Additional care needs to be taken when translating partial functions, such as division. In SMT solving, they are treated as total underspecified functions. For example, when \(\mathcal {T}\) is integer arithmetic with division, interpretations for \(\mathcal {T}\) are defined in such a way that for all integers a, b and interpretation \(\mathcal {I}\), the theory also has the interpretation defined exactly as \(\mathcal {I}\) apart from having \(a/0 = b\). In a way, division by 0 behaves as an uninterpreted function.
Due to this convention, Z3 may generate an arbitrary value for the result in order to satisfy a given query. As a result, Z3 can produce a model that is output as an ordinary solution except for the assumptions about division by 0. For example solving \(2 / x = 1\) can return \(x = 0\). If we accept that \(x \simeq 0\) is a solution, the theorem prover may become unsound. As an example, consider a problem consisting of the following two clauses
The example is satisfiable as witnessed by an interpretation that assigns false to p(z) for every real number z and interprets 1 / 0 as a non-zero real, e.g. 1. However, the \( TheoryInst \) rule could produce conflicting instances p(0) and \(\lnot p(0)\) of the two clauses, internally assuming \(1/0=0\) for the first instances and \(1/0 \ne 0\) for the second.
To deal with this issue, we assert that \(s \not \simeq 0\) whenever we translate a term of the form t / s. This implies that we do not pass to the SMT solver terms of the form t / 0.
Instance Generation. The next step is to understand when and how we can turn the model returned by the SMT solver into a substitution making T valid. Recall that T can contain
-
1.
interpreted symbols that have a fixed interpretation in \(\mathcal {T}\), such as 0 or \(+\);
-
2.
other interpreted symbols, such as division;
-
3.
variables of T.
In general, there are no standards on how SMT solvers return models or solutions. We assume that the model returned by the underlying SMT solver can be turned into a conjunction S of literals such that
-
1.
S is satisfiable in \(\mathcal {T}\);
-
2.
\(S \rightarrow T\) is valid in \(\mathcal {T}\).
Note that checking that T is satisfiable and returning T as a model satisfies both conditions, but does not give a substitution that can be used to apply the \( TheoryInst \) rule.
To apply this rule, we need models of a special form defined below. A conjunction S of literals is said to be in triangle form if S has the form
such that for all \(i = 1,\ldots ,n\) the variable \(x_i\) does not occur in \(t_i,\ldots ,t_n\). Any model S in a triangle form can be converted into a substitution \(\theta \) such that \(x_i\theta = t_i\theta \) for all \(i = 1,\ldots ,n\). Note that \(S\theta \) is then valid, hence (by validity of \(S \rightarrow T\)), \(T\theta \) is valid too, so we can use \(\theta \) to apply \( TheoryInst \).
Practically, we must evaluate the introduced constants (i.e. those introduced for each of the variables in the above step) in the given model. In some cases, this evaluation fails to give a numeric value. For example, if the result falls out of the range of values internally representable by Vampire or when the value is a proper algebraic number, which currently also cannot be represented internally by our prover. In this case, we cannot produce a substitution and the inference fails.
Theory Tautology Deletion. As we pointed out above, if the SMT solver returns unsatisfiable then C is a theory tautology and can be removed. We only do it when we do not pass to the solver additional assumptions related to division by 0.
4 Abstraction Through Unification
As shown earlier, there are cases where we cannot perform a necessary inference step, because we are using a syntactic notion of equality rather than a semantic one. We have introduced an inference rule (\( TheoryInst \)) able to derive p(7) from the clause
but unable to deal with a pair of clauses such as
as it only performs theory reasoning inside a clause whereas this requires us to reason between clauses. Semantically, the terms 14y and \(x^2 + 49\) can be made equal when \(y=x=7\) so we would like to get the result p(7) here also.
Notice that if the clauses had been abstracted as follows:
then the resolution step would have been successful, producing
which could be given to \( TheoryInst \) to produce p(7). One solution would be to store clauses in abstracted form, but we argued earlier why this is not suitable and later confirm this experimentally. Instead of abstracting fully we incorporate the abstraction process into unification so that only abstractions necessary for a particular inference are performed. This is a lazy approach, i.e., we delay abstraction until it is needed.

Unification with Abstraction. Here we define a partial function \(\mathsf{mgu_{Abs}}\) on pairs of terms and pairs of atoms such that \(\mathsf{mgu_{Abs}}(t,s)\) is either undefined, in which case we say that it fails on (s, t), or \(\mathsf{mgu_{Abs}}(t,s) = (\theta ,D)\) such that
-
1.
\(\theta \) is a substitution and D is a (possibly empty) disjunction of disequalities;
-
2.
\((D \vee t \simeq s)\theta \) is valid in the underlying theory (and even valid in predicate logic).
Algorithm 1 gives a unification algorithm extended so that it implements \(\mathsf{mgu_{Abs}}\). The algorithm is parameterised by a \(\mathtt {canAbstract}\) predicate. The idea here is that some abstractions are not useful. For example, consider the two clauses
Allowing 1 and 2 to unify and produce \(1 \not \simeq 2\) is not useful in any context. Therefore, \(\mathtt {canAbstract}\) will always be false if the two terms are always non-equal in the underlying theory, e.g. if they are distinct numbers in the theory of arithmetic. Beyond this obvious requirement we also want to control how prolific such unifications can be. Therefore, we include the following options here:
-
interpreted_only: only produce a constraint if the top-level symbol of both terms is a theory symbol,
-
one_side_interpreted: only produce a constraint if the top-level symbol of at least one term is a theory symbol,
-
one_side_constant: only produce a constraint if the top-level symbol of at least one term is a theory symbol and the other is an uninterpreted constant,
-
all: allow all terms of theory sort to unify and produce constraints.
Updated Calculus. So far we have only considered resolution as a rule that could use this new form of unification, but in principle it can be used wherever we use unification. In the extended version of this paper [32] we describe how to update the full superposition and resolution calculus to make use of unification with abstraction. Here we give the rules for resolution and factoring:

where, for both inferences, \((\theta ,D) = \mathsf{mgu_{Abs}}{}(A,A')\) and A is not an equality literal.
Now given the problem from the introduction involving p(2x) and \(\lnot p(10)\) we can apply Resolution-wA to produce \(2x \not \simeq 10\) which can be resolved using evaluation and equality resolution as before. We note at this point that a further advantage of this updated calculus is that it directly resolves the issue of losing proofs via eager evaluation, e.g. where \(p(1+3)\) is evaluated to p(4), missing the chance to resolve with \(\lnot p(x+3)\).
Implementation. In Vampire, as in most modern theorem provers, inferences involving unification are implemented via term indexing [30]. Therefore, to update how unification is applied we need to update our implementation of term indexing. As the field of term indexing is highly complex we only give a sketch of the update here.
Term indices provide the ability to use a query term t to extract terms that unify (or match, or generalise) with t along with the relevant substitutions. Like many theorem provers, Vampire uses substitution trees [14] to index terms. The idea behind substitution trees is to abstract a term into a series of substitutions required to generate that term and store these substitutions in the nodes of the tree. To search for unifying terms we perform a backtracking search over the tree, composing substitutions from the nodes when descending down edges and checking at each node whether the query term is consistent with the current substitution. This involves unifying subterms of the query term against terms at nodes and a backtrackable result substitution must be maintained to store the results of these unifications. The result substitution must be backtracked as appropriate i.e. when backtracking past the point of unification.
To update this process we do two things. Firstly, wherever previously a unification failed we will produce a set of constraints using Algorithm 1. Secondly, alongside the backtrackable result substitution we maintain a backtrackable stack of constraints so that whenever we backtrack past a point where we made a unification that produced some constraints we remove those constraints from the stack.
5 Experimental Results
We present experimental results evaluating the effectiveness of the new techniques. Our experiments were carried out on a cluster on which each node is equipped with two quad core Intel processors running at 2.4 GHz and 24 GiB of memory.
Comparing New Options. We were interested in comparing how various proof option values affect the performance of a theorem prover. We consider the two new options referred to here by their short names: uwa (unification with abstraction) and thi (theory instantiation). In addition, we consider the boolean option fta (full theory abstraction), applying full abstract to input clauses as implemented in previous versions of Vampire.
Making such a comparison is hard, since there is no obvious methodology for doing so, especially considering that Vampire has over 60 options commonly used in experiments (see [24]). The majority of these options are Boolean, some are finitely-valued, some integer-valued and some range over other infinite domains. The method we used here was based on the following ideas, already described in [17].
-
1.
We use a subset of problems with quantifiers and theories from the SMTLIB library [5] (version 2016-05-23) that (i) do not contain bit vectors, (ii) are not trivially solvable, and (iii) are solvable by some approach.
-
2.
We repeatedly select a random problem P in this set, a random strategy S and run P on variants of S obtained by choosing possible values for the three options using the same time limit.
We consider combinations of option values satisfying the following natural conditions: either fta or uwa must be off, since it does not make sense to use unification with abstraction when full abstraction is performed. This resulted in 24 possible combinations of values. We ran approximately 100 000 tests with the time limit of 30 s, which is about 4000 tests per a combination of options. The results are shown in Table 1.
It may seem surprising that the overall best strategy has all the three options turned off. This is due to what we have observed previously: many SMTLIB problems with quantifiers and theories require very little theory reasoning. Indeed, Vampire solves a large number of problems (including problems unsolvable by existing SMT solvers) just by adding theory axioms and then running superposition with no theory-related rules. Such problems do not gain from the new options, because new inference rules result only in more generated clauses. Due to the portfolio approach of modern theorem provers, our focus is on cases where new options are complementary to existing ones.
Let us summarise the behaviour of three options, obtained by a more detailed analysis of our experimental results.
Full Theory Abstraction. Probably the most interesting observation from these results is that the use of full abstraction (fta) results in an observable degradation of performance. This confirms our intuition that unification with abstraction is a good replacement for abstraction. As a result, we will remove the fta option from Vampire.
Unification with Abstraction. This option turned out to be very useful. Many problems had immediate solutions with uwa turned on and no solutions when it was turned off. Further, the value all resulted in 12 unique solutions. We have decided to keep the values all, interpreted_only and off.
Theory Instantiation. This option turned out to be very useful too. Many problems had immediate solutions with thi turned on and no solutions when it was turned off. We have decided to keep the values all, strong and off.
Contribution of New Options to Strategy Building. Since modern provers normally run a portfolio of strategies to solve a problem (strategy scheduling), there are two ways new strategies can be useful in such a portfolio:
-
1.
by reducing the overall schedule time when problems are solved faster or when a single strategy replaces one or more old strategies;
-
2.
by solving previously unsolved problems.
While for decidable classes, such as propositional logic, the first way can be more important, in first-order logic it is usually the second way that matters. The reason is that, if a problem is solvable by a prover, it is usually solvable with a short running time.
We ran Vampire trying to solve, using the new options, problems previously unsolved by Vampire. We took all such problems from the TPTP library [33] and SMT-LIB [5] and Table 2 shows the results. In the table, new solutions are meant with respect to what Vampire could previously solve and uniquely solved stands for the number of new problems with respect to what can be solved by other entrants into SMT-COMPFootnote 1 and CASCFootnote 2 where the main competitors are SMT solvers such as Z3 [11] and CVC4 [4] and ATPs such as Beagle [6] and Princess [28, 29].
With the help of the new options Vampire solved 20 problems previously unsolved by any other theorem prover or SMT solver.
6 Related Work
We review relevant related work. A more thorough review can be found in [32].
SMT Solving. SMT solvers such as Z3 [11] and CVC4 [4] implement E-matching [9, 12], model based quantifier instantiation [9, 12] and conflict instantiation [27] to handle quantifiers. Although complete on some fragments, these instantiation techniques are generally heuristic and cannot be directly applied in our setting (see [26]).
In \(DPLL(\varGamma )\) [10] a superposition prover is combined with an SMT solver such that ground literals implied by the SMT solver are used as hypotheses to first-order clauses.
AVATAR Modulo Theories. Our previous work on AVATAR Modulo Theories [21] uses the AVATAR architecture [23, 34] for clause splitting to integrate an SMT solver with a superposition prover. The general idea is to abstract the clause search space as a SMT problem and use a SMT solver to decide on at least one literal per clause to have in the current search space of the superposition prover. To abstract the clause search space, non-ground components (sub-clauses sharing variables) are abstracted as propositional symbols whilst ground literals are translated directly. The result is that the superposition prover only deals with a set of clauses that is theory-consistent in its ground part.
Theory Resolution. Stickel’s Theory Resolution [31] is a generalisation of the resolution inference rule whose aim is to exclude the often prolific theory axioms from the explicit participation on reasoning about the uninterpreted part of a given problem. In [32] we show that the theory resolution rule is a re-definition of \(\mathcal {T}\)-sound inferences. Given this, it is too abstract per se to bear practical relevance to our approach.
Hierarchic Superposition. Hierarchic Superposition (HS) [3] is a generalisation of the superposition calculus for black-box style theory reasoning. The approach uses full abstraction to separate theory and non-theory parts of the problem and introduces a conceptual hierarchy between uninterpreted reasoning (with the calculus) and theory reasoning (delegated to a theory solver) by making pure theory terms smaller than everything else. HS guarantees refutational completeness under certain conditions that can be rather restrictive, e.g., the clauses p(x) and \(\lnot p(f(c))\) cannot be resolved if the return sort of function f is a theory sort. The strategy of weak abstractions introduced by Baumgartner and Waldmann [7] partially addresses the downsides of the original approach. However, their approach requires some decisions to be made, for which there currently does not seem to be a practical solution. See [32] for more details.
Other Theory Instantiation. SPASS+T [20] implements a theory instantiation rule that is analogous to E-matching in the sense that it uses ground theory terms from the search space to perform instantiations as a last resort. This is not related to our approach.
Unification Modulo Theories. There is a large amount of work on unification modulo various theories, such as AC. This work is not related since we are not looking for the set of all or most general solutions to unification. Instead, we postpone finding such solutions by creating constraints, which can then be processed by the SMT solver.
7 Conclusion
We have introduced two new techniques for reasoning with problems containing theories and quantifiers. The first technique allows us to utilise the power of SMT solving to find useful instances of non-ground clauses. The second technique presents a solution to the issue of full abstraction by lazily abstracting clauses to allow them to unify under theory constraints. Our experimental results show that these approaches can solve problems previously unsolvable by Vampire and other solvers.
There are two directions for future research that we believe will further increase the power of this technique. Firstly, to explore the relationship between this approach and the AVATAR modulo theories work and, secondly, to relax the restriction of theory instantiation to single concrete models.
References
Akbarpour, B., Paulson, L.C.: Extending a resolution prover for inequalities on elementary functions. In: Dershowitz, N., Voronkov, A. (eds.) LPAR 2007. LNCS (LNAI), vol. 4790, pp. 47–61. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75560-9_6
Althaus, E., Kruglov, E., Weidenbach, C.: Superposition modulo linear arithmetic SUP(LA). In: Ghilardi, S., Sebastiani, R. (eds.) FroCoS 2009. LNCS (LNAI), vol. 5749, pp. 84–99. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04222-5_5
Bachmair, L., Ganzinger, H., Waldmann, U.: Refutational theorem proving for hierarchic first-order theories. Appl. Algebra Eng. Commun. Comput. 5, 193–212 (1994)
Barrett, C., Conway, C.L., Deters, M., Hadarean, L., Jovanović, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_14
Barrett, C., Stump, A., Tinelli, C.: The Satisfiability Modulo Theories Library (SMT-LIB) (2010). www.SMT-LIB.org
Baumgartner, P., Bax, J., Waldmann, U.: Beagle – a hierarchic superposition theorem prover. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 367–377. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_25
Baumgartner, P., Waldmann, U.: Hierarchic Superposition with weak abstraction. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 39–57. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_3
Bonacina, M.P., Lynch, C., de Moura, L.M.: On deciding satisfiability by theorem proving with speculative inferences. J. Autom. Reasoning 47(2), 161–189 (2011)
de Moura, L., Bjørner, N.: Efficient E-matching for SMT solvers. In: Pfenning, F. (ed.) CADE 2007. LNCS (LNAI), vol. 4603, pp. 183–198. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73595-3_13
de Moura, L., Bjørner, N.: Engineering DPLL(T) + Saturation. In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS (LNAI), vol. 5195, pp. 475–490. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71070-7_40
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Detlefs, D., Nelson, G., Saxe, J.B.: Simplify: a theorem prover for program checking. J. ACM 52(3), 365–473 (2005)
Ganzinger, H., Korovin, K.: Theory instantiation. In: Hermann, M., Voronkov, A. (eds.) LPAR 2006. LNCS (LNAI), vol. 4246, pp. 497–511. Springer, Heidelberg (2006). https://doi.org/10.1007/11916277_34
Graf, P.: Substitution tree indexing. In: Hsiang, J. (ed.) RTA 1995. LNCS, vol. 914, pp. 117–131. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-59200-8_52
Hoder, K., Reger, G., Suda, M., Voronkov, A.: Selecting the selection. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016. LNCS (LNAI), vol. 9706, pp. 313–329. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40229-1_22
Korovin, K., Voronkov, A.: Integrating linear arithmetic into superposition calculus. In: Duparc, J., Henzinger, T.A. (eds.) CSL 2007. LNCS, vol. 4646, pp. 223–237. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74915-8_19
Kovács, L., Robillard, S., Voronkov, A.: Coming to terms with quantified reasoning. In: Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, Paris, France, 18–20 January 2017, pp. 260–270. ACM (2017)
Kovács, L., Voronkov, A.: First-order theorem proving and Vampire. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 1–35. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_1
Nonnengart, A., Weidenbach, C.: Computing small clause normal forms. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning (in 2 volumes), pp. 335–367. Elsevier and MIT Press, Cambridge (2001)
Prevosto, V., Waldmann, U.: SPASS+T. In: Proceedings of the FLoC 2006 Workshop on Empirically Successful Computerized Reasoning, 3rd International Joint Conference on Automated Reasoning, vol. 192, CEUR Workshop Proceedings, pp. 19–33 (2006)
Reger, G., Bjørner, N., Suda, M., Voronkov, A.: AVATAR modulo theories. In: 2nd Global Conference on Artificial Intelligence, GCAI 2016, EPiC Series in Computing, vol. 41, pp. 39–52. EasyChair (2016)
Reger, G., Suda, M.: Set of support for theory reasoning. In: IWIL Workshop and LPAR Short Presentations, Kalpa Publications in Computing, vol. 1, pp. 124–134. EasyChair (2017)
Reger, G., Suda, M., Voronkov, A.: Playing with AVATAR. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 399–415. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_28
Reger, G., Suda, M., Voronkov, A.: The challenges of evaluating a new feature in vampire. In: Proceedings of the 1st and 2nd Vampire Workshops, EPiC Series in Computing, vol. 38, pp. 70–74. EasyChair (2016)
Reger, G., Suda, M., Voronkov, A.: New techniques in clausal form generation. In: 2nd Global Conference on Artificial Intelligence, GCAI 2016, EPiC Series in Computing, vol. 41, pp. 11–23. EasyChair (2016)
Reger, G., Suda, M., Voronkov, A.: Instantiation and pretending to be an SMT solver with Vampire. In: Proceedings of the 15th International Workshop on Satisfiability Modulo Theories, CEUR Workshop Proceedings, vol. 1889, pp. 63–75 (2017)
Reynolds, A., Tinelli, C., de Moura, L.M.: Finding conflicting instances of quantified formulas in SMT. In: Formal Methods in Computer-Aided Design, FMCAD 2014, Lausanne, Switzerland, 21–24 October 2014, pp. 195–202 (2014)
Rümmer, P.: A constraint sequent calculus for first-order logic with linear integer arithmetic. In: Cervesato, I., Veith, H., Voronkov, A. (eds.) LPAR 2008. LNCS (LNAI), vol. 5330, pp. 274–289. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89439-1_20
Rümmer, P.: E-matching with free variables. In: Bjørner, N., Voronkov, A. (eds.) LPAR 2012. LNCS, vol. 7180, pp. 359–374. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28717-6_28
Sekar, R., Ramakrishnan, I., Voronkov, A.: Term indexing. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. II, pp. 1853–1964. Elsevier Science, Amsterdam (2001). Chap. 26
Stickel, M.E.: Automated deduction by theory resolution. J. Autom. Reasoning 1(4), 333–355 (1985)
Suda, M., Reger, G., Voronkov, A.: Unification with abstraction and theory instantiation in saturation-based reasoning. EasyChair Preprint no. 1. EasyChair (2017). https://easychair.org/publications/preprint/1
Sutcliffe, G.: The TPTP problem library and associated infrastructure. J. Autom. Reasoning 43(4), 337–362 (2009)
Voronkov, A.: AVATAR: the architecture for first-order theorem provers. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 696–710. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_46
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis> This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara> <SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Reger, G., Suda, M., Voronkov, A. (2018). Unification with Abstraction and Theory Instantiation in Saturation-Based Reasoning. In: Beyer, D., Huisman, M. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2018. Lecture Notes in Computer Science(), vol 10805. Springer, Cham. https://doi.org/10.1007/978-3-319-89960-2_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-89960-2_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89959-6
Online ISBN: 978-3-319-89960-2
eBook Packages: Computer ScienceComputer Science (R0)