Abstract
We study the round complexity of zero-knowledge (ZK) proof systems. While five round ZK proofs for \({\mathsf {NP}}\) are known from standard assumptions [Goldreich-Kahan, J. Cryptology’96], Katz [TCC’08] proved that four rounds are insufficient for this task w.r.t. black-box simulation. In this work, we study the feasibility of ZK proofs using non-black-box simulation. Our main result is that three round private-coin ZK proofs for \({\mathsf {NP}}\) do not exist (even w.r.t. non-black-box simulation), under certain assumptions on program obfuscation. Our approach builds upon the recent work of Kalai et al. [Crypto’17] who ruled out constant round public-coin ZK proofs under the same assumptions as ours.
N. Fleischhacker and V. Goyal—We acknowledge the generous support of Northrop Grumman.
N. Fleischhacker and A. Jain—Supported in part by a DARPA/ARL Safeware Grant W911NF-15-C-0213 and a sub-award from NSF CNS-1414023.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The notion of zero-knowledge (ZK) proofs [32] is fundamental in cryptography. Intuitively, ZK proofs allow one to prove a statement without revealing anything beyond the validity of the statement.
An important measure of efficiency of ZK protocols is round complexity. Ever since the introduction of ZK proofs nearly three decades ago, an extensive amount of research has been dedicated towards minimizing their round-complexity. Protocols with smaller round complexity are more desirable so as to minimize the effect of network latency, which in turn decreases the time complexity of the protocol.
Round-Complexity of ZK. In this work, we study the exact round complexity of ZK proofs that achieve soundness even against computationally unbounded adversarial provers (as opposed to arguments that achieve soundness only against polynomial-time adversarial provers). While initial constructions of ZK proofs required a polynomial number of rounds, the seminal work of Goldreich and Kahan [29] constructed a five round ZK proof system for \({\mathsf {NP}}\) based on collision-resistant hash functions.
In the negative direction, two-round ZK arguments for \({\mathsf {NP}}\) were ruled out by Goldreich and Oren [31]. Later, Goldreich and Krawcyzk [30] ruled out three round ZK arguments for \({\mathsf {NP}}\) where the ZK property holds w.r.t. a black-box simulator. More recently, Katz [37] proved that four round ZK proofs with black-box simulation only exist for languages whose complement is in \(\mathsf {MA}\).
The above state of the art motivates the following intriguing question:

In this work, we investigate precisely this question.
Private-coin vs Public-coin. In the study of ZK proofs, whether or not the verifier makes its random coins public or keeps them private has a strong bearing on the round-complexity. Indeed, constructing public-coin ZK proofs is viewed as a harder task. Very recently, Kalai et al. [36] ruled out constant round public-coin ZK proof systems for \({\mathsf {NP}}\), even w.r.t. non-black-box simulation, assuming the existence of certain kinds of program obfuscation [7]. However, their approach breaks down in the private coin setting, where a verifier may keep its random coins used during the protocol private from the prover. This is not surprising, since five round private-coin ZK proofs are already known [29].
In this work, we investigate the feasibility of constructing private-coin ZK proofs (via non-black-box techniques) in less than five rounds. We remark that a candidate construction of three-round (private-coin) ZK proof system was given by Lepinski [40] based on a highly non-standard “knowledge-type” assumption; we discuss the bearing of our results on Lepinski’s protocol (and the underlying assumption) below.
1.1 Our Results
We revisit the round complexity of zero-knowledge proof systems. As our main result, we rule out the existence of three round private-coin ZK proofs for languages outside \(\mathsf {BPP}\), under certain strong assumptions.
Theorem 1
(Informal). Three round ZK proofs against non-uniform verifiers and distinguishers only exist for languages in \(\mathsf {BPP}\), assuming the following:
-
Sub-exponentially secure one-way functions.
-
Sub-exponentially secure indistinguishability obfuscation for circuits [7, 25].
-
Exponentially secure input-hiding obfuscation for multi-bit point functions [5, 11].
Our result relies on the same assumptions as those used in the recent work of Kalai et al. [36]. In their work, Kalai et al. use these assumptions to instantiate the Fiat-Shamir heuristic [24] and then rely upon its connection with public-coin ZK proofs [22] to rule out constant round public-coin ZK proofs. Naturally, this approach does not extend to the private coin setting. Nevertheless, we are able to build upon their techniques to obtain our result in Theorem 1.
Further, we note that our result contradicts the work of Lepinski [40] and thus refutes the knowledge-type assumption underlying Lepinski’s protocol. We further elaborate on this in Sect. 1.3.
On our assumptions. Starting with the work of [25], several candidate constructions of indistinguishability obfuscation (iO) have been proposed over the last few years (see, e.g., [2,3,4, 15, 26, 27, 41,42,43,44,45, 47]). During this time, (sub-exponentially secure) iO has also led to numerous advances in theoretical cryptography (see, e.g., [13, 21, 25, 46]). Nevertheless, no iO scheme whose security is based on standard cryptographic assumptions is presently known.
Our second assumption on program obfuscation concerns with the notion of input-hiding obfuscation [5] for the class of multi-bit point functions \(\mathcal {I}_{\alpha ,\beta }\), where \(\mathcal {I}_{\alpha ,\beta }(\alpha )=\beta \) and 0, otherwise. Roughly speaking, an input-hiding obfuscator for this family is said to be T-secure, if any PPT adversary can succeed in guessing \(\alpha \) with probability at most \(T^{-1}\). For our purposes, we require T to be exponential in the security parameter. Candidate constructions of such obfuscation based on a strong variant of the DDH assumption are known from the works of [11, 19] (see Sect. 2 for a more detailed discussion.)
Pessimistic Interpretation. While it is natural to be somewhat skeptical about the obfuscation assumptions we make, we note that our result implies that constructing three-round zero-knowledge proofs would require overcoming significant technical barriers. In particular, it would require disproving the existence of sub-exponentially secure iO, or the existence of exponentially secure input-hiding obfuscation for multi-bit point functions (or, less likely, disproving the existence of sub-exponentially secure one-way functions).
What about four rounds? Our result in Theorem 1 also extends to a specific relaxation of ZK, referred to as \(\epsilon \)-ZK [14]. In this relaxed notion, the simulator’s running time may grow polynomially with the distinguishing gap, which is allowed to be an inverse polynomial (unlike standard ZK, where the distinguishing gap must be negligible).
In a recent work, Bitansky et al. [14] construct a four round private coin \(\epsilon \)-ZK proof system for \({\mathsf {NP}}\), assuming the existence of keyless multi-collision-resistant hash functions (MCRH) [9, 14, 39]. Multi-collision-resistant hash functions weaken the standard notion of collision-resistant hash functions by only guaranteeing that an adversary cannot find many (rather than two) inputs that map to the same image. Presently, no constructions of keyless MCRH based on standard assumptions are known; however, unlike collision-resistant hash functions that cannot be secure against non-uniform adversaries in the keyless setting, keyless MCRH are meaningful even in the non-uniform setting if the number of required collisions are larger than the non-uniform advice to the adversary.
Their result serves as evidence that our techniques are unlikely to extend to the four round case, since otherwise it would imply the non-existence of keyless MCRH. While this is not implausible based on current evidence, in our eyes, it would be a rather surprising outcome.
It is of course possible that while four round private-coin \(\epsilon \)-ZK proofs exist, four round private-coin ZK proofs do not. However, in light of the above, it seems that ruling out four round private-coin ZK proofs (w.r.t. non-black-box simulation) would require substantially new techniques.
1.2 Technical Overview
In order to rule out the existence of three-round zero knowledge proofs, we need to show that for any imaginable three round proof system, there exists a non-uniform adversarial verifier whose view cannot be efficiently simulated by any non-black-box simulator. Since a non-black-box simulator has access to the adversary’s code, an immediate challenge is to “hide” the random coins of the adversarial verifier from the simulator.
Our starting approach to address this issue is to use program obfuscation. Let \(\varPi \) be any three-round private-coin proof system. To prove that \(\varPi \) is not ZK, we construct a “dummy” adversarial verifier \(V^*\) who receives as auxiliary input \(\mathsf {aux}\), an obfuscation of the next-message function of the honest verifier algorithm of \(\varPi \). More concretely, the auxiliary input \(\mathsf {aux}\) consists of an obfuscated program that has a key k for a pseudorandom function (PRF) hardwired in its description:
-
1.
Upon receiving a message \(\alpha \) from the prover, the program computes a message \(\beta \) of the honest verifier (as per protocol \(\varPi \)) using randomness \(r=\mathsf {PRF}_k(\alpha )\).Footnote 1
-
2.
Upon receiving a protocol transcript \((\alpha ,\beta ,\gamma )\), it recomputes the randomness r used to compute \(\beta \). Using the randomness r and the transcript, it honestly computes the verifier’s output (i.e., whether to accept or reject the proof).
The adversarial verifier’s code does not do anything intelligent on its own, and simply uses its auxiliary input \(\mathsf {aux}\) to compute its protocol message.
Ruling out Rewinding Simulators. The above strategy for hiding the random coins of the verifier runs into the following problem: a simulator may fix the first two messages \((\alpha ,\beta )\) of the protocol, and then observe the verifier’s output on many different third messages to learn non-trivial information about the private randomness of the verifier. Indeed, it was recently shown in the work of Jain et al. [35] that in certain protocols, a simulator can learn the verifier’s random tape by observing whether the verifier accepts or rejects in multiple trials.
A naive approach to address this problem is to simply modify the adversary and remove the protocol output from adversary’s view. This can be achieved by deleting the second instruction in the obfuscated program \(\mathsf {aux}\). This approach, however, immediately fails because now a simulator can simply simulate a “rejecting” transcript and succeed in fooling any distinguisher.
We address this problem by using non-uniform distinguishers, in a manner similar to Goldreich and Oren [31] and the recent work of [1]. Specifically, we modify the adversarial verifier to be such that it simply outputs the protocol transcript at the end of the protocol. The revised auxiliary input \(\mathsf {aux}\) only contains the first instruction described above. The PRF key k used to compute the verifier’s randomness inside \(\mathsf {aux}\) is given as non-uniform advice to the distinguisher. Note that this information is not available to the simulator. Now, given k and the protocol transcript, the distinguisher can easily decide whether or not to accept the transcript. Therefore, a simulator can no longer fool the distinguisher via a rejecting transcript.
How to rule out any Simulator? Of course the main problem remains. While the above approach constitutes a meaningful first step, we still need to formally argue that there does not exist any efficient simulator for the aforementioned adversarial verifier.
In prior works such as [31], this is achieved by showing that any efficient simulator algorithm can be used by a cheating prover to break the soundness of candidate protocol, which leads to a contradiction. It is, however, not immediately clear how to implement this strategy in our setting since a cheating prover does not have access to the code of the verifier (which is required for running the simulator algorithm).
We instead show that the existence of an efficient simulator can be used to disprove the computational soundness of a different protocol that is provably sound, leading to a contradiction.
Contradiction via Round Compression. We implement a compiler for compressing any three round private coin proof system into a two round argument system. Our round compression strategy is in fact very similar to the one developed in the recent work of Kalai et al. [36] in the context of public-coin ZK proofs. We then show that a simulator for the three round proof w.r.t. the aforementioned non-uniform verifier can be used to construct a cheating prover for the two round argument system.
We now elaborate on the round compression strategy. Consider the prover and verifier of the three-round proof to be two-stage algorithms. That is, \(\mathsf {P}_1\) produces the prover’s first message \(\alpha \), \(\mathsf {V}_1\) is the verifier’s next message function that on input \(\alpha \) outputs the verifier’s message \(\beta \), \(\mathsf {P}_2\) on input \(\beta \) produces the prover’s second message \(\gamma \) and finally \(\mathsf {V}_2\) is the decision procedure which uses the random tape to decide whether \((\alpha ,\beta ,\gamma )\) is an accepting transcript. The compressed two-round argument works as follows:
-
1.
In the first round, the verifier obfuscates the code of a slightly modified \(\mathsf {V}_1\) that upon input \(\alpha \), computes its message \(\beta \) using randomness \(r=\mathsf {PRF}_k(\alpha )\) generated via a hardcoded PRF key k. The verifier then sends the obfuscated program to the prover.
-
2.
The prover now runs \(\mathsf {P}_1\) to get \(\alpha \), evaluates the obfuscated program on \(\alpha \) to receive \(\beta \) and finally runs \(\mathsf {P}_2\) on \(\alpha ,\beta \) to get \(\gamma \). The prover then sends \(\alpha ,\beta ,\gamma \) to the verifier.
-
3.
Finally, the verifier can use k to recompute the random tape \(\mathsf {PRF}_k(\alpha )\) and run \(\mathsf {V}_2\) to validate the transcript.
A minor variant of the above strategy was recently used by Kalai et al. [36] in the case of public-coin ZK proofs. In their case, the obfuscated program simply corresponds to a PRF algorithm since it suffices to implement the strategy of a public-coin verifier.Footnote 2
Now, using the above round compression strategy, we can compress any three-round proof system \(\varPi \) into a two-round argument system \(\varPi '\). Now suppose that there exists an efficient zero-knowledge simulator \(\mathsf {Sim}\) for \(\varPi \) w.r.t. the adversarial verifier \(\mathsf {V}^*\) with auxiliary input \(\mathsf {aux}\), as described earlier. It is easy to see that such a simulator \(\mathsf {Sim}\) can be used to construct an efficient cheating prover \(\mathsf {P}^*\) for \(\varPi '\). Indeed, the view of \(\mathsf {Sim}\) in \(\varPi \) against \(\mathsf {V}^*\) with \(\mathsf {aux}\) is the same as the view of \(\mathsf {P}^*\) against an honest verifier in \(\varPi '\).
Thus, the main challenge now is to prove that our round-compression strategy indeed yields two-round arguments.
How to prove Soundness? To prove computational soundness of the two-round protocol, we proceed in two main steps:
-
1.
First, we establish that there exists only a very small set of “bad” first messages \(\alpha \) for which the cheating prover can even hope to be successful.
-
2.
Second, we prove that the obfuscation sufficiently hides this small set to ensure that the cheating prover cannot find such an \(\alpha \).
Below, we elaborate on each of these steps.
Step 1: Upper bounding Bad \(\alpha \)’s. Imagine for a moment, that the three-round proof system is public coin. Then, for any \(x \not \in \mathcal {L}\) and any \(\alpha \), there can only exist a negligible fraction of random tapes (and therefore \(\beta \)) for which an accepting \(\gamma \) even exists. This is true because otherwise the computationally unbounded prover could simply exhaustively search for this \(\gamma \) once they receive \(\beta \). Now, if the random tape, as in the two-round argument, is chosen pseudorandomly as a function of \(\alpha \), then only a very small set of \(\alpha \)’s will lead to such bad random tapes. This is because a distinguisher against the pseudorandom function can test for bad \(\alpha \)’s by exhaustively enumerating \(\gamma \)’s because the PRF is assumed to be \(2^n\)-secure. This small set would then be the set of bad \(\alpha \)’s. Clearly any successful cheating prover must use a bad \(\alpha \), since those are the only ones for which an accepting \(\gamma \) even exists.
In a private coin protocol, however, this notion of bad \(\alpha \)’s does not work. In fact in a private coin protocol, for any \(\alpha \) and any random tape, an accepting \(\gamma \) may always exist! Indeed, any three-round proof system can be transformed into another proof system that has this property: the verifier in the new protocol acts exactly as the original verifier, except that it also chooses a random \(\gamma ^*\) that it keeps private. Now, once it receives \(\gamma \) from the prover in the third round, the verifier accepts if either the original verifier accepts or \(\gamma =\gamma ^*\). Clearly in this protocol, there always exists an accepting \(\gamma \) but the protocol nevertheless remains sound. To break soundness, a prover must either break soundness of the original protocol or guess \(\gamma ^*\) which is only possible with negligible probability, because the entire transcript is independent of \(\gamma ^*\).
This example does not only show that the notion of bad \(\alpha \)’s from the public coin case does not work in the private-coin case, it also helps to illustrate how we can try to fix it. While an accepting \(\gamma \) may always exist, the prover only learns \(\beta \) and cannot tell which random tape was used by the verifier, beyond the obvious fact that it must have been consistent with \(\beta \). Therefore, the only \(\gamma \) a prover can hope to use to break the soundness of the protocol are those that, for a fixed \(\beta \), are accepted by many consistent random tapes.
We use this key observation to derive our new notion of bad \(\alpha \)’s. For any \(\alpha \) there exists only a negligible fraction of random tapes that are consistent with a \(\beta \) such that there exists a \(\gamma \) that is accepted with high probability over all the random tapes consistent with \(\beta \). This is true, because otherwise an unbounded prover could choose a random \(\alpha \) and after receiving \(\beta \), exhaustively search for all consistent random tapes and then search for the \(\gamma \) accepted by many of them. And then again, if the random tape, as is done in the two-round argument, is chosen pseudorandomly as a function of \(\alpha \), then only a very small set of \(\alpha \)’s will lead to such bad random tapes.
However, must a cheating prover in the two-round protocol necessarily use such a bad \(\alpha \) to convince a verifier? While in the public coin case this was a trivial fact, this is not at all obvious in the more general private-coin case. Since even for “good” random tapes accepting \(\gamma \)’s may exist, it is necessary to show that these remain hidden and cannot be used to cheat.
Here indistinguishability obfuscation comes to the rescue. Using iO and puncturable PRFs, we can show that a cheating prover must remain oblivious about which consistent random tape was used to compute \(\beta \). This allows us to argue that a cheating prover cannot make use of \(\gamma \)’s that are only accepting for a small number of consistent random tapes. Therefore, with overwhelming probability, a successful cheating prover must use a bad \(\alpha \).
Step 2: Hiding Bad \(\alpha \)’s. Now, it remains to argue that this set of bad \(\alpha \) is hidden by the obfuscation. Once we have established that a cheating prover must output a bad \(\alpha \), the most obvious idea would be to try and lead this to a contradiction with the soundness of the three-round proof. However, to translate this into an attack, we need to use the security of the PRF. And while using iO, that means we need to puncture. Since the puncturing must be done before we learn \(\alpha \) used by the cheating prover, we would incur an exponential loss in the success probability of the hypothetical three-round cheating prover. We can therefore only bring this to a contradiction if the three-round proof is exponentially sound, which would severely weaken the result. Instead, we follow the same approach as Kalai et al. [36] and “transfer” the exponential loss to another cryptographic primitive.
The idea is to use the security of another primitive to argue that bad \(\alpha \)’s are hidden. Since the goal is to argue that bad inputs to a circuit remain hidden a natural candidate for this primitive is input-hiding obfuscation. And indeed, sufficiently strong input-hiding obfuscation for multibit point functions allows to lead the existence of a cheating prover to a contradiction. Some technical issues arise in this proof due to the distribution of bad \(\alpha \)’s not being uniform. However, using a clever trick of a “relaxed” verifier it is possible to show that the distributions are sufficiently close. In this part of the proof, we are able to adapt the elegant strategy of Kalai et al. [36] with only minor modifications.
Extension to \(\epsilon \) -ZK. To extend our result to also rule out three-round \(\epsilon \)-ZK proofs, we mainly need to argue that the cheating prover we described above is still successful in breaking soundness of the two-round argument, even if our starting point is an \(\epsilon \)-ZK simulator instead of a regular ZK simulator.
Towards this, we note that the \(\epsilon \)-ZK simulator, for every noticeable function \(\epsilon \), is required to output a distribution that is \(\epsilon \)-indistinguishable from the real distribution. Thus, we can choose any small noticeable function \(\epsilon \), and then this means that, while the cheating prover against the two-round argument is no longer successful with all but negligible probability, it is still successful with probability \(1-\epsilon \). This is sufficient to break soundness and our main theorem therefore extends to \(\epsilon \)-ZK proofs.
1.3 Implications to Lepinski’s Protocol
Lepinski’s 3-round ZK proof protocol [40] is based on a clever combination of the three round honest-verifier ZK protocol of Blum [16] for Hamiltonian Graphs and a special kind of oblivious transfer. While Lepinski chose to give a more direct description of his protocol, a more modular high-level construction is implicit in his thesis. His construction makes use of two building blocks:
-
1.
The three round honest-verifier ZK protocol of Blum for Hamiltonian Graphs.
-
2.
A three round string OT protocol with the following properties:
-
The protocol is “delayed input” on the sender’s side. I.e., the first round of the OT can be computed independently of the sender’s inputs \((m_0, m_1)\).
-
The protocol achieves indistinguishability based security against a computationally unbounded malicious sender.
-
The protocol achieves simulation based security against a malicious polynomial time receiver.
-
Based on these assumptions a three-round ZK proof can be constructed as described below. In the description we focus on soundness 1 / 2. For this specific protocol, smaller soundness error can be achieved by parallel repetition without affecting the ZK property.
-
1.
In the first round, the prover sets up the OT by sending the first message.
-
2.
In the second round, the verifier sends the OT receiver message corresponding to their random challenge for Blum’s protocol. I.e. the Blum challenge is used as the selection bit b in the OT.
-
3.
In the third round the prover sends the first message of Blum’s protocol. Additionally he sends the sender message of the OT, corresponding to the two possible prover responses to the (as of yet unknown) challenge. I.e. the prover sets \(m_b\) in the OT to be the response to challenge b.
-
4.
Finally the verifier receives the OT message, thus learning \(m_b\) and verifies that \(m_b\) is a valid response in Blum’s protocol.
It is easy to verify that this protocol is indeed sound: since the OT is secure against an unbounded sender, the prover must choose his first message without knowledge of the challenge and if the graph does not contain a Hamiltonian cycle then it can only give a valid response to one of the challenges and is thus only successful with probability 1 / 2. The soundness of this protocol is uncontested by our result.
To prove that the above protocol is also zero-knowledge, one can leverage the simulation-based security of the OT against malicious receivers. In particular, the ZK simulator uses the OT simulator to learn the OT selection bit, and then uses it to invoke the honest-verifier ZK simulator for Blum’s protocol. This part is disputed by our result. Since the security of Blum’s protocol is not in question, this means that our result disputes the existence of an OT protocol with the properties described above.
However, Lepinski implicitly gives a number-theoretic construction of such an OT protocol using a very specific “knowledge-type” assumption that is referred to as the “proof of knowledge assumption (POKA)” in this thesis. This assumption essentially states that a specific three-round public-coin proof of knowledge protocol remains a proof of knowledge even if the verifier’s challenge is computed using a fixed hash function. This assumption is necessary to facilitate extraction of the receiver’s selection bit in his OT protocol, which is the key to proving simulation-based security against malicious receivers.
The question, of course, remains how this protocol and the underlying assumption exactly relate to our impossibility result. For that, we should first note that Lepinski does not explicitly prove his protocol to be zero-knowledge relative to non-uniform verifiers. Since our impossibility result only rules out three-round ZK with non-uniform verifiers, our result – taken literally – does not directly apply to the protocol as stated. However, it is easy to see that Lepinski’s protocol does, in fact, achieve ZK against non-uniform verifiers if the POKA assumption is suitably augmented so that it holds even against provers with arbitrary auxiliary input. This augmented assumption is therefore what is specifically refuted by our result.
In a bit more detail, what does it mean exactly to apply our result to Lepinski’s protocol? As mentioned earlier, the soundness of the protocol is not in question. Therefore, the round compression part of our proof works exactly as stated, i.e., we are able to compress Lepinski’s three-round proof into a two round argument. It is the second part of our result, where we show that the soundness of the two round argument and the zero-knowledge property of the three-round proof contradict each other, where we get the refutation of the POKA assumption.
Essentially, in this part of the proof, we show that in the compressed two-round argument, a malicious prover is capable of using the ZK-simulator for the three-round proof to cheat and break soundness. Since the soundness of the protocol is not in question, this means that we are refuting the existence of the ZK-simulator and thus, that the 3-round protocol can be zero-knowledge. In the generalized terms in which we described Lepinski’s protocol above the ZK-simulator only requires the HVZK-simulator of Blum’s protocol and the OT-simulator to work. This means that our work specifically refutes the simulation based receiver-security of the OT protocol. If we look at our result in a bit more detail, it is also clear why this is the case. Essentially, we are constructing a malicious prover who is capable of running the ZK-simulator for the 3-round proof. For Lepinski’s construction to work, this simulator must be able to extract the selection bit in the OT from the verifier’s message. This means that we are constructing an algorithm capable of extracting the selection bit of the receiver while acting as a malicious sender in the OT protocol. Clearly, this immediately implies that the OT is broken.
1.4 Related Work
There is a large body of work dedicated to the study of round complexity of zero-knowledge protocols. Below, we provide a brief (and incomplete) summary of some of the prior work in this area.
ZK Proofs. Five-round ZK proofs are known based on collision-resistant hash functions [29], and four-round \(\epsilon \)-ZK proofs were recently constructed based on keyless multi-collision-resistant hash functions [14]. Both of these constructions require the verifier to use private coins. There also exists a candidate for a three-round ZK proof due to Lepinski [40], which ultimately clashes with our result. Lepinski’s protocol is based on a highly non-standard knowledge-type assumption which our result refutes. We explain the exact relationship and implications in Sect. 1.3.
Dwork et al. [22] (and independently, Hada and Tanaka [33]) established an intimate connection between the Fiat-Shamir paradigm [24] and constant-round public-coin ZK proofs. Using their result, [36] recently ruled out the existence of constant-round public-coin ZK proofs, under the same assumptions as in our work. Previously, such protocols were only ruled out w.r.t. black-box simulation by [30]. We refer the reader to [36] for further discussion on public-coin ZK proofs.
ZK Arguments. Four-round ZK arguments are known based on one-way functions [8, 23]. Goldreich and Krawcyzk [30] ruled out the existence of three-round ZK arguments for \({\mathsf {NP}}\) w.r.t. black-box simulation. While three-round ZK arguments with non-black-box simulators were unknown for a long time, some recent works have studied them w.r.t. weaker adversaries such as uniform provers [10], or uniform verifiers [12], while finally Bitansky et al. [14] were very recently able to construct general three round ZK arguments for non-uniform provers and verifiers based on keyless multi-collision-resistant hash functions.
2 Preliminaries
We denote by \(n\in \mathbb {N}\) the security parameter that is implicitly given as input to all algorithms in unary representation \(1^n\). We denote by \(\{0,1\}^\ell \) the set of all bit-strings of length \(\ell \). For a finite set S, we denote the action of sampling x uniformly at random from S by  , and we denote the cardinality of S by \(\left|S \right|\). Al algorithms are assumed to be randomized, unless explicitly stated otherwise. An algorithm is efficient or \(\mathsf {PPT}\) if it runs in time polynomial in the security parameter. If \(\mathcal {A}\) is randomized then by
, and we denote the cardinality of S by \(\left|S \right|\). Al algorithms are assumed to be randomized, unless explicitly stated otherwise. An algorithm is efficient or \(\mathsf {PPT}\) if it runs in time polynomial in the security parameter. If \(\mathcal {A}\) is randomized then by  we denote that \(\mathcal {A}\) is run on input x and with random coins r and produced output y. If no randomness is specified, then it is assumed that \(\mathcal {A}\) is run with freshly sampled uniform random coins, and write this as
we denote that \(\mathcal {A}\) is run on input x and with random coins r and produced output y. If no randomness is specified, then it is assumed that \(\mathcal {A}\) is run with freshly sampled uniform random coins, and write this as  . For a circuit C we denote by \(\left|C \right|\) the size of the circuit. A function \({\mathsf {negl}(n)}\) is negligible if for any positive polynomial \(\mathsf {poly}(n)\), there exists an \(N \in \mathbb {N}\), such that for all \(n> N\), \({\mathsf {negl}(n)} \le \frac{1}{\mathsf {poly}(n)}\).
. For a circuit C we denote by \(\left|C \right|\) the size of the circuit. A function \({\mathsf {negl}(n)}\) is negligible if for any positive polynomial \(\mathsf {poly}(n)\), there exists an \(N \in \mathbb {N}\), such that for all \(n> N\), \({\mathsf {negl}(n)} \le \frac{1}{\mathsf {poly}(n)}\).
2.1 Interactive Proofs and Arguments
An interactive proof for an \({\mathsf {NP}}\) language \(\mathcal {L}\) is an interactive protocol between two parties, a computationally unbounded prover and a polynomial-time verifier. The two parties receive a common input x and the prover tries to convince the verifier that \(x\in \mathcal {L}\). Intuitively the prover should (almost) always be successful if x is indeed in \(\mathcal {L}\), but should be limited in its ability to convince the verifier if \(x\not \in \mathcal {L}\). An interactive proof, as formally introduced by Goldwasser et al. [32] is defined as follows.
Definition 1
(Interactive Proof). An r-round 2-Party protocol \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) between a polynomial-time verifier \(\mathsf {V}\) and an unbounded prover \(\mathsf {P}\) is an interactive proof with soundness error \(\epsilon \) for language \(\mathcal {L}\) if the following two conditions hold:
-
1.
Completeness: For all \(x \in \mathcal {L}\) it holds that
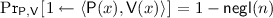 .
. -
2.
Soundness: For all \(x^* \not \in \mathcal {L}\) and all computationally unbounded malicious provers \(\mathsf {P}^*\) it holds that
 .
.
An interactive argument is very similar to an interactive proof, except that soundness is only required to hold relative to polynomial time malicious provers. Since also the honest prover is required to run in polynomial time, it receives an \({\mathsf {NP}}\) witness for x as an additional input. Formally, this leads to the following definition.
Definition 2
(Interactive Argument). An r-round 2-Party protocol \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) between a polynomial-time verifier \(\mathsf {V}\) and a polynomial-time prover \(\mathsf {P}\) is an interactive argument with soundness error \(\epsilon \) for language \(\mathcal {L}\) with associated relation \(\mathcal {R}\) if the following two conditions hold:
-
1.
Completeness: For all \((x,w) \in \mathcal {R}\) it holds that
 .
. -
2.
Soundness: For all \(x^* \not \in \mathcal {L}\) and all polynomial-time malicious provers \(\mathsf {P}^*\) it holds that
 .
.
An especially powerful class of interactive proofs and arguments are those that are zero-knowledge. Intuitively a zero-knowledge proof or argument ensures that a malicious polynomial time verifier cannot learn anything from an execution of the protocol, except that \(x\in \mathcal {L}\). This was first formalized in [32] by requiring the existence of a polynomial time simulator capable of – without knowledge of an \({\mathsf {NP}}\) witness for x – simulating any interaction a malicious verifier might have with the prover. This implies that anything the verifier learns from a protocol execution it could have also learned without interacting with the prover. To obtain a contradiction in the main proof in Sect. 3 we will use the notion of non-uniform zero-knowledge, where both the malicious verifier as well as the distinguisher may be non-uniform.
Definition 3
(Non-uniform Zero-Knowledge with Auxiliary Input). Let \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) be a 2-Party protocol. \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) is said to be non-uniformly zero-knowledge with auxiliary input, if for all (possibly malicious) \(\mathsf {PPT}\) algorithms \(\mathsf {V}^*\) there exists a \(\mathsf {PPT}\) simulator \(\mathsf {Sim}\), such that for all \(\mathsf {PPT}\) distinguishers \(\mathcal {D}\) and all auxiliary inputs \(\mathsf {aux}\) and \(\mathsf {aux}'\), it holds that for all statements x

2.2 Puncturable Pseudorandom Functions
The notion of puncturable pseudorandom functions was independently introduced in [17, 18, 38]. A puncturable pseudorandom function allows to puncture a key k on some fixed input x. This punctured key should still allow to correctly evaluate the PRF on any input other than x. However, the value of the function on input x should be indistinguishable from a unform random value, even given the punctured key. We define a strong notion of puncturable pseudorandom functions in the following.
Definition 4
(T-Secure Puncturable Pseudorandom Functions). A pair of probabilistic polynomial time algorithms \((\mathsf {PRF},\mathsf {Puncture})\) is a T-secure puncturable pseudorandom function with key length \(\kappa (n)\) input length \(i(n)\) and output length \(o(n)\) if the following conditions hold:
-
1.
Functionality Preserved Under Puncturing: For every \(n\in \mathbb {N}\), every key
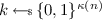 , every input \(x\in \{0,1\}^{i(n)}\), every punctured key \(\mathsf {k}\{x\}\), and every input \(x'\in \{0,1\}^{i(n)}\setminus {\{x\}}\) it holds that \(\mathsf {PRF}_k(x') = \mathsf {PRF}_{\mathsf {k}\{x\}}(x')\).
, every input \(x\in \{0,1\}^{i(n)}\), every punctured key \(\mathsf {k}\{x\}\), and every input \(x'\in \{0,1\}^{i(n)}\setminus {\{x\}}\) it holds that \(\mathsf {PRF}_k(x') = \mathsf {PRF}_{\mathsf {k}\{x\}}(x')\). -
2.
Pseudorandomness: For any fixed \(x\in \{0,1\}^{i(n)}\) it holds that for every distinguisher \(\mathcal {D}\) that runs in time at most \(\mathsf {poly}(T(n))\) it holds that
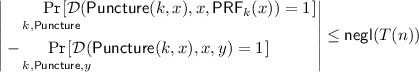
Our impossibility result uses \(2^{2n}\)-secure puncturable pseudorandom functions. Note that these can be constructed using the GGM construction from any subexponentially secure one-way function [28, 34] by for example using keys length \(\kappa (n)=n^2\).
2.3 Obfuscation
Our impossibility result uses two different kinds of obfuscation, indistinguishability obfuscation and input-hiding obfuscation for multi-input point functions. Indistinguishability obfuscation (iO) was first suggested as a notion by Barak et al. [7] as a weaker form of obfuscation. The security guarantee of iO is that the obfuscation of two functionally equivalent circuits should result in indistinguishable output distributions. That is, any polnomial-time reverse engineering cannot detect which of two equivalent implementations was the source of an obfuscated program. This security may seem rather weak at first glance. However, following the introduction of a first candidate construction by Garg et al. [25] it has been shown in several works that even this seemingly weak notion of obfuscation is a very powerful tool. We formally define indistinguishability obfuscation below.
Definition 5
(T-Secure Indistinguishability Obfuscation). Let \(\mathbb {C}\) be a family of polynomial size boolean circuits. Let \(\mathsf {iO}\) be a probabilistic polynomial time algorithm, which takes as input a circuit \(\mathbf {C}\in \mathbb {C}\) and a security parameter \(1^n\), and outputs a boolean circuit \(\mathbf {B}\) (not necessarily in \(\mathbb {C}\)). \(\mathsf {iO}\) is a T-secure indistinguishability obfuscator if the following two conditions hold:
-
1.
Correctness: For every \(n\in \mathbb {N}\), every circuit \(\mathbf {C}\in \mathbb {C}\) with input length \(\ell \), every obfuscated circuit
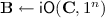 and every \(x\in \{0,1\}^{\ell }\) it holds that \(\mathbf {B}(x) = \mathbf {C}(x)\).
and every \(x\in \{0,1\}^{\ell }\) it holds that \(\mathbf {B}(x) = \mathbf {C}(x)\). -
2.
Indistinguishability: For every \(n\in \mathbb {N}\), every pair of circuit \(\mathbf {C}_1,\mathbf {C}_2\in \mathbb {C}\) with identical input length \(\ell \) and \(\left|\mathbf {C}_1 \right| = \left|\mathbf {C}_2 \right|\), and every \(\mathsf {poly}(T(n))\)-time distinguisher \(\mathcal {D}\) it holds that

Our impossibility result uses a strong notion of \(2^{2n}\)-secure indistinguishability obfuscation for general circuits. This notion is implied by any subexponentially secure indistinguishability obfuscator by instantiating the security parameter with \(\kappa (n)=n^2\).
The second form of obfuscation used in our result is input-hiding obfuscation for multi-bit point functions. The notion of input-hiding obfuscation was first suggested by Barak et al. in [5]. An input-hiding obfuscator for a family of circuits \(\mathbb {C}\) guarantees that, given an obfuscation of a circuit \(\mathbf {C}\) drawn uniformly at random from \(\mathbb {C}\) it is hard for an adversary to find any input on which the circuit doesn’t output 0.
Definition 6
(T-Secure Input-Hiding Obfuscation). Let \(\mathbb {C}= \{\mathbb {C}_n\}_{n\in \mathbb {N}}\) be a family of polynomial size boolean circuits, where \(\mathbb {C}_n\) is a set of circuits operating on inputs of length \(n\). A polynomial time obfuscator \(\mathsf {hideO}\) is a T-secure input hiding obfuscator for \(\mathbb {C}\) if the following two conditions hold:
-
1.
Correctness: For every \(n\in \mathbb {N}\), every circuit \(\mathbf {C}\in \mathbb {C}_n\), every obfuscated circuit
 and every \(x\in \{0,1\}^{n}\) it holds that \(\mathbf {B}(x) = \mathbf {C}(x)\).
and every \(x\in \{0,1\}^{n}\) it holds that \(\mathbf {B}(x) = \mathbf {C}(x)\). -
2.
Input Hiding: For every \(n\in \mathbb {N}\), and all probabilistic polynomial time adversary \(\mathcal {A}\) it holds that

Note that this security definition differs from previous definitions of T-security in so far as it requires the adversary to run in polynomial time (in \(n\)). Our result specifically uses input-hiding obfuscation for multi-bit point functions. A multi-bit point function is characterized by two values x and y and is defined as the function that on input x outputs y and outputs 0 on all other inputs.
Definition 7
(T-Secure Input-Hiding Obfuscation for Multi-bit Point Functions). Let \(I_{x,y}\) denote the multi-bit point function with \(I_{x,y}(x)=y\) and \(I_{x,y}(x')=0\) for all \(x'\ne x\) and let k be a function \(k : \mathbb {N}\rightarrow \mathbb {N}\). A polynomial time obfuscator \(\mathsf {hideO}\) is a T-secure input hiding obfuscator for \((n,k)\)-multi-bit point functions if it is a T-secure input-hiding obfuscator for all circuit families \(\mathbb {C}\) for which the following properties hold.
-
1.
All circuits in
 describe point functions with \(n\)-bit input and \(k(n)\)-bit output. I.e.,
describe point functions with \(n\)-bit input and \(k(n)\)-bit output. I.e.,  .
. -
2.
The marginal distribution on x is uniform for a uniformly sampled circuit
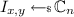 .
.
This notion was first studied by Bitansky and Cannetti in [11]. They also showed that an earlier candidate construction by Cannetti and Dakdouk [19] can be proven secure in the generic group model based on a strong variant of the DDH assumption. Our impossibility result requires \(2^{n}\)-secure input hiding obfuscator for multi-bit point functions. This may on first glance seem problematic, since DDH (and thereby the instantiation due to Cannetti and Dakdouk [19]) can be broken in time less than \(2^n\) even in the generic group model. However, in Definition 6 we explicitly – and in contrast to the other definitions in this section – require that the adversary runs in polynomial time. And known subexponential time attacks do not imply a polynomial time attack that is successful with probability greater than \(\mathsf {poly}/2^{(n)}\).
3 Impossibility of Three-Round Zero-Knowledge Proofs
In this section we will prove our main result, i.e., that under the stated assumptions, zero-knowledge 3-round interactive proof systems for non-trivial languages cannot exist. Our result is formally stated in Theorem 2.
Theorem 2
Let \(\hat{\varPi }\) be a 3-round interactive proof system for a language \(\mathcal {L}\not \in \mathsf {BPP}\) with negligible soundness error \(\mu \). Assume the existence of a \(2^{2n}\)-secure puncturable pseudorandom function, a \(2^{2n}\)-secure indistinguishability obfuscator, and a \(\mu \,\cdot \,2^{n}\mathsf {poly}(n)\)-secure input-hiding obfuscator for multi-bit point functions. Then \(\hat{\varPi }\) cannot be non-uniformly zero-knowledge with auxiliary input.
Proof
(Theorem 2). Let \(\hat{\varPi }=\mathchoice{\left\langle \hat{\mathsf {P}},\hat{\mathsf {V}}\right\rangle }{\langle \hat{\mathsf {P}},\hat{\mathsf {V}}\rangle }{\langle \hat{\mathsf {P}},\hat{\mathsf {V}}\rangle }{\langle \hat{\mathsf {P}},\hat{\mathsf {V}}\rangle }\) be a 3-round interactive proof system as described in Theorem 2. We consider the prover and verifier as two-stage algorithms, \(\hat{\mathsf {V}} = (\hat{\mathsf {V}}_{1},\hat{\mathsf {V}}_{2})\), \(\hat{\mathsf {P}} = (\hat{\mathsf {P}}_{1},\hat{\mathsf {P}}_{2})\). The first stage of the prover  on input the statement x, witness w and random coins r outputs the prover’s first message \(\alpha \). The first stage of the verifier
on input the statement x, witness w and random coins r outputs the prover’s first message \(\alpha \). The first stage of the verifier  on input the statement x, the prover’s first message \(\alpha \) and random coins s outputs the verifier’s message \(\beta \). The second stage of the prover
on input the statement x, the prover’s first message \(\alpha \) and random coins s outputs the verifier’s message \(\beta \). The second stage of the prover  on input the statement x, witness w, the verifier’s message \(\beta \) and random coins r outputs the prover’s second message \(\gamma \). The second stage of the verifier
on input the statement x, witness w, the verifier’s message \(\beta \) and random coins r outputs the prover’s second message \(\gamma \). The second stage of the verifier  on input the statement x, the prover’s messages \(\alpha ,\gamma \) and random coins s outputs a bit b indicating whether the proof is accepted of not. Note that without loss of generality we assume that the second stages do not take their own messages as input and instead recompute them when necessary.
on input the statement x, the prover’s messages \(\alpha ,\gamma \) and random coins s outputs a bit b indicating whether the proof is accepted of not. Note that without loss of generality we assume that the second stages do not take their own messages as input and instead recompute them when necessary.
First we slightly modify the protocol \(\hat{\varPi }\) into the protocol \(\varPi =\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\). The protocol behaves exactly as \(\hat{\varPi }\), except that \(\mathsf {V}_1\) takes as its random coins \(s=\sigma \Vert \hat{s}\) with \(\left|\sigma \right| = \left\lceil \log \mu ^{-1}\right\rceil \) and after running  outputs \(\beta := \sigma \Vert \hat{\beta }\). The prover’s second stage \(\mathsf {P}_2\) then again behaves exactly as \(\hat{\mathsf {P}}_2\), and ignores \(\sigma \). The following claim is immediately apparent.
outputs \(\beta := \sigma \Vert \hat{\beta }\). The prover’s second stage \(\mathsf {P}_2\) then again behaves exactly as \(\hat{\mathsf {P}}_2\), and ignores \(\sigma \). The following claim is immediately apparent.
Claim 3
If \(\hat{\varPi }\) is a 3-round interactive proof system with negligible soundness error \(\mu \), then \(\varPi \) is also a 3-round interactive proof system for the same language with the same negligible soundness error \(\mu \).
This modification is therefore without loss of generality and will allow us to cleanly define a relaxed version of the verifier later in the proof, leading to a much simpler proof.
The two-round argument system \(\bar{\varPi } = \mathchoice{\left\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\right\rangle }{\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\rangle }{\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\rangle }{\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\rangle }\) resulting from compressing the three-round proof system \(\varPi =\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) into two rounds. The round compression is achieved by sending an obfuscated version of the verifier’s own code to the prover as a first message. This allows the prover to compute the verifier’s response to their first message without additional interaction. This construction is proven sound in Lemma 4.
Now, we use the pseudorandom function \(\mathsf {PRF}\) the indistinguishability obfuscator \(\mathsf {iO}\) to construct a two-round protocol \(\bar{\varPi } = \mathchoice{\left\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\right\rangle }{\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\rangle }{\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\rangle }{\langle \bar{\mathsf {P}},\bar{\mathsf {V}}\rangle }\) as depicted in Fig. 1. The circuit \(\mathbf {C}_{\mathsf {V}_1}\) is defined as follows:

To prove Theorem 2 we will now use the following two lemmas proven in Sects. 3.1 and 3.2 respectively.
Lemma 4
Let \(\hat{\varPi }\) be a 3-round interactive proof system with negligible soundness error \(\mu \) as in Theorem 2. Let \(\varPi \) be the modified 3-round interactive proof system as described above. Assume that \(\mathsf {PRF}\) is a \(2^{2n}\)-secure puncturable pseudorandom function, and \(\mathsf {iO}\) is a \(2^{2n}\)-secure indistinguishability obfuscator. Further assume that \(\mathsf {hideO}\) is a \(2^{n}\)-secure input-hiding obfuscator for multi-bit point functions. Then \(\bar{\varPi }\), described in Fig. 1 is a 2-round interactive argument system with negligible soundness error \(\bar{\mu }\).
Lemma 5
Let \(\varPi \) be a 3-round interactive proof system for a language \(\mathcal {L}\not \in \mathsf {BPP}\). Let \(\bar{\varPi }\) be the transformed 2-round argument system described in Fig. 1 with soundness error \(\bar{\mu }\). If \(\bar{\mu } \le {\mathsf {negl}(n)}\) then \(\varPi \) is not non-uniformly zero-knowledge with auxiliary input.
Theorem 2 now follows as a simple corollary from combining Lemmas 4 and 5. By our assumption, \(\varPi \) has a negligibly small soundness error \(\mu \), which by Lemma 4 also implies a negligible soundness error \(\bar{\mu }\) for \(\bar{\varPi }\). Since a negligible soundness error of \(\bar{\varPi }\) implies that \(\varPi \) is not non-uniformly zero-knowledge with auxiliary input, the theorem trivially follows. \(\square \)
3.1 Proof of Lemma 4
Fix a modified 3-round interactive proof system \(\varPi = \mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\). Let \(\mu \le {\mathsf {negl}(n)}\) be the soundness error of \(\varPi \). We assume without loss of generality, that all messages of the protocol have length \(n\).
Assume towards contradiction that there exists a cheating \(\mathsf {PPT}\) prover \(\mathsf {P}^*\) breaking the soundness of \(\bar{\varPi }\) for some \(x^*\not \in \mathcal {L}\) with probability \(\nu = 1/\mathsf {poly}(n)\). I.e., we have that

To obtain a contradiction we analyze a variant of the protocol \(\varPi \) that works with a relaxed verifier \(\mathsf {V}'\). The relaxed verifier \(\mathsf {V}'\) works exactly as \(\mathsf {V}\), except that in addition to accepting whenever \(\mathsf {V}\) does, it also accepts if \(\beta = 0^{\left\lceil \log \nu /\mu \right\rceil }\Vert \beta '\) for some arbitrary \(\beta '\). Remember, that \(\beta = \sigma \Vert \hat{\beta }\) with \(\left|\sigma \right| = \left\lceil \log \mu ^{-1}\right\rceil \). I.e., \(\mathsf {V}'\) also accepts if the first \(\left\lceil \log \nu /\mu \right\rceil \) bits of \(\sigma \) are zero. In particular since \(\mathsf {V}'\) always accepts if \(\mathsf {V}\) accepts, it remains true that

Further, using a union bound, we can bound the soundness error \(\mu '\) of the relaxed 3-round protocol \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}'\right\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }\) to be
In particular, for any negligible \(\mu \), \(\mu '\) remains negligible.
Let  denote the set of all random tapes that given \(\alpha \) lead to the second message \(\beta \). We define the following set of pairs \((\alpha ,\beta )\), for which a malicious \(\gamma \) exists that will be accepted by the verifier for a large fraction of the random tapes that given \(\alpha \) lead to \(\beta \).
denote the set of all random tapes that given \(\alpha \) lead to the second message \(\beta \). We define the following set of pairs \((\alpha ,\beta )\), for which a malicious \(\gamma \) exists that will be accepted by the verifier for a large fraction of the random tapes that given \(\alpha \) lead to \(\beta \).

Observe, that membership in \(\mathsf {ACC}\) can be tested in time  by enumerating all messages \(\gamma \) and all random tapes s, checking whether \(\beta = \mathsf {V}'_1(x^*,\alpha ;s)\) and \(\mathsf {V}'_2(x^*,\alpha ,\gamma ;s) = 1\) and then computing the probability.Footnote 3 Given the cheating prover \(\mathsf {P}^*\), there exists an efficient algorithm \(\mathcal {A}\) that outputs \(\alpha \), such that \((\alpha ,\mathsf {V}'_1(\alpha ;\mathsf {PRF}_k(\alpha ))) \in \mathsf {ACC}\) with high probability. Formally this is stated in the following claim that is proven in Sect. 3.1.1.
by enumerating all messages \(\gamma \) and all random tapes s, checking whether \(\beta = \mathsf {V}'_1(x^*,\alpha ;s)\) and \(\mathsf {V}'_2(x^*,\alpha ,\gamma ;s) = 1\) and then computing the probability.Footnote 3 Given the cheating prover \(\mathsf {P}^*\), there exists an efficient algorithm \(\mathcal {A}\) that outputs \(\alpha \), such that \((\alpha ,\mathsf {V}'_1(\alpha ;\mathsf {PRF}_k(\alpha ))) \in \mathsf {ACC}\) with high probability. Formally this is stated in the following claim that is proven in Sect. 3.1.1.
Claim 6
If there exists a malicious prover \(\mathsf {P}^*\) as assumed above, then for the efficient algorithm \(\mathcal {A}\) that on input  runs
runs  , discards \(\gamma \) and outputs \(\alpha \) the following holds:
, discards \(\gamma \) and outputs \(\alpha \) the following holds:

Now consider the punctured version of the verifier circuit \(\mathbf {C}_{\mathsf {pct}}\) defined follows:

We will use the following claim, which essentially states that, when given an obfuscation of the verifier’s circuit punctured at \(\alpha ^*\), the \(\mathcal {A}\) from Claim 6 will output \(\alpha ^*\) with a probability slightly above random chance. The claim is proven in Sect. 3.1.2.
Claim 7
If \(\mathsf {PRF}\) is \(2^{2n}\)-secure and \(\mathsf {iO}\) is \(2^{2n}\)-secure, then it must hold that

This property of \(\mathcal {A}\) contradicts the security of the input hiding obfuscator \(\mathsf {hideO}\) as shown in the following. We claim that



where \(\mathbf {C}_{\mathsf {hide}}[k,\mathbf {B}]\) is a circuit that defined as follows

Equation 4 follows by reduction to the \(2^{2n}\) security of the indistinguishability obfuscator as depicted in Fig. 2. Clearly, the two circuits are functionally equivalent. Further, if it holds that \((\alpha ^*,\beta ^*) \in \mathsf {ACC}\) then the two cases of the security definition of indistinguishability obfuscation directly correspond to the two cases of Eq. 4. The reduction \(\mathcal {B}^\mathsf {iO}\) runs in time \(\mathcal {O}{2^{2n}}\) and therefore, Eq. 4 follows. Equation 5 then follows simply by upper bounding the probability with 1 and the negligible function by \(2^{-2n}\). Finally Eq. 6 follows directly from Claim 7 and the last inequality follows by loosely upper bounding the negligible function \(2^{-2n}\).
The reduction from the claim of Eq. 4 to the \(2^{2n}\) security of the indistinguishability obfuscator.
Closely following [36], it remains to be shown that the distribution defined by uniformly sampling \((\alpha ^*,\beta ^*)\) from \(\mathsf {ACC}\) is close to the distribution defined by uniformly sampling \(\alpha ^*\) and then sampling \(\beta ^*\) conditioned on \((\alpha ^*,\beta ^*) \in \mathsf {ACC}\).
Formally, we define two distributions. Let \(\mathsf {D}_0\) be the distribution over pairs \((\alpha ^*,\beta ^*)\) defined by uniformly sampling  . Let \(\mathsf {D}_1\) be the distribution over pairs \((\alpha ^*,\beta ^*)\) defined by uniformly sampling
. Let \(\mathsf {D}_1\) be the distribution over pairs \((\alpha ^*,\beta ^*)\) defined by uniformly sampling  and then uniformly sampling
and then uniformly sampling  . We denote by \(\mathsf {D}_b[\alpha ^*,\beta ^*]\) the probability of the pair \((\alpha ^*,\beta ^*)\) by distribution \(\mathsf {D}_b\).
. We denote by \(\mathsf {D}_b[\alpha ^*,\beta ^*]\) the probability of the pair \((\alpha ^*,\beta ^*)\) by distribution \(\mathsf {D}_b\).
Claim 8
For any \((\alpha ^*,\beta ^*) \in \{0,1\}^{n} \times \{0,1\}^{2n}\) it holds that
It follows from Claim 8 that by drawing from \(\mathsf {D}_1\) instead of \(\mathsf {D}_0\), the probability of \(\mathcal {A}\) outputting \(\alpha ^*\) can decrease at most by a multiplicative factor of \(4/\nu \). Therefore, Claim 8 and Eq. 6 imply that there exists a \(\mathsf {PPT}\) algorithm \(\mathcal {A}\) such that

Since the distribution of \(\alpha ^*\) drawn from \(\mathsf {D}_1\) is uniform, and \(\nu \) is an inverse polynomial, this contradicts the \(T = \mu \cdot 2^{n}\cdot \mathsf {poly}(n)\) security of the input hiding obfuscator and Lemma 4 follows. \(\square \)
It remains to show that the various claims used in the above proof actually hold. The proofs for these claims are detailed in the following sections.
3.1.1 Proof of Claim 6
By definition of \(\mathcal {A}\) we specifically need to show that

To do so, we will use the following claim, stating that if the cheating prover is successful in getting \(\mathsf {V}'_2\) to accept using the random tape \(\mathsf {PRF}_k(\alpha )\), then \(\mathsf {V}'_2\) would accept with almost the same probability if the random tape were replaced with a randomly chosen  .
.
Claim 9
If \(\mathsf {PRF}\) is \(2^{2n}\)-secure and \(\mathsf {iO}\) is \(2^{2n}\)-secure, then it must hold for any malicious prover \(\mathsf {P}^*\) as assumed above, that

We observe the following




where Eq. 7 follows from the definition of \(\mathsf {P}^*\) and Eq. 8 follows directly from Claim 9. Equation 9 simply splits the probability into two cases and Eq. 10 upper bounds the probability of the verifier accepting in the two cases.
The above observation gives us

as claimed. \(\square \)
Proof of Claim 9. Let \(\delta \) be any function such that

In this case, we also have that for a uniformly chosen value \(\alpha \),

Now consider the punctured version of the verifier circuit defined as before. By the \(2^{2n}\) security of the obfuscator, the fact that the two circuits \(\mathbf {C}_{\mathsf {V}_1}[k,x^*]\) and \(\mathbf {C}_{\mathsf {pct}}[\mathsf {k}\{\alpha \},\alpha ,\mathsf {V}'_1(\alpha ;\mathsf {PRF}_k(\alpha ))]\) are functionally equivalent and the fact that  can be sampled in time \(\mathcal {O}({2^n})\), it follows that
can be sampled in time \(\mathcal {O}({2^n})\), it follows that

Further, by the \(2^{2n}\) security of the pseudorandom function and the fact that  can be sampled in time \(\mathcal {O}{(2^n)}\), it follows that
can be sampled in time \(\mathcal {O}{(2^n)}\), it follows that

where the last inequality is obtained by loosely upper bounding the negligible functions. The circuit \(\mathbf {C}_{\mathsf {pct}}[\mathsf {k}\{\alpha \},\alpha ,\beta ]\) no longer contains any information about s besides the fact that \(s \in S_{\alpha ^*,\beta ^*}\). In the case where \(\alpha ^* = \alpha \), s and \(s'\) are, therefore, distributed identically and the two probabilities must in fact also be identical. Therefore, \(2^{-n}\cdot \delta (n)- 2^{-2n} \le 0\), giving us \(\delta (n) \le 2^{-n}\). The claim thus follows. \(\square \)
3.1.2 Proof of Claim 7
By definition of conditional probability, we have that

where we can easily bound  using the soundness error \(\mu '\) of \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}'\right\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }\). This is due to the fact that otherwise a (computationally unbounded) malicious prover could simply send a randomly sampled \(\alpha ^*\). Upon receiving \(\beta ^*\), it would hold that \((\alpha ^*,\beta ^*) \in \mathsf {ACC}\) with probability greater than \(2\mu '/\nu \). In this case, the prover could exhaustively search for a message \(\gamma ^*\) that would lead many verifiers to accept. By definition of \(\mathsf {ACC}\), such a prover would win with probability greater than \((2\mu '/\nu )\cdot (\nu /2) = \mu '\), contradicting the soundness of the underlying protocol. It remains to bound the numerator, which we will do in two hops.
using the soundness error \(\mu '\) of \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}'\right\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }\). This is due to the fact that otherwise a (computationally unbounded) malicious prover could simply send a randomly sampled \(\alpha ^*\). Upon receiving \(\beta ^*\), it would hold that \((\alpha ^*,\beta ^*) \in \mathsf {ACC}\) with probability greater than \(2\mu '/\nu \). In this case, the prover could exhaustively search for a message \(\gamma ^*\) that would lead many verifiers to accept. By definition of \(\mathsf {ACC}\), such a prover would win with probability greater than \((2\mu '/\nu )\cdot (\nu /2) = \mu '\), contradicting the soundness of the underlying protocol. It remains to bound the numerator, which we will do in two hops.



Equation 11 follows by reduction to the \(2^{2n}\) security of the puncturable pseudorandom function as depicted in Fig. 3. Clearly, the two cases of the security definition for puncturable pseudorandom functions directly map to the two cases of Eq. 11. Further, the reduction \(\mathcal {B}^\mathsf {PRF}\) runs in time \(\mathcal {O}{\smash {(2^{2n})}}\) and therefore, Eq. 11 follows.
The reduction from the claim of Eq. 11 to the \(2^{2n}\) security of the puncturable pseudorandom function.
Equation 12 follows by reduction to the \(2^{2n}\) security of the indistinguishability obfuscator as depicted in Fig. 4. Clearly, the two circuits are functionally equivalent and the two cases of the security definition for puncturable pseudorandom functions directly map to the two cases of Eq. 11. The reduction \(\mathcal {B}^\mathsf {iO}\) runs in time \(\mathcal {O}{\smash {(2^{2n})}}\) and therefore, Eq. 12 follows. Finally, Eq. 13 then follows by the fact that the sum of two negligible functions is negligible and by loosely upper bounding the resulting negligible functions (note that \(2^{-2n}\) is an inverse polynomial in \(2^{2n}\)).
The reduction from the claim of Eq. 12 to the \(2^{2n}\) security of the indistinguishability obfuscator.
Using basic probability theory and Claim 6, we get

Combining this with Eq. 13, we get

where the last inequality follows by loosely upper bounding the negligible function \(2^{1-n}\) by the inverse polynomial \(\nu /4\). Finally Claim 7 follows by

\(\square \)
3.1.3 Proof of Claim 8
For any \(\alpha ^*\) denote by  . By construction of the relaxed verifier we have that \(B_{\alpha ^*}\) contains at least a \(\mu /\nu \) fraction of all \(\beta \). On the other hand, soundness of the protocol \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}'\right\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }\) guarantees, that \(B_\alpha \) does not contain more than a \(2\mu '/\nu \le 4\mu /\nu ^2\) fraction of all \(\beta \). Thus, we have
. By construction of the relaxed verifier we have that \(B_{\alpha ^*}\) contains at least a \(\mu /\nu \) fraction of all \(\beta \). On the other hand, soundness of the protocol \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}'\right\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }{\langle \mathsf {P},\mathsf {V}'\rangle }\) guarantees, that \(B_\alpha \) does not contain more than a \(2\mu '/\nu \le 4\mu /\nu ^2\) fraction of all \(\beta \). Thus, we have
In particular, for any \(\alpha \) and \(\alpha ^*\), we have that
which gives us
\(\square \)
3.2 Proof of Lemma 5
Consider the following malicious verifier \(\mathsf {V}^* = (\mathsf {V}^*_1,\mathsf {V}^*_2)\). The first stage \(\mathsf {V}^*_1\) on input the statement x, the prover’s first message \(\alpha \) and auxiliary input \(\mathsf {aux}\) simply interprets the auxiliary input as a circuit, evaluates it on \(x,\alpha \), and outputs the result  . The second stage \(\mathsf {V}^*_2\) on input the statement x, the prover’s messages \(\alpha ,\gamma \) and auxiliary input \(\mathsf {aux}\) recomputes
. The second stage \(\mathsf {V}^*_2\) on input the statement x, the prover’s messages \(\alpha ,\gamma \) and auxiliary input \(\mathsf {aux}\) recomputes  and then simply outputs \(\alpha ,\beta ,\gamma \).
and then simply outputs \(\alpha ,\beta ,\gamma \).
Now, assume towards contradiction, that \(\varPi \) is zero-knowledge, i.e., in particular for \(\mathsf {V}^*\) as described above there exists a \(\mathsf {PPT}\) simulator \(\mathsf {Sim}\) such that for all \(\mathsf {PPT}\) distinguishers \(\mathcal {D}\), all auxiliary inputs \(\mathsf {aux}\) and \(\mathsf {aux}'\), and all statements x it holds that

We will use said simulator to construct a malicious prover \(\mathsf {P}^*\) against \(\bar{\varPi }\) as follows: On input x and the verifier’s message \(\mathbf {B}= \mathsf {iO}(\mathbf {C}_{\mathsf {V}_1}[k])\), \(\mathsf {P}^*\) invokes the simulator \(\mathsf {Sim}\) on x and auxiliary input \(\mathbf {B}\). The simulator will produce a transcript \(\alpha ,\beta ,\gamma \) that \(\mathsf {P}^*\) also outputs.
If \(x \in \mathcal {L}\), then the zero-knowledge property and the completeness guarantee that \(\bar{\mathsf {V}}_2\) will accept the proof with probability \(1-{\mathsf {negl}(n)}\), since otherwise we could easily construct a successful distinguisher against \(\mathsf {Sim}\) as follows. The distinguisher \(\mathcal {D}\) on input \((\alpha ,\beta ,\gamma )\) and auxiliary input \(\mathsf {aux}'\) simply runs \(\bar{\mathsf {V}}_2\) on \((\alpha ,\gamma )\) and random coins \(\mathsf {aux}'\) and outputs  . Further, even if \(x \not \in \mathcal {L}\), \(\bar{\mathsf {V}}_2\) must still accept with all but negligible probability, since otherwise the combination of \(\mathsf {P}^*\) and \(\bar{\mathsf {V}}\) could be used to decide \(\mathcal {L}\), implying that \(\mathcal {L}\in \mathsf {BPP}\).
. Further, even if \(x \not \in \mathcal {L}\), \(\bar{\mathsf {V}}_2\) must still accept with all but negligible probability, since otherwise the combination of \(\mathsf {P}^*\) and \(\bar{\mathsf {V}}\) could be used to decide \(\mathcal {L}\), implying that \(\mathcal {L}\in \mathsf {BPP}\).
Therefore, \(\mathsf {P}^*\) succeeds in convincing \(\bar{\mathsf {V}}\) of false statements with all but negligible probability. Since this contradicts the premise that \(\bar{\mu } \le {\mathsf {negl}(n)}\), \(\mathsf {Sim}\) cannot exist and therefore \(\varPi \) is not zero-knowledge. \(\square \)
4 Extending the Lower Bound to \(\epsilon \)-Zero Knowledge
In [14] Bitansky et al. introduced a weaker notion of zero-knowledge they called \(\epsilon \)-zero-knowledge. In this weaker notion, the outputs of the simulator may be distinguishable with non-negligible probability, but the distinguishing advantage is upper bounded by any inverse monomial in the length of the statement. In this section we prove that our lower bound extends to this weaker notion of zero-knowledge. This is particularly interesting because Bitansky et al. [14] are able to construct a 4-round \(\epsilon \)-zero-knowledge proof protocol from keyless multi-collision-resistant hash functions (MCRH). This provides evidence that our technique is unlikely to be extend to the case of 4-round proofs, since that would rule out MCRHs.
We start by defining \(\epsilon \)-zero-knowledge. The definition is almost identical to regular zero-knowledge, except that the advantage of the distinguisher is not bounded by a negligible function.
Definition 8
(Non-uniform \(\epsilon \)-Zero-Knowledge with Auxiliary Input). Let \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) be a 2-Party protocol. \(\mathchoice{\left\langle \mathsf {P},\mathsf {V}\right\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }{\langle \mathsf {P},\mathsf {V}\rangle }\) is said to be non-uniformly \(\epsilon \)-zero-knowledge with auxiliary input, if for all (possibly malicious) \(\mathsf {PPT}\) algorithms \(\mathsf {V}^*\) there exists a \(\mathsf {PPT}\) simulator \(\mathsf {Sim}\), such that for all \(\mathsf {PPT}\) distinguishers \(\mathcal {D}\) and all auxiliary inputs \(\mathsf {aux}\) and \(\mathsf {aux}'\), it holds that for all statements x with \(\left|x \right|=\lambda \) and every noticeable function \(\epsilon (\lambda ) = \lambda ^{-\mathcal {O}{(1)}}\)

Next, we state our generalized lemma about 3-round \(\epsilon \)-zero-knowledge proofs. This lemma is a straightforward adaption of Lemma 5 to the \(\epsilon \)-zero-knowledge case.
Lemma 10
Let \(\varPi \) be a 3-round interactive proof system for a language \(\mathcal {L}\not \in \mathsf {BPP}\). Let \(\bar{\varPi }\) be the transformed 2-round argument system described in Fig. 1 with soundness error \(\bar{\mu }\). If \(\bar{\mu } \le {\mathsf {negl}(n)}\) then \(\varPi \) is not non-uniformly \(\epsilon \)-zero-knowledge with auxiliary input.
From combining Lemmas 4 and 10 a statement equivalent to Theorem 2 for \(\epsilon \)-zero-knowledge follows as a simple corollary.
4.1 Proof of Lemma 10
Just like the lemma itself, the proof is a straightforward adaption of the proof for Lemma 5. We only need to make sure that the weaker requirement on the simulator does not cause the success probability of the cheating prover to deteriorate too much.
Consider the following malicious verifier \(\mathsf {V}^* = (\mathsf {V}^*_1,\mathsf {V}^*_2)\). The first stage \(\mathsf {V}^*_1\) on input the statement x, the prover’s first message \(\alpha \) and auxiliary input \(\mathsf {aux}\) simply interprets the auxiliary input as a circuit, evaluates it on \(x,\alpha \), and outputs the result  . The second stage \(\mathsf {V}^*_2\) on input the statement x, the prover’s messages \(\alpha ,\gamma \) and auxiliary input \(\mathsf {aux}\) recomputes
. The second stage \(\mathsf {V}^*_2\) on input the statement x, the prover’s messages \(\alpha ,\gamma \) and auxiliary input \(\mathsf {aux}\) recomputes  and then simply outputs \(\alpha ,\beta ,\gamma \).
and then simply outputs \(\alpha ,\beta ,\gamma \).
Now, assume towards contradiction, that \(\varPi \) is \(\epsilon \)-zero-knowledge, i.e., in particular for \(\mathsf {V}^*\) as described above there exists a \(\mathsf {PPT}\) simulator \(\mathsf {Sim}\) such that for all \(\mathsf {PPT}\) distinguishers \(\mathcal {D}\), all auxiliary inputs \(\mathsf {aux}\) and \(\mathsf {aux}'\), all statements x and all noticeable function \(\epsilon (\lambda ) = \lambda ^{-\mathcal {O}{(1)}}\) it holds that

We will use said simulator to construct a malicious prover \(\mathsf {P}^*\) against \(\bar{\varPi }\) as follows: On input x and the verifier’s message \(\mathbf {B}= \mathsf {iO}(\mathbf {C}_{\mathsf {V}_1}[k])\), \(\mathsf {P}^*\) invokes the simulator \(\mathsf {Sim}\) on \(1/\epsilon (\lambda )\), x and auxiliary input \(\mathbf {B}\). The simulator will produce a transcript \(\alpha ,\beta ,\gamma \) that \(\mathsf {P}^*\) also outputs.
If \(x \in \mathcal {L}\), then the zero-knowledge property guarantees that \(\bar{\mathsf {V}}_2\) will accept the proof with probability greater than \(1-\left|x \right|^{-c}\) for any constant \(c\in \mathbb {N}\), since otherwise we could easily construct a successful distinguisher against \(\mathsf {Sim}\) as follows. The distinguisher \(\mathcal {D}\) on input \((\alpha ,\beta ,\gamma )\) and auxiliary input \(\mathsf {aux}'\) simply runs \(\bar{\mathsf {V}}_2\) on \((\alpha ,\gamma )\) and random coins \(\mathsf {aux}'\) and outputs  . This distinguisher would therefore be able to distinguish between a real transcript and a simulated transcript with probability greater than \(\left|x \right|^{-c}\) for some constant \(c\in \mathbb {N}\), thus clearly clearly contradicting the fact that \(\mathsf {Sim}\) is a valid simulator. Further, even if \(x \not \in \mathcal {L}\), \(\bar{\mathsf {V}}_2\) must still accept with probability at least \(1-\left|x \right|^{-c}-{\mathsf {negl}(n)}\), since otherwise the combination of \(\mathsf {P}^*\) and \(\bar{\mathsf {V}}\) could be used to decide \(\mathcal {L}\), implying that \(\mathcal {L}\in \mathsf {BPP}\).
. This distinguisher would therefore be able to distinguish between a real transcript and a simulated transcript with probability greater than \(\left|x \right|^{-c}\) for some constant \(c\in \mathbb {N}\), thus clearly clearly contradicting the fact that \(\mathsf {Sim}\) is a valid simulator. Further, even if \(x \not \in \mathcal {L}\), \(\bar{\mathsf {V}}_2\) must still accept with probability at least \(1-\left|x \right|^{-c}-{\mathsf {negl}(n)}\), since otherwise the combination of \(\mathsf {P}^*\) and \(\bar{\mathsf {V}}\) could be used to decide \(\mathcal {L}\), implying that \(\mathcal {L}\in \mathsf {BPP}\).
Therefore, \(\mathsf {P}^*\) succeeds in convincing \(\bar{\mathsf {V}}\) of false statements with probability greater than \(1-\left|x \right|^{-c}-{\mathsf {negl}(n)}\) for any constant \(c\in \mathbb {N}\), which is clearly non-negligible. Since this contradicts the premise that \(\bar{\mu } \le {\mathsf {negl}(n)}\), \(\mathsf {Sim}\) cannot exist and therefore \(\varPi \) is not zero-knowledge. \(\square \)
Notes
- 1.
- 2.
In particular, in the public-coin case, the obfuscated program can be interpreted as an instantiation of the random oracle in the Fiat-Shamir heuristic.
- 3.
This assumes without loss of generality that \(\left|\gamma \right|=\left|s \right|=n\).
References
Ananth, P., Jain, A.: On secure two-party computation in three rounds. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 612–644. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_21
Ananth, P., Jain, A., Sahai, A.: Indistinguishability obfuscation from functional encryption for simple functions. Cryptology ePrint Archive, Report 2015/730 (2015). http://eprint.iacr.org/2015/730
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_6
Applebaum, B., Brakerski, Z.: Obfuscating circuits via composite-order graded encoding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 528–556. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_21
Barak, B., Bitansky, N., Canetti, R., Kalai, Y.T., Paneth, O., Sahai, A.: Obfuscation for evasive functions. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 26–51. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_2
Barak, B., Goldreich, O., Goldwasser, S., Lindell, Y.: Resettably-sound zero-knowledge and its applications. In: 42nd Annual Symposium on Foundations of Computer Science, pp. 116–125. IEEE Computer Society Press, Las Vegas, 14–17 October 2001
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_1
Bellare, M., Jakobsson, M., Yung, M.: Round-optimal zero-knowledge arguments based on any one-way function. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 280–305. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_20
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N.: Multi collision resistant hash functions and their applications. Cryptology ePrint Archive, Report 2017/489 (2017). http://eprint.iacr.org/2017/489
Bitansky, N., Brakerski, Z., Kalai, Y., Paneth, O., Vaikuntanathan, V.: 3-message zero knowledge against human ignorance. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 57–83. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_3
Bitansky, N., Canetti, R.: On strong simulation and composable point obfuscation. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 520–537. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_28
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: Shmoys, D.B. (ed.) 46th Annual ACM Symposium on Theory of Computing, pp. 505–514. ACM Press, New York, 31 May–3 June 2014
Bitansky, N., Goldwasser, S., Jain, A., Paneth, O., Vaikuntanathan, V., Waters, B.: Time-lock puzzles from randomized encodings. In: Sudan, M. (ed.) ITCS 2016: 7th Innovations in Theoretical Computer Science, pp. 345–356. Association for Computing Machinery, Cambridge, 14–16 January 2016
Bitansky, N., Kalai, Y.T., Paneth, O.: Multi-collision resistance: a paradigm for keyless hash functions. Cryptology ePrint Archive, Report 2017/488 (2017). http://eprint.iacr.org/2017/488
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: Guruswami, V. (ed.) 56th Annual Symposium on Foundations of Computer Science, pp. 171–190. IEEE Computer Society Press, Berkeley, 17–20 October 2015
Blum, M.: How to prove a theorem so no one else can claim it. In: Proceedings of the International Congress of Mathematicians, vol. 1, p. 2 (1986)
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_15
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
Canetti, R., Dakdouk, R.R.: Obfuscating point functions with multibit output. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 489–508. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_28
Canetti, R., Goldreich, O., Goldwasser, S., Micali, S.: Resettable zero-knowledge (extended abstract). In: 32nd Annual ACM Symposium on Theory of Computing, pp. 235–244. ACM Press, Portland, 21–23 May 2000
Cohen, A., Holmgren, J., Nishimaki, R., Vaikuntanathan, V., Wichs, D.: Watermarking cryptographic capabilities. In: Wichs, D., Mansour, Y. (eds.) 48th Annual ACM Symposium on Theory of Computing, pp. 1115–1127. ACM Press, Cambridge, 18–21 June 2016
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. In: 40th Annual Symposium on Foundations of Computer Science, pp. 523–534. IEEE Computer Society Press, New York, 17–19 October 1999
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: 22nd Annual ACM Symposium on Theory of Computing, pp. 416–426. ACM Press, Baltimore, 14–16 May 1990
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual Symposium on Foundations of Computer Science, pp. 40–49. IEEE Computer Society Press, Berkeley, 26–29 October 2013
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_10
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: Guruswami, V. (ed.) 56th Annual Symposium on Foundations of Computer Science, pp. 151–170. IEEE Computer Society Press, Berkeley, 17–20 October 2015
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986)
Goldreich, O., Kahan, A.: How to construct constant-round zero-knowledge proof systems for NP. J. Cryptol. 9(3), 167–190 (1996)
Goldreich, O., Krawczyk, H.: On the composition of zero-knowledge proof systems. SIAM J. Comput. 25(1), 169–192 (1996)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems (extended abstract). In: 17th Annual ACM Symposium on Theory of Computing, pp. 291–304. ACM Press, Providence, 6–8 May 1985
Hada, S., Tanaka, T.: On the existence of 3-round zero-knowledge protocols. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 408–423. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055744
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Kalai, Y.T., Rothblum, G.N., Rothblum, R.D.: From obfuscation to the security of Fiat-Shamir for proofs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 224–251. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_8
Katz, J.: Which languages have 4-round zero-knowledge proofs? In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 73–88. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_5
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013: 20th Conference on Computer and Communications Security, pp. 669–684. ACM Press, Berlin, 4–8 November 2013
Komargodski, I., Naor, M., Yogev, E.: Collision resistant hashing for paranoids: dealing with multiple collisions. Cryptology ePrint Archive, Report 2017/486 (2017). http://eprint.iacr.org/2017/486
Lepinski, M.: On the existence of 3-round zero-knowledge proofs. Ph.D. thesis, Massachusetts Institute of Technology (2002)
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_2
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 599–629. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_20
Lin, H., Tessaro, S.: Indistinguishability obfuscation from trilinear maps and block-wise local PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 630–660. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_21
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: Dinur, I. (ed.) 57th Annual Symposium on Foundations of Computer Science, pp. 11–20. IEEE Computer Society Press, New Brunswick, 9–11 October 2016
Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation from semantically-secure multilinear encodings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 500–517. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_28
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) 46th Annual ACM Symposium on Theory of Computing, pp. 475–484. ACM Press, New York, 31 May–3 June 2014
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_15
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Fleischhacker, N., Goyal, V., Jain, A. (2018). On the Existence of Three Round Zero-Knowledge Proofs. In: Nielsen, J., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2018 . EUROCRYPT 2018. Lecture Notes in Computer Science(), vol 10822. Springer, Cham. https://doi.org/10.1007/978-3-319-78372-7_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-78372-7_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78371-0
Online ISBN: 978-3-319-78372-7
eBook Packages: Computer ScienceComputer Science (R0)





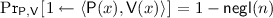 .
. .
. .
. .
.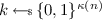 , every input
, every input 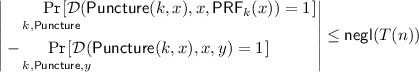
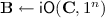 and every
and every 
 and every
and every 
 describe point functions with
describe point functions with  .
.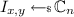 .
.



