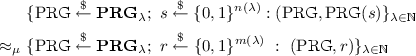Abstract
We consider the question of finding the lowest degree L for which L-linear maps suffice to obtain IO. The current state of the art (Lin, EUROCRYPT’16, CRYPTO ’17; Lin and Vaikunthanathan, FOCS’16; Ananth and Sahai, EUROCRYPT ’17) is that L-linear maps (under suitable security assumptions) suffice for IO, assuming the existence of pseudo-random generators (PRGs) with output locality L. However, these works cannot answer the question of whether \(L < 5\) suffices, as no polynomial-stretch PRG with locality lower than 5 exists.
In this work, we present a new approach that relies on the existence of PRGs with block-wise locality L, i.e., every output bit depends on at most L (disjoint) input blocks, each consisting of up to \(\log \lambda \) input bits. We show that the existence of PRGs with block-wise locality is plausible for any \(L \ge 3\), and also provide:
-
A construction of a general-purpose indistinguishability obfuscator from L-linear maps and a subexponentially-secure PRG with block-wise locality L and polynomial stretch.
-
A construction of general-purpose functional encryption from L-linear maps and any slightly super-polynomially secure PRG with block-wise locality L and polynomial stretch.
All our constructions are based on the SXDH assumption on L-linear maps and subexponential Learning With Errors (LWE) assumption, and follow by instantiating our new generic bootstrapping theorems with Lin’s recently proposed FE scheme (CRYPTO ’17). Inherited from Lin’s work, our security proof requires algebraic multilinear maps (Boneh and Silverberg, Contemporary Mathematics), whereas security when using noisy multilinear maps is based on a family of more complex assumptions that hold in the generic model.
Our candidate PRGs with block-wise locality are based on Goldreich’s local functions, and we show that the security of instantiations with block-wise locality \(L \ge 3\) is backed by similar validation as constructions with (conventional) locality 5. We further complement this with hardness amplification techniques that further weaken the pseudorandomness requirements.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Indistinguishability obfuscation (IO), first defined in the seminal work of Barak et al. [16], aims to obfuscate functionally equivalent programs into indistinguishable ones while preserving functionality. IO is an extraordinarily powerful object that has been shown to enable a large set of new cryptographic applications. All existing IO constructions [4, 5, 10, 15, 24, 36, 39, 41, 45, 52, 53, 56, 63, 65] rely on multilinear maps or graded encodings. In particular, the power of an L-linear map – first made explicit by Boneh and Silverberg [23] – stems from the fact that it essentially allows to evaluate degree-L polynomials on secret encoded values, and to test whether the output of such polynomials is zero or not.
The case \(L = 2\) corresponds to bilinear maps, which can be efficiently instantiated from elliptic curves. In contrast, the instantiation of L-linear maps with \(L \ge 3\) has turned to be a far more challenging problem. Garg et al. [38] proposed in particular noisy (i.e., approximate) versions of L-linear maps for \(L \ge 3\), and gave the first candidate construction. Unfortunately, vulnerabilities [6, 27, 28, 31, 59] were later demonstrated against this and subsequent candidates [32, 33, 44, 51]. Of course, this does not mean that the resulting constructions are insecure. In fact, this has motivated the search for IO constructions which withstand all existing attacks [41].
IO from Low-Degree Multilinear Maps. This paper addresses the problem of finding the smallest L such that degree-L mutlilinear maps are sufficient for constructing IO. This fits within the more general goal of ultimately assessing whether bilinear maps are sufficient. While first-generation IO constructions all required polynomial-degree multilinear maps, a series of recent works [4, 52, 53, 56] reduced the required degree to \(L = 5\), assuming the existence of PRGs with output locality 5 and subexponential LWE, and under suitable assumption on the 5-linear maps. However, these works left open the question of whether multilinear maps with degree \(L < 5\) are sufficient.
Further reducing the degree is important. On the one hand, if IO can be achieved from bilinear maps, this is going to take us one step closer. On the other hand, even if bilinear maps would not suffice, it is potentially easier to find secure algebraic instantiations for low degree multilinear maps. Moreover, we want to understand the precise power these maps would enable.
Our Contributions, in a Nutshell. This paper presents a new paradigm for IO constructions which admits instantiations with L-linear maps for \(L \ge 3\), provided the SXDH assumption holds for the L-linear map. While this falls short of achieving IO from bilinear maps, our result shifts the focus on the fact that the gap between two- and three-linear maps is a seemingly fundamental barrier to be overcome. In particular, under the assumptions needed for our construction be secure, this shows that building three-linear maps is as difficult as getting full-blown IO.
We fundamentally rely on the recent line of works on building IO from constant-degree multilinear maps [4, 52, 53, 56], which all rely on so-called local pseudo-random generators (PRGs) – a PRG with locality L has every output bit depend on L input bits. It is known that if PRGs with locality L and polynomial stretch exist, then IO can be constructed from L-linear maps [4, 53]. Unfortunately, we do not even have locality-4 (polynomial stretch) PRGs [34, 60], and candidate PRGs only exist starting from locality 5 [47, 60, 61]. To circumvent the lower bound on PRG locality, we propose a new, relaxed, notion of locality, called block-wise locality. We build upon Lin’s [53] recent IO construction, but show that in order to obtain IO from L-linear maps, it suffices to use PRGs with block-wise locality L. As we will discuss below, such PRGs can exist for L as low as three.
Block-Wise Locality and IO. We say that a PRG mapping \(n\times \ell \) input bits to m output bits has block-wise locality L and block-size \(\ell \), if when viewing its input (i.e., the seed) as a matrix of \(n\times \ell \) bits, every output bit depends on at most L columns in the matrix (as opposed to L input bits), as depicted in Fig. 1. Observe that that the actual locality of such PRGs can go up to \(L\times \ell \), yet, it has the special structure that all these input bits come from merely L input columns. This special structure is the key feature that allows for replacing local PRGs with block-wise-local PRGs, in the following applications.
-
Application I: If there exists a subexponentially-secure PRG with block-wise-locality L, and any block-size
 , then we can construct general-purpose IO from L-linear maps.
, then we can construct general-purpose IO from L-linear maps. -
Application II: If the block-wise local PRG is only slightly superpolynomially secure, we can still build special-purpose IO for circuits with super-logarithmic length inputs, which implies full-fledged Functional Encryption (FE), from L-linear maps.
All our constructions come with security reductions to (1) the security of block-wise-local PRGs, (2) the SXDH assumption on L-linear maps, and (3) the subexponential Learning With Errors (LWE), where (2) and (3) have the same level of hardness as that of the PRG.
Concurrently, we investigate the existence of block-wise local PRGs. In particular, we propose candidates following the common paradigm for candidate local PRGs [7, 12, 34, 60, 61], which are variants of Goldreich’s functions [46]. We simply replace every PRG input bit with a column of \(\ell \) input bits. Such a block-wise local PRG is parameterized by a bipartite expander graph and a predicate (or potentially a set of predicates) over \(L \times \ell \) input bits. We discuss the security of these candidates, against known attacks, in relation to the choice of graph and predicate. Furthermore, aiming at weakening the assumption on our candidates, we present two hardness amplification techniques that amplify respectively the weaker next-bit-unpredictability property and pseudo-min-entropy generation property to different levels of pseudorandomness guarantees.
Instantiating the Underlying Multilinear Maps. We note that the results of this paper, per se, are merely new bootstrapping theorems, which do not rely, by themselves, on multilinear maps. More specifically, we show how to boostrap a FE scheme for computing degree-L polynomials to an IO scheme, using a PRG with block-wise-locality L, and then rely on Lin’s [53] FE construction. Some remarks on instantiations of the underlying multilinear maps are in order.
Concretely, the FE scheme from [53] relies on algebraic L-linear maps, for which to date no candidate for \(L \ge 3\) is known to exist. The alternative approach would be to instantiate them with existing noisy multilinear-map candidates. As discussed in [53, Sect. 2.6], the existing proof would however fail in this case, in addition to the SXDH assumption itself being false on exiting noisy multilinear-map candidates. Still, a proof for ideal multilinear maps would be valid, but it is not known whether (1) existing cryptanalytic attacks can be adapted to break a construction, or (2) whether a proof in a weak ideal model as in [41] is possible.
Background on Previous Versions of This Work. In a previous version of this paper, we incorrectly claimed that our approach can be extended to bilinear maps. Two subsequent works, one by Barak et al. [14], the other by Lombardi and Vaikuntanathan [57], have presented attacks against PRGs with block-wise locality two. Strictly speaking, these results leave a narrow window of expansion factors open where block-wise PRGs could exist, but we are not aware whether our approach could be modified to use such low-stretch PRGs, or whether the attacks can be extended. We discuss these results more in detail further below in Sect. 1.3.
In contrast, attacks for \(L \ge 3\) appear out of reach, as our assumption is implied by that made by recent works in the area of local PRGs and PRFs, c.f. e.g. the pseudorandomness assumptions from the recent work by Applebaum and Raykov [13]—and in fact, our amplification results show that even less needs to be achieved by the local function.
1.1 Block-Wise Locality
A \((n\times \ell , m)\)-PRG maps \(n\times \ell \) input bits to m output bits. As introduced above, a PRG has block-wise locality L and block-size \(\ell \), if when viewing the input as a \(n\times \ell \) matrix, every output bits depend on input bits in at most L columns. Such a function is fully specified by the input-output dependency graph G describing which input columns each output bit depends on, and the set of predicates \(\{P_j\}_{j \in [m]}\) that each output bit is evaluated through.
In all our applications, we consider block-wise local PRGs with sufficiently large polynomial input- and output-lengths, n and m (in the security parameter \(\lambda \)) and logarithmic block-size \(\ell = O(\log (\lambda ))\). In this setting, a PRG has polynomial-stretch if \(m = n^{1+\alpha }\) for some positive constant \(\alpha > 0\). For convenience, below we assume such parameters are fixed in our discussion.
When compared with traditional local PRGs (which can be thought as the special case with block size \(\ell = 1\)), the advantage of block-wise local PRGs is that while they will still permit instantiations with L-linear maps in our applications, their output bits depend on \(L \times \ell \) input bits, and hence we can use more complex, say logarithmic-degree, predicates. For this reason, known lower bounds on the locality of PRGs do not apply to block-wise locality, even when \(L < 5\), when the block size satisfies \(\ell = \varOmega (\log (\lambda ))\). Effectively, such PRGs can be seen as operating on input symbols with polynomial alphabet size. Moreover, the lower bounds in [34, 60] show that for conventional locality, PRGs with polynomial stretch require \(L \ge 5\), but they crucially rely on the fact that any locality-4 predicate is correlated with two of its input bits to rule out the existence of locality-4 PRGs. In contrast, a PRG with block-wise locality L can use predicates that depend on \(L\log \lambda \) input bits; setting the predicate to be uncorrelated with any subset of \(\log \lambda \) input bits circumvents the lower bound argument in [34, 60].
Block-Wise Local PRGs via Local PRGs. Every function with block-wise locality L and block size \(\ell \) is a function with locality \(L\ell \). Therefore, the rich literature on the security of Goldreich’s local functions (see Applebaum’s survey [8]) provides guidelines on how to choose candidate block-wise local PRGs, more specifically, the dependency graph G and predicates \(\{P_j\}\). In particular, the graph G should be (k, c)-expanding, i.e., every subset of \(k' \le k\) output bits depends on at least \(c\times k'\) input columns, for appropriately large k and c. We show that for \(L \ge 3\), a large \(1-o(1)\) fraction of graphs G is \((n^{1-\eta }, (1-\eta )L)\)-expanding. This in turn means that we can think of this as an instance of Goldreich’s function with locality \(L\ell \) built from a graph which is \((n^{1-\eta }, (1-\eta )L\ell )\)-expanding, thus taking us back to the classical setting studied in the literature.
Using this analogy, we can show for example that for block-wise locality 3 and block size 2, for most graphs G, the resulting function withstands all linear attacks with sub-exponential bias \(\epsilon \) when using the predicate outputting \(x_1^0 \oplus x_2^0 \oplus x_3^0 \oplus (x_1^1 \wedge x_2^1)\) on input three columns \((x_1^0, x_1^1), (x_2^0, x_2^1), (x_3^0, x_3^1)\). This is a criterion that has been adopted so far to validate PRG security of local functions.
Moving even one step further, Applebaum and Raykov [13] recently postulated the following (even stronger) pseudorandomness assumption on functions with logarithmic locality:
Assumption 1
(Informal). For locality \(D = O(\log \lambda )\), and arbitrarily polynomial output length \(m = n^{1 + \alpha }\), there exist a suitable predicate, \(P'\), such that, for any dependency graph \(G'\) that is \((n^{1-\eta }, (1-\eta )D)\)-expanding for some \(0< \eta < 1/2\), the locality-D function specified by \(P'\) and \(G'\) is \(2^{-n^{1-\eta }}\)-pseudorandom again \(2^{n^{1-\eta }}\)-time distinguishers.
In our setting, for block-wise locality \(L \ge 3\) and block-size \(\log \lambda \), we show that when choosing the dependency graph G at random, the obtained block-wise local function can be thought as a function with locality \(D = L\log \lambda \) satisfying the properties specified by the Applebaum-Raykov assumption, with \(1-o(1)\) probability. In particular, such functions withstand myopic inversion attacks (cf. e.g. [30]). In fact, our applications only need pseudorandomness to hold for output length \(m = n^{1+\alpha }\) for some arbitrarily small constant \(\alpha > 0\), and against polynomial time attackers, thus a much weaker requirement than what is guaranteed by the Applebaum-Raykov assumption.
For the case \(L = 2\), the assumption that a block-wise local PRG exists is not backed by any of the past results, and indeed, recent works (following up on an earlier version of this paper) show that blockwise-local PRGs with sufficient stretch do not exist. We discuss this further below in Sect. 1.3.
Amplification. In order to validate our assumptions even further, we present two transformations meant to enhance security of functions with block-wise locality. We consider two different techniques:
-
Amplification Technique I: produces a PRG construction with quasi-polynomial indistinguishability-gap (to polynomial-time distinguishers), from any unpredictable generator satisfying just polynomial next-bit unpredictability (i.e., the probability of predicting any output bit given previous output bits is at most
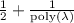 , albeit for predictors in quasi-polynomial time). Though such PRGs are not strong enough for constructing IO, it suffices for constructing FE from L-linear maps; see the next section.
, albeit for predictors in quasi-polynomial time). Though such PRGs are not strong enough for constructing IO, it suffices for constructing FE from L-linear maps; see the next section. -
Amplification Technique II: produces a PRG construction with sub-exponential indistinguishability-gap, from certain special pseudo-min-entropy-generator whose output has sufficiently-high pseudo-min-entropy.
1.2 From Block-Wise Locality to IO and FE
We now move to an overview of our constructions from block-wise local PRGs.
IO from Subexponentially Secure Block-Wise-Local PRGs. Recent IO constructions from low-degree multilinear maps [4, 53, 56] follow a common two-step approach: They first implement appropriate FE schemes, and then transform them into an IO scheme; we refer to the second step as the (FE-to-IO) bootstrapping step. In more detail, they use locality-L PRGs in the bootstrapping step in order to start with FE schemes that support only computation of degree-L polynomials; they then show that such FE schemes can be constructed from L-linear maps. In this work, following the blueprint and technique in [53], we show how to replace the use of local PRGs with block-wise local PRGs within the bootstrapping step.
Theorem 1
(Bootstrapping using block-wise local PRGs). Let L be any positive integer. There is a construction of IO for \({\mathsf {P/poly}}\) from the following primitives:
-
Public-key fully-selectively-secure (collusion-resistant) FE for degree-L polynomials whose encryption time is linear in the input length (i.e., \({\mathrm {poly}}(\lambda )N\)); or with a secret-key FE scheme with the same properties, assuming additionally the subexponential hardness of LWE with subexponential modulus-to-noise ratio.
-
a PRG with block-wise locality L, block-size \(\log \lambda \), and \(n^{1+\alpha }\)-stretch for some positive constant \(\alpha \).
where both FE and PRG need to have subexponential security.
The type of secret-key FE schemes for degree-L polynomials needed above was constructed by Lin [53] assuming the SXDH assumption on L-linear maps.
Theorem 2
[53]. Let L be any positive integer. Assuming the SXDH assumption on asymmetric L-linear maps, there is a construction of secret-key fully-selectively-secure (collusion-resistant) FE schemes for degree-L polynomials whose encryption time is linear in the input length (i.e., \({\mathrm {poly}}(\lambda )N\)). Moreover, the security reduction has a polynomial security loss.
Therefore, combining our new bootstrapping theorem with Lin’s FE construction, we obtain IO from the subexponential SXDH assumption on L-linear maps, subexponentially-secure PRG with block-wise locality L, and subexponential LWE.
The Power of Super-Polynomially Secure Block-Wise Local PRGs. While constructing full-fledged IO for all polynomial-sized programs requires block-wise local PRGs with subexponentially-security, we ask what can be built from PRGs with weaker (slightly) superpolynomial-security. In particular, such PRGs can be obtained using the aforementioned amplification technique I, from unpredictable generator satisfying just polynomial next-bit unpredictability. To this end, we first give a parameterized version of Theorem 1 showing that if the PRG and L-linear maps are \((2^{-{\mathrm {i}\ell }}\mathrm {negl})\)-secure, then we can build IO schemes for circuits with \({\mathrm {i}\ell }\)-bit inputs.
Theorem 3
(Parameterized version of Theorem 1 ). Let L be any positive integer. Then, there is a construction of IO for the class of polynomial-sized circuits with \({\mathrm {i}\ell }\)-bit inputs from the same primitives as in Theorem 1, and if FE and PRG are \((2^{-({\mathrm {i}\ell }+{\kappa })}\mathrm {negl})\)-secure, the resulting IO scheme is \((2^{-{\kappa }}\mathrm {negl})\)-secure.
Therefore, as discussed above, from slightly superpolynomially secure L-linear maps, a PRG with block-wise locality L, and subexponential LWE, we obtain IO for circuits with super-logarithmic, \(\omega (\log \lambda )\), length inputs, and if the primitives are quasi-polynomially secure, we obtain IO for circuits with poly-logarithmic \(\log ^{1+\varepsilon }(\lambda )\) length inputs. Such IO schemes are already sufficient for two types of natural applications of IO:
-
Type 1: Applications where IO is used to obfuscate a circuit with short inputs. For instance, for building FHE without relying on circular security [25], and constructing succinct randomized encoding for bounded space Turning machines [17]. In these applications, IO is used to obfuscate a circuit that receive as input an index from an arbitrary polynomial range.
-
Type 2: Applications where the input length of the obfuscated circuit is determined by the security parameter of some other primitive. Then, by assuming exponential security of the other primitive, the input length can be made poly-logarithmic. For instance, as observed in [18, 50], in the construction of public key encryption from one-way functions via IO, if assuming exponentially secure one-way functions, then IO for circuits with \(\omega (\log \lambda )\) bit inputs suffices for the application.
We further show that IO for circuits with super-logarithmic length inputs implies full-fledged functional encryption.
Theorem 4
(Functional Encryption from \(\omega (\log \lambda )\) -Input IO). Let \({\mathrm {i}\ell }\) be any super-logarithmic polynomial, that is, \({\mathrm {i}\ell }= \omega (\log \lambda )\). Assume IO for the class of polynomial-sized circuits with \({\mathrm {i}\ell }\)-bit inputs and public key encryption, both with \((2^{-{\mathrm {i}\ell }}\mathrm {negl})\)-security. Then, there exist collusion resistant (compact) public-key functional encryption for \({\mathsf {P/poly}}\), satisfying adaptive-security.
Combining the above two theorems, we immediately have that the existence of a PRG with block-wise locality L and L-linear maps, both with slighly super-polynomial security (and assuming subexponential LWE), implies the existence of full-fledged functional encryption, and all its applications, including, for instance, non-interactive key exchange (NIKE) for unbounded users [43], trapdoor permutations [43], PPAD hardness [19, 42], publicly-verifiable delegation schemes in the CRS model [62], and secure traitor tracing scheme [22, 29, 39], which further implies hardness results in differential privacy [37, 64].
1.3 Subsequent Works
Two recent works by Lombardi and Vaikuntanathan (LV) [57], and Barak, Brakerski, Komargodski, and Kothari (BBKK) [14] essentially rule out the existence of PRGs with block-wise locality \(L = 2\), except for a very narrow window of expansion, as we explain next.
The LV Attack. The LV attack considers generators whose output bits are evaluated using the same predidate P, and whose dependency graph G is chosen at random. LV show that for any predicate P and a \(1-o(1)\) fraction of the graphs, the output can be efficiently distinguished from random, if its length reaches  , where recall that
, where recall that  is the block size. Their attack relies on two important ingredient. The first ingredient consists of techniques for refuting random L-CSPs over large q-ary alphabets, which corresponds to PRGs with block-wise locality-L and block-size \(\ell = \log q\). Allen, O’Donnell, and Witmer [1] presented an efficient algorithm for this, which succeeds when the number of constraints is roughly
is the block size. Their attack relies on two important ingredient. The first ingredient consists of techniques for refuting random L-CSPs over large q-ary alphabets, which corresponds to PRGs with block-wise locality-L and block-size \(\ell = \log q\). Allen, O’Donnell, and Witmer [1] presented an efficient algorithm for this, which succeeds when the number of constraints is roughly  , where \(\varepsilon \) controls the “quality” of refutation. The second ingredient is a novel structural lemma showing that any locality-2 balanced predicate P over alphabet \(\mathbb {Z}_q\) must be \((1/2 + O(1)/\sqrt{q})\)-correlated with a locality-2 predicate Q over the constant-sized alphabet \(\mathbb {Z}_{16}\). Roughly speaking, to distinguish the output of a PRG with predicate P, they apply the refutation technique on CSPs w.r.t. the predicate Q correlated with P. This allows them to rule out PRGs with output length as short as
, where \(\varepsilon \) controls the “quality” of refutation. The second ingredient is a novel structural lemma showing that any locality-2 balanced predicate P over alphabet \(\mathbb {Z}_q\) must be \((1/2 + O(1)/\sqrt{q})\)-correlated with a locality-2 predicate Q over the constant-sized alphabet \(\mathbb {Z}_{16}\). Roughly speaking, to distinguish the output of a PRG with predicate P, they apply the refutation technique on CSPs w.r.t. the predicate Q correlated with P. This allows them to rule out PRGs with output length as short as  .
.
The BBKK Attack. BBKK considered the more general case where the generators use an arbitrary set of predicates \(\{P_j\}\) and arbitrary dependency graph G. They show that PRGs with block-wise locality 2 and output length  do not exist. The bound on the output length can be improved to
do not exist. The bound on the output length can be improved to  for the case where G is randomly chosen, and so is the predicate (in particular, the predicate is the same for all output bits). In fact, they proved a more general lower bound: There is no PRG whose outputs are evaluated using polynomials of degree at most d involving at most s monomials, and of output length \(\tilde{O}(s n^{\lceil d/2\rceil })\). Note that every block-wise locality L PRG can be written as such a generator, with \(n 2^{\ell }\) input bits, and using polynomials of degree L and at most \(2^{L\ell }\) monomials. Their result is based on semidefinite programming and in particular the sum of squares (SOS) hierarchy.
for the case where G is randomly chosen, and so is the predicate (in particular, the predicate is the same for all output bits). In fact, they proved a more general lower bound: There is no PRG whose outputs are evaluated using polynomials of degree at most d involving at most s monomials, and of output length \(\tilde{O}(s n^{\lceil d/2\rceil })\). Note that every block-wise locality L PRG can be written as such a generator, with \(n 2^{\ell }\) input bits, and using polynomials of degree L and at most \(2^{L\ell }\) monomials. Their result is based on semidefinite programming and in particular the sum of squares (SOS) hierarchy.
BV and BBKK essentially rule out the existence of PRGs with block-wise locality 2, except for the corner case where the generator can use a set of different predicates \(\{P_j\}\), a specific or random graph, and the output length is \(\tilde{O}(n 2^{(1+\varepsilon )\ell })\), for some \(0< \varepsilon < 1\). However, it is unclear to us whether PRGs with such small expansion is sufficient for constructing IO, or whether the attacks can be extended to cover this case.
Outline of This Paper
Section 2 discusses candidate constructions of block-wise local PRGs. Section 3 discusses our bootstrapping method using block-wise local PRGs. Finally, in Sect. 4, we discuss constructions of functional-encryption schemes in Sect. 4.
Further, the paper employs standard notation and terminology on functional encryption and IO. We refer the reader to the full version for the complete formalism [55].
2 Block-Wise Local PRGs
In this section, we introduce the notion of a block-wise local PRG. We start with formal definitions, in Sect. 2.1, which we refer to throughout the rest of the paper. Then, the remaining sub-sections will discuss a graph-based framework for block-wise local functions, and discuss candidates.
2.1 Pseudorandom Generators, Locality, and Block-Wise Locality
We review the notion of a PRG family, and its locality.
Definition 1
(Family of Pseudo-Random Generators (PRGs)). Let n and m be polynomials. A family of \((n(\lambda ),m(\lambda ))\)-PRG is an ensemble of distributions \(\mathbf{PRG}= \{\mathbf{PRG}_\lambda \}\) satisfying the following properties:
- Syntax::
-
For every \(\lambda \in \mathbb {N} \), every \(\mathrm {PRG}\) in the support of \(\mathbf{PRG}_\lambda \) defines a function mapping \(n(\lambda )\) bits to \(m(\lambda )\) bits.
- Efficiency::
-
There is a uniform Turning machine M satisfying that for every \(\lambda \in \mathbb {N} \), every \(\mathrm {PRG}\) in the support of \(\mathbf{PRG}_\lambda \), and every \(x \in \{0,1\}^{n(\lambda )}\), \(M(\mathrm {PRG}, x) = \mathrm {PRG}(x)\).
- \(\mu \)-Indistinguishability::
-
The following ensembles are \(\mu \)-indistinguishable
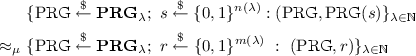
Definition 2
(Block-Wise Locality of PRGs). Let n, m, L, and \(\ell \) be polynomials. We say that a family of \((n(\lambda )\ell (\lambda ),m(\lambda ))\)-PRGs has block-wise locality-\((L(\lambda ),\ell (\lambda ))\) if for every \(\lambda \) and every \(\mathrm {PRG}\) in the support of \(\mathbf{PRG}_\lambda \), inputs of \(\mathrm {PRG}\) are viewed as \(n(\lambda )\times \ell (\lambda )\) matrices of bits, and every output bit of \(\mathrm {PRG}\) depends on input bits contained in at most \(L(\lambda )\) columns.
2.2 Graph-Based Block-Wise Local Functions
In this section, we discuss candidate PRGs with block-wise locality d, where d can be as small as two. Here, we start with the notational framework and then move on to discussing concrete assumptions on them in Sect. 2.3.
Goldreich’s Function. We will consider local functions based on Goldreich’s construction [46], which have been the subject for extensive study (cf. e.g. Applebaum’s survey [8]).
Recall first that an [n, m, d]-hypergraph is a collection \(G = (S_1, \ldots , S_m)\) where the hyerpedges \(S_i\) are elements of \([n]^d\), i.e., \(S_i = (i_1, \ldots , i_d)\), where \(i_j \in [n]\) (note that we allow for potential repetitions, merely for notational convenience). We use hypergraphs to build functions as follows.
Definition 3
(Goldreich’s function). Let \(\mathbf {G} = \{{\mathbf {G}}_{\lambda }\}_{\lambda \in \mathbb {N}}\) be an ensemble such that \(\mathbf {G}_{\lambda }\) is a distribution on \([n(\lambda ), m(\lambda ), d(\lambda )]\)-hypergraphs, for polynomial functions m, n, d. Also let \(P = \{{P}_{\lambda }\}_{\lambda \in \mathbb {N}}\)q be a family of predicates, where \(P_{\lambda }\) operates on \(d(\lambda )\)-bit strings. Then, define the function ensemble \(\mathbf {GF}^{\mathcal {G}, P} = \{\mathbf {GF}^{\mathcal {G}, P}_{\lambda }\}_{\lambda \in \mathbb {N}}\), where \(\mathbf {GF}^{\mathcal {G},P}_{\lambda }\) samples first a graph \(G = (S_1, \ldots , S_m) \mathop {\leftarrow }\limits ^{\$}\mathbf {G}_{\lambda }\), and then outputs the function \(\mathrm {GF}_{G, P}: \{0,1\}^n \rightarrow \{0,1\}^m\) such that for all n-bit x,
where x[S] denotes the d-bit sub-string obtained by concatenating the bits at positions indexed by S.Footnote 1
Functions with Block-Wise Locality. We want to extend the notation used above to consider the case where an edge of G does not solely give a pointer to individual bits to be injected in the computation, but rather, to “chunks” consisting of \(\ell \)-bit strings, and the predicate is applied to the concatenation of these bits. The resulting function clearly then satisfies block-wise locality d with block size \(\ell \).
Definition 4
(Block-wise local graph-based function). Let \(\mathbf {G} = \{{\mathbf {G}}_{\lambda }\}_{\lambda \in \mathbb {N}}\) be such that \(\mathbf {G}_{\lambda }\) is a distribution on \([n(\lambda ), m(\lambda ), d(\lambda )]\)-hypergraphs, for polynomial functions m, n, d. Also let \(\ell (\lambda )\) be a polynomial function, and \(P = \{{P}_{\lambda }\}_{\lambda \in \mathbb {N}}\) a family of predicates, where \(P_{\lambda }\) operates on \((d(\lambda ) \times \ell (\lambda ))\)-bit strings. Then, define the function ensamble \(\mathbf {GF}^{\mathcal {G}, P, \ell } = \{\mathbf {GF}^{\mathcal {G}, P, \ell }_{\lambda }\}_{\lambda \in \mathbb {N}}\), where \(\mathbf {GF}^{\mathcal {G},P, \ell }_{\lambda }\) samples first a graph \(G = (S_1, \ldots , S_m) \mathop {\leftarrow }\limits ^{\$}\mathbf {G}_{\lambda }\), and then outputs the function \(\mathrm {GF}_{G, P, \ell }: \{0,1\}^{n \cdot \ell } \rightarrow \{0,1\}^m\) such that for all \((n \times \ell )\)-bit inputs \(\mathbf {x}= (\mathbf {x}[1], \ldots , \mathbf {x}[n])\), where \(\mathbf {x}[1], \ldots , \mathbf {x}[n] \in \{0,1\}^{\ell }\),
where \(\mathbf {x}[S]\) denotes the \(d \cdot \ell \)-bit sub-string obtained by concatenating \(\ell \)-bit input chunks indexed by S.
We typically refer to the graph G describing \(\mathrm {GF}_{G, P, \ell }\) as the base graph. This is because \(\mathrm {GF}_{G, P, \ell }\) can be seen as a special case of Goldreich’s function defined above, for a suitable graph. Namely, the base graph G can be extended to an \([n \cdot \ell , m, d \ell ]\)-hypergraph \(\overline{G}\) naturally, where each edge \(S_i = (i_1, \ldots , i_d)\) from G is mapped into a new hyper-edge \(\overline{S}_i\) with \(d \cdot \ell \) elements such that
then clearly \(\mathrm {GF}_{G, P, \ell } = \mathrm {GF}_{\overline{G}, P, 1}= \mathrm {GF}_{\overline{G}, P}\). This view will be convenient to connect back to the body of work on studying the security of Goldreich’s function on suitable graphs, for which our block-wise local designs serve as a special case.
Expansion Properties. In general, we will want to instantiate our framework with functions where the base graph G is a good expander graph. Recall the following.
Definition 5
\(G = (S_1, \ldots , S_m)\) is a (k, c)-expander (or, equivalently, is (k, c)-expanding) if for all sets \(J\,\subseteq \,[m]\) with \(|J| \le k\), we have \(|{\bigcup _{j \in J} S_j}| \ge c\cdot |J|\).
Ideally, we will want in fact \(\overline{G}\) to be a good expander (in order to resort to large body of analyses for such functions). This will follow by making the base graph a good expander. In particular, the following simple fact stems from the observation that when going from G to \(\overline{G}\), we have \(|{\overline{S}_j}| = \ell |{S_j}|\), and hence the (relative) expansion factors of G and \(\overline{G}\) are identical.
Lemma 1
Let G be an [n, m, d]-hypergraph which is \((k, (1- \gamma )d)\)-expanding. Then, for any block-size \(\ell \), the resulting \([n \cdot \ell , m, d\ell ]\)-hypergraph \(\overline{G}\) is \((k, (1 - \gamma ) d\ell )\)-expanding.
In general, if we have high degree (say \(O(\log \lambda )\)), we can prove the existence (at least probabilistically) of very good expanders with expansion rate very close to the degree. Unfortunately, our construction of \(\overline{G}\) imposes some structure, and the actual expansion factor is dictated by the graph G with much lower degree d. The following lemma establishes the existence of good expander graphs, which we summarize below in a corollary with more useful parameters. While the proof of the lemma is folklore (we take notational inspiration from the one in [9]), we give it for completeness in the full version [55].
Lemma 2
(Strong expansion lemma). Let \(d \ge 2\), and let \(\gamma \in (0,1)\) and \(\beta \in (0, 1/2)\) be such that \(d \gamma = 1 + \beta \). Further, let \(1 \le \varDelta \le n^{\beta }/\log (n)\). Then, there exists a constant \(\alpha > 0\) such that a random \([n,m=\varDelta n, d]\)-hypergraph G is a \((k = \alpha n/\varDelta ^{1/\beta }, d(1 - \gamma ))\)-expander with probability \(1 - o(1)\).
Corollary 1
For every \(\gamma \) and d such that \(1< \gamma d < 1.5\), and every \(\eta \in (0,1)\), there exists a \([n, n^{1 + \zeta }, d]\)-hypergraph (for some \(\zeta > 0\)) which is a \((n^{1 - \eta }, (1 - \gamma )d)\)-expander.
2.3 Pseudorandom and Unpredictability Generators
We are interested in the question of finding [n, m, d]-hypergraphs for \(m = n^{1 + \alpha }\) and a constant \(d \ge 2\) such that \(\mathrm {GF}_{G, P, \ell }\) is a good PRG, for \(\ell = O(\log \lambda )\). We consider a parameterized assumption on such functions (in terms of unpredictability), and discuss it briefly. Below, we are then going to show how strong indistinguishability follows from (potentially) weaker versions of this assumption.
Unpredictability Generator and Assumptions. Let \(\mathbf {UG} = \{{\mathbf {UG}}_{\lambda }\}_{\lambda \in \mathbb {N}}\) be a function ensemble, where \(\mathbf {UG}_{\lambda }\) is a distribution on functions from \(n(\lambda )\) to \(m(\lambda )\) bits, for some polynomial functions m and n.
Definition 6
(Unpredictability generator). We say that \(\mathbf {UG}\) is an (s, \(\delta \) )-unpredictability generator (or \((s, \delta )\)-UG, for short) if for all (non-uniform) adversaries \(A = \{{A}_{\lambda }\}_{\lambda \in \mathbb {N}}\) with size at most \(s(\lambda )\) and all sequences of indices \(i(\lambda ) \in \{0, \ldots , i(\lambda ) - 1\}\), we have
where \(\mathrm {UG}_{\le j}(x)\) and \(\mathrm {UG}_j(x)\) denote the first j bits and the j-th bit of \(\mathrm {UG}(x)\), respectively.
Note that by a standard argument, being a \((s, \delta )\)-UG implies being a (family of) \((s, O(m \cdot \delta ))\)-PRGs. We now consider the following assumption, which parametrizes the fact that \(\mathrm {GF}_{G, P,\ell }\) is a good PRG.
Definition 7
( \(\mathsf {BLUG}\) -assumption). Let \(n, \ell ,s : \mathbb {N}\rightarrow \mathbb {N}\), and let \(d \ge 2\) and \(\alpha > 0\) be constants. Also, let \(\delta : \mathbb {N}\rightarrow [0,1]\). Then, the \((d, \ell )\)-\(\mathsf {BLUG}(n, \alpha , s, \delta )\) assumption is the assumption that there exists a family \(G = \{G_{\lambda }\}_{\lambda \in \mathbb {N}}\) of \([n(\lambda ), n(\lambda )^{1 + \alpha }, d]\) hypergraphs, and a family \(P = \{P_{\lambda }\}_{\lambda \in \mathbb {N}}\) of predicates on \((d(\lambda ) \times \ell (\lambda ))\)-bit strings such that \(\mathbf {GF}^{G, P, \ell }\) is an \((s, \delta )\)-UG.
We are being a bit informal here, in the sense that obviously we would like \(\mathbf {GF}^{G, P, \ell }\) to additionally be efficiently computable in a uniform sense. Our candidates will not have this property, as we are only able to infer the existence of suitable G’s probabilistically. There are two ways of thinking about the resulting ensemble: Either non-uniformly – the graph \(G_{\lambda }\) is given as advice for security parameter \(\lambda \) – but usually we actually show that a \(1 - o(1)\) fraction of the \([n, n^{1 + \alpha }, d]\)-hypergraphs are good choices. In that case, we replace G with \(\mathbf {G}\) where \(\mathbf {G}_{\lambda }\) chooses a random \([n(\lambda ), n(\lambda )^{1 + \alpha }, d(\lambda )]\)-hypergraph G, which is bad with vanishing probability o(1). This is of course not good enough, yet the problem can often be by-passed in an application-dependent way, by considering the fact that the end scheme using \(\mathbf {GF}^{\mathbf {G}, P, \ell }\) will also be insecure with probability o(1). One can then consider \(\omega (1)\)-instances of this scheme, each using an independent instance from \(\mathbf {GF}^{\mathbf {G},P,\ell }\), and then combine them with a combiner, if it exists.
Our constructions below require \((d, O(\log (\lambda )))\)-\(\mathsf {BLUG}(n, \alpha , {\mathrm {poly}}(\lambda ), 2^{-\omega (\log \lambda )})\) to be true for some \(n(\lambda ) = {\mathrm {poly}}(\lambda )\) and \(\alpha > 0\). For stronger results, we are going to replace \(2^{-\omega (\log \lambda )}\) with \(2^{-\lambda ^{\epsilon }}\) for some \(\epsilon > 0\). Below, we will discuss whether this assumption can be implied by (qualitatively) weaker properties. We will show in particular that \((d, O(\log ^{1 - \varepsilon }(\lambda )))\)-\(\mathsf {BLUG}(n, \alpha , 2^{\omega (\log \lambda )}, 1/\lambda ^{\varOmega (1)})\) implies \((d, O(\log (\lambda )))\)-\(\mathsf {BLUG}(n, \alpha , {\mathrm {poly}}(\lambda ), 2^{-\omega (\log \lambda )})\).
Here, we briefly discuss what can be expected to start with.
The case \(d \ge 3\) . For the case \(d \ge 3\), a good candidate to study is the case where \(\ell = O(\log (\lambda ))\) and \(G = \{G_{\lambda }\}_{\lambda \in \mathbb {N}}\) is such that \(G_{\lambda }\) is an \([n(\lambda ), n(\lambda )^{1 + \alpha }, d]\)-hypergraph which is a good \((n^{1 - \gamma }, (1 - \gamma )d)\)-expander where \(\gamma < \frac{1}{2}\), which exists (for some suitable \(\alpha > 0\)) by Corollary 1. The corresponding \(\overline{G}_{\lambda }\) are then in turn also \((n^{1 - \gamma }, (1 - \gamma )d \ell )\)-expanders by Lemma 1.
Applebaum and Raykov [13] recently justify the assumption that for suitable predicates, P, the function family \(\mathbf {GF}^{\overline{\mathcal {G}}, P}\) is one way and a PRG against adversary running in time \(2^{n^{1 - \gamma }}\), which cannot succeed with probability larger than \(2^{-n^{1- \gamma }}\). In the same paper, they also give a decision-to-search reduction for such functions, which however applies only for degrees where we can accommodate some \(\gamma \) with \(3 \gamma < 1\). In particular, such functions withstand existing attacks, such as myopic inversion attacks [30]. Also, the degree of P can be high, e.g., \(O(\log (\lambda ))\), and this prevents a number of attacks exploiting weakness of the predicate [21, 34].
Also, as we show in the next section, it is possible to adopt the techniques from [9] to show that we can get good \(\epsilon \)-biased generators (for a sub-exponential \(\epsilon \)) with block-wise locality (3, 2). This has been the main technique in validating PRG assumptions on graph-based local functions [9, 60, 61].
The special case \(d = 2\) . The case \(d = 2\) is particularly important, as it does allow instantiations from bilinear maps in our applications. Note that algebraic attacks are mitigated here – in contrast to the case of plain locality, i.e., \(\ell = 1\), we can set \(\ell = O(\log \lambda )\) and achieve sufficiently high algebraic degree of the predicate P. Unfortunately, this is not sufficient to prove pseudorandomness, as shown by recent attacks [14, 57], which we have discussed above in Sect. 1.3.
2.4 Block-Wise Local Small-Bias Generators
Several works [9, 12, 34, 60] have focused on studying weaker properties achieved by local generators. In particular, a standard statement towards validating their security is that of showing that the meet the definition of being a small-bias generator.
Definition 8
We say \(\mathrm {SB}: \{0,1\}^n \rightarrow \{0,1\}^m\) is an \(\epsilon \) -small biased generator if \(\max _{J \subseteq [n], J \ne \emptyset } \bigl | \Pr [x \mathop {\leftarrow }\limits ^{\$}\{0,1\}^n \;:\; \bigoplus _{j \in J} \mathrm {SB}_j(x) = 1] - \tfrac{1}{2} \bigr | \le \epsilon \), where \(\mathrm {SB}_j(x)\) denotes the j-th bit of \(\mathrm {SB}(x)\).
We show that \(\mathrm {GF}_{G, Q, 2}\) is a good small-biased generator for a sub-exponential \(\epsilon \), where G is an [n, m, 3]-hypergraph, and Q is the predicate which given three 2-bit blocks \(\mathbf {x}_1,\mathbf {x}_2, \mathbf {x}_3\) where \(\mathbf {x}_i = (x_i^l, x_i^h)\), outputs
Another convenient way to think about \(\mathrm {GF}_{G, Q, 2}\) is as
where \(Q^l(x_1, x_2, x_3) = x_1 \oplus x_2 \oplus x_3\) and \(Q^h(x_1, x_2, x_3) = x_1 \wedge x_2\). To show that \(\mathrm {GF}_{G, Q, 2}\) has small bias, the main idea is fairly straightforward. Indeed, current analyses of local small-biased generators give two separate analyses for so called “light tests” and “heavy tests”, where the “weight” of a test amounts to the cardinality of |J|. For standard locality, withstanding both at the same time forces the graph degree to be at least five, since the predicate needs to be “non-degenerate” for the construction to withstand tests (and the theorem of [9] to apply), and all predicates up to \(d = 4\) are degenerate (cf. e.g. [34]). This will not be a problem here, as we only target block-wise locality, and thus effectively the predicate can be non-degenerate. The proof is in the full version [55].
Lemma 3
For all \(\delta > 0\) and \(\alpha < \frac{1 - \delta }{4}\), for a fraction of \(1 - o(1)\) of all \([n, n^{1 + \alpha }, 3]\)-hypergraphs G, and Q as defined above, \(\mathrm {GF}_{G, Q, 2}\) is an \(\left( e^{-\frac{n^{\delta }}{4}}\right) \)-biased generator.
2.5 Hardness Amplification via the XOR Construction
In this paper, we rely on the assumption that \(\mathbf {GF}^{G,P,\ell }\) is a good PRG for an appropriate family G of expanders. However, we want to add additional justification to our assumptions. Here, in particular, we discuss how weak unpredictability for graph-based block-wise local functions can be amplified to super-polynomially small unpredictability generically. This means in particular that block-wise local PRGs have strong self-amplifying properties, and that for any G and P, in order to invalidate our assumption, we need to find an attack which succeeds in predicting the next bit with large (i.e., polynomial) advantage over \(\frac{1}{2}\). For otherwise, the lack of such an attack would imply that for the same G and (a related) \(P'\) and \(\ell '\), \(\mathbf {GF}^{G, P', \ell '}\) is a strong PRG.
To this end, we use a simple construction xoring the outputs of generators, which has already been studied to amplify PRG security [35, 58]. Our analysis resembles the one from [35], but is given for completeness. Also, a more general construction, with xoring replaced by a general extractor, was considered by Applebaum [7]. The use of xor, however, is instrumental to preserve block-wise locality. The main drawback of this construction is that it can at best ensure \(2^{-\varOmega (\log ^{1+\theta } \lambda )}\) distinguishing gap for some \(\theta \in (0, 1]\) while retaining block size \(\ell = O(\log \lambda )\). In the full version [55], we explain a different approach which relies on a different assumption. and potentially guarantees \(2^{-\lambda ^{\varOmega (1)}}\) distinguishing gap.
The XOR Construction. Let \(\mathbf {UG}= \{\mathbf {UG}_{\lambda }\}_{\lambda \in \mathbb {N}}\) be an \((s, \delta )\)-UG, where \(\mathbf {UG}_{\lambda }\) is a distribution on functions \(\{0,1\}^{n(\lambda )} \rightarrow \{0,1\}^{m(\lambda )}\). For an additional parameter \(k = k(\lambda ) \ge 1\), we define the ensemble \(\mathbf {UG}^k = \{\mathbf {UG}^k_{\lambda }\}_{\lambda \in \mathbb {N}}\), where \(\mathbf {UG}^k_{\lambda }\) samples functions \(\mathrm {UG}_1, \ldots , \mathrm {UG}_k \mathop {\leftarrow }\limits ^{\$}\mathbf {UG}_{\lambda }\) and output the description of a function \(\mathrm {UG}^k: \{0,1\}^{n \times k} \rightarrow \{0,1\}^{m}\) which, on input \(x = x^1 \;\Vert \;\cdots \;\Vert \;x^{k}\), where \(x^i \in \{0,1\}^{n(\lambda )}\), outputs
We prove the following in the full version [55].
Theorem 5
(Security of the XOR Construction). If \(\mathbf {UG}\) is a \((s, \delta )\)-UG and \(k = k(\lambda )\) is polynomial in \(\lambda \), then \(\mathbf {UG}^{k}\) is a \((s', \epsilon )\)-PRG, where
Block-Wise Local Instantiation. We instantiate the construction with parameter k when \(\mathbf {UG}= \mathbf {GF}^{G, P, \ell }\) for a family of [n, m, d]-hypergraphs \(G = \{{G}_{\lambda }\}_{\lambda \in \mathbb {N}}\), some \(\ell = \ell (\lambda )\), and a family P of \((d \times \ell )\)-bit predicates. Since the resulting function \(\mathrm {UG}_{\lambda }^k\) uses k instances of the same function \(\mathrm {GF}_{G_\lambda , P_{\lambda }, \ell }\), it can equivalently be thought as having the form (up to re-arranging the order of the input bits) \(\mathrm {GF}_{G_{\lambda }, P_{\lambda }^{k}, \ell (\lambda ) \cdot k(\lambda )}\), where the predicate \(P^{k}\) on input d \((k \cdot \ell )\)-bit blocks \(\mathbf {x}_1, \ldots , \mathbf {x}_d\), it interprets each of them as k \(\ell \)-bit blocks \(\mathbf {x}_{i} = \mathbf {x}_{i,1} \;\Vert \;\cdots \;\Vert \;\mathbf {x}_{i, k}\) and outputs
To instantiate our transformation, we assume that for some \(\ell (\lambda ) = \varOmega (\log ^{1- \theta }(\lambda ))\) and a family of \([n(\lambda ), m(\lambda ), d]\)-hypergraphs \(G = \{{G}_{\lambda }\}_{\lambda \in \mathbb {N}}\), the function family \(\mathrm {UG}= \mathbf {GF}^{G, P, \ell }\) is a \((s(\lambda ) = 2^{\log ^3(\lambda )}, \delta (\lambda ) = \lambda ^{-\varOmega (1)})\)-UG. Now, set \(k(\lambda ) = \log ^{\theta }(\lambda )\). Then, \(\mathrm {UG}^k\) is by the above \((d, O(\log (\lambda )))\)-block-wise local, and it is also \((s', \epsilon )\)-UG for \(s'(\lambda ) = {\mathrm {poly}}(\lambda )\), and
In other words, we have just established the following corollary.
Corollary 2
For any \(\beta > 0\), \(d \ge 2\), and \(\theta \in (0,1]\), if the \((d, O(\log ^{1 - \theta }(\lambda )))\)-\(\mathsf {BLUG}(n, \beta , 2^{\log ^3(\lambda )}, 1/\lambda ^{\varOmega (1)})\) assumption holds, then the assumption \((d, O(\log (\lambda )))\)-\(\mathsf {BLUG}(n, \beta , {\mathrm {poly}}(\lambda ), 2^{-\varOmega (\log ^{1 + \theta }(\lambda ))})\) also holds true.
3 IO from Block-Wise Locality-\((L, \log \lambda )\) PRG and L-Linear Maps
In this section, we prove the following bootstrapping theorem.
Theorem 6
(Bootstrapping via block-wise local PRGs). Let \(\mathcal {R}= \{{\mathcal {R}_\lambda }\}\) be any family of rings, \(\varepsilon \) be any positive constant, L any positive integer, n any sufficiently large polynomial, and \({\mathrm {i}\ell }\) and \({\kappa }\) any polynomials. There is a construction of \({\mathrm {i}\ell }(\lambda )\)-bit-input IO for \({\mathsf {P/poly}}\), from the following primitives:
-
A family of \((n(\lambda )\times \log \lambda , n(\lambda )^{1+\varepsilon })\)-PRGs with block-wise locality \((L,\log \lambda )\).
-
A public-key FE for degree-L polynomials in \(\mathcal {R}\), with linear efficiency and \({\mathsf {Full - Sel}}\)-security; or with a secret-key FE with the same properties, assuming additionally LWE with subexponential modulo-to-noise ratio.
The IO scheme is \((2^{-{\kappa }(\lambda )}\mathrm {negl}(\lambda ))\)-secure, if the PRG and FE schemes are \((2^{-{\mathrm {i}\ell }(\lambda )+{\kappa }(\lambda )}\mathrm {negl}(\lambda ))\)-secure, and LWE is \((2^{-{\mathrm {i}\ell }(\lambda )+{\kappa }(\lambda )}\mathrm {negl}(\lambda ))\)-hard.
Theorem 6 follows the same approach as Lin’s recent bootstrapping theorem [53], but modifies it in two ways. First, it uses block-wise local PRGs to replace local PRGs. Second, it makes explicit the relation between the security level (more precisely, the maximal distinguishing gap) of the underlying PRG and FE, and the input-length and security level of the resulting IO—if the underlying primitives are \(2^{-{\mathrm {i}\ell }+{\kappa }}\mathrm {negl}\)-secure, then the resulting IO scheme is for \({\mathrm {i}\ell }\)-bit-input circuits and \(2^{{\kappa }}\mathrm {negl}\)-security. Such relations are implicit in previous works, and not as tight as shown here.
Overview of Proof of Theorem 6 . To show the theorem, similar to previous works [53, 56], we take two steps:
Step 1. Construct a single-key public-key (or secret-key) FE schemes \(\mathbf{CFE}= \{{\mathbf{CFE}}^{N,D,S}\}\) for \({\mathsf {P/poly}}\), with \((1-\varepsilon )\)-sublinear compactness and \(2^{-{\mathrm {i}\ell }+{\kappa }}\mathrm {negl}\)-\({\mathsf {Full - Sel}}\)-security, starting from a public-key (or secret-key) FE for degree-L polynomials in  , with linear efficiency and \({\mathsf {Full - Sel}}\)-security.
, with linear efficiency and \({\mathsf {Full - Sel}}\)-security.
Previously, the work of [56] showed how to achieve this transformation from a locality-L PRGs and FE for computing degree  polynomials. Following that, the two recent works of [4, 53] used a pre-processing technique to relax the requirement on the underlying FE to supporting only degree-L polynomials. In this work, we extend their pre-processing technique even further, in order to relax the requirement on the underlying PRGs from having locality L to having block-wise locality \((L, \log \lambda )\). We describe this step in full detail in Sect. 3.1.
polynomials. Following that, the two recent works of [4, 53] used a pre-processing technique to relax the requirement on the underlying FE to supporting only degree-L polynomials. In this work, we extend their pre-processing technique even further, in order to relax the requirement on the underlying PRGs from having locality L to having block-wise locality \((L, \log \lambda )\). We describe this step in full detail in Sect. 3.1.
In the case that the obtained FE scheme \(\mathbf{CFE}\) is a secret-key one, we invoke the result of [18] to transform it into a public key FE scheme with the same properties, assuming LWE with subexponential modulus-to-noise ratio.
Since our transformation from FE for low-degree computations to weakly-compact FE for \({\mathsf {P/poly}}\) in Sect. 3.1 incurs only a polynoimal security loss, and so does the transformation of [18], the resulting weakly-compact FE has essentially the same level of security as that of underlying primitives.
Step 2. Apply an FE-to-IO transformation to obtain \({\mathrm {i}\ell }\)-bit-input IO for \({\mathsf {P/poly}}\), with \(2^{-{\kappa }}\mathrm {negl}\)-security.
The literature already offers three FE-to-IO transformations [2, 20, 54] that start from a public key FE scheme \(\mathbf{CFE}=\{{\mathbf{CFE}}^{N,D,S}\}\) as described above w.r.t. any positive constant \(\varepsilon \). In this work, we reduce the security loss incurred in the transformation so as to start with \(2^{-{\mathrm {i}\ell }+{\kappa }}\mathrm {negl}\)-secure FE (as opposed to \(2^{-O({\mathrm {i}\ell }^2)+{\kappa }}\mathrm {negl}\)-secure or \(2^{-O(\log \lambda ) {\mathrm {i}\ell }+{\kappa }}\mathrm {negl}\)-secure FE as in previous works). To do so, we present a new FE-to-IO transformation inspired by that of [54] and present a tight analysis. We describe this step in the full version [55].
3.1 Step 1: Constructing Weakly-Compact FE
Proposition 1
Let \(\mathcal {R}\), \(\varepsilon \), L, and n be defined as in Theorem 6, and \({\bar{\kappa }}\) be any polynomial. There is a construction of 1-key weakly-compact public-key FE for \({\mathsf {P/poly}}\) from the following primitives:
-
A family of \((n(\lambda )\times \log \lambda , n(\lambda )^{1+\varepsilon })\)-PRGs with block-wise locality \((L,\log \lambda )\).
-
Public-key FE for degree-L polynomials in \(\mathcal {R}\), with linear efficiency and \({\mathsf {Full - Sel}}\)-security; or secret-key FE with the same properties, assuming additionally LWE with subexponential modolus-to-noise ratio.
The weakly-compact FE is \((2^{-{\bar{\kappa }}(\lambda )}\mathrm {negl}(\lambda ))\)-\({\mathsf {Full - Sel}}\)-secure, if the underlying PRG and FE are \((2^{-{\bar{\kappa }}(\lambda )}\mathrm {negl}(\lambda ))\)-secure and LWE is \((2^{-{\bar{\kappa }}(\lambda )}\mathrm {negl}(\lambda ))\)-hard.
It was shown in [53] that 1-key weakly-compact FE for \({\mathsf {P/poly}}\) can be constructed from locality-L PRG and (unbounded collusion) FE for degree-L polynomials. Their construction of weakly-compact FE follows from the blue-print of previous works [52, 56], which uses FE for low degree polynomials to compute a randomized encoding of a computation in \({\mathsf {P/poly}}\), with pseudo-randomness generated through a local PRG. The locality of RE and PRG ensures that their composition can be computed in low degree. However, the straightforward composition of RE and PRG leads to a computation with degree \(3L+2\). The key idea in [53] and the concurrent work of [4] is that part of the RE computation can already be done at encryption time, that is, by asking the encryptor to pre-process the inputs (of the computation in \({\mathsf {P/poly}}\)) and seeds of PRG, and encrypt the pre-processed values, the composition of RE and PRG can be computed in just degree L from the pre-processed values, at decryption time—This is called the preprocessing technique. We take this technique one step further: By also performing part of the PRG computation at encryption time, we can replace local PRG with block-wise local PRG (with appropriate parameters) at “no cost”.
Below, we first briefly review the blueprint of [56], then describe the pre-processing idea of [53] and how to use it to accommodate PRG with block-wise locality.
The General Blueprint of [56]. To construct 1-key weakly-compact FE for \({\mathsf {P/poly}}\), Lin and Vaikuntanathan [56] (LV) first observed that, using the Trojan Method [26], it suffices to construct 1-key weakly-compact FE for \(\mathsf {NC}^1\) functions with some fixed depth \(D(\lambda ) = O(\log \lambda )\); denote this class of functions as \(\mathsf {NC}^1_D\).
Next, to bootstrap a low-degree FE scheme to FE for \(\mathsf {NC}_D^1\), the idea is using randomized encoding to “compress” any function \(h({{\mathbf {x}}}) \in \mathsf {NC}^1_D\) into a function \(g({{\mathbf {x}}},{{\mathbf {s}}}) = \mathsf{REnc}(f, {{\mathbf {x}}}\, ;\ \mathrm {PRG}({{\mathbf {s}}}))\) with small degree in \(\mathcal {R}\). The reason that local PRG is used is that the locality of a Boolean function bounds the degree of computing this function in any ring. Then, plugging-in randomized encodings with small locality like that of [11] the overall degree of g is small. For the security proof to work out, the actual functions used in the LV construction are more complicated and has form
where \({{\mathbf {CT}}}\) is a ciphertext hardwired in the secret key, and serves as “space” to hide values in the secret key in the security proof.
A formal description of the LV public key FE scheme \(\mathbf{CFE}^{N,D,S}\) for \(\mathsf {NC}^1\) circuits with input-length \(N = N(\lambda )\), depth \(D = D(\lambda ) = O(\log \lambda )\), and size \(S = S(\lambda )\) is in Fig. 2. (The secret-key case has almost identical construction.) The scheme uses the following tools:
-
\({\mathsf {Full - Sel}}\)-secure (collusion resistant) FE schemes for degree-\((3L+2)\) polynomials in some \(\mathcal {R}\), \(\{\mathbf{FE}^{N'} = (\mathsf{FE.Setup}, \mathsf{FE.KeyGen},\mathsf{FE.Enc},\mathsf{FE.Dec})\}\), with linear efficiency.
-
A \((n, n^{1+\alpha })\)-pseudorandom generator \(\mathrm {PRG}\) with locality L, for a sufficiently large polynomial input length \(n = n(\lambda )\) and any positive constant \(\alpha \).
-
The AIK randomized encoding scheme in \(\mathsf {NC}^0\) [11]; denote the encoding algorithm as \(\mathsf {AIK}(f, {{\mathbf {x}}}\, ; \ {{\mathbf {r}}})\).
We refer the reader to [56] for the correctness and security of the scheme. The compactness of the scheme \(\mathbf{CFE}\) follows from the following two facts:
-
1.
The length of the input \(({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {s}}}', 0)\) encrypted using \(\mathbf{FE}\) is \(N + 2\varGamma + 1 = N + S(\lambda )^{1/(1+\alpha )}{\mathrm {poly}}(\lambda )\).
-
2.
\(\mathbf{FE}\) has linear efficiency.
Putting them together, we have,

which is sublinear in the function size as desired. Furthermore, to see why degree-\((3L+2)\) FE suffices for the construction, note that the construction uses the underlying FE to generate keys computing the function g in Fig. 2, and hence it suffices to argue that g can be computed in degree \(3L+2\). By definition of g, when \(b=1\), the output can be computed in degree L as the PRG can be computed in degree L in \(\mathcal {R}\) (XOR with \({{\mathbf {CT}}}\) does not incur additional degree as \({{\mathbf {CT}}}\) are constants hardwired in the function g); when \(b=0\), the output can be computed in degree \(3L+1\), since the AIK randomized encoding has degree 3 in the random bits (i.e. PRG output) and 1 in the input \({{\mathbf {x}}}\). Therefore, g has exactly degree \(3L+2\), as selection by b can be done with one multiplication.
Single-key compact FE \(\mathbf{CFE}\) by [56]
The Idea of Preprocessing in [53]. Towards reducing the degree of the underlying FE and accommodating PRGs with block-wise locality-\((L, \log \lambda )\), the idea is letting the encryptor pre-process the input \(({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {s}}}', b)\) to produce certain intermediate values, from which the output of function g can be computed in exactly degree L. To see this, the output of g is viewed as corresponding to S AIK randomized encodings for functions \(\{{h_i}\}_{i \in [S]}\). If the \(l^\mathrm{th}\) output bit belongs to the \(i^\mathrm{th}\) randomized encoding for \(h_i\) with random tape \({{\mathbf {r}}}[i]\), the function \(g_l\) computing it can be written as a sum of monomials as follows:

where \({{\mathbf {r}}}[i]\) is the \(i^\mathrm{th}\) portion in \({{\mathbf {r}}}= \mathrm {PRG}({{\mathbf {s}}})\), and \({{\mathbf {r}}}' = \mathrm {PRG}({{\mathbf {s}}}')\). This is because in the case of \(b = 0\), the output is a bit in the AIK encoding of \(h_i\) and hence has degree 1 in the input \({{\mathbf {x}}}\) and degree 3 in \({{\mathbf {r}}}[i]\), while in the case of \(b = 1\), the output has degree 1 in \({{\mathbf {r}}}'\).
When \(\mathrm {PRG}\) has locality L, the straightforward way of computing a degree-3 monomial \({{\mathbf {r}}}[i]_{i_1} {{\mathbf {r}}}[i]_{i_2} {{\mathbf {r}}}[i]_{i_3}\) from the seed \({{\mathbf {s}}}\) requires degree 3L. The works of [4, 53] showed how to reduce the degree to just L. First, they use a different way to compute each \({{\mathbf {r}}}[i]\). View the seed \({{\mathbf {s}}}\) as a \(Q \times \varGamma '\) matrix with \(Q = Q(\lambda ) = {\mathrm {poly}}(\lambda )\) rows and \(\varGamma ' = S^{1/1+\alpha }\) columns; apply PRG on each row of \({{\mathbf {s}}}\) to expand the seed matrix into a \(Q \times S\) matrix \({{\mathbf {r}}}\) of pseudo-random bits. That is, denote the \(q^\mathrm{th}\) row of \({{\mathbf {s}}}\) and \({{\mathbf {r}}}\) as \({{\mathbf {s}}}_q\) and \({{\mathbf {r}}}_q\); \({{\mathbf {r}}}_q = \mathrm {PRG}({{\mathbf {s}}}_q)\). Finally, set the random tape for computing the \(i^\mathrm{th}\) AIK encoding to be the \(i^\mathrm{th}\) column \({{\mathbf {r}}}[i]\) of \({{\mathbf {r}}}\).
In [53], they used PRGs with locality L. Let \(\mathrm {PRG}[i]\) denote the function computing the \(i^\mathrm{th}\) output bit of \(\mathrm {PRG}\), and let \(\mathsf{Nbr}(i) = \{{\gamma _1, \cdots , \gamma _L}\}\) be the indexes of the L seed bits that the \(i^\mathrm{th}\) output bit depends on. Therefore,
Suppose that one has pre-computed all degree \(\le 3\) monomials over bits in each column \({{\mathbf {s}}}[\gamma ]\) of \({{\mathbf {s}}}\).
Given \(\mathsf{Mnml}^{\le 3}({{\mathbf {s}}}[\gamma ])\) for every \(\gamma \in \mathsf{Nbr}(i)\), one can compute \({{\mathbf {r}}}[i]_{i_1}{{\mathbf {r}}}[i]_{i_2}{{\mathbf {r}}}[i]_{i_3}\) in Eq. (2) using just degree L. Similarly, given \(\mathsf{Mnml}^{\le 3}({{\mathbf {s}}}[\gamma ])\) for all \(\gamma \in [\varGamma ']\), one can compute any degree 3 monomials over bits in \({{\mathbf {r}}}[i]\) for any i, sufficient for the computation of g.
Furthermore, the size of each set \(\mathsf{Mnml}^{\le 3}({{\mathbf {s}}}[\gamma ])\) is bounded by \((Q+1)^{3} = {\mathrm {poly}}(\lambda )\), and thus the size of their union for all \(\gamma \) is bounded by \(\varGamma '{\mathrm {poly}}(\lambda ) = S^{1/1+\alpha }{\mathrm {poly}}(\lambda )\)—only a polynomial factor (in \(\lambda \)) larger than the original seed \({{\mathbf {s}}}\) itself. Therefore the encryptor can afford to precompute all these monomials and encrypt them, without compromising the weak-compactness of the resulting FE for \(\mathsf {NC}^1_D\) scheme.
This Work: Handling Block-Wise Local PRG. Our new observation is that the above technique naturally extends to accommodate block-wise local PRGs. Consider a family of \((n(\lambda ) \times \log \lambda , n(\lambda )^{1+\alpha })\)-PRGs with block-wise locality-\((L, \log \lambda )\). As before, we think of the seed of such PRGs as a vector \({{\mathbf {t}}}\) of length n, where every element \(t_i\) is a block of \(\log \lambda \) bits, and each output bit \(\mathrm {PRG}[i]({{\mathbf {t}}})\) depends on at most L blocks.
Correspondingly, think of the seed matrix \({{\mathbf {s}}}\) described above as consisting of \(Q \times \varGamma '\) blocks of \(\log \lambda \) bits. When \({{\mathbf {r}}}[i]\) is computed using block-wise local PRGs, the degree-3 monomial \({{\mathbf {r}}}[i]_{i_1}{{\mathbf {r}}}[i]_{i_2}{{\mathbf {r}}}[i]_{i_3}\) in Eq. (2) now depends on a set of blocks \(\{{s_{i_t, \gamma _s}}\}_{t \in [3], s \in [L]}\). Though the actual locality of the PRG is \(L \log \lambda \), due to its special structure, we can still pre-process the seed \({{\mathbf {s}}}\) to enable computing any degree-3 monomial over \({{\mathbf {r}}}[i]\) for any i using degree L, in the following two steps.
-
1.
Precompute all multilinear monomials over bits in each block \(s_{q, \gamma }\) in \({{\mathbf {s}}}\).
$$\begin{aligned} \text{ Define } \qquad \mathsf{Mnml}(A) := \{{a_{i_1}a_{i_2}\cdots a_{i_{q}} \ | \ q \le |A| \ \text{ and } \forall j, k \ a_{i_j}\ne a_{i_k} \in A}\}. \end{aligned}$$More precisely, precompute \(\mathsf{Mnml}(s_{q, \gamma })\) for all \(q \in [Q]\) and \(\gamma \in [\varGamma ']\). Note that each set \(\mathsf{Mnml}(s_{q, \gamma })\) has exactly size \(\lambda \).
-
2.
For every column \(\gamma \in [\varGamma ']\), take the union of monomials over blocks in column \(\gamma \), that is, \(\cup _{q} \mathsf{Mnml}(s_{q, \gamma })\). Then, precompute all degree-\(\le 3\) monomials over this union, that is, \(\mathsf{Mnml}^{\le 3}(\cup _{q} \mathsf{Mnml}(s_{q,\gamma }))\), for each \(\gamma \). Observe that from \(\{{\mathsf{Mnml}^{\le 3}(\cup _q \mathsf{Mnml}(s_{q, \gamma }))}\}_{\gamma \in [\varGamma ']}\), one can again compute any degree-3 monomial in \({{\mathbf {r}}}[i]\) for any i in just degree L.
Furthermore, since \(|\mathsf{Mnml}(s_{q,\gamma })| = \lambda \) for any \(q, \gamma \), the number of monomials in \(\mathsf{Mnml}^{\le 3}(\cup _{q} \mathsf{Mnml}(s_{q,\gamma }))\) is bounded by \((Q\lambda + 1)^{3} = {\mathrm {poly}}(\lambda )\). Therefore, the total size of pre-computed monomials is
which is still sublinear in the circuit size S and does not compromise the weak-compactness of the resulting FE for \(\mathsf {NC}^1_D\) scheme.
Putting Things Together. So far, we showed how to “compress” the computation of degree 3 monomials over \({{\mathbf {r}}}[i]\), for any i, into a degree-L computation. To compute function g in Eq. (1) in degree L, we need to additionally pre-compute multiplications with \({{\mathbf {x}}}\) and b. As described in [53], this can be done easily by pre-computing the following:
(where the sets of monomials are first interpreted as a vector before taking tensor product). Given the tensor product, one can compute any monomial with degree \(\le 3\) in \({{\mathbf {r}}}[i]\) for any i, degree \(\le 1\) in \({{\mathbf {x}}}\), and degree \(\le 1\) in b, in just degree L, which is sufficient for computing the first additive term in \(g_l\) in Eq. (1). Similarly, to compute the second additive term in \(g_l\), it suffices to precompute all multilinear monomials over every block in \({{\mathbf {s}}}'\) (of length \(\varGamma \)), and compute their tensor product with b||1, that is,
In summary, for every \(l \in [\ell ]\), there exists a degree-L polynomial \(P_l\) that on input \((\mathbf {V}_1, \mathbf {V}_2)\) outputs \(g_l({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {s}}}', b)\).
Moreover, we show that both \(\mathbf {V}_1\) and \(\mathbf {V}_2\) have length sublinear in the circuit size. First, combining Eq. (3) with the fact that \(|({{\mathbf {x}}}||b||1)| = N+ 2\), we have that
The size of \(\mathbf {V}_2\) is
Finally, to construct a 1-key weakly-compact FE scheme for \(\mathsf {NC}^1_D\) from FE for just degree L polynomials. We modify the LV construction as follows: (1) Instead of encrypting \(({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {s}}}',b)\), the encryptor pre-computes and encrypts \(\mathbf {V}_1||\mathbf {V}_2\) as described above, and (2) instead of generating secret keys for functions \(\{{g_l}\}_{l \in [\ell ]}\) which have degree \(3L+2\), generate secret keys for \(\{{P_l}\}_{l \in [\ell ]}\) which have only degree L. This way, at decryption time, the decryptor computes the correct output \(\{{P_l(\mathbf {V}_1||\mathbf {V}_2) = g_l({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {s}}}', b)}\}\). The resulting new compact FE scheme \(\mathbf{CFE}\) is described in Fig. 3 (with key difference from the LV scheme highlighted). The compactness of the new scheme follows directly from the fact that the encrypted input \(\mathbf {V}_1,\mathbf {V}_2\) have length sublinear in \(S(\lambda )\), and that the degree-L \(\mathbf{FE}\) scheme has linear efficiency. Moreover, its correctness and security follows from the same proof as that in [56]; since their security proof incur only a polynomial security loss, we conclude Proposition 1.
4 FE from \(\omega (\log \lambda )\)-Bit-Input IO for \({\mathsf {P/poly}}\)
In this section, we show Theorem 4, i.e., we prove via a new transformation that adaptively-secure collusion-resistant public-key functional encryption for \({\mathsf {P/poly}}\) is implied by IO for circuits with short, \(\omega (\log \lambda )\)-bit, inputs and public key encryption, both with slightly super-polynomial security. Note that, in contrast, previous constructions of collusion-resistant FE for \({\mathsf {P/poly}}\) either rely on multilinear maps [40], or require IO for all \({\mathsf {P/poly}}\), including circuits with long (polynomial) inputs [39].
Our proof generically transforms any 1-key (public key) FE scheme for any circuit class \(\mathcal{C} \) into a collusion-resistant (public key) FE scheme for the same circuit class, using IO for circuits with \(\omega (\log \lambda )\)-bit inputs. The encryption time of the resulting FE schemes is polynomial in the encryption time of the original schemes, and hence if the original scheme is (non-)compact, so is the resulting FE scheme. The transformation also preserves the same type of security—namely \({\mathsf {Full - Sel}}\)- or \({\mathsf {Adap}}\)-security—and incurs a \(2^{\omega (\log \lambda )}\) security loss.
More precisely, we prove the following below in Sect. 4.1.
Proposition 2
Let \(\mathcal{C} \) be any circuit class, \({\tau }\) be any polynomial, and \({\mathrm {i}\ell }\) be any polynomial such that \({\mathrm {i}\ell }(\lambda ) = \omega (\log \lambda ) \le \lambda \). Assume the existence of an \({\mathrm {i}\ell }(\lambda )\)-bit-input indistinguishability obfuscator \({i\mathcal {O}}\) for \({\mathsf {P/poly}}\). Then, any 1-key public-key FE schemes \(\mathbf{OFE}\) for \(\mathcal{C} \) can be generically transformed into collusion-resistant FE schemes \(\mathbf{CRFE}\) for \(\mathcal{C} \), with the following properties:
-
The encryption time of \(\mathbf{CRFE}\) is polynomial in the encryption time of \(\mathbf{OFE}\).
-
If \({i\mathcal {O}}\) is \(2^{-({\mathrm {i}\ell }(\lambda ) + {\tau }(\lambda ))}\mathrm {negl}(\lambda )\)-secure and \(\mathbf{OFE}\) is \(2^{-({\mathrm {i}\ell }(\lambda ) + {\tau }(\lambda ))}\mathrm {negl}(\lambda )\)-(\({\mathsf {Adap}}\) or \({\mathsf {Full - Sel}}\))-secure, then \(\mathbf{CRFE}\) is \(2^{-{\tau }(\lambda )}\mathrm {negl}(\lambda )\)-(\({\mathsf {Adap}}\) or \({\mathsf {Full - Sel}}\))-secure.
It is known that adaptively-secure 1-key non-compact public-key FE for \({\mathsf {P/poly}}\) can be constructed from just public key encryption [48].
Theorem 7
(1-Key \({\mathsf {Adap}}\) -Secure Public-Key FE for \({\mathsf {P/poly}}\) [48]). Let \(\mu \) be any function from \(\mathbb {N} \) to [0, 1]. Assuming public key encryption with \(\mu (\lambda )\mathrm {negl}(\lambda )\)-security, there exist \(\mu (\lambda )\mathrm {negl}(\lambda )\)-\({\mathsf {Adap}}\)-secure 1-key non-compact public-key FE schemes for \({\mathsf {P/poly}}\).
Now, applying the transformation of Proposition 2 to the \(\mu \mathrm {negl}\)-\({\mathsf {Adap}}\)-secure 1-key FE schemes for \({\mathsf {P/poly}}\) with \(\mu = 2^{-({\mathrm {i}\ell }+{\tau })}\), yields \(2^{-{\tau }}\mathrm {negl}\)-\({\mathsf {Adap}}\)-secure collusion-resistant (non-compact public-key) FE for \({\mathsf {P/poly}}\). Finally, note that it follows from [3] that collusion-resistant non-compact FE schemes implies collusion-resistant compact FE schemes with the same level of security, which yields Theorem 4.
4.1 From 1-Key to Collusion-Resistant FE, Generically
In this section, we prove Proposition 2. Let us fix any circuit class \(\mathcal{C} \), and any \({\mathrm {i}\ell }\) such that \({\mathrm {i}\ell }(\lambda ) = \omega (\log \lambda )\le \lambda \). The resulting collusion-resistant FE scheme for \(\mathcal{C} \), denoted \(\mathbf{CRFE}= (\mathsf{CRFE.Setup}, \mathsf{CRFE.KeyGen}, \mathsf{CRFE.Enc}, \mathsf{CRFE.Dec})\), relies on the following building blocks:
-
An \({\mathrm {i}\ell }\)-bit-input indistinguishability obfuscator \({i\mathcal {O}}\) for \({\mathsf {P/poly}}\).
-
A 1-key FE scheme \(\mathbf{OFE}= (\mathsf{OFE.Setup}, \mathsf{OFE.KeyGen}, \mathsf{OFE.Enc}, \mathsf{OFE.Dec})\) for \(\mathcal{C} \).
-
A puncturable PRF scheme \(\mathsf{PPRF}= (\mathsf {PRF{.}Gen},\mathsf {PRF{.}Punc},{\mathsf {F}})\).
Given the above building blocks, to construct collusion resistant FE \(\mathbf{CRFE}\) for \(\mathcal{C} \), we start with the following intuition. If efficiency were not a problem, we could trivially construct a FE scheme that support releasing any polynomial number of secret keys, essentially by using a super-polynomial number of instances of \(\mathbf{OFE}\). Concretely, we would proceed as follows:
-
Setup: Generate a super-polynomial number, \(M = 2^{{\mathrm {i}\ell }(\lambda )} = 2^{\omega (\lambda )}\), of \(\mathbf{OFE}\) instances with master keys \(\{{({\mathsf {OMPK}}_i, {\mathsf {OMSK}}_i)\mathop {\leftarrow }\limits ^{\$}\mathsf{OFE.Setup}(1^\lambda )}\}_{i \in [M]}\).
-
Key Generation: To generate a key for a function f, sample an index at random \(i_f \mathop {\leftarrow }\limits ^{\$}[M]\) and generate a secret key using the \(i_f^\mathrm{th}\) master secret key \({\mathsf {OSK}}_{i_f} \mathop {\leftarrow }\limits ^{\$}\mathsf{OFE.KeyGen}({\mathsf {OMSK}}_{i_f}, f)\). Since there are at most a polynomial number of secret keys ever generated, the probability that every \(\mathbf{OFE}\) instance is used to generate at most one secret key is overwhelming.
-
Encryption: To encrypt any input x, simply encrypt the input x under all master public keys, \(\{{\mathsf{OCT}_i \mathop {\leftarrow }\limits ^{\$}\mathsf{OFE.Enc}({\mathsf {OMPK}}_i, x)}\}_{i \in [M]}\). Given the set of ciphertexts, one can compute the output f(x) of any function f for which a secret key \({\mathsf {OSK}}_{i_f}\) has been generated, by decrypting the appropriated ciphertext \(\mathsf{OCT}_{i_f}\) using the secret key \({\mathsf {OSK}}_{i_f}\).
Of course, the only problem with this FE scheme is that its setup and encryption algorithms run in super-polynomial time. To address this, we follow the previously adopted idea (e.g. [17, 25]) of using IO to “compress” these super-polynomially many \(\mathbf{OFE}\) instances into “polynomial size”. More precisely, instead of having the setup algorithm publish all M master public keys, let it generate an obfuscated circuit that on input \(i \in [M]\) outputs the \(i^\mathrm{th}\) master public key. Similarly, instead of having the encryption algorithm publish M ciphertexts, let it generate an obfuscated circuit that on input \(i \in [M]\) outputs the \(i^\mathrm{th}\) ciphertext under the \(i^\mathrm{th}\) master public key. Since the inputs to the obfuscated circuits are indexes from the range [M], which could be represented in \({\mathrm {i}\ell }\) bits, it suffices to use \({\mathrm {i}\ell }\)-bit-input IO. Furthermore, for “compression” to the possible, all M master public and secret keys, as well as all M ciphertexts, need to be sampled using pseudo-randomness generated by puncturable PRFs. The resulting obfuscated circuits have polynomial size, since generating individual master public keys and ciphertexts using pseudorandomness is efficient, and hence the new FE scheme becomes efficient. Finally, the security of the new FE scheme follows from the common “one-input-at-a-time” argument, which incurs a \(2^{-|i|} = 2^{-{\mathrm {i}\ell }}\) security loss. We formally describe the collusion-resistant FE scheme \(\mathbf{CRFE}\) for \(\mathcal{C} \) in Fig. 4.
We postpone the analysis of correctness, efficiency, and security of the \(\mathbf{CRFE}\) scheme to the full version [55].
Notes
- 1.
The notion could be block-wise to the cases where predicates are drawn by a distribution, and possibly differ from each output bit. We are going to dispense with such extensions, which are straightforward but easily lead to notational overhead.
References
Allen, S.R., O’Donnell, R., Witmer, D.: How to refute a random CSP. In: 56th FOCS, Berkeley, CA, USA, pp. 689–708, 17–20 October 2015
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Achieving compactness generically: indistinguishability obfuscation from non-compact functional encryption. IACR Cryptology ePrint Archive, vol. 2015, p. 730 (2015)
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. Cryptology ePrint Archive, Report 2016/1097 (2016). http://eprint.iacr.org/2016/1097
Ananth, P.V., Gupta, D., Ishai, Y., Sahai, A.: Optimizing obfuscation: avoiding Barrington’s theorem. In: ACM CCS 2014, Scottsdale, AZ, USA, pp. 646–658, 3–7 November 2014
Apon, D., Döttling, N., Garg, S., Mukherjee, P.: Cryptanalysis of indistinguishability obfuscations of circuits over GGH13. In: ICALP 2017. LNCS, vol. 80. Springer, Heidelberg (2017)
Applebaum, B.: Pseudorandom generators with long stretch and low locality from random local one-way functions. In: 44th ACM STOC, New York, NY, USA, pp. 805–816, 19–22 May 2012
Applebaum, B.: The cryptographic hardness of random local functions – survey. Cryptology ePrint Archive, Report 2015/165 (2015). http://eprint.iacr.org/2015/165
Applebaum, B., Bogdanov, A., Rosen, A.: A dichotomy for local small-bias generators. J. Cryptol. 29, 577–596 (2016)
Applebaum, B., Brakerski, Z.: Obfuscating circuits via composite-order graded encoding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 528–556. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_21
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in NC\(^{\text{0}}\). In: FOCS, pp. 166–175 (2004)
Applebaum, B., Lovett, S.: Algebraic attacks against random local functions and their countermeasures. In: 48th ACM STOC, Cambridge, MA, USA, pp. 1087–1100, 18–21 June 2016
Applebaum, B., Raykov, P.: Fast pseudorandom functions based on expander graphs. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 27–56. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53641-4_2
Barak, B., Brakerski, Z., Komargodski, I., Kothari, P.K.: Limits on low-degree pseudorandom generators (or: sum-of-squares meets program obfuscation). Cryptology ePrint Archive, Report 2017/312 (2017). http://eprint.iacr.org/2017/312
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_13
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Bitansky, N., Garg, S., Lin, H., Pass, R., Telang, S.: Succinct randomized encodings and their applications. In: Proceedings of 47th Annual ACM on Symposium on Theory of Computing, STOC 2015, 14–17 June 2015, Portland, OR, USA, pp. 439–448 (2015)
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_15
Bitansky, N., Paneth, O., Rosen, A.: On the cryptographic hardness of finding a nash equilibrium. In: Guruswami [49], pp. 1480–1498 (2015)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, 17–20 October 2015, Berkeley, CA, USA, pp. 171–190 (2015)
Bogdanov, A., Qiao, Y.: On the security of Goldreich’s one-way function. Comput. Complex. 21(1), 83–127 (2012)
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). doi:10.1007/11761679_34
Boneh, D., Silverberg, A.: Applications of multilinear forms to cryptography. Contemp. Math. 324, 71–90 (2002)
Brakerski, Z., Rothblum, G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 1–25. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_1
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_19
Caro, A., Iovino, V., Jain, A., O’Neill, A., Paneth, O., Persiano, G.: On the achievability of simulation-based security for functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 519–535. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_29
Chen, Y., Gentry, C., Halevi, S.: Cryptanalyses of candidate branching program obfuscators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 278–307. Springer, Cham (2017). doi:10.1007/978-3-319-56617-7_10
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_1
Chor, B., Fiat, A., Naor, M.: Tracing traitors. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 257–270. Springer, Heidelberg (1994). doi:10.1007/3-540-48658-5_25
Cook, J., Etesami, O., Miller, R., Trevisan, L.: Goldreich’s one-way function candidate and myopic backtracking algorithms. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 521–538. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_31
Coron, J.-S., et al.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_12
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_26
Coron, J.-S., Lepoint, T., Tibouchi, M.: New multilinear maps over the integers. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 267–286. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_13
Cryan, M., Miltersen, P.B.: On pseudorandom generators in NC0. In: Sgall, J., Pultr, A., Kolman, P. (eds.) MFCS 2001. LNCS, vol. 2136, pp. 272–284. Springer, Heidelberg (2001). doi:10.1007/3-540-44683-4_24
Dodis, Y., Impagliazzo, R., Jaiswal, R., Kabanets, V.: Security amplification for Interactive cryptographic primitives. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 128–145. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_9
Döttling, N., Garg, S., Gupta, D., Miao, P., Mukherjee, P.: Obfuscation from low noise multilinear maps. Cryptology ePrint Archive, Report 2016/599 (2016). http://eprint.iacr.org/2016/599
Dwork, C., Naor, M., Reingold, O., Rothblum, G.N., Vadhan, S.P.: On the complexity of differentially private data release: efficient algorithms and hardness results. In: 41st ACM STOC, Bethesda, MD, USA, pp. 381–390, 31 May–2 June 2009
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2013, 26–29 October 2013, Berkeley, CA, USA, pp. 40–49 (2013)
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_18
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_10
Garg, S., Pandey, O., Srinivasan, A.: Revisiting the cryptographic hardness of finding a nash equilibrium. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 579–604. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_20
Garg, S., Pandey, O., Srinivasan, A., Zhandry, M.: Breaking the sub-exponential barrier in obfustopia. Cryptology ePrint Archive, Report 2016/102 (2016). http://eprint.iacr.org/2016/102
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_20
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: Guruswami [49], pp. 151–170 (2015)
Goldreich, O.: Candidate one-way functions based on expander graphs. In: Electronic Colloquium on Computational Complexity (ECCC), vol. 7, no. 90 (2000)
Goldreich, O.: Foundations of Cryptography – Basic Tools. Cambridge University Press, Cambridge (2001)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Guruswami, V. (ed.) IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, Berkeley, CA, USA, 17–20 October 2015. IEEE Computer Society (2015)
Komargodski, I., Segev, G.: From minicrypt to obfustopia via private-key functional encryption. Cryptology ePrint Archive, Report 2017/080 (2017). http://eprint.iacr.org/2017/080
Langlois, A., Stehlé, D., Steinfeld, R.: GGHLite: more efficient multilinear maps from ideal lattices. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 239–256. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_14
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_2
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: CRYPTO 2017. LNCS. Springer, Heidelberg (2017)
Lin, H., Pass, R., Seth, K., Telang, S.: Output-compressing randomized encodings and applications. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 96–124. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_5
Lin, H., Tessaro, S.: Indistinguishability obfuscation from trilinear maps and block-wise local PRGs. Cryptology ePrint Archive, Report 2017/250 (2017). http://eprint.iacr.org/2017/250
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: IEEE 57th Annual Symposium on Foundations of Computer Science, FOCS 2016, New Brunswick, NJ, USA, 9–11 October 2016
Lombardi, A., Vaikuntanathan, V.: On the non-existence of blockwise 2-local PRGs with applications to indistinguishability obfuscation. Cryptology ePrint Archive, Report 2017/301 (2017). http://eprint.iacr.org/2017/301
Maurer, U., Tessaro, S.: A hardcore lemma for computational indistinguishability: security amplification for arbitrarily weak PRGs with optimal stretch. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 237–254. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11799-2_15
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_22
Mossel, E., Shpilka, A., Trevisan, L.: On e-biased generators in NC0. In: 44th FOCS, Cambridge, MA, USA, pp. 136–145, 11–14 October 2003
O’Donnell, R., Witmer, D.: Goldreich’s PRG: evidence for near-optimal polynomial stretch. In: IEEE 29th Conference on Computational Complexity, CCC 2014, 11–13 June 2014, Vancouver, BC, Canada, pp. 1–12 (2014)
Parno, B., Raykova, M., Vaikuntanathan, V.: How to delegate and verify in public: verifiable computation from attribute-based encryption. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 422–439. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28914-9_24
Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation from semantically-secure multilinear encodings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 500–517. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_28
Ullman, J.: Answering \(n_{2+o(1)}\) counting queries with differential privacy is hard. In: 45th ACM STOC, Palo Alto, CA, USA, pp. 361–370, 1–4 June 2013
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_15
Acknowledgements
The authors thank Benny Applebaum and Vinod Vaikuntanathan for many helpful discussions and insights.
Huijia Lin was supported in part by NSF grants CNS-1528178, CNS-1514526, and CNS-1652849 (CAREER). Stefano Tessaro was supported in part by NSF grants CNS-1423566, CNS-1528178, CNS-1553758 (CAREER), and IIS-152804.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Lin, H., Tessaro, S. (2017). Indistinguishability Obfuscation from Trilinear Maps and Block-Wise Local PRGs. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)





 , then we can construct general-purpose IO from L-linear maps.
, then we can construct general-purpose IO from L-linear maps.
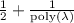 , albeit for predictors in quasi-polynomial time). Though such PRGs are not strong enough for constructing IO, it suffices for constructing FE from L-linear maps; see the next section.
, albeit for predictors in quasi-polynomial time). Though such PRGs are not strong enough for constructing IO, it suffices for constructing FE from L-linear maps; see the next section.