Abstract
Photoacoustic (PA) imaging has been gaining attention as a new imaging modality that can non-invasively visualize blood vessels inside biological tissues. In the process of imaging large body parts through multi-scan fusion, alignment turns out to be an important issue, since body motion degrades image quality. In this paper, we carefully examine the characteristics of PA images and propose a novel registration method that achieves better alignment while effectively decomposing the shot volumes into low-rank foreground (blood vessels), dense background (noise), and sparse complement (corruption) components on the basis of the PA characteristics. The results of experiments using a challenging real data-set demonstrate the efficacy of the proposed method, which significantly improved image quality, and had the best alignment accuracy among the state-of-the-art methods tested.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Photoacoustic (PA) imaging is a promising new technology for early clinical diagnosis of cancer, tumor angiogenesis, and many other diseases [1]. PA takes advantage of the thermoacoustic effect; that is, objects (i.e., blood vessels) absorb short-pulsed near-infrared irradiation and emit ultrasonic waves thereafter. 3D structures of objects can be reconstructed by sensing the thermoacoustic waves [2]. This technique can non-invasively visualize blood vessels in vivo with high spatial resolution without any contrast media. In order for PA imaging to capture entire portions of the human body, multi-scan and registration systems [3] have been developed that separately scan local areas of the sample and merge them. A single-shot volume reconstructed by PA technology usually suffers from severe noise caused by sound and light scattering and sensor layout limitations (Fig. 1). The goal of this study is to generate high-quality 3D volumes from these noisy shot volumes, in which vessels become clearly visible.
To reduce such noise, image averaging techniques have often been used, where the average of the random noise in the background becomes a small constant, and the linearly correlated foreground becomes apparent. Image averaging is effective as long as the sample is static or the size of the target is much larger than the motion. However, in the case of PA images reconstructed by merging shot-volumes of local scans, the patient often moves during scanning, and this assumption rarely holds true. It should be easy to imagine that even small motions adversely affect the image quality, considering the fact that blood vessels are thin (0.5 mm). What is required, therefore, is an accurate alignment of multiple shot volumes that can cope with such body motion.
A low-rank based alignment framework has a potential to address aligning such challenging data that contain severe dense noise and small foreground area. In the low-rank based alignment framework, an observation matrix D is first generated from given multiple images, where the i-th row indicates the i-th vectorized image. If we successfully make images well-aligned and eliminate the differences among aligned images, this results in making the data matrix low-rank. The low-rank based alignment framework achieves this by searching for the transform function \(\tau \) and the difference component \(\alpha \) that convert D into a low-rank component as \(D\circ \tau -\alpha \). Since this optimization problem is basically ill-posed, it is usually required to introduce some assumptions for the difference components in the optimization.
Contribution: The main contribution of this work is designing the difference component and the optimization method for aligning multiple PA volumes that contain small foreground, severe dense noise, and corrupted foregrounds based on the characteristics of PA images. To achieve this goal, we propose a coarse-to-fine approach to correctly extract the small blood vessel area without falling into a local minimum. For coarse-alignment, Frangi-filter [4] is first applied to the PA volumes to reduce the background noise and enhance blood vessels. A multi-scale pyramid scheme is then used for optimizing the transform function that converts the aligned data into low-rank. Given the initial estimate of transformation function at the previous step, we further align the data by decomposing it into a low-rank foreground (blood vessels), dense background (severe noise), and sparse complement components (complementary parts of the foreground) based on characteristics of PA imaging. A key novelty here is effective use of a statistical prior of PA imaging for optimization, in which the average of the dense noise background at each spatial voxel is forced to be a constant. Experimental results using real PA data demonstrate that the propose approach is effective for aligning and finding blood vessels without suffering from severe dense noise and corruption, and yields high quality 3D volumes with clear vascular structures.
Related works: Many registration methods have been proposed for aligning multiple images in medical imaging [5–7]. Since it is difficult to segment blood vessels in PA shot-volumes because of severe noise and corruption, modeling-and-alignment methods [8] do not work well. Blood vessels observed in PA images tend to be sparsely distributed throughout a dense noisy background, and it is difficult to align such images by using these alignment methods that rely on image similarities computed from both foreground and background. To reduce the influence of image corruption, a robust alignment method (RASL) [9] has been proposed, and successfully applied to registration problems in medical imaging [10, 11]. RASL optimizes an image transformation while separating an image into a low-rank foreground and sparse error components, where they assume that the differences among aligned images are caused from sparse corruptions. Compared with the images handled by RASL, the area of blood vessels is small with severe noise in vascular images in PA imaging. The error component becomes no longer sparse in this case, and RASL does not work properly; the low-rank component is optimized by adjusting the error component instead of properly transforming the data. To relax this sparse assumption, new decomposition methods have been proposed for recovering low-rank, sparse, and Gaussian noise components from the input data [12]. These methods assume that the foreground area is not small and the magnitude of the Gaussian noise is small. Thus, they are not suitable for PA images that contain heavy dense noise and the small area of blood vessels. In addition, these decomposition methods consider images that are well aligned and thus alignment problems were not considered before. In this paper, we propose a unified framework which simultaneously estimates the transformation and three-component decomposition.
2 Characteristics of PA Image
Figure 1 shows examples of x-y MIPs of PA shot volumes obtained from the same position, where the intensity range of each volume is −1 to 1. Let us first define the three components in these images. The first component is the foreground that represents blood vessels with high intensities. The second component is the background that represents noise that is in parts other than the blood vessels. The third is the complement that represents parts where foreground corruption occurs; in PA images, parts of vessels are corrupted by inhomogeneous light irradiation in vivo. For instance, in Fig. 1, the blood vessel in the red circle of the right image is not visible, while the corresponding vessel is visible in the left image. This missing portion corresponds to the complement. By examining real PA data, we found a statistical prior wherein the intensity distribution of the background is close to a Gaussian distribution with a large standard deviation (0.249), and the distribution of the averages of the aligned background at each spatial voxel is close to a Gaussian distribution with a constant mean (−0.001) and a small standard deviation (0.081), as shown in Fig. 2. By contrast, the average intensity in the vessels has a high value since the vessels are linearly correlated among well-aligned shot volumes. Note that this statistical prior is often true not only in our PA imaging system but also in many applications since the traditional image averaging techniques, which are widely used for reducing noise, use this prior implicitly. We effectively use these characteristics for simultaneously estimating the transform and the three-component decomposition.
3 Coarse-to-Fine Low-Rank-Based Alignment
In the case of PA images that contain dense noise and small foreground area, the current low-rank based methods tend to optimize the low-rank component by adjusting the difference component. To avoid this problem, we take a coarse-to-fine approach. For coarse alignment, we use a multi-scale pyramid scheme for optimizing the transformation using the noise-reduced data, without considering any difference components. This helps to find a proper transformation without falling into a such local minimum. To further refine the alignment, we optimize the transform function while decomposing the properly aligned data into three components, i.e., the low-rank foreground, dense noisy background, and sparse complement on the basis of the characteristics of PA imaging. The details of this procedure are described in the following sections.
3.1 Coarse Alignment by Low-Rank Minimization with Pyramid
Suppose we are given m volume data \(I_1^0,...,I_m^0 \in \mathcal {R}^{n=w \times h \times d}\) of a certain specimen, which might have moved during scanning. This step roughly aligns these volumes by using preprocessed foreground data, in which the background noise is reduced by enhancing the blood vessels with a Frangi filter [4], which uses the eigenvectors of the Hessian to compute the likeliness of tubular structures. The filtered data still include false positives in the background, and the vessels are corrupted. Yet, it is good enough for coarse alignment.
To find a proper transform function instead of adjusting the difference components, we only optimize the transform function \(\tau \) to convert the preprocessed data matrix D into a low-rank component, \(A=D\circ \tau \), without considering any difference components. \(D \in \mathcal {R}^{m \times n}\) is the observation data matrix, and n is the number of voxels in each shot volume. \(\tau \) denotes a certain transformation, such as the affine transform. According to [9], when the change in \(\tau \) is small, \(D\circ \tau =A\) can be approximated by linearizing about the current estimate of \(\tau \), and the rank minimization is relaxed into minimizing the nuclear norm \(\Vert A\Vert _*\).
where \(\varDelta \tau \) denotes the variance of \(\tau \) in each iteration, \(J_i \doteq \frac{\delta }{\delta \zeta }(I_i\circ \zeta )\mid _{\zeta =\tau _i} \in \mathcal {R}^{n \times p}\) is the Jacobian of the i-th data, and \(\epsilon _i\) denotes the standard basis for \(\mathcal {R}^m\). Equation (1) can be efficiently solved using augmented Lagrange multiplier (ALM) algorithm [13], in a similar manner to [9]. This optimization is applied with a multi-scale pyramid scheme, which successively aligns data with finer Gaussian pyramids.
3.2 Fine Alignment via Three Components Decomposition
The aforementioned preprocessed data may include false-positive and false-negative noise, which lead to small alignment errors because the optimization in the previous step does not consider noise. We further refine the results from the coarse alignment by using original volumes considering noise. To handle images that contains dense noise, we introduce a dense-noise term in the alignment, wherein our method aligns the data while decomposing it into a low-rank foreground A, dense noisy background B, and sparse complement C, by using characteristics of the dense noisy background. Specifically, the distribution of the averages of the aligned dense noise at the same positions becomes a Gaussian distribution with a constant mean and small variance. We introduce this statistical prior into the formulation of the decomposition problem as follows:
where A and B denote the aligned foreground and background data matrix respectively, and C denotes the complement matrix. The sum of A, B, and C equals the aligned data \(D\circ \tau \). \(\varvec{a}\) denotes a \(1 \times m\) vector whose elements are all 1. \(\varvec{b}\) denotes a \(1 \times n\) vector whose elements are all constant value b that is the mean of the Gaussian. We set b to 0 on the basis of our observations of real PA data. The term \(\lambda _1\Vert \varvec{a}B-\varvec{b} \Vert ^2\) penalizes the optimization function when the mean of the aligned backgrounds in the same positions stays away from the mean of the Gaussian. We set the weighting parameters \(\lambda _1\) as \(\kappa _1/(m \times d \times \sqrt{n})\), and \(\lambda _2\) as \(\kappa _2/\sqrt{n}\), where \(\kappa _1=1\), \(\kappa _2=3\) in all our experiments.

Algorithm 1 shows the complete procedure. At each iteration of the outer loop, we need to solve a linearized optimization problem by linearizing the transformation at the current estimate of \(\tau \). This optimization problem is convex and thus solvable via ALM. Specifically, the optimization problem to minimize the augmented Lagrange function is as follows:
where \(Y \in \mathcal {R}^{m \times n}\) is a Lagrange multiplier matrix, \(\mu \) is a positive scalar, and \(\langle \cdot , \cdot \rangle \) denotes the matrix inner product. This problem is iteratively minimized as follows:
where \(\mathrm{svd}(\cdot )\) denotes the singular value decomposition operator, and shrinkage operator \(S_{\beta }[\cdot ]=sign(x)\cdot \max {\{ \mid x \mid - \beta , 0 \}}\) is for the singular value thresholding algorithm to optimize the nuclear norm. \(\mu _k\) is a monotonically increasing positive sequence. We set \(\mu _k=(1.25)^{k}/\Vert D \Vert \), according to [9].
4 Experimental Evaluation
First, we evaluated the robustness and accuracy of the proposed method on shot volumes of real 3D PA data. We created five ground-truth data-sets by fixing the body during the scanning so that, there would be no pixel-level misalignment. We synthetically added different levels of position gaps to the shot volumes of the ground-truth, wherein the original volumes were randomly displaced with a uniformly distributed pseudorandom number \([-d \, d]\) of voxels along each axis (x, y, z). The voxel size was [0.25 0.25 0.25] mm, and the thickness of a vessel was 0.5 to 2 mm. We set the misalignment level d from 1 to 10. In total, we generated \(10\times 5\) data-set, in which each data-set included 21 to 36 shot volumes.
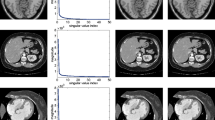
For comparison, we compared our results with those obtained by the following state-of-the-art methods: B-spline free-form deformation(B-FFD) [6] which optimizes the control points while minimizing the similarity function; spectral log demon registration [7], which finds the pointwise correspondence between images with simple nearest-neighbor searches (called Log-demon); and RASL [9] with the pyramid scheme. These methods were applied to vessel-enhanced data for a fair comparison. Figure 4 shows the results for each method, where a small value on the vertical axis indicates that the method successfully aligned the data-set. It shows that the proposed method works well until misalignment level 7; it should be good enough for dealing with real body motions. The other methods could not align the data so well, even with very low misalignment levels. Figure 3 shows examples of the x-y MIPs of the average images of the aligned results obtained by each method at misalignment level 6. The computational time of the proposed method is comparable with that of the other methods.
Figure 3(a) shows the ground-truth, in which the vessels are clearly visible. The synthetic misalignment makes the image quality significantly worse (Fig. 3(b)). The result of the proposed method (Fig. 3(f)) shows clear vessels, and the image is similar to the ground-truth. This indicates that the proposed method properly aligned the shot volumes. By contrast, vessels are still hard to identify in the results of the other methods (Figs. 3(c), (d), and (e)).
Now let us examine how well the proposed method decomposes real PA data into three components. For example, Fig. 5 shows the results at misalign level 6. The background noise is correctly decomposed in B, all vessels clearly appear in the low-rank component A, and the sparse corruptions of the vessels appear in the complement component C. This results show that the proposed method successfully decomposed the original noisy and misaligned PA data into three meaningful components.
Next, let us examine the robustness of the proposed method against real body motion. To get the real data, a hand was scanned using a wide-field range PA imaging system that scans local areas multiple times with a spiral pattern, and real body motions were added during scanning. The total number of shot volumes was 2048, and the total scanning time was about 2 min. Successive local shot volumes were overlaid over 85 %. The entire data was \(512\times 512\times 100\). Since each shot volume is a peace of local-area data, we first generated the data-sets of the local areas (\(168\times 168\times 100\)), which included 16 to 59 shot volumes. Next, we aligned the shot volumes in each data-set, then stitched together the aligned average volumes in order to generate the entire data. For comparison, an image averaging technique without alignment was applied to the data.
Figures 6(a), (c), and (d) show the average data without alignment. In the images, the contrast of the vessels is low, and some vessels are blurry because of body motion. Figures 6(b), (e), and (f) show the registration results from the proposed method. Here, the vessels are obviously clearer than in the original image and some vessels that are hard to see in the averages data without alignment become visible. Here, we should note that the vessels that appear thrice in the red box in Fig. 6(b), where two veins run side-by-side with artery, are not blurry. These image features were confirmed by a doctor of anatomy. The results show that our method significantly improved the image quality of PA imaging.
5 Conclusions
We examined the characteristics of PA images and proposed a registration method for PA imaging to generate high-quality 3D volumes in which vessels become clearly visible. By introducing the statistical prior, in which the mean of the values in the same position of the aligned background data tends to be a constant, our alignment method is capable of handling challenging PA data with strong noise and large misalignments. The experimental results on real data-sets demonstrate the effectiveness of our method; it significantly improved image quality and achieved the best alignment accuracy in the comparison. Currently, our method can only handle one global domain transformation per image, such as affine transformation. We will address the deformable transformation problems in future work. Besides PA imaging, the proposed method has the potential to be applied to many other sorts of medical imaging; these will be explored in our future work.
References
Kitai, T., Torii, M., Sugie, T., et al.: Photoacoustic mammography: initial clinical results. Breast Cancer 21, 146–153 (2014)
Li, C., Wang, L.V.: Photoacoustic tomography and sensing in biomedicine. Phys. Med. Biol. 54(19), 5997 (2009)
Kruger, R.A., Kuzmiak, C.M., Lam, R.B., et al.: Dedicated 3D photoacoustic breast imaging. Med. Phys. 40(11), 1–8 (2013). 113301
Frangi, A.F., Niessen, W.J., Vincken, K.L., Viergever, M.A.: Multiscale vessel enhancement filtering. In: Wells, W.M., Colchester, A.C.F., Delp, S.L. (eds.) MICCAI 1998. LNCS, vol. 1496, pp. 130–137. Springer, Heidelberg (1998)
Sotiras, A., Davatzikos, C., Paragios, N.: Deformable medical image registration: a survey. IEEE Trans. Med. Imaging 32, 1153–1190 (2013)
Rueckert, D., Sonoda, L.I., Hayes, C., Hill, D.L.G., Leach, M.O., Hawkes, D.J.: Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans. Med. Imaging 8, 712–721 (1999)
Lombaert, H., Grady, L., Pennec, X., et al.: Spectral log-demons: diffeomorphic image registration with very large deformations. IJCV 107, 254–271 (2014)
Aylward, S.R., Jomier, J., Weeks, S., Bullitt, E.: Registration and analysis of vascular images. IJCV 55(2/3), 123–138 (2003)
Peng, Y., Ganesh, A., Wright, J., et al.: RASL: robust alignment by sparse and low-rank decomposition for linearly correlated images. IEEE Trans. PAMI 34(11), 2233–2246 (2012)
Liu, X., Niethammer, M., Kwitt, R., McCormick, M., Aylward, S.: Low-rank to the rescue – atlas-based analyses in the presence of pathologies. In: Golland, P., Hata, N., Barillot, C., Hornegger, J., Howe, R. (eds.) MICCAI 2014, Part III. LNCS, vol. 8675, pp. 97–104. Springer, Heidelberg (2014)
Baghaie, A., D’souza, R.M., Yu, Z.: Sparse and low rank decomposition based batch image alignment for speckle reduction of retinal oct images, ISBI, pp. 226–230 (2015)
Tao, M., Yuan, X.: Recovering low-rank and sparse components of matrices from incomplete and noisy observations. SIAM J. Optim. 21(1), 57–81 (2011)
Lin, Z., Chen, M., Wu, L., Ma, Y.: The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices, UIUC Technical report UILU-ENG-09-2215 (2009)
Acknowledgments
This work was funded by ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Bise, R., Zheng, Y., Sato, I., Toi, M. (2016). Vascular Registration in Photoacoustic Imaging by Low-Rank Alignment via Foreground, Background and Complement Decomposition. In: Ourselin, S., Joskowicz, L., Sabuncu, M.R., Unal, G., Wells, W. (eds) Medical Image Computing and Computer-Assisted Intervention - MICCAI 2016. MICCAI 2016. Lecture Notes in Computer Science(), vol 9902. Springer, Cham. https://doi.org/10.1007/978-3-319-46726-9_38
Download citation
DOI: https://doi.org/10.1007/978-3-319-46726-9_38
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46725-2
Online ISBN: 978-3-319-46726-9
eBook Packages: Computer ScienceComputer Science (R0)