Abstract
We give an overview of completeness and incompleteness results within proof-theoretic semantics. Completeness of intuitionistic first-order logic for certain notions of validity in proof-theoretic semantics has been conjectured by Prawitz. For the kind of semantics proposed by him, this conjecture is still undecided. For certain variants of proof-theoretic semantics the completeness question is settled, including a positive result for classical logic. For intuitionistic logic there are positive as well as negative completeness results, depending on which variant of semantics is considered. Further results have been obtained for certain fragments of first-order languages.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
In proof-theoretic semantics (see Schroeder-Heister [34]; cf. Wansing [36]) for logical constants several related notions of validity have been proposed. We mention Kreisel (cf. Gabbay [6]), Prawitz [18–22], Dummett [3] and Sandqvist [26]. Overviews and discussions of such proof-theoretic notions of validity can be found in Schroeder-Heister [31] and Read [24].
What these notions of validity have in common is that the validity of an atomic formula, or atom, is defined in terms of the derivability of that atom in a given system of atomic rules, that is, of rules which can only contain atoms. Let \(a, b, \ldots , a_1, a_2, \ldots \) be atoms. Then

is an example of a system S of atomic rules (the first two having the form of atomic axioms), in which \(c\) is derivable by

and therefore valid with respect to S. Atomic rules are also called boundary rules (cf. Dummett [3]) or production rules. Atomic systems S are also called bases; they can have the form of Post systems, definite Horn clause logic programs etc.
The validity of complex formulas \(A,B,\ldots ,A_1,A_2,\ldots \) (constructed as usual from atoms with logical constants) with respect to an atomic system S can then be defined inductively by giving semantic clauses for the logical constants. The validity of implications \(A \mathbin {\rightarrow }B\) with respect to an atomic system S is usually defined by taking into account arbitrary atomic extensions \(S'\) of S. Let \(\vDash _S\) stand for ‘valid with respect to S’; then the semantic clause for implication has the form

where in the definiens all extensions \(S'\) of S have to be considered. This ensures that implications \(A \mathbin {\rightarrow }B\) cannot become valid with respect to S just because some atom on which the validity of A depends is not derivable in S. Considering extensions thus guarantees monotonicity for validity with respect to S.
It was conjectured by Prawitz [19, 22] that intuitionistic first-order logic is complete with respect to certain notions of validity for inference rules. This conjecture is still undecided. There are, however, several negative as well as positive results about completeness for certain plausible variants of this notion of validity, formulated not for inference rules but for formulas. One kind of variants considers only certain fragments of first-order languages. Other variants are based on different kinds of atomic systems which allow for atomic rules of a more general form than production rules only. Further variants are given through different treatments of negation or absurdity, and by different notions of what an extension of an atomic system is.
In the following, we present several of these variants together with their respective completeness or incompleteness results.
2 Prawitz’s Conjecture
Prawitz has given several definitions of proof-theoretic validity (see Prawitz [18–22]), and he has conjectured completeness of intuitionistic first-order logic for some of them. We here present a formulation for the fragment \(\{\mathbin {\rightarrow },\mathbin {\vee },\mathbin {\wedge }\}\) as given by Schroeder-Heister [33], which captures the main ideas underlying Prawitz’s definitions. The restriction to the fragment \(\{\mathbin {\rightarrow },\mathbin {\vee },\mathbin {\wedge }\}\) is only made to keep the exposition simple; the definitions can be extended to the first-order case in a more or less straightforward way.
We first define some preliminary notions:
Definition 1
A (first-level) atomic system S is a (possibly empty) set of atomic rules of the form

where the \(a_i\) and \(b\) are atoms. The set of premises \(\{a_1,\ldots ,a_n\}\) in a rule can be empty; in this case the rule is an atomic axiom and of level 0. First-level atomic systems that do not contain atomic axioms are called proper first-level atomic systems.
Definition 2
An arbitrary inference rule has the form

The notation is the same as the one used for the logical rules of natural deduction (see Gentzen [7]). That is, rules of this form allow one to conclude C from the set of premises \(\{B_1,\ldots ,B_n\}\) and to discharge any of the assumptions \(A_{ij}\), written in square brackets \([\;]\), on which premises \(B_i\) might depend.
Definition 3
A derivation structure is a derivation tree composed of arbitrary inference rules. (Derivation structures correspond to what Prawitz calls ‘(argument or proof) schemata’ or ‘(argument or proof) skeletons’.)
The notions open/closed and canonical/non-canonical as used for derivations in natural deduction are carried over to derivation structures. That is, a derivation structure with no open assumptions is closed, otherwise open. It is canonical, if it ends with one of the introduction rules

It is non-canonical, if it does not.
Definition 4
A reduction procedure transforms a given derivation structure into another derivation structure.
A justification J of an arbitrary inference rule R, excluding introduction rules, is a set of reduction procedures which transform derivation structures \(\mathscr {D}\) ending with an application of R into another derivation structure with the same end formula as \(\mathscr {D}\) and having no more open assumptions than \(\mathscr {D}\) (see Prawitz [22]).
Now validity with respect to atomic systems S and justifications J (short: (S, J)-validity) can be defined as follows:
Definition 5
-
(i)
Every closed derivation in an atomic system S is (S, J)-valid (for every justification J).
-
(ii)
A closed canonical derivation structure is (S, J)-valid, if all its immediate substructures are (S, J)-valid.
-
(iii)
A closed non-canonical derivation structure is (S, J)-valid, if it reduces, with respect to J, to a canonical derivation structure, which is (S, J)-valid.
-
(iv)
An open derivation structure
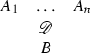
where all open assumptions of \(\mathscr {D}\) are in \(\{A_1,\ldots ,A_n\}\), is (S, J)-valid, if for every extension \(S'\) of S and every extension \(J'\) of J, and for every list of closed derivation structures
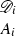 (for \(1 \le i \le n \)) which are \((S',J')\)-valid, the derivation structure
(for \(1 \le i \le n \)) which are \((S',J')\)-valid, the derivation structure 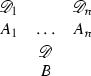
is \((S',J')\)-valid.
Extensions \(S'\) of S and \(J'\) of J are here understood in the set-theoretic sense as \(S' \supseteq S\) and \(J' \supseteq J\). Taking extensions into account ensures that (S, J)-validity of derivation structures is monotone with respect to extensions of S and J. This is an important constraint, if atomic systems S and justifications J are understood to represent, for example, states of knowledge.
In [18, Appendix A.1], Prawitz gave a definition of ‘valid derivation’, which makes use of extensions of atomic systems. However, in definitions of the more general notion of ‘valid derivation structure’ (i.e., of ‘valid argument schema’ or ‘valid argument’) he uses (consistent) extensions of justifications, but no extensions of atomic systems. Completeness of minimal logic for one such notion was conjectured in Prawitz [19]. A completeness conjecture for intuitionistic logic and a similar notion of validity is made in Prawitz [22]:
Conjecture 1
(Prawitz [22, p. 274]) Every valid inference rule that can be formulated within first-order languages holds as a derivable inference rule within the system of natural deduction for intuitionistic logic.
Prawitz’s motivation for considering proof-theoretic notions of validity is to give an answer to the question of whether the elimination rules of Gentzen’s intuitionistic system of natural deduction are the strongest possible ones justifiable in terms of the introduction rules of that system. Gentzen’s idea that the introduction rules define the logical constants and that the elimination rules have to be justified on the basis of the introduction rules (see Gentzen [7]; cf. [1]) is reflected in the notion of validity by the fact that priority is given to canonical derivation structures, that is, to derivation structures ending with an introduction rule, to which non-canonical derivation structures have to be reduced. The (as yet unsettled) completeness conjecture implies a positive answer to that question.
In [22], Prawitz also gives a further modification of the notion of validity with respect to the role played by justifications. We will not discuss this modification here. Moreover, in what follows we will focus on proof-theoretic notions of validity for formulas instead of validity for derivation structures or inference rules. This approach has the advantage that justifications J (i.e., sets of reduction procedures for derivation structures) do not need to be considered at all. We here only mention that certain notions of validity for inference rules were given in Schroeder-Heister [28, 30], and that intuitionistic logic was claimed to be complete with respect to them there.
3 Failure of Completeness for Intuitionistic Logic
Our first example of a notion of validity for formulas is due to Kreisel [10]. We follow the expositions given by Gabbay in [5] and [6, Chap. 13], adjust the notation and speak of ‘Kreisel validity’.
Let \(\mathscr {A}\) be a fixed alphabet and S a Post system on \(\mathscr {A}\). If a word w over \(\mathscr {A}\) is derivable in S, we write \({}\vdash _S w\). Let h be any function which assigns words over \(\mathscr {A}\) to all variables \(x,y,x_1,x_2,\ldots \) and relation symbols R of a first-order language, and let  for all \(y \ne x\).
for all \(y \ne x\).
Definition 6
Kreisel S -validity (\(\vDash _S^h\)) and Kreisel validity (\(\vDash \)) are defined as follows:
-
(K1)
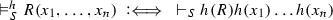 (where \(R(x_1,\ldots ,x_n)\) is an atom),
(where \(R(x_1,\ldots ,x_n)\) is an atom), -
(K2)
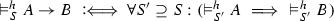 ,
, -
(K3)
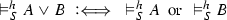 ,
, -
(K4)
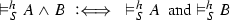 ,
, -
(K5)
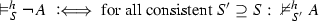 (where \(S'\) is consistent iff \({}\nvdash _{S'} w\) for some word w),
(where \(S'\) is consistent iff \({}\nvdash _{S'} w\) for some word w), -
(K6)
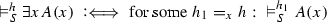 ,
, -
(K7)
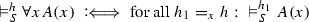 ,
, -
(K8)
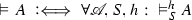 .
. -
(K9)
A is substitution-Kreisel-valid
 all substitution instances of A are Kreisel valid (where substitutions are uniform substitutions of formulas for atoms in A).
all substitution instances of A are Kreisel valid (where substitutions are uniform substitutions of formulas for atoms in A).
Note that clause (K5) for negation is restricted to consistent extensions, and that extensions \(S' \supseteq S\) are understood in the normal set-theoretic sense, that is, the Post system \(S'\) contains at least all the rules of the Post system S. Alternatively, extensions \(S'\) of S can be understood to mean that the implication \({}\vdash _S w \implies {}\vdash _{S'} w\) holds for all words w over \(\mathscr {A}\). In this latter case, Gabbay speaks of weak validity.
Intuitionistic first-order logic is neither complete for weak validity nor for Kreisel validity. Completeness already fails in the propositional case for both notions (we now consider weak validity and Kreisel validity restricted to the propositional fragment):
Theorem 1
(Gabbay [6, p. 224]) Intuitionistic propositional logic is not complete for weak validity. The formula \(((\lnot \lnot A \mathbin {\rightarrow }A) \mathbin {\rightarrow }(\lnot A \mathbin {\vee }\lnot \lnot A)) \mathbin {\rightarrow }(\lnot A \mathbin {\vee }\lnot \lnot A)\) is a counterexample.
Theorem 2
(Gabbay [6, p. 225]) Intuitionistic propositional logic is not complete for Kreisel validity. The set of Kreisel valid sentences is not closed under substitution. The formula \((a\mathbin {\rightarrow }(b\mathbin {\vee }c)) \mathbin {\rightarrow }((a\mathbin {\rightarrow }b) \mathbin {\vee }(a\mathbin {\rightarrow }c))\), for propositional atoms \(a,b,c\), is a counterexample.
Considering only the propositional fragment, completeness has been conjectured for substitution-Kreisel-validity:
Conjecture 2
(Gabbay [6, p. 226]) Intuitionistic propositional logic is complete for substitution-Kreisel-validity (restricted to the propositional fragment).
4 Goldfarb’s Account of Dummett’s Approach
Dummett [3, Chaps. 11–13] made an approach to proof-theoretic validity for inference rules (or arguments) which is similar to Prawitz’s (cf. Sect. 2). It is supposed to yield a justification of intuitionistic first-order logic. Goldfarb [8] (this volume) has given an analysis of the propositional part of Dummett’s approach, resulting in a notion of validity for formulas (instead of inference rules).
Goldfarb first gives a formulation for atomic systems of axioms only, that is, for sets of atoms. It is presumed that there are infinitely many atoms available and that only finite sets of atoms \(\alpha ,\beta \) are ever considered. We follow his notation in writing \(\alpha ,\beta \) for such sets but adjust it to ours otherwise:
Definition 7
-
(G1)
 ,
, -
(G2)
 ,
, -
(G3)
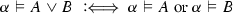 ,
, -
(G4)
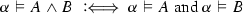 ,
, -
(G5)
There is no \(\alpha \) such that \(\alpha \vDash {\perp }\).
This notion of validity (\(\vDash \)) can be discarded right away, since it validates formulas which are not even derivable in classical logic (see Goldfarb [8]):
Lemma 1
-
(i)
Suppose A does not contain \({\perp }\). Then \(\alpha \vDash (A \mathbin {\rightarrow }{\perp }) \mathbin {\rightarrow }{\perp }\).
-
(ii)
Let \(a\) and \(b\) be two distinct atoms. Then \(\alpha \vDash (a\mathbin {\rightarrow }b) \mathbin {\rightarrow }b\).
Goldfarb then modifies this notion of validity by relativizing the relation \(\vDash \) to proper first-level atomic systems S (i.e., in Dummett’s terminology, to sets of boundary rules) as in Dummett’s approach. He points out that in order to avoid cases like Lemma 1 (i), atomic rules with conclusion \({\perp }\) have to be allowed as well. The modified notion can be given by rewriting clauses (G1)–(G5) with \(\vDash _S\) instead of \(\vDash \), together with the condition that sets \(\alpha ,\beta \) have now to be closed under the rules in S and do not contain \({\perp }\):
Definition 8
Let S be a proper first-level atomic system. Let the sets \(\alpha ,\beta \) be closed under the rules in S, and \({\perp }\notin \alpha ,\beta \).
- (G1\(^{\prime }\)):
-
 ,
, - (G2\(^{\prime }\)):
-
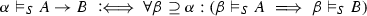 ,
, - (G3\(^{\prime }\)):
-
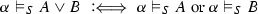 ,
, - (G4\(^{\prime }\)):
-
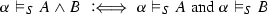 ,
, - (G5\(^{\prime }\)):
-
There is no \(\alpha \) such that \(\alpha \vDash _S {\perp }\).
According to Goldfarb, this notion of validity is a revision of Dummett’s approach in that it considers in principle all atomic systems S instead of only a fixed one.
For this revised notion of validity all valid formulas are classically valid. Completeness for intuitionistic logic does not hold (see Goldfarb [8]):
Lemma 2
-
(i)
Every valid formula is derivable in classical logic.
-
(ii)
The formula \((a\mathbin {\rightarrow }(B \mathbin {\vee }C)) \mathbin {\rightarrow }((a\mathbin {\rightarrow }B) \mathbin {\vee }(a\mathbin {\rightarrow }C))\) is valid for any atom \(a\) and any formulas B and C, but it is not intuitionistically derivable for all B, C.
The counterexamples to completeness given in Lemmas 1 and 2 are not schematic in the sense that all substitution instances of the valid formulas presented there are valid too. Goldfarb introduces the relation of schematic validity, which holds for a formula A if and only if all instances of A resulting from uniform substitutions of formulas for atoms in A are valid (cp. substitution-Kreisel-validity). He shows that the intuitionistically non-derivable formula \(\lnot A \mathbin {\vee }\lnot \lnot A\) is schematically valid for atomic systems which do only contain atoms (i.e., for atomic systems of level 0). In other words:
Theorem 3
(Goldfarb [8]) Intuitionistic logic is not complete for schematic validity for sets of atoms \(\alpha \) (i.e., for the notion of schematic validity based on validity (\(\vDash \)) according to Definition 7).
However, for the schematically understood revised notion of validity the following completeness result holds:
Theorem 4
(Goldfarb [8]) Intuitionistic propositional logic is complete for schematic validity based on the revised notion of validity (i.e., for the notion of schematic validity based on validity (\(\vDash _S\)) according to Definition 8).
We note that this completeness result depends on the restriction to consistent sets of atoms \(\alpha ,\beta \) in the sense that \({\perp }\notin \alpha ,\beta \). A restriction to consistent extensions is also made in Definition 6 of (substitution-) Kreisel validity, namely in clause (K5) for negation. If negation is understood as  , and \({\perp }\) is explained by
, and \({\perp }\) is explained by  , then
, then
Since \(\alpha ,\beta \) are consistent, this is equivalent to clause (K5), where \({\perp }\) is a word w such that \(\nvdash _{S'} w\). However, in the case of (substitution-) Kreisel validity this is the only clause where a restriction to consistent atomic systems (resp. Post systems) \(S,S'\) is made, whereas such a restriction applies in general in the case of (schematic) validity according to Definition 8. Assuming consistent extensions in general also in the case of Kreisel validity implies completeness for substitution-Kreisel-validity. That is, Conjecture 2 is decided positively in this case.
5 Proof-Theoretic Validity for Generalized Atomic Systems
We now consider atomic systems which are not restricted to first-level atomic rules but which can contain atomic rules that can also discharge assumptions of a certain kind. One can show that intuitionistic logic is not complete for a notion of proof-theoretic validity based on such generalized atomic systems (see [16]).
To motivate such a generalization one might argue that since the device of assumption discharge is available at the level of logical rules (e.g., in the rules of implication introduction and disjunction elimination of natural deduction), it should be available at the level of atomic rules, too. However, from the point of view of attempting a justification of a certain logic by giving a semantics based on atomic systems, such a generalization might be conceived as being counterproductive, as it introduces a feature of implication already at the level of atomic rules.
5.1 Generalized Atomic Systems
We generalize the notion of first-level atomic system to higher-level atomic systems by allowing for atomic rules that can discharge atomic assumptions (cf. [16]).
Definition 9
A second-level atomic system S is a (possibly empty) set of atomic rules of the form

where the \(a_i\) and \(b\) are atoms, and the \(\varGamma _i\) are finite sets of atoms. The sets \(\varGamma _i\) may be empty, in which case the rule is a first-level rule. The set of premises \(\{a_1,\ldots ,a_n\}\) can be empty as well; in this case the rule is an axiom.
Such a rule can be applied as follows: If the premises \(a_1,\ldots ,a_n\) have been derived in S from certain assumptions, then one may conclude \(b\), where, for each i, in the branch of the subderivation leading to \(a_i\) assumptions belonging to \(\varGamma _i\) may be discharged.
Second-level atomic systems are now further generalized to the higher-level case by allowing for atomic rules which can discharge not only atoms but atomic rules as assumptions (see Schroeder-Heister [29, 32] and Olkhovikov and Schroeder-Heister [15]; cf. [16]). We use the following linear notation for atomic higher-level rules:
Definition 10
-
(i)
Every atom \(a\) is a rule of level 0.
-
(ii)
If \(R_1,\ldots , R_n\) are rules (\(n \ge 1\)), whose maximal level is \(\ell \), and \(a\) is an atom, then \((R_1,\ldots ,R_n \mathbin {\rhd }a)\) is a rule of level \(\ell +1\).
Definition 11
A higher-level atomic system S is a (possibly empty) set of atomic rules of the form

(in linear notation: \((\varGamma _1 \mathbin {\rhd }a_1), \ldots , (\varGamma _n \mathbin {\rhd }a_n) \mathbin {\rhd }b\)), where the \(a_i\) and \(b\) are atoms, and the \(\varGamma _i\) are now finite sets \(\{R^i_1,\ldots ,R^i_k\}\) of rules, which may be empty. The set of premises \(\{a_1,\ldots ,a_n\}\) of such a rule can also be empty, in which case the rule is an axiom.
In the higher-level case atomic rules can be used as (dischargeable) assumptions, whereas in the second-level case only atoms could be used in that way. This difference requires a definition of the notion of derivation of an atom \(a\) from rules \(R_1,\ldots ,R_n\):
Definition 12
For a level-0 rule \(a\),

is a derivation of \(a\) from \(\{a\}\).
Now consider a level-\((\ell +1)\) rule \((\varGamma _1 \mathbin {\rhd }a_1), \ldots , (\varGamma _n \mathbin {\rhd }a_n) \mathbin {\rhd }b\). Suppose that for each i \((1 \le i \le n)\) a derivation

of \(a_i\) from \(\varSigma _i \cup \varGamma _i\) is given. Then

is a derivation of \(b\) from \(\varSigma _1 \cup \ldots \cup \varSigma _n \cup \{(\varGamma _1 \mathbin {\rhd }a_1), \ldots , (\varGamma _n \mathbin {\rhd }a_n) \mathbin {\rhd }b\}\).
An atom \(b\) is derivable from \(\varSigma \) in a higher-level atomic system S, symbolically \(\varSigma \vdash _S b\), if there is a derivation of \(b\) from \(\varSigma \cup S\).
As an example, consider the atomic system \(S =\{((b\mathbin {\rhd }e) \mathbin {\rhd }f), (((a\mathbin {\rhd }b) \mathbin {\rhd }c) \mathbin {\rhd }e)\}\) and the set of assumptions \(\varSigma = \{((a\mathbin {\rhd }b) \mathbin {\rhd }d), ((b,d) \mathbin {\rhd }c)\}\). The following derivation shows that \(\varSigma \vdash _S f\):

Angle brackets \(\langle \, \rangle \) are used to indicate the rules of S, and square brackets \([\;]\) with numerals indicate the discharge of assumptions.
5.2 Proof-Theoretic Validity
We now consider a notion of validity for intuitionistic propositional logic (see [16]), which will be based on the following clauses for the fragment \(\{\mathbin {\rightarrow },\mathbin {\vee },\mathbin {\wedge }\}\). Absurdity \({\perp }\) is taken as a distinguished atom. Extensions \(S'\) of atomic systems S are again understood in the set-theoretic sense: An atomic system \(S'\) is an extension of an atomic system S (written \(S' \supseteq S\)), if \(S'\) results from adding a (possibly empty) set of atomic rules to S.
Definition 13
S -validity (\(\vDash _S\)) and validity (\(\vDash \)) are defined as follows:
-
(S1)
 ,
, -
(S2)
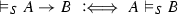 ,
, -
(S3)
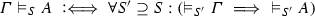 , where \(\varGamma \) is a set of formulas, and where \(\vDash _{S'} \varGamma \) stands for \(\{\vDash _{S'} A_i \mid A_i \in \varGamma \}\),
, where \(\varGamma \) is a set of formulas, and where \(\vDash _{S'} \varGamma \) stands for \(\{\vDash _{S'} A_i \mid A_i \in \varGamma \}\), -
(S4)
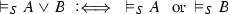 ,
, -
(S5)
 ,
, -
(S6)
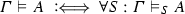 .
.
Since only the logical constants of the fragment \(\{\mathbin {\rightarrow },\mathbin {\vee },\mathbin {\wedge }\}\) are considered, and \({\perp }\) is just an atom, one could also speak of minimal validity or validity for minimal logic here. This notion is very similar to the ‘minimal part’ of Kreisel validity, given by clauses (K1)–(K4) and (K8) of Definition 6, when restricted to a propositional language and for words w identified with atoms \(a\).
In analogy to substitution-Kreisel-validity, we define in addition validity under substitution as validity for all substitution instances (resulting from uniform substitutions of formulas for atoms). Thus validity under substitution is by definition closed under substitution.
Definition 14
S -validity under substitution (\(\Vdash _S\)) and validity under substitution (\(\Vdash \)) are defined as follows:
-
(i)
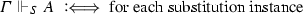 \(\varGamma ',A'\) of
\(\varGamma ',A'\) of 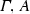 : \(\varGamma ' \vDash _S A'\).
: \(\varGamma ' \vDash _S A'\). -
(ii)
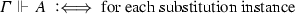 \(\varGamma ',A'\) of
\(\varGamma ',A'\) of 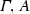 : \(\varGamma ' \vDash A'\).
: \(\varGamma ' \vDash A'\).
These notions of validity are now extended for intuitionistic propositional logic:
Definition 15
Intuitionistic
S
-validity (\(\vDash ^i_S\)) is defined as follows. Let \({({\perp })}\) stand for the set of rules  . Then
. Then  .
.
Correspondingly, \(\varGamma \vDash ^i A\), \(\varGamma \Vdash ^i_S A\) and \(\varGamma \Vdash ^i A\) are defined as \(\varGamma \vDash _{{({\perp })}} A\), \(\varGamma \Vdash _{S \cup {({\perp })}} A\) and \(\varGamma \Vdash _{{({\perp })}} A\), respectively.
The treatment of absurdity \({\perp }\), and therefore of negation if understood as \(\lnot A :=A \mathbin {\rightarrow }{\perp }\), differs from the one given by clause (K5) of Kreisel validity and from the one given by clauses (G5) or (G5\(^{\prime }\)). If \({\perp }\) were defined as a non-atomic constant by a semantical clause which says that there is no atomic system S such that \(\vDash _S {\perp }\), then \(\vDash _S \lnot \lnot a\) would hold for any atom \(a\); this is the case, since \(\nvDash _{S'} \lnot a\) for any \(S' \supseteq S\), as \(\vDash _{S''} a\) for some \(S'' \supseteq S'\).
We note the following properties of S-validity:
Lemma 3
-
(i)
\(\vDash _S\) is a consequence relation, that is,
-
(1)
\(A \vDash _S A\),
-
(2)
 ,
, -
(3)
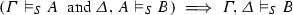 .
.
-
(1)
-
(ii)
\(\vDash _S\) is monotone with respect to S, that is, \(\varGamma \vDash _S A \implies {\forall }S' \supseteq S : \varGamma \vDash _{S'} A\).
-
(iii)
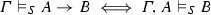 .
.
For intuitionistic S-validity (i.e., for \(\vDash _S\) replaced with \(\vDash ^i_S\)) these properties hold as well.
Atomic rules can be represented by formulas and vice versa (for details see [16]). Let \(\varSigma ^*\) stand for the set of formulas representing a finite set \(\varSigma \) of atomic rules. The following completeness and soundness result holds:
Lemma 4
\(\varSigma ^* \vDash _S a\iff \varSigma ^* \vdash _S a\).
5.3 Failure of Strong Completeness
We now consider the system \(\textit{NI}\) of natural deduction for intuitionistic propositional logic, for which one can show that it is not complete for validity.
Definition 16
Derivability of a formula A from a (possibly empty) set of assumptions \(\varGamma \) in \(\textit{NI}\) is written \(\varGamma \vdash A\).
Definition 17
-
(i)
Soundness of \(\textit{NI}\) means: \(\varGamma \vdash A \implies \varGamma \vDash ^i A\).
-
(ii)
Strong completeness of \(\textit{NI}\) means: \(\varGamma \vDash ^i A \implies \varGamma \vdash A\).
-
(iii)
Completeness (simpliciter) of \(\textit{NI}\) means: \(\varGamma \Vdash ^i A \implies \varGamma \vdash A\).
Soundness holds. Since derivability \(\varGamma \vdash A\) in \(\textit{NI}\) is closed under substitution, this implies \(\varGamma \Vdash ^i A\), that is, intuitionistic validity under substitution. The distinction between strong completeness and completeness (simpliciter) is useful, because one can show that validity is not closed under substitution; the given semantics validates a formula which is not derivable in \(\textit{NI}\). Thus strong completeness does not hold:
Theorem 5
\(\textit{NI}\) is not strongly complete. The set of valid formulas is not closed under substitution.
Three proofs of this result are discussed in [16]. Here we only mention the counterexample (cf. also Goldfarb [8] and Sect. 4)
which is already a counterexample for strong completeness of minimal logic, and hence of \(\textit{NI}\). This counterexample is independent of the level of atomic systems. There are other counterexamples, for which this is not the case. For example, \(\lnot \lnot a\vDash ^i a\) holds for first-level atomic systems, but fails for atomic systems of levels higher than 1. Thus certain counterexamples in the realm of first-level atomic systems can be avoided by allowing for higher-level atomic systems. What the given counterexample therefore also shows is that strong completeness already fails for the (more standard) notion of validity based on first-level atomic systems.
5.4 Strong Completeness Results
Strong completeness holds for the fragment of disjunction-free formulas and for the fragment of arbitrary negative formulas \(\lnot A\) (see [16]):
Lemma 5
Let \(\varGamma \) and A be disjunction-free. Then \(\varGamma \vDash ^i A \iff \varGamma \vdash A\).
Lemma 6
Let \(\varGamma \) and A be disjunction-free. Then \(\varGamma \vDash A \iff \varGamma \vdash ^m A\), where \(\vdash ^m\) denotes derivability in minimal logic. In other words, strong completeness holds for the \(\{\mathbin {\rightarrow },\mathbin {\wedge }\}\)-fragment of minimal (and intuitionistic) logic (see Schroeder-Heister [33]).
Lemma 7
For any formula of the form \(\lnot A\) it holds that \({}\vDash ^i \lnot A \iff {}\vdash \lnot A\).
These results depend on higher-level atomic systems, for which Lemma 4 holds.
5.5 Failure of Completeness
Theorem 6
Intuitionistic logic is not complete with respect to the semantics based on higher-level atomic systems.
This has been proved in [16] by showing that the intuitionistically non-derivable Harrop or Kreisel–Putnam formula (see Harrop [9], Kreisel and Putnam [11]) is intuitionistically valid under substitution, that is, that
holds. We emphasize that the given proof of this theorem depends on the fact that the considered semantics is based on higher-level atomic systems.
Since higher-level rules can be reduced to second-level rules by an appropriate coding (see Sandqvist [27]), it follows that intuitionistic logic is incomplete for S-validity based on second-level atomic systems. Whether intuitionistic logic is complete (simpliciter) for validity based on first-level atomic systems is an open problem.
Similarly to Gabbay’s completeness conjecture for substitution-Kreisel-validity, the following conjecture can be made for intuitionistic validity under substitution:
Conjecture 3
Intuitionistic propositional logic is complete (simpliciter) for intuitionistic validity based on first-level atomic systems. That is, \(\varGamma \Vdash ^i A \implies \varGamma \vdash A\), for first-level atomic systems only.
5.6 Comparison with Kripke Semantics
Proof-theoretic validity shares some similarities with the notion of validity in Kripke semantics, which is sound and complete for intuitionistic logic (see Kripke [12]; cf. Moschovakis [14]). We mention that the semantical clauses for conjunction and disjunction have the same form in both cases, and that the clauses for implication are similar in that they depend on the idea of extensions. In Kripke semantics the clause for implication is

for nodes \(k,k'\) and partial orders \(\ge \). The forcing relation for atoms \(a\) and nodes k is given by truth-value assignments \(v(k,a)\), which obey the monotonicity requirement that if \(k' \ge k\) and \(v(k,a) = \text {true}\), then \(v(k',a) = \text {true}\). Thus \(k'\) is an extension of k in the sense that \(\{a\mid k' \ \text {forces} \ a\} \supseteq \{a\mid k \ \text {forces} \ a\}\), just like \(S' \supseteq S\) for atomic systems \(S,S'\) of level 0 in the case of proof-theoretic validity.
Besides these similarities, there are the following main differences to Kripke semantics. In proof-theoretic validity, the S-validity of atoms is given by their derivability in S, whereas in Kripke semantics the validity (resp. the forcing relation) for nodes k and atoms \(a\) is given by truth-value assignments \(v(k,a)\).
In S-validity, atomic systems S are not only sets of atoms (which in Kripke semantics would be assigned to nodes k by v) but sets of atomic rules. This also means that \(S' \supset S\) can be the case, although \(\{a\mid {\vdash _{S'} a}\} = \{a\mid {\vdash _S a}\}\) (and consequently \(\{a\mid {\vDash _{S'} a}\} = \{a\mid {\vDash _S a}\}\)), simply because \(S'\) might contain inapplicable additional rules besides the ones in S, which therefore do not enlarge the set of atoms derivable in \(S'\). For example, let S contain only the axiom \(a\) and let  ; then \(S' \supset S\), while both in \(S'\) and S only \(a\) is derivable. A notion like weak validity (see Sect. 3), where
; then \(S' \supset S\), while both in \(S'\) and S only \(a\) is derivable. A notion like weak validity (see Sect. 3), where

is in this respect closer to the notion of validity in Kripke semantics than to S-validity.
In Kripke semantics, a formula has to be forced by every node in every Kripke structure in order to be Kripke valid. Besides different sets of nodes k and different truth-value assignments \(v(k,a)\), one therefore has to consider different partial orders \(\ge \), whereas in proof-theoretic validity only one kind of structure is taken into account (cf. Goldfarb [8]; see also [16]), namely the one where the partial order is set inclusion \(\supseteq \) for atomic systems S.
Furthermore, inconsistent extensions are possible in the case of S-validity, since absurdity \({\perp }\) could be added as an axiom to atomic systems S. This is not the case in Kripke semantics, where the forcing relation is consistent in the sense that a node k cannot force both A and \(\lnot A\) (cp., however, the modified Kripke models of Veldman [35]).
5.7 A Completeness Result for Intuitionistic Logic
A completeness result for intuitionistic propositional logic is available for the following notion of validity, which is given for second-level atomic systems S (see Sandqvist [27]; we adjust it to our notation):
Definition 18
-
(T1)
 ,
, -
(T2)
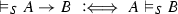 ,
, -
(T3)
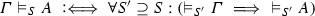 , where \(\varGamma \) is a set of formulas, and where \(\vDash _{S'} \varGamma \) stands for \(\{\vDash _{S'} A_i \mid A_i \in \varGamma \}\),
, where \(\varGamma \) is a set of formulas, and where \(\vDash _{S'} \varGamma \) stands for \(\{\vDash _{S'} A_i \mid A_i \in \varGamma \}\), -
(T4)
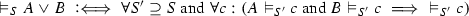 ,
, -
(T5)
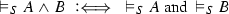 ,
, -
(T6)
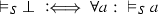 ,
, -
(T7)
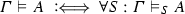 .
.
Compared to S-validity (see Definition 13) there are two differences (besides the restriction to second-level atomic systems S):
-
(i)
Clause (T4) for disjunction replaces (S4). It resembles the natural deduction elimination rule for disjunction. Note that the definiens is restricted to extensions \(S' \supseteq S\), and that propositional quantification is made use of in the universal quantification over all atoms \(c\) (not over all formulas; cf. Ferreira [4]).
-
(ii)
Absurdity \({\perp }\) is not an atom but a logical constant, whose meaning is given by clause (T6). This clause is based on Dummett’s introduction rule for \({\perp }\) (cf. Dummett [3, Chap. 13]).
Theorem 7
(Sandqvist [27]) Intuitionistic propositional logic is sound and complete for this semantics, that is, \(\varGamma \vDash A \iff \varGamma \vdash A\).
6 Completeness Results for Classical Logic
So far, we have only discussed notions of proof-theoretic validity intended for intuitionistic logic or for certain fragments thereof. Now we will discuss a notion of proof-theoretic validity for classical logic.
Sandqvist [26] gives a semantics for the fragment \(\{\mathbin {\rightarrow },{\perp },{\forall }\}\) of the language of first-order logic. He considers basic sequents of the form \((\varGamma :a)\), which are relations between finite sets \(\varGamma \) of basic sentences and basic sentences \(a\). Basic sentences are closed atomic formulas, that is, formulas containing neither logical constants nor free variables. Sets of basic sequents are called ‘bases’. In our terminology, basic sequents are first-level rules, and bases are first-level atomic systems S. Sandqvist shows that minimal logic can be justified and that the law of double negation elimination is valid for the fragment \(\{\mathbin {\rightarrow }, {\perp }, {\forall }\}\). The other logical constants can then be defined, and a justification of classical logic is achieved without making use of the principle of bivalence. That classical logic is sound and complete for the given semantics is surprising, since this semantics is very similar to semantics proposed for intuitionistic logic. Discussions of these results can be found in Makinson [13] and in [2].
Sandqvist’s semantics is the following (again, we use our notation):
Definition 19
-
(C1)
For closed atoms \(a\):
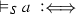 every set of closed atoms which is closed under S contains \(a\).
every set of closed atoms which is closed under S contains \(a\). -
(C2)
For non-empty \(\varGamma \):
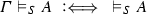 for every \(S' \supseteq S\) such that \(\vDash _{S'} B\) for every \(B \in \varGamma \).
for every \(S' \supseteq S\) such that \(\vDash _{S'} B\) for every \(B \in \varGamma \). -
(C3)
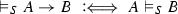 .
. -
(C4)
 for every closed atom \(a\).
for every closed atom \(a\). -
(C5)
 for every closed term t.
for every closed term t. -
(C6)
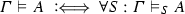 .
. -
(C7)
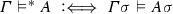 for all ground substitutions \(\sigma \).
for all ground substitutions \(\sigma \).
Note that the definiens in clause (C1) could be expressed equivalently as \(\vdash _S a\). Another (equivalent) formulation has been given by Makinson [13], where \(\underline{S}(\varDelta )\) is written for the closure of a set \(\varDelta \) of closed atoms under the rules in S. That is, \(\underline{S}(\varDelta )\) is the intersection of all sets \(\varLambda \) of closed atoms such that \(\varDelta \subseteq \varLambda \), and if  with \(\{a_1,\ldots ,a_n\} \subseteq \varLambda \), then \(b\in \varLambda \). Clauses (C1) and (C4) can then be written as follows:
with \(\{a_1,\ldots ,a_n\} \subseteq \varLambda \), then \(b\in \varLambda \). Clauses (C1) and (C4) can then be written as follows:
- (C1\(^{\prime }\)):
-
For closed atoms \(a\):
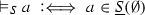 .
. - (C4\(^{\prime }\)):
-
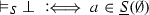 for every closed atom \(a\).
for every closed atom \(a\).
We point out that \({\perp }\) is not an atom here. In clause (C5), the notation A(x)[x / t] means that each occurrence of x in A is replaced by the term t. The relation \(\varGamma \vDash ^* A\) defined in clause (C7) deals with open formulas; a ground substitution is a substitution of variable-free terms for variables. The sets \(\varGamma \) of formulas are finite, but in Definition 19 infinite sets \(\varGamma \) could be allowed as well. The relation \(\vDash _S\) is called ‘valid inferability’ by Sandqvist; by ‘validity’ we refer to the relation \(\vDash \) defined in clause (C6).
The given semantics validates minimal logic (see Sandqvist [26, Lemma 3]). Furthermore, Sandqvist [26, Lemma 4] shows that the law of double negation elimination holds: \((A \mathbin {\rightarrow }{\perp }) \mathbin {\rightarrow }{\perp }\vDash ^* A\). Since minimal logic plus double negation elimination amounts to classical logic, the following soundness and completeness result for classical first-order logic holds:
Theorem 8
(Sandqvist [25, 26]) \(\varGamma \vDash A \iff \varGamma \vdash A\) in classical first-order logic.
The theorem is proved constructively by Sandqvist. An alternative proof is given by Makinson [13], who uses classical meta-reasoning.
Sandqvist [26] refers to the implication from right to left as soundness, whereas Makinson [13] takes the opposite perspective, in which the implication from right to left expresses that Sandqvist’s semantics is complete with respect to the usual model-theoretic semantics of classical logic. The implication from left to right, that is, completeness in the sense that Sandqvist validity (\(\varGamma \vDash A\)) implies classical derivability, or equivalently classical validity, holds as well.
6.1 Other Logical Constants
Sandqvist’s semantics contains clauses only for the logical constants of the fragment \(\{\mathbin {\rightarrow },{\perp },{\forall }\}\). A clause for conjunction \(\mathbin {\wedge }\) like (S5)

could be added without causing any problems with respect to completeness (cf. Makinson [13]). However, as noted by Sandqvist [26], if a clause for disjunction \(\mathbin {\vee }\) like (S4)

were added, then Theorem 8 would no longer hold. For example, the law of double negation elimination \((A \mathbin {\rightarrow }{\perp }) \mathbin {\rightarrow }{\perp }\vDash A\) does then not hold for each substitution instance anymore; a counterexample is \(A :=B \mathbin {\vee }(B \mathbin {\rightarrow }{\perp })\) (cf. [2]). In other words, validity fails to be closed under substitution, if disjunction is taken as primitive and understood according to the given semantical clause. This is also the case for the following stricter disjunction clauses (see Makinson [13]):

and

Similar observations can be made for the existential quantifier.
Makinson also gives an alternative clause for disjunction (see [13, p. 149]), which does not affect completeness. However, this clause is modeled on the definition \(A \mathbin {\vee }B :=(A \mathbin {\rightarrow }{\perp }) \mathbin {\rightarrow }B\), which represents a classical understanding of disjunction, whereas by clause (S4) disjunction is given its intuitionistic meaning.
6.2 Remarks
Theorem 8 still holds if atomic rules of S are allowed to have empty conclusions, and the closure \(\underline{S}(\varDelta )\) of a set \(\varDelta \) of closed atoms under the rules in S is understood as follows (see [13, p. 152]): \(\underline{S}(\varDelta )\) is the intersection of all sets \(\varLambda \) of closed atoms such that
-
(i)
\(\varDelta \subseteq \varLambda \), and if
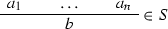 with \(\{a_1,\ldots ,a_n\} \subseteq \varLambda \), then \(b\in \varLambda \), and
with \(\{a_1,\ldots ,a_n\} \subseteq \varLambda \), then \(b\in \varLambda \), and -
(ii)
if
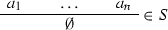 with \(\{a_1,\ldots ,a_n\} \subseteq \varLambda \), then \(b\in \varLambda \) for every closed atom \(b\) (where again \({\perp }\) is not an atom).
with \(\{a_1,\ldots ,a_n\} \subseteq \varLambda \), then \(b\in \varLambda \) for every closed atom \(b\) (where again \({\perp }\) is not an atom).
This generalization introduces a kind of negation at the level of atomic rules. In logic programming terms, this is a generalization of definite Horn clauses to Horn clauses.
Theorem 8 fails, however, if second-level rules are allowed in S. For example, consider the atomic system S which contains only the second-level rule

Then \(\vDash _S (a\mathbin {\rightarrow }b) \mathbin {\rightarrow }a\), but \(\nvDash _S a\), since \(\nvdash _S a\). Thus \(\nvDash ((a\mathbin {\rightarrow }b) \mathbin {\rightarrow }a) \mathbin {\rightarrow }a\), that is, Peirce’s law is no longer valid, and soundness fails.
We already remarked that absurdity \({\perp }\) is not an atom here. Furthermore, it is essential that there are infinitely many atoms in the language; otherwise completeness would be lost, since for finite sets of n atoms the classically non-derivable formula \(a_1 \mathbin {\rightarrow }(\ldots \mathbin {\rightarrow }(a_n \mathbin {\rightarrow }{\perp }) \ldots )\) becomes valid (see Makinson [13]). Soundness would fail if instead of clause (C4) the clause
were used (cf. [2, 13]). The use of a semantical clause for \({\perp }\) could also be avoided. Instead of showing the validity of the law of double negation, which depends both on clause (C3) for \(\mathbin {\rightarrow }\) and on clause (C4) for \({\perp }\), one can show the validity of Peirce’s law, which does not depend on clause (C4) at all (cf. [2, 26]).
Sandqvist’s result is remarkable, since it shows that the intuitionistically acceptable semantics given by Definition 19 allows for a justification of classical logic, as long as disjunction is understood classically.
The fact that the semantics is given for only a fragment of the language of first-order logic might be seen as a critical point. This leads to the question of whether such a semantics fulfills the requirements of proof-theoretic semantics for a justification of a logic. Makinson [13] argues that one might require to treat every logical constant used in informal mathematical discourse as a primitive in the formal language of the semantics and to give adequate semantical clauses for each of them. But, as he points out, such a requirement would be difficult to fulfill since it is too vague.
From the point of view of the formal systems used to represent logical reasoning in mathematical discourse one could argue that it is sufficient to have semantical clauses only for the standard logical constants present in the respective formal systems, such as the set \(\{\mathbin {\rightarrow },\mathbin {\vee },\mathbin {\wedge },{\perp },{\forall },{\exists }\}\) of logical constants in natural deduction for intuitionistic or classical logic. In the case of classical logic the restriction to a semantics for a fragment like \(\{\mathbin {\rightarrow },{\perp },{\forall }\}\), which is sufficient to define all the standard logical constants, should then be acceptable for the purpose of giving a justification for the whole logic.
7 Conclusion
We saw that within proof-theoretic semantics several similar notions of validity have been proposed. For some of these notions completeness results are available for certain fragments of intuitionistic (propositional) logic or for full intuitionistic (propositional) logic. In other cases, such as validity based on higher-level atomic systems, completeness for minimal and intuitionistic logic does not hold. For yet another notion a completeness result holds for classical logic, provided that disjunction is understood classically.
The considered notions of validity have in common that they are not closed under substitution. As derivability in intuitionistic or classical logic is closed under substitution, it seems questionable to even consider these notions as candidates for completeness. Indeed, for intuitionistic logic the failure of completeness with respect to validity based on first- or higher-level atomic systems could be proved by showing the validity of instances of classical laws which are not valid as a schema. For a notion of validity based on atomic systems of level 0, that is, for sets of atoms alone, there are counterexamples of not even classically derivable valid formulas.
As a way out, strengthened notions of validity have been proposed, which are by definition closed under substitution. Thus a formula can now only be valid (in the strengthened sense), if each of its substitution instances, resulting from uniform substitutions of arbitrary formulas for atoms, is valid (in the sense of the underlying, non-strengthened notion of validity). Intuitionistic propositional logic is complete with respect to two of these strengthened notions considered here. In the case of Goldfarb’s account, it is essential for completeness (Theorem 4) that only consistent extensions of atomic systems are taken into account. In the case of Sandqvist’s completeness result for intuitionistic propositional logic and validity based on second-level atomic systems (Theorem 7) it is crucial that disjunction is explained by the given clause (T4), and not by a more standard clause like (S4).
An essential component of all the considered notions of validity is their dependency on atomic systems. In each notion the validity of atoms \(a\) with respect to an atomic system S is defined by derivability of \(a\) in S (or as membership in a set of atoms closed under the rules of S), and the validity of implications (or of logical consequences \(\varGamma \vDash _S A\)) with respect to atomic systems S is defined by making use of extensions \(S'\) of S. Using extensions guarantees that validity is monotone with respect to atomic systems S. Whether extensions of atomic systems should be an integral part of any proof-theoretic notion of validity cannot be discussed here; we just point out that, for example, Prawitz has given up to consider extensions of atomic systems from the mid-1970s on and now emphasizes that this is not an intrinsic part of his analysis [personal communication]. His main argument is that atomic systems should not be looked at as descriptions of one’s knowledge but as rules defining the meaning of atomic propositions (cf. Prawitz [22, 23]), which would be changed by considering extensions (see [17] for a critical discussion).
With respect to completeness, the choice of the kind of atomic systems can be critical. For example, certain counterexamples to completeness of intuitionistic logic, namely examples of valid classically derivable formulas, can be prevented, if one allows for second-level instead of only first-level atomic systems. With regard to the completeness result for classical logic (Theorem 8) this means that the choice of first-level atomic systems is essential, since completeness does no longer hold for second-level atomic systems. Other results, such as strong completeness for certain fragments of intuitionistic logic, depend on the availability of arbitrary higher-level atomic systems.
For the philosophical endeavor of justifying a certain logic one might want to restrict oneself to first-level atomic systems in the first place, since higher-level systems already presuppose a feature of implication at the atomic level by allowing for the discharge of atomic assumptions. This presupposition might be deemed too strong for any adequate justification. For a justification of intuitionistic logic one would therefore prefer a proof-theoretic semantics which is restricted to first-level atomic systems, possibly allowing for inconsistent extensions. The question of whether intuitionistic logic is complete for such a semantics is still open.
References
de Campos Sanz, W., Piecha, T.: Inversion by definitional reflection and the admissibility of logical rules. Rev. Symb. Log. 2(3), 550–569 (2009)
de Campos Sanz, W., Piecha, T., Schroeder-Heister, P.: Constructive semantics, admissibility of rules and the validity of Peirce’s law. Log. J. IGPL 22(2), 297–308 (2014). First published online 6 August 2013
Dummett, M.: The Logical Basis of Metaphysics. Duckworth, London (1991)
Ferreira, F.: Comments on predicative logic. J. Philos. Log. 35, 1–8 (2006)
Gabbay, D.M.: On Kreisel’s notion of validity in Post systems. Studia Logica 35(3), 285–295 (1976)
Gabbay, D.M.: Semantical Investigations in Heyting’s Intuitionistic Logic. Reidel, Dordrecht (1981)
Gentzen, G.: Untersuchungen über das logische Schließen. Mathematische Zeitschrift, 39, 176–210, 405–431 (1934/35). English translation in: Szabo, M.E. (ed.) The Collected Papers of Gerhard Gentzen, pp. 68–131. North-Holland, Amsterdam (1969)
Goldfarb, W.: On Dummett’s “Proof-theoretic justifications of logical laws”. In: Piecha, T., Schroeder-Heister, P. (eds.) Advances in Proof-Theoretic Semantics. Springer, Dordrecht (2016). This volume (Circulated manuscript, 1998)
Harrop, R.: Concerning formulas of the types in intuitionistic formal systems. J. Symb. Log. 25, 27–32 (1960)
Kreisel, G.: Unpublished appendix to the paper “Set theoretic problems suggested by the notion of potential totality” in: Infinitistic Methods. Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 2–9 September 1959. Pergamon, Oxford (1961) (reference taken from [5]; unpublished appendix not found)
Kreisel, G., Putnam, H.: Eine Unableitbarkeitsbeweismethode für den intuitionistischen Aussagenkalkül. Archiv für mathematische Logik und Grundlagenforschung 3, 74–78 (1957)
Kripke, S.A.: Semantical analysis of intuitionistic logic I. In: Crossley, J., Dummett, M.A.E. (eds.) Formal Systems and Recursive Functions, pp. 92–130. North-Holland, Amsterdam (1965)
Makinson, D.: On an inferential semantics for classical logic. Log. J. IGPL 22(1), 147–154 (2014)
Moschovakis, J.: Intuitionistic logic. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy (2014). http://plato.stanford.edu/archives/fall2014/entries/logic-intuitionistic/
Olkhovikov, G.K., Schroeder-Heister, P.: Proof-theoretic harmony and the levels of rules: generalised non-flattening results. In: Moriconi, E., Tesconi, L. (eds.) Second Pisa Colloquium in Logic, Language and Epistemology, pp. 245–287. ETS, Pisa (2014)
Piecha, T., de Campos Sanz, W., Schroeder-Heister, P.: Failure of completeness in proof-theoretic semantics. J. Philos. Log. 44(3), 321–335 (2014). First published online 1 August 2014
Piecha, T., Schroeder-Heister, P.: Atomic systems in proof-theoretic semantics: two approaches. In: Redmond, J., Nepomuceno Fernández, A., Pombo, O. (eds.) Epistemology, Knowledge and the Impact of Interaction. Springer, Dordrecht (2016)
Prawitz, D.: Ideas and results in proof theory. In: Fenstad, J.E. (ed.) Proceedings of the Second Scandinavian Logic Symposium, Studies in Logic and the Foundations of Mathematics, vol. 63, pp. 235–307. North-Holland, Amsterdam (1971)
Prawitz, D.: Towards a foundation of a general proof theory. In: Suppes, P., et al. (eds.) Logic, Methodology and Philosophy of Science IV, pp. 225–250. North-Holland, Amsterdam (1973)
Prawitz, D.: On the idea of a general proof theory. Synthese 27, 63–77 (1974)
Prawitz, D.: Meaning approached via proofs. In: Kahle, R., Schroeder-Heister, P. (eds.) Proof-Theoretic Semantics. Synthese, vol. 148, pp. 507–524. Springer, Berlin (2006)
Prawitz, D.: An approach to general proof theory and a conjecture of a kind of completeness of intuitionistic logic revisited. In: Pereira, L.C., Haeusler, E.H., de Paiva, V. (eds.) Advances in Natural Deduction, Trends in Logic, vol. 39, pp. 269–279. Springer, Berlin (2014)
Prawitz, D.: On the relation between Heyting’s and Gentzen’s approaches to meaning. In: Piecha, T., Schroeder-Heister, P. (eds.) Advances in Proof-Theoretic Semantics. Springer, Dordrecht (2016). This volume
Read, S.: Proof-theoretic validity. In: Caret, C.R., Hjortland, O.T. (eds.) Foundations of Logical Consequence, Mind Association Occasional Series, pp. 136–158. Oxford University Press, Oxford (2015)
Sandqvist, T.: An inferentialist interpretation of classical logic. Ph.D. thesis, Department of Philosophy, Uppsala University (2005)
Sandqvist, T.: Classical logic without bivalence. Analysis 69, 211–217 (2009)
Sandqvist, T.: Basis-extension semantics for intuitionistic sentential logic (2014). To appear
Schroeder-Heister, P.: The completeness of intuitionistic logic with respect to a validity concept based on an inversion principle. J. Philos. Log. 12, 359–377 (1983)
Schroeder-Heister, P.: A natural extension of natural deduction. J. Symb. Log. 49, 1284–1300 (1984)
Schroeder-Heister, P.: Proof-theoretic validity and the completeness of intuitionistic logic. In: Dorn, G., Weingartner, P. (eds.) Foundations of Logic and Linguistics: Problems and Their Solutions, pp. 43–87. Plenum Press, New York (1985)
Schroeder-Heister, P.: Validity concepts in proof-theoretic semantics. In: Kahle, R., Schroeder-Heister, P. (eds.) Proof-Theoretic Semantics. Synthese, vol. 148, pp. 525–571. Springer, Berlin (2006)
Schroeder-Heister, P.: The calculus of higher-level rules, propositional quantification, and the foundational approach to proof-theoretic harmony. In: Indrzejczak, A. (ed.) Gentzen’s and Jaśkowski’s Heritage. 80 Years of Natural Deduction and Sequent Calculi. Studia Logica, vol. 103, pp. 1185–1216. Springer, Berlin (2014)
Schroeder-Heister, P.: Examples of proof-theoretic validity (Supplement to [34]). In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy (2012). http://plato.stanford.edu/entries/proof-theoretic-semantics/examples.html
Schroeder-Heister, P.: Proof-theoretic semantics. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy (2012). http://plato.stanford.edu/entries/proof-theoretic-semantics/
Veldman, W.: An intuitionistic completeness theorem for intuitionistic predicate logic. J. Symb. Log. 41, 159–166 (1976)
Wansing, H.: The idea of a proof-theoretic semantics and the meaning of the logical operations. Studia Logica 64, 3–20 (2000)
Acknowledgments
This work was supported by the French-German ANR-DFG project “Hypothetical Reasoning—Its Proof-Theoretic Analysis” (HYPOTHESES), DFG grant Schr 275/16-2. It was written during a research stay at the IHPST (Paris), and I am very grateful for the hospitality I received there. I would like to thank Grigory Olkhovikov and Tor Sandqvist for discussions, and Peter Schroeder-Heister for discussions and comments. The completion of this paper was supported by the French-German ANR-DFG project “Beyond Logic: Hypothetical Reasoning in Philosophy of Science, Informatics, and Law”, DFG grant Schr 275/17-1.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution Noncommercial License, which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Piecha, T. (2016). Completeness in Proof-Theoretic Semantics. In: Piecha, T., Schroeder-Heister, P. (eds) Advances in Proof-Theoretic Semantics. Trends in Logic, vol 43. Springer, Cham. https://doi.org/10.1007/978-3-319-22686-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-22686-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22685-9
Online ISBN: 978-3-319-22686-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



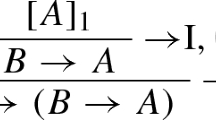

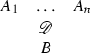
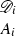 (for
(for 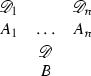
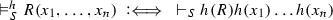 (where
(where 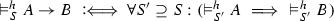 ,
,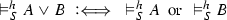 ,
,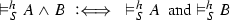 ,
,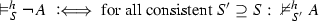 (where
(where 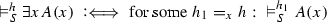 ,
,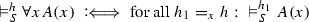 ,
,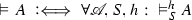 .
. all substitution instances of A are Kreisel valid (where substitutions are uniform substitutions of formulas for atoms in A).
all substitution instances of A are Kreisel valid (where substitutions are uniform substitutions of formulas for atoms in A). ,
, ,
,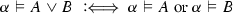 ,
,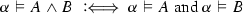 ,
, ,
,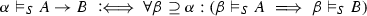 ,
,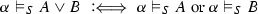 ,
,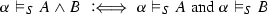 ,
, ,
,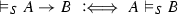 ,
,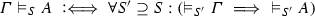 , where
, where 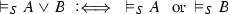 ,
, ,
,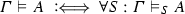 .
.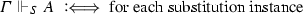
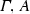 :
: 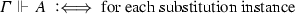
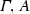 :
:  ,
,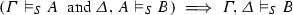 .
.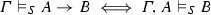 .
. ,
,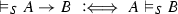 ,
,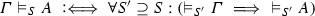 , where
, where 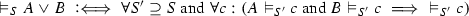 ,
,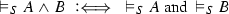 ,
,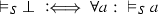 ,
,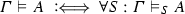 .
.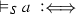 every set of closed atoms which is closed under S contains
every set of closed atoms which is closed under S contains 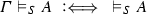 for every
for every 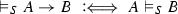 .
. for every closed atom
for every closed atom  for every closed term t.
for every closed term t.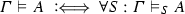 .
.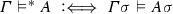 for all ground substitutions
for all ground substitutions 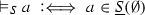 .
.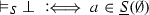 for every closed atom
for every closed atom 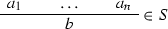 with
with 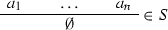 with
with