Abstract
This chapter constitutes the core of the part of the book devoted to spontaneously broken spacetime symmetry. It builds a framework for constructing effective actions for Nambu–Goldstone bosons, starting from the nonlinear realization of spacetime symmetry developed in the previous chapter. The framework is first applied to systems where the values of the order parameter at different spacetime points belong to the same orbit of the symmetry group. This case can be treated by a simple modification of the setup for broken internal symmetries. Next, the formalism is utilized to discuss the physical significance of so-called inverse Higgs constraints and the associated auxiliary vector fields. It is shown on concrete examples that while such fields may excite physical modes in the spectrum, these are not actual Nambu–Goldstone bosons. The rest of the chapter is devoted to genuine breaking of translation invariance by a coordinate-dependent order parameter. This requires a further improvement of the formalism to ensure proper realization of the symmetry and a one-to-one parameterization of all the fields.
You have full access to this open access chapter, Download chapter PDF
With the nonlinear realization of spacetime symmetry put forward in Chap. 12, we are now in the position to construct the low-energy effective field theory (EFT). As I already occasionally stressed, the EFT machinery for spontaneously broken spacetime symmetry is less developed than that for internal symmetry. As a consequence, I will not be able to offer an explicit general expression for the effective Lagrangian akin to what I did in Chap. 8. Instead, I will describe the basic framework in an algorithmic fashion, and then work out some illustrative examples.
In this chapter, I only consider systems where the symmetry group G is known and dictated by the microscopic dynamics. This has been the underlying assumption of the whole book so far. Yet, there are physical systems whose low-energy physics may feature additional symmetry which itself may but need not be spontaneously broken. Such symmetry is usually called emergent, and appears among others in classical systems such as fluids or solids. I will defer a detailed discussion of such emergent symmetries and their spontaneous breaking to the next chapter.
Following some preliminary work in Sect. 13.1, the survey of EFTs for spontaneously broken spacetime symmetry starts in Sect. 13.2. Here I deal with systems where the values of the order parameter at all points in space belong to the same orbit of the symmetry group. This requires a minimal modification of the setup for internal symmetries, but already involves some of the subtleties associated with the spacetime ones. A major issue is that the number of Nambu–Goldstone (NG) variables \(\pi ^a\) depends on the choice of order parameter realizing the given symmetry-breaking pattern. This means that some would-be NG variables are not required by the symmetry-breaking pattern per se. In Sect. 12.3.2, I suggested that such fields may, but need not, be physical. In case they are, they necessarily excite gapped modes in the spectrum, not true NG modes. I illustrate this dichotomy by several examples in Sect. 13.3. Then I offer some comments on the inverse Higgs constraints (IHCs) as an operational prescription for eliminating such spurious degrees of freedom.
The generic case of systems where the order parameter may depend on coordinates in an a priori arbitrary manner is considered in Sect. 13.4. Here the methods available for the construction of EFT appear to be least developed. I will therefore have to content myself with a careful discussion of the special case of one-dimensional order parameter modulation, augmented with a couple of illustrative examples.
1 Building Blocks for Construction of Effective Actions
In Chap. 8, I showed that the effective action for NG bosons of spontaneously broken internal symmetry can always be expressed in terms of the associated Maurer–Cartan (MC) form. I am not aware of any proof of the equivalent statement for spacetime symmetries. I will however make the common assumption that this is still the case.
1.1 Maurer–Cartan Form
Recall that we deal generally with a set of bosonic fields \(\psi ^i\), taking values from a target manifold \(\mathcal {M}\). The spacetime is treated as a possibly curved manifold M of dimension D, parameterized by local coordinates \(x^\mu \). Together, \(\psi ^i\) and \(x^\mu \) span the product manifold \(\mathcal {M}\times M\). In order to avoid excessive repetition, I will not review all the details of the standard nonlinear realization of spacetime symmetry. The reader is invited to consult Sect. 12.3 to refresh their memory. Let me just stress the important roles of the isotropy groups \(H_x\) of a spacetime point \(x\in M\), and \(H_{(\psi ,x)}\) of the point \((\psi ,x)\in \mathcal {M}\times M\). For chosen fixed \(\psi _0\in \mathcal {M}\), the coset space \(H_0/H_{(\psi _0,0)}\) spans a submanifold of \(\mathcal {M}\times \{0\}\simeq \mathcal {M}\), parameterized by NG coordinates \(\pi ^a\). These are generally accompanied by a set of matter variables \(\chi ^\varrho \). Together, \((\pi ^a,\chi ^\varrho ,x^\mu )\) constitute of a complete set of local coordinates on \(\mathcal {M}\times M\).
Let us first focus on the variables \((\pi ^a,x^\mu )\), required for a successful nonlinear realization of spacetime symmetry. I will represent these jointly as
where \(\mathcal {T}_{x}\) is a fixed purely spacetime transformation that transports the spacetime origin to the point x (cf. Sect. 12.2). Moreover, \(U(\pi )\) is a matrix representative of an element of the coset space \(H_0/H_{(\psi _0,0)}\). By (12.15), the action of any \(g\in G\) on \((\pi ^a,x^\mu )\) can then be expressed compactly as

where \(g_0(x,g)= \mathcal {T}_{\mathbb {X}(x,g)}^{-1}g\mathcal {T}_{x}\). Moreover, \(\pi ^{\prime a}(\pi ,g_0(x,g))\) and \(h(\pi ,g_0(x,g))\) are defined by (12.10). The MC form can now be introduced through
The first piece that depends solely on \(\pi ^a\) is familiar from our analysis of internal symmetries. The second piece is new and in some, as yet unclear, way reflects the action of the symmetry on the spacetime. Equation (13.2) induces the following transformation of the MC form,

where I for brevity dropped the arguments of \(g_0(x,g)\).
In order to understand better the structure of the MC form, we need to make a digression. By definition of spacetime symmetry, the transformation of coordinates \(x^\mu \) is independent of the field variables \(\psi ^i\) (or \(\pi ^a,\chi ^\varrho \)). One can thus restrict the action of G to the spacetime manifold, where it is defined by the maps  . Under this restricted action, the spacetime behaves as a homogeneous space, \(M\simeq G/H_0\). This implies the following local homeomorphism of manifolds,
. Under this restricted action, the spacetime behaves as a homogeneous space, \(M\simeq G/H_0\). This implies the following local homeomorphism of manifolds,
With the obvious notation for the Lie algebras of the three groups G, \(H_0\) and \(H_{(\psi _0,0)}\), the corresponding isomorphism of tangent spaces reads
Here \(\mathfrak {h}_0/\mathfrak {h}_{(\psi _0,0)}\) and \(\mathfrak {g}/\mathfrak {h}_0\) should be viewed as shorthand notation for the respective tangent spaces; these are themselves not Lie algebras without further qualifications.
I previously assumed that at the very least, the coset space \(H_0/H_{(\psi _0,0)}\) is reductive. This ensures that both \(\mathfrak {h}_{(\psi _0,0)}\) and \(\mathfrak {h}_0/\mathfrak {h}_{(\psi _0,0)}\) are invariant subspaces under the adjoint action of \(H_{(\psi _0,0)}\). In the following, I will need a stronger assumption, namely that all three components of the direct sum (13.6) are invariant under the adjoint action of \(H_{(\psi _0,0)}\). This is guaranteed if \(H_{(\psi _0,0)}\) is compact, but in general has to be viewed as an additional assumption.
Example 13.1
Let us check the validity of this assumption for the examples of nonlinear realization worked out in Sect. 12.4. In case of a theory of Lorentz scalars with an internal symmetry group \(G_{\mathrm {int}}\) (Sect. 12.4.1), we have \(H_{(\psi _0,0)}\simeq \mathrm {SO}(d,1)\times H_{\mathrm {int}}\). As long as the coset space \(G_{\mathrm {int}}/H_{\mathrm {int}}\) itself is reductive, the tangent space \(\mathfrak {h}_0/\mathfrak {h}_{(\psi _0,0)}\simeq \mathfrak {g}_{\mathrm {int}}/h_{\mathrm {int}}\) is naturally invariant under the adjoint action of \(H_{(\psi _0,0)}\). Likewise, the tangent space \(\mathfrak {g}/\mathfrak {h}_0\) of \(G/H_0\simeq M\simeq \mathbb {R}^D\) carries the vector representation of \(\mathrm {SO}(d,1)\). It is easy to check that also for the examples in Sects. 12.4.2 and 12.4.3, our assumption on the decomposition (13.6) is satisfied.
The case of Galilei symmetry (Sect. 12.4.4) is most nontrivial. Here the commutation relation \([P_r,K_s]=\mathrm{i} \delta _{rs}Q\) implies that the d-dimensional space spanned on the components of the momentum operator does not carry a representation of Galilei boosts. Hence the boosts should not be included in the isotropy subgroup \(H_{(\psi _0,0)}\). The way out, as shown in Sect. 12.4.4, is to introduce a vector order parameter \(A^\mu \) that gives a vector of NG variables \(\xi ^r\), carrying a nonlinear realization of the boosts. Then, \(H_{((\psi _0,A_0),0)}\) is either \(\mathrm {SO}(d)\) or \(\mathrm {SO}(d)\times \mathrm {U}(1)_Q\). In both cases, the Lie algebra \(\mathfrak {g}\) of G naturally splits into invariant subspaces of \(H_{((\psi _0,A_0),0)}\) as in (13.6). This observation lends further support to the mathematical realization of Galilei boosts in terms of the auxiliary vector of NG fields \(\xi ^r\). I will return to this in Sect. 13.3.3.
In order to reformulate the above basic assumption in a language more common in physics, we need a notation for the symmetry generators. In analogy with the treatment of internal symmetries in Chap. 7, I will denote generators that form a basis of \(\mathfrak {g}\) as \(Q_{A,B,\dotsc }\). A subset of these generators that spans a basis of \(\mathfrak {h}_{(\psi _0,0)}\) will be \(Q_{\alpha ,\beta ,\dotsc }\). Analogously, the basis of \(\mathfrak {h}_0/\mathfrak {h}_{(\psi _0,0)}\) will be \(Q_{a,b,\dotsc }\). Finally, for the basis of the complementary space \(\mathfrak {g}/\mathfrak {h}_0\), I will use the notation  . In the fixed basis \(Q_A\), the structure of the Lie algebra \(\mathfrak {g}\) is defined by the structure constants
. In the fixed basis \(Q_A\), the structure of the Lie algebra \(\mathfrak {g}\) is defined by the structure constants  via
via  . Then, our assumption that all the components of the direct sum (13.6) carry a representation of \(H_{(\psi _0,0)}\) restricts the commutators of \(Q_\alpha \) to
. Then, our assumption that all the components of the direct sum (13.6) carry a representation of \(H_{(\psi _0,0)}\) restricts the commutators of \(Q_\alpha \) to

The remaining commutators of the Lie algebra \(\mathfrak {g}\) take the generic form

There is no  term in \([Q_a,Q_b]\) since all the \(Q_\alpha \) and \(Q_a\) together span a basis of \(\mathfrak {h}_0\). As to
term in \([Q_a,Q_b]\) since all the \(Q_\alpha \) and \(Q_a\) together span a basis of \(\mathfrak {h}_0\). As to  , at this stage we do not need to assume that they are mutually commuting translation generators.
, at this stage we do not need to assume that they are mutually commuting translation generators.
We are now ready to return to the MC form. By its definition (13.3), \(\omega \equiv \omega ^AQ_A\) is a (locally defined) 1-form on \(H_0/H_{(\psi _0,0)}\times M\) that takes values in the Lie algebra \(\mathfrak {g}\) of G. It consists of three parts, corresponding to the three spaces on the right-hand side of (13.6),

The notation for \(\omega _\parallel \) and \(\omega _\perp \) follows the conventions introduced in Chap. 7 for internal symmetries. The \(\omega _P\) component, proportional to the generators  , is new here. Thanks to the assumption that both spaces \(\mathfrak {h}_0/\mathfrak {h}_{(\psi _0,0)}\) and \(\mathfrak {g}/\mathfrak {h}_0\) are invariant under the adjoint action of \(H_{(\psi _0,0)}\), the transformation rule (13.4) splits as
, is new here. Thanks to the assumption that both spaces \(\mathfrak {h}_0/\mathfrak {h}_{(\psi _0,0)}\) and \(\mathfrak {g}/\mathfrak {h}_0\) are invariant under the adjoint action of \(H_{(\psi _0,0)}\), the transformation rule (13.4) splits as

Following Chap. 7, it would now be possible to work out further technical details. These include for instance an explicit expression for the action of G on the coordinates \((\pi ^a,x^\mu )\), or the MC equations for the exterior derivative of \(\omega (\pi ,x)\). I will however not do so even though it would be straightforward, for we will not need these details. Let us instead turn to the physical interpretation of the various parts of the MC form.
1.2 Covariant Derivatives of Fields
The first part of the MC form in (13.3), \(-\mathrm{i} U(\pi )^{-1}\mathrm{d} U(\pi )\), obviously takes values from the Lie algebra \(\mathfrak {h}_0\). It follows that \(\omega _P\) does not contain any contributions proportional to \(\mathrm{d} \pi ^a\). In other words, \(\omega _P\) is a well-defined 1-form on the slice \(\{\pi \}\times M\simeq M\) for any fixed point \(\pi ^a\) in \(H_0/H_{(\psi _0,0)}\),

By assumption, the action of G on the spacetime M is transitive. This implies that at \(\pi ^a=0\), the components of  span the whole cotangent space to M. By continuity, the same must be true in some neighborhood of the origin of \(H_0/H_{(\psi _0,0)}\), \(\pi ^a=0\). We conclude that the 1-forms
span the whole cotangent space to M. By continuity, the same must be true in some neighborhood of the origin of \(H_0/H_{(\psi _0,0)}\), \(\pi ^a=0\). We conclude that the 1-forms  with fixed \(\pi ^a\) define a (local) coframe on the spacetime manifold M. We are of course free to use any (local) frame or coframe on M we wish. Nevertheless, it will be convenient to stick to \(\omega _P\) thanks to its covariant transformation properties under G, as shown in (13.10). This justifies a posteriori the notation
with fixed \(\pi ^a\) define a (local) coframe on the spacetime manifold M. We are of course free to use any (local) frame or coframe on M we wish. Nevertheless, it will be convenient to stick to \(\omega _P\) thanks to its covariant transformation properties under G, as shown in (13.10). This justifies a posteriori the notation  for the components of \(\omega _P\).
for the components of \(\omega _P\).
Next we have a look at the \(\omega _\perp \) part of the MC form,
The  piece comes from the \(-\mathrm{i} U(\pi )^{-1}\mathrm{d} U(\pi )\) term in (13.3) and is thus independent of the spacetime coordinates. The full 1-form \(\omega _\perp \) however contains components from cotangent spaces to both \(H_0/H_{(\psi _0,0)}\) and M. Unlike in the case of internal symmetries, it therefore cannot be interpreted as giving rise to a coframe on \(H_0/H_{(\psi _0,0)}\).
piece comes from the \(-\mathrm{i} U(\pi )^{-1}\mathrm{d} U(\pi )\) term in (13.3) and is thus independent of the spacetime coordinates. The full 1-form \(\omega _\perp \) however contains components from cotangent spaces to both \(H_0/H_{(\psi _0,0)}\) and M. Unlike in the case of internal symmetries, it therefore cannot be interpreted as giving rise to a coframe on \(H_0/H_{(\psi _0,0)}\).
At this point, recall that we eventually want to treat \(\pi ^a\) as fields. These naturally define maps from M to \(H_0/H_{(\psi _0,0)}\) that take any \(x\in M\) to \(\pi ^a(x)\in H_0/H_{(\psi _0,0)}\). Slightly more formally, one can view the fields as maps from M to \(H_0/H_{(\psi _0,0)}\times M\) that assign to \(x\in M\) the pair \((\pi ^a(x),x^\mu )\). This makes it possible to pull differential forms on \(H_0/H_{(\psi _0,0)}\times M\) back to M. Thus, the coframe (13.11) becomes  .Footnote 1 More interesting is the pull-back of (13.12) to M,
.Footnote 1 More interesting is the pull-back of (13.12) to M,
This obviously carries information about the derivatives of the NG fields \(\pi ^a(x)\). To extract the covariant derivative of the NG field, we decompose the spacetime 1-form \(\omega ^a(\pi (x),x)\) in the coframe
of the NG field, we decompose the spacetime 1-form \(\omega ^a(\pi (x),x)\) in the coframe  ,
,

Comparison with (13.13) then gives

where  is the local frame on M, dual to
is the local frame on M, dual to  . The covariant derivative can also be expressed compactly as
. The covariant derivative can also be expressed compactly as  .
.
I am using here the same symbol  for the covariant derivative as in Appendix A.5, yet the two objects do not seem to be the same. Let me clarify the difference. First, the first term on the right-hand side of (13.15) is not just the gradient of \(\pi ^a\) projected to the frame
for the covariant derivative as in Appendix A.5, yet the two objects do not seem to be the same. Let me clarify the difference. First, the first term on the right-hand side of (13.15) is not just the gradient of \(\pi ^a\) projected to the frame  . The extra factor
. The extra factor  , as well as the \(\omega ^a_\nu \) term, is needed to ensure covariance under the action of G. In particular the
, as well as the \(\omega ^a_\nu \) term, is needed to ensure covariance under the action of G. In particular the  factor is nontrivial even if G is an internal symmetry group. Second, we are not introducing here an all-purpose connection on M that would make
factor is nontrivial even if G is an internal symmetry group. Second, we are not introducing here an all-purpose connection on M that would make  covariant under the maximal structure group \(\mathrm {GL}(\dim M)\). As follows from (13.10), we only allow changes of the local frame induced by a representation of the structure group \(H_{(\psi _0,0)}\). This procedure is designed to give a G-invariant EFT for the NG fields. In spite of using covariant derivatives, the EFTs constructed below are not covariant under general coordinate transformations on M.
covariant under the maximal structure group \(\mathrm {GL}(\dim M)\). As follows from (13.10), we only allow changes of the local frame induced by a representation of the structure group \(H_{(\psi _0,0)}\). This procedure is designed to give a G-invariant EFT for the NG fields. In spite of using covariant derivatives, the EFTs constructed below are not covariant under general coordinate transformations on M.
The remaining part of the MC form (13.9) that we have not discussed yet is \(\omega _\parallel \). This, as the transformation rule (13.10) suggests, plays the role of an \(\mathfrak {h}_{(\psi _0,0)}\)-valued connection. Let us define the spacetime components of the connection after pull-back to M through
Then for a matter field \(\chi ^\varrho \) that transforms linearly in a representation D of \(H_{(\psi _0,0)}\), cf. (12.10), the covariant derivative can be defined as

This generalizes the covariant derivative we constructed in the context of internal symmetries in Sect. 8.2.4.
We conclude by checking in what precise sense the derivatives (13.15) and (13.17) of the NG and matter fields are covariant. To that end, consider a transformation by an element of \(g\in G\) infinitesimally close to unity, \(g\approx e+\mathrm{i} \epsilon ^AQ_A\), where \(\epsilon ^A\) is a set of small constant parameters. The element \(h(\pi ,g_0(x,g))\in H_{(\psi _0,0)}\), defined by (12.10) with  , then reads, to linear order in \(\epsilon ^A\),
, then reads, to linear order in \(\epsilon ^A\),
Here \(k^\alpha _A(\pi ,x)\) is a set of functions that are calculable following the guidance of Sect. 7.3, but we need not do so explicitly. It is easy to check that the last two lines of (13.10) now translate into the infinitesimal transformations

By the duality between the frame  and the coframe
and the coframe  , the transformation of the latter gives
, the transformation of the latter gives  . Equipped with these auxiliary identities, we arrive at the infinitesimal transformations of the covariant derivatives (13.15) and (13.17),
. Equipped with these auxiliary identities, we arrive at the infinitesimal transformations of the covariant derivatives (13.15) and (13.17),

The covariant derivatives transform linearly. This makes it possible to construct G-invariant Lagrangian densities out of the (possibly higher) covariant derivatives using standard methods of tensor algebra and representation theory.
Example 13.2
Recall the example worked out in Sect. 12.4.2. Here \(G\simeq \mathbb {R}^+\ltimes \mathrm {ISO}(d,1)\) acts on a set of relativistic scalars, where \(\mathrm {ISO}(d,1)\) is the Poincaré group and \(\mathbb {R}^+\) represents scale transformations of spacetime coordinates. Suppose that the ground state of the system carries a uniform condensate, spontaneously breaking the scale invariance. We choose accordingly \(\psi _0\in \mathcal {M}\) that breaks the dilatation group \(\mathbb {R}^+\). Thus, \(H_{(\psi _0,0)}\simeq \mathrm {SO}(d,1)\) whereas \(H_0\simeq \mathbb {R}^+\times \mathrm {SO}(d,1)\).
Let us disregard possible matter fields and focus on the dilaton field \(\pi \), parameterizing the coset space \(H_0/H_{(\psi _0,0)}\simeq \mathbb {R}\). We fix \(x^\mu \) to be the standard Minkowski coordinates, and  the energy–momentum operator. The manifold \(H_0/H_{(\psi _0,0)}\times M\simeq \mathbb {R}^{d+2}\) is naturally parameterized by \(\mathfrak {U}(\pi ,x)=\mathrm{e} ^{\mathrm{i} x\cdot P}\mathrm{e} ^{\mathrm{i} \pi D}\).Footnote 2 With the help of the commutation relation
the energy–momentum operator. The manifold \(H_0/H_{(\psi _0,0)}\times M\simeq \mathbb {R}^{d+2}\) is naturally parameterized by \(\mathfrak {U}(\pi ,x)=\mathrm{e} ^{\mathrm{i} x\cdot P}\mathrm{e} ^{\mathrm{i} \pi D}\).Footnote 2 With the help of the commutation relation  , we compute the MC form
, we compute the MC form
From the second term, we extract the spacetime coframe  and the corresponding dual frame,
and the corresponding dual frame,  . The dual frame can be used as a covariant derivative operator,
. The dual frame can be used as a covariant derivative operator,  , that is scale-invariant.
, that is scale-invariant.
To produce an action, we still need a volume element. This is most easily obtained by constructing a volume form on the Minkowski spacetime using the coframe,
A generic Poincaré- and scale-invariant effective action for the dilaton then reads
The Lagrangian \(\mathcal {L}_{\mathrm {eff}}\) can be built by writing down the most general Lorentz-invariant operator in terms of the derivatives of \(\pi \), and then replacing \(\partial _\mu \) with \(\nabla _\mu \) everywhere.
2 Twisting Order Parameter for Internal Symmetry
We have reached the point where we can start dealing with concrete systems featuring spontaneous breakdown of spacetime symmetry. As mentioned above, I will always assume that the effective action can be constructed solely out of the MC form. Any claim of having found the most general invariant action therefore has to be interpreted accordingly. It is not always straightforward to construct the most general effective action even in this restricted sense. To make further progress, it is convenient to narrow down the landscape of systems that we consider.
In this section, I will elaborate on the example of nonlinear realization worked out in Sect. 12.4.1. Here is a brief reminder. Suppose that the symmetry group factorizes as \(G\simeq G_{\mathrm {s.t.}}\times G_{\mathrm {int}}\), where “s.t.” and “int” stand respectively for “spacetime” and “internal.” Moreover, suppose that the target manifold \(\mathcal {M}\) is parameterized by a set of fields \(\psi ^i\) that are scalar in the sense that \(\mathbb {F}^i(\psi ,x,g_{\mathrm {s.t.}})=\psi ^i\) for all \(g_{\mathrm {s.t.}}\in G_{\mathrm {s.t.}}\). This is equivalent to requiring that \(G_{\mathrm {s.t.}}\) is a purely spacetime symmetry. Likewise, \(G_{\mathrm {int}}\) is internal in the sense that \(\mathbb {F}^i(\psi ,x,g_{\mathrm {int}})\) is independent of \(x^\mu \) and \(\mathbb {X}^\mu (x,g_{\mathrm {int}})=x^\mu \) for all \(g_{\mathrm {int}}\in G_{\mathrm {int}}\). The action of the symmetry group G on the standard coordinates \((\pi ^a,\chi ^\varrho ,x^\mu )\) is then given by (12.19). The isotropy group of the spacetime origin is \(H_0\simeq H_{\mathrm {s.t.}}\times G_{\mathrm {int}}\), and the spacetime manifold M is equivalent to the homogeneous space \(G_{\mathrm {s.t.}}/H_{\mathrm {s.t.}}\). Similarly, the isotropy group of \((\psi _0,0)\in \mathcal {M}\times M\) is \(H_{\mathrm {s.t.}}\times H_{\mathrm {int}}\), hence \(H_0/H_{(\psi _0,0)}\simeq G_{\mathrm {int}}/H_{\mathrm {int}}\).
I will now make one additional, important assumption. Let us choose the reference point \(\psi _0\in \mathcal {M}\) so that it represents the actual value of the order parameter at the spacetime origin, \(\langle {\psi ^i(0)}\rangle =\psi ^i_0\). Suppose that in the resulting standard coordinates on \(\mathcal {M}\), the vacuum expectation value (VEV) of all the matter fields, \(\langle {\chi ^\varrho (x)}\rangle \), is zero. This is equivalent to requiring that the order parameter is fully specified by the VEVs \(\langle {\pi ^a(x)}\rangle \). The values of the order parameter at different spacetime points lie on the same orbit of \(G_{\mathrm {int}}\) in \(\mathcal {M}\). It is then mathematically consistent to eliminate the matter fields from the EFT altogether. After all, they are expected to excite gapped modes in the spectrum, which can be ignored at sufficiently low energies.
Example 13.3
Consider a theory of a single real relativistic scalar field \(\phi \), equipped with an internal shift symmetry,  . This corresponds to \(G_{\mathrm {s.t.}}\simeq \mathrm {ISO}(d,1)\), \(H_{\mathrm {s.t.}}\simeq \mathrm {SO}(d,1)\), and \(G_{\mathrm {int}}\simeq \mathbb {R}\). For any choice of the reference point \(\phi _0\), the internal isotropy group is trivial, \(H_{\mathrm {int}}\simeq \{e\}\). In this case, the only degree of freedom, that is \(\phi \) itself, is of the NG type. There are no matter-type variables. Therefore, our assumption that the VEV of all \(\chi ^\varrho \) be vanishing is trivially satisfied.
. This corresponds to \(G_{\mathrm {s.t.}}\simeq \mathrm {ISO}(d,1)\), \(H_{\mathrm {s.t.}}\simeq \mathrm {SO}(d,1)\), and \(G_{\mathrm {int}}\simeq \mathbb {R}\). For any choice of the reference point \(\phi _0\), the internal isotropy group is trivial, \(H_{\mathrm {int}}\simeq \{e\}\). In this case, the only degree of freedom, that is \(\phi \) itself, is of the NG type. There are no matter-type variables. Therefore, our assumption that the VEV of all \(\chi ^\varrho \) be vanishing is trivially satisfied.
A slightly less trivial example is that of a complex relativistic scalar \(\phi \), subject to the action of \(G_{\mathrm {int}}\simeq \mathrm {U}(1)\) via  . For any nonzero \(\phi _0\in \mathbb {C}\), we have again \(H_{\mathrm {int}}\simeq \{e\}\). The field is then naturally parameterized by its modulus and phase, \(\phi =\varrho \mathrm{e} ^{\mathrm{i} \theta }\), where \(\theta \) is the sole NG variable. Provided \(\langle {\varrho (x)}\rangle \equiv \varrho _0\) is constant, \(\varrho \) can be traded for a matter field with vanishing VEV as desired, \(\chi \equiv \varrho -\varrho _0\). On the other hand, the VEV of the phase, \(\langle {\theta (x)}\rangle \), can have arbitrary coordinate dependence. This kind of order parameter describes relativistic superfluids.
. For any nonzero \(\phi _0\in \mathbb {C}\), we have again \(H_{\mathrm {int}}\simeq \{e\}\). The field is then naturally parameterized by its modulus and phase, \(\phi =\varrho \mathrm{e} ^{\mathrm{i} \theta }\), where \(\theta \) is the sole NG variable. Provided \(\langle {\varrho (x)}\rangle \equiv \varrho _0\) is constant, \(\varrho \) can be traded for a matter field with vanishing VEV as desired, \(\chi \equiv \varrho -\varrho _0\). On the other hand, the VEV of the phase, \(\langle {\theta (x)}\rangle \), can have arbitrary coordinate dependence. This kind of order parameter describes relativistic superfluids.
Discarding the matter fields amounts to restricting our basic setup to the manifold \(H_0/H_{(\psi _0,0)}\times M\simeq G_{\mathrm {int}}/H_{\mathrm {int}}\times G_{\mathrm {s.t.}}/H_{\mathrm {s.t.}} \). Henceforth, I will only consider flat spacetimes such that \(G_{\mathrm {s.t.}}\) possesses a set of D mutually commuting translation generators  . With the parameterization \(\mathfrak {U}(\pi ,x)=\mathrm{e} ^{\mathrm{i} x\cdot P}U(\pi )\), the MC form becomes
. With the parameterization \(\mathfrak {U}(\pi ,x)=\mathrm{e} ^{\mathrm{i} x\cdot P}U(\pi )\), the MC form becomes
The spacetime coframe is trivial,  , and it is not necessary to distinguish frame and coordinate-basis indices. The \(\omega _\parallel \) and \(\omega _\perp \) parts of the MC form (13.24) are fixed by the internal symmetry. We can therefore reuse the wealth of information accumulated in Chap. 7 to evaluate them.
, and it is not necessary to distinguish frame and coordinate-basis indices. The \(\omega _\parallel \) and \(\omega _\perp \) parts of the MC form (13.24) are fixed by the internal symmetry. We can therefore reuse the wealth of information accumulated in Chap. 7 to evaluate them.
So far, I have not made any assumptions about the coordinate dependence of the order parameter beyond the requirement that all \(\langle {\chi ^\varrho (x)}\rangle \) vanish. Whether or not the order parameter breaks any spacetime symmetries has no bearing on the set of degrees of freedom \(\pi ^a\) of the EFT, their transformation under G, or the MC form. Yet, the devil is in the details, as we shall now see.
2.1 New Features of the Old Setup
A consistent low-energy EFT setup requires a number of ingredients to be in place. The first is of course having a set of well-defined degrees of freedom, well separated from whatever high-energy modes have been ignored. This is generally guaranteed by the broken symmetry. These low-energy degrees of freedom should map to positive-energy excitations of a stable ground state. Failure to satisfy this condition indicates that we have not identified the correct ground state. Finally, in the absence of further physical input, it is necessary to include in the effective Lagrangian all operators consistent with the given symmetry. Typically, infinitely many such operators exist. Hence, we need an organizing principle to decide which operators are relevant and which can be neglected: power counting.
Stability of the Ground State
Our choice of the reference point, \(\psi ^i_0\equiv \langle {\psi ^i(0)}\rangle \), corresponds to \(\langle {\pi ^a(0)}\rangle =0\), or \(\langle {U(\pi (0))}\rangle =e\). The actual order parameter defines a map from M to the coset space \(G_{\mathrm {int}}/H_{\mathrm {int}}\), \(\langle {U(\pi (x))}\rangle \equiv U_0(x)\). Nontrivial coordinate dependence indicates that the order parameter is twisted. Importantly, not every choice of \(U_0(x)\) is physically consistent. A necessary condition is that \(U_0(x)\) is a local minimum of the energy functional of the EFT. This is straightforward to check in two steps. First, \(U_0(x)\) should be a stationary state, that is a solution of the equation of motion (EoM); see Sect. 8.3 for details on the latter. Second, the spectrum of small fluctuations about this state should only contain positive-energy excitations.
Example 13.4
Recall the helimagnetic state, introduced in Example 6.5,
where k is a positive constant. In this case, the order parameter is \(\boldsymbol n\in \mathrm {SO}(3)/\mathrm {SO}(2)\simeq S^2\). It is spatially twisted so that it forms a helix oriented along the z-axis, with pitch \(2\pi /k\). In Example 9.10, I showed that this order parameter minimizes the energy in the EFT for ferromagnets augmented with the Dzyaloshinskii–Moriya (DM) interaction. The precise value of k is fixed by the coupling of the DM term.
Ensuring the stability of the ground state is an integral part of the construction of the low-energy EFT. The requirement was already implicitly present in our analysis of internal symmetries in Part III of the book. The fact that the vacuum, \(\pi ^a=0\), is a solution of the EoM was guaranteed by the absence of terms linear in \(\pi ^a\) in the effective Lagrangian. Such terms were typically forbidden by the nonlinearly realized symmetry. Only in one exceptional example, namely the class of Galileon theories (Sect. 10.3.2), I enforced the absence of linear terms ad hoc by discarding the tadpole operator. Furthermore, stability under small fluctuations was ensured by fixing the signs of the parts of the effective Lagrangian bilinear in \(\pi ^a\), carrying respectively two temporal or two spatial derivatives.
Power Counting
Eventually, we would like to parameterize the EFT by NG fields \(\tilde \pi ^a(x)\) such that \(\langle {\tilde \pi ^a(x)}\rangle =0\). This makes it easy to distinguish the ground state from its fluctuations. It is often convenient to factorize the matrix variable \(U(\pi )\) as
This maintains a simple transformation rule for \(\tilde \pi ^a\) under the action of \(G_{\mathrm {int}}\). Indeed, a comparison with (12.19) shows that

In other words, the action of \(G_{\mathrm {int}}\) by left multiplication is simply conjugated by \(U_0^{-1}\).
The challenge to face is that following blindly the machinery of Chap. 8, we arrive at an effective Lagrangian where derivatives act on \(U(\pi )\) rather than on \(U(\tilde \pi )\). This is not a problem if the characteristic length scale of the symmetry breaking \(G_{\mathrm {int}}\to H_{\mathrm {int}}\) is much shorter than the scale of variations of the ground state \(U_0(x)\). Such a hierarchical symmetry breaking occurs for instance in helimagnets. Indeed, the helix pitch in FeGe is about \(70\,\mathrm {nm}\) [1], which is much longer than the scale of the crystal lattice at which the magnetic order is formed. In such systems, derivatives of both \(U(\tilde \pi (x))\) and \(U_0(x)\) can be considered small and counted together. Should, however, the order parameter feature short-distance variations, a different power counting is needed. The precise setup of the power counting that renders the EFT predictive is then best considered case by case.
2.2 Case Study: Relativistic Superfluids
From the point of view of symmetry, a superfluid is an ordered phase of matter where an internal \(\mathrm {U}(1)\) symmetry is spontaneously broken. We therefore need an order parameter charged under this symmetry. The simplest choice is to take a complex scalar field \(\phi \) carrying the action of \(G_{\mathrm {int}}\simeq \mathrm {U}(1)\) via  . We then assume that due to microscopic dynamics, this field develops a nonzero VEV. That is however not enough. We want the vacuum to describe matter, that is a state with nonzero density of the \(\mathrm {U}(1)\) charge. In a Lorentz-invariant scalar theory, a state of uniform nonzero charge density corresponds to a time-dependent VEV,
. We then assume that due to microscopic dynamics, this field develops a nonzero VEV. That is however not enough. We want the vacuum to describe matter, that is a state with nonzero density of the \(\mathrm {U}(1)\) charge. In a Lorentz-invariant scalar theory, a state of uniform nonzero charge density corresponds to a time-dependent VEV,
The constants \(\varphi _0\) and \(\mu \) are without loss of generality assumed to be positive. See Chap. 3 of [2] for an introduction to superfluidity from the field theory point of view.
The same superfluid state can also be represented by a constant order parameter at the cost of redefining the Lagrangian. Indeed, introduce a new scalar field, \(\Phi (x)\equiv \mathrm{e} ^{\mathrm{i} \mu t}\phi (x)\), so that our superfluid state amounts to \(\langle {\Phi (x)}\rangle =\varphi _0\). As a consequence of the field redefinition, \(\partial _0\phi =(\partial _0-\mathrm{i} \mu )\Phi \). This agrees with my previous observation (see Example 8.7) that an equilibrium state parameterized by the chemical potential \(\mu \) can be described in the Lagrangian formalism by a constant background gauge field, \(A_\mu =(\mu ,\mathbf 0)\). It is now clear that the order parameter (13.28) corresponds to a superfluid at rest. Using Lorentz invariance, a superfluid state in uniform motion can likewise be parameterized by a constant timelike \(A_\mu \), or equivalently by the VEV \(\varphi (x)=\varphi _0\mathrm{e} ^{-\mathrm{i} A\cdot x}\).
As we already saw in Example 13.3, the condensate (13.28) satisfies our technical assumption underlying the construction of EFT for systems with a twisted order parameter. Here we have \(U(\pi (x))=\mathrm{e} ^{\mathrm{i} \pi (x)Q}\), where \(\pi (x)\) is the phase of \(\phi (x)\) and Q is the generator of \(G_{\mathrm {int}}\simeq \mathrm {U}(1)\). The NG field transforms under the internal symmetry as  . The MC form (13.24) reduces to \(\omega (\pi ,x)=Q\mathrm{d} \pi +P\cdot \mathrm{d} x\). Upon dropping the tadpole operator, \(\pi \), which is itself quasi-invariant, the most general Poincaré- and \(\mathrm {U}(1)\)-invariant effective action can be written as
. The MC form (13.24) reduces to \(\omega (\pi ,x)=Q\mathrm{d} \pi +P\cdot \mathrm{d} x\). Upon dropping the tadpole operator, \(\pi \), which is itself quasi-invariant, the most general Poincaré- and \(\mathrm {U}(1)\)-invariant effective action can be written as
The effective Lagrangian \(\mathcal {L}_{\mathrm {eff}}\) is an arbitrary function of the derivatives of \(\pi \) in which all Lorentz indices have been contracted in a Lorentz-invariant manner.
Let us check that the tentative ground state, \(\langle {\pi (x)}\rangle =-\mu t\), satisfies the EoM. This follows from the equivalence of the EoM and the conservation of the Noether current of the internal \(\mathrm {U}(1)\) symmetry; see Example 4.2 for a proof of the equivalence. The current carried by the condensate (13.28) is necessarily constant, and thus automatically conserved for any values of \(\varphi _0\) and \(\mu \).
Next, we have to deal with power counting. I will follow closely the logic of Sect. 9.1.1, where a power-counting scheme for relativistic EFTs was worked out. A new complication is that we do not know a priori how large the chemical potential \(\mu \) is, and thus whether \(\partial _\mu \pi \) can be considered small. We therefore cannot naively expand the effective Lagrangian in the derivatives of \(\pi \). However, we can use the fact that every \(\pi \) in the Lagrangian always carries at least one “persistent” derivative and only count additional derivatives. This makes sense: introducing the fluctuation field \(\tilde \pi \) via (13.26), that is \(\pi (x)\equiv \tilde \pi (x)-\mu t\), any higher derivative kills the chemical potential and thus captures directly the variation of \(\tilde \pi \).
To formalize this observation, expand the effective Lagrangian as
were  collects all Lorentz-invariant operators with n additional derivatives. Now consider a generic Feynman diagram \(\Gamma \), contributing to a given observable. Denote as I the number of internal propagators in \(\Gamma \), as E the number of external legs, as L the number of loops, and as \(V_n\) the number of interaction vertices from each of
collects all Lorentz-invariant operators with n additional derivatives. Now consider a generic Feynman diagram \(\Gamma \), contributing to a given observable. Denote as I the number of internal propagators in \(\Gamma \), as E the number of external legs, as L the number of loops, and as \(V_n\) the number of interaction vertices from each of  . Think of the Fourier representation, in which the diagram amounts to a homogeneous function of energy–momenta on the external legs. Loop integration contributes altogether DL powers of energy–momenta, the internal propagators contribute \(-2I\) powers. The persistent derivatives on each field give \(2I+E\) powers of energy–momenta. Finally, the additional derivatives add up to \(\sum _{n\geq 0}nV_n\). Altogether, the naive degree of the diagram becomes
. Think of the Fourier representation, in which the diagram amounts to a homogeneous function of energy–momenta on the external legs. Loop integration contributes altogether DL powers of energy–momenta, the internal propagators contribute \(-2I\) powers. The persistent derivatives on each field give \(2I+E\) powers of energy–momenta. Finally, the additional derivatives add up to \(\sum _{n\geq 0}nV_n\). Altogether, the naive degree of the diagram becomes
For any given observable, E is fixed and \(\deg \Gamma \geq E\). The leading-order (LO) contribution comes from diagrams with \(L=0\) and \(V_n=0\) for any \(n\geq 1\). Accordingly, the LO effective Lagrangian for a relativistic superfluid is  : an arbitrary Lorentz-invariant function of \(\partial _\mu \pi \). The next-to-leading-order (NLO) Lagrangian requires two additional derivatives, \(n=2\). For any \(D\geq 3\), the NLO contribution to any observable corresponds to \(\deg \Gamma =E+2\) and amounts to tree-level (\(L=0\)) diagrams with one interaction vertex from
: an arbitrary Lorentz-invariant function of \(\partial _\mu \pi \). The next-to-leading-order (NLO) Lagrangian requires two additional derivatives, \(n=2\). For any \(D\geq 3\), the NLO contribution to any observable corresponds to \(\deg \Gamma =E+2\) and amounts to tree-level (\(L=0\)) diagrams with one interaction vertex from  and all others from
and all others from  . Interestingly, the contributions from loop diagrams only start to matter beyond NLO of the derivative expansion. Most important is that at any finite degree, only a finite number of Lagrangians
. Interestingly, the contributions from loop diagrams only start to matter beyond NLO of the derivative expansion. Most important is that at any finite degree, only a finite number of Lagrangians  and a finite number of Feynman diagrams is required. This renders the power-counting scheme consistent and predictive.
and a finite number of Feynman diagrams is required. This renders the power-counting scheme consistent and predictive.
It might still look troublesome that the LO Lagrangian can be an arbitrary Lorentz-invariant function of \(\partial _\mu \pi \). This surely contains an infinite number of unknown parameters, so how could such an EFT be useful? To address this question, note there is only one way to make such Lagrangians Lorentz-invariant, namely by contracting the Lorentz indices on \(\partial _\mu \pi \) pairwise. Then, upon separating the ground state from the fluctuations, the LO Lagrangian becomes
where P is some as yet unknown function. In the superfluid ground state, the Lagrangian reduces to a function of the chemical potential, \(P(\mu )\). This can be related to the energy density of the equilibrium state by Legendre transformation,
The prime indicates a derivative of P with respect to its argument. Also, I used that  and that \(\langle {\pi (x)}\rangle =-\mu t\). Equation (13.33) looks familiar: \(P(\mu )\) can be interpreted as the thermodynamic pressure of the superfluid at zero temperature, and \(P'(\mu )\equiv n(\mu )\) as the density of the \(\mathrm {U}(1)\) charge. Our main result therefore is that the LO EFT for superfluids at zero temperature (13.32) is completely fixed by the thermodynamic equation of state [3].
and that \(\langle {\pi (x)}\rangle =-\mu t\). Equation (13.33) looks familiar: \(P(\mu )\) can be interpreted as the thermodynamic pressure of the superfluid at zero temperature, and \(P'(\mu )\equiv n(\mu )\) as the density of the \(\mathrm {U}(1)\) charge. Our main result therefore is that the LO EFT for superfluids at zero temperature (13.32) is completely fixed by the thermodynamic equation of state [3].
To get a flavor of the physical content of the EFT, let us expand (13.32) to second order in the NG field,
This shows that the NG bosons propagate with the phase velocity
where I used the thermodynamic relations \(\mathrm{d} U=\mu \mathrm{d} n\) and \(\mathrm{d} P=n\mathrm{d} \mu \). It is remarkable that the phase velocity of the superfluid NG boson at zero temperature is given by the same expression (13.35) as that of hydrodynamic sound.
Example 13.5
For an illustration of these general results, let us have a look at dense matter consisting of relativistic (Dirac) fermions in \(d=3\) dimensions [3]. Provided the interactions between the particles are sufficiently weak and their mass sufficiently small, the equation of state can be well approximated by that of a free gas of massless fermions,Footnote 3
Suppose that the interaction between the fermions is attractive so that they form Cooper pairs in the spin-singlet, s-wave state. The fermionic quasiparticles near the Fermi surface then become gapped and decouple at sufficiently low energies. The low-energy physics of the system reduces to the dynamics of the condensate of scalar Cooper pairs. This is an example of a fermionic superfluid. According to (13.32), the low-energy EFT of such a system is dominated by a LO Lagrangian that is polynomial in the NG field,
The NG bosons propagate at the speed \(v=1/\sqrt {3}\), characteristic of a gas of weakly interacting ultrarelativistic particles. Note that in this case, the microscopic energy scale of the system is set by the chemical potential itself. The scale associated with the spontaneous breakdown of the \(\mathrm {U}(1)\) symmetry is assumed to be much smaller, which is ensured by the weak binding of the Cooper pairs. Thus, \(\mu \) could not have been treated as a small parameter in any reasonable sense.
3 Vector Modes: The Relevant, the Irrelevant and the Unphysical
As demonstrated in the previous chapter, the same symmetry-breaking pattern can be realized with various choices of order parameter. This ambiguity is innocuous for internal symmetries. On the other hand, in case of spacetime symmetries, it can lead to nonlinear realizations with apparently different numbers of NG variables. For instance, the superfluid order parameter (13.28) breaks the combined spacetime and internal symmetry in a rather nontrivial manner. First, it obviously breaks Lorentz boosts. Second, it breaks time translations and the internal \(\mathrm {U}(1)\) symmetry down to a “diagonal” subgroup, where the phase generated by a time translation is compensated by a \(\mathrm {U}(1)\) rotation. In the setup of Sect. 13.2.2, all this is implicitly taken into account. However, as pointed out in Sect. 12.4.3, it might be meaningful to add a secondary, vector order parameter, representing the VEV of the Noether current of the \(\mathrm {U}(1)\) symmetry. This requires introducing an additional vector of NG fields. Similarly, we saw in Sect. 12.4.4 that nonlinear realization of Galilei symmetry is easier to implement if one adds a vector of NG variables corresponding to Galilei boosts.
These observations raise obvious questions. Are the additional vector NG variables merely a useful mathematical tool, or do they correspond to actual modes in the spectrum? In case they are physical, what is their exact nature? To answer these questions, I will now work out several physically distinct examples, from nonlinear realization to concrete effective actions. With the additional insight, I will then in Sect. 13.3.4 attempt to draw general conclusions.
3.1 The Relevant: Helimagnets
Let us start with a familiar system where a vector field turns out to excite a physical, gapless NG mode. This will set a benchmark for our discussion of the role of vector NG modes. At the same time, it will provide the first example of an EFT going beyond the class of systems covered by Sect. 13.2. I already addressed spin systems in detail in Chap. 9. Moreover, I mentioned the exotic case of helimagnets on several occasions. I will therefore not spend time on reviewing the basic phenomenology, and instead start right away with a symmetry-based analysis.
We are talking about a condensed-matter system whose symmetry is captured by the Aristotelian group in three spatial dimensions, \(G\simeq \mathrm {SO}(3)\ltimes \mathbb {R}^4\). Unlike in Chap. 9, I will not include a separate internal symmetry under spin rotations. This is broken by the spin-orbit coupling, which plays a key role in the formation of the helimagnetic order. The order parameter is the local magnetization density, which is a vector under spatial rotations, hence \(\mathcal {M}\simeq \mathbb {R}^3\). We are of course interested in the physics of ordered states where the magnetization is nonzero. This fixes the two isotropy groups \(H_0\simeq \mathrm {SO}(3)\) and \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\). The local manifold decomposition (13.5) in this case becomes
The submanifold relevant for the nonlinear realization of the symmetry on the NG variables is \(H_0/H_{(\psi _0,0)}\times M\simeq S^2\times \mathbb {R}^4\). I will parameterize the spacetime using the translation operator \(\mathcal {T}_{\boldsymbol x,t}=\mathrm{e} ^{\mathrm{i} tH}\mathrm{e} ^{\mathrm{i} \boldsymbol {x}\cdot \boldsymbol {P}}\). The coset space \(S^2\) is parameterized by two local coordinates \(\pi ^a\), encoded in an \(\mathrm {SO}(3)\)-valued matrix \(U(\pi )\).
Having fixed the basic setup, we can read off the MC form from (13.3),

The second equality follows from the fact that the momentum operator carries a vector representation of \(\mathrm {SO}(3)\) under the adjoint action thereof.Footnote 4 Using (13.9), we subsequently identify the elements of the spacetime coframe,

The \(\omega _\perp \) part of the MC form comes entirely from \(-\mathrm{i} U(\pi )^{-1}\mathrm{d} U(\pi )\), i.e. is given by \(\omega ^a(\pi )=\omega ^a_b(\pi )\mathrm{d} \pi ^b\). The related covariant derivatives of the NG variables \(\pi ^a\) are extracted using (13.15),

Under the action of \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\), these split into the irreducible multiplets

Those on the first line of (13.42) are singlets, while the first two items on the second line transform as vectors under \(\mathrm {SO}(2)\). Finally, the last operator in (13.42) transforms as a traceless symmetric tensor of \(\mathrm {SO}(2)\). That is also a two-dimensional real representation, but carries a double charge of \(\mathrm {SO}(2)\) compared to the vector representation. This is important when combining the irreducible multiplets into an effective Lagrangian in a way that preserves invariance under \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\).
Before we can construct an effective action, we still need to consider power counting. Here I will, unlike for superfluids in Sect. 13.2.2, assume that the spatial variation of the order parameter is slow. This allows us to apply the naive scheme where each (covariant) derivative counts. The EFT will then be dominated by operators with the lowest number of derivatives. It is convenient to express the effective Lagrangian in terms of a unit-vector parameterization of the coset space, \(\boldsymbol n(\pi )\in S^2\). This is related to \(U(\pi )\) via \(\boldsymbol n(\pi )=U(\pi )\boldsymbol n_0\), where \(\boldsymbol n_0\in S^2\) is an arbitrary but fixed reference vector. The advantage of using the \(\boldsymbol n\) variable is that it makes invariance under the whole \(H_0\simeq \mathrm {SO}(3)\) manifest. Dropping surface terms, the most general invariant Lagrangian with up two derivatives consists of
All the operators in (13.43) are clearly invariant under spatial rotations. What is less obvious is that there are no other algebraically independent contributions to the invariant Lagrangian with up to two derivatives. This follows from the formalism based on the MC form, but would not be straightforward to check in the language using the \(\boldsymbol n\) field. Let me at least clarify why some apparent candidate operators do not give anything new. Starting with  , there is no operator of the type \((\boldsymbol \nabla \times \boldsymbol n)^2\), since this equals \(\delta ^{rs}\partial _r\boldsymbol n\cdot \partial _s\boldsymbol n-(\boldsymbol {\nabla }\cdot \boldsymbol {n})^2\) up to a surface term. Likewise, the operator \([\boldsymbol n\times (\boldsymbol \nabla \times \boldsymbol n)]^2\) is absent, being equal to \((\boldsymbol \nabla \times \boldsymbol n)^2-[\boldsymbol n\cdot (\boldsymbol \nabla \times \boldsymbol n)]^2\). Other candidate operators can be eliminated using the identity \((\boldsymbol {n}\cdot \boldsymbol {\nabla })\boldsymbol n=-\boldsymbol n\times (\boldsymbol \nabla \times \boldsymbol n)\), valid for a unit vector field \(\boldsymbol n\). Finally, there is no \(\partial _0\boldsymbol n\cdot (\boldsymbol \nabla \times \boldsymbol n)\) in
, there is no operator of the type \((\boldsymbol \nabla \times \boldsymbol n)^2\), since this equals \(\delta ^{rs}\partial _r\boldsymbol n\cdot \partial _s\boldsymbol n-(\boldsymbol {\nabla }\cdot \boldsymbol {n})^2\) up to a surface term. Likewise, the operator \([\boldsymbol n\times (\boldsymbol \nabla \times \boldsymbol n)]^2\) is absent, being equal to \((\boldsymbol \nabla \times \boldsymbol n)^2-[\boldsymbol n\cdot (\boldsymbol \nabla \times \boldsymbol n)]^2\). Other candidate operators can be eliminated using the identity \((\boldsymbol {n}\cdot \boldsymbol {\nabla })\boldsymbol n=-\boldsymbol n\times (\boldsymbol \nabla \times \boldsymbol n)\), valid for a unit vector field \(\boldsymbol n\). Finally, there is no \(\partial _0\boldsymbol n\cdot (\boldsymbol \nabla \times \boldsymbol n)\) in  , since this is itself a surface term. Similar reasoning shows that no new operators can be produced using second covariant derivatives such as
, since this is itself a surface term. Similar reasoning shows that no new operators can be produced using second covariant derivatives such as  or
or  .
.
The presence of  with a single spatial derivative is a new feature, arising from the vector order parameter. There is no invariant operator with a single time derivative. However, we know from Chap. 9 that an internal \(\mathrm {SU}(2)\) spin symmetry together with spatial rotational invariance admit a quasi-invariant Lagrangian,
with a single spatial derivative is a new feature, arising from the vector order parameter. There is no invariant operator with a single time derivative. However, we know from Chap. 9 that an internal \(\mathrm {SU}(2)\) spin symmetry together with spatial rotational invariance admit a quasi-invariant Lagrangian,
where \(a,b\in \{1,2\}\). Being free of spatial derivatives, this is also quasi-invariant under our \(H_0\simeq \mathrm {SO}(3)\) that acts on both \(\boldsymbol n\) and spatial coordinates. Finally, note that the coframe (13.40) yields the standard volume measure \(\mathrm{d} ^3\!\boldsymbol x\,\mathrm{d} t\) thanks to the fact that \(U(\pi )\) is an \(\mathrm {SO}(3)\)-valued matrix. This justifies a posteriori dropping surface terms from (13.43), and makes it actually possible to include a quasi-invariant Lagrangian such as (13.44).
In ferromagnets where the coupling \(c^{(0,1)}_1\) is nonzero, every time derivative counts as two spatial derivatives (see Sect. 9.2.1 for a detailed justification). We can then discard the  and
and  Lagrangians as subleading. Even with this simplification, there are still six independent operators in the
Lagrangians as subleading. Even with this simplification, there are still six independent operators in the  ,
,  and
and  Lagrangians. In order to make the analysis of the physical consequences of the EFT feasible, we need to take one more step to reduce the Lagrangian. Namely, the spin-orbit interaction in real materials is typically much weaker than other interactions. It therefore makes sense to treat the couplings of all the operators that lock the spin and orbital rotations together, namely
Lagrangians. In order to make the analysis of the physical consequences of the EFT feasible, we need to take one more step to reduce the Lagrangian. Namely, the spin-orbit interaction in real materials is typically much weaker than other interactions. It therefore makes sense to treat the couplings of all the operators that lock the spin and orbital rotations together, namely  ,
,  ,
,  and
and  , as small. Counting all of these formally as degree one in the derivative expansion, the entire LO (degree-two) effective Lagrangian will be just
, as small. Counting all of these formally as degree one in the derivative expansion, the entire LO (degree-two) effective Lagrangian will be just
Here I have already switched to the physical notation for the effective couplings: M for the local magnetization density, \(\varrho _{\mathrm {s}}\) for the spin stiffness, and \(\lambda _{\mathrm {DM}}\) for the length scale of the DM interaction. The latter is all that is left of the effects of the spin-orbit coupling at the LO of the derivative expansion.
I showed already in Example 9.10 that the DM interaction inevitably leads to the formation of a helical structure in the ground state. One can without loss of generality choose a Cartesian system of coordinates such that
where \(k\equiv 2\pi /\lambda _{\mathrm {DM}}\). Let us next focus on the excitation spectrum. The first step in that regard is to reparameterize the field following the logic of (13.26),
The variable \(\boldsymbol N(\boldsymbol x,t)\) is still a unit vector. Moreover, in the ground state it is constant, \(\langle {\boldsymbol N(\boldsymbol x,t)}\rangle \equiv \boldsymbol N_0=(1,0,0)\). This allows us to identify independent fluctuations around the ground state with the \(N^2\) and \(N^3\) components of \(\boldsymbol N\).
The task to express the Lagrangian (13.45) in terms of \(\boldsymbol N\) is a bit tedious, and the final result is not elegant. I will therefore skip the straightforward details and only spell out the part of the Lagrangian bilinear in \(N^2,N^3\). Up to a surface term,
where
The excitation spectrum is determined by the zero modes of the matrix differential operator in (13.48). Due to the explicit coordinate dependence, this is a complicated problem. I will therefore content myself with some simple observations that illustrate the peculiarities of helimagnets. To start with, the presence of operators with a single time derivative makes the two degrees of freedom \(N^2,N^3\) canonically conjugate to each other. The spectrum should therefore consist of a single type of magnon, just like in uniform ferromagnets in the absence of the DM interaction. The magnon dispersion relation can be calculated explicitly in the special case of propagation along the helix axis. The single-particle wave function is then independent of the \(x,y\) coordinates so that  . A Fourier transform in time and the z-coordinate then gives the energy as a function of momentum,
. A Fourier transform in time and the z-coordinate then gives the energy as a function of momentum,
The physical momentum \(p_z\) should be much smaller than the inverse of the length scale associated with the formation of the ferromagnetic order, which can be thought of as \(\sqrt {\varrho _{\mathrm {s}}}\). This defines the range of validity of the EFT. Within this range, however, there are two qualitatively different regimes. At long wavelengths, \(p_z\ll k\), (13.50) is well approximated by \(E(p_z)\approx (k\varrho _{\mathrm {s}}/M)\left \lvert {p_z}\right \rvert \). The dispersion relation is linear. The corresponding one-particle state is a linearly polarized spin wave with \(N^3\approx 0\). This amounts to spin oscillations in the xy plane along the direction perpendicular locally to \(\boldsymbol n_0(\boldsymbol x)\). On the other hand, at intermediate wavelengths, \(k\ll p_z\ll \sqrt {\varrho _{\mathrm {s}}}\), the dispersion relation (13.50) turns into \(E(p_z)\approx (\varrho _{\mathrm {s}}/M)p_z^2\). This reproduces the standard ferromagnetic magnon spectrum we found in Sect. 9.2.2. Physically, this means that such short-distance oscillations of spin are insensitive to the helical structure of the ground state. The magnon is circularly polarized in the plane perpendicular to the local magnetization \(\boldsymbol n_0(\boldsymbol x)\).
This concludes our excursion to helimagnetism. We have discovered very interesting physics, but no surprises as to the number and type of NG modes in the spectrum so far. To that end, we will capitalize on the experience we have collected here to explore another fascinating physical system: liquid crystals.
3.2 The Irrelevant: Smectic Liquid Crystals
Liquid crystals are an intriguing exotic state of matter; see [4] for a thorough account of the subject. The basic ingredient underlying the liquid crystal order is a strongly anisotropic microscopic constituent. This is typically an elongated organic molecule or a polymer, with a rigid, rod-like structure. An ordered ground state arises from a geometric arrangement of the molecules that breaks invariance under spatial translations or rotations, or both.
I will be mostly concerned with the interplay of two simple liquid crystal phases: the nematic phase and the smectic (or more precisely smectic-A) phase. In the nematic phase, the microscopic constituents are aligned along a common direction but their spatial positions remain disordered as in an ordinary liquid. See the left panel of Fig. 13.1 for a visualization. In the smectic phase, the alignment persists but the constituents are in addition organized in parallel layers. Within each layer, however, their positions remain disordered; see the right panel of Fig. 13.1. Both of these phases feature an order parameter that defines the axis of alignment, and can be viewed as an “unoriented vector.” To describe smectics, one needs in addition a secondary order parameter that accounts for the layered structure of the medium.
The microscopic symmetry governing the physics of liquid crystals is the same as that of spin systems with spin-orbit coupling, \(G\simeq \mathrm {SO}(3)\ltimes \mathbb {R}^4\). In the simpler nematic phase, which I will start with, the target space is \(\mathcal {M}\simeq \mathbb {R}^3/\mathbb {Z}_2\), where any vector in \(\mathbb {R}^3\) is identified with its opposite. This setup is almost identical to that of Sect. 13.3.1, and we can therefore largely reuse the EFT developed therein. The change in the global structure of \(\mathcal {M}\) from \(\mathbb {R}^3\) to \(\mathbb {R}^3/\mathbb {Z}_2\) affects the nature of topological defects in the medium. However, as far as the dynamics of small fluctuations of the order parameter is concerned, all we have to do is impose invariance under the reflection \(\boldsymbol n\to -\boldsymbol n\). This kills, first of all, the quasi-invariant Lagrangian (13.44), for there is no equivalent of “magnetization” in liquid crystals that the coupling  could measure. Moreover, the
could measure. Moreover, the  and
and  terms in (13.43) drop out, being odd in \(\boldsymbol n\). In materials that respect spatial parity, we can finally discard the
terms in (13.43) drop out, being odd in \(\boldsymbol n\). In materials that respect spatial parity, we can finally discard the  term.Footnote 5 All in all, the LO Lagrangian for the fluctuations of the order parameter in nematics consists of the
term.Footnote 5 All in all, the LO Lagrangian for the fluctuations of the order parameter in nematics consists of the  ,
,  ,
,  and
and  operators. However, a somewhat different basis of operators with spatial derivatives is more common in the literature, namely
operators. However, a somewhat different basis of operators with spatial derivatives is more common in the literature, namely
The advantage of this parameterization is that there are field configurations for which all but one of the operators in (13.51) vanish. Global stability of the uniform state with constant \(\langle {\boldsymbol n(x)}\rangle \equiv \boldsymbol n_0\) thus requires that all the couplings \(K_{1,2,3}\) are positive. For completeness, let me add that they are related to the parameters in (13.43) by  ,
,  and
and  up to integration by parts.
up to integration by parts.
Unlike in the case of helimagnets, I will not use the Lagrangian (13.51) to analyze the spectrum of excitations of a nematic. Namely, to get a physically correct picture of the dynamics, one would need to consider the interplay of the vector variable \(\boldsymbol n\) with hydrodynamic degrees of freedom (see Sect. 8.5 of [6]). After all, we are talking about liquids. Our restricted setting will however be sufficient to contrast the NG degrees of freedom in the nematic and smectic-A phases.
To describe the smectic state, we need an additional order parameter accounting for the layered structure as shown in the right panel of Fig. 13.1. This can be done with a single real scalar field \(\phi (x)\). The layers of the medium are then defined as surfaces of constant \(\phi \). The translation across one layer of molecules changes \(\phi (x)\) by a fixed amount; I will use a normalization of \(\phi (x)\) where the increment equals \(2\pi \). Interestingly, this picture implies the existence of a new, emergent symmetry. Namely, for the sake of identification of the individual strata of the smectic, it does not matter what the attached value of \(\phi \) is. None of the surfaces of constant \(\phi \) changes if we shift \(\phi (x)\) by a constant. The EFT for smectic liquid crystals should therefore be invariant under the internal symmetry  . This is our first example of an emergent symmetry arising from the spatial distribution of a medium; I will give a more systematic account of such symmetries in Chap. 14. The complete symmetry group of a smectic is then \(G\simeq [\mathrm {SO}(3)\ltimes \mathbb {R}^4]\times \mathbb {R}\). The corresponding isotropy groups are \(H_0\simeq \mathrm {SO}(3)\times \mathbb {R}\) and \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\). The degrees of freedom of the EFT are determined by the coset space \(H_0/H_{(\psi _0,0)}\simeq S^2\times \mathbb {R}\).
. This is our first example of an emergent symmetry arising from the spatial distribution of a medium; I will give a more systematic account of such symmetries in Chap. 14. The complete symmetry group of a smectic is then \(G\simeq [\mathrm {SO}(3)\ltimes \mathbb {R}^4]\times \mathbb {R}\). The corresponding isotropy groups are \(H_0\simeq \mathrm {SO}(3)\times \mathbb {R}\) and \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\). The degrees of freedom of the EFT are determined by the coset space \(H_0/H_{(\psi _0,0)}\simeq S^2\times \mathbb {R}\).
The values of the two order parameters in the smectic ground state are correlated. As indicated in Fig. 13.1, the axis of alignment \(\boldsymbol n_0\) of the molecules is perpendicular to the entire stack of parallel layers. Moreover, the individual molecular layers are equidistantly spaced. This implies that the VEV of the gradient \(\langle {\boldsymbol \nabla \phi (x)}\rangle \) is a constant nonzero vector, parallel to \(\boldsymbol n_0\). I will use the notation
where the parameter k defines the distance between neighboring layers, \(2\pi /k\).
The shift symmetry \(\mathbb {R}\) guarantees that \(\phi (x)\) can only enter the effective Lagrangian with derivatives. Being a scalar under rotations, its covariant derivatives are

where \(U(\pi )\) is still the matrix related to \(\boldsymbol n\) by \(\boldsymbol n(\pi )=U(\pi )\boldsymbol n_0\). Also, I used the previously derived coframe (13.40), which is not affected by adding the scalar field \(\phi (x)\). The appearance of these covariant derivatives in the effective Lagrangian is constrained by the isotropy group \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\) and the reflection \(\boldsymbol n\to -\boldsymbol n\). To these we should add the discrete symmetry under \(\phi \to -\phi \) which, just like the internal shifts of \(\phi \), preserves the identification of the layers of the smectic. With these constraints, the contributions of \(\phi (x)\) to the LO effective Lagrangian are reduced to
In order for the alignment of \(\boldsymbol \nabla \phi \) and \(\boldsymbol n\) to be energetically preferred, the spatial gradient couplings \(c_\parallel \) and \(c_\perp \) should satisfy \(c_\perp <c_\parallel \).
Let us now turn the argument around and see how the background (13.52) affects the vector field \(\boldsymbol n\). I will set without loss of generality \(\boldsymbol n_0=(0,0,1)\) so that the two independent fluctuations of \(\boldsymbol n\) correspond to \(n^1\) and \(n^2\). This reduces (13.54) to
Thanks to the stability constraint on the couplings, \(c_\parallel -c_\perp >0\). What we have here is therefore a well-defined, positive-definite mass term for the fluctuations of \(\boldsymbol n\).
Let us pause to appreciate the implications of this result. In the nematic phase, we dealt with two NG degrees of freedom, parameterizing via the unit vector \(\boldsymbol n\) the coset space \(S^2\). In the smectic phase, we extended the coset space to \(S^2\times \mathbb {R}\). The corresponding new NG variable parameterizes the fluctuations of \(\phi \) around its VEV (13.52). Given that \(\phi \) only enters the effective Lagrangian with derivatives, it necessarily couples to a NG mode in the spectrum. However, at the same time, the fluctuations of \(\boldsymbol n\) received a gap. Adding an extra NG field has reduced the number of NG modes from two to one!
To understand what is going on, think of the order parameter (13.52) alone. Being a spatial vector, the gradient \(\boldsymbol \nabla \phi \) spontaneously breaks spatial rotations in addition to the internal shift symmetry of \(\phi \) and translations in the direction of \(\boldsymbol n_0\). We may then treat \(\langle {\boldsymbol n(x)}\rangle \equiv \boldsymbol n_0\) as a secondary order parameter, since it does not break any symmetries that would be left intact by \(\langle {\phi (x)}\rangle \). This makes the \(\boldsymbol n\) mode redundant: its presence is not required to reproduce the symmetry-breaking pattern of a smectic. Consequently, the fluctuations of \(\boldsymbol n\) are not protected by symmetry from acquiring a gap.
This is an explicit realization of an issue I alerted the reader to already in Chap. 12. The number of true, gapless NG degrees of freedom (one) is fixed by the symmetry-breaking pattern. However, the additional, would-be NG modes contained in \(\boldsymbol n(x)\) are physical and may manifest themselves as low-lying excitations of the smectic ground state. The nematic and smectic phases of liquid crystals are separated by a continuous (second-order) phase transition. At the transition point, the scale k vanishes. Accordingly, near the phase transition, the gap of the \(\boldsymbol n\)-type fluctuations is very small and they need to be included in the low-energy EFT.
Further away from the phase transition, we expect the gapped modes to have little effect on the low-energy physics. In this regime, it should be possible to construct an EFT for smectics in terms of \(\phi (x)\) alone. This can be arrived at in two different ways. One possibility is to start from a combination of (13.51) and (13.54) and integrate out the vector \(\boldsymbol n\). The other possibility is to construct the EFT for \(\phi (x)\) alone from scratch. This is arguably more straightforward but less predictive, since the effective couplings of the EFT will be unrelated to those in (13.51) and (13.54). For illustration, I will nevertheless choose the latter option as it highlights the physics of the NG mode in the smectic phase.
The task to find an EFT for a scalar field \(\phi \), subject to an internal shift symmetry \(\mathbb {R}\), copies closely the construction of Sect. 13.2.2, with two differences. The first difference is minor. Namely, unlike in Sect. 13.2.2, we do not impose full Poincaré invariance, but merely the Aristotelian symmetry. The resulting effective Lagrangian is, in analogy with (13.29), a function of derivatives of \(\phi (x)\) where spatial indices are contracted in a way preserving invariance under spatial rotations. The second difference is absolutely essential: we want our EFT to stabilize the anisotropic smectic state (13.52). To that end, let us parameterize the fluctuations of \(\phi (x)\) by a NG field \(\pi (x)\) such that \(\phi (\boldsymbol x,t)=k\boldsymbol n_0\cdot \boldsymbol x+\pi (\boldsymbol x,t)\). The basic rotationally invariant building block for the construction of the Lagrangian is  . Dropping the constant piece, the part of the effective Lagrangian with one derivative per field will be a generic function of \(\partial _0\pi \) and \(k\boldsymbol n_0\cdot \boldsymbol \nabla \pi +(\boldsymbol \nabla \pi )^2/2\). The static part of the effective Lagrangian, bilinear in the NG field \(\pi (x)\), is thus contained in
. Dropping the constant piece, the part of the effective Lagrangian with one derivative per field will be a generic function of \(\partial _0\pi \) and \(k\boldsymbol n_0\cdot \boldsymbol \nabla \pi +(\boldsymbol \nabla \pi )^2/2\). The static part of the effective Lagrangian, bilinear in the NG field \(\pi (x)\), is thus contained in
The ellipsis includes operators that are bilinear in \(\pi (x)\) but contain more than one derivative per field. The leading operator of this kind is \(c_3(\boldsymbol \nabla ^2\phi )^2=c_3(\boldsymbol \nabla ^2\pi )^2\).
Remarkably, the \(c_1\) operator is forbidden. The easiest way to see this is to think of the gradient \(\boldsymbol \nabla \phi \) as a vector field, \(\boldsymbol A\equiv \boldsymbol \nabla \phi \). The part of the static Lagrangian with one derivative per \(\phi \) is then a mere function of \(\boldsymbol A\). Should the corresponding Hamiltonian density have a minimum for nonzero \(\langle {\boldsymbol A}\rangle =k\boldsymbol n_0\) as implied by (13.52), its Hessian matrix at the minimum must have two zero modes. This is just the statement of the Goldstone theorem in terms of the eigenvalues of the mass matrix, which we proved back in Sect. 3.1. Hence, for the smectic state (13.52) to be stable within the EFT, the Lagrangian (13.56) must not contain any terms quadratic in the part of the gradient of \(\pi \), perpendicular to \(\boldsymbol n_0\). It is the stability criterion together with the spontaneously broken rotational invariance that forbids the \(c_1\) operator.
We conclude that the leading contributions to the bilinear Lagrangian consist of the operators \((\partial _0\pi )^2\), \((\boldsymbol \nabla _\parallel \pi )^2\) and \((\boldsymbol \nabla _\perp ^2\pi )^2\), where \(\parallel \) and \(\perp \) denote projections to directions parallel and transverse to \(\boldsymbol n_0\). This suggests an unusual, anisotropic power counting. For all these operators to contribute at the same order, the time derivative should have the same counting degree as \(\boldsymbol \nabla _\parallel \) and \(\boldsymbol \nabla _\perp ^2\). The presence of a higher power of the transverse gradient has a profound impact on the stability of the smectic phase at nonzero temperature. I will relegate a more detailed discussion and further generalization of this observation to Chap. 15.
3.3 The Unphysical: Nonrelativistic Superfluids
The final example in our exploration of the role of vector modes will be nonrelativistic superfluids. Here we do know a priori that it is possible to construct an EFT solely in terms of a scalar degree of freedom. All one has to do is to take the EFT for a relativistic superfluid, developed in Sect. 13.2.2, and perform a nonrelativistic limit. It is however instructive to carry out the construction of the nonrelativistic version of the EFT from scratch.
To get started, recall the basic properties of Galilei symmetry from Sect. 12.4.4. The Lie algebra of the Galilei group in d spatial dimensions includes the generators  and H of space and time translations and
and H of space and time translations and  of spatial rotations. In addition, there is a vector generator
of spatial rotations. In addition, there is a vector generator  of Galilei boosts. I will add from the outset a central charge Q whose eigenvalues measure nonrelativistic mass. This turns the Galilei group into the Bargmann group. Altogether, the nontrivial part of the local structure of the symmetry group is determined by the commutation relations
of Galilei boosts. I will add from the outset a central charge Q whose eigenvalues measure nonrelativistic mass. This turns the Galilei group into the Bargmann group. Altogether, the nontrivial part of the local structure of the symmetry group is determined by the commutation relations

The commutators of  are fixed by rotation invariance and will not be needed. All the other commutators not listed here are vanishing. Mathematically, the Bargmann group has the structure \(G\simeq \mathrm {SO}(d)\ltimes \{\mathbb {R}^d_K\ltimes [\mathbb {R}^D\times \mathrm {U}(1)_Q]\}\). All the symmetry transformations but translations leave the spacetime origin fixed, hence its isotropy group is \(H_0\simeq [\mathrm {SO}(d)\ltimes \mathbb {R}^d_K]\times \mathrm {U}(1)_Q\). The translations themselves will be represented by the operator \(\mathcal {T}_{\boldsymbol x,t}\equiv \mathrm{e} ^{\mathrm{i} tH}\mathrm{e} ^{\mathrm{i} \boldsymbol {x}\cdot \boldsymbol {P}}\).
are fixed by rotation invariance and will not be needed. All the other commutators not listed here are vanishing. Mathematically, the Bargmann group has the structure \(G\simeq \mathrm {SO}(d)\ltimes \{\mathbb {R}^d_K\ltimes [\mathbb {R}^D\times \mathrm {U}(1)_Q]\}\). All the symmetry transformations but translations leave the spacetime origin fixed, hence its isotropy group is \(H_0\simeq [\mathrm {SO}(d)\ltimes \mathbb {R}^d_K]\times \mathrm {U}(1)_Q\). The translations themselves will be represented by the operator \(\mathcal {T}_{\boldsymbol x,t}\equiv \mathrm{e} ^{\mathrm{i} tH}\mathrm{e} ^{\mathrm{i} \boldsymbol {x}\cdot \boldsymbol {P}}\).
In order to describe the superfluid order, we need an order parameter that carries a nontrivial action of the internal \(\mathrm {U}(1)_Q\) subgroup. Similarly to relativistic superfluids, the simplest choice is a complex scalar field \(\psi \). For any \(\psi _0\neq 0\), the corresponding isotropy group is then \(H_{(\psi _0,0)}\simeq \mathrm {SO}(d)\ltimes \mathbb {R}^d_K\). However, as pointed out before, this is not satisfactory, since it violates our requirements on the decomposition (13.6) of the Lie algebra \(\mathfrak {g}\) of G. Namely, the operators  and H span a basis of \(\mathfrak {g}/\mathfrak {h}_0\) but do not carry a representation of \(H_{(\psi _0,0)}\). The way out is to add a secondary order parameter \(A^\mu \equiv (A^0,\boldsymbol A)\) that transforms as a vector under Galilei boosts. Choosing \(A^\mu _0=(a,\mathbf 0)\) with \(a\neq 0\) can be interpreted as specifying the density of the \(\mathrm {U}(1)_Q\) charge in the rest frame of the superfluid. It reduces the isotropy subgroup further to \(H_{((\psi _0,A_0),0)}\simeq \mathrm {SO}(d)\). The coset space
and H span a basis of \(\mathfrak {g}/\mathfrak {h}_0\) but do not carry a representation of \(H_{(\psi _0,0)}\). The way out is to add a secondary order parameter \(A^\mu \equiv (A^0,\boldsymbol A)\) that transforms as a vector under Galilei boosts. Choosing \(A^\mu _0=(a,\mathbf 0)\) with \(a\neq 0\) can be interpreted as specifying the density of the \(\mathrm {U}(1)_Q\) charge in the rest frame of the superfluid. It reduces the isotropy subgroup further to \(H_{((\psi _0,A_0),0)}\simeq \mathrm {SO}(d)\). The coset space  can be parameterized by NG variables \(\pi \) and \(\xi ^r\) through \(U(\pi ,\boldsymbol \xi )\equiv \mathrm{e} ^{\mathrm{i} \pi Q}\mathrm{e} ^{\mathrm{i} \boldsymbol {\xi }\cdot \boldsymbol {K}}\). In this parameterization, a Galilei boost with velocity \(\boldsymbol v\) acts on the NG variables and the spacetime coordinates as
can be parameterized by NG variables \(\pi \) and \(\xi ^r\) through \(U(\pi ,\boldsymbol \xi )\equiv \mathrm{e} ^{\mathrm{i} \pi Q}\mathrm{e} ^{\mathrm{i} \boldsymbol {\xi }\cdot \boldsymbol {K}}\). In this parameterization, a Galilei boost with velocity \(\boldsymbol v\) acts on the NG variables and the spacetime coordinates as
With all the pieces at hand, we can now compute the MC form (13.3),
The \(\omega _\parallel \) part of the MC form is trivial. From \(\omega _P=H\mathrm{d} t+\boldsymbol P\cdot (\mathrm{d} \boldsymbol x-\boldsymbol \xi \mathrm{d} t)\), we extract the spacetime coframe,  and
and  . The
. The  term in
term in  does not affect the spacetime volume form, we can thus use the volume measure \(\mathrm{d} ^d\!\boldsymbol x\,\mathrm{d} t\) to turn effective Lagrangians into effective actions. To construct covariant derivatives of the NG fields, we will also need the spacetime frame, dual to the above coframe,
does not affect the spacetime volume form, we can thus use the volume measure \(\mathrm{d} ^d\!\boldsymbol x\,\mathrm{d} t\) to turn effective Lagrangians into effective actions. To construct covariant derivatives of the NG fields, we will also need the spacetime frame, dual to the above coframe,

The covariant derivatives of \(\pi \) and \(\xi ^r\) are then extracted from the \(\omega _\perp \) part of the MC form (13.59) with the help of (13.15),

It is an easy exercise to check explicitly that all these covariant derivatives are invariant under the Galilei boost (13.58). Thanks to their simple form, it is not necessary to distinguish frame and coordinate-basis indices. In the following, I will therefore happily use \(\nabla _r\pi =\partial _r\pi -\xi _r\) and \(\nabla _s\xi ^r=\partial _s\xi ^r\).
In accord with the general machinery of nonlinear realizations, we could also add matter fields, organized in linear multiplets of \(H_{((\psi _0,A_0),0)}\simeq \mathrm {SO}(d)\). By (13.17), the covariant derivatives of a matter field \(\chi ^\varrho \) would then be  and
and  . This opens the possibility to promote (almost) any nonrelativistic theory with Aristotelian symmetry to a theory that is Galilei-invariant. Indeed, recall that in Part III of the book, we dealt largely with Aristotelian EFTs where we imposed invariance under linearly realized rotations by hand. What prevents us from introducing an auxiliary vector field \(\xi ^r\) and replacing \(\partial _0\to \nabla _0\equiv \partial _0+\boldsymbol {\xi }\cdot \boldsymbol {\nabla }\) everywhere? This will certainly work for strictly invariant Lagrangians. (The naive replacement \(\partial _0\to \nabla _0\) might spoil the quasi-invariance of Lagrangians that shift upon a symmetry transformation by a total time derivative.) The only fly in the ointment is that we do not have a physical interpretation for the \(\xi ^r\) field in terms of the NG degrees of freedom of the Aristotelian EFT. Rather, \(\xi ^r\) should be viewed as the local velocity of a medium carrying the NG modes; the combination \(\partial _0+\boldsymbol {\xi }\cdot \boldsymbol {\nabla }\) is often referred to as the material derivative. The Aristotelian EFTs constructed in Chap. 8 describe the low-energy physics in the rest frame of the medium. The same remark applies to relativistic systems. There, adding a NG field for Lorentz boosts allows one to promote an Aristotelian theory to one invariant under the full Poincaré group.
. This opens the possibility to promote (almost) any nonrelativistic theory with Aristotelian symmetry to a theory that is Galilei-invariant. Indeed, recall that in Part III of the book, we dealt largely with Aristotelian EFTs where we imposed invariance under linearly realized rotations by hand. What prevents us from introducing an auxiliary vector field \(\xi ^r\) and replacing \(\partial _0\to \nabla _0\equiv \partial _0+\boldsymbol {\xi }\cdot \boldsymbol {\nabla }\) everywhere? This will certainly work for strictly invariant Lagrangians. (The naive replacement \(\partial _0\to \nabla _0\) might spoil the quasi-invariance of Lagrangians that shift upon a symmetry transformation by a total time derivative.) The only fly in the ointment is that we do not have a physical interpretation for the \(\xi ^r\) field in terms of the NG degrees of freedom of the Aristotelian EFT. Rather, \(\xi ^r\) should be viewed as the local velocity of a medium carrying the NG modes; the combination \(\partial _0+\boldsymbol {\xi }\cdot \boldsymbol {\nabla }\) is often referred to as the material derivative. The Aristotelian EFTs constructed in Chap. 8 describe the low-energy physics in the rest frame of the medium. The same remark applies to relativistic systems. There, adding a NG field for Lorentz boosts allows one to promote an Aristotelian theory to one invariant under the full Poincaré group.
With the basic building blocks at hand, we can proceed to the construction of an EFT for the superfluid. Following closely the relativistic counterpart in Sect. 13.2.2, we first fix a power-counting scheme. We again count both \(\partial _0\pi \) and \(\boldsymbol \nabla \pi \) as degree zero. For the covariant derivatives in (13.61) to have a consistent counting degree, we have to assign \(\xi ^r\) degree zero as well. Any other derivative acting on \(\pi \) or \(\xi ^r\) will then have degree one. It follows that at the LO of the derivative expansion, we can ignore \(\nabla _\mu \xi ^r\). The LO Lagrangian will be some function of the rotationally invariant operators \(\nabla _0\pi \) and \(\delta ^{rs}\nabla _r\pi \nabla _s\pi \). This underlines the fact that the field \(\xi ^r\) is merely auxiliary and does not represent independent degrees of freedom. Indeed, it only enters the LO Lagrangian without any derivatives and can be eliminated algebraically by imposing its EoM,
The natural solution is \(\boldsymbol \xi =\boldsymbol \nabla \pi \), which turns the two building blocks for the LO Lagrangian to \(\nabla _0\pi \to \partial _0\pi +(\boldsymbol \nabla \pi )^2/2\) and \(\nabla _r\pi \to 0\). Of course, (13.62) can also be satisfied if the expression in square brackets vanishes. This would imply that the LO Lagrangian only depends on \(\nabla _0\pi +(1/2)\delta ^{rs}\nabla _r\pi \nabla _s\pi =\partial _0\pi +(\boldsymbol \nabla \pi )^2/2\). Either way, we end up with the same LO Lagrangian in terms of \(\pi \) alone.
Finally, recall the superfluid ground state can be described by a time-dependent VEV of a complex scalar field. This amounts to \(\langle {\pi (x)}\rangle =-\mu t\) where \(\mu \) is the chemical potential. The fluctuations around this background can be parameterized by a field \(\tilde \pi \) such that \(\pi (x)=\tilde \pi (x)-\mu t\). Following again the analogy with Sect. 13.2.2, we conclude that the LO effective Lagrangian for Galilei-invariant superfluids reads
The function \(P(\mu )\) represents the thermodynamic pressure of the superfluid in equilibrium at zero temperature.
Example 13.6
As a simple application of our new EFT, expand the Lagrangian (13.63) to second order in the NG field \(\tilde \pi \). Up to a surface term, we find
This gives immediately the phase velocity of the NG boson,
where \(n(\mu )\equiv P'(\mu )\) should be interpreted as the mass density of the superfluid. This matches the relativistic result \(v=\sqrt {\mathrm{d} {P}/\mathrm{d} {U}}\) in (13.35), since in the nonrelativistic limit, the energy density \(U(\mu )\) reduces to the density of the rest mass. Note that in spite of the appearance, the EFT (13.63) describes a type-A NG mode with a linear dispersion relation. This justifies a posteriori the use of the power-counting scheme where temporal and spatial derivatives are counted equally.
Before closing the discussion of nonrelativistic superfluids, I have a debt to pay off. Namely, when constructing the EFT, I tacitly assumed the effective Lagrangian to be strictly invariant. Could the Lagrangian also include some quasi-invariant contributions? The answer to this question is surprisingly rich, but luckily will not affect the LO Lagrangian (13.63).
As pointed out in Sect. 8.1, quasi-invariant Lagrangians for broken internal symmetries are classified by relative Lie algebra cohomology. It is not clear whether this elegant result survives all the complications of nonlinear realization of spacetime symmetries. Let us nevertheless take a leap of faith and see where it will lead us. We thus seek \((D+1)\)-forms that are closed and \(H_0\)-invariant. I will first split the MC form (13.59) into components corresponding to the individual generators,
We are now to take the exterior product of \(D+1\) of these 1-forms. Invariance under the whole isotropy group \(H_0\) is ensured by contracting vector indices in a rotationally invariant manner. It is the closedness requirement that poses a challenge. To that end, we take note of the MC equations, reflecting the commutation relations (13.57) between the generators,
These suggest a set of \(d+1\) naturally closed, rotationally invariant \((D+1)\)-forms,
where \(n=0,\dotsc ,d\). The corresponding effective Lagrangians are equivalent to the D-form potentials of these \((D+1)\)-forms, that is such  that
that  . These D-form potentials are obviously not unique, since they can be shifted without consequences by the exterior derivative of any \((D-1)\)-form. A suitable choice is
. These D-form potentials are obviously not unique, since they can be shifted without consequences by the exterior derivative of any \((D-1)\)-form. A suitable choice is
A reader wishing to check this may find the following identity useful,
Next, we eliminate the auxiliary field \(\xi ^r\) by imposing the same constraint as above, \(\boldsymbol \xi =\boldsymbol \nabla \pi \). After some manipulation, the D-form potentials (13.69) then give a set of \(d+1\) quasi-invariant Lagrangians (with adjusted overall normalization),

The form of the Lagrangians (13.71) should ring a bell. Indeed, except for replacing spacetime indices with spatial ones, these are exactly the Galileon Lagrangians (10.54). The similarity is not accidental. The generators \(Q,K_\mu \) of the constant and linear parts of the Galileon symmetry (10.53) and the energy–momentum operator \(P_\mu \) satisfy the commutation relation \([P_\mu ,K_\nu ]=\mathrm{i} g_{\mu \nu }Q\). This is identical to the centrally extended commutator in the Bargmann algebra. We have thus killed two birds with one stone, explaining the origin of the Galileon Lagrangians as a byproduct of our discussion of Galilei-invariant superfluids. Now back to the physical content of (13.71). The \(n=0\) Lagrangian,  , is a tadpole operator. This must be dropped to keep the EFT stable. The \(n=1\) Lagrangian is equivalent to \((\boldsymbol \nabla \pi )^2\) by partial integration. This is, in spite of appearance, already included in the LO effective Lagrangian (13.63). Namely, it is a part of \(\partial _0\pi +(\boldsymbol \nabla \pi )^2/2\) where \(\partial _0\pi \) itself is a surface term. Finally, all the quasi-invariant Lagrangians (13.71) with \(n\geq 2\) contain more than one derivative per field. Consequently, they will only contribute at higher, subleading orders of the derivative expansion of the superfluid EFT.
, is a tadpole operator. This must be dropped to keep the EFT stable. The \(n=1\) Lagrangian is equivalent to \((\boldsymbol \nabla \pi )^2\) by partial integration. This is, in spite of appearance, already included in the LO effective Lagrangian (13.63). Namely, it is a part of \(\partial _0\pi +(\boldsymbol \nabla \pi )^2/2\) where \(\partial _0\pi \) itself is a surface term. Finally, all the quasi-invariant Lagrangians (13.71) with \(n\geq 2\) contain more than one derivative per field. Consequently, they will only contribute at higher, subleading orders of the derivative expansion of the superfluid EFT.
3.4 Inverse Higgs Constraints
The analysis of concrete examples has given us enough experience to appreciate the broader spectrum of subtleties associated with spontaneous breaking of spacetime symmetries. Let us reevaluate what we have learned in particular about the role of vector fields. I should warn the reader that this matter is not yet quite settled. Hence, the content and organization of the discussion below is necessarily more subjective than elsewhere in the book.
In case of internal symmetries, the situation is clear. There is a one-to-one mapping between broken symmetry generators and NG fields in the low-energy EFT. The construction of the EFT itself is fairly streamlined. All one needs to know is the symmetry-breaking pattern. As shown in Chap. 8, finding the EFT then boils down to solving certain linear-algebraic constraints for the tensor couplings in the effective Lagrangian. The functional dependence of the Lagrangian on the NG fields is completely fixed by symmetry.
In case of spontaneously broken spacetime symmetry, we would hope to be able to do the same. This desire lies behind the agnostic nonlinear realization that I already mentioned in Sect. 12.3.2. In this framework, one starts with a separate NG field for each spontaneously broken symmetry generator. The actions of all the generators in an abstract group space are by construction independent of each other. This however leads to the surprising observation that the number of fields that ultimately couple to gapless excitations may be lower than that of the broken generators.Footnote 6 I will now outline the various mechanisms how the naively expected number of NG fields based on mere counting broken generators may be reduced. This will add nuance to the intuitive picture painted in Sect. 6.1 and summarized in Fig. 6.1 therein. The different mechanisms are listed in Fig. 13.2.
Various mechanisms whereby the number of physical NG fields coupling to gapless, true NG modes can be lower than the number of generators parameterizing the coset space \(H_0/H_{(\psi _0,0)}\). The detailed meaning of the keywords involved is explained in the main text. The physical NG fields are in turn in a one-to-one (type-A) or two-to-one (type-B) correspondence with the NG modes in the spectrum
Redundancy of Symmetries
Two symmetries that are locally equivalent necessarily lead to identical fluctuations of the order parameter. This is the simplest and most important of all the mechanisms, to which I already devoted the whole Chap. 11. Its advantage is that such a redundancy can be checked at the level of classical symmetry transformations. No specific choice of an order parameter or knowledge of the corresponding symmetry-breaking pattern is needed. See Sect. 11.3 for examples.
Redundancy of Order Parameter Fluctuations
Moving down the decision tree, the next possibility is that some symmetries are locally distinct, yet lead to equivalent fluctuations of the order parameter. An example of this type is the helimagnet; see Example 6.5 for details. Here spatial translations and rotations are not trivially redundant due to the vector nature of the order parameter. However, thanks to the particular spatial modulation of the order parameter, three independent broken symmetry generators lead to mere two distinct types of fluctuations. This type of redundancy requires detailed knowledge of the order parameter, but can still be detected straightforwardly following the approach of Sect. 6.3.1.
Both of the above types of redundancy are automatically accounted for by the standard nonlinear realization of Chap. 12. This ensures a one-to-one parameterization of whatever fields carrying the action of the symmetry one starts with. However, it is sometimes advantageous to add auxiliary would-be NG fields, even if these are known beforehand not to correspond to separate physical degrees of freedom. We saw an example in Sect. 13.3.3. The unphysical nature of the vector field \(\xi ^r\) therein manifested itself in the fact that we could eliminate it algebraically using its EoM. Such a procedure, while physically certainly correct, may however become exceedingly cumbersome beyond LO of the derivative expansion. There is an alternative that allows one to eliminate \(\xi ^r\) algebraically before one starts constructing the effective Lagrangian [7]. Indeed, note that the covariant derivative \(\nabla _r\pi \) in (13.61) is linear in \(\xi ^r\) without any derivatives on it. Setting it to zero gives \(\boldsymbol \xi =\boldsymbol \nabla \pi \), which is an algebraic condition that is covariant under all the symmetries of the EFT. This is an example of an IHC. Imposing the IHC brings us back to the nonlinear realization of Galilei symmetry solely in terms of the scalar \(\pi \). Yet, invariance under Galilei boosts is still automatically implemented. Galilei-invariant Lagrangians can be constructed using the same building blocks (13.61) while imposing by hand just invariance under spatial rotations. The latter can be ensured using standard tensor methods.
The auxiliary field \(\xi ^r\) in nonrelativistic superfluids is associated with Galilei boosts. In this concrete case, the corresponding would-be NG modes are clearly unphysical. However, it seems to be true generally that there are no observed single-particle NG states for which boosts would be the sole associated broken symmetry. Curiously, the Goldstone theorem for boosts can be saturated by states from a continuum spectrum rather than by stable bosonic quasiparticles, as in Fermi liquids [8, 9]. A class of mathematically consistent EFTs that feature NG bosons originating in boost symmetry has been proposed in [10].
Eliminating the auxiliary vector field using its EoM or using an IHC must lead to EFTs with the same functional form. The only difference is possibly in the identification of the effective couplings, but these are usually determined subsequently by matching the predictions of the EFT to selected observables. This makes the two approaches entirely equivalent. The advantage of using the classical EoM (or generally, at loop level, integrating the auxiliary field out) is that it is physically transparent. The IHC, on the other hand, is usually technically simpler. The drawback is that there is no universal algorithm how to find a suitable IHC. As a rule, one has to follow intuition combined with insight in the concrete problem at hand. See [11] for a discussion of some of the traps involved.
Gapped Modes from Secondary Order Parameter
Eliminating the redundancy of either type, we are back to the standard nonlinear realization of spacetime symmetry, developed in Sect. 12.3. Here all the fields, whether NG fields \(\pi ^a\) or matter fields \(\chi ^\varrho \), describe independent, physical degrees of freedom. Barring possible NG modes of spontaneously broken translation symmetry, the NG variables are classified as coordinates on the coset space \(H_0/H_{(\psi _0,0)}\). However, there may be different choices of the order parameter(s) leading to the same symmetry-breaking pattern but different coset spaces \(H_0/H_{(\psi _0,0)}\), hence different numbers of NG variables. This possibility owes its existence to the distinction between the isotropy groups \(H_0\), \(H_{(\psi _0,0)}\) and the unbroken subgroup \(H_\varphi \) in case of spacetime symmetries.
A phenomenologically relevant example is the smectic liquid crystal, discussed in Sect. 13.3.2. (Another, relativistic example of this type can be found in [12].) Let us inductively generalize what we observed therein. Suppose there is a secondary order parameter that can be removed from the EFT without affecting the symmetry-breaking pattern. Then the associated NG variables are not required to be present by the broken symmetry. By the same token, the corresponding modes in the spectrum are not protected by the symmetry from acquiring a gap.Footnote 7
Here one has two choices how to go about the construction of the EFT. If it is possible to identify the secondary order parameter beforehand, one can drop it from the outset. The resulting minimal nonlinear realization of the given symmetry-breaking pattern then only includes genuine NG fields. Accordingly, all modes described by the EFT are gapless, that is true NG bosons. Alternatively, one may proceed with the nonlinear realization that includes the secondary order parameter. The extra would-be NG fields are then dynamical and couple to gapped modes in the spectrum. If desired, these fields can be eliminated either by using their EoM or by imposing a suitable IHC.
Example 13.7
Let us have a closer look at smectic liquid crystals (Sect. 13.3.2). Here the primary order parameter is \(\langle {\phi (\boldsymbol x,t)}\rangle =k\boldsymbol n_0\cdot \boldsymbol x\). This breaks rotations that do not preserve the axis of alignment defined by \(\boldsymbol n_0\). Moreover, it breaks translations along \(\boldsymbol n_0\) together with the emergent shift symmetry of \(\phi (x)\) down to the “diagonal” subgroup. Altogether, there are three spontaneously broken symmetry generators. One of these corresponds to the genuine NG mode described by the EFT (13.56). In addition, there are two gapped modes that can be viewed as fluctuations of the secondary order parameter, \(\langle {\boldsymbol n(x)}\rangle =\boldsymbol n_0\).
Suppose we start from an EFT including all three degrees of freedom. This might even be desirable near the nematic–smectic phase transition at which the modes excited by the vector field \(\boldsymbol n(x)\) become gapless. However, should we decide to eliminate the gapped modes, we need a covariant IHC. To that end, note that the covariant derivative  in (13.53) splits under the action of the isotropy group \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\) into a singlet,
in (13.53) splits under the action of the isotropy group \(H_{(\psi _0,0)}\simeq \mathrm {SO}(2)\) into a singlet,  , and a doublet,
, and a doublet,  . The condition
. The condition  is covariant under all the symmetries of the smectic and moreover is algebraic in \(\pi ^a\). In a somewhat more human notation, it is equivalent to \(\boldsymbol n\times \boldsymbol \nabla \phi =0\). The solution to this IHC is, up to overall sign, \(\boldsymbol n=\boldsymbol \nabla \phi /\left \lvert {\boldsymbol \nabla \phi }\right \rvert \).
is covariant under all the symmetries of the smectic and moreover is algebraic in \(\pi ^a\). In a somewhat more human notation, it is equivalent to \(\boldsymbol n\times \boldsymbol \nabla \phi =0\). The solution to this IHC is, up to overall sign, \(\boldsymbol n=\boldsymbol \nabla \phi /\left \lvert {\boldsymbol \nabla \phi }\right \rvert \).
In fact, the IHC can do more than to eliminate unwanted degrees of freedom. According to (13.20), covariant derivatives of NG fields \(\pi ^a\) extracted from the \(\omega _\perp \) part of the MC form transform exactly as matter fields with respect to some linear representation of \(H_{(\psi _0,0)}\). The very fact that the constraint  can be solved for \(\pi ^a\) means that the Jacobian matrix
can be solved for \(\pi ^a\) means that the Jacobian matrix  is nonsingular, at least around the reference point \(\pi ^a=0\). Instead of setting it to zero, we can therefore treat
is nonsingular, at least around the reference point \(\pi ^a=0\). Instead of setting it to zero, we can therefore treat  as a new field variable that replaces \(\pi ^a\) in the EFT. We conclude that the gapped degrees of freedom are indistinguishable from ordinary matter fields. This is the underlying reason why they can be removed from the EFT without spoiling the nonlinear realization of the broken symmetry. And for the same reason, it is no wonder that the broken symmetry does not force them to remain gapless.
as a new field variable that replaces \(\pi ^a\) in the EFT. We conclude that the gapped degrees of freedom are indistinguishable from ordinary matter fields. This is the underlying reason why they can be removed from the EFT without spoiling the nonlinear realization of the broken symmetry. And for the same reason, it is no wonder that the broken symmetry does not force them to remain gapless.
The same reasoning applies to Galilei-invariant superfluids (Sect. 13.3.3). Even if one does not wish to eliminate the auxiliary field \(\xi ^r\) from the EFT, one can still trade it for \(\boldsymbol \chi \equiv \boldsymbol \xi -\boldsymbol \nabla \pi \). This is invariant under Galilei boosts and transforms as a matter field in the vector representation of the linearly realized isotropy group \(\mathrm {SO}(d)\). The observation that whenever a set of would-be NG fields can be eliminated from the EFT by imposing some IHCs, they can instead be kept and traded for a set of matter fields, is general [14]. The change from the would-be NG fields to the matter fields is a field redefinition that is nonsingular. This is guaranteed by the fact that the IHCs are algebraically solvable.
The distinction between the three mechanisms discussed so far crucially relies on the type of order parameter breaking the symmetry of the system. Within a naive EFT based on the agnostic nonlinear realization, there is therefore no way to distinguish these scenarios. One has to accept the possibility that some would-be NG degrees of freedom of the EFT couple to gapped states. Within the EFT itself, it is not possible to tell whether such states are physical or mere artifacts of the EFT setup. This suggests that when it comes to spacetime symmetries, the symmetry-breaking pattern itself is not restrictive enough. To get more detailed insight, one needs additional low-energy data such as the order parameter. See [15, 16] for further discussion.
Gapped Modes Required by Order Parameter
So far, generators not leading to independent NG degrees of freedom could always be identified by inspecting the classical symmetry transformations and the order parameter(s). Interestingly, that is not the end of the story. There are theories featuring would-be NG fields that couple to gapped modes which cannot be discarded by dropping a secondary order parameter. See [17] for an example and more details. It is then still possible to eliminate such fields using either the EoM or a suitably chosen IHC. One should however expect the resulting minimal nonlinear realization of symmetry to involve generalized local transformations that depend on derivatives of the NG fields. As long as one insists on using solely point symmetries, it is not possible to recover the minimal nonlinear realization by reducing the order parameter. In this sense, the presence of the gapped modes is required for a description of the symmetry-breaking pattern based on a local order parameter.
In all the scenarios outlined above and summarized in Fig. 13.2, the IHCs play a prominent role. It is therefore important to stress that they are just a technical tool. We always have the option to work with the full EFT based either on the agnostic nonlinear realization or the standard nonlinear realization of Chap. 12. We just have to live with the possibility that the EFT may include some gapped modes. These of course become irrelevant at sufficiently low energies. The set of genuine NG degrees of freedom is fixed unambiguously by the symmetry-breaking pattern.
How to choose the IHC in practice is a kind of art in its own right. The examples I presented above were all mercifully simple. Nonetheless, there is a useful rule of thumb rooted in the expression (13.3) for the MC form. Namely, if the commutator  contains \(Q_b\), then the NG field \(\pi ^a\) appears linearly and without derivatives in the \(\omega ^b\) component of the MC form. It therefore seems possible to eliminate \(\pi ^a\) by setting \(\omega ^b\) (or the irreducible multiplet of components of the MC form containing it) to zero. This naive algorithm however requires further conditions to work [18], and moreover depends sensitively on the exact choice of field parameterization [19]. It is therefore comforting to know that whether or not one chooses to impose some IHCs has no effect on the low-energy physics of the theory.
contains \(Q_b\), then the NG field \(\pi ^a\) appears linearly and without derivatives in the \(\omega ^b\) component of the MC form. It therefore seems possible to eliminate \(\pi ^a\) by setting \(\omega ^b\) (or the irreducible multiplet of components of the MC form containing it) to zero. This naive algorithm however requires further conditions to work [18], and moreover depends sensitively on the exact choice of field parameterization [19]. It is therefore comforting to know that whether or not one chooses to impose some IHCs has no effect on the low-energy physics of the theory.
4 Genuine Breaking of Translation Invariance
Until now I assumed that whatever the pattern of symmetry breaking, the low-energy physics is captured by an EFT that lives on the coset space \(H_0/H_{(\psi _0,0)}\). As we saw, this is appropriate for systems where the value of the order parameter at all spacetime points lies on the same orbit of the symmetry group. Any matter fields \(\chi ^\varrho \) that might be present can then be discounted. In this last section of the chapter, I will briefly outline the changes that are necessary to account for fluctuations of generic coordinate-dependent order parameters. The nonlinear realization of spacetime symmetry developed in Chap. 12 remains valid even in this general case. This is because the construction does not depend on the order parameter as a function on spacetime, merely on the choice of the representative point \(\psi _0\in \mathcal {M}\). By the same token, everything said in Sect. 13.1 about the MC form and covariant derivatives still applies.
The new complication is that we now have to explicitly include the matter fields \(\chi ^\varrho (x)\) in the game. These may contain NG degrees of freedom that are not detected by the \(H_0/H_{(\psi _0,0)}\) coset space, namely those of spontaneously broken translations. The challenge we face is to find a parameterization of the matter fields that makes the existence of the translation NG modes manifest. As of writing this book, there does not seem to be a general parameterization that would do the job in presence of other, possibly spontaneously broken, symmetries. I will thus merely sketch the basic idea in the simplest case of spacetime symmetry breaking by an otherwise featureless order parameter.
4.1 One-Dimensional Modulation of the Order Parameter
To further simplify the problem, consider a single real scalar field \(\phi (x)\) in a theory invariant under a purely spacetime symmetry group G. This may be the Aristotelian group or one of its extensions including boosts such as the Galilei or Poincaré group. The isotropy group \(H_0\) contains the transformations that act linearly on spacetime coordinates, that is rotations and boosts. For any choice of \(\phi _0\in \mathbb {R}\), the isotropy group \(H_{(\phi _0,0)}\simeq H_0\) makes the coset space \(H_0/H_{(\phi _0,0)}\) trivial. There are no NG variables and the sole degree of freedom, namely \(\phi \) itself, is of the matter type.
Suppose now that the VEV \(\langle {\phi (x)}\rangle \) varies along one particular direction in space. In order to maintain Poincaré (or Galilei) covariance if desired, I will characterize this preferred direction by a fixed spacelike vector \(n^\mu \). Our order parameter for spacetime symmetry breaking is then defined by a function \(\varphi \) of a single variable such that
We would eventually like to trade \(\phi (x)\) for a NG field \(\pi (x)\) that manifests spontaneous breaking of translations in the direction of \(n^\mu \). Before we proceed, let me stress that the order parameter (13.72) will as a rule also break rotations and (if present) Lorentz or Galilei boosts. However, these never enter our setup explicitly. For scalar fields, we already know that both spatial rotations and boosts are descendant symmetries in the sense of Chap. 11. Their nonlinear realization will therefore be automatically taken care of by the same NG field \(\pi (x)\).
Let us now start with a purely mathematical problem on functions of a single variable. I will call the latter z to distinguish it from the spacetime or spatial coordinates, \(x^\mu \) and \(x^r\). Suppose we are given a function \(\varphi (z)\) that “breaks translation invariance,” that is, it is strictly monotonic, \(\varphi '(z)\neq 0\). We would like to parameterize the “fluctuations” of \(\varphi (z)\) in a way that makes the breaking of translation invariance manifest. We do so by locally shifting the graph of the function by \(\pi (z)\) along the z-axis. This defines uniquely a new function \(\phi (z)\) via \(\phi (z)\equiv \varphi (z-\pi (z))\), see Fig. 13.3. Thanks to the assumed strict monotonicity of \(\varphi (z)\), the mapping between \(\pi (z)\) and \(\phi (z)\) for fixed \(\varphi (z)\) is one-to-one.
Two parameterizations of the fluctuations of a strictly monotonic function \(\varphi (z)\). The first amounts to a local shift \(\pi (z)\) of the graph of \(\varphi (z)\) in the horizontal direction. The second is given by the function \(\phi (z)\) corresponding to the shifted graph. Mathematically, the two parameterizations are related by \(\phi (z)=\varphi (z-\pi (z))\)
This little trick can be promoted to an arbitrary number D of spacetime dimensions, provided \(\varphi \) as assumed only varies in one particular direction. The coordinates corresponding to all the other directions in spacetime play a role of fixed parameters in the mapping between \(\phi \) and \(\pi \). Thus, I assume that \(\varphi (n\cdot x)\) in (13.72) is a strictly monotonic function of its argument. This is necessary for translations along \(n^\mu \) to be spontaneously broken at each spacetime point. The scalar field \(\phi (x)\) can then be traded for \(\pi (x)\), defined implicitly by
The function \(\varphi \) as defined by (13.72) obviously depends on the choice of coordinates. For instance, \(\varphi (n\cdot x)\) and \(\varphi (n\cdot x+c)\) with any \(c\in \mathbb {R}\) describe the same order parameter, differing only by a coordinate shift along \(n^\mu \). This is a hallmark of translation symmetry breaking. The introduction of the NG field \(\pi (x)\) makes it possible to map a fixed function \(\varphi \) to a scalar field \(\phi \). This requires that under a spacetime transformation, be it a translation, rotation or boost, the NG field transforms as
In the special case of spatial translations, \(\boldsymbol x\to \boldsymbol x+\boldsymbol \epsilon \), this boils down to \(\pi '(\boldsymbol x+\boldsymbol \epsilon ,t)=\pi (\boldsymbol x,t)-\boldsymbol {n}\cdot \boldsymbol {\epsilon }\), where \(\boldsymbol n\) is the spatial part of \(n^\mu \). Shifting the NG field by a constant is typical for spontaneously broken Abelian symmetries. We are on the right track.
Now that we have settled the parameterization, we would like to construct the most general effective action consistent with all the symmetries present. Since there were no NG variables to start with, the MC form (13.3) reduces to \(P\cdot \mathrm{d} x\). This gives a trivial spacetime coframe,  . Also, by (13.17), the covariant derivative of the matter field \(\phi \) is trivial,
. Also, by (13.17), the covariant derivative of the matter field \(\phi \) is trivial,  . Therefore, an invariant action can be built by taking any Lagrangian density that does not depend explicitly on spacetime coordinates. It can contain \(\phi (x)\) with an arbitrary number of derivatives (including zero). The indices on the derivatives are to be contracted in a way that preserves the linearly realized group \(H_0\). In case of a relativistic, that is Poincaré-invariant theory, any Lorentz-invariant Lagrangian density \(\mathcal {L}_{\mathrm {eff}}[\phi ]\) will do.
. Therefore, an invariant action can be built by taking any Lagrangian density that does not depend explicitly on spacetime coordinates. It can contain \(\phi (x)\) with an arbitrary number of derivatives (including zero). The indices on the derivatives are to be contracted in a way that preserves the linearly realized group \(H_0\). In case of a relativistic, that is Poincaré-invariant theory, any Lorentz-invariant Lagrangian density \(\mathcal {L}_{\mathrm {eff}}[\phi ]\) will do.
It looks like we have not made much progress. In particular, we have not learned anything so far about the possible dependence of the effective Lagrangian on the NG field \(\pi (x)\). However, there are still two requirements we have not addressed yet. The first of these is that the order parameter (13.72) is at least a local minimum of the energy functional of the EFT. This will constrain what the effective Lagrangian may look like. The second requirement is to have a consistent power-counting scheme that would allow us to decide which operators in the Lagrangian are most important. In order to understand what is at stake, it is best to work out an illustrative example.
4.2 Case Study: Fluctuations of a Domain Wall
Following Chap. 5 of [20], consider the class of relativistic scalar field theory models
where \(V(\phi )\) is a potential function, required for stability to be bounded from below. We can assume without loss of generality that \(\min V(\phi )=0\). The classical EoM of the model reads
Suppose the potential has (at least) two degenerate minima. Then the EoM has domain wall (or kink) solutions \(\varphi \) that interpolate between the minima. Such solutions depend on a single spatial coordinate, which I will denote as z, and converge to the respective minima of the potential for \(z\to \pm \infty \). Upon reduction to the single variable z, the EoM (13.76) has the first integral \((1/2)(\mathrm{d} {\phi }/\mathrm{d} {z})^2-V(\phi )\). For the domain wall solutions, this first integral evaluates to zero since for \(z\to \pm \infty \), \(\varphi (z)\) converges to a constant such that  . This reduces the EoM to the following first-order differential equation for \(\varphi (z)\),
. This reduces the EoM to the following first-order differential equation for \(\varphi (z)\),
The prime on \(\varphi \) indicates a derivative with respect to its argument.
Example 13.8
One of the most common scalar potentials is the double-well potential,
where \(\lambda \) and v are positive parameters. A simple calculation gives the corresponding domain wall solution, interpolating between the minima at \(\phi =\pm v\),
Here \(z_0\) is an integration constant that determines the center of the domain wall where \(\varphi (z_0)=0\). The width of the domain wall is given by \(1/(\sqrt {\lambda } v)\).
Another example of a phenomenologically important potential is
where m and v are positive parameters. This appears for instance in the low-energy effective theory (9.21) of quantum chromodynamics, when restricted to neutral pions. In this realization, m corresponds to the pion mass \(m_\pi \) and v to the pion decay constant, \(f_\pi \). The potential \(V(\phi )\) is now periodic with minima at \(\phi =2n\pi v\) for any \(n\in \mathbb {Z}\). The domain wall solution, connecting two neighboring minima, is
In this case, the width of the domain wall is fixed by the mass parameter to be \(1/m\).
Both concrete domain wall solutions in Example 13.8 satisfy our criteria for the translation-breaking order parameter modulated in one dimension. We would eventually like to derive a low-energy EFT for the fluctuations of the domain wall. The first step towards this goal is to use the general parameterization (13.73) with \(n\cdot x=z\). The potential term in (13.75) can then be eliminated by means of (13.77), upon which the Lagrangian becomes
The contribution of the \(1-\partial _z\pi \) piece to action is a mere boundary term independent of local variations of \(\pi (x)\). Namely,  where \(\tilde z\equiv z-\pi (x)\) and
where \(\tilde z\equiv z-\pi (x)\) and  . Dropping this contribution, we are left with the following effective action [16],
. Dropping this contribution, we are left with the following effective action [16],
The EFT (13.83) apparently describes a derivatively coupled NG field \(\pi (x)\) as we wanted. However, it is still not quite satisfactory due to the explicit appearance of the domain wall background \(\varphi (z)\). It is not even clear what the quasiparticle spectrum of the EFT is. To that end, we utilize the EoM, linearized in the NG field,
where the \(\approx \) symbol indicates the linear approximation. It is convenient to switch to the linear fluctuation of the order parameter, \(\chi (x)\equiv \phi (x)-\varphi (z)\).Footnote 8 The linearized EoM (13.84) is thus transformed to
As a simple check, note that the domain wall solution satisfies \(\varphi '''/\varphi '=\mathrm{d} ^2V(\varphi )/\mathrm{d} \varphi ^2\). Equation (13.85) then descends directly from the Lagrangian (13.75) by expanding the latter to second order in \(\chi (x)\). The form of (13.85) allows us to Fourier-transform in time and the transverse spatial coordinates (denoted collectively as \(\boldsymbol x_\perp \)). Parameterizing plane-wave solutions by energy E and transverse momentum \(\boldsymbol p_\perp \),
the profile function \(\hat \chi (z)\) solves the one-dimensional eigenvalue problem
In order to appreciate the content of this equation for single-particle states, let us return to the two concrete choices of potential introduced in Example 13.8. In both cases, I will for simplicity consider only the solution \(\varphi (z)\) centered at \(z_0=0\).
Example 13.9
For the double-well potential with the corresponding domain wall solution (13.79), \(\varphi '''(z)/\varphi '(z)=2\lambda v^2[2-3 \operatorname {\mathrm {sech}}^2(\sqrt {\lambda } vz)]\). Introducing a dimensionless coordinate \(Z\equiv \sqrt {\lambda } vz\) turns (13.87) into
The operator on the left-hand side is a special case of the Pöschl–Teller Hamiltonian, \(H_n\equiv -\partial _Z^2-n(n+1)/\cosh ^2Z\) with positive \(n\in \mathbb {Z}\). The spectrum of this Hamiltonian is well-known; see e.g. Chap. 11 of [21]. There are n bound states with eigenvalues \(-n^2,-(n-1)^2,\dotsc ,-1\). The continuous part of the spectrum covers the open interval \((0,\infty )\). In the \(n=2\) case of interest to us, the ground state with eigenvalue \(-4\) gives \(E=\left \lvert {\boldsymbol p_\perp }\right \rvert \). The corresponding profile function is \(\hat \chi (Z)\propto 1/\cosh ^2Z\). This solution is localized in the z-direction to the vicinity of the domain wall. It propagates as a plane wave in the transverse directions with a massless relativistic dispersion relation. The upper bound state of \(H_2\) with eigenvalue \(-1\) gives \(E^2=\boldsymbol p_\perp ^2+3\lambda v^2\). Its profile function is \(\hat \chi (Z)\propto \sinh Z/\cosh ^2Z\). This solution is also localized to the domain wall and propagates only in the transverse directions, but it has a nonzero mass of \(\sqrt {3\lambda }v\). Finally, the continuum part of the spectrum of the Pöschl–Teller Hamiltonian can be parameterized by the momentum variable \(p_z\) so that for \(z\to \pm \infty \), \(\hat \chi (z)\propto \exp (\mathrm{i} p_zz)\). The corresponding energy is \(E^2=\boldsymbol p_\perp ^2+p_z^2+4\lambda v^2\). This describes delocalized fluctuations of the domain wall that propagate in the entire space. They have a relativistic dispersion relation with mass \(2\sqrt {\lambda } v\).
In case of the cosine potential with its domain wall solution (13.81), \(\varphi '''(z)/\varphi '(z)=m^2[1-2 \operatorname {\mathrm {sech}}^2(mz)]\). With the dimensionless coordinate \(Z\equiv mz\), the eigenvalue problem (13.87) becomes
The left-hand side is again one of the Pöschl–Teller Hamiltonians, \(H_1\). Its sole bound state has the profile function \(\hat \chi (Z)\propto 1/\cosh Z\). This is a state localized to the domain wall that propagates in the transverse directions with the massless relativistic dispersion, \(E=\left \lvert {\boldsymbol p_\perp }\right \rvert \). The continuum part of the spectrum of this Pöschl–Teller Hamiltonian again amounts to delocalized fluctuations of the domain wall. Their dispersion relation is \(E^2=\boldsymbol p_\perp ^2+p_z^2+m^2\). Far away from the domain wall, they describe particles of mass m propagating in the bulk.
We are now ready to draw some general conclusions. Starting with any potential \(V(\phi )\) with degenerate minima, the domain wall solution will be localized in the z-direction. The linearized EoM (13.84) always admits plane-wave solutions, propagating in the transverse directions with the massless dispersion relation, \(E=\left \lvert {\boldsymbol p_\perp }\right \rvert \), and with a constant longitudinal profile, \(\hat \pi (z)\propto 1\). By (13.85), this corresponds to \(\hat \chi (z)\propto \varphi '(z)\). The existence of this solution is guaranteed by the spontaneously broken translation invariance. Indeed, the fact that \(\hat \pi (z)\) is constant indicates that this is the NG boson we are after. It does not propagate in the z-direction since translations in the z-direction are completely broken, hence there is no physical momentum \(p_z\) to label one-particle states with. The NG mode propagates solely along the directions in which translations remain unbroken.
The second observation is that there is a continuum of plane-wave-like solutions that propagate in the bulk. Far away from the domain wall where \(\varphi (z)\) goes to one of the minima of \(V(\phi )\), \(\varphi _0\), these are simple plane waves, \(\hat \chi (z)\propto \exp (\mathrm{i} p_zz)\). They have a relativistic dispersion relation with squared mass \(V''(\varphi _0)\). In fact, we could have guessed this much by expanding the Lagrangian (13.75) around the uniform solution \(\langle {\phi (x)}\rangle =\varphi _0\). In addition to the NG mode and the bulk plane-wave continuum, there may be further solutions to (13.85) that are localized on the domain wall and propagate only in the transverse directions. These correspond to excited bound states of the one-dimensional Hamiltonian on the left-hand side of (13.87). The presence of such massive excitations propagating along the domain wall depends on the concrete choice of the potential \(V(\phi )\).
It is not a priori obvious why the NG mode with \(\hat \pi (z)\propto 1\) is necessarily the lowest-lying excitation, that is, why the domain wall solution is stable. To understand this, let us assume without loss of generality that \(\phi (x)\) is monotonic in z and estimate its energy from below by completing the square,
where  . This estimate, known as the Bogomolny bound, shows that static solutions satisfying (13.77) minimize the energy per unit transverse volume on the class of field configurations with a fixed boundary condition at \(z\to \pm \infty \).
. This estimate, known as the Bogomolny bound, shows that static solutions satisfying (13.77) minimize the energy per unit transverse volume on the class of field configurations with a fixed boundary condition at \(z\to \pm \infty \).
We have discovered that our EFT (13.83) inevitably describes both the translation NG boson and specific gapped excitations. This is hardly surprising given that (13.83) is equivalent via a field redefinition to the original model (13.75). One might naively expect that an EFT for the NG mode alone could be extracted by integrating over z. After all, we found that the NG solution for \(\pi (x)\) does not depend on z at all. However, inserting a z-independent \(\pi (\boldsymbol x_\perp ,t)\) makes it possible to shift the z-coordinate in \(\varphi '(z-\pi )\), thus reducing (13.83) to
This is a noninteracting theory, describing free surface waves on the domain wall. We conclude that all interactions among the NG modes in the EFT (13.83) are mediated by the gapped modes.
The problem of disentangling the NG mode from the gapped excitations is related to our ability to organize contributions to the EFT by a derivative expansion. Also, we have so far been forced to work with specific domain wall solutions \(\varphi (z)\), descending from the chosen model potential \(V(\phi )\). We would rather have a model-independent EFT where the stability of the ground state and the existence of a power counting serve merely as constraints. I will now address these issues jointly in a framework inspired by the background gauge invariance approach of Sect. 8.2.
4.3 Effective Action from Background Gauge Invariance
The idea to use background gauging to derive an EFT for spontaneously broken translations has been utilized in multiple contexts, including inflationary cosmology [22] and superconductivity [23]. Here I will loosely follow the exposition in [16]. We are looking for an effective action \(S_{\mathrm {eff}}\{\pi \}\) for the NG mode of spontaneously broken translations in the z-direction. In the spirit of Sect. 8.2, we first promote the physical symmetry to a local invariance by adding a set of background gauge fields. Localizing spacetime translations leads to the group of spacetime diffeomorphisms. The precise choice of the corresponding background field is constrained by the physical symmetry and field content. In case of relativistic theories of scalar fields, one can use a spacetime metric, \(g_{\mu \nu }(x)\), to make the gauged action \(S_{\mathrm {eff}}\{\pi ,g\}\) diffeomorphism-invariant.
The transformation of the metric under a diffeomorphism of the spacetime manifold, \(x^\mu \to x^{\prime \mu }(x)\equiv x^\mu +\epsilon ^\mu (x)\), is given by the push-forward by the inverse of the diffeomorphism; see Appendix A.3.1. This must be augmented with a transformation rule for the NG field \(\pi (x)\). In order to maintain the relation \(\phi (x)=\varphi (z-\pi (x))\) between a scalar field \(\phi (x)\) and a fixed function \(\varphi (z)\), \(\pi (x)\) should transform as
The NG field can now be eliminated by choosing the diffeomorphism as \(\epsilon ^\mu (x)=-\delta ^\mu _z\pi (x)\). With a slight abuse of notation, I will denote this operation as \(\mathcal {T}_{-\pi }\). This reduces the action to \(S_{\mathrm {eff}}\{\pi ,g\}=S_{\mathrm {eff}}\{0,\mathcal {T}_{-\pi }g\}\). The dependence of the action on the composite gauge field \((\mathcal {T}_{-\pi }g)_{\mu \nu }\) is constrained by invariance under the residual group of diffeomorphisms that fix the point \(\pi =0\). These are (possibly z-dependent) \((D-1)\)-dimensional diffeomorphisms with \(\epsilon ^z(x)=0\). Once the most general admissible action  has been found, the EFT in flat Minkowski spacetime can be recovered by setting \(g_{\mu \nu }(x)\) to the Minkowski metric.
has been found, the EFT in flat Minkowski spacetime can be recovered by setting \(g_{\mu \nu }(x)\) to the Minkowski metric.
To constrain the form of  , it is convenient to separate the z-coordinate from the other spacetime coordinates. I will indicate those using lowercase Fraktur indices \(\mathfrak {m},\mathfrak {n},\dotsc \). It will also be more practical to work with the inverse of the metric, \(g^{\mu \nu }(x)\), rather than \(g_{\mu \nu }(x)\) itself. The transformation of the metric under diffeomorphisms then splits as
, it is convenient to separate the z-coordinate from the other spacetime coordinates. I will indicate those using lowercase Fraktur indices \(\mathfrak {m},\mathfrak {n},\dotsc \). It will also be more practical to work with the inverse of the metric, \(g^{\mu \nu }(x)\), rather than \(g_{\mu \nu }(x)\) itself. The transformation of the metric under diffeomorphisms then splits as
For the sake of brevity, I suppressed the arguments x of \(g^{\mu \nu }(x)\) and \(x'\) of \(g^{\prime \mu \nu }(x')\). The transformation rule for \(g^{z\mathfrak {m}}\) is analogous to that for \(g^{\mathfrak {m}z}\).
Under the restricted \((D-1)\)-dimensional diffeomorphisms with \(\epsilon ^z(x)=0\), \(g^{zz}(x)\) behaves as a scalar, \(g^{\prime zz}(x')=g^{zz}(x)\). On the other hand, \(g^{\prime \mathfrak {m}z}=g^{\alpha z}(\delta ^{\mathfrak {m}}_\alpha +\partial _\alpha \epsilon ^{\mathfrak {m}})\) depends on both \(g^{\mathfrak {m}z}\) and \(g^{zz}\). Finally,  depends on all \(g^{\mathfrak {mn}}\), \(g^{\mathfrak {m}z}\), \(g^{z\mathfrak {n}}\) and \(g^{zz}\). This suggests that our main ingredient for constructing diffeomorphism-invariant actions will be
depends on all \(g^{\mathfrak {mn}}\), \(g^{\mathfrak {m}z}\), \(g^{z\mathfrak {n}}\) and \(g^{zz}\). This suggests that our main ingredient for constructing diffeomorphism-invariant actions will be
where the argument of \((\mathcal {T}_{-\pi }g)^{zz}\) is \(\tilde x^\mu \equiv x^\mu -\delta ^\mu _z\pi (x)\). The z-component of \(\tilde x^\mu \), that is \(\tilde z\equiv z-\pi (x)\), is itself invariant under spacetime diffeomorphisms and can thus appear in the effective action without restrictions. Finally, the effective action may also contain \((\mathcal {T}_{-\pi }g)^{\mathfrak {m}z}\) and \((\mathcal {T}_{-\pi }g)^{\mathfrak {mn}}\). These, not being scalars, can however only enter through higher-derivative tensors such as the Riemann curvature tensor. See Appendix A of [22] for a discussion of geometric structures allowed by the restricted \((D-1)\)-dimensional diffeomorphism invariance. For our purposes, the main conclusion is that the part of the effective action dominant at low energies will be included in
Here f is a generic smooth function of two variables. The volume measure \( \operatorname {\mathrm {vol}}(g)\) for a metric of (timelike) Lorentzian signature equals \(\sqrt {(-1)^d\det g}\); cf. Appendix A.7.2.
Example 13.10
Using the specific choice \(f(u,v)\equiv (1/2)[\varphi '(u)]^2(v-1)\) and subsequently going back to the flat Minkowski spacetime gives
This reproduces our previous model result (13.82).
A systematic expansion in derivatives of the NG field is easier if one uses the combination \((\mathcal {T}_{-\pi }g)^{zz}+1\), which goes to \(2\partial _z\pi +(\partial _\mu \pi )^2\) in the flat-spacetime limit. This suggests expanding the function \(f(u,v)\) in (13.95) in powers of \(v+1\). Up to second order in \(v+1\) and thus in derivatives, we have \(f(u,v)=c_0(u)+c_1(u)(v+1)+c_2(u)(v+1)^2+\dotsb \), which translates to the Minkowski-spacetime action
This is the low-energy EFT we have been looking for. It remains to elucidate the consistency constraints on the functions \(c_i(z-\pi )\). To that end, we expand the Lagrangian in (13.97) to second order in the NG field,
Bulk stability requires absence of any terms linear in \(\pi \). This leads to the constraint
In fact, one can demand even \(c_0(z)+2c_1(z)=0\), since any constant offset of \(c_0(z)\) can be dropped from (13.97). This sharper relation is indeed satisfied by the choice of \(f(u,v)\) in Example 13.10, where \(c_0(u)=-[\varphi '(u)]^2\) and \(c_1(u)=(1/2)[\varphi '(u)]^2\). With the constraint (13.99), the first term on the second line of (13.98) automatically drops, and the Lagrangian boils down to \(c_1(z)(\partial _\mu \pi )^2+4c_2(z)(\partial _z\pi )^2\) up to a surface term. A necessary (though not inevitably sufficient) condition for the corresponding energy functional to be bounded from below is therefore
So far, I have not assumed any specific choice or properties of the profile functions \(c_i(z)\). The effective action (13.97) defines a generic EFT for the NG mode of spontaneously broken translations in the z-direction in a relativistic system. In particular, the functions \(c_i(z)\) in (13.97) do not have to arise from a topologically nontrivial background such as a domain wall. However, if that happens to be the case, we expect them to be localized to a finite range in z. The NG mode will then correspond to a surface wave and propagate solely in the transverse directions. I would now like to use the general EFT (13.95) to shed some light on the physics of these surface waves beyond the noninteracting approximation (13.91). To that end, it is convenient to switch to the \(\tilde x^\mu \) coordinates. Namely, \(\pi (x)\) measures the local fluctuation-induced displacement of the domain wall in the z-direction. Geometrically, the dynamical state of the domain wall can thus be viewed as a hypersurface in \(\mathbb {R}^D\) defined by a constant value of \(\tilde z\).
With the shorthand notation \(\tilde g\equiv \mathcal {T}_{-\pi }g\), the determinant of this D-dimensional metric can be decomposed as \(\det \tilde g=({\tilde g}^{zz})^{-1}\det \tilde {\mathfrak {g}}\). Here \(\tilde {\mathfrak {g}}_{\mathfrak {mn}}\) is a projection of \(\tilde g_{\mu \nu }\) to the \((D-1)\)-dimensional space of \(x^{\mathfrak {m}}\), which is nothing but the metric on the domain wall induced by the bulk Lorentzian metric in \(\mathbb {R}^D\). The factorization of \(\det \tilde g\) follows from the mathematical properties of block matrices [24]. Augmenting this observation with the constraint \(c_0(z)+2c_1(z)=0\) turns the first line of (13.95) to
So far this is an exact rewriting of (13.95) except for the truncation of the power expansion in \(\tilde g^{zz}+1\). Now we take the limit of flat spacetime. Simultaneously, we restrict to fields independent of the \(\tilde z\) coordinate, as appropriate for the NG mode. This makes it possible to do the integral over \(\tilde z\) independently of the NG field. We thus arrive at an effective \((D-1)\)-dimensional theory for the surface waves on the domain wall which, up to higher-order corrections, takes the form
In this approximation, the EFT for the domain wall fluctuations is completely geometric and fixed by the induced metric,
The expression for \( \operatorname {\mathrm {vol}}(\tilde {\mathfrak {g}})\) follows from the so-called Weinstein–Aronszajn identity for matrix determinants. The reader may recognize this as the Dirac–Born–Infeld (DBI) theory that we met previously in Sect. 10.3.1. All that is left of the profile of the domain wall is the overall prefactor in (13.102).
Example 13.11
The prefactor  measures, up to overall sign, the energy of the domain wall per unit transverse volume, that is its surface tension. For the class of models (13.75), it equals
measures, up to overall sign, the energy of the domain wall per unit transverse volume, that is its surface tension. For the class of models (13.75), it equals  ; see also (13.90). In case of the double-well potential with the domain wall solution (13.79), this gives
; see also (13.90). In case of the double-well potential with the domain wall solution (13.79), this gives  . For the cosine potential with the corresponding domain wall (13.81), one finds analogously \(-8mv^2\).
. For the cosine potential with the corresponding domain wall (13.81), one finds analogously \(-8mv^2\).
The \((D-1)\)-dimensional theory (13.102) obviously describes only the NG mode as we wanted; the gapped modes we found in Sect. 13.4.2 are gone. The price to pay is that the D-dimensional Lorentz symmetry is now realized in a nontrivial fashion beyond our spacetime symmetry paradigm; cf. (10.50).
The fact that all the modes propagating in the D-dimensional bulk are gapped is essential for the validity of the EFT (13.102). There are physical systems where the bulk modes are naturally gapless, for instance when two immiscible superfluids are separated by an interface. In this case, integrating the bulk modes out makes the EFT for the surface waves on the interface nonlocal. This leads to a fractional-power dispersion relation of the surface modes, \(E(\boldsymbol p)\propto \left \lvert {\boldsymbol p}\right \rvert ^{3/2}\). See [25] for a detailed discussion from an EFT perspective.
4.4 Further Possible Applications
In discussing spontaneous breaking of spatial translations, I have deliberately merely outlined the general approach and then focused on a specific type of system to illustrate it. There are however several natural, physically motivated modifications or generalizations of the setup. I will now at least briefly mention some of the possible avenues one might wish to follow.
Periodic Modulation of Order Parameter
Mathematically the simplest modification is one with a single, otherwise featureless real order parameter where the profile \(\varphi (z)\), or \(c_0(z)\), is not spatially localized. The most interesting situation arises when \(\varphi (z)\) is a periodic function of z. In this case the physics changes qualitatively. The eigenvalue problem (13.87) for linear fluctuations will have no bound states. Instead, its continuous spectrum will have a band structure. There should still be a NG mode of the spontaneously broken translations, but this will assume the form of a sound wave (phonon) on the crystalline background \(\varphi (z)\). In the limit where \(\varphi (z)\) consists of widely separated localized kinks, the propagation of sound in the z-direction arises from tunneling between states localized on the individual kinks.
The detailed structure of the dispersion relation of the low-lying phonon excitations will be no less interesting. Namely, it turns out that the spontaneously broken symmetry under spatial rotations forbids the \(c_1\) term in (13.97). As a consequence, the derivative expansion of the effective Lagrangian starts at second order in longitudinal derivatives \(\partial _z\) but fourth order in the transverse gradient \(\boldsymbol \nabla _\perp \) [16]. We already saw the same behavior in smectic liquid crystals (Sect. 13.3.2), and I will return to its physical implications in Chap. 15.
Other Spacetime Symmetries
Another natural possibility is to consider systems with a real order parameter modulated in one spatial dimension, but with a different spacetime symmetry than Poincaré. This is relevant in particular for any condensed-matter system. As long as one has a concrete microscopic model, the analysis proceeds along the same steps as in Sect. 13.4.2. One can however also adopt the model-independent approach of Sect. 13.4.3 based on background gauge invariance. This requires coupling the theory to an appropriate spacetime geometry. A basic discussion can be found in Appendix A of [16]. For a more complete, if mathematically also more advanced, overview of non-Lorentzian geometry, see [26].
Additional Degrees of Freedom
One might also want to study spontaneous breaking of translation invariance alongside other, possibly internal, broken symmetries. The field parameterization required then follows the general standard nonlinear realization of Sect. 12.3 combined with the identification of the translation NG field à la Sect. 13.4.1. The background gauge invariance approach may again prove helpful. Its application however relies on our ability to simultaneously gauge all the relevant symmetries by adding suitable background gauge fields. This is not guaranteed a priori without further qualifications. Finally, there are also physical systems where spacetime translations are spontaneously broken in more than one direction. In this case, the idea behind Sect. 13.4.1 might still be possible to apply provided one has at hand a sufficient number of fields to parameterize the order fluctuations uniquely.
Notes
- 1.
I take the liberty to denote 1-forms on \(H_0/H_{(\psi _0,0)}\times M\) and their pull-backs to M using the same symbol. It should be clear from the context which of the two is meant.
- 2.
In order to avoid notation clash with the dilatation operator D, I temporarily denote the dimension of spacetime as \(d+1\).
- 3.
This restriction is of course just a matter of convenience. Our general result for the LO EFT (13.32) applies equally well to a strongly-interacting gas of massive fermions.
- 4.
In Chap. 9, I worked out the EFT for spin systems using the fundamental (spinor) representation of \(\mathrm {SO}(3)\). It goes without saying that this is just a matter of convenience. The nonlinear realization of symmetry on coset spaces as detailed in Sect. 7.3 only depends on the structure of the symmetry group. In the present case, the use of the vector representation of \(H_0\simeq \mathrm {SO}(3)\) is suggested by the transformation properties of the momentum operator \(\boldsymbol P\).
- 5.
The
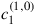 term is relevant for cholesteric liquid crystals whose building blocks possess intrinsic chirality. The mathematics of cholesterics is largely identical to that of helimagnets [5].
term is relevant for cholesteric liquid crystals whose building blocks possess intrinsic chirality. The mathematics of cholesterics is largely identical to that of helimagnets [5]. - 6.
Remember that these independent NG fields may still not be in a one-to-one correspondence with NG modes in the spectrum. Some of the fields may be pairwise canonically conjugated, leading to type-B NG bosons. The canonical conjugation mechanism is the same for internal and spacetime symmetries, and thus requires no further discussion.
- 7.
A similar phenomenon exists even for internal symmetries. As stressed in Sect. 8.3.2, the primary order parameter responsible for type-B NG modes in the spectrum is the commutator matrix (8.26). The presence of an additional, secondary order parameter may lead to gapped “partners” of the type-B NG modes. See [13] for a detailed discussion within Hamiltonian formalism, or Sect. 8.3.1 for an outline of how these gapped partner states manifest themselves in the effective Lagrangian.
- 8.
While \(\pi (z)\) is defined as the horizontal distance of the graphs of \(\phi (z)\) and \(\varphi (z)\) in Fig. 13.3 (the other spacetime coordinates being fixed), \(\chi (z)\) can be viewed as their vertical distance.
References
Y. Togawa, Y. Kousaka, K. Inoue, J.i. Kishine, J. Phys. Soc. Jpn. 85, 112001 (2016). https://doi.org/10.7566/JPSJ.85.112001
A. Schmitt, Introduction to Superfluidity: Field-theoretical Approach and Applications. Lecture Notes in Physics, vol. 888 (Springer, Berlin, 2015). https://doi.org/10.1007/978-3-319-07947-9
D.T. Son, https://arxiv.org/abs/hep-ph/0204199
P.G. de Gennes, J. Prost, The Physics of Liquid Crystals (Clarendon Press, Oxford, 1993)
L. Radzihovsky, T.C. Lubensky, Phys. Rev. E83, 051701 (2011). https://doi.org/10.1103/PhysRevE.83.051701
P.M. Chaikin, T.C. Lubensky, Principles of Condensed Matter Physics (Cambridge University Press, Cambridge, 1995). https://doi.org/10.1017/CBO9780511813467
E. Ivanov, V.I. Ogievetsky, Theor. Math. Phys. 25, 1050 (1975). https://doi.org/10.1007/BF01028947
I.Z. Rothstein, P. Shrivastava, J. High Energy Phys. 05, 014 (2018). https://doi.org/10.1007/JHEP05(2018)014
L. Alberte, A. Nicolis, J. High Energy Phys. 07, 076 (2020). https://doi.org/10.1007/JHEP07(2020)076
A. Nicolis, R. Penco, F. Piazza, R. Rattazzi, J. High Energy Phys. 06, 155 (2015). https://doi.org/10.1007/JHEP06(2015)155
B. Finelli, J. High Energy Phys. 03, 075 (2020). https://doi.org/10.1007/JHEP03(2020)075
I. Kharuk, A. Shkerin, Phys. Rev. D98, 125016 (2018). https://doi.org/10.1103/PhysRevD.98.125016
T. Hayata, Y. Hidaka, Phys. Rev. D91, 056006 (2015). https://doi.org/10.1103/PhysRevD.91.056006
T. Brauner, H. Watanabe, Phys. Rev. D89, 085004 (2014). https://doi.org/10.1103/PhysRevD.89.085004
A. Nicolis, R. Penco, F. Piazza, R.A. Rosen, J. High Energy Phys. 11, 055 (2013). https://doi.org/10.1007/JHEP11(2013)055
Y. Hidaka, T. Noumi, G. Shiu, Phys. Rev. D92, 045020 (2015). https://doi.org/10.1103/PhysRevD.92.045020
S. Endlich, A. Nicolis, R. Penco, Phys. Rev. D89, 065006 (2014). https://doi.org/10.1103/PhysRevD.89.065006
R. Klein, D. Roest, D. Stefanyszyn, J. High Energy Phys. 10, 051 (2017). https://doi.org/10.1007/JHEP10(2017)051
I.N. McArthur, J. High Energy Phys. 11, 140 (2010). https://doi.org/10.1007/JHEP11(2010)140
N. Manton, P. Sutcliffe, Topological Solitons (Cambridge University Press, Cambridge, 2004). https://doi.org/10.1017/CBO9780511617034
K.T. Hecht, Quantum Mechanics (Springer-Verlag, New York, 2000). https://doi.org/10.1007/978-1-4612-1272-0
C. Cheung, P. Creminelli, A.L. Fitzpatrick, J. Kaplan, L. Senatore, J. High Energy Phys. 03, 014 (2008). https://doi.org/10.1088/1126-6708/2008/03/014
K. Samokhin, Phys. Rev. B81, 224507 (2010). https://doi.org/10.1103/PhysRevB.81.224507
P.D. Powell, https://arxiv.org/abs/1112.4379
H. Watanabe, H. Murayama, Phys. Rev. D89, 101701 (2014). https://doi.org/10.1103/PhysRevD.89.101701
E. Bergshoeff, J. Figueroa-O’Farrill, J. Gomis, SciPost Phys. Lect. Notes 69 (2023). https://doi.org/10.21468/SciPostPhysLectNotes.69
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this chapter
Cite this chapter
Brauner, T. (2024). Broken Spacetime Symmetry in Quantum Matter. In: Effective Field Theory for Spontaneously Broken Symmetry. Lecture Notes in Physics, vol 1023. Springer, Cham. https://doi.org/10.1007/978-3-031-48378-3_13
Download citation
DOI: https://doi.org/10.1007/978-3-031-48378-3_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48377-6
Online ISBN: 978-3-031-48378-3
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)





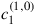 term is relevant for cholesteric liquid crystals whose building blocks possess intrinsic chirality. The mathematics of cholesterics is largely identical to that of helimagnets [
term is relevant for cholesteric liquid crystals whose building blocks possess intrinsic chirality. The mathematics of cholesterics is largely identical to that of helimagnets [