1 Introduction

Many industrial and engineering applications exploit thermo-fluid flow processes under thermodynamically subcritical, trans-critical, or supercritical regimes. As is well-known injection processes in transportation, propulsion, power generation and other high temperature applications are commonlly used. Thereby, liquid fuels are preferred as they feature high energy density (energy per unit volume), and thus mostly easy to store and transport. However, their use suffers from complex fuel atomization phenomena (primary and secondary breakup), evaporation and mixing that represent the major performance limiting factors of specific technologies in which these fuels are utilized.

A widespread tendency is to obviate this limitation by moving the operating conditions into supercritical state in which the fuel is able to evaporate directly without phase change. Such a behavior is due to the liquid surface tension and the latent heat which gradually diminish and even vanish when the ambient condition lies above the critical point of the injected fuel. In this way, a higher specific energy conversion can be achieved in combination with an improvement in the thermodynamic efficiency, or heat and mass transport can be enhanced along with reduction of harmful gas emissions (see [12, 26]). Examples of such techniques are found in propulsion rocket engines, modern gas turbines, diesel engines, and also in supercritical drying, cooling and cleaning, etc. Thereby, the majority of fuels reach supercritical conditions for pressures in the range of about 1.5–3 Mpa. In modern aircraft combustors the pressure is now exceeding values of 2–2.5 MPa at cruise conditions and 5–6 MPa during ground power generation, takeoff, and landing, while even higher values are expected for the future generation of gas turbines. In a naturally aspirated diesel engine, air at close-to-atmospheric pressure is inducted during the intake stroke and then compressed to a pressure of about 5 MPa and temperature of about 900 K during the compression stroke [7].

In such applications, when the fuel is injected as a compact, continuous stream and not as a disperse cloud of individual droplets, dispersed droplets can also be observed under supercritical pressure conditions. In fact, Roy et al. [43] experimentally investigated an initially supercritical fluid injected into a supercritical pressure environment. The jet undergoes for sufficiently low ambient temperatures phase separation leading to the formation of droplets and ligaments in the jet. This mainly stems from the interaction between the injectant and the surrounding gas, see also [55]. For more details, the reader may refer to the works by Anitescu et al. [6], Chehroudi [12], Klima et al. [21], Oefelein [33], and therein included references. Additional observations have been reported in which the droplets undergo a gradual transition from subcritical evaporation to mixing regime at different pressure and temperature above the pure fuel critical point. This gives a hint to state that the fuel still stays in the subcritical two-phase state for some time before fully entering the diffusion mixing regime, and the transition time varies with fuel types and droplet size [14]. It turns out that in the whole injection process, the combination of classical evaporation regime for the main liquid core and transition to the dense gas mixing state is possible at high ambient temperature especially for the droplets formed by possible primary atomization near the nozzle or at the end of the injection events.

In a case of mixture evolving in a combustor that experiences a pressure above the critical value of the mixture, the investigated mixture will behave as a supercritical fluid. Since the critical pressure strongly depends on the composition of the mixture in presence, the critical pressure for hydrocarbon-gas mixtures, for example, can reach very high values beyond the application relevant pressure levels. Furthermore, only in rare cases the liquid fuel is preheated to supercritical temperatures before injection into the combustion chamber. For hydrocarbons, these are in the range of 400-500 K [20]. After the injection, other processes may occur in the combustion chamber, such as heating by the combustion products and evaporative cooling. Therefore, the occurrence of subcritical and supercritical phenomena in combustion chambers might likely be expected in vicinity of the injector [14, 16, 26]. Due to the complexity of the evolving multi-scale and multi-physical processes, and to the urgent need of designing and improving the performance of the involved technologies, understanding and modelling of supercritical process or processes implying supercritical region of the fuel have become a relevant issue.

Focusing on numerically based investigations, various approaches for the spray simulation, namely the Eulerian-Lagrangian (EL) method, the Eulerian-Eulerian (EE) or multi-fluid approach and the Transported Probability Density Function (T-PDF), are usually applied. A recent review is provided by Ries and Sadiki [42].

Reported investigations of supercritical injection processes range from individual jets (e.g. [17, 24]) to sprays in the entire combustion chamber [50]. Mixing processes within such configurations were examined on different numerical scales by means of direct numerical simulations (DNS) [11, 27, 47], Large Eddy simulations (LES) [23, 33, 49] or Reynolds Averaged Numerical Simulation (here RANS) descriptions [10, 48]. Thereby, the main focus was on the mixture formation [23], the phase separation [39, 40] or the effects at the phase boundary [15, 28]. For the model validation in this class of investigations the detailed study by Chehroudi [12], who neatly generated and compared various experimental data from different liquid and gas jets as function of pressures, remains state of the art. The contribution by Mayer et al. [26] can be considered as standard configuration for non-reacting flow studies. The fuel flow system is usually described as a single phase dense gas with real gas effects within an Eulerian framework. This method, also known as single fluid mixing (SFM) model, corresponds to a so-called homogeneous EE model. As it is valid to decouple real and ideal fluid behavior, Banuti [8, 9] suggested an extension by considering a multi-fluid mixing (MFM) modeling.

Focusing on LES modeling, some studies report on a priori investigations that are based on a gaseous phase description while taking into account real gas properties. Two aspects are essentially addressed, namely the inclusion of necessary physics in subgrid scale (SGS) models into the governing filtered equations and into the real fluid EoS. First, the consistency of existing classic LES models primary designed for atmospheric environments was evaluated ([11, 27, 47]). Then, a posteriori validation has been reported. Finally, first comparisons with experimental data in the supercritical range were carried out by e.g. Miller et al. [27, 28], Petit et al. [38]. All these investigations were limited to comparisons of prediction obtained with different SGS models developed for subcritical flow situations in connection with various real gas descriptions. It turns out that LES modelling based on single-fluid mixture models is not able to provide a detailed description of all fluid states, such as liquid, gaseous, supercritical up to multi-phase mixtures including spray dynamics and phase changes. Furthermore, the consideration of SGS in dealing with the real fluid EoS has been often neglected as reviewed by Ries and Sadiki [42].

Despite the limitations observed with single fluid models, several researchers employed the pure Eulerian modeling within the framework of LES (e.g. [23, 28, 38, 46]). The broad consensus is that LES allows an accurate prediction of such supercritical fluid flows, whereby species mixing and combustion within supercritical injection conditions could be addressed in a satisfactory way (e.g. [18, 33, 51, 52]).

In the case of coexistence of supercritical states and multi-component subcritical two-phase states, Matheis and Hickel [25] presented and evaluated a two-phase model for Eulerian LES of liquid-fuel injection and mixing at high pressure. This model is based on cubic EoS and VLE (vapor-liquid equilibrium) calculations via a homogeneous mixture approach. Such an approach holds only for dense and moderately dense high-pressure injection cases which feature typically high Weber number and low Stokes number. The droplet diameters are small and surface tension is low giving raise to droplet vaporization time scale and droplet inertial time scales sufficiently small compared to hydrodynamic time scales and of the order of the computational time step [25]. For liquid fuel injection which includes dilute spray region and intrinsically permits significant slip velocity between the dispersed liquid and the gas phase, the above pure Eulerian approach with a single-valued velocity for both phases is invalid.

A coupling between the Eulerian VLE-based two-phase model for the primary jet breakup and an appropriate subsequent approach to describe the evolvement of the spray is necessary.This allows to make a clear difference between the classical multifluid model (EE) family [45] which is rather well suitable to describe two-phase flow processes (see [22, 36]) and the pure Eulerian modeling appropriate for single phase multi-species mixing. Indeed, in the latter the thermodynamic mixing process is retrieved using either the SFM or the MFM models [9], whereas the multifluid (EE) methods offer a versatile framework to deal with two-phase flows, as different levels of disequilibrium between phases can be treated, and physical effects (e.g. surface tension, phase change) easily be integrated [36].

Accordingly, the EE-methods are able to treat formation and disappearance of interfaces, even though they may require several grid cells to capture the interface while being subject to progressive interface smearing. The review paper by Ries and Sadiki [42] and the comprehensive contribution by Pelletier [36] provide more description details. Ping et al. [57] suggested recently an EE- multicomponent real-fluid fully compressible four-equation model for two-phase flow with phase change. Thereby, the balance equations for distinct species in gas and liquid phases are considered, while a mixture momentum and mixture specific internal energy are solved. They are completed by real gas equations of state for both gas and liquid phases. As long as the multicomponent mixture is outside the vapor dome (i.e., single phase), the system of governing equations is closed by PR EoS. Once, the mixture is inside the vapor dome (i.e., two phase), the system is closed by the composite EoS connected with the set of algebraic equations for each phase (equilibrium connection constraints). In particular, in the composite EoS, each phase always follows its own EoS (here Peng-Robinson), and the equilibrium connection constraints ensure that the mixture speed of sound is always defined.

Under supercritical/transcritical conditions, the most comprehensive spray simulation following an EL framework as adopted by Oefelein [33] and Yang [56] represents an alternative to EE. Thereby both EE and EL methods adapted for supercritical conditions have been employed, see also [54]. Nishad et al. [32] investigated the effect of real gas behavior on the evaporation of isolated droplets subject to transcritical operating environments. Thereby, a multicomponent evaporation model has been developed and applied. The model includes following effects: (a) the gas solubility in the liquid phase; (b) the diffusion inside the droplet, including internal flow recirculation with effective thermal conductivity and mass diffusivity; (c) the gradients on the gas phase side by Nusselt and Sherwood numbers using the effective film method; (d) the real gas behavior in the gas and liquid phases by using the PR equation of state; (e) the spatial and temporal variation of the thermophysical properties. In particular, the impact of Nu- and She-number correlations has been appraised.

The present paper aims at developing a generally valid, consistent numerical description of a turbulent multi-component two-phase flow that experiences processes that may occur under both subcritical and trans-critical or supercritical operating conditions. Within an appropriate LES methodology, focus is put on an Euler-Eulerian description method suitable for trans- and supercritical sprays under consideration of multi-component mixture properties along with phase change process.

The paper is organized as follows. In Sect. 2, the LES-based numerical modelling approach adopted is outlined. Thereby, the governing filtered equations, the sub-grid scale models applied, the real fluid thermodynamic and transport models are introduced. Subsequently, the numerical procedure and the numerical setup are provided. In Sect. 3, the investigated configuration is outlined along with the computational domain and the inflow/boundary conditions. In Sect. 4 relevant results of this paper are presented and discussed before concluding and addressing open issues and challenges in the last section (Sect. 5)

2 Methods and Models

In this section, the required Favre-filtered governing equations for LES and the thermophysical models are briefly introduced. Subsequently the numerical procedure employed in this work is concisely described.

2.1 Governing Filtered Equations and Modeling

A Large Eddy Simulation (LES) framework with an incompressible low-Mach solver capable to simulate configurations with Mach-numbers up to 0.35 is utilized. In order to capture turbulent multiphase flow characteristics along with phase change processes, the original low-Mach approach in accordance to Ries et al. [41] and Müller et al. [29], is developed and extended to obtain an Eulerian-Eulerian approach for multi-species mixtures under consideration of multicomponent aspects in line with [25, 44] and [57]. This results in the following set of governing filtered Eulerian-Eulerian equations for mass, momentum, species and sensible enthalpy, respectively, which is solved for the two phases considered as multi-species mixtures:

$$\begin{aligned} \frac{\partial {{\alpha }_{p}\bar{\rho }}}{\partial t} + \frac{\partial }{\partial x_{j}} \left( {\alpha }_{p}\bar{\rho }\tilde{u}_{j}\right) = 0 \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial {\alpha }_{p}\bar{\rho }\tilde{u}_{j}}{\partial t} + \frac{\partial }{\partial x_{j}} \left( {\alpha }_{p}\bar{\rho }\tilde{u}_{i}\tilde{u}_{j}\right) = -\frac{\partial {\alpha }_{p}\tilde{p}}{\partial x_{j}} + \frac{\partial }{\partial x_{j}} \left( {\alpha }_{p}\bar{\tau }_{ij}-{\alpha }_{p}\bar{\rho }\tau _{ij}^{SGS}\right) \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial {\alpha }_{p}\bar{\rho }Y_{S}}{\partial t} + \frac{\partial }{\partial x_{j}} \left( {\alpha }_{p}\bar{\rho }Y_{S}\tilde{u}_{j}\right) = -\frac{\partial }{\partial x_{j}}\left( {\alpha }_{p}j_{S,j}+\bar{{\alpha }_{p}\rho }j_{S,j}^{SGS}\right) \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial {\alpha }_{p}\bar{\rho }\tilde{h}}{\partial t} + \frac{\partial }{\partial x_{j}} \left( {\alpha }_{p}\bar{\rho }\tilde{u}_{j}\tilde{h}\right) = -\frac{\partial }{\partial x_{j}}\left( {\alpha }_{p}q_{j}+{\alpha }_{p}\bar{\rho }q_{j}^{SGS}\right) \end{aligned}$$
(4)

In these equations and throughout the paper, filtered variables are denoted by \((\tilde{*})\) while \(({*}^{SGS})\) represents sub-grid-scale quantities. In Eqs. (1)–(4) the phase fractions \(\alpha _{p}\) of the mixture are calculated by \(\alpha _{p}=\frac{\partial {V}_{p}}{\partial V}\) with \(\sum {\alpha }_{p}=1\), where the index p (with \(p=\)liquid, gas) denotes the phase state. It is worth noting that once Eq. 1 is written for each phase, the phase change terms denoted as \(\pi _{p, S_{\kappa }}\) appear, but are constrained by \(\sum _{p}\pi _{p, S_{\kappa }}=0\) for the whole mixture. On the left hand side of the equations, t represents time and \(\bar{\rho }\) the density with \(\bar{\rho }=\sum {\alpha }_{p}\bar{\rho }_{p}\). In particular, \(\tilde{u}_{i}\) represents the mixture velocity components with \(i=1, 2, 3\) denoting the Cartesian coordinates, \(\tilde{h}\) the sensible enthalpy and \({Y}_{S}\) the volume fraction of each specie. According to the low Mach approach, \(\tilde{p}\) is the modified thermodynamic pressure in which sub-grid-scales are not accounted for.

On the right hand side of these equations appear several flux terms, namely molecular contribution and its SGS counterpart for the stress tensor \(\tau _{ij}\), \(\tau _{ij}^{SGS}\), the heat flux \(q_{j}\), \(q_{j}^{SGS}\) and the mass flux of species \(j_{S,j}\), \(j_{S,j}^{SGS}\), in Eqs. (2), (3) and (4), respectively. These quantities are very complex and need to be modelled.

Dealing with Newtonian fluid flows, the molecular stress tensor obeys the Newtonian law given as

$$\begin{aligned} \tau _{ij} = -\nu \left( \frac{\partial \tilde{u}_{i}}{\partial x_{j}}+\frac{\partial \tilde{u}_{j}}{\partial x_{i}}-\frac{2}{3}\frac{\partial \tilde{u}_{k}}{\partial x_{k}}\delta _{ij}\right) \,, \end{aligned}$$
(5)

where \(\delta _{ij}\) is the Kronecker-delta function. The mixture viscosity \(\nu \) is determined by means of the correlations of Chung et al. [13]:

$$\begin{aligned} \nu = {\nu }_{p} + {\nu }_{k}\,, \end{aligned}$$
(6)

consisting of a temperature and a pressure depending viscosity \({\nu }_{k}\) and \({\nu }_{p}\) given as:

$$\begin{aligned} {\nu }_{k} = \nu _{0}\left[ \frac{1}{{G}_{2}} + {A}_{6}Y\right] \,, \qquad {\nu }_{p} = \left[ 36.344\cdot {10}^{6}\frac{{\left( M{T}_{c}\right) }^{\frac{1}{2}}}{{{V}_{c}}^\frac{2}{3}}\right] \,, \end{aligned}$$
(7)

respectively. In these expressions, \(\nu _0\) is the dilute gas viscosity, \({T}_{c}\) the critical temperature of the mixture and \({V}_{c}\) the critical volume. M, \(A_n\), \(G_o\) and Y represent linear functions depending on a set of empirical linear equations. Further information regarding Chung et al. correlations can be found in [13].

As pointed out in [34, 42] and elsewhere, the molecular flux vectors for the system consisting of multiple species \({S}_{\kappa }\); \((\kappa \in [1, N-1]; N: \text{ number } \text{ of } \text{ species})\) can have very complex forms based on the full matrices of mass-diffusion coefficients and thermal-diffusion factors with consideration of the Soret and Dufour effects. As for the viscosity, the thermal conductivity are computed using mixture rules. In this paper, such molecular fluxes are simply modeled according to [34] as:

$$\begin{aligned} j_{{S}_{\kappa },j} = -\left[ j_{{S}_{\kappa },j}^{\prime }+\left( \alpha _{IK}-\alpha _{h}\right) Y_{{S}_{\kappa }}Y_{{S}_{\gamma }}\frac{\rho D}{T}\frac{\partial T}{\partial x_{j}}\right] \,, \end{aligned}$$
(8)

where \(\alpha _{IK}\) and \(\alpha _{h}\) are transport coefficients associated to molar and heat fluxes. The diffusion factor D is derived from \(Sc = \nu \alpha _{D}D\), with mass diffusion factor \(\alpha _{D}\), and

$$\begin{aligned} j_{{S}_{\kappa },j}^{\prime } = \bar{\rho }D\left[ \alpha _{D}\frac{\partial Y_{{S}_{\kappa }}}{\partial x_{j}}+\frac{Y_{{S}_{\kappa }}Y_{{S}_{\gamma }}}{R\, T}\frac{m_{{S}_{\kappa }}m_{{S}_{\gamma }}}{{m}_{m}}\left( \frac{v_{{S}_{\kappa }}}{m_{{S}_{\kappa }}}-\frac{v_{{S}_{\gamma }}}{m_{{S}_{\gamma }}}\right) \frac{\partial p}{\partial x_{j}}\right] . \end{aligned}$$
(9)

In this Eq. (9) R stands for the universal gas constant, the quantity \(m_{{S}_{z}}; \left( z=\kappa ,\gamma \right) \) are the molar mass of species \({S}_{z}\) and \({m}_{m}\) the molar mass of the mixture, while \(v_{{S}_{z}}\) expresses the partial molar volume of species z with \(v_{{S}_{z}}=\left( \partial v / \partial X_{{S}_{z}}\right) \) and \(X_{{S}_{z}}\) the molar fraction of species \({S}_{z}\) given as \(X_{{S}_{z}} = {m}_{m}\, Y_{{S}_{z}}/m_{{S}_{z}}\)). Relying on the low-Mach solver approach, the quantity \(\partial p / \partial x_{j}\) is negligibly small. The heat flux vector is modeled as:

$$\begin{aligned} q_{j} = -\lambda \frac{\partial T}{\partial x_{j}}-\alpha _{IK}R\,T\frac{m}{m_{{S}_{1}}m_{{S}_{2}}}j_{{S}_{1},j}^{\prime }\,, \end{aligned}$$
(10)

where \(\lambda \) is the thermal conductivity.

Concerning the SGS counterparts, various modelling approaches and their consistency have been discussed in Ries and Sadiki [42]. The modeling approach used in the present paper follows the outcome from [42] by applying the simplest consistent reduced framework provided by the zero-equation approach. Correspondingly, the simple gradient approach is used for both the SGS stress tensor, the mass flux and heat flux vectors as:

$$\begin{aligned} \tau _{ij}^{SGS} = -\nu ^{SGS}\left( \frac{\partial \tilde{u}_{i}}{\partial x_{j}}+\frac{\partial \tilde{u}_{j}}{\partial x_{i}}-\frac{2}{3}\frac{\partial \tilde{u}_{k}}{\partial x_{k}}\delta _{ij}\right) \end{aligned}$$
(11)

with \(\nu ^{SGS}\) the SGS kinematic viscosity expressed by the Smagorinsky SGS approximation. Accordingly

$$\begin{aligned} \nu ^{SGS}=C\Delta ^{2}{\sqrt{2{\bar{S}}_{ij}{\bar{S}}_{ij}}}=C{\Delta }^{2}\left| {\bar{S}}\right| \,, \end{aligned}$$
(12)

where \(\Delta \) represents the filter width of the underlying numerical domain, and \({\bar{S}}_{ij}={\frac{1}{2}}\left( {\frac{\partial {\bar{u}}_{i}}{\partial x_{j}}}+{\frac{\partial {\bar{u}}_{j}}{\partial x_{i}}}\right) \) stands for the rate-of-strain tensor. C is a constant model coefficient calculated here according to \(C=\frac{1}{\pi }{\left( \frac{2}{3{\alpha }_{S}}\right) }^{\frac{3}{4}}\). With the Kolmogorov constant \({\alpha }_{S}=1.5\) this leads to \(C=0.173\). The mass and the heat flux vectors are modelled as

$$\begin{aligned} j_{S,j}^{SGS} = -\frac{\nu ^{SGS}}{Sc^{SGS}}\frac{\partial {{Y}_{{S}_{\kappa }}}}{\partial x_{j}}\,, \qquad q_{j}^{SGS} = -\frac{\nu ^{SGS}}{Pr^{SGS}} \frac{\partial \tilde{h}}{\partial x_{j}}\,,\end{aligned}$$
(13)

respectively, where \(Sc^{SGS}\) is the SGS Schmidt number and \(Pr^{SGS}\) the SGS Prandtl number.

2.2 Thermodynamic and Transport Models

In the present study a heat transfer fluid [53] and more exotic fire extinguishing fluid (see, e.g. [30]), fluoroketone is investigated under supercritical conditions. As already pointed out above, constitutive equations or closures for \(\rho \), \(\mu \), \(\lambda \), Cp and h as functions of local temperature and pressure are required. Once under supercritical conditions, non-ideal gas behavior must be accounted for. The commonly used Peng-Robinson equation of state (PR-EOS) [37] is employed in the present study. With supercritical conditions are meant pressure levels above the mixtures critical pressure as well as temperature higher than the mixture critical temperatures. To remedy the limitations of the PR-EOS at operation conditions near the critical point, a generalized volume translation method proposed by Abudour et al. [5] can be applied. Non-ideal corrections of \(c_p\) and h are thus expressed in terms of departure functions derived from the PR-EOS, where the contributions from the hypothetical, ideal gas are calculated using the 7-coefficients NASA polynomials. Regarding transport properties, the correlations of Chung [13], applicable for dilute and dense fluids, are utilized for \(\mu \) and \(\lambda \) as outlined above. Indeed, dealing with two-phase flow considered as multicomponent mixtures, the Peng-Robinson equation of state is applied separately for each phase of the multi-species mixture:

$$\begin{aligned} p = \frac{RT}{\tilde{v}-b_{m}} - \frac{\left( \alpha a\right) _{m}}{\tilde{v}^{2}+2b\tilde{v}-b^{2}} \end{aligned}$$
(14)

with

$$\begin{aligned} \alpha = \left[ 1+\left( 0.37464+1.54226\omega -0.26992\omega ^{2}\right) \left( 1-\sqrt{\frac{T}{T_{c}}}\right) \right] \,. \end{aligned}$$
(15)

In this equation,

$$\begin{aligned} a = 0.45724\frac{\left( R\, T_{c}\right) ^{2}}{P_{c}}\,, \qquad b = 0.0778\frac{R\,T_{c}}{P_{c}} \end{aligned}$$
(16)

where \(T_{c}\) expresses the critical temperature, \(P_c\) the critical pressure and \(\omega \) the acentric factor. The mixture parameters \(\left( \alpha a\right) _{m}\) and \(b_{m}\) are defined by means of the Van-der-Waals mixing rules:

$$\begin{aligned} \left( \alpha a\right) _{m} = \sum _{\kappa }\sum _{\gamma } X_{\kappa }X_{\gamma }\left( \alpha a\right) _{\kappa \gamma }\,,&\quad \left( \alpha a\right) _{\kappa \gamma } = \sqrt{\left( \alpha a\right) _{\kappa }\left( \alpha a\right) _{\gamma }}\left( 1-k_{\kappa \gamma }\right) \,, \\ b_{m} =&\sum _{\kappa }X_{\kappa }b_{\kappa }\,, \end{aligned}$$

where \(k_{\kappa \gamma }\) is representing the binary interaction parameter.

Table 1 Operating conditions of fluoroketone and helium
Full size table

Table 1 summarizes the initial critical and flow properties of fluoroketone and helium under consideration in the investigated configuration in Sect. 3. The simulation conditions are far from the vicinity of the critical point for helium. Fig. 1 shows that the thermodynamic and transport models are in good agreement with the reference data owing to the fact that helium is by far more volatile in comparison to fluoroketone.

Fig. 1
figure 1

NASA fitted curves of relevant thermodynamic data in respect to data sets obtained from REFPROP [4] and 3M [1]

Full size image

It is worth mentioning that in subcritical conditions, the cubic Peng-Robinson equation EOS is first solved resulting in three roots. The smallest positive one is calculated to obtain the liquid molar volume. The remaining roots of the Peng-Robinson EOS are used to determine the gas molar volume, which corresponds to the larger root. Under single-phase conditions, the Peng Robinson EOS is calculated only once and the real positive root is considered to obtain the molar volume. When the phase molar volume is known, other values including phase density and mixture density can be calculated. The phase composition can then be used for the calculation of the thermal properties of each phase. In supercritical conditions the process follows the same procedure with respect to the critical point of species and mixtures.

2.3 Numerical Procedure and Setup

The governing filtered Eulerian-Eulerian low-Mach equations (Eqs. 1–4) are phase dependent solved by calculating a chain of predictor-corrector steps. A combination of PISO [19] and SIMPLE [35] algorithms is applied for coupling phase velocities and pressure. A schematic representation of the solution algorithm is depicted in Fig. 2.

Fig. 2
figure 2

Flow chart of the low Mach Eulerian-Eulerian PISO-SIMPLE algorithm

Full size image

Beginning in the global SIMPLE loop, a density predictor is solved by means of the continuity equation. Next, the phases in the simulation domain are rebalanced according to thermodynamic states. Then, momentum is predicted using previous iteration field variables. Moving into the PISO loop, the enthalpy equation is calculated and temperature is iteratively derived. Then, the thermodynamic pressures and temperatures are updated and eventually, the pressure equation is solved and the velocity is corrected. The whole process is iteratively repeated in the related SIMPLE and PISO loops until convergence is reached.

Regarding temporal as well as spatial discretization, a central differencing scheme of second order is utilized for the convection terms. In addition a conservative second order scheme is used for the Laplacian terms. The time derivative terms are solved by a second order backward integration method. A preconditioned conjugate gradient solver is deployed for the density predictor and geometric algebraic multi grid solvers are utilized for pressure, momentum and enthalpy equations in order to increase computation speed by multi grid resolutions. Details about the discretization procedure and the numerical schemes can be found in the OpenFOAM programmers guide [3].

This Eulerian-Eulerian algorithm is implemented in the OpenSource computational fluid dynamics software framework, OpenFOAM Version 7.0 [2].

3 Investigated Configuration

The configuration under study corresponds to the experimentally investigated jet of fluoroketone by Muthukumaran et al. [30, 31]. Fluoroketone finds applications as a heat transfer fluid in cooling applications [53] and as fire extinguishing fluid.

3.1 Experimental Reference

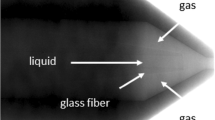
In [30, 31] a supercritical elliptical jet of fluoroketone is injected into a high pressure and temperature chamber, see Fig. 3. The chamber design is based on the experimental study of Roy et al. [43]. It features a 55 mm square cross section and a chamber length of 190.5 mm. On each side a window in the chamber provides a field of observation of 22 mm width and 86 mm length. The injector orifice is of elliptic shape with a 4 to 1 mm ratio. The elliptic inlet orifice is intentionally used to detect effects of surface tension in the experiment. In the presence of surface tension the initial elliptic jet is forced from the elliptic surface into a round surface. The chamber is initially filled with helium at supercritical pressure and temperature. Finally the elliptic jet of supercritical fluoroketone is injected into the chamber. The elliptic jet evolves from a fully developed elliptic pipe flow with a hydraulic diameter of \({d}_{H} \approx 1.45\) mm, a corresponding Reynolds number of \(Re \approx 13000\) and a inlet Mach-number \(Ma<< 0.1\).

Fig. 3
figure 3

Computational domain embedded in a drawing which corresponds to the experimental setup used in [30, 43]

Full size image

3.2 Computational Domain, Initial and Boundary Conditions

In order to increase the computational efficiency and to avoid unnecessary computational costs, only a conical cutout of the experimental chamber, representing the primary region of interest, is considered in the present study. By maintaining a sufficient distance of the numerical domain to the walls present in the experimental setup and under consideration of the fact that the ambient fluid in the chamber is a quiescent medium of very low density, the effect of the wall is neglected in the simulation domain. The chamber simulation domain consists of a conical domain with a length of 90 mm and a \(5\,{d}_{H}\) diameter at the narrow inlet side gradually increasing to a \(10\,{d}_{H}\) diameter at the outlet end. A three-dimensional, block structured numerical grid consisting of \(\approx 3\) million numerical control volumes, is employed after a preliminary grid resolution study. The numerical grids finest solution is located at the inlet walls and slightly spreads out radial and downstream in control volume dimensions. The mentioned inlet data simulation numerical grid fits exactly to the inlet of the jet injection simulation domain in order to avoid any numerical disturbances.

Fig. 4
figure 4

Inlet velocity fluctuations \(u_{mean}\) normalized by injection velocity \({u}_{i}\)  in m/s on the inlet pipe centerline

Full size image

In particular a full simulation of the injector pipe was conducted to generate proper inlet data for the jet injection case. For that purpose a elliptic pipe of \(20\,{d}_{H}\) length was utilized. By applying recycling boundary conditions at the pipe inlet/outlet a numerically infinite elliptic pipe corresponding to the given diameters is simulated and slices of the flow field are extracted from the middle section of the pipe. The pressure gradient along the pipe flow direction, that drives the flow, is adjusted dynamically to maintain a constant mass flux for the resulting inlet data. The latter is recorded after two full passes of fluid through the simulation domain in order to avoid artificial numerical artifacts in the inlet data that may result from minor fluctuating inaccuracies in the initial conditions of the pipe simulation. In this elliptical cross section a velocity field data set is subsequently stored in a database at each relevant time step, see Fig. 4. This inlet data set is interpolated with second order accuracy in space and time in order to match the inlet of the jet and utilized as inflow conditions of the jet simulation. On the outlet and conical domain shell surface, a velocity inlet/outlet boundary condition is imposed to enable fluctuating fluxes of fluid from the surrounding domain. Thereby, the incoming velocity is calculated from the internal cell value. In the opposite direction a Neumann condition is applied in the case of outflow. At the walls next to the inlet orifice, a no-slip condition is utilized. In the case of temperature boundary conditions, a Dirichlet condition is set for the inlet, while Neumann conditions are imposed at the outflow and domain shell.

4 Results and Discussions

First, turbulent flow dynamics and thermal properties are examined in order to identify the distinctive features of the jet disintegration process under the operating supercritical thermodynamic conditions.

Fig. 5
figure 5

Representation of the medium temperature of the simulated jet (Contour in foreground). Back plane: Mean temperature in K. Horizontal plane: Instantaneous temperature in K. Turquoise contour: Potential core

Full size image

Figure 5 depicts a spatial representation of the simulated elliptical fluoroketone jet injection. The foreground contour represents the medium temperature, while the turquoise colored contour is wrapping the main core of the jet. Moving downstream, the jet begins to disintegrate and the main core vanishes. On the back plane the mean temperature of the jet is shown. The increasing widening in the direction of flow, as well as the slowly decreasing temperature profile of the jet is clearly visible. On the lower plane an instantaneous image of the temperature is given. In contrast to the mean temperature field, turbulent structures are clearly visible. In terms of the temperature field, it ranges from high values at the core of the jet to small values in the ambient helium. However no sharply defined interface exists in the temperature distribution of the jet. Close to the inlet, the elliptic jet surface is nearly unaffected by the surrounding. Further downstream, turbulent and diffusive effects begin to influence the jet and lead to an increasing jet disintegration. Due to the absence of surface tension in supercritical environments, finger-like structures begin to stretch out of the jet interface into the ambient helium atmosphere. Finally these structures dissolve and accelerate the disintegration process of the temperature interface.

Fig. 6
figure 6

Experiment: Density of the fluoroketone jet in \(kg/m^3\) in the centerline axial plane, according to [30]

Full size image
Fig. 7
figure 7

Simulation: Density of the fluoroketone jet in \(kg/m^3\) in the centerline axial plane

Full size image

Figure 6 depicts the experimental result of an instantaneous shot of an elliptical jet injection of fluoroketone into a helium environment. Some scattering effects due to the utilized measurement methods are visible in the resulting density fields. The jet has a visible length of \(x \approx 60\) mm and is fully disintegrating in the observation area. The main core of the jet breaks up at \(x \approx 12\) mm downstream. It further disintegrates and begins to fall apart at \(\approx 28\) mm. The main core maximum density is \(478\, \frac{kg}{{m}^{3}}\) while the spreading angle of the jet in between the two dashed lines amounts \(20^{\circ }\).

Figure 7 shows an instantaneous shot of an elliptical jet simulation on the center plane and the obtained jet spreading angle of 19 degrees. This value is slightly narrower than in the experiment, suggesting that the velocity in downstream direction is a little elevated in comparison to the experiment. The main core has a slightly higher density of \(493\,\frac{kg}{{m}^{3}}\) in comparison to experimental data. One can observe a constriction of the main core of the jet at \(x \approx 13\) mm downstream. This fits very well to the primary main core breakup in the experimental data from Fig. 6. A temporal observation of the primary breakup shows that this point fluctuates from \(x \approx 11\,\) to 13 mm, and the secondary breakup fluctuates subsequently from \(x \approx 29\,\) to \(34\, mm\). It turns out that the secondary breakup is numerically well reproduced and the pseudo-liquid pockets are more visible in contrast to the experiment. This is also depicted in Fig. 8 which compares the density profiles along the centerline in experiment and simulation. Thereby it is visible that the simulated density result is following the global trend of the experimental data.

Fig. 8
figure 8

Comparison of density profile along centerline of the fluoroketone jet

Full size image

As pointed out above, some minor density aggregations are observable downstream the secondary breakup in contrast to measurement result. This indicates a slightly over prediction and delayed full dilution of the mixture density in the wake flow as already seen in Fig. 8. This prediction divergence might be due to the still coarser mesh resolution downstream and the more sensitive numerical capturing of density fragments in comparison to the low experimental resolution under high pressure conditions. Finally, to note is that the liquid jet is not forced into a round shape; it rather preserves an elliptical shape until the disintegration process is completed.

Fig. 9
figure 9

Isobaric mixture heat capacity at six different downstream cross sections, representing the main core disintegration. (Red area: Disintegration interface)

Full size image

Figure 9 displays the isobaric heat capacity of the mixture at six different downstream cross sections. Close to the injection \(\left( x= 5\,\textrm{mm}\right) \), the jet is expanding out of the elliptic injection outline, due to the injection velocity differences across the injection cross section. The velocity is significantly larger in the inner section and therefore the jet expands from the narrow diameter in radial direction. Further downstream the main core becomes subject to turbulent and thermodynamic mixing processes and thereby varies considerably in its shape, with a clearly defined interface. The interfaces fades out and finally disappears while the processes of turbulent mixing and resulting jet disintegration take place.

Fig. 10
figure 10

Instantaneous velocity field u of the fluoroketone jet, in the centerline axial plane, normalized by \(u_{i}\)

Full size image
Fig. 11
figure 11

Fluctuations of velocity \(u^{'}\), of the fluoroketone jet, in the centerline axial plane, normalized by \(u_{mean}\)

Full size image

To get further insights into the turbulent fluctuations, the flow field is examined. Even though experimental data is not available, Figs. 10 and 11 allow to gain a view of the velocity field. Figure 10 shows an instantaneous view of the velocity \(u/u_{i}\) of the fluoroketone jet in the main cross section, ranging up to a ratio of \(\approx 1.1\) in good agreement with Fig. 4. One can recognize that tiny turbulent disturbances in the sharp interface region \(\left( x \approx < 12\, mm \right) \) modulate the turbulent turn over in the further downstream region and thereby initialize the turbulent mixing.

Figure 11 illustrates the fluctuations of velocity of the jet in terms of \(u^{'}/u_{mean}\) which indicates areas of high turbulent effects penetrating the jet interface. In the sharp interface region these disturbing effects are more concentrated leading to the relatively intense breakup of the main core further downstream. It appears clearly that under trans- and supercritical conditions very complex thermodynamic processes occur in the fluid systems in which the fluid properties vary significantly. In particular, the changes in entropy production are very large, so that an analysis using the second law of thermodynamics appears essential in order to delimit sub-processes and identify the causes of possible inefficiencies of these sub-processes. Such an approach has been utilized, and results have already been reported by Ries and Sadiki [42] for similar configurations as investigated in the present paper.

5 Conclusions

Relying on a low-Mach Eulerian-Eulerian based real fluid system modelling, an LES approach has been developed which is able to describe turbulent two-phase flow fluids with phase change as multi-component mixtures in which the real fluid properties are accounted for by a composite Peng-Robinson equation of state. Thereby each phase is governed by its own PR EoS. The numerical model allowed to perform qualitative and quantitative analyses. The results showed significant coupled effect of the turbulence and the thermodynamic on the jet disintegration along with the mixing processes of a supercritical jet of fluoroketone fluid injected into an environment of helium.

To appraise the prediction capability of the model suggested, comparisons of the achieved numerical results with available experimental data have been carried out. The numerical simulations could reproduce correctly the jet disintegration regimes as observed experimentally in terms of penetration length, fluoroketone mass density and jet spreading angle. In addition, the effect chain of the evolving processes was especially consistently reproduced under such operating conditions.

The prediction evaluation of the validated model needs to be further assessed. For that purpose, simulations of trans-critical jet injection are being carried out. A comparison of the expected results with those obtained from an Euler-Lagrangian approach which is extended to integrate the arising effects of vanishing surface tension is left for future work.