Social Network Tools for the Evaluation of Individual and Group Scientific Performance

Abstract

Over the past few decades, scientific collaboration has been widely considered an important driver of research innovation. By collaborating together, scientists can benefit from both methodological and technological complementarities and synergy, improving the quality and quantity of their research outputs. As evidence of this, collaboration among scientists is increasing in all disciplines and government policies in international exchange programs are aimed at promoting collaboration among researchers. Collaboration among scientists can be represented as a network, usually adopting co-authorship as linkages. In this view, Social Network Analysis provides a useful theoretical and methodological approach because collaboration features can be related to the topological characteristics of the network. Recently, several empirical studies have found positive associations between researchers’ position in the co-authorship network and their productivity, although the results can be different depending on the discipline, scientific performance measure, and data source retrieved to construct the co-authorship networks. In this contribution, we propose the use of SNA tools for scientific evaluation purposes. Network indices at the individual and subgroup levels will be introduced to analyze the relation with both the individual research productivity and scientific output quality measure provided by the Italian academic researchers involved in VQR from the period 2011–2014.

1 Introduction

Over the past few decades, scientific collaboration has been considered an important driver of research progress that supports researchers in generating novel ideas (see, among others, Beaver 2001). The role of scientific collaboration has been emphasized in recent government policies and international exchange programs that aim at stimulating the mobility of researchers and fostering scientific collaboration and productivity (Wuchty et al. 2007; Defazio et al. 2009; Leone Sciabolazza et al. 2020). Recently, university administrations and research funders have explored a variety of programs and policies to stimulate interdisciplinary collaboration. Among them, it is worth recalling the funding initiatives targeting: interdisciplinary projects, such as the INSPIRE program of the US National Science Foundation (NSF), the Interdisciplinary Research Consortia program of the US National Institutes of Health (National Institute of Health 2007), the EU funding research network (Commission of European Communities 2006), and the national Spanish Ingenio 2010 Program (Ministry of Education and Science 2006); interdisciplinary training programs such as the NSF Integrative Graduate Education and Research Traineeship (IGERT); and interdisciplinary university fellowship programs (Sà 2008). Scientific collaboration has also been recognized as a key factor in measuring and evaluating scholars’ scientific performance (Ferligoj et al. 2015; De Stefano & Zaccarin 2016).

Moving from this perspective, this chapter aims at presenting the main results of the SnEval (Social Network tools for the Evaluation of individual and group scientific performance) research project. The main contribution of the project was to show novel results based on a network analysis on the ANVUR VQR data. The proposed methodology can be adopted in future research evaluation exercises.

The analysis focuses on the co-authorship networks among academic scholars in two research areas of the Italian university system, namely Area 2—Physics and Area 13—Economics and Statistics. These areas have different characteristics in the evaluation exercise. In particular, Area 2 is classified as a fully “bibliometric” area,¹ that is, the majority of scientific products in the area are published in international journals and bibliometric indicators (journal metrics and citations indicators) are commonly used for evaluation purposes. Conversely, Area 13 is classified as a “non-bibliometric” area. Although a few disciplines in this area are characterized by bibliometric-like publication behavior, the evaluation of scientific products is performed mainly by a peer-review process (or informed peer review where reviewers additionally take into account a number of bibliometric indicators). Co-authorship information has been derived from the scientific products scholars in the two areas submitted for the VQR exercise in the period 2011–2014. Co-authorship networks were built at different levels of the official aggregations (macro-sectors and meso-sectors or Settore concorsuale) of the disciplines² belonging to the two abovementioned areas in the VQR exercise period (see Sect. 4).

We then selected some of the most appropriate network indices—at the individual and subgroup network levels—and some useful techniques (as described in Sect. 3) to disentangle the different publication and collaboration styles characterizing the two areas. These indices are used both to characterize the structure of the disciplines and to look for their effect on the quality of the research outputs. More specifically, we compared the different co-authorship networks by considering their topology and authors’ position. This analysis is crucial to understand how the authors are related and how the collaboration patterns change across time and between disciplines. In particular, we considered the structural properties of the observed networks and their local characteristics. Furthermore, we fitted a regression model to provide empirical evidence of the relation between the network results, here at the author and network levels, and the VQR scores at the individual level, the latter representing the “dependent variables” in the model.

The results suggest that even in the Italian scenario, it would be worth fostering intra and interdisciplinary collaboration to improve group and individual productivity. We show how the proposed analytical tools can provide useful insights on the co-authorship network topology and detect those researchers in certain structural positions who can be the target of some network-based interventions (for instance, in scale-free networks, few important nodes act as hubs). Furthermore, the fitted models affirm that the researchers in a central position in the co-authorship network are also those scholars whose performance is significantly higher than the researchers in a more peripheral position.

2 Related Literature

Collaboration in science is a complex phenomenon that affects scientific productivity in various ways, as well as knowledge diffusion within and between disciplines.

It is straightforward to represent collaboration among scientists as a network, in which the nodes are scholars tied by the various forms of scientific collaboration among them. In this view, Social Network Analysis (SNA) (Wasserman & Faust 1994) provides a useful theoretical and methodological approach for studying collaboration among these individuals. Because collaboration features can be related to the network properties, this approach can help in the understanding of the structure and the evolution of research collaboration over topics and time (Yan & Guns 2014), as well as to cluster researchers and determine research groups (see, among others, Mali et al. 2012 and their related references).

Most of the empirical studies on scientific collaboration mainly refer to the analysis of co-authorship networks, with co-authorship ties being used as a proxy of scholars’ collaborative behavior (Ponomariov & Boardman 2016). The increasing availability of electronic databases allows for good-quality data on co-authorship to be collected in a relatively inexpensive way. Over the past few decades, several SNA co-authorship studies have been carried out in various fields. Among them, seminal papers can be found in Albert and Barabási (2002) and Newman (2004) for physics and biomedical research, in Goyal et al. (2006) for economics, and in Moody (2004) for sociology. More recently, Abel et al. (2019) investigated the driving factors behind co-authorship both within and across institutions among demographers. The common aims of these network-based studies were understanding of the topological properties of networks and their implications for the evolution of topics and methods. For instance, a “small-world” pattern (Watts 1999) can support disciplinary fragmentation and specialty areas that are clustered into distinct groups of scientists, mainly because of scientists’ research group membership, university affiliations, or geographic proximity. On the contrary, a broad connectivity among a large proportion of scientists can suggest theoretical integration, while more centralized structures that are driven by few highly connected scientists (usually called “stars”) can imply the existence of a peculiar tie formation mechanism named “preferential attachment” (Albert & Barabási 2002). Clear evidence of the presence of small-world properties has been observed in the fields of economics (Goyal et al. 2006; Maggioni & Uberti 2011) and physics (Newman 2004). Physics, mathematics, neurosciences (Albert & Barabási 2002), and economics (Goyal et al. 2006) have also shown statistical properties consistent with a preferential attachment mechanism. Sociology is the one exception because it is better represented by an integrated (cohesive) collaboration network structure resembling a random network (Moody 2004).

Co-authorship networks can also be exploited to predict the scientific performance of researchers, that is, evaluating the effect of actors’ embeddedness in co-authorship networks and their individual research outputs (Abbasi et al. 2011). Several empirical studies found positive correlations between researchers’ position in the co-authorship network and their productivity (e.g., see Fischbach et al. 2011; Abbasi et al. 2012; Uddin et al. 2013; Ferligoj et al. 2015), even if the results depend on disciplines and by the measures used for scientific productivity or scientific performance (Melin 2000; Lee & Bozeman 2005), as well as by the characteristics of the data sources retrieved to construct the co-authorship networks (De Stefano & Zaccarin 2016).

A myriad of studies also focuses on specific scientific communities at the country level. Among them, see, for example, the contributions of Kronegger et al. (2012) on Slovenian scientists, Digiampietri et al. (2017) on Brazilian PhDs working in probability and statistics field, and Leone Sciabolazza et al. (2017) on researchers hired at the University of Florida. In Italy, Maggioni and Uberti (2011) analyzed co-authorship networks among academic economists, while De Stefano et al. (2013) and Fuccella et al. (2016) studied academic statisticians. Bellotti (2012) considered the links among Italian physicists participating in funded national projects, and Bellotti et al. (2016) extended the analysis to several disciplines in Italian academia. Abramo et al. (2018) examined the collaboration behavior of stars and top scientists among Italian academic scientists, while gender and academic rank differences in collaboration were analyzed, respectively, in Abramo et al. (2014) and Abramo et al. (2019).

3 Basic Concepts on Networks

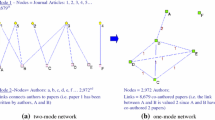
The basic notations and concepts to formally describe a co-authorship network in the SNA context are presented below. Co-authorship data are extracted from a set of authors and their papers and are arranged in an affiliation matrix that represents a bipartite network (i.e., two-mode network).

Let $\mathcal {N}=\{1, 2, \ldots , n\}$ be the set of n authors and $\mathcal {P}=\{1, 2, \ldots , p\}$ the set of p papers observed on n authors. An affiliation matrix A(n × p) author-by-paper is defined with the elements a_ik, assuming a value of 1 if $i \in \mathcal {N}$ authored the paper $k \in \mathcal {P}$, and 0 otherwise. The co-authorship network is derived from the matrix product Y = AA′, which helps in defining the undirected and valued n × n adjacency matrix (i.e., one-mode network) Yauthor-by-author. The element y_ij of Y is greater than 0 if $i,j \in \mathcal {N}$ co-authored one or more papers in $\mathcal {P}$, and y_ij = 0 otherwise. The relations embedded in Y can be represented by a graph $G(\mathcal {N},\mathcal {L})$, that is, a collection of a set $\mathcal {N}$ of nodes (authors in our case) connected by the set $\mathcal {L}$ of their links (co-authorship relationships). The cardinality of $\mathcal {L}$ is $l = \left | \mathcal {L} \right | =1/2 \sum _i \sum _j y_{ij}$, ∀i ≠ j.

Several network statistics at the global and individual levels have been defined both to describe the structural characteristics of G and to test the consistency of G with theoretical network structures that have well-known topological features and properties.

The most basic network statistics at the global level is the density Δ(G) = 2l∕n(n − 1), which measures the cohesion of G. When Δ(G) ≈ 0, G is said to be sparse. The network connectivity is described by the average path length ℓ(G), which is defined as the average number of links along the shortest paths (geodesic distance ℓ(i, j)) for all possible ${n}\choose {2}$ pairs of nodes (Watts 1999). The largest ℓ(i, j) over all pairs of nodes is called the diameter of G. In the presence of disconnected graphs, ℓ(G) is computed on the so-called giant component, which is the largest subgraph in terms of the number of reachable connected nodes (that is a path connecting two randomly selected nodes).

Besides global network statistics, node-level centrality indices refer to the position of each node (or actor) in the network according to various definitions of “centrality”. The most used centrality measures are: degree, closeness, and betweenness (Freeman 1979). The degree d_i of the i-th node is the basic one among these measures. It expresses the number of links that i has with the other nodes in the network. If d_i = 0, the node i is isolated; on the contrary, if d_i = n − 1 (the maximum value for degree), the node is the most central one in terms of its overall connectivity. In co-authorship networks, d_i indicates the number of distinct co-authors of the i-th author. Denoting with σ_j,k = σ_k,j the number of shortest paths from node j to k and with σ_j,k(i) the number of those shortest paths passing through i, a further centrality measure is the so-called betweenness b_i. This is related to the bridging role of an actor and his/her potential to control the flow of information or the exchange of resources (e.g., knowledge). The authors with large betweenness values denote the propensity to connect otherwise disconnected groups of researchers (e.g., connecting members of different labs or departments). In general, in network studies, high betweenness is observed for the authors with high interdisciplinary behavior.

Let $\mathcal {N}_i= \left \{v:\ell (i,v)=1 \right \}$ be the neighborhood of the i-th node, so that $i \notin \mathcal {N}_i$. A measure of the overlap between the links of distinct nodes in $\mathcal {N}_i$ is the (local) clustering coefficients (also called transitivity) (Fronczak et al. 2003) of the i-th node: $\Gamma _i= \left | \mathcal {L}_i \right | / {{d_i}\choose {2}}$, where $\left | \mathcal {L}_i \right |$ is the total number of links in the subnetwork $\mathcal {N}_i$. The network clustering coefficient Γ(G) is defined as the average of the Γ_i, $\forall i \in \mathcal {N}$. Γ(G) represents the average number of closed triplets of nodes (triangles) in the network out of the total number of triads, that is, arbitrary connected (or disconnected) triplets of nodes. Hence, this measure captures the extent to which authors are embedded in cohesive clusters characterized by high collaboration. High Γ(G) is a characteristic associated with the so-called small-world behavior in networks.

Furthermore, following the procedure proposed by Albert et al. (2000), degree centrality can also be used to analyze the extent to which most connected authors (i.e., scientists with the highest degree centrality) are crucial for the connectivity in the network. To this purpose, the consequences of deleting nodes at random and nodes that are highly connected could also be investigated.

The interest in the analysis of co-authorship networks lies in the fact that collaborative behavior within a scientific community closely depends on the network topological features. In particular, a frequent finding in co-authorship networks is that they are consistent with some theoretical network models with well-defined topological and relational properties, which have a meaningful interpretation in terms of knowledge diffusion in specific discipline. The simplest network models start with the idea that the connections between actors occur at random, as in the Erdos–Renyi (ER) random graphs, a family of networks in which the probability of a tie between actors’ pairs is equal to p, independently of the rest of the network and actor neighborhood (i.e., actors do not have any preference to connect with other nodes). This model represents the baseline model for assessing evidence of non-random behaviors in the observed co-authorship networks.

Empirical evidence shows that co-authorship networks are usually nonrandom because they tend to exhibit distinctive statistical properties deriving from peculiar attachment mechanisms among authors. In particular, scale-free (Albert & Barabási 2002) and small-world (Watts 1999) configurations are the theoretical models that most frequently emerge in a co-authorship analysis.

Looking at the degree distribution, that is, the frequency distribution of the number of co-authors per author, if a power law distribution is observed, then there is evidence for the emergence of a scale-free structure in the network. This implies the existence of a peculiar tie formation mechanism named preferential attachment, which formally accounts for the tendency to interact with the best connected authors (i.e., the authors with the highest degree, usually called stars or hubs). A strategy to test if the degree distribution of the network is consistent with a power law distribution is provided in Clauset et al. (2009). This strategy generates ER random networks equivalent to the observed network to check the departure from the pure randomness of the co-authorship network under study.

The small-world configuration, instead, describes the simultaneous presence of dense local clustering (i.e., high value of a clustering coefficient) with short network distances (i.e., shortest path length) that can facilitate knowledge flows inside a network. In a co-authorship network, this means that there exist small cohesive groups of researchers with few connections between them that strategically reduce the overall distance among actors. Specifically, networks consistent with this topology have high node connectivity with a low average distance among regions of the network, that is, the average path length is not greater than the value observed in random networks of equal size together with a high tendency toward author clustering. Also, in small-world structures, the diameter is lower than the one observed in ER graphs.

4 The VQR 2011–2014 Data

The data used in this analysis are bibliographic information (authors, co-authors, and the quality of the paper according to the assigned VQR scores) derived from the publications submitted by the academic researchers for the evaluation exercise VQR 2011–2014, which assesses the quality of the scientific products published in the period 2011–2014. According to the official governmental Italian classification, scientific disciplines are classified in several research areas. For the VQR, these areas are divided into bibliometric and non-bibliometric classes, depending on the use of bibliometric indicators for the research quality assessment or the use of peer-review mechanism, respectively). In particular, we analyze Area 2 (Physics) and Area 13 (Economics and Statistics) scientific areas.

Area 2 comprises four macro-sectors: Physics of Fundamental Interactions (02/A), Physics of Matter (02/B), Astronomy, Astrophysics Earth and Planetary Physics, Applied Physics (02/C), and Physics Teaching and History of Physics (02/D). Each macro-sector encompasses one or two meso-sectors. Meso-sector 02/C1 is associated with a unique micro-sector, while each of the remaining meso-sectors comprises two micro-sectors. This categorization is non-mutually exclusive, meaning that a researcher can be affiliated with multiple micro- and meso-sectors.³

Similarly, Area 13 is composed of four macro-sectors: Economics (13/A), Business Administration and Management (13/B), Economic History (13/C), and Statistics and Mathematical Methods for Decisions (13/D). Also, in this case, each macro-sector consists of one or more meso-sectors. The details of the classification of both scientific areas and the corresponding macro and meso-sectors are reported in Table 1

Table 1 Scientific areas 2 (Physics) and 13 (Economics and Statistics) and macro and meso-sectors according to the official Italian classification

As a result of the evaluation, a VQR score on a 5-point scale, as shown in Table 2, was assigned to each product submitted by the academic researchers. In Table 3, the average VQR scores for each analyzed macro-sectors are reported. We can notice a slightly higher overall VQR performance of the physics macro-sectors with respect to the economics and statistics macro-sectors. A transformation of such scores, representing the “excellence” of the individual research outputs, will be used as the dependent variable in the regression model illustrated in Sect. 5.4.

Table 2 Labels and associated numerical scores in the VQR 2011–2014 evaluation exercise

Table 3 Average VQR scores at the macro-sector level

The co-authorship networks at different levels of aggregation (macro- and meso-sectors) are built by retrieving all co-authors from the scientific production submitted for the evaluation exercise. To this end, it is worth noting that, on average, we observe two publications per author. In fact, in the VQR, each evaluated researcher should submit at most two scientific products (however, some researchers can appear as a co-author in a paper submitted by someone else). For this reason, the co-authorship network under analysis is a sample of the overall co-authorship networks among Area 2 and Area 13 researchers. Despite this limitation, we can consider these co-authorship networks as determined by the most significant production according to each researcher’s auto-evaluation.

4.1 Co-authorship Networks

For each macro- and meso-sector considered, we create a co-authorship network, where each node indicates a researcher involved in the VQR exercise, and a link registers the presence and intensity of the collaboration between the two of them. Intensity is proxied by the number of times two researchers co-authored a paper together.

Table 4 summarizes the main characteristics of the co-authorship networks at the macro-sector level. Networks are often composed of more than 500 authors (the number of nodes), who are linked by rare collaborations among them. The average number of co-authors of a scientist (i.e., degree centrality) is either zero or one, and the density of the network is in the order of 10⁻³.

Table 4 Areas 2 and 13 macro-sectors—descriptive table

The number of scientists involved in a collaboration is extremely small in each macro-sector; hence, it is plausible to expect that the circulation of knowledge and information is relatively limited. In all networks, 90% of the collaborations are activated by no more than 80 researchers, and at least 40% of the researchers are isolated. Moreover, most of the collaborations occur within small components, that is, a set of authors directly or indirectly connected among them. In fact, the density × 1000 is barely larger than 1 for most cases. The denser network is the macro-sector 02/D (physics teaching and history of physics). The giant component (largest component) in each network never comprises more than 6% of the total number of nodes. This suggests that the diffusion of information among connected scientists is likely to become rapidly redundant. Notably, however, the low propensity to collaboration is higher in Area 13 than in Area 2.

A similar picture emerges when considering the statistics relative to the networks of collaborations at the meso-level sectors, which are reported in Table 5. Density and degree centrality are extremely low in each meso-sector, and most of the authors are either isolated or embedded in a very small number of components. Also, in this case, scientists from Area 13 show the smallest propensity to collaborate.

Table 5 Areas 2 and 13 meso-sectors—descriptive table

The comparison between the largest components of the networks of area 13 and area 2 shed some light on the different behaviors of the researchers in these two areas. At the macro level, scientists in Area 2 tend to share a higher number of collaborators with respect to the scientists in Area 13, as shown by their highest clustering coefficient. However, we observe the opposite when considering networks at the meso-level: scientists from Area 13 feature a higher number of co-authors with respect to their colleagues from Area 2. This suggests that the scientists from Area 2 are more inclined to activate collaborations across meso-sectors, while those from Area 13 are more prone to work with those belonging to their own meso-sector.

5 Network Analysis Results

In this section, we investigate the main features of the largest components of the networks, both at the macro- and at the meso-levels, to infer some relevant insights into the co-authorship behavior of the scientists considered in the current study.

5.1 Analysis at the Global Level

We begin by investigating the overall architecture of the networks’ largest component, with the aim of finding evidence of specific model of interactions among scientists.

First, we find that scientists tend to form dense collaborations in the largest components, and many of them share one or more collaborators: that is, they feature a relatively high clustering coefficient. In Table 6, we compare this metric with that obtained from equivalent random (ER) networks, where macro-sector collaborations are formed by chance. We find that the clustering coefficient registered in the actual networks (C_gC) is always higher than that observed in simulated networks (C_rand). This is not surprising, and it is consistent with the fact that the scientists did not activate collaborations at random. On the contrary, scientists tend to choose a new collaborator among those already in contact with one of their co-authors, thus creating groups of collaborations presumably focused on a specific field of research, where skills are likely to be compatible.⁴ The same behavior is observed when considering the networks at the meso- level, as reported in Table 7.

Table 6 Areas 2 and 13 macro-sectors—model checking

Table 7 Areas 2 and 13 meso-sectors—model checking

Second, we observe that the transmission of information among groups of scientists in the same component tends to be rather inefficient. This can be inferred by comparing the actual value of average path length (L_gC) with that registered in ERs (L_rand). In most cases, the distance among nodes which are linked by the relations formed at random in ERs, is lower than that among the nodes connected by actual relations. It follows that scientists tend to interact in small groups, being clumped into different and distant areas, even when embedded in the same largest component. However, this is not always the case. A more efficient configuration of the distance among nodes, similar to that observed in ERs, is observed in macro-sectors 13/B and 13/C (Table 6) and meso-sectors 02/B1, 02/C1, 13/A2, 13/B2, 13/B4, 13/B5, 13/C1, and 13/D2 (Table 7).

Taken together, our results point to the presence of a specific model of interaction for researchers in some sectors. When the clustering coefficient is higher than that registered in ERs, that is, some sort of specialized collaborations emerge among groups of scientists, and the distance between scientists is similar to that observed in ER, which means that the diffusion of information is relatively fast, we then find evidence for small-world behavior: a peculiar network structure with unique properties of local specialization and efficient information transfer. Such small-world behavior seems to be compatible with all networks found with a high value of average path length: that is, macro-sectors 13/B and 13/C and meso-sectors 02/B1, 02/C1, 13/A2, 13/B2, 13/B4, 13/B5, 13/C1, and 13/D2. The researchers affiliated with these sectors can rely on the fast and efficient exchange of information with their colleagues because of the network structure in which they are embedded. Overall, it seems that the researchers in Area 13 tend to interact more according to this mechanism with respect to researchers affiliated to Area 2.

Finally, we focus on the degree distribution of large components. In particular, we are interested in finding evidence in favor of or against a power law distribution with the parameter α ranging between 2 and 3 (for more details, see Albert & Barabási 2002; Clauset et al. 2009). When this is the case, the authors follow a preferential attachment behavior, that is, scientists prefer to activate collaborations with those who already have many collaborations in place and who are pivotal in their sector. By looking at Tables 6 and 7, almost none of the network degree distributions fit with a true power law distribution in the macro-sectors and meso-sectors. The only exception is the network of those affiliated with meso-sector 13/B5, for which there is evidence of a preferential attachment behavior.

5.2 Analysis at the Local Level: Centrality Measures

We now turn to an analysis of the centrality measures (Freeman 1979) associated with the largest component of the networks. In particular, we focus on the relation between (i) degree centrality vs betweenness centrality and (ii) degree centrality vs the clustering coefficient (or local transitivity).

When the degree centrality is positively correlated with both betweenness centrality and the clustering coefficient, the network features a core-periphery structure where nodes located at the core of the subnetwork are densely connected with one another (high degree centrality), acting as brokers (high betweenness) for the nodes situated at the periphery of the network. A core-periphery structure points to an uneven exposure to information among researchers: only those located at the core of the network can easily access to new information, while those located at the periphery tend to be excluded from the process of knowledge diffusion.

By contrast, when degree centrality is positively correlated with betweenness centrality and negatively correlated with the clustering coefficient, we say that the network has a structure similar to that of interlinked stars: few researchers play the role of a hub (high betweenness centrality) for others who are loosely connected with each other (low clustering coefficient). In this case, the diffusion of information becomes problematic. Most researchers will rely on a small number of colleagues to access knowledge produced in different areas of the networks. In other words, a small number of scientists act as information gatekeepers in these networks because the diffusion of knowledge heavily depends on the extent to which they are prone to receive new information from one part of the network and transmit it to different parts.

The analysis of the correlation between centrality measures is summarized in Tables 6 and 7. We observe that many of the largest components feature a core-periphery structure (02/A, 02/B, 13/B, 13/C) at the macro-level, and only macro-sector 02/C is characterized by relations arranged like interlinked stars. Moreover, no clear structure arises for the largest component of macro-area 02/D. As for meso- sectors, we detect the presence of a core-periphery structure in more than 60% of the giant components (meso-sectors 02/A1, 02/A2, 02/B1, 02/B2, 02/C1, 13/A2, 13/B2, 13/B3, and 13/B4).

5.3 Network Attack

Next, we test the resilience of the networks’ architecture in macro-sectors by simulating different breakdown scenarios. Specifically, this is done by looking at global changes in the network topology after deleting 5% of the nodes. The results of our simulations for the macro-level networks are presented in Table 8.

Table 8 Areas 2 and 13 macro-sectors—network attack

The first row of the table indicates the number of components generated after deleting random nodes in the network. The third row reports the same statistics when attacking the topmost connected nodes (i.e., those with the highest degree centrality). The second and fourth rows report the ratio between the number of nodes in the giant component before and after the attack, respectively, when this is random or targeted. We see that by targeting random nodes, giant components remain substantially unaltered. By contrast, when an attack is targeted, the giant components of macro-sectors 02/A, 02/B, and 02/C lose 50% of the nodes. This is somewhat similar to what happens to macro-sector 13/B. This means that the topmost connected scientists in these networks are almost all embedded in the giant component, and they play a crucial role in sustaining the core of the collaborations in the macro-sectors. Even stronger is the effect in macro-sector 13/C, where the giant component loses about 70% of its members. Interestingly, there is no effect in macro-sector 02/D. This suggests that most collaborative scientists in this network are not embedded in the giant component; instead they work separately from the area where most researchers are involved.

The effect of random failures is less drastic than that produced by a targeted attack when evaluating the number of components generated by our simulations. The latter attacks consistently produce a higher number of components. This suggests that scientists benefiting from the diffusion of information channeled throughout network components heavily rely on the presence of the topmost connected authors.

The results remain substantially unchanged when testing the same effect at the meso-level, as reported in Table 9. Most meso-sectors rely on the topmost connected authors for the general connectivity of their networks.

Table 9 Areas 2 and 13 meso-sectors—network attack

Our findings hint to some policy indications: for example, replacing an eminent scientist collaborating with many laboratories (e.g., a node with high degree centrality) may compromise the chances of his/her colleagues rapidly finding in both macro- and meso-level networks new collaborators outside their research group or to access new information. In fact, by removing him/her from the network, his/her collaborators will remain isolated in small components with no direct or indirect connections to colleagues located in different zones of the network.

5.4 Co-authorship Networks and Scientific Performance: A Regression Analysis

In this section, we provide some insights into the relation between individual researchers’ network position and their average VQR scores as obtained by the evaluation of the papers they submitted for the evaluation exercise in 2011–2014. We carry out a linear regression analysis where the dependent variable is the “excellence” measure (VQR scores) of researchers active in physics or economics and covariates represented by some of the available individual characteristics and individual network indices. In particular, as individual characteristics, we used the scientific areas (physics and economics and statistics, the latter treated as a reference category), gender (female as the reference category), and geographic location of the university to which researchers were affiliated (S, Southern Italy, I, Islands, NE, North-Eastern Italy, NO, North-Western Italy, and C, Central Italy, this latter considered as reference category). The distribution of such covariates is reported in Tables 10, 11, and 12, respectively. As far as the individual network indices are concerned, we adopted the centrality measures defined in Sect. 3, namely node degree, betweenness, and transitivity (i.e., clustering coefficient). The variable excellence of the authors is the average VQR score of the authors’ papers. As already stated, the VQR score is a 5-point scale with the scores reported in Table 2 and described in Sect. 4. In this analysis, we used the scores in Table 2 to compute the average VQR evaluation for each author. In Fig. 1, we depict the distribution of the log transform of the excellence variable that we used as dependent variable in the regression model.

Fig. 1

Histogram of log(excellence). 19 researchers with an overall excellence value equal to 0 are excluded

Table 10 Distribution of researchers according to scientific area

Table 11 Distribution of researchers according to their gender

Table 12 Distribution of researchers according to geographic location of their hiring university

One of the distinct properties of several network characteristics measured on the level of researchers is their asymmetric distribution. A specific feature of the analyzed network is its high level of fragmentation with a large number of small components and isolates, hence preventing the calculation of network statistics for some of the units.

To meet the assumptions of the regression analysis, the network-based variables included in the model were categorized. Transitivity and betweenness were dichotomized into categories indicating zero and nonzero values; degree (number of connections) was categorized into three categories (0, 1–10, and 11–66) indicating degree centrality of the researchers.

Model and Interpretation

Model results are reported in Table 13. It can be noted that gender differences have no significant effect on scientific performance; this means that after controlling for the geographical area and network characteristics of the researchers, the gender gap is not present in the analyzed scientific areas, differently from other studies (Aksnes et al. 2019). Moving to the geographic location, the model assumes universities located in Central Italy a reference category (baseline). The category indicating researchers working in universities in North-Eastern Italy has negative and significant effect, so their performance is significantly lower than Central Italy. No significant differences are found among Central, Islands, South, and North-Western Italy.

Table 13 Regression model estimates and fit

As can be noted from the Physics coefficient value, the authors in the physics area have higher performance than the authors in economics and statistics area (baseline category of Physics).

For the network indices of co-authorship network, the authors are more likely to achieve a higher VQR score if they have a greater degree and betweenness higher than 0. The same holds for transitivity as an indicator of working in clustered research groups. This shows that working with several co-authors (high degree) and being part of multiple clustered research groups (high betweenness) matter in terms of successful research.

The differences between disciplines become even higher when the authors have between 1 and 10 co-authors (estimated parameter of the interaction effect between Physics and Degree[1,10)), which means that highly central researchers are more successful in a bibliometric discipline, likewise physics macro-sectors. Above this threshold (so for very high degree values), the effect of the number of co-authors on performance is positive on average, independently on the scientific area. This latter effect is in line with previous findings (Abbasi et al. 2011; De Stefano & Zaccarin 2016; Lee & Bozeman 2005) and shows that having high number of different co-authors can lead to positive effects on scholars’ scientific performance in different fields.

6 Concluding Remarks

The present chapter illustrated the use of SNA tools for co-authorship in the context of the Italian research evaluation exercise that ran from 2011 to 2014. In particular, we analyzed the results at the different network levels (global, subgroup, and individual actor levels), here considering their relations with the performance of researchers. The analysis is in line with the literature on scientific collaboration. In fact, research collaboration is often reported as a driver of scientific quality and productivity (Abbasi et al. 2011). For this reason, the analysis of collaboration and co-authorship networks provides essential information for the design of many academic policies. An in-depth understanding of the interactions among scientists provides useful insights into the conditions underlying creativity and genesis of scientific discovery, and it may provide information on new tools and policies that have the potential to accelerate science (Fortunato et al. 2010). This is particularly relevant when considering the interdisciplinary fields required to tackle complex problems in innovative ways and bridge disciplinary silos, such as the fight against climate change or the current COVID-19 crisis. The study of collaboration networks can also be leveraged to provide scientists with access to new and non-redundant information allowing them to engage in more innovative studies. For this reason, the researchers have been progressively stimulated by new policies to activate new forms of collaboration and improve their position in the co-authorship network. For instance, this is the case of scientific policies providing research funding conditional on the activation of a new intellectual collaboration or the case of internal department tenure policies that require candidates to have a minimum amount of publications but that do not fully discount articles by the number of authors (see Ductor 2015 for a recent discussion). Knowledge of one’s collaboration network is also an essential tool to forecast one’s future research output and productivity (Ductor et al. 2014); therefore, it provides crucial information for conducting good recruitment in a department and hiring talented researchers. Moreover, the structure of scientific collaboration networks is a powerful source of information on the dependence of a research team from the presence of so-called academic stars (Azoulay et al. 2010; Waldinger 2010). Therefore, this finding provides useful suggestions to design a system of incentives for “superstar” scholars to (i) remain in the university and maintain an efficient network of collaborations and (ii) increase the involvement of their collaborators in research projects, to reduce the dependency of the overall network from their own work. Finally, collaboration networks are important predictors of the level of peer pressure suffered by an individual; this can be altered to improve a scientist’s working environment and correct undesired situations, such as the presence of gender or other kinds of disparities (Lindenlaub & Prummer 2021). The results presented in the work, despite being retrieved from a small sample of publications of scholars in specific areas, suggest that even in the Italian scenario, it would be worth fostering intra and interdisciplinary collaboration to improve group and individual scientific productivity and performance. This is especially true based on the insights on the importance of a network position in producing quality research outputs. To perform this task and introducing new policies in this direction, comprehensive knowledge of the network structure in disciplines is crucial. The understanding of network patterns by means of the tools presented can guide in the detection of those researchers in certain structural position who may be the target of some network-based interventions (e.g., scale-free networks because the one observed on meso-sector 13/B5 relies on few important nodes acting as hubs). We believe that the results are promising, but we think that a future analysis would benefit from the availability of richer datasets containing a larger set of individual publication records for retrieving a more comprehensive co-authorship network.