1 Introduction

The advancement of modern science has led to an increase in the complexity of scientific problems, and a rise in the cost of scientific instruments, resulting in the emergence of big science [1–5]. This paradigm shift has led to the accumulation of knowledge, making it almost impossible for a single scientist to possess comprehensive expertise required for one scientific project, known as the burden of knowledge [6]. Therefore, scientists have increasingly formed scientific teams to address these challenges [3, 4, 7, 8]. Previous research has demonstrated that teams dominate knowledge creation in contemporary science, operating across institutional and national boundaries [8–10]. Collaboration networks have thus become a powerful tool for studying team structures and scientific collaborations [7].

Past two decades have witnessed numerous studies on the properties of collaboration networks, suggesting that collaboration networks exhibit scale-free, small-world, assortativity and strong community structures [7, 11–13]. Recent studies expanded the scope of collaboration networks from binary to weighted [14, 15], temporal [16–18] and multilayer networks [19]. The availability of large-scale bibliometric datasets as well as quantitative tools enables the study of the relationship between collaboration network structure and scientific performance. From the macroscopic point of view, previous studies showed that macroscopic network properties significantly affect scientists’ academic performance, including productivity and citation impact [20–28]. From the individual paper’s point of view, empirical studies explored microscopic team formation, examining the association between team diversity, team structures and paper citation, novelty, disruption and multidisciplinarity [9, 28–39]. However, existing studies mainly constructed collaboration networks at a dyadic level, potentially overlooking valuable information, as scientific collaboration now is dominated by group interactions beyond dyadic levels.

In recent years, researchers have made substantial progress in network science and computational topology, leading to the emergence of higher-order representations that capture multi-agent relationships beyond conventional dyadic interactions. Notable examples include simplicial complexes [40, 41] and hypergraphs [42, 43], which have been widely applied in analyzing various types of networks across social systems [44], neuroscience [45, 46], ecology [47, 48], and other biological systems [49, 50]. Despite of similar frameworks in the field of science of science [51–55], to the best of our knowledge, there is limited research exploring the association between higher-order properties and individual scientific productivity. In fact, prior research demonstrated that higher-order holes play necessary roles in biological systems especially the brain functioning [56, 57]. This highlights an encouraging and promising direction in the collaboration system, i.e., investigating how these higher-order characteristics affect scientific outcomes. This calls for a further analysis into translating the original co-authorship data into structures that preserve group interactions. Additionally, existing studies have drawn conclusions from specific scientific domains, raising questions regarding the generalizability of the findings.

In this paper, we fill this gap by leveraging the Microsoft Academic Graph data (MAG), a large-scale scholarly dataset. We utilize a simplicial complex framework to construct local collaboration networks for a cohort of more than 3.7 million scientists. Our primary objective is to investigate the association between higher-order structural properties of local collaboration networks and scientists’ productivity. Specifically, we delve into two key higher-order characteristics: the 0th Betti number (\(\beta _{0}\)), representing the number of disconnected components, and the 1st Betti number (\(\beta _{1}\)), indicating the presence of higher-order loops. There are three key findings. Firstly, we find that there is an intriguing inverted U-shaped relationship between the number of disconnected components and individual productivity. Secondly, we observe that the presence of higher-order loops within local co-authorship networks is positively associated with scientists’ productivity, suggesting interesting underlying forces related to group interactions. Thirdly, the uncovered relationship can be generalizable to major scientific domains, indicating strong generalizability of our results. This study has several contributions. First, we use a simplicial complex approach to depict scientific collaboration networks, which helps to capture group interactions and higher-order structural properties that cannot be obtained in the conventional dyadic view. Second, our work encompasses scientists from diverse scientific disciplines, offering insights that extend beyond specific scientific domains. These results may help us better understand individual careers and have policy implications for nurturing scientists towards high academic performance.

2 Related work

2.1 The impact of macroscopic collaboration structure on scientific output

Recently, there has been significant interest in the science of team science [8, 9, 37, 38, 58, 59]. Previous studies documented several fundamental characteristics of collaboration networks [7, 11–13]. The availability of computational tools also pushes scientists to extend conventional binary collaboration networks to weighted, temporal, multilayer and higher-order networks, enabling a more nuanced analysis of collaboration patterns [14–19, 51–55]. Numerous studies demonstrate the impact of collaboration networks on individual scientist’s academic performance. For example, prior studies focus on the association between centrality, tie strength and its configuration, structural hole and scientific productivity and citation impact [20–28, 60]. Recent research has also explored the relationship between collaboration networks and innovative research. Using patent datasets, Wang et al. showed that inventors with a high degree centrality in patent collaboration networks often exhibit low exploratory innovation, whereas inventors spanning structural holes produce more innovative outputs [61]. Using the American Physical Society data, Wang et al. observed that scientists spanning over structural holes in scientific collaboration networks produced more novel and disruptive research and had a higher chance to publish novel/disruptive papers [60].

2.2 The impact of microscopic team structure on scientific output

Recent studies delved into the relationship between microscopic team structures and scientific outputs. For example, Zeng et al. proposed the concept of team freshness, and found that team freshness strongly predicts multidisciplinarity and disruption of individual papers [38]. Liu et al. focused on link freshness and demonstrated an inverted U-shaped relationship between link freshness and citation impact [34]. Xu et al. discovered that author contribution within a team is associated with long-term citations, novelty and disruption [36]. Furthermore, Chen et al. explored new author combinations within scientific teams, revealing that new author combinations positively inspire the emergence of new knowledge units and combinations of knowledge elements [33]. Recent studies also focused on team diversity. Yang et al. demonstrated that gender-diverse teams produce novel and impactful papers [37]. In addition to gender diversity, researchers have examined other dimensions of diversity, including ethnicity, nationality, affiliations, discipline and academic age, finding consistently that diverse teams produce impactful papers [9, 29–32]. Finally, Lin et al. studied the association between collaboration distance and disruption, revealing that remote teams were less likely to produce disruptive research compared with onsite teams [39].

2.3 Higher-order network representations in science of science

Conventional research primarily focused on pairwise interactions in collaboration networks, overlooking higher-order interactions involving three or more researchers [51–54]. To fill this gap, algebraic topologists and network scientists have introduced higher-order network representations such as simplicial complexes [40, 41] and hypergraphs [42, 43]. These advancements have enabled the application of higher-order networks in various fields, including social systems, neuroscience, ecology, and other biological systems [44–50]. In science of science domain, there are a few studies exploring higher-order network representations. For example, Carstens and Horadam were among the first to introduce persistent homology to analyze Betti numbers in weighted collaboration networks, distinguishing them from random networks [51]. Patania et al. studied topological structures by analyzing the distribution of facet size, simplicial degrees, homological hole lengths, and community sizes [54]. Similarly, Salnikov et al. constructed sequential knowledge networks using simplicial complexes, and analyzed the persistence of homological holes [55]. Gebhart and Funk used simplicial complexes to study the evolution of homological holes and their correlations with traditional network properties, as well as their impact on the novelty and impact of papers and patents [52]. Juul et al. investigated the frequency of different hypergraph patterns in random models and empirical data, and explored the relationship between citations and hypergraph patterns [53].

In summary, previous research has explored the relationships between the structural attributes of macroscopic collaboration networks and microscopic team structures and how these factors impact scientists’ academic performance. Nonetheless, significant gaps remain within the current body of literature. Firstly, there has been limited emphasis on local collaboration networks, despite their potential role in knowledge spillovers and individual outcomes. Furthermore, while earlier studies have indeed investigated higher-order structural features, the precise influence of these structures on scientists’ performance remains an open question. To add to this complexity, the generalizability of these findings across a wide array of scientific domains has yet to be fully addressed. In this paper, we seek to address these gaps by examining the impact of higher-order structural properties within local collaboration networks on the productivity of scientists from diverse academic fields. Our study aims to contribute valuable insights and extend the understanding of these intricate relationships.

3 Data

In this paper, we leverage the Microsoft Academic Graph dataset (MAG), which comprises more than 260 million digital publications spanning from 1800 to 2021. MAG offers comprehensive information regarding each publication, including publication year, scientific field(s), and author name(s). It has emerged as a pivotal data source for research on individual careers [62–68]. MAG employs cutting-edge techniques for distinguishing author identities. In addition to machine learning algorithms that leverage publication records for author disambiguation, MAG goes further by harnessing the power of web search engines to access public information such as personal websites and public curricula vitae [69]. Recent studies have established a gold standard dataset for author name disambiguation based on ORCID, finding that MAG author IDs achieve an impressive 81.87% accuracy, 78.13% F1 score, and 98.49% precision, underscoring the reliability of MAG’s author identification methods [34, 70].

In this study, we focus on journal articles and conference papers published prior to 2011. Our analysis includes papers with scientific field information as well as venue information, resulting in a dataset of 56,895,201 papers. Furthermore, we focus on scientists who published at least 5 papers and no more than 500 papers during their entire career. This approach helps us mitigate potential errors related to author name disambiguation within the Microsoft Academic Graph (MAG), including instances of author under-conflation, where an author’s publication count may be erroneously lower than the actual number, or over-conflation, which involves wrongly assigning additional publication records to an author. This method also allows us to reduce the influence of outliers, which could include authors with very few or exceptionally high numbers of publications. This selection criterion aligns with recent research practices [38, 60]. Moreover, we exclude scientists who have collaborated with more than 36 distinct partners in any given year. The reason for this exclusion is rooted in the considerable computational complexities associated with high-order network analyses. In particular, the computation of homology necessitates enumerating all conceivable combinations of simplices, with computational complexity growing exponentially with the dimension of the simplicial complex [54]. This threshold helps us manage these computational challenges, balancing the need for accuracy with the constraints of available computational resources. Additionally, we focus on scientists who published his/her first paper later than 1960 in order to reduce the noise derived from the relatively small number of publications before.

Our final sample comprises a total of 3,785,807 scientists. For each scientist, we construct his/her yearly local collaboration networks by considering interactions among collaborators (see details in Methodology), resulting in a total of 27,786,774 scientist-year observations till 2011 (see the data frame of “scientist-year observations” in the Appendix, Table A1). Note that scientists with less than a 3-year publication history were excluded to ensure the consistency of the number of samples included into the regression analysis of the panel data.

4 Methodology

4.1 Simplicial complexes

Basic notations and definitions

We provide several basic notations and definitions related to simplicial complexes. First, a d-simplex α represents a set of interacting nodes, where d denotes the dimensionality of the simplex. For example, a single node is a 0-simplex, a link between two nodes is a 1-simplex, and a (filled) triangle is a 2-simplex, and so on. Second, a face of a d-simplex α is a lower-dimensional simplex \(\alpha '\) formed by a proper subset of nodes of α, i.e., \(\alpha ' \subset \alpha \). For instance, in the case of a 2-simplex, its faces include three 0-simplices and three 1-simplices. Third, a simplicial complex γ is a collection of simplices that satisfies closure under the inclusion of faces, indicating that for every simplex α belonging to γ, all of its faces \(\alpha '\) also belong to γ. For more details, please refer to [71, 72].

Why using simplicial complexes?

The use of simplicial complexes can be justified for several reasons. First, it is a natural approach when investigating scientific collaborations, considering that it allows to model multi-agent interactions. Over recent decades, science has witnessed a remarkable increase in complexity and scale, with most knowledge creation by teamwork, or group interactions [8]. When studying collaboration networks through dyadic aspects that originated from scientist-paper bipartite networks, we risk losing crucial information regarding these group interactions. In response to this, recent advancements have been made in higher-order network representations, and such frameworks have found widespread application in the analysis of various network types [44–50]. Second, the use of a simplicial framework is advantageous because it explicitly preserves group interactions that involve more than two scientists. One key benefit of this approach is its ability to encode higher-order “holes” within the collaboration network [54]. To illustrate this, consider two cases: in the first case, three scientists have never co-authored a paper together, but any two of them have collaborated on at least one paper. In the second case, all three scientists have indeed published a paper together previously. When using conventional methods, both situations might be represented as triangles. However, we recognize that only the former case is accurately depicted by an empty triangle, while the latter should be represented by a filled triangle. Similarly, conventional methods cannot distinguish whether quadrilaterals or pentagons are empty or filled. Lastly, the application of higher-order structures empowers us to delve deeper into understanding the functions of these topological features within scientific collaboration networks. Significantly, prior research has illuminated the crucial roles played by higher-order holes in the functioning of the human brain [56, 57]. Nonetheless, it remains unclear how these higher-order holes within collaboration networks are linked to individual scientific careers. This underscores the need to translate original co-authorship data into structures that accurately represent and preserve these group interactions.

4.2 Local collaboration networks

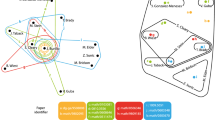
We construct yearly local collaboration networks for each scientist at year t, by extracting his/her collaboration records from preceding year t-5 to t-1 among his/her collaborators. Figure 1 shows an illustrative example of a selected scientist. At year t, the focal scientist collaborated with six scientists (see Fig. 1a). We then identify collaboration relationships among collaborators using publication data between t-5 and t-1 (see Fig. 1b). For example, [1, 5] indicates that scientists 1 and 5 have co-authored a paper during this period, while [1, 2, 6] suggests that scientists 1, 2, and 6 have published a paper together. Using these collaboration records, we obtain the local collaboration network for the selected scientist at year t (see Fig. 1d). It is important to note that we construct this network using higher-order interactions, which differs markedly from the conventional bipartite network projection (see Fig. 1c).

Figure 1
figure 1

An illustration of constructing higher-order local collaboration networks. (a) shows the individual scientist’s egocentric network at year t. The links indicate that two scientists collaborated at year t. (b) shows the publication records and collaboration relationships among collaborators between t-5 and t-1. Note that grey person represents scientists who did not collaborate with the focal scientist at year t. (c) depicts the individual scientist’s local collaboration network based on conventional bipartite network projections. Solid lines suggest that connected two scientists have collaborated at least once between t-5 and t-1. (d) depicts the higher-order local collaboration network with a simplicial description. Solid lines represent that two scientists have collaborated at least once between t-5 and t-1. Filled triangles indicate that the connected three scientists have at least one joint publication during this period. The empty triangle means the connected three scientists have not collaborated together, whereas any two of them have a pairwise collaboration

Full size image

4.3 Betti numbers

In this study, we characterize higher-order structural properties of local collaboration networks using the Betti number, which is a topological measure to quantify the presence of holes in higher-order networks. Each Betti number corresponds to a specific dimension of holes within the network. We provide several related notations below. For details, we refer to these references [73–75].

Boundary operation, d-chain, d-cycles and d-boundary

Here, we provide a brief description of key definitions. The boundary of a d-simplex is defined as the sum of its \((d-1)\)-dimensional faces, denoted as \(\partial _{d}\). A d-chain is defined as the sum of d-simplices in a simplicial complex. The group of d-chains is defined as the d-chains with the addition modulo 2, denoted as \(C_{d}\). A d-cycle is defined as a d-chain with a boundary of zero. The group of d-cycles is defined as the d-cycles with the addition modulo 2, denoted as \(Z_{d}\). A d-boundary refers to a d-chain that is the boundary of a \((d + 1)\)-chain. The group of d-boundaries refers to the d-boundaries with the addition modulo 2, denoted as \(B_{d}\). Note that \(B_{d} \subset Z_{d} \subset C_{d}\).

Homomorphism, kernel and image

If there is a map \(f: M\rightarrow S\), which satisfies that \(\forall a, b\in M\), \(f(a * b)= f(a) \cdot f (b) \in S\), then f is a homomorphism from M to S. Here M and S are two nonempty sets; ∗ and ⋅ are two operations defined on these two sets, respectively. So the boundary operator \(\partial _{d}\) is a homomorphism from \(C_{d+1}\) to \(C_{d}\). The kernel of a homomorphism \(f: M\rightarrow S\) is the set of all elements in M that are mapped to zero. Therefore, \(Z_{d}\) is the kernel of \(\partial _{d}\). The image of a homomorphism f: \(M\rightarrow S\) is the set of all elements in S. As a result, \(B_{d}\) is the image of \(\partial _{d+1}\).

Homology group and Betti numbers

The dth homology group is defined as the quotient between \(Z_{d}\) and \(B_{d}\), denoted as

$$ H_{d} ( \gamma ) = \frac{Z_{d}}{B_{d}} = \frac{\ker ( \partial _{d} )}{\operatorname{im} ( \partial _{d+1} )}. $$

The elements of \(H_{d} ( \gamma )\) refers to the d-cycles that are not induced by a d-boundary, namely the d-dimensional holes of our simplicial complex γ. The rank of \(H_{d} ( \gamma )\) is defined as the dth Betti number of γ, denoted as

$$ \beta _{d} =\operatorname{rank} \bigl( H_{d} ( \gamma ) \bigr) =\operatorname{rank} ( Z_{d} ) -\operatorname{rank} ( B_{d} ), $$

which indicates the number of different d-dimensional holes. In this study, we only focus on the effects of \(\beta _{0}\) and \(\beta _{1}\). \(\beta _{0}\) counts the number of disconnected components, and \(\beta _{1}\) counts the number of higher-order loops, capturing the presence of circular relationships or cycles within the network.

To illustrate the concept more, let’s consider the local collaboration network shown in Fig. 1d. In this network, there are two disconnected components, one consists of node 3, and the other is formed by the rest nodes. Hence, \(\beta _{0}\) is 2. Additionally, we observe two empty triangles. One is formed by nodes 1, 5, and 6, while the other is formed by nodes 1, 4, and 5. Therefore, \(\beta _{1}\) is also 2. It is worth noting that in the dyadic view, there is no filled triangle within collaboration networks. If the focal scientist has no coauthors at year t, then \(\beta _{0}\) and \(\beta _{1}\) are set to zero.

4.4 Variables in regression analysis

In this study, we consider scientific productivity, which refers to the total number of papers published at year t as the dependent variable. For independent and control variables, we utilize the 0th Betti number (\(\beta _{0}\)) and 1st Betti number (\(\beta _{1}\)) to quantify the higher-order structural properties of local collaboration networks. It is important to note that \(\beta _{0}\) is a continuous variable, while \(\beta _{1}\) is transformed into a binary variable as the majority of observed values are zero. We consider several explanatory variables that may affect the performance of individual scientists. Specifically, we consider network size, network density, average tie strength and collaborative strength. Network size refers to the number of collaborators at year t. Network density is defined as the fraction of real links with respect to all possible links in conventional collaboration networks [34]. Average tie strength is the average number of papers coauthored between individual scientist and collaborators from t-5 to t-1 [22]. The collaborative strength is the ratio of collaborative papers among all collaborators to the total number of papers published by all collaborators between t-5 and t-1. Prior studies demonstrated that such network properties may be associated with scientists’ academic performance [20, 22, 24, 25, 34]. Moreover, we also consider career age at year t [76]. Finally, given that the scientist’s academic performance at year t can be affected by previous records [22], we control for the productivity at the last year in which the scientist has publication records. The details of variables are shown in Table 1.

Table 1 Variables description
Full size table

4.5 Regression models

We use Poisson regressions to quantify the relationship between high-order properties and scientific productivity. The application of a Poisson model in our study is grounded in its suitability for regressions where the dependent variable is counted and follows a Poisson distribution. In our context, productivity is denoted by the number of publications, which inherently assumes non-negative integer values. While the distribution of publication counts exhibits characteristics of a fat-tailed distribution [77], it is important to note that prior research has demonstrated the Poisson estimator’s reliability in panel data models. This reliability is maintained even when the actual data distribution does not precisely conform to the Poisson distribution, as long as the mean specification remains accurate [78]. The regression equations are as follows:

$$ \begin{aligned} &\ln ( \mathrm{Productivity}_{i,t} ) \\ &\quad = a_{0} + a_{1} ( \beta _{i, \Delta t} ) + a_{3} ( \mathrm{Network}\ \mathrm{density}_{i, \Delta t} ) + a_{4} \bigl( \log_{2} ( \mathrm{Average}\ \mathrm{tie}\ \mathrm{strength}_{i, \Delta t} +1 ) \bigr) \\ &\quad \quad {}+ a_{5} \bigl( \log_{2} ( \mathrm{Collaborative}\ \mathrm{strength}_{i, \Delta t} +1 ) \bigr) + a_{6} \bigl( \log_{2} ( \mathrm{Career}\ \mathrm{age}_{i,t} +1 ) \bigr) \\ &\quad \quad {}+ a_{7} \bigl( \log_{2} ( \mathrm{Productivity}_{i, \overleftarrow{t}} ) \bigr) + \sum _{j} b_{j} \sigma _{ji,t} + \mu _{i} + \tau _{t} + \varepsilon _{i,t}, \end{aligned} $$

where Δt refers to the period from t-5 to t-1, \(\overleftarrow{t}\) indicates the last year in which the scientist has publication records. \(\mu _{i}\) represents individual fixed effects, which is a vector of unobserved but fixed confounders depending only on individual i [79]. The rationale for adding individual fixed effects is to control for individuals’ unobservable characteristics [80]. \(\tau _{t} \) represents year fixed effects, and the rationale for adding year fixed effects is to take into account unobserved variables that evolve over time but are constant across entities [80]. \(\sigma _{jit}\) indicates network size fixed effects, and we categorize the network size into six bins: \([0, 6]\), \([7, 12]\), \([13, 18]\), \([19, 24]\), \([25, 30]\), and \([31, 36]\). The reason why we consider fixed effects instead of controlling for its continuous form is that there is collinearity between \(\beta _{0}\) and network size, which may influence the precision of estimations [37]. Note that in the regression model we add quadratic terms of \(\beta _{0}\) in order to check whether there is an inverted U-shaped relationship, and we also control for \(\beta _{0}\) when exploring the effect of \(\beta _{1}\). We take logarithms for variables with fat-tail distributions.

We use scientific fields provided by the MAG data to categorize scientists into different scientific domains. This categorization is based on scientific domains to which more than half of a scientist’s papers belong to. The Appendix Table A2 shows the number of scientists, as well as scientist-year observations across 19 scientific domains.

5 Results

5.1 Descriptive statistics

Table 2 shows the descriptive statistics of the variables used in our analysis. To assess the presence of multicollinearity, we calculate the variance inflation factor (VIF), and find that the VIFs for \(\beta _{0}\), \(\beta _{1}\), network density, average tie strength, collaborative strength, career age are 1.23, 1.05, 1.71, 1.56, 1.42 and 1.04, respectively. These values suggest that there is no strong multicollinearity among these variables.

Table 2 Descriptive statistics of different variables
Full size table

Figures 2a and 2b display the distribution of \(\beta _{0}\) and \(\beta _{1}\), respectively. We find that over 90% of local collaboration networks exhibit less than eight disconnected components. Moreover, the occurrence of higher-order loops in these networks is relatively rare. Specifically, local collaboration networks that contain at least one higher-order loop account for around 5% of the total networks. Figure 2c illustrates the temporal evolution of \(\beta _{0}\) and \(\beta _{1}\). We observe that the average number of components in local collaboration networks steadily increased. Additionally, there is a significant rise in the proportion of local collaboration networks that exhibit at least one higher-order loop. Notably, approximately 11% of the local collaboration networks display the presence of higher-order loop structures at year 2011, highlighting the growing prevalence of higher-order structures within local collaboration networks. Figure 2d illustrates the average value of \(\beta _{0}\) and probability of \(\beta _{1} =1\) across different scientific domains, revealing distinct disciplinary variations. Generally, scientists in medicine, biology, material science and environmental science are more likely to have local collaboration networks with disconnected components and higher-order loops. Besides, additional descriptive analyses show that scientists with higher-order loops are typically more senior, with higher productivity and citation impact than those without higher-order loops.

Figure 2
figure 2

The distribution, evolution and disciplinary variations of \({\beta}_{{0}}\) and \({\beta}_{{1}}\).(a-b) The distribution of \(\beta _{0}\) and \(\beta _{1}\). (c) \(\langle \beta _{0}\rangle\), and \(\mathrm{P}( \beta _{1} =1)\) as a function of time. (d) \(\langle \beta _{0}\rangle \) and \(\mathrm{P}( \beta _{1} =1)\) across different scientific domains

Full size image

5.2 Scientific productivity

Figures 3a and 3b show the relationship between \(\beta _{0}\), \(\beta _{1}\), and the number of papers published at year t, respectively. We find several noteworthy patterns. First, scientific productivity shows an initial increase with each additional component until \(\beta _{0}\) reaches 22, beyond which it starts to decline, suggesting that having a moderate number of disconnected components in the collaboration network is associated with high productivity. Second, scientists whose local collaboration networks contain at least one higher-order loop tend to publish more papers compared to those without loops, indicating the positive impact of higher-order loops on scientific productivity (2.00 versus 3.65, Two-sided Welch’s t-test, p-value < 0.001).

Figure 3
figure 3

The relationship between \({\beta}_{{0}}\), \({\beta}_{{1}}\) and scientific productivity. (a) The scatter plot between \(\beta _{0}\) and scientific productivity. The point represents mean value and the error bar represents standard error of the mean. (b) The bar chart between \(\beta _{1}\) and scientific productivity. The bar represents mean value and the error bar represents standard error of the mean. (c) The estimated association between \(\beta _{0}\) and scientific productivity based on Table 3 model (5) using the “margins” function of STATA. The red cross mark represents the turning point. The error bar represents the 95% confidence interval

Full size image

To eliminate the effects of potential explanatory factors, we perform fixed effects Poisson regressions (see Table 3). The results confirm an inverted U-shaped relationship between \(\beta _{0}\) and scientific productivity, with a turning point estimated at 15 (Table 3 model 5). Figure 3c visualizes the estimated scientific productivity as a function of \(\beta _{0}\) based on the regression, holding other variables at the sample means. And it demonstrates that the productivity increases by 645.0% when \(\beta _{0}\) rises from 0 to 15, but decreases by 94.7% when \(\beta _{0}\) increases from 15 to 36. We find that \(\beta _{1}\) is positively associated with scientific productivity (Table 4 model 5). Adjusting for all factors, having at least a higher-order loop in local collaboration networks is associated with an increase of 11.7%, on average, more publications for individual scientists. Overall, these observations highlight the critical role of higher-order structures of local collaboration networks.

Table 3 Fixed-effects Poisson regressions regarding the association between \(\beta _{0} \) and scientific productivity
Full size table
Table 4 Fixed-effects Poisson regressions regarding the association between \(\beta _{1} \) and scientific productivity
Full size table

Moreover, we run the same fixed-effects Poisson regression separately for each scientific field. Table 5 indicates that the findings are strongly generalizable across various scientific domains. The 19 scientific domains are sorted according to the number of scientists in descending order. Specifically, we find that all scientific domains have significantly positive coefficients of \(\beta _{0}\) and significantly negative coefficients of \(\beta _{0}^{2}\), indicating that there is an inverted U-shaped relationship between \(\beta _{0}\) and scientific productivity. Moreover, we observe that \(\beta _{1}\) is significantly and positively associated with scientific productivity for scientists in 18 out of 19 fields (except for art). For example, forming at least one higher-order loop is associated with an increase of 8.9% more papers in medicine, 9.1% in biology, and 12.2% in chemistry.

Table 5 Fixed-effects Poisson regressions on scientific productivity across fields
Full size table

5.3 Robustness checks

We conduct a series of robustness tests to strengthen the validity of our findings. Initially, we run Poisson regressions separately for each year. Since each scientist occurs exactly once in a given year, we thus eliminate the effect of duplicated scientist has in the aggregated regression. In this analysis, we consider the same control variables as the main regression, while we do not add individual and year fixed effects, as each scientist only has one row in the dataset. We observe that the inverted U-shaped with \(\beta _{0}\) and the positive effects of \(\beta _{1}\) on productivity remain statistically significant across years (see Fig. 4).

Figure 4
figure 4

The regression coefficients of \({\beta}_{{0}}\), \({\beta}_{{0}}^{{2}}\) and \({\beta}_{{1}}\) across years. The point represents the coefficient and the error bar represents the 95% confidence interval. Darker coloring represents significant coefficients (p-value < 0.05), whereas lighter coloring represents insignificant coefficients (p-value > 0.05)

Full size image

Besides, we separate scientists into subgroups according to their number of “rows” in the data, and run the Poisson regressions separately for each group. The distribution of the number of rows is depicted in Fig. 5a, and we find that most scientists show less than 10 years of observations. Figure 5b-d depicts the coefficients of \(\beta _{0}\), \(\beta _{0}^{2}\) and \(\beta _{1}\) for different subgroups. We observe that the inverted U-shaped associations induced by \(\beta _{0}\) and the positive effects of \(\beta _{1}\) on productivity remain statistically significant for every subgroup, indicating that our results are not affected by high-prolific scientists.

Figure 5
figure 5

(a) The distribution of the number of rows per scientist. (b-d) The coefficients \(\beta _{0}\), \(\beta _{0}^{2}\) and \(\beta _{1}\) in Poisson regression models across rows. The point represents the coefficient and the error bar represents the 95% confidence interval. The grey line indicates y = 0. Darker coloring represents significant coefficients (p-value < 0.05), whereas lighter coloring represents insignificant coefficients (p-value > 0.05)

Full size image

In addition, we separate scientists according to their citation impact (i.e., average citations within 10 years after publication, i.e., \(c_{10}\)), i.e., less-impact scientists whose average \(c_{10}\) are in the bottom 25% (949,048 scientists and 5,791,795 observations), median-impact scientists whose average \(c_{10}\) are between 37.5% and 62.5% (948,860 scientists and 7,547,067 observations), as well as high-impact scientists whose average \(c_{10}\) are in the top 25 percent (946,512 scientists and 7,165,398 observations). We run Poisson regressions for each group separately. Figure 6a depicts the coefficients of \(\beta _{0}\), \(\beta _{0}^{2}\) and \(\beta _{1}\) in Poisson regression models for each group. We again observe that the inverted U-shaped associations induced by \(\beta _{0}\) and the positive effects of \(\beta _{1}\) on productivity remain statistically significant. This finding suggests that the main results hold for scientists with different citation impact.

Figure 6
figure 6

(a) The coefficients \(\beta _{0}\), \(\beta _{0}^{2}\) and \(\beta _{1}\) in Poisson regression models across low-impact, median, and high-impact scientists. (b) The coefficients of \(\beta _{0}\), \(\beta _{0}^{2}\) and \(\beta _{1}\) in Poisson regression models when adopting different time window thresholds. (c) The coefficients of \(\beta _{0}\), \(\beta _{0}^{2}\) and \(\beta _{1}\) in Poisson regression models when excluding samples with popular surnames. The point represents the coefficient and the error bar represents the 95% confidence interval. The grey line indicates y = 0. Darker coloring represents significant coefficients (p-value < 0.05), whereas lighter coloring represents insignificant coefficients (p-value > 0.05)

Full size image

Furthermore, we employ various thresholds to construct local collaboration networks, from 1 to 4 years. Through these iterations, we perform the same regression analyses as in our primary investigation. Notably, the inverted U-shaped associations influenced by \(\beta _{0}\) and the positive effects of \(\beta _{1}\) persisted as statistically significant (see Fig. 6b).

To address concerns related to the accuracy of disambiguation methods for common names, we compile a list of the 1000 most popular surnames worldwide, which encompass commonly occurring surnames from both Asian and Western regions [accessed from https://forebears.io/earth/surnames]. We repeat the analyses and find the primary findings in our study still hold (see Fig. 6c). Moreover, we repeat our analysis by employing the conventional Ordinary Least Squares (OLS) regression model. In this model, the dependent variable is the logarithm of productivity. It is noteworthy that the outcomes of these analyses aligned with the results of our primary Poisson regression approach, providing further evidence of the robustness of our findings.

6 Conclusions

In an era where scientific knowledge creation is dominated by collaborative teams, it is of paramount importance to delve into the higher-order structures inherent in scientific collaboration networks. The conventional approach, which primarily adopts a dyadic perspective to construct local collaboration networks, may inadvertently overlook invaluable information for group interactions. Leveraging a vast dataset encompassing over 56 million research articles from 1960 to 2011 from the Microsoft Academic Graph, our objective is to explore the intricate link between the higher-order structural features characterizing local collaboration networks and their impact on scientific productivity. Furthermore, we endeavor to ascertain the generalizability of these findings across a diverse set of scientific domains. Throughout our analysis, a noteworthy trend becomes apparent – both the number of disconnected components and the prevalence of higher-order holes exhibit a consistent upward trajectory over time. The fraction of local networks featuring higher-order holes reached 11% in 2011. This surge may be attributed to the remarkable expansion of the scientific community during this period. While higher-order holes are indeed evident in various domains, with domains such as medicine and biology sharing common features, the dominance of triatic closure remains a prevailing characteristic within scientific collaboration networks.

Furthermore, our investigation reveals an intriguing inverted U-shaped association between the number of disconnected components in local collaboration networks and scientific productivity. These results partly speak to the strength of weak tie theory [81], which suggests that individuals spanning over structural holes in social networks can gain significant advantages in accessing new opportunities, fostering innovation [82], and enhancing their overall performance [83]. Previous research, largely rooted in macroscopic collaboration networks, has consistently demonstrated the advantages reaped by scientists who span structural holes. These benefits include paper publication, citation counts, and a higher likelihood of contributing novel research [20, 25, 60]. However, such studies have rarely ventured into the intricate realm of scientists’ local networks. Structural holes [84, 85], which foster diversity within local collaboration networks, are primed to play a pivotal role [86]. One would expect significant advantages upon scientists in the realms of productivity. It is plausible that structural diversity acts as a catalyst for resource-sharing and the seamless transmission of knowledge, empowering scientists to harness a spectrum of expertise, diverse ideas, and even the valuable lessons extracted from failure across a heterogeneous pool of collaborators [87–91]. These diverse local collaboration structures equip scientists to acquire a wide array of skills. Ultimately, this dynamic bolsters their productivity. This interpretation aligns with prior findings that suggest novel and multidisciplinary research flourishes within newly-formed teams [38]. This research reinforces this perspective by illuminating a positive correlation between the number of disconnected components within local collaboration networks and scientific productivity – up to a certain threshold. These empirical results effectively substantiate the tenets of structural holes and the significance of weak ties.

This study reveals that as the number of disconnected components reaches a certain threshold, a negative correlation emerges with regard to productivity. This intriguing discovery propels us to explore the potential underlying forces at play. In the realm of scientific collaborations, where the advantages of structural holes and disconnected team members are evident, effective communication and coordination between individuals remain critical [92, 93]. A key facilitator in this regard is familiarity, which results in positive outcomes. Earlier research spotlighted the benefits of strong ties between scientists, often referred to as “super-ties,” underscoring their substantial contributions to productivity and citations [94]. Furthermore, the diverse structures present within local collaboration networks can have the unintended consequence of slowing down the assimilation of ideas, leading to lower consensus and, in some cases, potential conflicts [32, 95, 96]. For example, international collaborations tend to produce less novel papers [32], and remote collaborations show a negative association with disruptive research [39]. Similarly, Liu et al. found an inverted-U shaped relationship between team freshness and citations using paper-level data [34].

This study makes a pivotal observation: the presence of higher-order loops within local collaboration networks is positively correlated with productivity in scientific careers. These higher-order loops shed light on the dynamic interplay among multiple agents that goes beyond the typical dyadic interactions. For instance, the phenomena of complex contagion, where an influence requires the involvement of more than two individuals, may exhibit unique characteristics. As highlighted by Iacopini et al. [97], “the simplicial model of contagion is able to capture the basic mechanisms and effects of higher-order interactions in social contagion processes.” In scientific collaboration, researchers engage in discussions, knowledge diffusion, and the adoption of innovative ideas. Describing these intricate interactions through the lens of higher-order networks provides invaluable insights. This leads to intriguing questions about how resources and knowledge are transmitted within these higher-order loops, as well as the underlying forces driving the positive correlation between higher-order loops and scientific performance. As we conclude, these findings not only provide answers but also raise stimulating questions, paving the way for promising directions in future research within this domain.

In conclusion, these results remain consistent across a spectrum of scientific domains, highlighting its generalizability. This work contributes significantly to the understanding of higher-order collaboration networks by delving into the roles of higher-order holes. Furthermore, it advances our comprehension of how network structures can influence the scientific performance of researchers. Of paramount significance is our discovery of an intriguing inverted U-shaped relationship driven by the number of disconnected components within local collaboration networks. This insight offers a nuanced understanding of the interplay between structural complexity and scientific output. Additionally, our work transcends disciplinary boundaries by encompassing scientists from diverse fields. The insights gleaned from this study hold the potential to benefit a wide array of research areas, extending beyond specific scientific domains. Our findings have important policy implications for nurturing scientific personnel and accelerating innovative breakthroughs. Scientists need to carefully consider the structure of his/her collaboration network. It is crucial for scientists to strive for a well-balanced and properly disconnected or loosely connected local co-authorship network, which is crucial to high productivity.

This study contains several limitations. First, we use publication data to describe collaboration patterns, while collaborative work does not always result in written outputs, and the presence of ghost authors, where individuals contribute to research but are not acknowledged as authors, cannot be ruled out [34, 98, 99]. This may introduce possible biases in our findings and limit the generalizability of our results to all forms of scientific collaboration. Secondly, we gauge scientific productivity using the number of publications. However, the number of publications alone may not be a perfect indicator that captures scientists’ scientific performance [100]. Prior research proposed various indicators to measure the quality of academic outputs, such as citations [101], novelty indicators [102, 103] aligning with Schumpeter’s innovation economics that “innovation combines components in a new way” [104], disruption index [59, 105], as well as other metrics capturing the interdisciplinarity [106]. It is thus interesting to understand the effect of higher-order structures on scientists’ academic performance taking into account the quality of works. Thirdly, it is worth noting that despite we control for possible confounding variables, our study is still of a correlational nature and does not establish causal relationships. Despite these limitations, our study offers valuable insights into the relationship between higher-order structural properties and scientific outcomes, contributing to a growing body of literature in the field of science of science and data science.

Further research is needed to conduct systematic investigations to unravel the underlying mechanisms driving these associations between higher-order properties and productivity. What are the factors that prompt scientists with higher-order structures to publish significantly more papers than their counterparts without higher-order structures? In an era of big science, there are a tremendous number of publications and citations each year, future work could examine the evolution of the effect of high-order structures on scientific achievements, which may untangle the effect of the growth of science and higher-order structures. Finally, future research could go beyond scientific productivity and explore how higher-order structures affect knowledge recombination, originality and interdisciplinarity.