Modelling Our Sense of Smell

Abstract

The first step in our sensing of smell is the conversion of chemical odorants into electrical signals. This happens when odorants stimulate ion channels along cilia, which are long thin cylindrical structures in our olfactory system. Determining how the ion channels are distributed along the length of a cilium is beyond current experimental methods. Here we describe how this can be approached as a mathematical inverse problem. Identification of specific functions of receptor neuron arrays is a major challenge today in both Mathematics and Biosciences. In this paper, two integral equations based mathematical models are studied for the inverse problem of determining the distribution of ion channels in cilia of olfactory neurons from experimental data.

1 Introduction

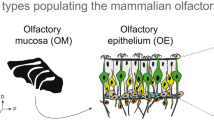
The first step in sensing smell is the transduction (or conversion) of chemical information into an electrical signal that goes to the brain. Pheromones and odorants, which are small molecules with the chemical characteristics of an odor are found all throughout our environment. The olfactory system (part of the sensory system we use to smell) performs the task of receiving these odorant molecules in the nasal mucosa, and triggering the physical-chemical processes that generates the electric current that travels to the brain. see Fig. 1 and Sect. 1.1.

What happens next is a mystery. Intuition tells us that the electrical wave generated gives rise to an emotion in the brain, which in turn affects our behavior. Of course, the workings of our other four senses is similarly a mystery. And so, we quickly come to perhaps one of the most fundamental questions in neurosciences for the future: How does our consciousness processes external stimuli once reduced to electro-chemical waves and, over time, how does this mechanism lead us to become who we are?

How can we approach this problem with mathematics? Faced with these reflections, applied mathematicians take time to stop and wonder if it is possible to provide such far-reaching phenomena with a mathematical representation that allows us to understand and act. Biology is synonymous with “function”, so the study of biological systems should start by understanding the corresponding underlying physiology. Consequently, to obtain a proper mathematical representation of the transduction of an odor into an electrical signal, and before any mathematical intervention, we must first detect which atomic populations are involved in the process and identify their respective functions.

1.1 Transduction of Olfactory Signals

The molecular machinery that carries out this work is in the olfactory cilia. Cilia are long, thin cylindrical structures that extend from an olfactory receptor neuron into the nasal mucus (Fig. 1).

Fig. 1

Odorants reaching the nasal mucus (left) and structure of an olfactory receptor neuron (right)

The transduction of an odor begins with pheromones binding to specific receptors on the external membrane of cilia. When an odorant molecule binds to an olfactory receptor on a cilium membrane, it successively activates an enzyme, which increases the levels of a ligand or chemical messenger named cyclic adenosine monophosphate (cAMP) within the cilia. As a result of this, cAMP molecules diffuse through the interior of the cilia. Some of the cAMP molecules binds to cyclic nucleotide-gated (CNG) ion channels, causing them to open. This allows an influx of positively charged ions into the cilium (mostly Ca$^{2+}$ and Na$^+$ as illustrated in Fig. 2), which causes the neuron to depolarize, generating an excitatory response. This response is characterized by a voltage difference on one side and another of the membrane, which in turn initiates the electrical current. This is the overall process that human beings share with all mammals and reptiles to smell and differentiate odors.

Fig. 2

Signal transduction mechanism for the olfactory system. a In the absence of stimulus channels are closed, system is at resting state. b Binding of odorants triggers cAMP synthesis and opening of CNG channels, leading to Ca$^{2+}$ and Na$^+$ transport and a Cl$^-$ flux

1.2 Kleene’s Experimental Procedure

Experimental techniques for isolating a single cilium (from a grass frog) were developed by biochemist and neuroscientist Steven J. Kleene and his research team at the University of Cincinnati in the early 1990s [5, 6]. One olfactory cilium of a receptor neuron is detached at its base and stretched tight into a recording pipette. The cilium is immersed in a cAMP bath. As a result of the phenomenon previously described inside the cilium, the intensity of the current generated is recorded.

Although the properties of a single channel have been described successfully using these experimental techniques, the distribution of these channels along the cilia still remains unknown, and may well turn out to be crucial in determining the kinetics of the neuronal response. Ionic channels, in particular, CNG channels are called “micro-domains” in biochemistry, because of their practically imperceptible size. This makes their experimental description using the current technology very difficult.

1.3 An Integral Equation Model

Given the experimental difficulties, there is a clear opportunity for mathematics to inform biology. Determining ion channels distribution along the length of a cilium using measurements from experimental data on transmembrane current is usually categorized in physics and mathematics as an inverse problem. Around 2006, a multidisciplinary team (which brought together mathematicians with biochemists and neuroscientists, as well as a chemical engineer) developed and published a first mathematical model [4] to simulate Kleene’s experiments. The distribution of CNG channels along the cilium appears in it as the main unknown of a nonlinear integral equation model.

This model gave rise to a simple numerical method for obtaining estimates of the spatial distribution of CNG ion channels. However, specific computations revealed that the mathematical problem is poorly conditioned. This is a general difficulty in inverse problems, where the corresponding mathematical problem is usually ill-posed (in the sense of Hadamard, which requires the problem to have a solution that exists, is unique, and whose behavior changes continuously with the initial conditions), or else it is unstable with respect to the data. As a consequence, its numerical resolution often results in ill-conditioned approximations.

The essential nonlinearity in the previous model arises from the binding of the channel activating ligand (cAMP molecules) to the CNG ion channels as the ligand diffuses along the cilium. In 2007, mathematicians D. A. French and C. W. Groetsch introduced a simplified model, in which the binding mechanism is neglected, leading to a linear Fredholm integral equation of the first kind with a diffusive kernel. The inverse mathematical problem consists of determining a density function, say $\rho =\rho (x)\ge 0$ (representing the distribution of CNG channels), from measurements in time of the transmembrane electrical current, denoted $\text {I}_0[\rho ]$. This mathematical equation for $\rho$ is the following integral equation: for all $t \ge 0$,

$$\begin{aligned} \text {I}_0[\rho ](t) = \int \limits _0^L\rho (x)\, \, \mathbbm {P}(c(t,x)) {\,\mathrm {d}x}, \end{aligned}$$

(1)

where $\, \mathbbm {P}$ is known as the Hill function of exponent $n>0$ (see Fig. 3). It is defined by:

$$\begin{aligned} \nonumber \forall w\ge 0, \qquad \, \mathbbm {P}(w) = \frac{w^n}{w^n+K_{1/2}^n}. \end{aligned}$$

In this definition, the exponent n is an experimentally determined parameter and $K_{1/2}>0$ is a constant which represents the half-bulk (i.e., the ligand concentration for which half the binding sites are occupied); typical values for n in humans are $n\simeq 2$. Besides, in the linear integral equation above, c(t, x) denotes the concentration of cAMP that diffuses along the cilium with a diffusivity constant that we denote as D; L denotes the length of the cilium, which for simplicity is assumed to be one-dimensional. Here, by concentration we mean the molar concentration, i.e., the amount of solute in the solvent in a unit volume; it is a nonnegative real number.

Fig. 3

The Hill function $\, \mathbbm {P}$

Hill-type functions are extensively used in biochemistry to model the fraction of ligand bound to a macromolecule as a function of the ligand concentration and, hence, the quantity $\, \mathbbm {P}(c(t,x))$ models the probability of the opening of a CNG channel as a function of the cAMP concentration. The diffusion equation for the concentration of cAMP can be explicitly solved if the length of the cilium L is supposed to be infinite. It is given by:

$$\begin{aligned} \nonumber c(t,x) = c_0 \text {erfc}\left( \frac{x}{2 \sqrt{D t}} \right) , \end{aligned}$$

where $c_0>0$ is the maintained concentration of cAMP with which the pipette comes into contact at the open end ($x=0$) of the cilium (while $x=L$ is the closed end). Here, $\text {erfc}$ is the standard complementary Gauss error function,

$$ \text {erfc}(x) := 1- \frac{2}{\sqrt{\pi }} \int \limits _0^x e^{-\tau ^2} {\,\mathrm {d}}\tau . $$

Accordingly, it is straightforward to check that c is decreasing in both its variables and that it remains bounded for all (t, x), $0 < c(t,x)\le c_0$.

Despite its elegance (by virtue of the simplicity of its formulation), this new model does not overcome the difficulties encountered in its non-linear version. In fact the mathematical inverse problem associated to model (1) can be shown to be ill-posed. More precisely, since $\, \mathbbm {P}(c(t,x))$ is a smooth mapping, the operator $\rho \mapsto \text {I}_0[\rho ]$ is compact from $\text {L}^p(0,L)$ to $\text {L}^p(0,T)$ for every $L,T>0$, $1<p<\infty$. Thus, even if the operator $\text {I}_0$ were injective, its inverse would not be continuous because, if so, then the identity map in $\text {L}^p(0,L)$ would be compact, which is known to be false.

1.4 Non-diffusive Kernels

This last result certainly has a more general character. In fact, it is clear from its proof that any model based on a first-order integral equation with a diffusive smooth kernel necessarily results in the problem of recovering the density from measurements of the electrical current being ill-posed.

An initial, natural approach to tackling this anomaly in model (1) was developed in Conca et al. [3]. This exploited the fact that the Hill function converges point-wise to a single step function as the exponent n goes to $+\infty$, the strategy was to approximate $\, \mathbbm {P}$ using a multiple step function.

Based on different assumptions of the spaces where the unknown $\rho$ is sought, theoretical results of identifiability, stability and reconstruction were obtained for the corresponding inverse problem. However, numerical methods for generating estimates of the spatial distribution of ion channels revealed that this class of models is not satisfactory for practical purposes. The only feasible estimates for $\rho$ are obtained for multiple step functions that are very close to a single-step function or, equivalently, for Hill functions with very large exponents, which imply the use of unrealistic models.

Another way to overcome the ill-posedness of the inverse problem in (1) consists of replacing the kernel of the integral equation with a non-smooth variant of the Hill function.

Specifically, let $a\in (0, c_0)$ be a given real parameter. A discontinuous version of $\, \mathbbm {P}$ is obtained by forcing a saturation state for concentrations higher than a. By doing so, one is led to introduce the following disruptive variant of $\, \mathbbm {P}$ (shown in Fig. 4):

$$\begin{aligned} \nonumber \, \mathbbm {H}(c) = \, \mathbbm {P}(c) \, \mathbbm {1}_{c\le a} + \, \mathbbm {1}_{a < c\le c_0}, \end{aligned}$$

where $\, \mathbbm {1}_J$ denotes the characteristic function of the interval J. The mathematical problem that recovers $\rho$ from the electrical current data is therefore modelled by

$$\begin{aligned} \text {I}_1[\rho ](t) = \int \limits _0^L \rho (x) \, \, \mathbbm {H}(c(t,x)){\,\mathrm {d}}x, \end{aligned}$$

(2)

where c(t, x) is still defined as before. The introduction of this disruptive Hill function can be understood mathematically as follows: as $t\rightarrow \infty$, the factor $x/\sqrt{D t}$ in the complementary error function defining the concentration tends to 0, and consequently c(t, x) tends pointwise to $c_0$. An inverse mathematical problem and a direct problem are associated with both models (1) and (2). In the first, the electric current is measured and the unknown is the density $\rho$ of ion channels, while in the direct problem the opposite is true. Since these are Fredholm equations of the first type, it is natural to tackle them using convolution. Once the variable $\rho$ has been extended to $[0, \infty )$ by zero, the Mellin transform is revealed as being the most appropriate tool for carrying out this task (see the overview section “Mellin transform”).

Fig. 4

A disruptive variant of $\, \mathbbm {P}$ ($a=0.157$)

2 A General Convolution Equation

The Mellin transform is the appropriate tool to study model (2). It allows to reduce it in a convolution equation of the Mellin type. To do so, the key observation is the fact that $\, \mathbbm {H}(c(t,x))$ can be written in terms of $\frac{\sqrt{t}}{x}$. Indeed, defining G as

$$\begin{aligned} \nonumber G(z) = \, \mathbbm {H}\left( c_0 \text {erfc}\left( \frac{1}{2\sqrt{D} z}\right) \right) , \end{aligned}$$

we have $\text {I}_1[\rho ](t) = \int \nolimits _0^L \rho (x) G(\frac{\sqrt{t}}{x}){\,\mathrm {d}}x$. Thus, by extending $\rho$ by zero to $[0,\infty )$, and rescaling time t in $t^2$, we obtain

$$ \text {I}_1[\rho ](t^2) = \int \limits _0^{\infty } x \rho (x) G\left( \frac{t}{x} \right) \frac{{\,\mathrm {d}}x}{x} = \Big (x \rho (x)\Big ) * G $$

which is a convolution equation in $x\rho (x)$.

Taking Mellin transform on both sides and using its operational properties, we formally obtain

$$ \frac{1}{2} \mathcal {M}\text {I}_1[\rho ](s/2) = \mathcal {M}G(s) \mathcal {M}\rho (s+1) $$

or equivalently,

$$\begin{aligned} \mathcal {M}\rho (s+1) = \frac{1}{2} \frac{\mathcal {M}\text {I}_1[\rho ] \left( s/2\right) }{\mathcal {M}G(s)}. \end{aligned}$$

(3)

Mellin Transform

Austrian mathematician Robert Hjalmar Mellin (1854–1933) gave his name to the so-called Mellin transform, whose definition and properties are recalled below. The interested reader is referred to §2 of [1] or Lindelöf [7] for a summary of his work, and proof of the main results around this transform.

For $q\in \, \mathbbm {R}$, $q+i\, \mathbbm {R}$ will denote the vertical line $\{q+it, t\in \, \mathbbm {R}\}$ of the complex plane having abscissa q, and for $p\in \, \mathbbm {R}$ ($p\ge 1$), $\text {L}^p\left( [0,\infty ), x^q\right)$, or simply $\text {L}^p_q$, will stand for the Lebesgue space with the weight $x^q$, i.e.,

$$ \text {L}^p_q = \left\{ f:[0,\infty )\rightarrow \, \mathbbm {R}\ | \ \Vert f\Vert _{\text {L}^p_q} < +\infty \right\} , $$

where $\Vert f\Vert _{\text {L}^p_q} = (\int \limits _0^{\infty } | f(x) |^p x^q {\,\mathrm {d}}x)^{1/p}$. $\text {L}^p_q$, endowed with this norm, is a Banach space.

Let f be in $\text {L}^1\left( [0,\infty ), x^q\right)$. The Mellin transform of f is a complex-valued function defined on the vertical line $q+1+i\, \mathbbm {R}$ by

$$ \mathcal {M}f(s) = \int \limits _0^{\infty } x^s f(x) \frac{{\,\mathrm {d}}x}{x} $$

From its very definition, it is observed that the Mellin transform maps functions defined on $[0,\infty )$ into functions defined on $q + 1+ i\, \mathbbm {R}$. Like in the Fourier transform, $\mathcal {M}f$ is continuous whenever f is in $\text {L}^1\left( [0,\infty ), x^q\right)$. Specifically, we have

Theorem 1 (Riemann-Lebesgue) The Mellin transform is a linear continuous map from $\text {L}^1\left( [0,\infty ), x^q\right)$ into $\mathcal {C}^0(q+1+i\, \mathbbm {R};\, \mathbbm {C})\hookrightarrow \text {L}^\infty (q+1+i\, \mathbbm {R};\, \mathbbm {C})$; its operator norm is 1.

Proposition 1 If f is in $\mathrm{L}^{1}_q$ for every real number q in (a, b) then its Mellin transform $\mathcal {M}f(\cdot )$ is holomorphic in the strip $S=\{s\in \, \mathbbm {C}\mid a+1< \mathrm Re(s)< b+1\}$.

The following table summarizes the main operational properties of the Mellin transform:

Function	Mellin transform
$f(at), \ a>0$	$a^{-s} \mathcal {M}f(s)$
$f(t^a), \ a\ne 0$	$|a|^{-1} \mathcal {M}f(a^{-1} s)$
$f^{(k)}(t)$	$(-1)^k (s-k)_k \mathcal {M}f(s-k)$

where, $\forall x\in \, \mathbbm {R}$ and $\forall k\ge 1$, $(x)_{k}$ stands for the so-called Pochhammer symbol, which is defined by

$$ (x)_{k} = x \cdots (x-k+1) = \prod _{j=0}^{k-1} (x-j) \quad \text{ if } k\ge 1, $$

and $(x)_{0} = 1$, where x is in $\, \mathbbm {R}$.

2.1 A Priori Estimates

Seeking continuity and observability inequalities for model (2) is then reduced to find lower and upper bounds for $\mathcal {M}G (\cdot )$ in suitable weighted Lebesgue’s spaces. Doing so, one obtains

Theorem 2

(A Priori Estimates) Let $k \in \mathbb {N}\cup \{0\}$ and $r\in \, \mathbbm {R}$ be arbitrary. Assume that the Mellin transforms of $\rho$ and $\text {I}_1[\rho ]$ satisfy (3), then

$$ C_{\ell }^{k} \Vert \rho \Vert _{\text {L}^2_r} \le \Vert (\text {I}_1[\rho ])^{(k)}\Vert _{\text {L}^2_{2k+\frac{r-3}{2}}} \le C_u^{k} \Vert \rho \Vert _{\text {L}^2_r}, $$

where

$$\begin{aligned} C_{\ell }^{k} \ {\buildrel \mathrm (def) \over =}&\sqrt{2}\inf \limits _{s \in \frac{r-1}{2}+i\, \mathbbm {R}} \left| \left( \frac{s}{2} \right) _{k} \mathcal {M}G(s)\right| \\ C_u^{k} \ {\buildrel \mathrm (def) \over =}&\sqrt{2}\sup \limits _{s\in \frac{r-1}{2}+i\, \mathbbm {R}}\left| {\left( \frac{s}{2} \right) _{k}\mathcal {M}G(s)}\right| , \end{aligned}$$

and $\text {L}^p_q = \text {L}^p\left( [0,\infty ), x^q\right)$ stands for the Lebesgue space with the weight $x^q$, $p\ge 1$, $q\in \, \mathbbm {R}$.

Remark 1

It is worth noting that $C_{\ell }^{k}, C_u^{k}$ could a priori range from 0 to $+\infty$.

Proof

Using the properties of the Mellin transform in Eq. (3), it follows that

$$\begin{aligned} \begin{aligned} (s-k)_{k} \; \mathcal {M}\text {I}[\rho ](s-k)&= 2 (s-k)_{k} \; \mathcal {M}G(2(s-k)) \; \mathcal {M}\rho (2(s-k)+1) \end{aligned} \end{aligned}$$

(4)

Thanks to Parseval-Plancherel’s isomorphism, for every s in $q+i\, \mathbbm {R}$, we have

$$\begin{aligned} \begin{aligned} \left\| (\text {I}[\rho ])^{(k)}\right\| _{\mathrm{L}^{2}_{2q-1}}&= \frac{1}{\sqrt{(2\pi )}} \left\| (-1)^k (s-k)_{k} \, \mathcal {M}\text {I}[\rho ](s-k)\right\| _{\mathrm{L}^{2}\left( q+i\, \mathbbm {R}\right) }\\&= \frac{2}{\sqrt{(2\pi )}} \Big \Vert {(s-k)_{k} \, \mathcal {M}G(2(s-k)) \, \mathcal {M}\rho (2(s-k)+1)}\Big \Vert _{\mathrm{L}^{2}\left( q+i\, \mathbbm {R}\right) } \\&= \frac{2}{\sqrt{(2\pi )}} \Big \Vert {(s)_{k} \, \mathcal {M}G(2s) \, \mathcal {M}\rho (2s+1)}\Big \Vert _{\mathrm{L}^{2}\left( q-k+i\, \mathbbm {R}\right) }\\&= \frac{1}{\sqrt{\pi }}\left\| \left( \frac{s}{2}\right) _{k} \, \mathcal {M}G(s) \, \mathcal {M}\rho (s+1)\right\| _{\mathrm{L}^{2}\left( 2(q-k)+i\, \mathbbm {R}\right) } \end{aligned} \end{aligned}$$

(5)

As $\mathcal {M}$ is an isometry from $\mathrm{L}^{2}\left( 2(q-k)+1+i\, \mathbbm {R}\right)$ on $\mathrm{L}^{2}_{4(q-k)+1}$,

$$\begin{aligned} \left\| \mathcal {M}\rho (s+1)\right\| _{\mathrm{L}^{2}\left( 2(q-k)+i\, \mathbbm {R}\right) } = \left\| \mathcal {M}\rho (s)\right\| _{\mathrm{L}^{2}\left( 2(q-k)+1+i\, \mathbbm {R}\right) } = \sqrt{2\pi } \left\| \rho \right\| _{\mathrm{L}^{2}_{4(q-k)+1}} \end{aligned}$$

(6)

Thanks to (5) and (6) and the definitions of $C_l^k, C_u^k$, we get

$$ C_l^k\left\| \rho \right\| _{\mathrm{L}^{2}_{4(q-k)+1}} \le \left\| (\text {I}[\rho ])^{(k)}\right\| _{\mathrm{L}^{2}_{2q-1}} \le C_u^k \left\| \rho \right\| _{\mathrm{L}^{2}_{4(q-k)+1}} $$

Taking $r=4(q-k)+1$, that is $q=k+\frac{r-1}{4}$, provides the result.

Mellin Convolution

For two given functions f, g, the multiplicative convolution $f*g$ is defined as follows

$$ (f*g)(x) = \int \limits _0^{\infty } f(y)\, g\left( \frac{x}{y} \right) \frac{{\,\mathrm {d}}y}{y} $$

Theorem 3 (Mellin Transform of a Convolution) Whenever this expression is well defined, we have

$$ \mathcal {M}(f*g)(s) = \mathcal {M}f(s) \, \mathcal {M}g(s) $$

Finally, the classical $L^2$-isometry has his Mellin counterpart.

Theorem 4 (Parseval-Plancherel’s Isomorphism) The Mellin transform can be extended in a unique manner to a linear isometry (up to the constant $(2\pi )^{-1/2}$) from $\text {L}^2_{2q-1}$ onto the classical Lebesgue space $\text {L}^2(q+i\, \mathbbm {R})$:

$$ \mathcal {M}\in \mathcal {L}\left( \text {L}^2_{2q-1} ; \text {L}^2(q+i\, \mathbbm {R}, {\,\mathrm {d}}x)\right) $$

3 Observability of CNG Channels

The a priori estimates in the theorem above also allow to determine a unique distribution of ion channels along the length of a cilium from measurements in time of the transmembrane electric current.

Theorem 5

(Existence and uniqueness of $\rho$) Let $a>0$ and $r<1$ be given. If $\text {I}_1 \in \text {L}^2\left( [0,\infty ), t^{\frac{r-3}{2}}\right)$, $\text {I}_1^\prime \in \text {L}^2\left( [0,\infty ), t^{2+\frac{r-3}{2}}\right)$ and a is small enough, then there exists a unique $\rho \in \text {L}^2([0,\infty ), x^r)$ which satisfies the following stability condition:

where $C>0$ depends only on a and r.

Proof

The proof is based on the following technical lemmas and its corollaries.

Lemma 1

Let A and B be two elements of $\ [0,\infty ]$, $k\in \cup \{0\} \mathbb {N}$ be a nonnegative integer and f a function such that $f^{(j)}$ is in $\mathrm{L}^{1}_j(A,B)$ for every $j=0,\ldots ,k$. For every real number t, we have

$$ \int \limits _A^B f(x) x^{it} \,\mathrm {d}x = \sum _{j=0}^{k-1} (-1)^j Q_j \left[ x^{j+1} f^{(j)}(x) x^{it} \right] _A^B + (-1)^k Q_{k-1}\int \limits _A^B x^{k} f^{(k)}(x) x^{it} \,\mathrm {d}x, $$

where $Q_j=Q_j(t) = \left( \prod _{l=0}^{j} (1+l+it )\right) ^{-1}$.

Proof

We use induction on $k\in \mathbb {N}$. For $k=0$, since $Q_{-1}=1$, there is nothing to prove. We assume that the formula is true for an integer $k \in \mathbb {N}$. As $(k+1+it) Q_k = Q_{k-1}$, it remains to prove that

$$ (k+1+it) \int \limits _A^B x^{k} f^{(k)}(x) x^{it} \,\mathrm {d}x = \left[ x^{k+1} f^{(k)}(x) x^{it} \right] _A^B - \int \limits _A^B x^{k+1} f^{(k+1)}(x) x^{it} \,\mathrm {d}x $$

As $\frac{\,\mathrm {d}}{\,\mathrm {d}x} x^{it} = \frac{it}{x} x^{it}$, the previous relation follows by integration by parts. Indeed, we have

$$\begin{aligned} it \int \limits _A^B x^{k} f^{(k)}(x) x^{it} \,\mathrm {d}x= & {} \int \limits _A^B x^{k+1} f^{(k)}(x) (x^{it})^\prime \,\mathrm {d}x \\= & {} \left[ x^{k+1} f^{(k)}(x) x^{it} \right] _A^B - (k+1) \int \limits _A^B x^{k} f^{(k)}(x) x^{it} \,\mathrm {d}x \\&- \int \limits _A^B x^{k+1} f^{(k+1)}(x) x^{it} \,\mathrm {d}x \end{aligned}$$

Corollary 1

Let $f:[A,B]\rightarrow \, \mathbbm {R}$ with $A,B \in [0,\infty ]$ be a piecewise $C^1$ function. If f is non-negative, $f^\prime$ is non-positive, $f\in \mathrm{L}^{1}(A,B), f^\prime \in \mathrm{L}^{1}_1(A,B)$ and for all $t\in \, \mathbbm {R}$: $[xf(x)x^{it}]_A^B=0$, then

$$ \sqrt{1+t^2} \left| \int \limits _{A}^B f(x) x^{it} \,\mathrm {d}x \right| \le \int \limits _{A}^B f(x) \,\mathrm {d}x. $$

Proof

From Lemma 1 with $k=1$ one obtains

$$ \forall t\in \, \mathbbm {R}, \quad (1+it) \int \limits _{A}^B f(x) x^{it} \,\mathrm {d}x = - \int \limits _{A}^B x f^\prime (x) x^{it} \,\mathrm {d}x $$

As $A,B\ge 0$ and $f^\prime \le 0$, using this previous identity twice, for $t\ne 0$ and for $t=0$, we get

$$\begin{aligned} \sqrt{1+t^2} \left| \int \limits _{A}^B f(x) x^{it} \,\mathrm {d}x \right| \le \int \limits _{A}^B \left| x f^\prime (x) \right| \,\mathrm {d}x = \int \limits _{A}^B f(x) \,\mathrm {d}x \end{aligned}$$

Lemma 2

Let $n, K>0,q\in \, \mathbbm {R}$ and $f=\frac{\text {erfc}^n}{\text {erfc}^n+K}$. There exists $x_q>0$ such that the function $g_q:x\in [x_q,\infty ) \mapsto f(x) \, x^{q-1}$ is decreasing. Let $\tilde{q} = \inf E_q$ where $E_q=\{c \ge 0 \mid g_q^\prime (x) < 0\, \forall x \ge c \}$. The function $q \mapsto \tilde{q}$ is increasing and $\tilde{q} = (q/(2n))^{1/2} + o\left( q^{1/2} \right)$ as $q \rightarrow \infty$.

Proof

As $f >0$, the inequality $g_q^\prime (x) \le 0$ is equivalent to

$$\begin{aligned} \frac{f^\prime (x)}{f(x)} \le - \frac{q-1}{x} \end{aligned}$$

(7)

Let us compute $\frac{f^\prime }{f}$. To do so, let $u=\text {erfc}^n$, so that $f=\frac{u}{u+K}$. We have

$$\begin{aligned} \frac{f^\prime }{f} = \frac{u^\prime }{u} \frac{K}{u+K} = n \frac{\text {erfc}^\prime }{\text {erfc}} \frac{K}{u+K} \end{aligned}$$

(8)

Since $\text {erfc}^\prime (x) = - 2 \pi ^{-1/2} e^{-x^2}$, for x large enough, $\text {erfc}(x) = \pi ^{-1/2} x^{-1} e^{-x^2} + o\left( x^{-1} e^{-x^2}\right)$, and so

$$\begin{aligned} \frac{f^\prime (x)}{f(x)} = n \frac{\text {erfc}^\prime (x)}{\text {erfc}(x)} (1+o(1)) = -2 n x + o(x) \end{aligned}$$

(9)

This asymptotic expansion proves that the inequality (7) is satisfied for large enough values of x. As a consequence, for every q in $\, \mathbbm {R}$, the set $E_q$ is not empty, which justifies the definition of $\tilde{q}$. Note that the definition of $\tilde{q}$ implies $g^\prime _q(\tilde{q}) = 0$, and hence, thanks to (7), $\frac{f^\prime (\tilde{q})}{f(\tilde{q})} = - \frac{q-1}{\tilde{q}}$. Let $q_1 \ge q_2$ be two real numbers. In order to show that $\tilde{q_2} \le \tilde{q_1}$, it is enough to prove that $g_{q_1}^\prime (\tilde{q_2}) \ge 0$. This holds true because

$$\begin{aligned} g_{q_1}^\prime (\tilde{q_2})= & {} \tilde{q_2}^{q_1-2} (f^\prime (\tilde{q_2}) \tilde{q_2} + f(\tilde{q_2}) (q_1-1)) \ge \tilde{q_2}^{q_1-2} (f^\prime (\tilde{q_2}) \tilde{q_2} + f(\tilde{q_2}) (q_2-1)) \\= & {} \tilde{q_2}^{q_1-q_2} g_{q_2}^\prime (\tilde{q_2}) = 0 \end{aligned}$$

To find an expansion for $\tilde{q}$, let us recall the following classical lower bound on $\text {erfc}(x)$ for $x \ge 0$,

$$ \frac{1}{x+(x^2+2)^{1/2}} \le \frac{1}{2} \pi ^{1/2} \exp (x^2)\, \text {erfc}(x) $$

As the function $u=\text {erfc}^n$ takes its values in (0, 1], $\frac{nK}{1+K} \le \frac{nK}{u+K} \le n$. Consequently, the identities (8) yield

$$\begin{aligned} -n \left( x+(x^2+2)^{1/2} \right) \le \frac{f^\prime (x)}{f(x)} \end{aligned}$$

(10)

Let $q>1$ and set $x_q = \frac{q-1}{(2n)^{1/2} (n+q-1)^{1/2}}$. The inequality $-\frac{q-1}{x} \le -n \left( x+(x^2+2)^{1/2} \right)$ is equivalent to $x \left( x+(x^2+2)^{1/2} \right) \le \frac{q-1}{n}$. A simple computation shows that this inequality is satisfied for $x=x_q$ (and becomes and equality). Thanks to (10), we conclude that $x_q$ satisfies $\frac{f^\prime (x_q)}{f(x_q)} \ge - \frac{q-1}{x_q}$, which leads to $\tilde{q} \ge x_q$, by definition of $\tilde{q}$ and by (7). This last inequality implies that $\tilde{q}$ tends to $+\infty$ as q tends to $+\infty$. Finally, from (9), we get the asymptotic for $\tilde{q}$, namely

$$ - 2n \tilde{q} + o(\tilde{q}) = \frac{f^\prime (\tilde{q})}{f(\tilde{q})} = - \frac{q-1}{\tilde{q}} $$

This completes the proof of Lemma 2.

Proof of Theorem 5

We are now in a position to conclude the proof of Theorem 5. To do so, we begin by introducing

$$ J(x) \, {\buildrel \mathrm (def) \over =}\, \, \mathbbm {H}(c_0 \text {erfc}(x)) = f(x) \, \mathbbm {1}_{x \ge \alpha } + K \, \mathbbm {1}_{0< x < \alpha }, $$

where $f(x)=\frac{\text {erfc}(x)^n}{\text {erfc}(x)^n+c_0^{-n} K_{1/2}^n}$, $\alpha = \text {erfc}^{-1}\left( \frac{a}{c_0}\right)$, and $K=1$. A brief calculation shows that G and J, and their corresponding Mellin transforms are related as follows

$$\begin{aligned} G(x)=J\left( \frac{1}{2 \sqrt{D} x}\right) \quad \text {and} \quad \mathcal {M}G(s) = \frac{1}{2^{s}\sqrt{D^s} \mathcal {M}J(-s)} \end{aligned}$$

(11)

Thus, in terms of J, Eq. (3) becomes

$$\begin{aligned} \mathcal {M}\rho (s+1)= \frac{2^{s-1}}{\sqrt{D^s}} \frac{\mathcal {M}\text {I}[\rho ] \left( s/2\right) }{\mathcal {M}J(-s)} \end{aligned}$$

(12)

From the estimate for $\text {erfc}$ at $+\infty$, given in the proof of Lemma 2, the function $J_1$ is in $\mathrm{L}^{1}_k$ for every $k>-1$. Thus $\mathcal {M}J_1$ is holomorphic on the right half-plane, see Proposition 1. Using Lemma 3.2 in [1] on the vertical line $\frac{1-r}{2}+i\, \mathbbm {R}$ with $\frac{1-r}{2}>0$, one deduces that bounds for $\mathcal {M}J(-s)$ amounts to estimate $|{s\mathcal {M}J_1(s)}|$, from above or from below, on the vertical lines $q+i\, \mathbbm {R}$, for $q>0$. The Mellin transform of $J_1$ at $s=q+it$ is given by

$$ \mathcal {M}J_1(s) = K \int \limits _{0}^{\alpha } x^{s-1} \,\mathrm {d}x + c_0^n\int \limits _{\alpha }^{+\infty } f(x) x^{s-1} \,\mathrm {d}x = K \frac{\alpha ^{s}}{s} +c_0^n \int \limits _{\alpha }^{+\infty } f(x) x^{q-1} x^{it} \,\mathrm {d}x $$

For any $a\ge 0,q>0$ and $s\in q+i\, \mathbbm {R}$ we have

$$ \left| \mathcal {M}J_1(s)\right| \le K \frac{\alpha ^{q}}{q} + c_0^n\int \limits _{\alpha }^{+\infty } f(x) x^{q-1} \,\mathrm {d}x, $$

which is finite. Let $q>0$. According to Lemma 2 the function $x\mapsto f(x) x^{q-1}$ is decreasing for $x\ge x_0$. Let $a<c_0 \text {erfc}(x_0)$ so that $\alpha =\text {erfc}^{-1}\left( a/c_0\right) \ge x_0$. Let $g(x)=f(x) x^{q-1} \, \mathbbm {1}_{x\ge \alpha }$. For every $t\in \, \mathbbm {R}$, $\left[ f(x) x^{it} \right] _{x_0}^{\infty }=0$ because f vanishes for $x\le \alpha$ and $x_0 \le \alpha$, and $g(x) = \pi ^{-n/2} x^{-n+q-1} e^{-n x^2} + o\left( x^{-n+q-1} e^{-n x^2} \right)$. Then Corollary 1 can be applied to the function g, with $A=\alpha , B=+\infty$, for $s\in q+i\, \mathbbm {R}$, to give

$$\begin{aligned} \begin{aligned} \left| s \mathcal {M}J_1(s)\right|&\le K \left| \alpha ^s\right| + c_0^n \frac{\left| {s}\right| }{ \sqrt{1+t^2}} \sqrt{1+t^2} \left| \int \limits _{\alpha }^{\infty } f(x) \; x^{s-1} \,\mathrm {d}x \right| \\&\le K \alpha ^q +c_0^n \max (1,q) \int \limits _{\alpha }^{\infty } f(x) x^{q-1} \,\mathrm {d}x < \infty ,\\ \end{aligned} \end{aligned}$$

because $\frac{\left| s \right| }{ \sqrt{1+t^2}}\in [q,1] \cup [1,q]$, either $q\le 1$ or $q\ge 1$. For small values of a, the first term dominates the second one. The same calculation as above leads to

$$\begin{aligned} \left| s \mathcal {M}J_1(s)\right| \ge K \alpha ^q - c_0^n\max (1,q) \int \limits _{\alpha }^{\infty } f(x) x^{q-1} \,\mathrm {d}x \end{aligned}$$

This latter expression is equivalent to $K \alpha ^q$ as $\alpha$ tends to $+\infty$, therefore, it is positive for large values of $\alpha$.

4 Unstable Identifiability, Non Existence of Observability Inequalities

Since the French-Groetsch model is also a Fredholm integral equation of the first kind, it is natural to apply a Mellin transform here too. This leads to interesting results: neither an observability inequality nor a proper numerical algorithm for recovering $\rho$ can be established. However, an Identifiability result holds whenever the current is measured over an open time interval (see the Identifiability Theorem below).

Defining $\tilde{G}$ as

$$ \tilde{G}(z) = \, \mathbbm {P}\left( c_0 \text {erfc}\left( \frac{1}{2\sqrt{D} z}\right) \right) , $$

and rescaling time t in $t^2$, we obtain a convolution equation very similar to (3):

$$\begin{aligned} \mathcal {M}\rho (s+1) = \frac{1}{2} \frac{\mathcal {M}\text {I}_0[\rho ] \left( s/2\right) }{\mathcal {M}\tilde{G}(s)} \end{aligned}$$

(13)

A close study of the transform of $\tilde{G}(s)$ allows us to establish the following two theorems, which provide information about the behavior of the inverse problem associated with model (1). The proof of Theorems 3 and 4 requires to extend Mellin transform to functions in the Schwartz space and to prove that the Mellin transforms of such smooth and rapidly decreasing functions decay faster than polynomials on vertical lines.¹

Theorem 3

(Non Observability) Let $r<1$ be fixed. For every non-negative integer k there exists no constant $C_k > 0$ such that the observability inequality:

$$ \Vert (\text {I}_0[\rho ])^{(k)}\Vert _{\text {L}^2\left( [0,\infty ), t^{2k+\frac{r-3}{2}}\right) } \ge C_k \Vert \rho \Vert _{\text {L}^2_{r}}, $$

holds for every function $\rho \in \text {L}^2([0,\infty ), x^r)$.

Note that this result shows that $\text {I}_0\in \mathcal {L}(L^2_r ; L^2_{\frac{r-3}{2}})$, and that if the inverse problem were identificable (i.e., $\text {I}_0$ were injective), then $\text {I}_0^{-1}$ could not be continuous.

Theorem 4

(Identifiability) Let $r< 0$ and $\rho \in \text {L}^1([0,\infty ), x^r)$ be arbitrary. If there exists a nonempty open subset $\,\mathcal {U}$ of $(0,\infty )$ such that for all $t\in \mathcal {U},\ \text {I}_0[\rho ](t) = 0$, then $\rho = 0$ almost everywhere on $(0,\infty )$.

The interested reader is referred to [1, §4 and §5] for various numerical experiences associated with the different theoretical results of this paper. In particular, Theorems 5 and 6 are graphically illustrated in the quoted reference with data extracted from laboratory experiments carried out by Chen et al. [2] in the 1990s.

A Path Forward

The Mellin transform has been successful in mathematically analyzing models (1) and (2), allowing us to answer questions of existence (observability), uniqueness and identifiability of the distribution of ion channels along a cilium, as well as stability issues associated with both direct and inverse problems in these models. However, from a more holistic scientific point of view, not a purely mathematical one, the big question does not seem to be exactly this. Rather, it is about whether, by using and studying these models, Mathematics truly helps to improve our understanding of the olfactory system and, in general terms, the real world. In this sense, Kleene’s experiments have been a great contribution, albeit insufficient. Much stronger validation of the models is required, which can only be achieved by forming multidisciplinary teams and designing ad-hoc experiments.