Abstract
We present novel reductions of the propositional modal logics
 ,
,
 ,
,
 ,
,
 and
and
 to Separated Normal Form with Sets of Modal Levels. The reductions result in smaller formulae than the well-known reductions by Kracht and allow us to use the local reasoning of the prover
to Separated Normal Form with Sets of Modal Levels. The reductions result in smaller formulae than the well-known reductions by Kracht and allow us to use the local reasoning of the prover
 to determine the satisfiability of modal formulae in these logics. We show experimentally that the combination of our reductions with the prover
to determine the satisfiability of modal formulae in these logics. We show experimentally that the combination of our reductions with the prover
 performs well when compared with a specialised resolution calculus for these logics and with the b̆uilt-in reductions of the first-order prover SPASS.
performs well when compared with a specialised resolution calculus for these logics and with the b̆uilt-in reductions of the first-order prover SPASS.
C. Dixon was partially supported by the EPSRC funded RAI Hubs FAIR-SPACE (EP/R026092/1) and RAIN (EP/R026084/1), and the EPSRC funded programme Grant S4 (EP/N007565/1).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The main motivation for reducing problems in one logic (the source logic) to ‘equivalent’ problems in another logic (the target logic) is to exploit results and tools for the target logic to solve theoretical or practical problems in the source logic. For propositional modal logics this approach has been researched extensively for reductions of the satisfiability problem in these logics to the satisfiability problem in ‘stronger’ logics such as first-order logic [10, 20], the second-order theory of n successors [6], simple type theory [4], and regular grammar logics [19].
An alternative approach is to reduce propositional modal logics to a ‘weaker’ logic, in particular, the basic modal logic
 . For extensions of
. For extensions of
 with one of the axioms \(\mathsf {B}\), \(\mathsf {D}\), \(\mathsf {alt_1}\), \(\mathsf {T}\), and \(\mathsf {4}\), Kracht [12] defines reduction functions of their global and local satisfiability problem to the corresponding problem in
with one of the axioms \(\mathsf {B}\), \(\mathsf {D}\), \(\mathsf {alt_1}\), \(\mathsf {T}\), and \(\mathsf {4}\), Kracht [12] defines reduction functions of their global and local satisfiability problem to the corresponding problem in
 and proves their correctness. He also defines a reduction function for
and proves their correctness. He also defines a reduction function for
 , the extension of
, the extension of
 with \(\mathsf {5}\), to
with \(\mathsf {5}\), to
 , but this reduction is incorrect as not all theorems of
, but this reduction is incorrect as not all theorems of
 are theorems of
are theorems of
 . Several features of Kracht’s approach are relevant to our work. First, as is not uncommon in modal logic, he treats the modal operator \(\Diamond \) as abbreviation for \(\lnot \Box \lnot \), that is, \(\Box \) is the only modal operator occurring in modal formulae. Second, the basic idea underlying his reduction functions is for a given modal formula \(\varphi \) to generate sufficiently many instances \(\varDelta \) of a modal axiom \(\Lambda \) so that \(\varphi \) is
. Several features of Kracht’s approach are relevant to our work. First, as is not uncommon in modal logic, he treats the modal operator \(\Diamond \) as abbreviation for \(\lnot \Box \lnot \), that is, \(\Box \) is the only modal operator occurring in modal formulae. Second, the basic idea underlying his reduction functions is for a given modal formula \(\varphi \) to generate sufficiently many instances \(\varDelta \) of a modal axiom \(\Lambda \) so that \(\varphi \) is
 -satisfiable iff \(\varphi \wedge \varDelta \) is
-satisfiable iff \(\varphi \wedge \varDelta \) is
 -satisfiable. Third, Kracht is only concerned with preservation of the computational complexity of the satisfiability problem under consideration, as well as the preservation of other theoretical properties. For instance, the local satisfiability problem in the modal logics covered by Kracht is PSPACE-complete. So, it is sufficient to ensure that \(\varDelta \) is polynomial in size with respect to \(\varphi \). As Kracht himself concludes, his method offers a uniform way of transferring results about one modal logic to another, but may not be as useful for practical applications.
-satisfiable. Third, Kracht is only concerned with preservation of the computational complexity of the satisfiability problem under consideration, as well as the preservation of other theoretical properties. For instance, the local satisfiability problem in the modal logics covered by Kracht is PSPACE-complete. So, it is sufficient to ensure that \(\varDelta \) is polynomial in size with respect to \(\varphi \). As Kracht himself concludes, his method offers a uniform way of transferring results about one modal logic to another, but may not be as useful for practical applications.
In [15, 16] we have introduced a new normal form for basic multi-modal logic, called Separated Normal Form with Modal Levels,
 , that uses labelled modal clauses. These labels refer to the level within a tree Kripke structure at which a modal clause holds. This can be seen as a compromise between approaches that label formulae with worlds at unspecified level [1, 3] and approaches that label formulae with paths [5, 23]. A combination of a normal form transformation for modal formulae and a resolution-based calculus for labelled modal clauses can then be used to decide local and global satisfiability in basic modal logic. In [17, 18] we have presented
, that uses labelled modal clauses. These labels refer to the level within a tree Kripke structure at which a modal clause holds. This can be seen as a compromise between approaches that label formulae with worlds at unspecified level [1, 3] and approaches that label formulae with paths [5, 23]. A combination of a normal form transformation for modal formulae and a resolution-based calculus for labelled modal clauses can then be used to decide local and global satisfiability in basic modal logic. In [17, 18] we have presented
 , an implementation of that calculus, together with an experimental evaluation that indicates that
, an implementation of that calculus, together with an experimental evaluation that indicates that
 performs well if propositional variables are evenly spread across a wide range of modal levels within the formulae one wants to decide.
performs well if propositional variables are evenly spread across a wide range of modal levels within the formulae one wants to decide.
A feature of
 is its use of additional propositional symbols as ‘surrogates’ for subformulae of a modal formula \(\varphi \). In the following we take advantage of the availability of those surrogates to provide a novel transformation from extensions of
is its use of additional propositional symbols as ‘surrogates’ for subformulae of a modal formula \(\varphi \). In the following we take advantage of the availability of those surrogates to provide a novel transformation from extensions of
 with a single one of the axioms \(\mathsf {B}\), \(\mathsf {D}\), \(\mathsf {T}\), \(\mathsf {4}\) and \(\mathsf {5}\) to
with a single one of the axioms \(\mathsf {B}\), \(\mathsf {D}\), \(\mathsf {T}\), \(\mathsf {4}\) and \(\mathsf {5}\) to
 . Another novel aspect is that we modify the normal form so that it uses sets of modal levels as labels instead of a single modal level. In
. Another novel aspect is that we modify the normal form so that it uses sets of modal levels as labels instead of a single modal level. In
 we only need a definition of a surrogate at the modal level at which the corresponding subformula occurs in \(\varphi \). But in
we only need a definition of a surrogate at the modal level at which the corresponding subformula occurs in \(\varphi \). But in
 ,
,
 ,
,
 and
and
 , we need a definition at every reachable modal level, of which there can be many. We call the resulting normal form, Separated Normal Form with Sets of Modal Levels,
, we need a definition at every reachable modal level, of which there can be many. We call the resulting normal form, Separated Normal Form with Sets of Modal Levels,
 .
.
The structure of the paper is as follows. In Section 2 we recap common concepts of propositional modal logic including its syntax and semantics. Section 3 defines
 and the reductions of
and the reductions of
 ,
,
 ,
,
 ,
,
 ,
,
 and
and
 to
to
 . Correctness is proved in Section 4. Related work is discussed in Section 5. In Section 6 we compare the performance of a combination of our reductions and the modal-layered resolution calculus implemented in prover
. Correctness is proved in Section 4. Related work is discussed in Section 5. In Section 6 we compare the performance of a combination of our reductions and the modal-layered resolution calculus implemented in prover
 with resolution calculi specifically designed for the logics under consideration and with translation-based approaches built into the first-order theorem prover SPASS.
with resolution calculi specifically designed for the logics under consideration and with translation-based approaches built into the first-order theorem prover SPASS.
2 Preliminaries
The language of modal logic is an extension of the language of propositional logic with a unary modal operator \(\Box \) and its dual \(\Diamond \). More precisely, given a denumerable set of propositional symbols, \(P= \{p, p_0, q, q_0, t, t_0,\ldots \}\) as well as propositional constants \(\mathbf{true}\) and \(\mathbf{false}\), modal formulae are inductively defined as follows: Constants and propositional symbols are modal formulae. If \(\varphi \) and \(\psi \) are modal formulae, then so are \(\lnot \varphi \), \((\varphi \wedge \psi )\), \((\varphi \vee \psi )\), \((\varphi \rightarrow \psi )\), \(\Box \varphi \), and \(\Diamond \varphi \). We also assume that \(\wedge \) and \(\vee \) are associative and commutative operators and consider, e.g., \((p\vee (q\vee r))\) and \((r\vee (q\vee p))\) to be identical formulae. We often omit parentheses if this does not cause confusion. By  we denote the set of all propositional symbols occurring in \(\varphi \). This function straightforwardly extends to finite sets of modal formulae. A modal axiom (schema) is a modal formula \(\psi \) representing the set of all instances of \(\psi \).
we denote the set of all propositional symbols occurring in \(\varphi \). This function straightforwardly extends to finite sets of modal formulae. A modal axiom (schema) is a modal formula \(\psi \) representing the set of all instances of \(\psi \).
A literal is either a propositional symbol or its negation; the set of literals is denoted by \(L\). We denote by \(\lnot l\) the complement of the literal \(l\in L\), that is, \(\lnot l\) denotes \(\lnot p\) if l is the propositional symbol p, and \(\lnot l\) denotes p if l is the literal \(\lnot p\). A modal literal is either \(\Box l\) or \(\Diamond l\), where \(l \in L\).
A (normal) modal logic is a set of modal formulae which includes all propositional tautologies, the axiom schema \(\Box {(\varphi \rightarrow \psi )} \rightarrow (\Box {\varphi } \rightarrow \Box {\psi })\), called the axiom \(\mathsf {K}\), is closed under modus ponens (if \(\vdash {} \varphi \) and \(\vdash {} \varphi \rightarrow \psi \) then \(\vdash {}\psi \)) and the rule of necessitation (if \(\vdash {}\varphi \) then \(\vdash {} \Box {\varphi }\)).
 is the weakest modal logic, that is, the logic given by the smallest set of modal formulae constituting a normal modal logic. By
is the weakest modal logic, that is, the logic given by the smallest set of modal formulae constituting a normal modal logic. By
 we denote an extensions of
we denote an extensions of
 by a set \(\Sigma \) of axioms.
by a set \(\Sigma \) of axioms.
The standard semantics of modal logics is the Kripke semantics or possible world semantics. A Kripke frame \(F\) is an ordered pair \(\langle W, R \rangle \) where \(W\) is a non-empty set of worlds and \(R\) is a binary (accessibility) relation over \(W\). A Kripke structure \(M\) over \(P\) is an ordered pair \(\langle F,V \rangle \) where \(F\) is a Kripke frame and the valuation V is a function mapping each propositional symbol in \(P\) to a subset V(p) of \(W\). We say \(M= \langle F,V \rangle \) is based on the frame \(F\). A rooted Kripke structure is an ordered pair \(\langle M,w_0 \rangle \) with \(w_0\in W\). To simplify notation, in the following we write \(\langle W, R, V \rangle \) and \(\langle W, R, V,w_0 \rangle \) instead of \(\langle \langle W, R \rangle , V \rangle \) and \(\langle \langle \langle W, R \rangle , V \rangle ,w_0 \rangle \), respectively.
Satisfaction (or truth) of a formula at a world \(w\) of a Kripke structure \(M= \langle W, R, V \rangle \) is inductively defined by:

If \(\langle M, w \rangle \models \varphi \) holds then \(M\) is a model of \(\varphi \), \(\varphi \) is true at w in \(M\) and \(M\) satisfies \(\varphi \). A modal formula \(\varphi \) is satisfiable iff there exists a Kripke structure \(M\) and a world w in \(M\) such that \(\langle M, w \rangle \models \varphi \). A modal formula \(\varphi \) is globally true or valid in a Kripke structure \(M\) if it is true at all worlds of \(M\); it is valid if it is valid in all Kripke structures.
In the following we are interested in extensions of
 with the axiom schemata shown in Table 1. Each of these axiom schemata defines a class of Kripke frames where the accessibility relation \(R\) satisfies the first-order property stated in the table. Given a normal modal logic L with corresponding class of frames \(\mathfrak {F}\), we say a modal formula \(\varphi \) is L-satisfiable iff there exists a frame \(F\in \mathfrak {F}\), a valuation V and a world \(w_0\in F\) such that \(\langle F,V,w_0 \rangle \models \varphi \).
with the axiom schemata shown in Table 1. Each of these axiom schemata defines a class of Kripke frames where the accessibility relation \(R\) satisfies the first-order property stated in the table. Given a normal modal logic L with corresponding class of frames \(\mathfrak {F}\), we say a modal formula \(\varphi \) is L-satisfiable iff there exists a frame \(F\in \mathfrak {F}\), a valuation V and a world \(w_0\in F\) such that \(\langle F,V,w_0 \rangle \models \varphi \).
A path rooted at \(w\) of length k, \(k\ge 0\), in a frame \(F = \langle W,R \rangle \) is a sequence \(\vec {w} = (w_0,w_1,\ldots ,w_k)\) where for every i, \(1\le i\le k\), \(w_{i-1}\mathbin {R}w_i\). We say that the path \((w_0,w_1,\ldots ,w_k)\) connects \(w_0\) and \(w_k\). For a path \(\vec {w} = (w_0,\ldots ,w_k)\) and world \(w_{k+1}\) with \(w_k\mathbin {R}w_{k+1}\), \(\vec {w}\circ w_{k+1}\) denotes the path \((w_0,\ldots ,w_k,w_{k+1})\). A path \((w_0)\) of length 0 is identified with its root \(w_0\). We denote the set of all paths rooted at a world \(w_0\) in \(F\) by \(\vec {F}[w_0]\) and the set of all paths by \(\vec {F}\). The function  maps every path \(\vec {w} = (w_0,\ldots ,w_k)\) to its terminal world \(w_k\) while the function
maps every path \(\vec {w} = (w_0,\ldots ,w_k)\) to its terminal world \(w_k\) while the function  maps every path \(\vec {w} = (w_0,w_1,\ldots ,w_k)\) to its length k.
maps every path \(\vec {w} = (w_0,w_1,\ldots ,w_k)\) to its length k.
A rooted Kripke structure \(M = \langle W,R,V,w_0 \rangle \) is a rooted tree Kripke structure iff R is a tree, that is, a directed acyclic connected graph where each node has at most one predecessor, with root \(w_0\). It is a rooted tree Kripke model of a modal formula \(\varphi \) iff \(\langle W,R,V,w_0 \rangle \models \varphi \). In a rooted tree Kripke structure with root \(w_0\) for every world \(w_k\in W\) there is exactly one path \(\vec {w}\) connecting \(w_0\) and \(w_k\); the modal level of \(w_k\) (in M), denoted by  , is given by
, is given by  .
.
Let \(F = \langle W, R \rangle \) be a Kripke frame with \(w\in W\). The unravelling \(F^u[w]\) of \(F\) at \(w\) is the frame \(\langle \vec {W}, \vec {R} \rangle \) where:
-
\(\vec {W} = \vec {F}[w]\) is the set of all rooted paths at \(w\) in \(F\);
-
for all \(\vec {v},\vec {w} \in \vec {W}\), if \(\vec {w} = \vec {v}\circ w\) for some \(w\in W\), then \(\vec {v}\mathbin {\vec {R}}\vec {w}\).
Let \(F=\langle W, R \rangle \) and \(F'=\langle W', R' \rangle \) be two Kripke frames. A function \(f :W\mapsto W'\) is a p-morphism (or a bounded morphism) from \(F\) to \(F'\) if the following holds:
-
if \(v\mathbin {R}w\), then \(f(v)\mathbin {R'}f(w)\).
-
if \(f(u)\mathbin {R'}w\), then there exists \(v\in W\) s.t. \(f(v)=w\) and \(u\mathbin {R}v\).
Analogously for Kripke models. For \(F = \langle W,R \rangle \), \(M' = \langle F,V',w_0 \rangle \), and \(M = \langle F^u[w_0],V,(w_0) \rangle \), the function  is a p-morphism from \(M\) to \(M'\).
is a p-morphism from \(M\) to \(M'\).
When considering local satisfiability, the following holds (see, [8]):
Theorem 1
Let \(\varphi \) be a modal formula. Then \(\varphi \) is
 -satisfiable iff there is a finite rooted tree Kripke structure \(M=\langle F,V,w_0 \rangle \) such that \(\langle M, w_0 \rangle \models \varphi \).
-satisfiable iff there is a finite rooted tree Kripke structure \(M=\langle F,V,w_0 \rangle \) such that \(\langle M, w_0 \rangle \models \varphi \).
For the normal form transformation presented in the next section we assume that any modal formula \(\varphi \) has been simplified by exhaustively applying the rewrite rules in Table 2 and is in Negation Normal Form (NNF), that is, a formula where only propositional symbols are allowed in the scope of negations. We say that such a formula is in simplified NNF.
3 Layered Normal Form with Sets of Levels
A formula to be tested for satisfiability is first transformed into a normal form called Separated Normal Form with Sets of Modal Levels,
 , whose language extends that of modal logic with labels consisting of sets of modal levels. Informally, we write \(S: \varphi \), where S is a set of natural numbers, to denote that a formula \(\varphi \) is true at modal levels \(ml\in S\). We write
, whose language extends that of modal logic with labels consisting of sets of modal levels. Informally, we write \(S: \varphi \), where S is a set of natural numbers, to denote that a formula \(\varphi \) is true at modal levels \(ml\in S\). We write  instead of \(\mathbb N:\varphi \).
instead of \(\mathbb N:\varphi \).
We introduce some notation that will be used in the following. Let \(S^+= \{l + 1\in \mathbb N\mid l \in S\}\), \(S^- = \{ l - 1 \in \mathbb N\mid l \in S\}\), and \(S^\ge = \{n \mid n \ge \min (S)\}\), where \(\min (S)\) is the least element in S. Note that the restriction of the elements being in \(\mathbb N\) implies that \(S^-\) cannot contain negative numbers.
The labels in
 work as a kind of weak universal operator, allowing us to talk about formulae that are satisfied at all worlds in a given set of modal levels. Formally, we restrict ourselves to rooted tree Kripke structures \(M = \langle W,R,V,w_0 \rangle \) and if S is a set of modal levels, then by M[S] we denote the set of worlds that are at a modal level in S, that is,
work as a kind of weak universal operator, allowing us to talk about formulae that are satisfied at all worlds in a given set of modal levels. Formally, we restrict ourselves to rooted tree Kripke structures \(M = \langle W,R,V,w_0 \rangle \) and if S is a set of modal levels, then by M[S] we denote the set of worlds that are at a modal level in S, that is,  . The satisfaction of labelled formulae in a rooted tree Kripke structure M is then defined as follows:
. The satisfaction of labelled formulae in a rooted tree Kripke structure M is then defined as follows:

If \(M\models S: \varphi \), then we say that \(S: \varphi \) holds in \(M\). Note that if \(S=\emptyset \), then \(M\models S: \varphi \) trivially holds. For a set \(\varPhi \) of labelled formulae, \(M\models \varPhi \) iff \(M\models S:\varphi \) for every \(S:\varphi \) in \(\varPhi \), and we say \(\varPhi \) is
 -satisfiable.
-satisfiable.
A labelled modal formula is then an
 clause iff it is of one of the following forms:
clause iff it is of one of the following forms:
-
Literal clause \(S: \bigvee _{b=1}^{r} l_b\)
-
Positive modal clause \(S: l' \rightarrow \Box l\)
-
Negative modal clause \(S: l' \rightarrow \Diamond l\)
where \(S \subseteq \mathbb N\) and l, \(l'\), \(l_b\) are propositional literals with \(1 \le b \le r\), \(r \in \mathbb N\). Positive and negative modal clauses are together known as modal clauses. We regard a literal clause as a set of literals, that is, two clauses are the same if they contain the same set of literals.
We assume that the set \(P\) of propositional symbols is partitioned into two infinite sets Q and T such that for every modal formula \(\psi \) we have  and there exists a propositional symbol \(t_\psi \in T\) uniquely associated with \(\psi \).
and there exists a propositional symbol \(t_\psi \in T\) uniquely associated with \(\psi \).
Given a modal formula \(\varphi \) in simplified NNF and
 , then we can obtain a set \(\varPhi _L\) of clauses in
, then we can obtain a set \(\varPhi _L\) of clauses in
 such that \(\varphi \) is L-satisfiable iff \(\varPhi _L\) is
such that \(\varphi \) is L-satisfiable iff \(\varPhi _L\) is
 -satisfiable as \(\varPhi _L =\{\{ 0 \}: t_\varphi \}\cup \rho _{L}(\{0\}:t_\varphi \rightarrow \varphi )\), where \(\rho _{L}\) is defined as follows:
-satisfiable as \(\varPhi _L =\{\{ 0 \}: t_\varphi \}\cup \rho _{L}(\{0\}:t_\varphi \rightarrow \varphi )\), where \(\rho _{L}\) is defined as follows:

where \(\eta \) and \(\delta _{L}\) are defined as follows:

and functions \(P_{L}\), \(\varDelta _{L}\) are defined as shown in Table 3. The function \(\eta \) maps a propositional literal \(\psi \) to itself while it maps every other modal formula \(\psi \) to a new propositional symbol \(t_\psi \in T\) uniquely associated with \(\psi \). We call \(t_\psi \) the surrogate of \(\psi \) or simply a surrogate. The functions  and
and  introduce additional propositional symbols, called supplementary propositional symbols, \(t_{\Box \lnot t_{\Box \psi }}\in T\) and \(t_{\Diamond t_{\Box \psi }}\in T\), respectively, that do not correspond to subformulae of the formula we are transforming.
introduce additional propositional symbols, called supplementary propositional symbols, \(t_{\Box \lnot t_{\Box \psi }}\in T\) and \(t_{\Diamond t_{\Box \psi }}\in T\), respectively, that do not correspond to subformulae of the formula we are transforming.
Intuitively,  is based on the following consideration: Take a world w in a Kripke structure \(M\) with a symmetric accessibility relation \(R\). If there exists a world v with \(w\mathbin {R}v\) such that \(\langle M, v \rangle \models \Box \psi \), then \(\langle M, w \rangle \models \psi \). Now, take the contrapositive of that statement: If \(\langle M, w \rangle \not \models \psi \), then for every world v with \(w\mathbin {R}v\), \(\langle M, v \rangle \not \models \Box \psi \). Equivalently, \(\langle M, w \rangle \models \psi \) or \(\langle M, w \rangle \models \Box \lnot \Box \psi \). This is expressed by the formula \(\eta (\psi )\vee t_{\Box \lnot t_{\Box \psi }}\). For
is based on the following consideration: Take a world w in a Kripke structure \(M\) with a symmetric accessibility relation \(R\). If there exists a world v with \(w\mathbin {R}v\) such that \(\langle M, v \rangle \models \Box \psi \), then \(\langle M, w \rangle \models \psi \). Now, take the contrapositive of that statement: If \(\langle M, w \rangle \not \models \psi \), then for every world v with \(w\mathbin {R}v\), \(\langle M, v \rangle \not \models \Box \psi \). Equivalently, \(\langle M, w \rangle \models \psi \) or \(\langle M, w \rangle \models \Box \lnot \Box \psi \). This is expressed by the formula \(\eta (\psi )\vee t_{\Box \lnot t_{\Box \psi }}\). For  , the formula \(t_{\Diamond t_{\Box \psi }}\rightarrow \Box t_{\Diamond t_{\Box \psi }}\) expresses an instance of axiom schema
, the formula \(t_{\Diamond t_{\Box \psi }}\rightarrow \Box t_{\Diamond t_{\Box \psi }}\) expresses an instance of axiom schema  , \(\Diamond \varphi \rightarrow \Box \Diamond \varphi \), with \(\varphi = \Box {\psi }\), i.e., \(\Diamond \Box \psi \rightarrow \Box \Diamond \Box \psi \). The contrapositive of axiom schema \(\mathsf {5}\) is \(\Diamond \Box \varphi \rightarrow \Box \varphi \), equivalent to \(\lnot \Diamond \Box \varphi \vee \Box \varphi \). For \(\varphi =\psi \) this is expressed by the formula \(\lnot t_{\Diamond t_{\Box \psi }}\vee t_{\Box \psi }\). For the formula \(\lnot t_{\Diamond t_{\Box \psi }}\rightarrow \Box \lnot t_{\Box \psi }\), consider \(\lnot \Diamond \Box \psi \). By duality of \(\Box \) and \(\Diamond \), this is equivalent to \(\lnot \lnot \Box \lnot \Box \psi \) and \(\Box \lnot \Box \psi \). So, \(\lnot \Diamond \Box \psi \rightarrow \Box \lnot \Box \psi \) in every normal modal logic, not only
, \(\Diamond \varphi \rightarrow \Box \Diamond \varphi \), with \(\varphi = \Box {\psi }\), i.e., \(\Diamond \Box \psi \rightarrow \Box \Diamond \Box \psi \). The contrapositive of axiom schema \(\mathsf {5}\) is \(\Diamond \Box \varphi \rightarrow \Box \varphi \), equivalent to \(\lnot \Diamond \Box \varphi \vee \Box \varphi \). For \(\varphi =\psi \) this is expressed by the formula \(\lnot t_{\Diamond t_{\Box \psi }}\vee t_{\Box \psi }\). For the formula \(\lnot t_{\Diamond t_{\Box \psi }}\rightarrow \Box \lnot t_{\Box \psi }\), consider \(\lnot \Diamond \Box \psi \). By duality of \(\Box \) and \(\Diamond \), this is equivalent to \(\lnot \lnot \Box \lnot \Box \psi \) and \(\Box \lnot \Box \psi \). So, \(\lnot \Diamond \Box \psi \rightarrow \Box \lnot \Box \psi \) in every normal modal logic, not only
 . The remaining labelled formulae introduced by
. The remaining labelled formulae introduced by  and
and  ensure that supplementary propositional symbols are defined. For the remaining logics the additional clauses are also based directly on the axiom schemata.
ensure that supplementary propositional symbols are defined. For the remaining logics the additional clauses are also based directly on the axiom schemata.
To simplify presentation in the following, we define a function \(\eta _f\) as follows:
and we treat the two clauses \(S: \lnot t_{\psi _1\wedge \psi _2} \vee \eta (\psi _1)\) and \(S: \lnot t_{\psi _1\wedge \psi _2} \vee \eta (\psi _2)\) resulting from the normal form transformation of \(\psi _1\wedge \psi _2\) as a single ‘clause’ \(S: \lnot t_{\psi _1\wedge \psi _2} \vee \eta _f(\psi _1\wedge \psi _2)\). We also interchangeably write \(S:\lnot t_{\Box \psi }\vee \eta _f(\Box \psi )\) for \(S:t_{\Box \psi }\rightarrow \eta _f(\Box \psi )\) and, analogously, \(S:\lnot t_{\Diamond \psi }\vee \eta _f(\Diamond \psi )\) for \(S:t_{\Diamond \psi }\rightarrow \eta _f(\Diamond \psi )\). We then call any clause of the form \(S:\lnot t_\psi \vee \eta _f(\psi )\) a definitional clause.
Definition 1
Let \(\varPhi \) be a set of
 clauses. We say \(t_\psi \in T\) occurs at level ml in \(\varPhi \) iff either
clauses. We say \(t_\psi \in T\) occurs at level ml in \(\varPhi \) iff either
-
(a)
there exists a clause \(S:\vartheta \) in \(\varPhi \) with \(ml\in S\) such that \(\vartheta \) is a propositional formula and \(t_\psi \) occurs positively in \(\vartheta \), or
-
(b)
there exists a clause \(S:t_{\Box \psi }\rightarrow \Box t_\psi \) in \(\varPhi \) with \(ml-1\in S\), or
-
(c)
there exists a clause \(S:t_{\Diamond \psi }\rightarrow \Diamond t_\psi \) in \(\varPhi \) with \(ml-1\in S\).
Definition 2
Let \(\varPhi \) be a set of
 clauses. Then \(\varPhi \) is definition-complete iff for every \(t_\psi \in T\) and every level ml, if \(t_\psi \) occurs at level ml in \(\varPhi \) then there exists a clause \(S: \lnot t_\psi \vee \eta _f(\psi )\) in \(\varPhi \) with \(ml\in S\).
clauses. Then \(\varPhi \) is definition-complete iff for every \(t_\psi \in T\) and every level ml, if \(t_\psi \) occurs at level ml in \(\varPhi \) then there exists a clause \(S: \lnot t_\psi \vee \eta _f(\psi )\) in \(\varPhi \) with \(ml\in S\).
Theorem 2
Let
 . Then \(\varPhi _L =\{\{ 0 \}: t_\varphi \}\cup \rho _{L}(\{0\}:t_\varphi \rightarrow \varphi )\) is definition-complete.
. Then \(\varPhi _L =\{\{ 0 \}: t_\varphi \}\cup \rho _{L}(\{0\}:t_\varphi \rightarrow \varphi )\) is definition-complete.
Proof
By induction over the computation of \(\varPhi _L\). It is straightforward to see that the transformation of labelled formulae \(S: t\rightarrow (\psi _1\wedge \psi _2)\) and \(S: t\rightarrow (\psi _1\vee \psi _2)\) only introduces surrogates at levels in S and \(\varDelta _L\) then adds definitional clauses for those surrogates. The transformation of a labelled formula \(S: t_{\Diamond \psi }\rightarrow \Diamond \psi \) may introduce a surrogate at levels in \(S^+\) and \(\delta _L(S^+,\psi )\) then adds definitional clauses for those surrogates. The transformation of a labelled formula \(S: t_{\Box \psi }\rightarrow \Box \psi \) depends on the logic L. We can see that for every level at which a new surrogate occurs in \(P_L(S: t_{\Box \psi }\rightarrow \Box \psi )\), then \(\varDelta _L(S: t_{\Box \psi }\rightarrow \Box \psi )\) contains a definitional clause for it at that level.
4 Correctness
Due to space constraints we only prove the correctness of the transformation for
 . We first state several lemmata that are used in the correctness proofs for all logics.
. We first state several lemmata that are used in the correctness proofs for all logics.
Lemma 1
Let \(\varPhi \) be a set of definitional clauses such that every \(t_\psi \) occurring in \(\varPhi \) is an element of T and all other propositional symbols occurring in \(\varPhi \) are in Q. Let \(M=\langle W, R, V, w_0 \rangle \) be a rooted Kripke structure. Let \(\langle \vec {W},\vec {R} \rangle \) be the unravelling of \(\langle W, R \rangle \) at \(w_0\). Let \(\vec {M}= \langle \vec {W}, \vec {R}, \vec {V_\Sigma },(w_0) \rangle \) be a Kripke structure such that
-
 for every propositional symbol \(p\in Q\), and
for every propositional symbol \(p\in Q\), and -
\(\vec {V_\Sigma }(t_\psi ) = \{\vec {w}\in \vec {W}\mid \langle \vec {M}, \vec {w} \rangle \models \psi \}\) for every surrogate
 .
.
Then \(\vec {M}\models \varPhi \).
Lemma 2
Let \(\varphi \) be a L-satisfiable modal formula in simplified NNF where L is a normal modal logic and let  . Let \(M=\langle W, R, V, w_0 \rangle \) be a rooted
. Let \(M=\langle W, R, V, w_0 \rangle \) be a rooted
 model of \(\varphi \). Let \(\langle \vec {W},\vec {R} \rangle \) be the unravelling of \(\langle W,R \rangle \) at \(w_0\). Let \(\vec {M} = \langle \vec {W}, \vec {R}, \vec {V},(w_0) \rangle \) be a Kripke structure such that
model of \(\varphi \). Let \(\langle \vec {W},\vec {R} \rangle \) be the unravelling of \(\langle W,R \rangle \) at \(w_0\). Let \(\vec {M} = \langle \vec {W}, \vec {R}, \vec {V},(w_0) \rangle \) be a Kripke structure such that
-
 for every propositional symbol
for every propositional symbol  , and
, and -
\(\vec {V}(t_\psi ) = \{\vec {w}\in \vec {W}\mid \langle \vec {M}, \vec {w} \rangle \models \psi \}\) for every surrogate
 .
.
Then \(\vec {M}\models \varPhi \).
Lemma 3
Let \(M=\langle W, R, V, w_0\rangle \) be a rooted Kripke structure. Let \(\langle \vec {W},\vec {R} \rangle \) be the unravelling of \(\langle W, R \rangle \) at \(w_0\). Let \(\vec {M}= \langle \vec {W}, \vec {R}, \vec {V_\Sigma },(w_0)\rangle \) where  for every propositional symbol \(p\in Q\).
for every propositional symbol \(p\in Q\).
Then for every modal formula \(\psi \) over Q and for every world \(\vec {w}\in \vec {W}\), \(\langle \vec {M}, \vec {w} \rangle \models \psi \) iff  .
.
Lemma 4
Let \(\varphi \) be a modal formula in simplified NNF. Let  . Let
. Let  be a definition-complete set of
be a definition-complete set of
 clauses, let \(M = \langle W,R,V,w_0 \rangle \) be a tree
clauses, let \(M = \langle W,R,V,w_0 \rangle \) be a tree
 model of \(\varPhi \) and let \(M' = \langle W,R',V,w_0 \rangle \) be such that
model of \(\varPhi \) and let \(M' = \langle W,R',V,w_0 \rangle \) be such that
-
(4a)
\(R\subseteq R'\);
-
(4b)
for every modal clause \(S: t_{\Box \psi }\rightarrow \Box \eta (\psi )\) in \(\varPhi \) and every world \(w\in M[S]\), \(\langle M', w \rangle \models t_{\Box \psi }\rightarrow \Box \eta (\psi )\);
-
(4c)
for every modal clause \(S: t_{\Box \psi }\rightarrow \Box t_\psi \) in \(\varPhi \) and all worlds \(v,w\in W\), if (i) \(w\in M[S]\) and (ii) \(w\mathbin {R'}v\) then (iii) there exists a clause \(S':\lnot t_\psi \vee \eta _f(\psi )\) in \(\varPhi \) with \(v\in M[S']\).
Then \(\langle M', w_0 \rangle \models \varphi \).
Theorems 3 and 4 now state the correctness of our transformation for
 .
.
Theorem 3
Let \(\varphi \) be a modal formula in simplified NNF. Let  . If \(\varphi \) is
. If \(\varphi \) is
 -satisfiable, then \(\varPhi _B\) is
-satisfiable, then \(\varPhi _B\) is
 -satisfiable.
-satisfiable.
Proof
The main idea is to show that given a rooted
 model of \(\varphi \), then a small variation of its unravelling is a rooted tree
model of \(\varphi \), then a small variation of its unravelling is a rooted tree
 model of \(\varPhi _B\).
model of \(\varPhi _B\).
Let \(M=\langle W, R, V, w_0 \rangle \) be a rooted
 model of \(\varphi \) with \(\langle M, w_0 \rangle \models \varphi \) and symmetric relationship \(R\). Let \(\langle \vec {W},\vec {R} \rangle \) be the unravelling of \(\langle W,R \rangle \) at \(w_0\). Let
model of \(\varphi \) with \(\langle M, w_0 \rangle \models \varphi \) and symmetric relationship \(R\). Let \(\langle \vec {W},\vec {R} \rangle \) be the unravelling of \(\langle W,R \rangle \) at \(w_0\). Let  where
where
-
 for every propositional symbol
for every propositional symbol 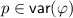 ,
, -
 for every surrogate
for every surrogate  introduced by rewriting, and
introduced by rewriting, and -
 for every supplementary propositional symbol \(t_{\Box \lnot t_{\Box \psi }} \) introduced in the normal form transformation of a labelled formula \(S:t_{\Box \psi }\rightarrow \Box \psi \).
for every supplementary propositional symbol \(t_{\Box \lnot t_{\Box \psi }} \) introduced in the normal form transformation of a labelled formula \(S:t_{\Box \psi }\rightarrow \Box \psi \).
Note that  is well-defined as for every surrogate \(t_\psi \in T\), \(\psi \) only contains propositional symbols in Q. Let
is well-defined as for every surrogate \(t_\psi \in T\), \(\psi \) only contains propositional symbols in Q. Let  .
.
We now consider the clauses occurring in  and show that they hold in
and show that they hold in  . By Lemma 2 it follows that
. By Lemma 2 it follows that  . Also, all definitional clauses in
. Also, all definitional clauses in  are true in
are true in  by Lemma 1.
by Lemma 1.
Next consider clauses of the form

where \(t_{\Box \psi } \) is a surrogate for \(\Box \psi \). These are not in  . We show both are true in
. We show both are true in  . We do so by first considering that \(t_{\Box \lnot t_{\Box \psi }} \) is true at a world and then that it is false.
. We do so by first considering that \(t_{\Box \lnot t_{\Box \psi }} \) is true at a world and then that it is false.
-
Case (a):
Let
 with
with  . Clearly,
. Clearly,  . Also, by definition of
. Also, by definition of  ,
,  . So, for every \(\vec {v}\in \vec {W}\) with \(\vec {w}\mathbin {\vec {R}}\vec {v}\),
. So, for every \(\vec {v}\in \vec {W}\) with \(\vec {w}\mathbin {\vec {R}}\vec {v}\),  . As \(t_{\Box \psi } \) is a surrogate for \(\Box \psi \), by definition of \(\vec {V_B}\), \(\vec {v}\not \in \vec {V_B}(t_{\Box \psi })\) and
. As \(t_{\Box \psi } \) is a surrogate for \(\Box \psi \), by definition of \(\vec {V_B}\), \(\vec {v}\not \in \vec {V_B}(t_{\Box \psi })\) and  . Thus,
. Thus,  and, by the semantics of implication,
and, by the semantics of implication,  .
. -
Case (b):
Let
 with
with  . Clearly, by the semantics of implication,
. Clearly, by the semantics of implication,  . Also, by definition of \(\vec {V_B}\), \(\vec {w}\not \in \vec {V_B}(t_{\Box \lnot t_{\Box \psi }})\) implies
. Also, by definition of \(\vec {V_B}\), \(\vec {w}\not \in \vec {V_B}(t_{\Box \lnot t_{\Box \psi }})\) implies  which in turn implies
which in turn implies  . So, there exists \(\vec {v}\in \vec {W}\) with \(\vec {w}\mathbin {\vec {R}}\vec {v}\) and
. So, there exists \(\vec {v}\in \vec {W}\) with \(\vec {w}\mathbin {\vec {R}}\vec {v}\) and  . Since
. Since  is a p-morphism from
is a p-morphism from  to M,
to M,  . Since \(R\) is symmetric, we also have
. Since \(R\) is symmetric, we also have  and by construction of
and by construction of  , for
, for  we have \(\vec {v}\mathbin {\vec {R}}\vec {u}\). Since
we have \(\vec {v}\mathbin {\vec {R}}\vec {u}\). Since  ,
,  . As
. As  is a p-morphism and
is a p-morphism and  and since
and since  ,
,  . By Lemma 3, from
. By Lemma 3, from  we obtain
we obtain  . If \(\psi \) is a literal, then \(\eta (\psi ) = \psi \) and \(\langle M, \vec {w} \rangle \models \eta (\psi )\). If \(\psi \) is not a literal, then \(\eta (\psi ) = t_\psi \) and from
. If \(\psi \) is a literal, then \(\eta (\psi ) = \psi \) and \(\langle M, \vec {w} \rangle \models \eta (\psi )\). If \(\psi \) is not a literal, then \(\eta (\psi ) = t_\psi \) and from  , by definition of
, by definition of  ,
,  and
and  . So, \(\langle M, \vec {w} \rangle \models \eta (\psi )\vee t_{\Box \lnot t_{\Box \psi }} \).
. So, \(\langle M, \vec {w} \rangle \models \eta (\psi )\vee t_{\Box \lnot t_{\Box \psi }} \).
Thus, in both cases, for arbitrary  , \(\eta (\psi )\vee t_{\Box \lnot t_{\Box \psi }} \) and \(t_{\Box \lnot t_{\Box \psi }} \rightarrow \Box \lnot t_{\Box \psi } \) and therefore Clauses (1) and (2) are true in
, \(\eta (\psi )\vee t_{\Box \lnot t_{\Box \psi }} \) and \(t_{\Box \lnot t_{\Box \psi }} \rightarrow \Box \lnot t_{\Box \psi } \) and therefore Clauses (1) and (2) are true in  .
.
Theorem 4
Let \(\varphi \) be a modal formula in simplified NNF. Let  . If
. If  is
is
 -satisfiable, then \(\varphi \) is
-satisfiable, then \(\varphi \) is
 -satisfiable.
-satisfiable.
Proof
The main idea is to show that given a rooted tree
 model of
model of  , its symmetric closure is a rooted
, its symmetric closure is a rooted
 model of \(\varphi \).
model of \(\varphi \).
Let \(M = \langle W,R,V,w_0 \rangle \) be a rooted tree
 model of
model of  . Let
. Let  be a structure such that
be a structure such that
-
(a)
 is the symmetric closure of \(R\), that is,
is the symmetric closure of \(R\), that is,  is the smallest relation on \(W\) such that
is the smallest relation on \(W\) such that 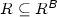 and for every \(v,w\in W\),
and for every \(v,w\in W\),  implies
implies  ;
; -
(b)
 for every propositional symbol.
for every propositional symbol.
Let  . We show that
. We show that  satisfies the three preconditions of Lemma 4. By Lemma 4 this in turn implies that
satisfies the three preconditions of Lemma 4. By Lemma 4 this in turn implies that  .
.
-
Condition 4a holds as
 .
. -
For Condition 4b let
 be a modal clause in
be a modal clause in  . Then
. Then  also contains the additional clauses
also contains the additional clauses
 and
and
 . Let \(w\in M[S]\). We have to show that
. Let \(w\in M[S]\). We have to show that

 . Assume
. Assume  . As
. As  this implies \(\langle M, w \rangle \models t_{\Box \psi }\). Let \(v\in W\) such that
this implies \(\langle M, w \rangle \models t_{\Box \psi }\). Let \(v\in W\) such that  .
.Case (a): Assume \(w\mathbin {R}v\). As \(\langle M, w \rangle \models t_{\Box \psi }\) and \(\langle M, w \rangle \models t_{\Box \psi }\rightarrow \Box \eta (\psi )\), we have \(\langle M, w \rangle \models \Box \eta (\psi )\). As \(w\mathbin {R}v\), \(\langle M, v \rangle \models \eta (\psi )\). As \(\eta (\psi )\) is a literal and
 we obtain
we obtain  . So,
. So,  .
.Case (b): Assume v is not reachable from w via \(R\). Then
 was introduced by the symmetric closure operation on \(R\) and we must have \(v\mathbin {R}w\). That is, v is a \(R\)-predecessor of w and from \(w\in M[S]\) it follows that \(v\in M[S^-]\). So,
was introduced by the symmetric closure operation on \(R\) and we must have \(v\mathbin {R}w\). That is, v is a \(R\)-predecessor of w and from \(w\in M[S]\) it follows that \(v\in M[S^-]\). So,
 and
and
 . From \(v\mathbin {R}w\), \(\langle M, w \rangle \models t_{\Box \psi }\) and (8), it follows that \(\langle M, v \rangle \models \lnot t_{\Box \lnot t_{\Box \psi }}\). This together with (7) implies \(\langle M, v \rangle \models \eta (\psi )\). As \(\eta (\psi )\) is a literal and
. From \(v\mathbin {R}w\), \(\langle M, w \rangle \models t_{\Box \psi }\) and (8), it follows that \(\langle M, v \rangle \models \lnot t_{\Box \lnot t_{\Box \psi }}\). This together with (7) implies \(\langle M, v \rangle \models \eta (\psi )\). As \(\eta (\psi )\) is a literal and  we obtain
we obtain  . So,
. So,  .
.Case (a) and Case (b) together show that Property (6) holds.
-
For Condition 4c let
 be in
be in 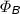 , \(v,w\in W\),
, \(v,w\in W\),  (i.e., \(w\in M[S]\)) and
(i.e., \(w\in M[S]\)) and  . We need to show that there exists a clause \(S':\lnot t_\psi \vee \eta _f(\psi )\) in
. We need to show that there exists a clause \(S':\lnot t_\psi \vee \eta _f(\psi )\) in  with \(v\in M[S']\).
with \(v\in M[S']\).As in the previous case
 implies either \(w\mathbin {R}v\) or \(v\mathbin {R}w\). In the first case
implies either \(w\mathbin {R}v\) or \(v\mathbin {R}w\). In the first case  while in the second case
while in the second case  .
.As
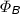 contains Clause (9), \(t_\psi \) occurs at level \(ml+1\) in
contains Clause (9), \(t_\psi \) occurs at level \(ml+1\) in  . By definition of
. By definition of  ,
, 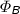 also contains the clause
also contains the clause
 . As \(ml\in S\), \(ml-1\in S^-\) and therefore \(t_\psi \) also occurs at level \(ml-1\) in
. As \(ml\in S\), \(ml-1\in S^-\) and therefore \(t_\psi \) also occurs at level \(ml-1\) in  . By Theorem 2,
. By Theorem 2,  is definition-complete, so there must be a clause \(S':\lnot t_\psi \vee \eta _f(\psi )\) in
is definition-complete, so there must be a clause \(S':\lnot t_\psi \vee \eta _f(\psi )\) in  such that \(ml+1\) and \(ml-1\) in \(S'\).
such that \(ml+1\) and \(ml-1\) in \(S'\).
Theorem 5
Let \(\varphi \) be a modal formula in simplified NNF,
 , and \(\varPhi _L = \{\{ 0 \}: t_\varphi \}\cup \rho _{L}(\{0\}:t_\varphi \rightarrow \varphi )\). Then \(\varphi \) is
, and \(\varPhi _L = \{\{ 0 \}: t_\varphi \}\cup \rho _{L}(\{0\}:t_\varphi \rightarrow \varphi )\). Then \(\varphi \) is
 -satisfiable iff \(\varPhi _{L}\) is
-satisfiable iff \(\varPhi _{L}\) is
 -satisfiable.
-satisfiable.
5 Comparison With Related Work
The approaches most closely related to ours are Kracht’s reductions of normal modal logics to basic modal logic [11, 12], the global modal resolution calculus [14], and Schmidt and Hustadt’s axiomatic translation principle for translations of normal modal logics to first-order logic [24].
The first significant difference to our approach is that Kracht’s reductions and the axiomatic translation exclude the modal operator \(\Diamond \) from the language and only consider the modal operator \(\Box \).
In order to present Kracht’s approach, we need some additional notions. Let  ,
,  , and |S| denote the set of all subformulae of \(\varphi \), the maximum nesting of modal operators in \(\varphi \), and the cardinality of the set S, respectively. Let \(\Diamond ^0\psi =\Box ^0\psi =\Box ^{<1}\psi = \psi \), \(\Box ^{<n+1}\psi = (\psi \wedge \Box \Box ^{<n}\psi )\), \(\Box ^{n+1}\psi =\Box \Box ^n\psi \), and \(\Diamond ^{n+1}\psi =\Diamond \Diamond ^n\psi \). We can then define a reduction function \(\rho ^\mathsf {K}_L\) for a normal modal logic L in
, and |S| denote the set of all subformulae of \(\varphi \), the maximum nesting of modal operators in \(\varphi \), and the cardinality of the set S, respectively. Let \(\Diamond ^0\psi =\Box ^0\psi =\Box ^{<1}\psi = \psi \), \(\Box ^{<n+1}\psi = (\psi \wedge \Box \Box ^{<n}\psi )\), \(\Box ^{n+1}\psi =\Box \Box ^n\psi \), and \(\Diamond ^{n+1}\psi =\Diamond \Diamond ^n\psi \). We can then define a reduction function \(\rho ^\mathsf {K}_L\) for a normal modal logic L in
 as follows:
as follows:

where  Kracht shows that \(\varphi \) is L-satisfiable iff \(\rho ^\mathsf {K}_L(\varphi )\) is \(\mathsf {K}{}{}\)-satisfiable. There are three differences to our approach. First, \(P^\mathsf {K}_L(\varphi )\) will include an axiom instance for every occurrence of a subformula \(\lnot \Box \psi \), equivalent to \(\Diamond \lnot \psi \), in \(\varphi \). In contrast, our approach requires no logic specific treatment of such subformulae. Second, the use of \(\Box ^{<n} P^\mathsf {K}_L(\varphi )\) in \(\rho ^\mathsf {K}_L\) means that the axiom instance is available at every modal level. This means, for example, that for \(\vartheta _1 = \Diamond ^{100}(\lnot p\wedge \Box p)\), the formula
Kracht shows that \(\varphi \) is L-satisfiable iff \(\rho ^\mathsf {K}_L(\varphi )\) is \(\mathsf {K}{}{}\)-satisfiable. There are three differences to our approach. First, \(P^\mathsf {K}_L(\varphi )\) will include an axiom instance for every occurrence of a subformula \(\lnot \Box \psi \), equivalent to \(\Diamond \lnot \psi \), in \(\varphi \). In contrast, our approach requires no logic specific treatment of such subformulae. Second, the use of \(\Box ^{<n} P^\mathsf {K}_L(\varphi )\) in \(\rho ^\mathsf {K}_L\) means that the axiom instance is available at every modal level. This means, for example, that for \(\vartheta _1 = \Diamond ^{100}(\lnot p\wedge \Box p)\), the formula  contains the axiom instance \(\Box p\rightarrow p\) over 100 times, although it is only required at the level at which \(\Box p\) occurs. Third, this is further compounded if the formula \(\psi \) in \(\Box \psi \) is itself a complex formula. We try to avoid that by using a surrogate propositional symbol \(t_\psi \) instead, but this will only have a positive effect if the definitional clauses for \(t_\psi \) do not have to be repeated.
contains the axiom instance \(\Box p\rightarrow p\) over 100 times, although it is only required at the level at which \(\Box p\) occurs. Third, this is further compounded if the formula \(\psi \) in \(\Box \psi \) is itself a complex formula. We try to avoid that by using a surrogate propositional symbol \(t_\psi \) instead, but this will only have a positive effect if the definitional clauses for \(t_\psi \) do not have to be repeated.
 (EUC1 and EUC2).
(EUC1 and EUC2).The global modal resolution (GMR) calculus operates on
 clauses, that is, clauses of the form
clauses, that is, clauses of the form
where l, \(l'\), \(l_b\) are propositional literals with \(1 \le b \le r\), \(r \in \mathbb N\), and \(\Box ^*\) is the universal operator. The calculus has specific inference rules for normal modal logics such as
 ,
,
 ,
,
 ,
,
 ,
,
 . Table 4 shows the two additional rules for
. Table 4 shows the two additional rules for
 , the only logic for which there are rules for both \(\Box \) and \(\lnot \Box \lnot \), i.e., \(\Diamond \). These inference rules can be seen to perform an ‘on-the-fly’ computation of a transformation. Note that the clauses produced by
, the only logic for which there are rules for both \(\Box \) and \(\lnot \Box \lnot \), i.e., \(\Diamond \). These inference rules can be seen to perform an ‘on-the-fly’ computation of a transformation. Note that the clauses produced by  differ from those produced by GMR for
differ from those produced by GMR for
 . Implicitly, our results here also show that it should be possible to eliminate EUC1 from the GMR calculus.
. Implicitly, our results here also show that it should be possible to eliminate EUC1 from the GMR calculus.
For the axiomatic translation, we only present the function \(P^\mathsf {RS}_L\) that computes the logic dependent first-order clausal formulae that are part of the overall translation.

The predicate symbols \(Q_\psi \) correspond to our surrogate symbols \(t_\psi \). The clausal formulae used in the treatment of
 and
and
 are translations of the
are translations of the
 clauses we use (or vice versa).
clauses we use (or vice versa).
 and
and
 are handled in a different way as the first-order clausal formulae refer directly the accessibility relation and can therefore more easily express the transfer of information to a predecessor world. The universal quantification over worlds also means that the constraints expressed by the formulae hold at all modal levels without the need of any repetition.
are handled in a different way as the first-order clausal formulae refer directly the accessibility relation and can therefore more easily express the transfer of information to a predecessor world. The universal quantification over worlds also means that the constraints expressed by the formulae hold at all modal levels without the need of any repetition.
In Section 6 we will also use the relational and semi-functional translation of modal logics to first-order logic combined with structural transformation to clause normal form. In both approaches \(\Box \psi \) is translated as \(\forall x y (\lnot Q_{\Box \psi }(x)\vee \lnot R(x,y)\vee Q_\psi \), while \(\Diamond \psi \) becomes \(\forall x\exists y (\lnot Q_{\Diamond \psi }(x)\vee R(x,y))\) and \(\forall x\exists \alpha (\lnot Q_{\Diamond \psi }(x)\vee R(x,[x\alpha ]))\) in the relational and semi-functional translation, respectively. Then, depending on the modal logics, further formulae representing the semantic properties of the accessibility R are added. For the relational translation these will simply be the formulae in the fourth column of Table 1. The semi-functional translation uses collections of partial accessibility function in addition to the accessibility relation. A predicate \(\mathrm {def}\) is used to represent on which worlds a partial accessibility function is defined. For each modal logic there is then again a background theory consisting of formulae over \(\mathrm {def}\) and R that represents the properties of the underlying accessibility relation which is added to the translation of a formula. For example, for
 the background theory is: \( \forall x y\forall \alpha \beta ((\lnot \mathrm {def}(x)\vee \mathrm {def}(y))\wedge (\lnot \mathrm {def}(\mathrm {w_0})\vee R(\mathrm {w_0},[\mathrm {w_0}\alpha ]))\wedge (\lnot \mathrm {def}(x)\vee \lnot \mathrm {def}(y)\vee R([x\alpha ],[y\beta ]))), \) where \(\mathrm {w_0}\) is a constant representing the root world in a rooted Kripke structure.
the background theory is: \( \forall x y\forall \alpha \beta ((\lnot \mathrm {def}(x)\vee \mathrm {def}(y))\wedge (\lnot \mathrm {def}(\mathrm {w_0})\vee R(\mathrm {w_0},[\mathrm {w_0}\alpha ]))\wedge (\lnot \mathrm {def}(x)\vee \lnot \mathrm {def}(y)\vee R([x\alpha ],[y\beta ]))), \) where \(\mathrm {w_0}\) is a constant representing the root world in a rooted Kripke structure.
6 Evaluation
We have compared the performance of the following approaches: (i) the combination of our reductions with the modal-layered resolution (MLR) calculus for
 clauses [15] implemented in the modal theorem prover
clauses [15] implemented in the modal theorem prover
 , with three different refinements for resolution inferences on labelled propositional clauses (ii) the global modal resolution (GMR) calculus, also implemented in
, with three different refinements for resolution inferences on labelled propositional clauses (ii) the global modal resolution (GMR) calculus, also implemented in
 , with three different refinements for resolution inferences on propositional clauses (iii) the combinations of the relational and semi-functional translation of modal logics to first-order logic with ordered first-order resolution implemented in the first-order theorem prover SPASS. In total this gives us eight different approaches to compare. The axiomatic translation is currently not implemented in SPASS. Other provers, such as LEO-III [26], LWB [9], MleanCoP [21], do not have built-in support for the full range of logics considered here. LoTREC 2.0 [7] supports all the logics, but is not intended as automatic theorem prover.
, with three different refinements for resolution inferences on propositional clauses (iii) the combinations of the relational and semi-functional translation of modal logics to first-order logic with ordered first-order resolution implemented in the first-order theorem prover SPASS. In total this gives us eight different approaches to compare. The axiomatic translation is currently not implemented in SPASS. Other provers, such as LEO-III [26], LWB [9], MleanCoP [21], do not have built-in support for the full range of logics considered here. LoTREC 2.0 [7] supports all the logics, but is not intended as automatic theorem prover.
The modal-layered resolution calculus operates on
 clauses, that is, clauses of the form
clauses, that is, clauses of the form
where  and l, \(l'\), \(l_b\) are propositional literals with \(1 \le b \le r\), \(r \in \mathbb N\). In the implementation of the reductions presented in Section 3, we take a
and l, \(l'\), \(l_b\) are propositional literals with \(1 \le b \le r\), \(r \in \mathbb N\). In the implementation of the reductions presented in Section 3, we take a
 clause \(S:\psi \) simply as an abbreviation of the set of
clause \(S:\psi \) simply as an abbreviation of the set of
 clauses \(\{ml:\psi \mid ml\in S\}\). Note that this also means that we will have to repeat similar resolution inferences for different modal levels.
clauses \(\{ml:\psi \mid ml\in S\}\). Note that this also means that we will have to repeat similar resolution inferences for different modal levels.
 [13] implements the reductions presented in Section 3 as well as a normal form transformation of modal formulae to sets of
[13] implements the reductions presented in Section 3 as well as a normal form transformation of modal formulae to sets of
 clauses. It implements both the MLR and the GMR calculus. Resolution inferences between (labelled) propositional clauses can either be unrestricted (cplain option), restricted by an ordering (cord option), that is, clauses can only be resolved on their maximal literals with respect to an ordering chosen by the prover in such a way to preserve completeness, restricted to negative resolution (cneg option), that is, one of the premises in an inference has to be a negative clause, or restricted to positive resolution. We do not include the last option in our evaluation as it typically performs worse.
clauses. It implements both the MLR and the GMR calculus. Resolution inferences between (labelled) propositional clauses can either be unrestricted (cplain option), restricted by an ordering (cord option), that is, clauses can only be resolved on their maximal literals with respect to an ordering chosen by the prover in such a way to preserve completeness, restricted to negative resolution (cneg option), that is, one of the premises in an inference has to be a negative clause, or restricted to positive resolution. We do not include the last option in our evaluation as it typically performs worse.
 also implements a range of simplification rules that are applied to modal formulae before their transformation to normal form. Of those we have enabled pure literal elimination (early_ple option), simplification using the Box Normal Form [22] and Prenex Normal Form (bnfsimp and prenex options) [17]. For clause processing, unit resolution and pure elimination are enabled (unit, lhs_unit, and ple options).
also implements a range of simplification rules that are applied to modal formulae before their transformation to normal form. Of those we have enabled pure literal elimination (early_ple option), simplification using the Box Normal Form [22] and Prenex Normal Form (bnfsimp and prenex options) [17]. For clause processing, unit resolution and pure elimination are enabled (unit, lhs_unit, and ple options).
SPASS 3.9 [27, 28] supports automated reasoning in extended modal logics, including all logics considered here, PDL-like modal logics as well as description logics. It includes eight different translations of modal logics to first-order logic. In our evaluation we have used the relational translation and the semi-functional translation. For the local satisfiability problem in
 to
to
 , for the relational translation we have added the first-order frame properties given in Table 1 while for the semi-functional translation we have added the background theories devised by Nonnengart [20]. For the transformation to first-order clausal form, we have enabled renaming of quantified subformulae. The only inference rules used are ordered resolution and ordered factoring, the reduction rules used are condensing, backward subsumption and forward subsumption. For the relational and semi-functional translation for
, for the relational translation we have added the first-order frame properties given in Table 1 while for the semi-functional translation we have added the background theories devised by Nonnengart [20]. For the transformation to first-order clausal form, we have enabled renaming of quantified subformulae. The only inference rules used are ordered resolution and ordered factoring, the reduction rules used are condensing, backward subsumption and forward subsumption. For the relational and semi-functional translation for
 ,
,
 ,
,
 , and
, and
 we thereby obtain a decision procedure, while for the other logics we do not. For
we thereby obtain a decision procedure, while for the other logics we do not. For
 and
and
 , the fragment of first-order clausal logic corresponding to the semi-functional translation of modal formula and their background theories is decidable by ordered resolution with selection [25]. However, the non-trivial ordering and selection function required is not currently implemented in SPASS.
, the fragment of first-order clausal logic corresponding to the semi-functional translation of modal formula and their background theories is decidable by ordered resolution with selection [25]. However, the non-trivial ordering and selection function required is not currently implemented in SPASS.
For our evaluation we have chosen the LWB basic modal logic benchmark collection [2], with 20 formulae in each of 18 parameterised classes. For
 , all formulae in 9 classes are satisfiable while all formulae in the other 9 classes are unsatisfiable. In their negation normal form, 63% of modal operators are \(\Box \) and 37% are \(\Diamond \) operators. We have used the collection for each of the six logics. If a formula is unsatisfiable in
, all formulae in 9 classes are satisfiable while all formulae in the other 9 classes are unsatisfiable. In their negation normal form, 63% of modal operators are \(\Box \) and 37% are \(\Diamond \) operators. We have used the collection for each of the six logics. If a formula is unsatisfiable in
 then it remains unsatisfiable in the other five logics, while the opposite is not true. As we move to logics other than
then it remains unsatisfiable in the other five logics, while the opposite is not true. As we move to logics other than
 , it is also no longer the case that all formulae in a class have the same satisfiability status.
, it is also no longer the case that all formulae in a class have the same satisfiability status.
The third column in Table 5 indicates the total number of satisfiable and unsatisfiable formulae for each logic. In the last two lines of the table we sum up the results for all logics. The last eight columns in the table show how many formulae each of the approaches were able to solve with a time limit of 100 CPU seconds for each formula. Benchmarking was performed on a PC with an AMD Ryzen 5 5600X CPU @ 4.60GHz max and 32GB main memory using Fedora release 33 as operating system.
As we can see, the new reductions combined with the modal-layered resolution (MLR) calculus and ordered resolution refinement (cord) perform best, achieving the highest number of solved formulae in 8 out of 12 individual categories in the table, on two of those equal with the global modal resolution (GMR) calculus. On 3 categories, GMR outperfoms MLR. On both satisfiable and unsatisfiable formulae in
 this can be seen as evidence that ‘on-the-fly’ transformation offers a (slight) advantage over our approach given that the additional clauses hold universally in both approaches. For SPASS we see a clear advantage of the semi-functional translation over the relational one, on both satisfiable and unsatisfiable formulae.
this can be seen as evidence that ‘on-the-fly’ transformation offers a (slight) advantage over our approach given that the additional clauses hold universally in both approaches. For SPASS we see a clear advantage of the semi-functional translation over the relational one, on both satisfiable and unsatisfiable formulae.
7 Conclusion and Future Work
We have presented new reductions of propositional modal logics
 ,
,
 ,
,
 ,
,
 ,
,
 to Separated Normal Form with Sets of Modal Levels. We have shown experimentally that these reductions allow us to reason effectively in these logics.
to Separated Normal Form with Sets of Modal Levels. We have shown experimentally that these reductions allow us to reason effectively in these logics.
The obvious next step is to consider extensions of the basic modal logic
 with combinations of the axioms \(\mathsf {B}\), \(\mathsf {D}\), \(\mathsf {T}\), \(\mathsf {4}\), and \(\mathsf {5}\). Unfortunately, a simple combination of the reductions for each of the axioms is not sufficient to obtain a satisfiability-preserving reduction for the such modal logics. An example is the simple formula \(\lnot p\wedge \Diamond \Diamond \Box p\) which is
with combinations of the axioms \(\mathsf {B}\), \(\mathsf {D}\), \(\mathsf {T}\), \(\mathsf {4}\), and \(\mathsf {5}\). Unfortunately, a simple combination of the reductions for each of the axioms is not sufficient to obtain a satisfiability-preserving reduction for the such modal logics. An example is the simple formula \(\lnot p\wedge \Diamond \Diamond \Box p\) which is
 -unsatisfiable. If we define
-unsatisfiable. If we define

that is,  is the union of
is the union of  and
and  , then the clause set obtained from
, then the clause set obtained from  is
is
 -satisfiable. The same issue also occurs in the axiomatic translation of modal logics to first-order logic where the translation for
-satisfiable. The same issue also occurs in the axiomatic translation of modal logics to first-order logic where the translation for
 is not simply the combination of the translations for
is not simply the combination of the translations for
 and
and
 [24, Theorem 5.6]. We are currently exploring solutions to this problem.
[24, Theorem 5.6]. We are currently exploring solutions to this problem.
Regarding practical applications, it would be advantageous to have an implementation of a calculus that operates directly
 clauses. This would greatly reduce the number of
clauses. This would greatly reduce the number of
 performed on satisfiable formulae and simplify proof search in general. Again, such an implementation is future work.
performed on satisfiable formulae and simplify proof search in general. Again, such an implementation is future work.
References
Balbiani, P., Demri, S.: Prefixed tableaux systems for modal logics with enriched languages. In: IJCAI 1997. pp. 190–195. Morgan Kaufmann (1997)
Balsiger, P., Heuerding, A., Schwendimann, S.: A benchmark method for the propositional modal logics K, KT, S4. J. Autom. Reasoning 24(3), 297–317 (2000)
Basin, D., Matthews, S., Vigano, L.: Labelled propositional modal logics: Theory and practice. J. Log. Comput. 7(6), 685–717 (1997)
Benzmüller, C., Paulson, L.C.: Multimodal and intuitionistic logics in simple type theory. Log. J. IGPL 18(6), 881–892 (2010)
Fitting, M.: Prefixed tableaus and nested sequents. Ann. Pure Appl. Log. 163(3), 291–313 (2012)
Gabbay, D.M.: Decidability results in non-classical logics: Part I. Ann. Math. Log. 8, 237–295 (1975)
Gasquet, O., Herzig, A., Longin, D., Sahade, M.: LoTREC: Logical tableaux research engineering companion. In: TABLEAUX 2005. LNCS, vol. 3702, pp. 318–322. Springer (2005). https://doi.org/10.1007/11554554_25
Halpern, J.Y., Moses, Y.: A guide to completeness and complexity for modal logics of knowledge and belief. Artif. Intell. 54(3), 319–379 (1992)
Heuerding, A., Jäger, G., Schwendimann, S., Seyfried, M.: The Logics Workbench LWB: A snapshot. Euromath Bulletin 2(1), 177–186 (1996)
Horrocks, I., Hustadt, U., Sattler, U., Schmidt, R.A.: Computational modal logic. In: Blackburn, P., van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic, chap. 4, pp. 181–245. Elsevier (2006)
Kracht, M.: Reducing modal consequence relations. J. Log. Comput. 11(6), 879–907 (2001)
Kracht, M.: Notes on the space requirements for checking satisfiability in modal logics. In: Advances in Modal Logic 4, pp. 243–264. King’s College Publications (2003)
Nalon, C.: KSB (2021), https://cic.unb.br/~nalon/#software
Nalon, C., Dixon, C.: Clausal resolution for normal modal logics. J. Algorithms 62, 117–134 (2007)
Nalon, C., Dixon, C., Hustadt, U.: Modal resolution: Proofs, layers, and refinements. ACM Trans. Comput. Log. 20(4), 23:1–23:38 (2019)
Nalon, C., Hustadt, U., Dixon, C.: A modal-layered resolution calculus for K. In: TABLEAUX 2015. LNCS, vol. 9323, pp. 185–200. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-319-24312-2_13
Nalon, C., Hustadt, U., Dixon, C.: KSP: A resolution-based prover for multimodal K. In: IJCAR 2016. LNCS, vol. 9706, pp. 406–415. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-319-40229-1_28
Nalon, C., Hustadt, U., Dixon, C.: KSP: Architecture, refinements,strategies and experiments. J. Autom. Reason. 64(3), 461–484(2020)
Nguyen, L.A., Szalas, A.: Exptime tableau decision procedures for regular grammar logics with converse. Studia Logica 98(3), 387–428 (2011)
Ohlbach, H.J., Nonnengart, A., de Rijke, M., Gabbay, D.M.: Encoding two-valued nonclassical logics in classical logic. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, chap. 21, pp. 1403–1485. Elsevier (2001)
Otten, J.: MleanCoP: A connection prover for first-order modal logic. In: IJCAR 2014. LNCS, vol. 8562, pp. 269–276. Springer (2014). https://doi.org/10.1007/978-3-319-08587-6_20
Pan, G., Sattler, U., Vardi, M.Y.: BDD-based decision procedures for the modal logic K. J. Appl. Non-Class. Log. 16(1–2), 169–208 (2006)
Schmidt, R.A.: Decidability by resolution for propositional modal logics. J. Autom. Reasoning 22(4), 379–396 (1999)
Schmidt, R.A., Hustadt, U.: The axiomatic translation principle for modal logic. ACM Trans. Comput. Log. 8(4), 19 (2007)
Schmidt, R.A., Hustadt, U.: First-order resolution methods for modal logics. In: Programming Logics: Essays in Memory of Harald Ganzinger. LNCS, vol. 7797, pp. 345–391. Springer (2013). https://doi.org/10.1007/978-3-642-37651-1_15
Steen, A., Benzmüller, C.: The higher-order prover Leo-III. In: ECAI 2020. Frontiers in Artificial Intelligence and Applications, vol. 325, pp. 2937–2938. IOS Press (2020). https://doi.org/10.3233/FAIA200462
The SPASS Team: Spass 3.9 (2016), http://www.spass-prover.org/
Weidenbach, C.: Combining superposition, sorts and splitting. In: Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning, pp. 1965–2013. Elsevier and MIT Press (2001)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Papacchini, F., Nalon, C., Hustadt, U., Dixon, C. (2021). Efficient Local Reductions to Basic Modal Logic. In: Platzer, A., Sutcliffe, G. (eds) Automated Deduction – CADE 28. CADE 2021. Lecture Notes in Computer Science(), vol 12699. Springer, Cham. https://doi.org/10.1007/978-3-030-79876-5_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-79876-5_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79875-8
Online ISBN: 978-3-030-79876-5
eBook Packages: Computer ScienceComputer Science (R0)




 for every propositional symbol
for every propositional symbol  .
. for every propositional symbol
for every propositional symbol  , and
, and .
. for every propositional symbol
for every propositional symbol  ,
, for every surrogate
for every surrogate  introduced by rewriting, and
introduced by rewriting, and for every supplementary propositional symbol
for every supplementary propositional symbol  with
with  . Clearly,
. Clearly,  . Also, by definition of
. Also, by definition of  ,
,  . So, for every
. So, for every  . As
. As  . Thus,
. Thus,  and, by the semantics of implication,
and, by the semantics of implication,  .
. with
with  . Clearly, by the semantics of implication,
. Clearly, by the semantics of implication,  . Also, by definition of
. Also, by definition of  which in turn implies
which in turn implies  . So, there exists
. So, there exists  . Since
. Since  is a p-morphism from
is a p-morphism from  to M,
to M,  . Since
. Since  and by construction of
and by construction of  , for
, for  we have
we have  ,
,  . As
. As  is a p-morphism and
is a p-morphism and  and since
and since  ,
,  . By Lemma
. By Lemma  we obtain
we obtain  . If
. If  , by definition of
, by definition of  ,
,  and
and  . So,
. So,  is the symmetric closure of
is the symmetric closure of  is the smallest relation on
is the smallest relation on  and for every
and for every  implies
implies  ;
; for every propositional symbol.
for every propositional symbol. .
. be a modal clause in
be a modal clause in  . Then
. Then  also contains the additional clauses
also contains the additional clauses
 and
and
 . Let
. Let 
 . Assume
. Assume  . As
. As  this implies
this implies  .
. we obtain
we obtain  . So,
. So,  .
. was introduced by the symmetric closure operation on
was introduced by the symmetric closure operation on  and
and
 . From
. From  we obtain
we obtain  . So,
. So,  .
. be in
be in 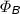 ,
,  (i.e.,
(i.e.,  . We need to show that there exists a clause
. We need to show that there exists a clause  with
with  implies either
implies either  while in the second case
while in the second case  .
.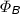 contains Clause (
contains Clause ( . By definition of
. By definition of  ,
, 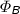 also contains the clause
also contains the clause
 . As
. As  . By Theorem
. By Theorem  is definition-complete, so there must be a clause
is definition-complete, so there must be a clause  such that
such that