Abstract
We are interested in widening the reasoning support for propositional modal logics in the so-called modal cube. The modal cube consists of extensions of the basic modal logic \(\textsf{K}_{}\) with an arbitrary combination of the modal axioms \(\textsf{B}\), \(\textsf{D}\), \(\textsf{T}\), \(\textsf{4}\) and \(\textsf{5}\). We revisit recently developed local reductions from all logics in the modal cube to a normal form comprising sets of clausal formulae with associated modal levels. We extend these reductions further to the basic modal logic \(\textsf{K}_{}\), called definitional reductions. This enables any prover for \(\textsf{K}_{}\) to be used to solve the satisfiability problem for all logics in the modal cube. We also present alternative, axiomatic, reductions based on ideas originally proposed by Kracht, providing new theoretical results and improved bounds on the size of the reductions. We compare both sets of reductions combined with state-of-the-art provers for \(\textsf{K}_{}\) on a large set of parametric benchmarks for all logics in the modal cube. The results show that the provers perform better with reductions based on the clausal normal form than the axiomatic reductions.
C. Nalon was partially supported by FAPDF 11/2021, DPG/UnB 004/2022. C. Dixon was partially supported by the EPSRC funded RAI Hubs FAIR-SPACE (EP/R026092/1) and RAIN (EP/R026084/1), and the EPSRC funded programme Grant S4 (EP/N007565/1).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Following [4], modal logics can be seen as simple but expressive languages for talking about relational structures that provide an internal and local perspective on those structures. The most intensively studied modal logics are the basic modal logic \(\textsf{K}_{}\) and its extensions with one or more of the axioms \(\textsf{B}\) (symmetry), \(\textsf{D}\) (seriality), \(\textsf{T}\) (reflexivity), \(\textsf{4}\) (transitivity) and \(\textsf{5}\) (Euclideaness), that form the so-called modal cube. There are numerous reasons for this. To name just three: (i) relations which are serial, symmetric, transitive, etc. are very common; (ii) the logics in the modal cube can be used to represent and reason about idealised mental attitudes such as knowledge, belief, desire and intention; (iii) mathematical techniques, algorithms, calculi, as well as implemented reasoning tools for these logics provide building blocks for the study and application of more complex modal logics.
In [27], we have presented a reduction from each of the 15 distinct logics in the modal cube to Separated Normal Form with Sets of Modal Levels, \(\textsf{SNF}_{sml}\), a clausal normal form for basic modal logic in which clauses are labelled with possibly infinite sets of modal levels, and to Separated Normal Form with Modal Levels, \(\textsf{SNF}_{ml}\), where each clause is given a natural number label. The latter reduction then allowed us to use the modal-layered clausal resolution (MLR) calculus [22], implemented in the modal logic theorem prover
 [19, 26] to reason in these logics. We evaluated this approach on a new collection of benchmark formulae for all 15 logics and compared its performance with that of the global modal resolution (GMR) calculus also implemented in
[19, 26] to reason in these logics. We evaluated this approach on a new collection of benchmark formulae for all 15 logics and compared its performance with that of the global modal resolution (GMR) calculus also implemented in
 and with Leo-III, an automated theorem prover for polymorphic higher-order logic [32]. The GMR calculus has specific rules for each logic while Leo-III reasons about modal logics using a translation approach and has translations for each of the 15 logics built in. The evaluation showed that the approach performs better than Leo-III but not as well as the GMR calculus in
and with Leo-III, an automated theorem prover for polymorphic higher-order logic [32]. The GMR calculus has specific rules for each logic while Leo-III reasons about modal logics using a translation approach and has translations for each of the 15 logics built in. The evaluation showed that the approach performs better than Leo-III but not as well as the GMR calculus in
 . We identified the reduction from \(\textsf{SNF}_{sml}\) to \(\textsf{SNF}_{ml}\) as the main contributing factor, in particular, on satisfiable formulae where the MLR calculus has to fully saturate the corresponding set of \(\textsf{SNF}_{ml}\) clauses up to redundancy before it can conclude that the original formula is satisfiable.
. We identified the reduction from \(\textsf{SNF}_{sml}\) to \(\textsf{SNF}_{ml}\) as the main contributing factor, in particular, on satisfiable formulae where the MLR calculus has to fully saturate the corresponding set of \(\textsf{SNF}_{ml}\) clauses up to redundancy before it can conclude that the original formula is satisfiable.
In this paper, we investigate and evaluate an alternative use of our reductions from logics in the modal cube to \(\textsf{SNF}_{ml}\). A finite set of clauses in \(\textsf{SNF}_{ml}\) can straightforwardly be transformed into a formula in the basic modal logic \(\textsf{K}_{}\). Such a transformation then allows the use of any existing approach to solving the satisfiability problem in \(\textsf{K}_{}\) to the satisfiability problem in all logics in the modal cube. An advantage of the use of this transformation over a translation from each of the 15 logics to first-order (or higher-order) logic [1, 5, 9, 14] is the availability of implemented decision procedures for basic modal logic. In contrast, while many decidable fragments of first-order logics are known, including decidable fragments that are suitable targets of translations of modal logic formulae, implemented decision procedures for these fragments are rare. See also related discussions in [27, 30].
The original motivation for our work on reductions to \(\textsf{SNF}_{sml}\) and \(\textsf{SNF}_{ml}\) were Kracht’s reductions of the normal modal logics \(\textsf{KB}_{}\), \(\textsf{KD}_{}\), \(\textsf{KT}_{}\), and \(\textsf{K4}_{}\) to \(\textsf{K}_{}\) [17, 18]. Extending our reduction from \(\textsf{SNF}_{ml}\) to \(\textsf{K}_{}\) to obtain a reduction from the modal cube to \(\textsf{K}_{}\) raises first the question whether one can devise a reduction based on the same idea as Kracht’s for the remaining logics of the modal cube. We will call such a reduction axiomatic as the idea is to use certain instances of axiom schemata embedded into modal contexts of nested \(\Box \)-operators up to a certain depth bound. We answer this question positively by providing the reductions missing in Kracht’s work. The second question then raised is how well provers for \(\textsf{K}_{}\) perform on our reduction compared to an axiomatic reduction. Our empirical evaluation indicates that the definitional reduction appears to result in better performance overall when combined with state-of-the-art \(\textsf{K}_{}\) provers.
The structure of the paper is as follows. In Sect. 2 we recall common concepts of propositional modal logics and the definition of our normal form \(\textsf{SNF}_{ml}\). Section 3 recalls our reduction from logics in the modal cube to \(\textsf{SNF}_{ml}\), defines the transformation of a finite set of \(\textsf{SNF}_{ml}\) clauses to basic modal, and introduces the axiomatic reduction for the logics in the modal cube. In Sect. 4 we compare the performance of a combination of the reductions defined in Sect. 3 when combined with provers for basic modal logic as well as with the global resolution calculus for logics in the modal cube implemented in
 .
.
2 Preliminaries
The language of modal logic is an extension of the language of propositional logic with unary modal operators \(\Box \) and \(\Diamond \). More precisely, given a denumerable set of propositional symbols, \(P= \{p, p_0, q, q_0, t, t_0,\ldots \}\) as well as propositional constants \(\textbf{true}\) and \(\textbf{false}\), modal formulae are inductively defined as follows: constants and propositional symbols are modal formulae. If \(\varphi \) and \(\psi \) are modal formulae, then so are \(\lnot \varphi \), \((\varphi \wedge \psi )\), \((\varphi \vee \psi )\), \((\varphi \rightarrow \psi )\), \(\Box \varphi \), and \(\Diamond \varphi \). We also assume that \(\wedge \), and \(\vee \) are associative and commutative operators and consider, e.g., \((p\vee (q\vee r))\) and \((r\vee (q\vee p))\) to be identical formulae. We often omit parentheses if this does not cause confusion. The size of \(\varphi \) is the number of occurrences of propositional constants, propositional variable, boolean operators and modal operators in \(\varphi \). By \(\textsf{var}(\varphi )\) we denote the set of all propositional symbols occurring in \(\varphi \). This function easily extends to finite sets of modal formulae. A modal axiom (schema) is a modal formula \(\psi \) representing the set of all instances of \(\psi \).
A literal is either a propositional symbol or its negation; the set of literals is denoted by \(L_{P}\). By \(\lnot l\) we denote the complement of the literal \(l\in L_{P}\), that is, if l is the propositional symbol p then \(\lnot l\) denotes \(\lnot p\), and if l is the literal \(\lnot p\) then \(\lnot l\) denotes p. By |l| for \(l\in L_{P}\) we denote p if \(l = p\) or \(l = \lnot p\). A modal literal is either \(\Box l\) or \(\Diamond l\), where \(l \in L_{P}\).
An occurrence of a subformula has positive polarity if it is inside the scope of an even number of (explicit or implicit) negations, and it has negative polarity if it is one inside the scope of an odd number of negations. A literal is pure if all its occurrences have either a positive or a negative polarity.
The modal logic \(\textsf{K}_{}\) is given by the smallest set of modal formulae which includes all propositional tautologies, the axiom schema \(\Box {(\varphi \rightarrow \psi )} \rightarrow (\Box {\varphi } \rightarrow \Box {\psi })\), is closed under modus ponens and the rule of necessitation (if \(\varphi \in \textsf{K}_{}{}\) then \(\Box {\varphi }\in \textsf{K}_{}{}\)). Given a modal logic L and set of axioms \(\varSigma \), the smallest modal logic \(L' \supset L\cup \varSigma \) is an extension of L and we denote \(L'\) by \(L\varSigma \).
The standard semantics of modal logics is the Kripke semantics or possible world semantics. A Kripke frame \(F\) is an ordered pair \(\langle W, R \rangle \) where \(W\) is a non-empty set of worlds and \(R\) is a binary (accessibility) relation over \(W\). A Kripke structure \(M\) over \(P\) is an ordered pair \(\langle F,V \rangle \) where \(F\) is a Kripke frame and the valuation V is a function mapping each propositional symbol in \(P\) to a subset V(p) of \(W\). A rooted Kripke structure is an ordered pair \(\langle M,w_0 \rangle \) with \(w_0\in W\).
Satisfaction (or truth) of a formula at a world \(w\) of a Kripke structure \(M= \langle W, R, V \rangle \) is inductively defined by:

If \(\langle M, w \rangle \models \varphi \) then we say that \(\varphi \) is true at \(w\) in \(M\). A rooted Kripke structure \(M = \langle M,w_0 \rangle \) is a model of a modal formula \(\varphi \) iff \(\langle M, w_0 \rangle \models \varphi \) and \(M\) satisfies \(\varphi \). A modal formula is satisfiable iff there exists a Kripke structure \(M\) and a world \(w\in M\) such that \(\langle M, w \rangle \models \varphi \). A rooted Kripke structure \(M = \langle W,R,V,w_0 \rangle \) is a rooted tree Kripke structure iff R is a tree, that is, a directed acyclic connected graph where each node has at most one predecessor, with root \(w_0\).
A path from \(w'_0\) to \(w'_k\) of length k, \(k\ge 0\), in a frame \(F = \langle W,R \rangle \) is a sequence \((w'_0,w'_1,\ldots ,w'_k)\) where for every i, \(0\le i\le k-1\), \(w'_{i}\mathbin {R}w'_{i+1}\). A path \((w'_0)\) of length 0 is identified with its root \(w'_0\). In a rooted tree Kripke structure \(M\) with root \(w_0\) for every world \(w_k\in W\) there is exactly one path connecting \(w_0\) and \(w_k\); the modal level (in \(M\)), denoted by \(\textsf{ml}_{M}(w_k)\), is given by the length of the path from \(w_0\) to \(w_k\). More generally, for a rooted Kripke structure \(M\) with root \(w_0\), the depth of a world \(w_k\) (in \(M\)), denoted by \(\textsf{depth}_{M}(w_k)\), is the length of the shortest path from \(w_0\) to \(w_k\). The depth of \(M\) is the maximal depth of a world in \(M\). The outdegree of a world \(w\) in F is given by \(|\{w'\mid w\mathbin {R}w'\}|\).
The 15 logics in the modal cube consist of \(\textsf{K}_{}\) itself and its extensions with one or more of the modal axioms shown in Table 1. Each of these axioms defines a class of Kripke frames where the accessibility relation \(R\) satisfies the first-order property stated in the table. Combinations \(\varSigma \) of axioms then define a class \(\mathfrak {F}_\varSigma \) of Kripke frames where the accessibility relation satisfies the combination of their corresponding properties. Given a logic \(L = \textsf{K}_{}{}\!\varSigma \), a modal formula \(\varphi \) is L-satisfiable iff there exists a frame \(F\in \mathfrak {F}_\varSigma \), a valuation V and a world \(w\in F\) such that \(M = \langle F,V,w \rangle \models \varphi \) and we call \(M\) an L-model of \(\varphi \).
A modal formula is in simplified NNF (denoted by \(\textsf{nnf}(\varphi )\)), if it has been simplified by exhaustively applying the rewrite rules in Table 2, and it is in Negation Normal Form (NNF), that is, a formula where only propositional symbols are allowed in the scope of negations.
The reductions given in the next section produce formulae in a clausal normal form, called Separated Normal Form with Sets of Modal Levels \(\textsf{SNF}_{sml}\), given in [29]. The language of \(\textsf{SNF}_{sml}\) extends that of the basic modal logic \(\textsf{K}_{}\) with sets of modal levels as labels. Clauses in \(\textsf{SNF}_{sml}\) have one of the following forms:

where \(S\subseteq \mathbb {N}\) and l, \(l'\), \(l_i\) are propositional literals with \(1 \le i \le n\), \(n \in \mathbb {N}\). We write \({{\,\mathrm{{\star }}\,}}: \varphi \) instead of \(\mathbb {N}:\varphi \) and such clauses are called global clauses. Positive and negative modal clauses are together known as modal clauses.
Given a rooted tree Kripke structure M and a set S of natural numbers, by M[S] we denote the set of worlds that are at a modal level in S, that is, \(M[S] = \{w\in W\mid \textsf{ml}_{M}(w)\in S\}\). Then
The use of sets as labels allows a concise representation of clauses that might hold in a possibly infinite number of levels.
If \(M\models S: \varphi \), then we say that \(S: \varphi \) holds in \(M\) or is true in \(M\). For a set \(\varPhi \) of labelled formulae, \(M\models \varPhi \) iff \(M\models S:\varphi \) for every \(S:\varphi \) in \(\varPhi \), and we say \(\varPhi \) is K-satisfiable.
We introduce some notation that will be used in the following. For \(m,n\in \mathbb {N}\), \(m\le n\), let \([m.\, .n] = \{m,\ldots ,n\}\subseteq \mathbb {N}\). Let \(S^+= \{l + 1\in \mathbb {N}\mid l \in S\}\), \(S^- = \{ l - 1 \in \mathbb {N}\mid l \in S\}\), and \(S^\ge = \{ln \in \mathbb {N}\mid n \ge \min (S)\ge l\}\), where \(\min (S)\) is the least element in S. Note that the restriction of the elements being in \(\mathbb {N}\) implies that \(S^-\) cannot contain negative numbers.
A formula is in Separated Normal Form with Modal Levels (\(\textsf{SNF}_{ml}\)) [22, 23], if it is a conjunction of clauses in on of the following forms:

where \(ml \in \mathbb {N}\cup \{{{\,\mathrm{{\star }}\,}}\} \) and l, \(l'\), \(l_i\) are propositional literals with \(1 \le i \le n\), \(n \in \mathbb {N}\). Effectively, this normal form corresponds to a restriction on the \(\textsf{SNF}_{sml}\) where the sets are singletons or \({{\,\mathrm{{\star }}\,}}\), representing all levels.
3 Reductions
3.1 Definitional Reduction
In [27] we introduced a reduction \(\rho ^{ sml }_{L}(\varphi )\) that for any modal logic \(L = \textsf{K}_{}{}\mathrm {{\varSigma }}\) with \(\mathrm {{\varSigma }}\subseteq \{\textsf{B},\textsf{D},\textsf{T}, \textsf{4},\textsf{5}\}\), transforms a modal formula \(\varphi \) in simplified NNF to a finite set \(\varPhi ^{sml}_L\) of clauses in \(\textsf{SNF}_{sml}\) such that \(\varphi \) is L-satisfiable iff \(\varPhi ^{sml}_L\) is \(\textsf{K}_{}{}\)-satisfiable. For \(\textsf{K4}_{}\), \(\textsf{K5}_{}\) and their extensions by further axioms, \(\rho ^{ sml }_{L}\) produces sets of clauses where the labelling sets S are potentially infinite. However, depending on syntactic properties of \(\varphi \) it is possible to impose upper bounds on the maximal modal level that occurs in those sets so that the reduction remains satisfiability preserving. Table 3 shows such a bound for each logic in the modal cube. In the table and in the following, for a modal formula \(\varphi \) in simplified NNF, (i) \(d^\varphi _m\) is the modal depth of \(\varphi \), (ii) \(d^\varphi _\Diamond \) is the maximal nesting of \(\Diamond \)-operators not in the scope of any \(\Box \) operators in \(\varphi \), (iii) \(n^\varphi _\Box \) is the number of \(\Box \)-subformulae in \(\varphi \), and (iv) \(n^\varphi _\Diamond \) is the number of \(\Diamond \)-subformulae below \(\Box \)-operators in \(\varphi \). Using these bounds it is then possible to define a function \(\rho ^{ ml }_{L}\) that transforms a modal formula \(\varphi \) in simplified NNF to a finite set \(\varPhi ^{ml}_L\) of clauses in \(\textsf{SNF}_{ml}\) such that \(\varphi \) is L-satisfiable iff \(\varPhi ^{ml}_L\) is \(\textsf{K}_{}{}\)-satisfiable.
Table 4 shows the definitions of modified reductions \(\bar{\rho }^{ sml }_L\) and \(\bar{\rho }^{ ml }_L\) to \(\textsf{SNF}_{sml}\) and \(\textsf{SNF}_{ml}\), respectively. In contrast to \(\rho ^{ sml }_{L}\), \(\bar{\rho }^{ sml }_L\) already uses the bounds in Table 3 to ensure that all labelling sets S occurring in the reduction of a modal formula remain finite. The function \(\bar{\rho }^{ml}_L\) then does not enforce further restrictions, but straightforwardly transforms a finite set of \(\textsf{SNF}_{sml}\)-clauses with finite labelling sets into a finite set of \(\textsf{SNF}_{ml}\) clauses. This presentation of the reduction of modal formulae to a finite set of clauses in \(\textsf{SNF}_{ml}\) is closer to the implementation of the process in the prover
 .
.
Given a finite set \(\varPhi \) of clauses in \(\textsf{SNF}_{ml}\) we can use a function \(\tau ^\textsf{f}\) to obtain an equivalent modal formula as follows:
where \(\Box ^0\psi = \psi \) and \(\Box ^{n+1}\psi =\Box \Box ^n\psi \).
A smaller equivalent formula can be constructed as follows. For a finite set \(\varPhi \) of clauses in \(\textsf{SNF}_{ml}\) let \(\varPhi [ml] = \{C\;|\; ml:C\in \varPhi \}\) and \(ml_{max} = \max \{ml\;|\; ml:C\in \varPhi \}\). Then
Combining \(\bar{\rho }^{ml}_L\) and \(\tau ^\textsf{n}\) we can define a reduction \(\rho ^{ def }_{L}\) as
which we call the definitional reduction of \(\varphi \) for the modal logic L.
Theorem 1
([30]). Let \(L = \textsf{K}_{}{}\!\varSigma \) with \(\varSigma \subseteq \{\textsf{B},\textsf{D},\textsf{T},\textsf{4}{}{},\textsf{5}\}\) and \(\varphi \) be a modal formula in simplified NNF. Then \(\varphi \) is L-satisfiable iff \(\rho ^{ def }_{L}(\varphi )\) is \(\textsf{K}_{}{}\)-satisfiable.
This reduction allows us to use any reasoner for the basic modal logic \(\textsf{K}_{}{}\) as a reasoner for all the logics in the modal cube.
3.2 Axiomatic Reduction
The reductions \(\rho ^{ sml }_{L}\) and \(\rho ^{ ml }_{L}\) in [27] were developed as an alternative to and improvement on reductions from the modal logics \(\textsf{KB}_{}{}\), \(\textsf{KD}_{}{}\), \(\textsf{KT}_{}{}\), and \(\textsf{K4}_{}{}\) to \(\textsf{K}_{}{}\) introduced by Kracht [18]. In contrast to \(\rho ^{ sml }_{L}\) and \(\rho ^{ ml }_{L}\) which require modal formulae to be in NNF and treat the modal operators \(\Box \) and \(\Diamond \) differently, Kracht’s reductions assumes that (i) modal formulae are not necessarily in NNF and (ii) the only modal operator occurring in modal formulae is \(\Box \) and no distinction is made between positive and negative occurrences of this operator. In the following we extend Kracht’s reduction to all logics in the modal cube while adhering to those two assumptions.
Let
 and
and
 . We can then define a reduction \(\rho ^{ax}_{L}\) for all modal logics L in the modal cube as follows:
. We can then define a reduction \(\rho ^{ax}_{L}\) for all modal logics L in the modal cube as follows:

where \(b^{ ax }_L(\varphi )\) and \(P^{ ax }_{L}(\varphi )\) are as defined in Table 5. We call \(\rho ^{ ax }_{L}(\varphi )\) the axiomatic reduction of \(\varphi \) for the modal logic L.
Theorem 2
Let \(L = \textsf{K}_{}{}\!\varSigma \) with \(\varSigma \subseteq \{\textsf{B},\textsf{D},\textsf{T},\textsf{4},\textsf{5}\}\) and \(\varphi \) be a modal formula in simplified NNF. Then \(\varphi \) is L-satisfiable iff \(\rho ^{ ax }_{L}(\varphi )\) is \(\textsf{K}_{}{}\)-satisfiable.
Just as the definitional reduction, the axiomatic reduction allows us to use any reasoner for basic modal logic as a reasoner for all the logics in the modal cube.
3.3 Discussion
There are five main differences between the definitional reduction and the axiomatic reduction, and between the axiomatic reduction and the work in [18]:
-
1.
The axiomatic reduction for all logics except the logics \(\textsf{KB}_{}\), \(\textsf{KD}_{}\), \(\textsf{KT}_{}\), \(\textsf{K4}_{}\) is new. Kracht [18] did define a reduction from \(\textsf{K5}_{}\) to \(\textsf{K4}_{}\), but since \(\textsf{K5}_{}\) is not a subset of \(\textsf{K4}_{}\), this reduction is not correct. Our definition of the axiomatic reduction corrects that mistake while remaining close to the Kracht’s original idea by adding instances of \(\textsf{4}\) at modal levels greater than 0.
The bounds given for \(\textsf{KB}_{}\), \(\textsf{KD}_{}\), and \(\textsf{KT}_{}\) given in Table 5 are the same as Kracht’s [18]. However, for \(\textsf{K4}_{}\) he used a bound given by the number of distinct subformulae of the formula \(\varphi \) under consideration. We are able to show that a bound given by the number of distinct \(\Box \)-subformulae is sufficient. For the remaining logics, the bounds are new.
-
2.
The definitional reduction introduces new propositional symbols for complex subformulae, so-called surrogate propositional symbols. For the modal resolution calculi implemented in
 [22, 26] this is necessary to obtain the clausal normal form on which the calculi operate. However, in the context of our reductions, where we have to add instances of axiom schemata for \(\Box \)-subformulae, the use of surrogate propositional symbols offers the advantage that repeated occurrences of the same complex subformula can be replaced by the same surrogate symbol. Each surrogate propositional symbol then requires a definition at every modal level at which it occurs, but overall there should still be a benefit in relation to the size of the resulting formula.
[22, 26] this is necessary to obtain the clausal normal form on which the calculi operate. However, in the context of our reductions, where we have to add instances of axiom schemata for \(\Box \)-subformulae, the use of surrogate propositional symbols offers the advantage that repeated occurrences of the same complex subformula can be replaced by the same surrogate symbol. Each surrogate propositional symbol then requires a definition at every modal level at which it occurs, but overall there should still be a benefit in relation to the size of the resulting formula. -
3.
The bounds shown in Table 3 for the definitional reduction and in Table 5 for the axiomatic reduction, have different effects on the modal formulae produced. For the definitional reduction, the modal depth of \(\rho ^{ def }_{L}(\varphi )\) is at most \(d^{ sml }_L(\varphi _L)+1\), that is, the bound shown for L in Table 3 plus one. In contrast, for the axiomatic reduction, \(b^{ ax }_L\) in Table 5 only states the modal depth of
 where the propositional symbol \(p_a\) will then be replaced by a conjunction of instances of axiom schemata for \(\Box \)-subformulae of \(\varphi \). For all logics except \(\textsf{K}_{}{}\) and \(\textsf{KD}_{}{}\), the modal depth of these axiom schemata will be between \(d^\varphi _m\) and \(d^\varphi _m+2\). Thus, the overall modal depth of \(\rho ^{ ax }_{L}(\varphi )\) is bound by \(b^{ ax }_L+d^\varphi _m+2\), not just by the bound shown in Table 5.
where the propositional symbol \(p_a\) will then be replaced by a conjunction of instances of axiom schemata for \(\Box \)-subformulae of \(\varphi \). For all logics except \(\textsf{K}_{}{}\) and \(\textsf{KD}_{}{}\), the modal depth of these axiom schemata will be between \(d^\varphi _m\) and \(d^\varphi _m+2\). Thus, the overall modal depth of \(\rho ^{ ax }_{L}(\varphi )\) is bound by \(b^{ ax }_L+d^\varphi _m+2\), not just by the bound shown in Table 5.For example, consider the formula \(\Box \Box p\) in \(\textsf{KB}_{}\). Then with the axiomatic reduction we obtain the formula

which itself is a formula of modal depth 5. With the definitional reduction, we obtain
$$\begin{array}{@{}l@{}l@{}}&t_{\Box \Box p} \hbox {}\wedge \hbox {} (t_{\Box \Box p} \rightarrow \Box t_{\Box p}) \hbox {}\wedge \hbox {} \Box (t_{\Box p} \rightarrow \Box p) \hbox {}\wedge \hbox {} (p\vee t_{\Box \lnot t_{\Box p}}) \hbox {}\wedge \hbox {} (t_{\Box \lnot t_{\Box p}}\rightarrow \Box \lnot t_{\Box p}) \end{array}$$which is a formula of modal depth 2.
Taking this into account we can see that for \(L = \textsf{K}_{}{}\!\varSigma \) where \(\varSigma \subseteq \{\textsf{B},\textsf{D},\textsf{T}\}\) we can expect the modal depth of \(\rho ^{ def }_{L}(\varphi )\) to be less than or equal to that of \(\rho ^{ ax }_{L}(\varphi )\), while for the remaining logics of the modal cube it depends on the individual formula which reduction will produce a formula of greater modal depth. Nevertheless, for logics such as \(\textsf{K4}_{}\) we expect that the modal depth of \(\rho ^{ ax }_{L}(\varphi )\) will often be drastically lower than that of \(\rho ^{ def }_{L}(\varphi )\).
-
4.
The definitional reduction makes a distinction between \(\Box \)- and \(\Diamond \)-operators and only introduces additional clauses for \(\Box \)-subformulae. For logics except \(\textsf{KB4}_{}\), \(\textsf{K5}_{}\) and their extensions, it also carefully tracks at which modal levels additional clauses are required for which occurrences of surrogate symbols that were introduced for \(\Box \)-subformulae. The ‘price’ paid for the fact that for these logics additional clauses are not also introduced for \(\Diamond \)-subformulae is in the higher bounds for the modal levels up to which additional clauses and definitions of surrogate symbols need to be added. The reason is that the presence of axiom instances for negative occurrences of \(\Box \)-subformulae in the axiomatic reduction for \(\textsf{K4}_{}\), \(\textsf{K5}_{}\) and their extensions allows the ‘back-propagation’ of \(\Box \)-subformulae that occur negatively, namely, if \(\lnot \Box \psi \) is true at a world w at modal level 2 or higher in a tree \(\textsf{K}_{}{}\)-model of \(\rho ^{ ax }_{L}(\varphi )\), then it is also true at a predecessor world v of w. Provers that do not construct tree Kripke structures, but general Kripke structure, or use caching, can potentially take advantage of this and construct ‘shallower’ models. On the hand, the outdegree of worlds increases.
-
5.
The definitional reduction for \(\textsf{K45}_{}\), \(\textsf{KD45}_{}\) and \(\textsf{KT45}_{}\) takes account of the fact that instances of \(\textsf{4}\) are only required to hold at the root world. At all other worlds, instances of \(\textsf{5}\) are already sufficient to enforce transitivity of the accessibility relation in Kripke structures for these logics. This restriction to the root world is in line with the construction of the definitional reduction \(\rho ^{ def }_{L}\) in Eq. 1, namely, that we have different sets of clauses associated with each modal level. In contrast, the construction of the axiomatic reduction \(\rho ^{ ax }_{L}\) in Eq. 2 assumes that we use the same set of axiom instances at every modal level.
We will revisit the effect that Points 2, 3, and 4 have on the size and modal depths of formulae, on the performance of provers, and the models they may produce in the next section.
4 Evaluation
In our evaluation we compare the effect of using the definitional reduction and the axiomatic reduction as input for three provers for \(\textsf{K}_{}\): CEGARBox [10], Spartacus [13], and
 [24, 30]. Spartacus and CEGARBox were included as they presented best performance in recent evaluations [10, 24,25,26, 29, 30] when compared with several other provers with built-in support for modal logics: BDDTab [12], FaCT++ [34], InKreSAT [16], SPASS [33], and Leo-III+E [8, 31].
[24, 30]. Spartacus and CEGARBox were included as they presented best performance in recent evaluations [10, 24,25,26, 29, 30] when compared with several other provers with built-in support for modal logics: BDDTab [12], FaCT++ [34], InKreSAT [16], SPASS [33], and Leo-III+E [8, 31].
We have included two more approaches in the comparison: (i) the global modal resolution (GMR) calculi [21] that include specific inference rules for each of the logics in the modal cube, implemented in
 ; (ii) modal layered resolution (MLR) calculi [22] together with the reductions given in Table 4, again implemented in
; (ii) modal layered resolution (MLR) calculi [22] together with the reductions given in Table 4, again implemented in
 . The first is an example of ‘native’ reasoning in the logics concerned, while the inclusion of latter allows us to investigate the effect of ‘internalising’ the reduction and having inference rules that operate on modal clauses. Both calculi support several refinements of resolution. We report only results for the ordered refinement (cord) as it was the best performing overall.
. The first is an example of ‘native’ reasoning in the logics concerned, while the inclusion of latter allows us to investigate the effect of ‘internalising’ the reduction and having inference rules that operate on modal clauses. Both calculi support several refinements of resolution. We report only results for the ordered refinement (cord) as it was the best performing overall.
The two reductions combined with CEGARBox, Spartacus, and
 and the GMR and MLR calculi in
and the GMR and MLR calculi in
 give us a total of eight different approaches.
give us a total of eight different approaches.
We have used the benchmarks introduced in [27], which compriseFootnote 1 (i) 100 unsatisfiable formulae for each of the logics being considered; these are based on 20 formulae each from 5 classes of the LWB benchmark collection [3] modified so that the formulae for logic L are only unsatisfiable in L and its extensions; and also (ii) 100 formulae that are \(\textsf{S5}_{}\)-satisfiable, that is, formulae that are satisfiable in all 15 logics; these consist of 20 formulae each from 5 classes of the LWB benchmark collection.
We have supplied all reductions and provers with preprocessed formulae extracted from
 . The simplified negation normal form for a formula \(\varphi \), \(\textsf{nnf}({\varphi })\), is generated by
. The simplified negation normal form for a formula \(\varphi \), \(\textsf{nnf}({\varphi })\), is generated by
 as follows. First, the formula is rewritten into box normal form [28], a normal form similar to the negation normal form, but where the operator \(\Diamond \) is rewritten as \(\lnot \Box \lnot \). To the resulting formula, we apply prenexing [20], that is, moving the modal operators outwards as much as possible. The simplification rules given in Table 2 are then applied together with pure literal elimination (i.e. replacing occurrences of pure literals by true) and constant propagation. Table 6 shows the effect of all these preprocessing steps on average size, average modal depth, and average number of boxes in our benchmark formulae, separately for unsatisfiable (U) and satisfiable (S) formulae. Over all formulae we get a 20% reduction in size and a 66% reduction in the number of \(\Box \)-operators. The modal depth remains unchanged which is an indication of the robustness of the benchmarks.
as follows. First, the formula is rewritten into box normal form [28], a normal form similar to the negation normal form, but where the operator \(\Diamond \) is rewritten as \(\lnot \Box \lnot \). To the resulting formula, we apply prenexing [20], that is, moving the modal operators outwards as much as possible. The simplification rules given in Table 2 are then applied together with pure literal elimination (i.e. replacing occurrences of pure literals by true) and constant propagation. Table 6 shows the effect of all these preprocessing steps on average size, average modal depth, and average number of boxes in our benchmark formulae, separately for unsatisfiable (U) and satisfiable (S) formulae. Over all formulae we get a 20% reduction in size and a 66% reduction in the number of \(\Box \)-operators. The modal depth remains unchanged which is an indication of the robustness of the benchmarks.
For the axiomatic reduction, the resulting formula is then extracted from
 and the reduction according to Eq. 2 and Table 5 is applied externally. For the definitional reduction, the formula is not extracted but transformed by
and the reduction according to Eq. 2 and Table 5 is applied externally. For the definitional reduction, the formula is not extracted but transformed by
 into \(\textsf{SNF}_{ml}\) according to Tables 3 and 4. During the transformation into the normal form, complex subformulae are replaced by the same symbol in all positions they might occur. After transformation into \(\textsf{SNF}_{ml}\), the kept clauses are extracted from
into \(\textsf{SNF}_{ml}\) according to Tables 3 and 4. During the transformation into the normal form, complex subformulae are replaced by the same symbol in all positions they might occur. After transformation into \(\textsf{SNF}_{ml}\), the kept clauses are extracted from
 and used to produce the modal formula for the definitional reduction according to Eq. 1.
and used to produce the modal formula for the definitional reduction according to Eq. 1.
Table 7 shows experimental results comparing the performance of the eight approaches. The first three columns of the table show the logic, the satisfiability status of the formulae for our benchmark collection used for this logic (‘U’ for ‘unsatisfiable, ‘S’ for ‘satisfiable’), and their number. In total we have 30 sets of benchmark formulae. The next eight columns then show how many of those formulae were solved by each of the eight approaches. A time limit of 100 CPU seconds was set for each formula and where a reduction is used the time taken includes the computation of the reduction. The highest number or numbers in each row are highlighted in bold. The last six columns show the results for \(\rho ^{ def }_{L}\) and \(\rho ^{ ax }_{L}\) combined with CEGARBox, Spartacus, and
 . Here, for each logic L and each satisfiability status we have indicated with italics which reduction resulted in better performance for each of the three provers. In the following we call each such pair a comparison point. Benchmarking was performed on a PC with an AMD Ryzen 5 5600X CPU @ 4.60 GHz max and 64 GB main memory using Fedora release 37 as operating system.
. Here, for each logic L and each satisfiability status we have indicated with italics which reduction resulted in better performance for each of the three provers. In the following we call each such pair a comparison point. Benchmarking was performed on a PC with an AMD Ryzen 5 5600X CPU @ 4.60 GHz max and 64 GB main memory using Fedora release 37 as operating system.
For both satisfiable and unsatisfiable benchmark formulae, the combination of the definitional reduction with CEGARBox performs best. Overall, it solves 25% more formulae than the second best approach, the GMR calculi in
 . CEGARBox with the definitional reduction also outperforms CEGARBox with the axiomatic reduction on both satisfiable and unsatisfiable benchmark formulae. The same is true for the MLR calculus in
. CEGARBox with the definitional reduction also outperforms CEGARBox with the axiomatic reduction on both satisfiable and unsatisfiable benchmark formulae. The same is true for the MLR calculus in
 when combined with one of the two reductions and for Spartacus on satisfiable benchmark formulae when combined with one of the two reductions.
when combined with one of the two reductions and for Spartacus on satisfiable benchmark formulae when combined with one of the two reductions.
We can see that the internal transformation to \(\textsf{SNF}_{ml}\) together with the MLR calculus in
 performs better than first computing the definitional reduction \(\rho ^{ def }_{L}\) and then handing the resulting formula to
performs better than first computing the definitional reduction \(\rho ^{ def }_{L}\) and then handing the resulting formula to
 . The former approach performs better on 26 out of 30 sets of benchmark formulae. This is not surprising since in the latter case
. The former approach performs better on 26 out of 30 sets of benchmark formulae. This is not surprising since in the latter case
 does apply the transformation into \(\textsf{SNF}_{ml}\) again. This implies that new propositional symbols are introduced when applying renaming and new clauses are added defining those symbols. Also, for the ordered resolution refinement we use, all literals in the scope of modal operators will be renamed in order to retain completeness [22]. Again, for each renamed literal there will be an additional clause. Overall,
does apply the transformation into \(\textsf{SNF}_{ml}\) again. This implies that new propositional symbols are introduced when applying renaming and new clauses are added defining those symbols. Also, for the ordered resolution refinement we use, all literals in the scope of modal operators will be renamed in order to retain completeness [22]. Again, for each renamed literal there will be an additional clause. Overall,
 will perform inferences with a larger set of \(\textsf{SNF}_{ml}\) clauses over a larger set of propositional symbols. This is bound to degrade performance in most cases.
will perform inferences with a larger set of \(\textsf{SNF}_{ml}\) clauses over a larger set of propositional symbols. This is bound to degrade performance in most cases.
Looking at individual logics, a more varied picture is evident. Consider both satisfiable and unsatisfiable benchmark formulae for the logics \(\textsf{K5}_{}\), \(\textsf{KD5}_{}\), \(\textsf{K4B}_{}\) (which is the same logic as \(\textsf{K5B}_{}\)), \(\textsf{K45}_{}\), \(\textsf{KD45}_{}\), and \(\textsf{S5}_{}\) and the behaviour of Spartacus and
 with one of the two reductions on these. Of these 24 comparison points, the axiomatic reduction results in better performance on 21 and the definitional reduction only on 3. In particular, Spartacus with the axiomatic reduction consistently shows better performance for these logics than with the definitional reduction. In stark contrast, CEGARBox with the definitional reduction still performs better on 10 out of 12 comparison points. Interestingly, this advantage of the axiomatic reduction does not carry over to \(\textsf{K4}_{}\) and its extensions \(\textsf{KD4}_{}\) and \(\textsf{S4}_{}\). Here, with exceptions of 3 out of 18 comparison points, the definitional reduction with one of CEGARBox,
with one of the two reductions on these. Of these 24 comparison points, the axiomatic reduction results in better performance on 21 and the definitional reduction only on 3. In particular, Spartacus with the axiomatic reduction consistently shows better performance for these logics than with the definitional reduction. In stark contrast, CEGARBox with the definitional reduction still performs better on 10 out of 12 comparison points. Interestingly, this advantage of the axiomatic reduction does not carry over to \(\textsf{K4}_{}\) and its extensions \(\textsf{KD4}_{}\) and \(\textsf{S4}_{}\). Here, with exceptions of 3 out of 18 comparison points, the definitional reduction with one of CEGARBox,
 , and Spartacus leads to better performance than the axiomatic reduction.
, and Spartacus leads to better performance than the axiomatic reduction.
 on unsatisfiable benchmark formulae.
on unsatisfiable benchmark formulae.We can gain additional insight by looking in more detail at the behaviour of provers. While this would be most beneficial for CEGARBox, this tool currently only outputs the satisfiability status of formulae but neither models nor proofs. Instead we turn to Spartacus which can output models for satisfiable formulae. Table 8 shows information on the input formulae that were given to Spartacus, resulting from one of our reductions, and the models that Spartacus produced. The first four columns show the logic, the reduction that was used, how many satisfiable benchmark formulae (out of 100) Spartacus was able to solve, and how many formulae it was able to solve with both reductions. The number in the fourth column is not necessarily the minimum of the two numbers in the third column for a particular logic. The next two columns contain the average size and average modal depth of \(\rho ^{ def }_{L}\) and \(\rho ^{ ax }_{L}\) where Spartacus solve both. Finally, the last three columns contain the average number of worlds, number of edges, and depth of the models for these formulae. Spartacus uses blocking, even for the modal logic \(\textsf{K}_{}\), and the models it produces are not trees but general graphs. A fine-grained analysis on the level of individual formulae shows that, with the exception of the logic \(\textsf{KB4}_{}\), it is generally the case that the reduction that produces smaller formulae leads Spartacus to produce smaller models, and thereby also leads to more formulae being solved. Only for \(\textsf{KB4}_{}\) are there more instances where a larger formula resulting from a reduction, namely the definitional reduction, lead to smaller models. However, it is still the case that axiomatic reduction then allows more formulae to be solved for \(\textsf{KB4}_{}\).
For unsatisfiable formulae we consider
 . Table 9 shows information on the input formulae that were given to
. Table 9 shows information on the input formulae that were given to
 , resulting from one of our reductions, and the proof search conducted by
, resulting from one of our reductions, and the proof search conducted by
 . The first six columns correspond to those in Table 8. The final three columns contain the average number of inference steps
. The first six columns correspond to those in Table 8. The final three columns contain the average number of inference steps
 requires to find a proof, the average size of those proofs, and the average maximal modal level of a clause in those proofs. Again we see that the reduction that produces smaller formulae, with few exceptions, also leads
requires to find a proof, the average size of those proofs, and the average maximal modal level of a clause in those proofs. Again we see that the reduction that produces smaller formulae, with few exceptions, also leads
 to find proofs in fewer inference steps and allows it to solve more formulae.
to find proofs in fewer inference steps and allows it to solve more formulae.
5 Conclusions
The axiomatic and the definitional reductions from logics in the modal cube to basic modal logic that we have presented in this paper allow any decision procedure for basic modal logic to be used to solve the satisfiability problem in all 15 logics of the modal cube. This is of particular interest as over the last 25 years, a range of decision procedures for basic modal logic have been implemented and improved [2, 6, 7, 10,11,12,13, 15, 34] but only few implemented decision procedures for all logics of the modal cube exist. Our empirical results also indicate that such reductions are not only a theoretical possibility but are effective and efficient: the combination of the definitional reduction with CEGARBox is currently the best performing approach on our collection of benchmark formulae for the modal cube. There are a number of other contributing factors to the efficiency of the approach that are also beneficial outside the context of reductions. Pre-processing techniques such as simplification and prenexing can reduce the size and, in the context of modal logics, the number of modal operators in a modal formula. The use of surrogate propositional symbols and of a clausal normal form allows to again reduce the size and structural complexity of formulae.
Despite the positive empirical results, we nevertheless hope that more provers that natively support all the logics of the modal cube will be implemented. At the moment our comparison is limited to our own resolution-based prover
 . Support for modal logics except \(\textsf{K}_{}\) in other provers is often limited to \(\textsf{KD}_{}\), \(\textsf{KT}_{}\), and \(\textsf{S4}_{}\). A wider range of provers for all logic in the modal cube would allow us to establish the robustness of our empirical results and possibly enable us to identify strength and weaknesses relative to native provers. It would be beneficial if such support for native reasoning in a logics of the modal cube would also include the provisions of proofs for unsatisfiable formulae and models for satisfiable formulae as well as some abstract measure of the computational effort expended in finding those. This is paramount for our ability to explain the behaviour of prover on our benchmarks.
. Support for modal logics except \(\textsf{K}_{}\) in other provers is often limited to \(\textsf{KD}_{}\), \(\textsf{KT}_{}\), and \(\textsf{S4}_{}\). A wider range of provers for all logic in the modal cube would allow us to establish the robustness of our empirical results and possibly enable us to identify strength and weaknesses relative to native provers. It would be beneficial if such support for native reasoning in a logics of the modal cube would also include the provisions of proofs for unsatisfiable formulae and models for satisfiable formulae as well as some abstract measure of the computational effort expended in finding those. This is paramount for our ability to explain the behaviour of prover on our benchmarks.
Finally, our collection of benchmark formulae requires further refinement. Some of the satisfiable formulae in that collection seem to allow rather small models and overall do not appear to be sufficiently challenging across all the logics. We will need to investigate whether this can be remedied simply by moving to higher parameter values for these parameterised classes of formulae or whether completely new classes of formulae are required.
Notes
- 1.
Input files for the provers used here and the source for
 are available at http://nalon.org/#software.
are available at http://nalon.org/#software.
References
Areces, C., Gennari, R., Heguiabehere, J., de Rijke, M.: Tree-based heuristic in modal theorem proving. In: Horn, W. (ed.) ECAI 2000, pp. 199–203. IOS Press (2000)
Balbiani, P., Demri, S.: Prefixed tableaux systems for modal logics with enriched languages. In: Pollack, M.E. (ed.) IJCAI 1997, pp. 190–195. Morgan Kaufmann (1997)
Balsiger, P., Heuerding, A., Schwendimann, S.: A benchmark method for the propositional modal logics K, KT, S4. J. Autom. Reasoning 24(3), 297–317 (2000). https://doi.org/10.1023/A:1006249507577
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge Tracts in Theoretical Computer Science, Cambridge University Press, Cambridge (2002)
Demri, S., de Nivelle, H.: Deciding regular grammar logics with converse through first-order logic. J. Logic Lang. Inform. 14(3), 289–329 (2005)
Girlando, M., Straßburger, L.: MOIN: a nested sequent theorem prover for intuitionistic modal logics (system description). In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI), vol. 12167, pp. 398–407. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-51054-1_25
Giunchiglia, F., Sebastiani, R.: Building decision procedures for modal logics from propositional decision procedures—the case study of modal K. In: McRobbie, M.A., Slaney, J.K. (eds.) CADE 1996. LNCS, vol. 1104, pp. 583–597. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61511-3_115
Gleißner, T., Steen, A.: LEO-III (2022). https://doi.org/10.5281/zenodo.4435994
Gleißner, T., Steen, A., Benzmüller, C.: Theorem provers for every normal modal logic. In: Eiter, T., Sands, D. (eds.) LPAR 2017. EPiC Series in Computing, vol. 46, pp. 14–30. EasyChair (2017). https://doi.org/10.29007/jsb9
Goré, R., Kikkert, C.: CEGAR-tableaux: improved modal satisfiability via modal clause-learning and SAT. In: Das, A., Negri, S. (eds.) TABLEAUX 2021. LNCS (LNAI), vol. 12842, pp. 74–91. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-86059-2_5
Goré, R., Nguyen, L.A.: Clausal tableaux for multimodal logics of belief. Fundam. Inform. 94(1), 21–40 (2009)
Goré, R., Olesen, K., Thomson, J.: Implementing tableau calculi using BDDs: BDDTab system description. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 337–343. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_25
Götzmann, D., Kaminski, M., Smolka, G.: Spartacus: a tableau prover for hybrid logic. Electron. Notes Theor. Comput. Sci. 262, 127–139 (2010)
Horrocks, I., Hustadt, U., Sattler, U., Schmidt, R.A.: Computational modal logic. In: Blackburn, P., van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic, chap. 4, pp. 181–245. Elsevier (2006)
Hustadt, U., Schmidt, R.A.: MSPASS: modal reasoning by translation and first-order resolution. In: Dyckhoff, R. (ed.) TABLEAUX 2000. LNCS (LNAI), vol. 1847, pp. 67–71. Springer, Heidelberg (2000). https://doi.org/10.1007/10722086_7
Kaminski, M., Tebbi, T.: InKreSAT: modal reasoning via incremental reduction to SAT. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 436–442. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_31
Kracht, M.: Reducing modal consequence relations. J. Log. Comput. 11(6), 879–907 (2001)
Kracht, M.: Notes on the space requirements for checking satisfiability in modal logics. In: Balbiani, P., Suzuki, N.Y., Wolter, F., Zakaryaschev, M. (eds.) Advances in Modal Logic 4, pp. 243–264. King’s College Publications (2003)
Nalon, C.: K\(_{\rm S}\)P (2022). https://www.nalon.org/#software
Nalon, C., Dixon, C.: Anti-prenexing and prenexing for modal logics. In: Fisher, M., van der Hoek, W., Konev, B., Lisitsa, A. (eds.) JELIA 2006. LNCS (LNAI), vol. 4160, pp. 333–345. Springer, Heidelberg (2006). https://doi.org/10.1007/11853886_28
Nalon, C., Dixon, C.: Clausal resolution for normal modal logics. J. Algorithms 62, 117–134 (2007)
Nalon, C., Dixon, C., Hustadt, U.: Modal resolution: proofs, layers, and refinements. ACM Trans. Comput. Log. 20(4), 23:1–23:38 (2019)
Nalon, C., Hustadt, U., Dixon, C.: A modal-layered resolution calculus for K. In: De Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 185–200. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24312-2_13
Nalon, C., Hustadt, U., Dixon, C.: K\(_{\rm S}\)P: a resolution-based prover for multimodal K. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016. LNCS (LNAI), vol. 9706, pp. 406–415. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40229-1_28
Nalon, C., Hustadt, U., Dixon, C.: K\(_{\rm S}\)P: a resolution-based prover for multimodal K, abridged report. In: Sierra, C. (ed.) IJCAI 2017, pp. 4919–4923. IJCAI/AAAI Press (2017). https://doi.org/10.24963/ijcai.2017/694
Nalon, C., Hustadt, U., Dixon, C.: K\(_{\rm S}\)P: Architecture, refinements, strategies and experiments. J. Autom. Reason. 64(3), 461–484 (2020)
Nalon, C., Hustadt, U., Papacchini, F., Dixon, C.: Local reductions for the modal cube. In: Blanchette, J., Kovács, L., Pattinson, D. (eds.) IJCAR 2022. LNCS, vol. 13385, pp. 486–505. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-10769-6_29
Pan, G., Sattler, U., Vardi, M.Y.: BDD-based decision procedures for the modal logic K. J. Appl. Non-Class. Log. 16(1–2), 169–208 (2006)
Papacchini, F., Nalon, C., Hustadt, U., Dixon, C.: Efficient local reductions to basic modal logic. In: Platzer, A., Sutcliffe, G. (eds.) CADE 2021. LNCS (LNAI), vol. 12699, pp. 76–92. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79876-5_5
Papacchini, F., Nalon, C., Hustadt, U., Dixon, C.: Local is best: efficient reductions to modal logic K. J. Autom. Reason. 66(4), 639–666 (2022). https://doi.org/10.1007/s10817-022-09630-6
Schulz, S.: E 2.6 (2022). https://wwwlehre.dhbw-stuttgart.de/~sschulz/E/Download.html
Steen, A., Benzmüller, C.: The higher-order prover Leo-III. In: Giacomo, G.D., Catalá, A., Dilkina, B., Milano, M., Barro, S., Bugarín, A., Lang, J. (eds.) ECAI 2020. Frontiers in Artificial Intelligence and Applications, vol. 325, pp. 2937–2938. IOS Press (2020). https://doi.org/10.3233/FAIA200462
The SPASS Team: SPASS 3.9 (2016). https://www.spass-prover.org/
Tsarkov, D., Horrocks, I.: FaCT++ description logic reasoner: system description. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 292–297. Springer, Heidelberg (2006). https://doi.org/10.1007/11814771_26
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Nalon, C., Hustadt, U., Papacchini, F., Dixon, C. (2023). Buy One Get 14 Free: Evaluating Local Reductions for Modal Logic. In: Pientka, B., Tinelli, C. (eds) Automated Deduction – CADE 29. CADE 2023. Lecture Notes in Computer Science(), vol 14132. Springer, Cham. https://doi.org/10.1007/978-3-031-38499-8_22
Download citation
DOI: https://doi.org/10.1007/978-3-031-38499-8_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38498-1
Online ISBN: 978-3-031-38499-8
eBook Packages: Computer ScienceComputer Science (R0)



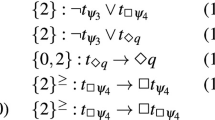

 [
[ where the propositional symbol
where the propositional symbol 
 are available at
are available at