Robust Topology Optimization of Truss-Like Space Structures

Abstract

Due to the additional design freedom and manufacturing possibilities of additive manufacturing compared to traditional manufacturing, topology optimization via mathematical optimization gained importance in the initial design of complex high-strength lattice structures. We consider robust topology optimization of truss-like space structures with multiple loading scenarios. A typical dimensioning method is to identify and examine a suspected worst-case scenario using experience and component-specific information and to incorporate a factor of safety to hedge against uncertainty. We present a quantified programming model that allows us to specify expected scenarios without having explicit knowledge about worst-case scenarios, as the resulting optimal structure must withstand all specified scenarios individually. This leads to less human misconduct, higher efficiency and, thus, to cost and time savings in the design process. We present three-dimensional space trusses with minimal volume that are stable for up to 100 loading scenarios. Additionally, the effect of demanding a symmetric structure and explicitly limiting the diameter of truss members in the model is discussed.

1 Introduction

Robust Truss Topology Optimization (RTTO) deals with the structural design optimization problem to find a truss that is stable subjected to loading, material or geometric uncertainty. We examine loading uncertainty [1, 2]. Most research in this area considers perturbations of loads and focuses on robust compliance topology optimization often resulting in semidefinite programs [4, 7]. We aim at minimizing the volume of truss-like structures under multiple-load uncertainty and assume a static system in order to provide an initial design proposal. A robust mixed integer program arises that can be tackled with high performance standard solvers. We utilize the expressiveness of Quantified Mixed-Integer Linear Programming (QMIP) [5] to model the robust optimization problem.

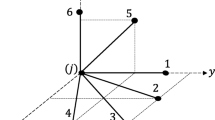
Our approach simultaneously considers sizing and topology optimization and utilizes the so-called ground structure [9], see Fig. 1, which is given by a set of vertices (fixed nodal points) $V \in \mathbb {R}^3$ and a set of edges (possible structural members) $E \subseteq V \times V$. The resulting structure must be adequately dimensioned for any of the anticipated loading scenarios. Therefore, the challenging task of identifying, analyzing, and quantifying the worst-case scenario [7], which thus far highly depends upon practical engineering experience, can be bypassed, leading to less human misconduct, higher efficiency and, thus, to cost and time savings.

Fig. 1.

(Left) The ground structure; (Right) Symmetry and bearing positions

In structural mechanics symmetry is often exploited to effectively optimize and analyze structural systems [8]. From the viewpoint of mathematical optimization, enforcing symmetry is often computationally beneficial, as it results in a reduction of free variables. In general, however, demanding symmetry results in suboptimal solutions, as optimal solutions can be asymmetric even if the design domain, the external loads, and the boundary conditions are symmetric [12]. We optionally consider two vertical planes of symmetry, as shown in Fig. 1. Hence, specifying the structure of the representative region suffices.

We introduce the robust optimization model in Sect. 2. In Sect. 3 we discuss two three-dimensional examples: a ground structure with 296 members and 128 loading scenarios as well as a 1720-member ground structure with 8 loading scenarios, before we summarize and conclude in Sect. 4.

2 Robust Truss Topology Optimization

We utilize QMIP, which is a formal extension of Mixed Integer Programming (MIP) where variables are either existentially or universally quantified resulting in a robust multistage optimization problem. For more details, we refer to [5]. A solution is a strategy for assigning existentially quantified variables such that a linear constraint system is fulfilled. In particular, in a solution it is ensured that even for the worst-case assignment of universally quantified variables the system holds. The following model features two quantifier changes and therefore also can be interpreted as adjustable robust optimization problem with right-hand side uncertainty [15]. The model aims at finding a truss-like space structure with minimal volume such that for any anticipated loading scenario the structure remains in a static equilibrium position. Restated in the quantification context:

$$\begin{aligned} \exists \ \text {structure}\quad \forall \ \text {loading scenarios}\quad \exists \ \text {static equilibrium, } \end{aligned}$$

(1)

i.e., does a truss-like structure exist such that for all anticipated loading scenarios a static equilibrium exists. Within the ground structure (see Fig. 1), given by the undirected graph $G=(V,E)$, edges must be selected at which straight and prismatic members should be placed and for each member its cross-sectional area must be determined. The locations of vertices, i.e., nodal points, are fixed in space, to allow a preprocessing of the spatial and angular relationships between edges and vertices. Additionally, a set of bearings $B\subset V$ must be specified, see Fig. 1. We also want to be able to demand symmetrical structures and therefore introduce the function $R:E \rightarrow E$, for which R(e) maps to the edge representing e. In contrast to the established design variable linking technique [10], only variables that characterize representative members need to be deployed in order to enforce that members at edges e and R(e) are equally dimensioned. We use $R(e)=e$ if no symmetry is demanded.

As a minimum cross-sectional area is essential due to manufacturing restrictions, we use the combination of a binary variable $x_e$ and a continuous variable $a_e$ in order to indicate the existence of a member at edge $e\in E$ (with specified minimum area) and its potential additional cross-sectional area. The minimum area $A_{\min }$ can either be a fixed value or optionally adhere to design rules VDI 3405-3-4, VDI 3405-3-3 [13, 14]. In the latter case, the minimum area of each member is computed separately depending on its length and its spatial orientation, cf. [11]. Note that these design rules are only enforced locally for each edge: if multiple members with identical beam axes form one long structural member, post-processing is necessary. Both $\mathbf {x}$ and $\mathbf {a}$ are first stage existential variables, as they represent the selected structure. Binary universal variables $\mathbf {y}$ are used to specify the loading scenario, consisting of $C\in \mathbb {N}$ loading cases: the binary universal variable $y_i$ indicates whether loading case i is active, while the variable vector $\mathbf {y}$ indicates the selected loading scenario. For each anticipated loading scenario the structure given by $\mathbf {x}$ and $\mathbf {a}$ must have the following properties: each nodal point as well as the entire structure must be in a static equilibrium position and the longitudinal stress within each structural member—induced by the normal force per cross-sectional area—must not exceed the member’s yield strength. The existential variables $n_e$ and $r_b$ represent the normal force in a structural member at e and the bearing reaction force at bearing b, respectively. The variables used in our model are given in Table 1 and the parameters are listed in Table 2. We use bold letters when referring to a vector or matrix.

Table 1. Variables

Table 2. Sets, Parameters and Functions

$$\begin{aligned} \min&\sum _{e \in E}L_e\left( A_{\min } \cdot x_{R(e)} + a_{R(e)} \right) \end{aligned}$$

(2)

$$\begin{aligned} \text {s.t.}\,\,&{\exists \mathbf {x} \in \{0,1\}^E\ \mathbf {a} \in \mathbb {Q}_+^E \quad \forall \mathbf {y} \in \{0,1\}^C \quad \exists \mathbf {r} \in \mathbb {Q}^{B\times 3}\ \mathbf {n} \in \mathbb {Q}^E :}~ \end{aligned}$$

(3)

$$\begin{aligned}&S\vert n_e \vert \le \sigma _y \left( A_{\min } x_{R(e)} + a_{R(e)}\right) \qquad \forall \, e \in E \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{e \in I(b)} n_{e}^d + \sum _{i =1}^{C} y_i F_{i,b}^d +r_{b}^d =0 \qquad \forall \, b \in B ,\, d\in \{x,y,z\}\end{aligned}$$

(5)

$$\begin{aligned}&\sum _{e \in I(v)} n_{e}^d + \sum _{i =1}^{C} y_i F_{i,v}^d =0 \qquad \forall \, v \in V\setminus B ,\, d\in \{x,y,z\}\end{aligned}$$

(6)

$$\begin{aligned}&a_{R(e)} \le (A_{\max } - A_{\min })x_{R(e)}\qquad \forall \, e \in E \end{aligned}$$

(7)

$$\begin{aligned}&\sum _{v \in V} \sum _{i=1}^C \mathbf {V}(b,v) \times y_i\mathbf {F}_{i,v} + \sum _{b' \in B} \mathbf {V}(b,b')\times \mathbf {r}_{b'}=\mathbf {0} \qquad \forall \, b \in B \end{aligned}$$

(8)

$$\begin{aligned}&\sum _{v \in V} \sum _{i=1}^C y_i \mathbf {F}_{i,v} + \sum _{b \in B}\mathbf {r}_b=\mathbf {0} \qquad \end{aligned}$$

(9)

The Objective Function (2) aims at minimizing the volume of the structure. Note that the objective value does not reflect the exact volume of the corresponding structure: overlapping parts of members at vertices are not merged but counted multiple times. The Quantification Sequence (3) defines the variables’ domain and order, as outlined in Expression (1). If $R(e)\ne e$, $\mathbf {x}$ and $\mathbf {a}$ variables are deployed only for edges in the image of E under function R, i.e., only for the representative edges. Constraint (4) ensures that the local longitudinal stress must not exceed the member’s yield strength considering a factor of safety. In particular, modifying the cross-sectional area given by $A_{\min }+a_{R(e)}$, alters the stress in a member. Constraint (4) is linearized by writing the constraint once with the left-hand side $+n_e$ and once with $-n_e$. Constraints (5) and (6) ensure the static equilibrium at each vertex. The decomposition $n_e^d$ of the normal force $n_e$ into each spatial direction $d \in \{x,y,z\}$ is obtained by multiplying $n_e$ with $\sin (\theta )$, where $\theta$ is the angle between the member and the corresponding d-axis. As the ground structure is fixed in space those coefficients can be preprocessed. With Constraint (7), $a_e$ must be zero if no member is present at edge e. Constraints (8) and (9) define the equilibrium of moments by resolution of the external forces and ensure, in combination with Constraints (5) and (6), that the resulting structure is always a static system of purely axially loaded members. In particular, the cross product $\mathbf {V}(b,v) \times \mathbf {F}_{i,v}$ characterizes the moment induced by external force $\mathbf {F}_{i,v}$ on bearing b with lever arm $\mathbf {V}(b,v)$. Analogously, $\mathbf {V}(b,b')\times \mathbf {r}_{b'}$ is the moment about bearing b caused by the bearing reaction force at $b'$.

The resulting structure is ensured to be adequately dimensioned for any of the $2^C$ loading scenarios resulting from the combination of C loading cases. However, if the resulting structure only needs to be adequately dimensioned for each individual loading case, the model can be altered by enforcing $\sum _{i=1}^C y_i=1$ on the universal variables. In this case only C loading scenarios, which correspond to the loading cases, are of interest. As such a constraint cannot simply be added to the constraint system, see [6], this case is implemented using a single integer universal variable specifying the load case, which is then transformed into existential indicator variables.

In order to illustrate our approach we use a 40-member planar rectangular grid with fixed bearing at the bottom left, floating bearing at the bottom right, and four loading cases color-coded in Fig. 2. Note that the dimensions and color-coded loading cases of all figures in this work are not to scale.

Fig. 2.

Optimal solutions for (a) $A_{\min }=0\,\mathrm{mm}$, without symmetry, combined cases, (b) $A_{\min }\equiv A_{\text {VDI}}$, without symmetry, combined cases, (c) $A_{\min }\equiv A_{\text {VDI}}$, without symmetry, single cases, (d) $A_{\min }\equiv A_{\text {VDI}}$, with symmetry, single cases

In Fig. 2a the optimal solution for $A_{\min }=0\,\mathrm{mm}$ is displayed, which is stable for any combination of the loading case. Figure 2b contains the optimal solution if each single member must be dimensioned according to VDI 3405-3-3, 3405-3-4. For the case that the loading cases can only occur individually the optimal solution is shown in Fig. 2c. Figure 2d displays the optimal solution if we additionally demand symmetry around the vertical mid-axis. Note that in neither case one has to explicitly deal with any kind of worst-case scenario, but can be assured that a solution is in a static equilibrium in every scenario. Most importantly, in general one cannot assume the worst-case scenario to be the one where all loading cases are active, as compensation of forces might occur.

3 Computational Experiments

We conduct experiments on three-dimensional ground structures with artificial loading cases. The first example showcases that a large number of scenarios can be considered, while the second example demonstrates that large three-dimensional ground structures can be used. We assume a basic vertex distance of 10 mm, two fixed bearings on the two lower left corners, and two floating bearings on the lower right corners. The considered material is fine polyamide PA 2200, with layer thickness of 0.12 mm for Selective Laser Sintering (SLS) and a yield strength of $\sigma _y=45 \pm 0\,\mathrm{N\, mm}^{-2}$. For each QMIP instance we built the corresponding Deterministic Equivalent Problem (DEP) [3] and used CPLEX to solve the arising MIP instance¹. For each instance we limit the runtime to 240 h.

Table 3. Computational results for the 296-member space truss

296-member Space Truss with 128 Loading Scenarios

We assume seven loading cases and are interested in structures that are able to withstand each of the $2^7$ loading scenarios resulting from combining the single loading cases. We examine the optimization results for several values of $A_{\min }$, but refer to the minimum diameter $D_{\min }$ for presentation reasons. The individual loading cases are given in Fig. 3a–3g. Additionally, optimal structures for each individual case are displayed for better comprehensibility. In Fig. 3h the best found robust solution for $D_{\min }=1\,\mathrm{mm}$ is displayed, which is stable in any of the $2^7$ loading scenarios.

Table 3 contains the objective values of the best found solutions, the best lower bounds, and the corresponding optimality gap for different settings.

Fig. 3.

Loading cases (a-g) and robust solution (h) for $R(e)=e$ and $D_{\min }=1\, \mathrm{mm}$

Fig. 4.

Non-symmetric solutions for (a) $D_{\min }= 0\, \mathrm{mm}$, (b) $D_{\min }\equiv D_{\text {VDI}}$, (c) $D_{\min }= 3\,\mathrm{mm}$, and symmetric solution for (d) $D_{\min }= 3\, \mathrm{mm}$

For $D_{\min }=0\,\mathrm{mm}$ the DEP of the QMIP instance can be preprocessed to be a Linear Programming (LP) problem, as the binary $\mathbf {x}$ variables can be fixed to 1. The corresponding optimal solutions where found within 2 and 0.5 h for the non-symmetrical and symmetrical case, respectively. For all other instances, except for the symmetric instance with $D_{\min }=1\,\mathrm{mm}$, the optimality gap was not closed sufficiently within 240 h. Table 3 indicates, that for increasing $D_{\min }$ it becomes computationally more expensive to obtain small optimality gaps, which is partially due to the worsening of the corresponding LP-relaxation. Four best found solutions for various values of $D_{\min }$ are shown in Fig. 4.

The solutions differ considerably: with increasing $D_{\min }$ the number of structural members tends to decrease and when additionally enforcing the VDI design rules, long members—in particular diagonal members—are avoided. Note that only the structure given in Fig. 4a is optimal. In Fig. 4d the drawback of demanding symmetry becomes apparent: the sufficient triangular structure at the bottom is no longer feasible.

Symmetry. Demanding a symmetrical structure reduces the number of continuous $\mathbf {a}$ and binary $\mathbf {x}$ variables from 296 to 94. This results in a computational benefit which is reflected in Table 3; in particular when comparing the optimality gap. Obviously, the volume of the optimal symmetrical structure cannot be lower than for the one without symmetry. Nevertheless, in some cases the incumbent symmetrical solution has lower volume when the time limit was reached. The solutions for $D_{\min }=0\,\mathrm{mm}$ and $D_{\min }=1\,\mathrm{mm}$ indicate the price of demanding a symmetric structure: the volume of the symmetric solution increased by about $\frac{1}{6}$ for this instance.

Minimal Diameter. The manufacturable minimal diameter depends on the manufacturing process and is obviously always larger than zero. The computational results for $D_{\min }=0\,\mathrm{mm}$, however, invite to use these quickly obtained solutions, but the resulting structures exhibit several structural members with extremely small diameter of $<0.1 \,\mathrm{mm}$. Hence, solving this LP formulation is computational efficient but unsuitable for direct application in engineering. However, in order to utilize this stable solution one can inflate small members until they have the desired diameter. Table 4 shows the resulting volumes of the structures when—starting from the optimal solution for $D_{\min }=0\,\mathrm{mm}$—the diameter of affected members is increased to the actual value of $D_{\min }$. In all cases the volume dramatically exceeds the corresponding best structure found during the optimization process, cf. Table 3. Therefore, when disregarding the runtime, solving the model with explicitly stated minimum diameter is preferable to postprocessing the quickly obtained optimal solutions for $D_{\min }=0 \,\mathrm{mm}$.

Table 4. Truss volumes when inflating members to $D_{\min }$ based on LP solution

1720-member Space Truss with 8 Loading Scenarios

We assume a $90\,\mathrm{mm} \times 30 \,\mathrm{mm}\times 50\,\mathrm{mm}$ ground structure with $10\,\mathrm{mm}$ basic vertex distance and 8 loading cases. We are interested in symmetrical structures that are stable in each individual loading case.

Table 5. Computational results for the 1720-member space truss

In Table 5 computational results for various values of $D_{\min }$ are presented. Only for $D_{\min }=0\,\mathrm{mm}$ the optimal solution was found (in 104 min).

Fig. 5.

$D_{\min }=1\,\mathrm{mm}$ (left) and $D_{\min }\equiv D_{\text {VDI}}$ (right) with eight loading scenarios

In Fig. 5 the eight (colored) loading cases as well as the best found solutions for $D_{\min }=1\,\mathrm{mm}$ and $D_{\min }\equiv D_{\text {VDI}}$ with 479 and 320 members, respectively, are displayed. For comparison: the optimal solution for $D_{\min }=0\,\mathrm{mm}$ exhibits 1004 members. Hence, changing the minimal diameter significantly alters the structure’s topology.

4 Conclusion

We utilized quantified programming to introduce a robust formulation for the shape and topology optimization of truss-like structures. Instead of determining and optimizing a worst-case scenario based on engineering experience and prone to human error, our approach allows to state loading cases while the resulting structure is ensured to be stable, even in the (unknown) worst-case. A distinction can be made as to whether the loading cases can only occur individually or whether they can occur in any combination. We presented results on a 296-member space truss, considering the combination of seven loading cases resulting in 128 scenarios. A 1720-member space truss with 8 individually occurring loading cases demonstrates the applicability of our approach for large-scale structures. Additionally, we highlighted advantages and disadvantages of explicitly enforcing a minimal cross-sectional area of structural members and a symmetric structure. Future work has to deal with the distortion of the objective value due to overlapping members and the development of problem specific heuristics.