Truss topology optimization with discrete design variables—Guaranteed global optimality and benchmark examples

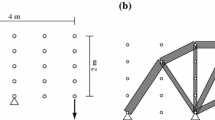
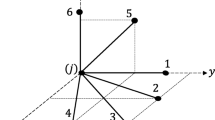
Abstract

This paper considers the problem of optimal truss topology design subject to multiple loading conditions. We minimize a weighted average of the compliances subject to a volume constraint. Based on the ground structure approach, the cross-sectional areas are chosen as the design variables. While this problem is well-studied for continuous bar areas, we consider in this study the case of discrete areas. This problem is of major practical relevance if the truss must be built from pre-produced bars with given areas. As a special case, we consider the design problem for a single available bar area, i.e., a 0/1 problem. In contrast to the heuristic methods considered in many other approaches, our goal is to compute guaranteed globally optimal structures. This is done by a branch-and-bound method for which convergence can be proven. In this branch-and-bound framework, lower bounds of the optimal objective function values are calculated by treating a sequence of continuous but non-convex relaxations of the original mixed-integer problem. The main effect of using this approach lies in the fact that these relaxed problems can be equivalently reformulated as convex problems and, thus, can be solved to global optimality. In addition, these convex problems can be further relaxed to quadratic programs for which very efficient numerical solution procedures exist. By exploiting this special problem structure, much larger problem instances can be solved to global optimality compared to similar mixed-integer problems. The main intention of this paper is to provide optimal solutions for single and multiple load benchmark examples, which can be used for testing and validating other methods or heuristics for the treatment of this discrete topology design problem.