1 Introduction

The numerical solution of transport phenomena in complex geometrical domains is a subject of continuous development regarding three characteristics: accuracy, robustness and efficiency. The geometrical complexity can be handled with different grid topologies and the understanding of their issues is relevant for industrial applications. High-order computation is a demanding issue, motivated by a potential reduction of computational cost for complex computational fluid dynamics (CFD) problems.

High-order accurate methods for unstructured grids have historically been focused on hyperbolic equations, see e.g. Lê et al. [1]. Barth and Frederickson [2] developed a high-order Finite Volume Methods (FVM) for the resolution of the Euler equations, using a quadratic polynomial. The coupling of Euler system with viscous terms, which requires diffusive schemes was achieved by Ollivier-Gooch et al. [3].

In the last years, the development of high-order methods was applied for the resolution of parabolic and elliptic problems in unstructured grids, see e.g. Boularas et al. [4]. The range of possible applications varies from Poisson problems, see Batty [5], heat transfer problems, see e.g. Chantasiriwan [6], diffusion equations with variable coefficients, see Zhai [7], or discontinuous coefficients, see e.g. Clain et al. [8].

Several polynomial reconstruction techniques applied to FVM can be highlighted: the fourth-order methods of Ollivier-Gooch et al. [9], Cueto-Felgueroso et al. [10], and Nogueira et al. [11], also sixth-order results have been reported by Clain et al. [12]. The objective of this work is to extend the weighted least-squares (WLS) method to very high-order schemes and polyhedral unstructured grids.

In terms of other applications with the weighted least-squares technique. Magalhaes et al. [13] and Albuquerque et al. [14] have developed, respectively, relative and absolute error estimators for second-order finite volume schemes with unstructured grids. Martins et al. [15, 16] has created a third-order interpolation method with divergence free constraint for immersed boundary applications, respectively, for Cartesian and unstructured polyhedral grids.

The following manuscript is divided in four sections: in Sect. 2 the implemented method for two dimensions is briefly described, in Sect. 3 the verification of the implemented schemes, with Cartesian and perturbed grids, is carried out. Section 4 shows the results for a case with irregular polyhedral and triangular grids and proposes a novel method to treat the Neumann boundary conditions, Sect. 5 concludes the manuscript with a summary of the principal achievements of this work.

2 Elliptical Operator for Unstructured Grids with the Least Squares Technique

In this work, the Poisson equation will be solved, which is defined by:

$$\displaystyle \begin{aligned} \nabla\cdot\nabla\phi=\varphi_{\phi}, \end{aligned} $$
(1)

where ϕ is the transported variable and φ ϕ is the source term that is required when using manufactured analytical solutions and it is equal to its own Laplacian. After applying the classic Finite Volume method in a Poisson equation the following equation is obtained:

$$\displaystyle \begin{aligned} \sum_{f\in\mathcal{F}\left(P\right)}{\sum_{g\in\mathcal{G}\left(f\right)}\nabla \phi_{g}w_{G_g} \cdot \mathbf{S_{f}}}=\int_{CV}{\varphi_{\phi}}dV, \end{aligned} $$
(2)

where \(\mathcal {F}\left (P\right )\) is the set of faces of cell P, \(\mathcal {G}\left (f\right )\) is the set of Gauss points of the face f, S f is the face normal vector and w G is the weight of Gauss-Legendre Quadrature. The important part of this method is how the calculation of the face gradient ∇ϕ g is carried out at each Gauss point. This will be explained in the next subsection.

2.1 Polynomial Reconstructions

To obtain the gradients values at the integration points, a reconstruction of the unknown primitive variable is performed at the face centroid, using a polynomial expansion.

The number of terms of the polynomial has to take into account the required order of the scheme and it has the following form:

$$\displaystyle \begin{aligned} \begin{gathered} \phi_{f}^R\left(x,y\right)=C_1+C_2\left(x-x_f\right)+C_3\left(y-y_f\right)+ \hfill \\ \quad \quad \quad \quad +C_4\left(x-x_f\right)^2+C_5\left(x-x_f\right)\left(y-y_f\right)+C_6\left(y-y_f\right)^2+\cdots \hfill. \end{gathered} \end{aligned} $$
(3)

Expression (3) can be written in a more compact form, a vectorial one, as:

$$\displaystyle \begin{aligned} \phi_{f}^R\left(\mathbf{x}\right)={\mathbf{d}}_f\left(\mathbf{x}\right){\mathbf{c}}_f. \end{aligned} $$
(4)

where the subscript f refers that the reconstruction is made at the face f and \({\mathbf {d}}_f\left (\mathbf {x}\right )=\left [1,\;\left (x-x_f\right ),\;\left (y-y_f\right ),\;\left (x-x_f\right )^2,\;\left (x-x_f\right )\left (y-y_f\right ),\;\left (y-y_f\right )^2,\!\!\right .\) \(\left .\cdots \right ]\), \({\mathbf {x}}_f=\left (x_f,\;y_f\right )\) is the face centroid coordinates vector, \(\mathbf {x}=\left (x,\;y\right )\) is the coordinates vector of a point used for the reconstruction and \({\mathbf {c}}_f=\left [C_1,\;C_2,\;C_3,\;C_4,\;C_5,\;C_6,\;\cdots \right ]^T\) are the reconstruction constants.

Table 1 lists the number of terms of the expansion for each polynomial used in this work.

Table 1 Number of terms of the Taylor expansion required for a pth order polynomial at two dimensional (2D) cases
Full size table

The order of accuracy of the numerical scheme is p + 1, consequently the linear reconstruction will be second order accurate, the cubic reconstruction will be fourth order accurate, the fifth polynomial will have sixth order accurate and finally the seventh polynomial will be eighth order accurate. The numerical schemes will be called of \(\mathit {FLS}\left (p+1\right )\) according to the global order of the implemented method. For each order a minimum number of Gauss points are required to maintain the respective Quadrature order.

2.2 General Approach

The Weighted Least Squares (WLS) method is a technique used to solve overdetermined problems, where there are more independent equations than unknowns.

Equation (4) results in a system of linear equations, which the form as:

$$\displaystyle \begin{aligned} {\mathbf{D}}_f\,{\mathbf{c}}_f=\boldsymbol{\upphi}_s, \end{aligned} $$
(5)

where D f is a combination of \({\mathbf {d}}_f\left (\mathbf {x}\right )\) for every point of the reconstruction resulting in a matrix with n s × n coefs entries. The c f is a column vector with n coefs entries, ϕ s is a column vector with n s entries, n coefs is the number of constants of the p th polynomials and n s the size of the computational stencil, which is the set of the computational values and points used in the reconstruction and is made of cell neighbours of the face. Since n s > n coefs, the problem is overdetermined and so the WLS technique is used in order to minimize the weighted residual of the problem.

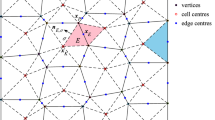
To solve this problem, specific stencils must be used for each scheme order. This is done by using vertex neighbours according to the experience of the Authors in a previous work [14]. Each successive order scheme requires an higher stencil to respect the n s > n coefs condition. Figure 1 shows examples of these stencils for a regular polyhedral and triangular grid. Basically each successive vertex neighbours (from 1 to 4) is used for a scheme with an even order accuracy. For example the second order scheme only needs a first order of vertex neighbours from the face marked in red.

Fig. 1
figure 1

Examples of different vertex neighbours order from the red face

Full size image

Other details used in the global matrix construction A ij are described in the work of Vasconcelos et al. [17]. Each line of the global matrix A ij corresponds to the diffusive discretization of the cell i and has to consider the diffusive flux integral for each face of the cell. This flux integral is computed from the polynomial reconstruction centered in the respective face and which was described previously. Finally the high-order diffusive fluxes can be written in the following matrix form:

$$\displaystyle \begin{aligned} {\mathbf{A}}_{ij}\phi_{j}=\sum_{f\in\mathcal{F}\left(i\right)} \left( \sum_{g\in\mathcal{G}\left(f\right)} w_{Gg}\mathbf{t_f}_j\left({\mathbf{x}}_g\right)\phi_{j} \right) \cdot {\mathbf{S}}_f,\end{aligned} $$
(6)

where \(\mathcal {F}(i)\) is the set of faces from cell i, \(\mathcal {G}(f)\) is the set of Gauss-Legendre points of face f, w Gg is the weight, x g are the coordinates of each Gauss-Legendre point g and t f j is the contribution from cell j to the face f diffusive flux from the reconstructed polynomial. The set of cells j is defined by the used stencil in the polynomial reconstructed at each face f, globally each line i will have contributions from all cells that result from the junction of sets from all faces of cell i.

3 Order Convergence Verification with Cartesian and Perturbed Non-uniform Grids

A numerical test is performed in non-uniform grids with an certain imposed displacement. This perturbation is done by moving randomly the grid lines in a range between zero and a % (γ) of the grid size from the Cartesian grid counterpart. This perturbation can be done in either a positive or negative direction. The cells of the grids are always squares and a reference grid without any perturbation is used, i.e. a Cartesian one. For this case, the following analytical solution was used and solved in a 1 × 1 square domain:

$$\displaystyle \begin{aligned} \phi\left(x,y\right)=\exp\left(-\frac{\left(x-0.5\right)^2+\left(y-0.5\right)^2}{0.0175}\right), \end{aligned} $$
(7)

Table 2 lists the error ratios, r, between a grid with an imposed perturbation and a regular one. Showing the ratio for both the mean and maximum error of the finest grid at study. Particularly for the FLS6 and FLS8 schemes, the error could be one order of magnitude greater than the obtained with the Cartesian grid. It is also shown that an imposed perturbation up to 20% has a low numerical error penalization.

Table 2 Ratio of mean and maximum error norms for all schemes between grids with an imposed perturbation and a Cartesian one with 25,600 cells
Full size table

Figure 2 shows the convergence curves obtained but only with the FLS4 and FLS8 schemes. It is possible to observe that the theoretical convergence orders is achieved for every perturbed grid.

Fig. 2
figure 2

Convergence curves for the imposed perturbed grids with FLS4 and FLS8

Full size image

Figure 3 shows the error distribution for the FLS8 scheme with a Cartesian and perturbed grid with γ = 30%. It is shown that the error distribution is severally changed by the imposed perturbation at the grid.

Fig. 3
figure 3

Error distribution for FLS8 scheme and two grid with 25,600 cells: one without any perturbation (left) and one with an imposed perturbation (right)

Full size image

4 Results for Several Grid Types and with Neumann Boundary Conditions

To verify the applicability of the proposed schemes to other grid types and Neumann boundary conditions. The numerical verification was performed with an analytical solution in a square domain, \(\left [0,1\right ]\). A Neumann boundary condition were imposed at the vertical faces and a Dirichlet boundary condition at the remaining ones.

Two different approaches were used when considering Neumann boundary conditions. The first approach is the classic one, which consists in simply derivation of the respective line from the least-squares matrix that represent the boundary face. It will be defined as the general case (GC) approach.

The second approach which is new to the Author’s knowledge and it consists on the multiplication of each line of the D f matrix referent to Neumann boundary face, b, by the respective face area, S b. That line will be written by \(\nabla {\mathbf {d}}_f\left ({\mathbf {x}}_b\right ){\mathbf {S}}_b\), instead of \(\nabla {\mathbf {d}}_f\left ({\mathbf {x}}_b\right ){\mathbf {n}}_b\) and the entry for the vector ϕ f is given by ∇ϕ b S b, instead of ∇ϕ b n b. Consequently, the problem will have the following aspect:

(8)

where the line in the matrix separates the contribution of the stencil cells and Dirichlet faces from the contribution of the Neumann faces of the current considered stencil.

The goal of this operation is to ensure that the vector ϕ s and each line of the least-squares matrix D f have the same unit dimensions, something that does not happen with the classic approach. This approach will be designed as dimensional correction (DCN) for Neumann boundary condition.

Numerical tests were performed for two grid types: irregular polyhedral and triangular grids. The analytical solution is given by:

$$\displaystyle \begin{aligned} \phi\left(x,y\right)=\sin\left(3\pi x\right)\sin\left(3\pi y\right), \end{aligned} $$
(9)

where in the Neumann boundaries the face flux will be ∇ϕ b ⋅S b ≠ 0.

Fig. 4
figure 4

Convergence curves of the mean error for mixed boundary conditions with irregular polyhedral and triangular grids for all schemes. The dotted lines are the convergence curves for the GC approach and the solid ones represent the convergence curves with the DCN approach

Full size image

Figure 4 shows the convergence curves to both approaches applied for all schemes with the irregular polyhedral (left) and triangular grids (right). The solid line represents the DCN approach and the dotted one represents the classic GC approach. The results point out that the theoretical convergence order is always achieved for both grids and indicates that the DCN approach improves the schemes performance, being more evident for the FLS2 and for FLS8 schemes, specially to the last one. The behaviour of the finest grids are more stable with the DCN.

Table 3 lists the comparison of the two approaches used for the Neumann BC for the irregular polyhedral grid, the comparison is made through the ratio between both approaches and using the mean and maximum error norm, r is computed by:

$$\displaystyle \begin{aligned} r_i=\frac{\Vert e\Vert_i^{GC}}{\Vert e\Vert_i^{DC_N}}, \end{aligned} $$
(10)

where i is the error norm used for the calculation.

Table 3 Comparison between the two approaches for a problem with an imposed Neumann BC for all schemes applied to the irregular polyhedral grids
Full size table

The results show that the biggest decrease of the error occurs for the maximum error. For the FLS8 scheme the error can be reduced up to 21 times, since the new method avoids the truncation error issue presented in the GC and showed in Fig. 4.

Table 4 lists the comparison between the two approaches used for the Neumann BC with the triangular grids. The results obtained allow to conclude that the major decrease of the numerical error occurs for the maximum error, which can be reduced almost one order of magnitude for the second-order scheme and to half with the fourth-order scheme. For the sixth-order scheme the maximum error with this new approach is slightly worse, almost 10%, than the general approach, however in terms of mean error the gain is evident since the mean error is reduced to half with the DCN approach. For the eighth-order scheme, it is possible to reduce the error in about three orders of magnitude since it avoids the truncation error issue.

Table 4 Comparison between the two approaches for a problem with an imposed not-null Neumann BC for all schemes applied to the triangular grids
Full size table

5 Conclusions

Verifications tests have been performed for a new high-order schemes based on the weighted least-squares technique for the Finite Volume method. The convergence curves have showed an excellent behaviour indicating that the theoretical order is achieved for cases at study. Also the new reconstruction method is not very sensitive to the imposed perturbations in the grid or either the topology of the cells.

Additionally, the results allowed to conclude that the novel proposed approach to treat the Neumann boundary conditions, improves the quality of the solution. These results are the expected ones, since in the WLS problem the dimensions of the matrices are identical to each other, when using this novel approach.