1 Introduction

Multiphase flow is not a canonical problem, therefore different models can be found in the literature. Volume Of Fluid (VOF) model [9] is amongst the simplest. It defines a single set of momentum equations shared by all phases, whilst the volume fraction (fraction of a particular infinitesimal control volume which is occupied by each phase) is tracked throughout the domain following an advection equation. Phase-field methods [11] conserve the simplicity of VOF whilst increasing the physical meaning of the evolution equation of the fluids present in the simulation. The volume fraction is substituted by a phase-field parameter, which identifies each phase. In this work, the Cahn–Hilliard equation [4] is chosen to model the evolution of the phase-field parameter.

The introduced model is discretised in space using a high-order discontinuous Galerkin method. These methods have been gaining popularity for the discretisation of conservation laws, such as the Navier–Stokes equations [5,6,7, 13, 16, 19, 23]. Specifically, we use a Discontinuous Galerkin Spectral Element Method (DGSEM) [2] that allows the generation of provably stable schemes [8]. These schemes provide enhanced robustness when compared to classical high-order methods [17]. As far as the temporal discretisation is concerned, we use an efficient implicit-explicit approach that permits maintaining the time step restriction of a typical one phase Navier–Stokes solver. It should be noticed that similar approaches to model multiphase flows have been proposed in the past, see for example [26], where an algorithm to model N immiscible incompressible fluids with high-order methods is described. However, according to the authors knowledge, this is the first implementation using the DGSEM.

The rest of the paper is organised as follows: in Sect. 2 the governing equations of the model are described. In Sect. 3 the numerical techniques to discretise the described model are introduced. Finally, in Sect. 4 the results of two validation test cases are shown.

2 Governing Equations

In this work we model multiphase flows with a phase field approach. The flow field is modelled by means of the incompressible Navier–Stokes equations. The evolution of each of the fluids is modelled with the Cahn–Hilliard equation, which defines a phase field variable, ϕ ∈ [−1, 1], that identifies spatial coordinates occupied by fluid 1, ϕ = −1, fluid 2, ϕ = 1, or an interface ϕ ∈ (−1, 1). The value of the thermodynamic properties of the fluids at each spatial coordinate can be computed as:

$$\displaystyle \begin{aligned} \rho(\phi) = \rho_1\left(\frac{1-\phi}{2}\right) + \rho_2\left(\frac{1+\phi}{2}\right),~~ \eta(\phi) = \eta_1\left(\frac{1-\phi}{2}\right) + \eta_2\left(\frac{1+\phi}{2}\right), \end{aligned} $$
(1)

where ρ i is the density of fluid i whilst η i is the dynamic viscosity of fluid i. The complete system is built considering first the momentum equation,

$$\displaystyle \begin{aligned} \frac{\partial\left(\rho\mathbf{v}\right)}{\partial t} + \nabla\cdot\left(\rho\mathbf{v}\mathbf{v}\right) = -\nabla p + \frac{1}{Re} \nabla\cdot\left(\eta\left(\nabla\mathbf{v} + \nabla{\mathbf{v}}^T\right)\right) + \frac{3}{\sqrt{2}\varepsilon ReCa}\mu\nabla\phi + \frac{1}{Fr^2}\rho{\mathbf{e}}_g, {} \end{aligned} $$
(2)

with velocity v, static pressure p, Reynolds number \(Re = \frac {\rho _1 u_0 L}{\eta _1}\) (where u o is a reference velocity whilst L is a reference length), Capillary number \(Ca=\frac {\eta _1 u_0}{\sigma }\) (where σ represents the surface tension), Froude number \(Fr = \frac {u_0}{\sqrt {gL}}\), (where g is the gravity acceleration) and e g is the gravity direction. Second, an artificial compressibility method [22] is used to couple the divergence-free condition,

$$\displaystyle \begin{aligned} \frac{\partial p }{\partial t} + \frac{\rho_0}{\rho_1} \frac{1}{M_0^2} \nabla\cdot\mathbf{v} = 0, {} \end{aligned} $$
(3)

where \(\rho _0 = \max \left (\rho _1,\rho _2\right )\) is a reference density, and M 0 is the artificial compressibility Mach number. Third, the Cahn–Hilliard equation for the phase field,

$$\displaystyle \begin{aligned} \frac{\partial \phi}{\partial t} + \nabla\cdot\left(\phi\mathbf{v}\right) = M\nabla^2 \mu, ~~\mu = -\phi + \phi^3 - \varepsilon^2 \nabla^2 \phi, {} \end{aligned} $$
(4)

with M the mobility, and ε the interface width, the two free parameters of the model. In (2) and (4), μ represents the chemical potential. Moreover, this equation is designed to minimize the free-energy functional [4], \(\mathcal F\),

$$\displaystyle \begin{aligned} \mathcal F(\phi,\nabla\phi) = \int_{\Omega}\left(\frac{1}{4}\left(1-\phi\right)^2\left(1+\phi\right)^2 + \frac{1}{2}\varepsilon^2|\nabla\phi|{}^2\right)dx. {} \end{aligned} $$
(5)

Note that the set of Eqs. (2)–(4) is written in non-dimensional form, where the thermodynamic variables of fluid 1 are taken as reference values, e.g.,

$$\displaystyle \begin{aligned} \rho(\phi) = \left(\frac{1-\phi}{2}\right) + \frac{\rho_2}{\rho_1}\left(\frac{1+\phi}{2}\right),~~ \eta(\phi) = \left(\frac{1-\phi}{2}\right) + \frac{\eta_2}{\eta_1}\left(\frac{1+\phi}{2}\right). \end{aligned} $$
(6)

The set (2)–(4) can be written as an advection-diffusion system:

$$\displaystyle \begin{aligned} \frac{\partial u}{\partial t} + \nabla\cdot\mathbf{F}(u) = \nabla\cdot{\mathbf{F}}_v(u,\mathbf{g}) + S(u,\mathbf{g}), {} \end{aligned} $$
(7)

where u = (ϕ, ρ v, p) is the state vector, g = (g ϕ, g v, g μ) = (∇ϕ, ∇v, ∇μ) is the gradients vector, F(u) and F v(u, g) are the inviscid and viscous fluxes respectively, and S(u, g) is a source term,

$$\displaystyle \begin{aligned} \mathbf{F}(u) &= \left[\begin{array}{c} \phi \mathbf{v} \\ \rho \mathbf{v}\mathbf{v} + p\boldsymbol{\mathcal I}_3 \\ \frac{\rho_0}{\rho_1} \frac{1}{M_0^2} \mathbf{v}\end{array}\right], {\mathbf{F}}_v(u,\mathbf{g}) = \left[\begin{array}{c} {\mathbf{g}}_\mu \\ \eta\left({\mathbf{g}}_v + {\mathbf{g}}_v^T\right) \\ 0 \end{array}\right], \\ &\quad S(u,\mathbf{g}) = \left[\begin{array}{c} 0 \\\displaystyle{ \frac{3}{\sqrt{2}\varepsilon ReCa}\mu{\mathbf{g}}_\phi+ \frac{1}{Fr^2}\rho{\mathbf{e}}_g} \\ 0 \end{array}\right]. \end{aligned} $$
(8)

3 Numerical Methods

The numerical implementation of (2)–(4) is performed using a high-order discontinuous Galerkin scheme for the spatial discretisation (DGSEM variant) and an implicit-explicit Euler scheme for the time discretisation.

3.1 Spatial Discretisation Using a Nodal Discontinuous Galerkin Scheme (DGSEM)

Discontinuous Galerkin (DG) schemes (see [15]) are constructed by tessellating the domain in non-overlapping elements, where the solution is approximated using polynomials of an arbitrary order, N. In this particular implementation, we use a nodal variant of the DG method, and we restrict ourselves to hexahedral elements.

In each element we approximate the solution using polynomials written in a set of local spatial coordinates ξ = (ξ, η, ζ) ∈ [−1, 1]3, which are related to the physical space by a transfinite mapping,

$$\displaystyle \begin{aligned} \mathbf{x}=(x,y,z) = \mathbf{X}(\mathbf{\xi}) = \mathbf{X}\left(\xi,\eta,\zeta \right). \end{aligned} $$
(9)

Using the local coordinates, we write the solution using tensor product Lagrange polynomials,

$$\displaystyle \begin{aligned} u(\mathbf{x})\big|{}_{E} \approx U(\mathbf{\xi}) = \sum_{i,j,k=0}^{N}U^{ijk}(t)l_i(\xi)l_j(\eta)l_k(\zeta), {} \end{aligned} $$
(10)

where the time-dependent coefficients U ijk(t) are the nodal values of the solution U, and l j(ξ) are the Lagrange polynomials based on a set of Gauss points \(\{\xi _j\}_{j=0}^N\). To handle curvilinear geometries, we use a mapping X that transforms local and physical spaces. With this mapping, we can construct covariant a i and contravariant a i basis, and their associated Jacobian J, and metrics matrix \(\boldsymbol {\mathcal M}\):

$$\displaystyle \begin{aligned} {\mathbf{a}}_i = \frac{\partial \mathbf{X}(\mathbf{\xi})}{\partial \xi_i},~~ {\mathbf{a}}^i = \nabla \xi_i = \frac{1}{J}{\mathbf{a}}_j \times {\mathbf{a}}_k,~~ J={\mathbf{a}}_i \cdot \left({\mathbf{a}}_j \wedge{\mathbf{a}}_k\right),~~\boldsymbol{\mathcal M}=[J{\mathbf{a}}^{\xi},J{\mathbf{a}}^{\eta},J{\mathbf{a}}^{\zeta}]. \end{aligned} $$
(11)

Following [14], we transform the system of Eqs. (7) to local coordinates,

$$\displaystyle \begin{aligned} \begin{aligned} \frac{\partial}{\partial t}\left\{\begin{array}{c} J \phi \\ J \rho \mathbf{v} \\ J p \end{array}\right\} + \nabla_\xi\cdot\left\{\begin{array}{c} \boldsymbol{\mathcal M}^T\mathbf{v}\phi \\ \boldsymbol{\mathcal M}^T\rho\mathbf{v}\mathbf{v} + \boldsymbol{\mathcal M}^Tp \boldsymbol{\mathcal I}_3 \\ \boldsymbol{\mathcal M}^T\frac{1}{{M_0}^2}\mathbf{v} \\ \end{array}\right\} &=\nabla_\xi\cdot\left\{\begin{array}{c} M\boldsymbol{\mathcal M}^T{\mathbf{g}}_\mu \\ \frac{1}{Re}\boldsymbol{\mathcal M}^T\left(\eta \left({\mathbf{g}}_{\mathbf{v}} + {\mathbf{g}}_{\mathbf{v}}^T\right)\right)\\ 0 \end{array}\right\} \\ + J \left\{\begin{array}{c} 0 \\ \frac{1}{Fr^2}\rho{\mathbf{e}}_g + \frac{3}{\sqrt{2}ReCa\varepsilon}\mu{\mathbf{g}}_\phi \\ 0 \end{array}\right\}, {} \end{aligned} \end{aligned} $$
(12)

with gradients,

$$\displaystyle \begin{aligned} J{\mathbf{g}}_{\mathbf{v}} = \boldsymbol{\mathcal M}\nabla_\xi\mathbf{v},~~J{\mathbf{g}}_\phi = \boldsymbol{\mathcal M}\nabla_\xi\phi, ~~J{\mathbf{g}}_\mu = \boldsymbol{\mathcal M}\nabla_\xi\mu, {} \end{aligned} $$
(13)

and the chemical potential definition,

$$\displaystyle \begin{aligned} J \mu = -J\phi + J\phi^3 - \varepsilon^2 \nabla_\xi\cdot\left(\boldsymbol{\mathcal{M}}^T {\mathbf{g}}_\phi\right). {} \end{aligned} $$
(14)

We obtain the DG scheme replacing the continuous solution by their polynomial counterpart (10), then multiplying (12), written in compact form (7), by a polynomial test function (with same order N as the solution) 𝜗, and we integrate the result in one element E = [−1, 1]3,

$$\displaystyle \begin{aligned} \int_{E} J \vartheta\frac{\partial U}{\partial t} + \int_{E}\vartheta\nabla_\xi\cdot\mathbf{F}(U) = \int_{E}\vartheta\nabla_\xi\cdot{\mathbf{F}}_v(U,\mathbf{G}) + \int_{E}J\vartheta S(U,\mathbf{G}). \end{aligned} $$
(15)

Next, we integrate by parts the terms containing divergences, which yields surface integrals. Since the solution is discontinuous at the inter-element faces, we replace the surface flux by a numerical flux, F ⋆,

$$\displaystyle \begin{aligned} \int_{E} J \vartheta\frac{\partial U}{\partial t} &+\int_{\partial E}\vartheta{\mathbf{F}}^\star\cdot\hat{n}dS-\int_{E}\nabla_\xi\vartheta \cdot \mathbf{F} = \int_{\partial E}\vartheta{\mathbf{F}}_v^\star\cdot\hat{n}dS \\ &-\int_{E}\nabla_\xi\vartheta \cdot {\mathbf{F}}_v + \int_{E} J \vartheta S(U,\mathbf{G}), {} \end{aligned} $$
(16)

where ∂E represents the six surfaces of the element E. For the inviscid numerical flux F ⋆, we use the exact Riemann solver derived in [1], whilst for the viscous numerical flux we use the Symmetric Interior Penalty (SIP) method [24], with the penalty parameter value derived in [21] and recently discussed for the DGSEM in [18]. In (16), \(\hat {n}\) is the surface outward normal vector in local coordinates. To obtain the evolution equations for each nodal degree of freedom U ijk, we let 𝜗 = l i(ξ)l j(η)l k(ζ), and compute the integrals using the Gauss quadrature points (and weights {w i}) associated to the interpolation points (which provide an accuracy of 2N + 1),

$$\displaystyle \begin{aligned} \begin{aligned} J^{ijk}\frac{dU^{ijk}}{dt} +& \frac{F_x^{\star}}{w_i}(\xi,\eta_j,\zeta_k)l_i(\xi)\bigg|{}_{\xi=-1}^{\xi=1} + \frac{F_y^{\star}}{w_j}(\xi_i,\eta,\zeta_k)l_j(\eta)\bigg|{}_{\eta=-1}^{\eta=1} \\ &+ \frac{F_z^{\star}}{w_k}(\xi_i,\eta_j,\zeta)l_k(\zeta)\bigg|{}_{\zeta=-1}^{\zeta=1}\\ &-\sum_{m=0}^N \left(\frac{w_m}{w_i} D_{mi}F_x^{mjk} + \frac{w_m}{w_j} D_{mj}F_y^{imk} + \frac{w_m}{w_k}D_{mk}F_z^{ijm} \right) = \\ &\frac{F_{v,x}^{\star ijk}}{w_i}(\delta_{iN}-\delta_{i0}) + \frac{F_{v,y}^{\star ijk}}{w_j}(\delta_{jN}-\delta_{j0}) + \frac{F_{v,z}^{\star ijk}}{w_k}(\delta_{kN}-\delta_{k0}) \\ &-\sum_{m=0}^N \left(\frac{w_m}{w_i} D_{mi}F_{v,x}^{mjk} + \frac{w_m}{w_j} D_{mj}F_{v,y}^{imk} + \frac{w_m}{w_k}D_{mk}F_{v,z}^{ijm} \right) + J^{ijk} S^{ijk}, \end{aligned} {} \end{aligned} $$
(17)

where F ijk = F(U ijk) and \(F_v^{ijk} = F_v(U^{ijk},{\mathbf {G}}^{ijk})\), being G ijk the nodal values of the gradient G. The symbol δ ik represents the Kronecker delta. The derivation matrix D ij is defined as \(D_{ij}=l_j^{\prime }(\xi _i)\). To compute the gradient G, we perform the weak formulation of (13),

$$\displaystyle \begin{aligned} \int_{E} J\mathbf{\tau}\cdot \mathbf{G} = \int_{\partial E} U^\star\boldsymbol{\mathcal M}^T\cdot\mathbf{\tau}dS - \int_{E}U\nabla_\xi\cdot\left(\boldsymbol{\mathcal M}^T \cdot\mathbf{\tau}\right), {} \end{aligned} $$
(18)

where τ is an arbitrary vector test function (from the order N polynomials space). Since we use the SIP method, we use solution averages to couple inter-element fluxes, U ⋆ = { {U} }. All the integrals involved in (18) are computed discretely similar to those in (16), i.e.,

$$\displaystyle \begin{aligned} \begin{aligned} J^{ijk} & \tau_{ijk}^d G^{ijk}_d = \frac{U^{\star}(\xi,\eta_j,\zeta_k)Ja_d^{\xi}(\xi,\eta_j,\zeta_k) }{w_i}l_i(\xi)\bigg|{}_{\xi=-1}^{\xi=1} \\ &+\frac{U^{\star}(\xi_i,\eta,\zeta_k)Ja_d^{\eta}(\xi_i,\eta,\zeta_k) }{w_j}l_j(\eta)\bigg|{}_{\eta=-1}^{\eta=1} +\frac{U^{\star}(\xi_i,\eta_j,\zeta)Ja_d^{\zeta}(\xi_i,\eta_j,\zeta) }{w_k}l_k(\zeta)\bigg|{}_{\zeta=-1}^{\zeta=1} \\ & -\sum_{m=0}^N \left(\frac{w_m}{w_i}Ja_d^{\xi,ijk} D_{mi}U^{mjk} + \frac{w_m}{w_j} Ja_d^{\eta,ijk} D_{mj}U^{imk} + \frac{w_m}{w_k}Ja_d^{\zeta,ijk}D_{mk}U^{ijm} \right). \end{aligned} \end{aligned} $$
(19)

The gradient nodal values \(G_d^{ijk}\) are introduced in the viscous fluxes F v(U ijk, G ijk) of (17) hence completing the discretisation of (16). Note that one needs to compute g ϕ before computing μ and its gradient g μ.

3.2 Time Integration Using IMplicit–EXplicit (IMEX) and Runge–Kutta Schemes

The time integration of (17) is performed with a combination of forward and backwards Euler and explicit Runge–Kutta schemes. On the one hand, the Navier–Stokes equations are integrated by means of a third order explicit Runge–Kutta (RK3) scheme [25]. On the other hand, the Cahn–Hilliard equation is integrated with a combination of explicit RK3 for the phase field advection, forward Euler for the chemical free-energy, and backwards Euler for the interfacial energy,

$$\displaystyle \begin{aligned} \frac{\phi^{n+1}-\phi^n}{\Delta t} + \nabla\cdot\left(\mathbf{v}\phi\right)^{RK3} = \nabla^2\left( -\phi^n + \left(\phi^n\right)^3 - \varepsilon^2 \nabla^2 \phi^{n+1}\right). \end{aligned} $$
(20)

The reason behind this choice, is that the numerical stiffness of the bi-Laplacian (∇4 ϕ) operator prevents from using an explicit method, as restricts the time-step Δt to unpractical values. We only treat implicitly the interfacial energy since it yields a constant Jacobian matrix, represented by \(J^{\nabla _2}\). In particular, the linear system to solve is,

$$\displaystyle \begin{aligned} \left[ J^{\nabla_2} + \frac{\mathcal I}{\Delta t}\right]\phi^{n+1} =\frac{\phi^n}{\Delta t} - \nabla\cdot\left(\mathbf{v}\phi\right)^{RK3}+ \nabla^2\left( -\phi^n + \left(\phi^n\right)^3\right). \end{aligned} $$
(21)

The Jacobian matrix is computed numerically (see [3]) and a LU factorisation is performed only at the first time step. In each following iteration, the RHS of (21) is computed and the linear system is solved by means of forward and backward substitutions. Both the LU factorisation and the forward and backward substitutions are performed with the library MKL--PARDISO [20].

4 Validation

The proposed methodology is tested with two test cases. First, the validity of the discontinuous Galerkin discretisation of the Cahn–Hilliard equation is tested with a benchmark spinodal decomposition problem [12]. Second, the validity of the coupled Cahn–Hilliard/Navier–Stokes system is tested with a two dimensional rising bubble test [10].

4.1 Spinodal Decomposition

This test problem considers an initial mixture of two fluids. These fluids are immiscible, therefore they tend to separate to minimise their free energy (5). As stated before, the geometry, initial condition and fluid parameters are taken from [12]. In particular, the initial condition for this benchmark problem is:

$$\displaystyle \begin{aligned} \begin{aligned} \phi(x,y) = -0.05 \left[ \cos{(0.105x)}\cos{(0.11y)} + \left[ \cos{(0.13x)}\cos{(0.087y)}\right]^2 \right.\\ \left.+\cos{(0.025x-0.15y)}\cos{(0.07x-0.02y)} \right]. \end{aligned} \end{aligned} $$
(22)

The physical domain is a “T” shape with a total height of 120 units, a total width of 100 units, and horizontal and vertical section widths of 20 units (Fig. 1). No-flux boundary conditions are applied at the boundaries. Following [12] mobility is set to M = 10, whilst the interface width is set to ε = 3.16. The physical domain is discretised with an unstructured mesh of 326 elements and a polynomial order of N = 4. For the time discretization, we use a time step Δt = 10−3.

Figure 1 shows qualitatively how the different phases separate, whilst Fig. 2 shows quantitatively the evolution of the total free energy with time. In Fig. 2 the results of this work are compared with those obtained in [12], validating the proposed method.

Fig. 1
figure 1

“T” domain for the spinodal decomposition. Initial condition (left figure) and evolution with time (the right figure is the steady-state solution)

Full size image
Fig. 2
figure 2

Evolution of total free energy (5) with time

Full size image

4.2 Rising Bubble

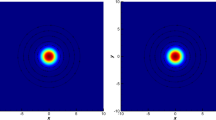
This test case considers a bubble of light fluid submerged in a heavy fluid, both subjected to a gravitational field. Following [10] the initial configuration, see Fig. 3, consists of a bubble of radius r = 0.25 centred at [0.5, 0.5] in a [1 × 2] domain. A no-slip boundary condition is used at the top and the bottom of the domain whilst a free slip condition is enforced at the vertical walls. Following [10], the Reynolds number is set to Re = 35 whilst σ and ε are set to 24.5 and 0.03125 respectively (this gives a Eötvös number Eo = 10) whilst both density and viscosity ratios are set to ρ 1∕ρ 2 = μ 1∕μ 2 = 10. The gravitational acceleration is g = 0.98. The problem is discretised with 16 × 32 elements with a polynomial order of N = 4, and a time step Δt = 4 ⋅ 10−6.

This test case is quantitively compared with the results of [10] in Fig. 4 with satisfactory results. It should be mentioned that the benchmark results of [10] are obtained with a sharp-interface model which may explain the small disagreement in the evolution of the center of mass shown in Fig. 4.

Fig. 3
figure 3

Initial condition of the rising bubble test problem

Full size image
Fig. 4
figure 4

Evolution of the center of mass of the bubble with time

Full size image

5 Conclusions

A method to model incompressible two phases flows is introduced. The model solves the incompressible Navier–Stokes equations coupled with the Cahn–Hilliard equation to track the evolution of the different fluids. The model is discretised in space using a discontinuous Galerkin spectral element method (DGSEM) whilst an efficient implicit-explicit approach is used to advance in time. The validity of the model is shown with two test cases. A spinodal decomposition benchmark problem is solved to validate the Cahn–Hilliard solver whilst a rising-bubble test problem is solved to validate the coupled Cahn–Hilliard–Navier–Stokes system. Both test cases are solved showing good agreement with the literature, and proving the accuracy and robustness of the proposed method.