1 Introduction

Multi-phase flows are ubiquitous in nature and engineering applications. The simplest flow of a liquid with free surface, such as a flowing river or a falling raindrop, already involves both the dynamics of the liquid phase and the surrounding air and can consequently be considered a two-phase flow. The application range is obviously much larger and includes, for example, and without pretending to be exhaustive, bubbly liquids and sprays, water flow with sediment transport, mist flows, two-phase flows with phase change as used in modern 3D printers, compressible multi-phase flows in internal combustion engines, flows in the paper, steel and food industry, etc. Such applications have motivated extensive efforts to study and develop multi-phase flow models that describe such phenomena with respect to physical principles and thermodynamics.

One particular aspect of multi-phase flows is that they involve moving interfaces between different bulk phases. From a physics perspective, the nature of the interface, that is, whether it is sharp or diffuse, has been subject to debate since the times of Rayleigh and Laplace. While both approaches have their advantages, it is admitted that diffuse interface approaches, in general, offer more flexibility, especially in the presence of strong deformations and topology changes in the interface geometry. In contrast, the sharp interface approach allows for a more rigorous treatment of the thermodynamics at the interface. In this paper, we are interested in diffuse interface approaches. Although a thorough review of diffuse interface approaches is beyond the scope of this work, the reader is, for example, referred to [1, 2, 7, 10, 18, 35, 36, 39, 46, 47, 50, 55, 65, 75] and references therein. For the incompressible case, see also [14, 37, 38] and related work.

Up to now, no universally accepted mathematical model exists for the whole range of different compressible multi-phase flows. Among the large number of different models that can be found in the literature, the one proposed by Baer and Nunziato [4] is one of the most widespread, see, for example, [3, 8, 41, 65], as well as the well-known Kapila model [46], which can be obtained from the Baer-Nunziato (BN) model in the stiff relaxation limit. The governing equations of the BN model form a hyperbolic system, because the associated eigenvalues are all real, and there exists a set of linearly independent eigenvectors. However, some of its equations cannot be written in the conservative form, which makes it difficult to deal with the appearance of discontinuities and the development of high-order numerical methods. Moreover, the BN model was modified by different authors in the literature, see, for example, Saurel and Abgrall [65], whose modification describes multi-phase mixtures and interface problems between pure compressible materials. An alternative two-phase flow model that is fully conservative is the one forwarded by Scannapieco and Cheng, see [66].

In addition to the previously mentioned models, there exists another class of models for compressible multi-phase flows that originates from the theory of Godunov and Romenski on symmetric hyperbolic and thermodynamically compatible (SHTC) systems [42, 44, 56, 57] and which was first introduced in [58, 59, 62, 63]. In this paper, we are therefore interested in the discretization of the SHTC model of barotropic compressible two-phase flows of Romenski et al. with different phase velocities and phase pressures in multiple space dimensions. The model consists of a first-order SHTC system of equations [58, 59, 62]. In the previous references, it was also shown that the SHTC equations, which are written in the conservative form, can be converted to the form of a BN-type model, where additional differential terms appear in the momentum equations, which were not included in the original BN model and which describe the so-called lift forces. Recently, an exact solution for the corresponding Riemann problem in the barotropic case was found in [69], and an all-Mach number flow solver was developed in [48].

The model proposed by Romenski et al. is strongly hyperbolic in one space dimension, and its homogeneous part without algebraic source terms is endowed with a curl involution on the relative velocity field. However, as we will show in this paper, the original model is only weakly hyperbolic in multiple space dimensions. To restore strong hyperbolicity, two different strategies can be followed: the first one consists in using the hyperbolic generalized Lagrangian multiplier (GLM) curl-cleaning methodology introduced in [11, 16, 20, 29], which is a natural extension of the original ideas presented by Munz et al. in [19, 49] on hyperbolic GLM divergence cleaning for the Maxwell and MHD equations, which contain the well-known divergence-free condition of the magnetic field. Curl constraints can also be found in many other first-order hyperbolic models, such as hyperbolic models for surface tension [15, 16, 67], first-order hyperbolic reformulations of the Navier-Stokes-Korteweg equations based on an augmented Lagrangian approach [20, 21], or first-order reductions of the Einstein field equations of general relativity [29]. The second methodology to recover the hyperbolicity involves the use of some extra terms in the momentum equation that symmetrize the system and is therefore directly based on the theory of SHTC systems following [43, 52,53,54]. In both cases, we will show that the system in the multidimensional case becomes again strongly hyperbolic.

In the setting of this model, the solutions are often discontinuous in space, that is, solutions to Riemann problems. Therefore, it is necessary to consider an approach that is robust and accurate even in the presence of shock waves or discontinuities. To address the sharp gradients of the numerical solutions, a high-order ADER discontinuous Galerkin (DG) finite-element framework with a posteriori subcell finite-volume limiter is considered, see [27, 34, 76] for further details. The proposed method is high order in space and time, thanks to the use of the ADER approach of Toro and Titarev [70, 73, 74]. To deal with spurious oscillations that may appear in the presence of discontinuities or shock waves, it makes use of a posteriori subcell finite-volume limiter for high-order fully discrete one-step ADER-DG schemes presented in [34, 76], which follows the multi-dimensional optimal order detection (MOOD) approach of Clain and Loubère [17, 22, 23].

This paper is organized as follows. Section 2 recalls the set of governing partial differential equations and shows the equation of state (EOS) that we will use in this work. In Sect. 2.2, the hyperbolicity of the system is studied in the multidimensional case, showing that the original model is only weakly hyperbolic, and two different strategies to recover strong hyperbolicity are presented. Section 3 introduces the high-order ADER-DG scheme used in this paper to solve the model numerically. Section 4 shows the results of several test cases and benchmark problems computed using the proposed method. Finally, Sect. 5 concludes the paper and summarizes the contributions of this work as well as its possible future extensions.

2 Governing Equations

The governing equations of the barotropic compressible two-velocity, two-pressure two-fluid model of Romenski, written in terms of the specific total energy potential \(E=E(\alpha _1,c_1,\rho ,w^k)\) are given by

where \(\alpha _1\) and \(\alpha _2\) are the volume fractions of the first and second phases, verifying the saturation constraint \(\alpha _1 + \alpha _2 = 1\), \(\rho _1\) and \(\rho _2\) are the mass densities of the first and second phases, \(\rho =\alpha _1\rho _1+\alpha _2\rho _2\) is the mixture mass density, \(c_j=\alpha _j\rho _j / \rho\) with \(j=1,2\) are the mass fractions of phase j which satisfy \(c_1+c_2=1\), and \(\varvec{g}=(g^1,g^2,g^3)^{\rm{T}}\) is the gravity acceleration. If \(\varvec{u}_1=(u_1^1,u_1^2,u_1^3)^{\rm{T}}\) and \(\varvec{u}_2=(u_2^1,u_2^2,u_2^3)^{\rm{T}}\) are the velocity vectors of each phase, then the mixture velocity \(\varvec{u}=(u^1,u^2,u^3)^{\rm{T}}\) is computed as \(u^k=c_1u^k_1+c_2u^k_2\) and the relative phase velocity, which is a primary evolution quantity in this model, is given by \(\varvec{w}=(w^1,w^2,w^3)^{\rm{T}}\) as \(w^k = u^k_1-u^k_2\). The source terms of Eqs. (1a) and (1e) are proportional to thermodynamic forces with \(\tau\) the rate of pressure relaxation and \(\zeta\) the inter-phase friction coefficient. The PDE system (1) is formed by two conservation laws for the volume and mass fractions, Eqs. (1a) and (1b), respectively, the conservation of the total mass, Eq. (1c), the conservation of the mixture momentum, Eq. (1d), and a balance law for the relative velocity, Eq. (1e). The algebraic source terms appearing in Eqs. (1a) and (1e) describe the interaction between the phases and are pressure relaxation and interfacial friction. The mixture EOS is given by, see [69],

$$\begin{aligned} E(\alpha_1,c_1,\rho ,w^1, w^2, w^3) = e(\alpha_{1},c_1,\rho )+c_1c_2\frac{w{^i}w^i}{2}, \end{aligned}$$

where the specific internal energy of the mixture reads as

$$\begin{aligned} e(\alpha _1,c_1,\rho )=c_1e_1(\rho _1)\,{+}\,c_2e_2(\rho _2) = c_1e_1\left( \frac{c_1\rho }{\alpha _1}\right) + c_2e_2\left( \frac{c_2\rho }{\alpha _2} \right) , \end{aligned}$$

where \(e_j(\rho _j)\) is the specific internal energy of the phase j. Since, in this work, an isentropic process is considered, the derivatives of e can be computed as

$$\begin{aligned} \frac{\partial e}{\partial \alpha _1} = \frac{p_2 -p_1}{\rho }, \qquad \frac{\partial e}{\partial c_1} = h_1(\rho _1) - h_2(\rho _2), \qquad \frac{\partial e}{\partial \rho } = \frac{p}{\rho ^2}, \end{aligned}$$

where \(h_j(\rho _j) = e_j(\rho _j)+\frac{p_j(\rho _j)}{\rho _j}, \, j=1,2\) is the specific enthalpy of the phase j. Then, the derivatives of the specific total energy E are given by

$$\begin{aligned} \frac{\partial E}{\partial \alpha _1}&= \frac{\partial e}{\partial \alpha _1} = \frac{p_2 -p_1}{\rho }, \quad \frac{\partial E}{\partial \rho } = \frac{\partial e}{\partial \rho }= \frac{p}{\rho ^2}, \quad \frac{\partial E}{\partial w^i} = c_1 (1-c_1) w^i, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial E}{\partial c_1}&= \frac{\partial e}{\partial c_1} + (1-2c_1)\frac{w^iw^i}{2} = h_1(\rho _1) - h_2(\rho _2) + (1-2c_1)\frac{w^iw^i}{2}. \end{aligned}$$
(3)

Considering the computations in [69], and taking into account (2) and (3), the following identities are obtained:

$$\begin{aligned}&\rho c_1 u^k + \rho E_{w^k}= \rho c_1 u_1^k, \quad \rho c_2 u^k - \rho E_{w^k}= \rho c_2 u_2^k,\\&\rho u^i u^k+p\delta _{ik}+\rho w^i E_{w^k}= \alpha _1 \rho _1 u_1^i u_1^k + \alpha _2 \rho _2 u_2^i u_2^k + p \delta _{ik},\\&(u_1^l-u_2^l) u^l + E_{c_1}= \frac{1}{2}(u_1^l)^2 -\frac{1}{2} (u_2^l)^2 + h_1-h_2. \end{aligned}$$

The PDE system (1) can now be rewritten in the following form, which is more convenient for numerical discretization:

The derivation of the PDE system (4) is based on the principles of thermodynamically compatible systems [44], and it consists of nine equations: the balance law for the volume fraction, the conservation laws of the two-phase masses, the conservation of the mixture momentum, and the balance law for the relative velocity field. Note that in the absence of source terms in (4e), i.e., for \(\zeta = 0\), the relative velocity is curl-free in the sense

$$\begin{aligned} \frac{\partial w^k}{\partial x_{l}}-\frac{\partial w^l}{\partial x_{k}} = 0. \end{aligned}$$

2.1 EOS

To close the two-phase model (4a)–(4e), it is necessary to define an EOS for each phase: throughout this paper, we will make use either of the ideal gas law or of the stiffened gas EOS, which will be used to model a liquid phase. For ideal gases, the EOS is defined as

$$\begin{aligned} E(\rho )=\frac{c_0^2}{\gamma (\gamma -1)} \quad \text{ with } c_0^2=\gamma \rho ^{\gamma -1}{\rm{e}}^{s/c_v}, \end{aligned}$$
(5)

where \(\gamma\) is the adiabatic index or the ratio of specific heats, \(c_0\) is the adiabatic sound speed, s is the specific entropy (which in our case will be constant), \(c_v\) is the specific heat capacity at constant volume, and the pressure is given by

$$\begin{aligned} p(\rho ) = \rho ^2 E_{\rho } = \rho ^\gamma {\rm{e}}^{s/c_v} = (\gamma -1)\rho E. \end{aligned}$$
(6)

For stiffened gases, the EOS reads as

$$\begin{aligned} E(\rho )=\frac{c_0^2}{\gamma (\gamma -1)}\left( \frac{\rho }{\rho _0}\right) ^{\gamma -1}{\rm{e}}^{s/c_v}+\frac{\rho _0 c_0^2 - \gamma p_0}{\gamma \rho }, \end{aligned}$$
(7)

where \(\rho _0\) and \(p_0\) are the reference density and pressure, respectively, and \(c_0\) is a constant reference sound speed. In this case, the pressure is computed as

$$\begin{aligned} p(\rho ) = \rho ^2 E_{\rho } = \frac{c_0^2 \rho _0}{\gamma } \left( \frac{\rho }{\rho _0} \right) ^\gamma {\rm{e}}^{s/c_v}- \frac{c_0^2 \rho _0 - \gamma p_0}{\gamma }. \end{aligned}$$
(8)

2.2 Hyperbolicity Analysis

In this section, we will study the hyperbolicity of the model (4a)–(4e). The one-dimensional (1D) case was already addressed in [69], and here, we briefly recall some results for the 1D case before moving to the more general multidimensional case. In particular, we will prove that the original system (4a)–(4e) is only weakly hyperbolic in the multidimensional case and show how the strong hyperbolicity can be restored considering two different strategies: on the one hand, using an extension of the hyperbolic GLM curl-cleaning approach, and on the other hand, modifying the original system of governing equations by adding the symmetrizing terms that allow rewriting the model in symmetric hyperbolic form, which is natural within the framework of SHTC equations. Defining the vectors of conserved and primitive variables as \(\textbf{Q}=(\alpha _1,\alpha _1\rho _1,\alpha _2\rho _2, \rho \varvec{u}^{\rm{T}}, \varvec{w}^{\rm{T}})^{\rm{T}}\) and \(\textbf{V}=(\alpha _1,\rho _1,\rho _2,\varvec{u}_1^{\rm{T}},\varvec{u}_2^{\rm{T}})^{\rm{T}}\), respectively, the PDE system (4) can be written as

$$\begin{aligned} \partial _t \textbf{Q}+ \nabla \cdot \textbf{F}(\textbf{Q}) + \textbf{B}_{}(\textbf{Q})\cdot \nabla \textbf{Q}=\textbf{S}(\textbf{Q}), \end{aligned}$$

where \(\textbf{S}(\textbf{Q})\) contains the source terms, \(\textbf{F}(\textbf{Q})\) is the nonlinear flux tensor, and \(\textbf{B}_{}(\textbf{Q})\cdot \nabla \textbf{Q}\) contains the non-conservative terms. Then, the quasi-linear form of the PDE in terms of the conserved variables \(\textbf{Q}\) is given by

$$\begin{aligned} \partial _t \textbf{Q}+ \textbf{A}(\textbf{Q})\cdot \nabla \textbf{Q}= \textbf{S}(\textbf{Q}), \end{aligned}$$

where \(\textbf{A}(\textbf{Q}) = \displaystyle {\frac{\partial \textbf{F}}{\partial \textbf{Q}} + \textbf{B}_{}}\). If the vector of primitive variables \(\textbf{V}\) is considered, the system can be written as

$$\begin{aligned} \partial _t \textbf{V}+ \textbf{C}(\textbf{V})\cdot \nabla \textbf{V}= \varvec{\mathcal {S}}(\textbf{V}), \end{aligned}$$
(9)

where \(\textbf{C}(\textbf{V}) = \displaystyle {\frac{\partial \textbf{V}}{\partial \textbf{Q}} \frac{\partial \textbf{F}}{\partial \textbf{V}} + \frac{\partial \textbf{V}}{\partial \textbf{Q}} \textbf{B}_{}\frac{\partial \textbf{Q}}{\partial \textbf{V}}}\) and \(\varvec{\mathcal {S}}(\textbf{V})=\displaystyle {\frac{\partial \textbf{V}}{\partial \textbf{Q}} \, \textbf{S}(\textbf{Q})}\). Throughout this section, for the sake of the readability and since it does not contribute anything to the study of the hyperbolicity of the system, the source terms are set to 0.

2.2.1 1D Case

The hyperbolicity analysis of the system (4) in one dimension has been done in detail in [69], so here, only a summary of the main points will be made that will be useful for a better understanding of the multidimensional case. If \(u= c_1 u_1+ c_2 u_2\) is the mixture velocity with \(u_j,\, j=1,2\) the velocity of the phase j and \(w=u_1-u_2\) is the relative velocity, the 1D system results in

Then, the matrix \(\textbf{C}\) in (9) is given by

$$\begin{aligned} \textbf{C}(\textbf{V}) = \left( \begin{array}{ccccc} u&{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _1}{\alpha _1} \left( u_1-u\right) &{} u_1 &{} 0 &{} \rho _1 &{} 0 \\ \frac{ \rho _2}{\alpha _2} \left( u-u_2\right) &{} 0 &{} u_2 &{} 0 &{} \rho _2 \\ \beta &{} \frac{a_1^2}{\rho _1} &{} 0 &{} u_1 &{} 0 \\ \beta &{} 0 &{} \frac{a_2^2}{\rho _2} &{} 0 &{} u_2 \\ \end{array} \right) \end{aligned}$$

with \(a_j\) the sound speed of phase j, that is defined as \(a^2_j=\rho _j\left( \frac{\partial h_j}{\partial \rho _j}\right) , \, j=1,2\) and \(\beta =\frac{1}{\rho }\left( \frac{a_1^2\rho _1}{\gamma _1}- \frac{a_2^2\rho _2}{\gamma _2}\right) = \frac{1}{\rho }\left( p_1- p_2\right)\). It is easy to show that \(\textbf{C}(\textbf{V})\) admits five eigenvalues, whose expressions are given hereafter

$$\begin{aligned} \lambda _1 = u_1+a_1, \,\, \lambda _2 = u_1-a_1, \,\, \lambda _3 = u, \,\, \lambda _4 = u_2+a_2,\,\, \lambda _5 = u_2-a_2. \end{aligned}$$

In this case, all five eigenvalues are real, and a complete set of five linearly independent eigenvectors exists, which means that the system in one space dimension is strongly hyperbolic, see [69] for further details about the eigenvalues and eigenvectors in the 1D case.

2.2.2 Multidimensional Case

Now, we are in the position to study the multidimensional case. In the following, we use the property of rotational invariance of Newtonian mechanics, and hence, it is enough to consider the matrix \(\textbf{C}(\textbf{V})\) only in the x-direction and not all possible space directions. The system under consideration is (4) and, in this case, the matrix \(\textbf{C}(\textbf{V})\) in the x-direction is given by

$$\begin{aligned} \textbf{C}(\textbf{V}) = \left( \begin{array}{ccccccccc} u^1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _1}{\alpha _1}\vartheta _2^1 &{} u^1_1 &{} 0 &{} \rho _1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _2}{\alpha _2}\vartheta _1^1&{} 0 &{} u_2^1 &{} 0 &{} 0 &{} 0 &{} \rho _2 &{} 0 &{} 0 \\ \beta &{} \frac{a_1^2}{\rho _1} &{} 0 &{} u_1^1 &{} \vartheta _{22}^2 &{} \vartheta _{22}^3&{} 0 &{} \vartheta _{12}^2&{} \vartheta _{12}^3\\ 0 &{} 0 &{} 0 &{} 0 &{} \xi _2 &{} 0 &{} 0 &{} -\vartheta _{12}^1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \xi _2 &{} 0 &{} 0 &{} -\vartheta _{12}^1\\ \beta &{} 0 &{} \frac{a_2^2}{\rho _2} &{} 0 &{} -\vartheta _{12}^2 &{} -\vartheta _{12}^3 &{} u_2^1 &{} -\vartheta _{11}^2 &{} -\vartheta _{11}^3 \\ 0 &{} 0 &{} 0 &{} 0 &{} \vartheta _{12}^1 &{} 0 &{} 0 &{} \xi _1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \vartheta _{12}^1 &{} 0 &{} 0 &{} \xi _1 \\ \end{array} \right) . \end{aligned}$$

As in the previous section, we make use of the following auxiliary variables to ease the expressions in the matrix:

$$\left\{\begin{aligned} \left. \begin{array}{l} \beta = \frac{1}{\rho }(p_1-p_2),\\ \vartheta _j^i=c_j w^i,\,\, \vartheta _{jk}^i=c_j c_k w^i,\,\, i=1,2,3,\,\, j=1,2,\,\, k=1,2,\\ \xi _1 = c_1u^1+c_2u_2^1 = u_2^1 + c_1^2 w^1 = u_2^1 + c_1 \vartheta _1^1, \\ \xi _2 = c_1u_1^1+c_2u^1 = u_1^1 - c_2^2 w^1= u_1^1 - c_2 \vartheta _2^1. \end{array}\right. \end{aligned}\right.$$
(11)

The matrix \(\textbf{C}\) admits 9 eigenvalues \(\lambda _{1-9}\) that are given by

$$\begin{aligned} \lambda _1 = u_1^1-a_1, \,\, \lambda _2 = u_1^1+a_1, \,\, \lambda _{3} = u_2^1-a_2,\,\, \lambda _{4} = u_2^1+a_2, \,\, \lambda _{5-9} = u^1, \end{aligned}$$

where the sound speed of each phase \(a_j\) again is defined as \(a^2_j=\rho _i\left( \frac{\partial h_j}{\partial \rho _j}\right) ,\,\,j=1,2\). The eigenvalues are all real. To prove whether the system is weakly or strongly hyperbolic, it is necessary to compute the associated eigenvectors. The right eigenvectors are the columns in the matrix below and are given in the same order as the eigenvalues

$$\begin{aligned} \textbf{R}_{\scriptscriptstyle {1-4}}=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0\\ {-\frac{\rho _1}{a_1}} &{} {\frac{\rho _1}{a_1}} &{} 0 &{} 0\\ 0 &{} 0 &{} {-\frac{\rho _2}{a_2}} &{} {\frac{\rho _2}{a_2}}\\ 1 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 1\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right) , \,\, \textbf{R}_{\scriptscriptstyle {5-7}}=\left( \begin{array}{ccc} {-\frac{\alpha _1\,\alpha _2\,Z_{2}}{\eta _2\,\vartheta _{1}^1}} &{} 0 &{} 0 \\ {\frac{\rho _1\,\zeta _1\,Z_{2}}{\eta _2\,\vartheta _{1}^1 Z_{1}}} &{} {-\frac{ \rho _1 \,\vartheta _{2}^3}{Z_{1}}} &{} {-\frac{ \rho _1\,\vartheta _{2}^2}{Z_{1}}} \\ {\frac{\rho _2\,\zeta _2}{\eta _2\,\vartheta _{1}^1}} &{} {\frac{\rho _2\, \vartheta _{1}^3}{Z_{2}}} &{} {\frac{\rho _2\,\vartheta _{1}^2}{Z_{2}}}\\ {-\frac{c_2\,\eta _1\,\vartheta _{2}^1}{c_1\,\eta _2\,Z_{1}}} &{} {\frac{\vartheta _{2}^1\,\vartheta _{2}^3}{Z_{1}}} &{} {\frac{\vartheta _{2}^1\, \vartheta _{2}^2}{Z_{1}}} \\ 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ 1 &{} {\frac{\vartheta _{1}^1\,\vartheta _{1}^3}{Z_{2}}} &{} {\frac{\vartheta _{1}^1\, \vartheta _{1}^2}{Z_{2}}} \\ 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ \end{array} \right) , \end{aligned}$$

where the auxiliary variables that are used to ease the notation are defined as

$$\begin{aligned} &Z_{1}= a_1^2-(\vartheta _{2}^1)^2, \quad Z_{2}=a_2^2-(\vartheta _{1}^1)^2, \quad \eta _1 = \alpha _2(a_1^2-\alpha _1\beta ), \nonumber \\ &\eta _2 = \alpha _1(a_2^2+\alpha _2\beta ), \quad \zeta _1 = \alpha _2\left( \alpha _1\beta -(\vartheta _2^1)^2\right) , \quad \zeta _2 = \alpha _1\left( \alpha _2\beta +(\vartheta _1^1)^2\right) . \end{aligned}$$

All eigenvalues are real, but two eigenvectors are missing (in fact, if we are working in dimension d, there are \(d-1\) missing eigenvectors), so the system is only weakly hyperbolic. Hereafter, we will show two different methodologies that can be used to restore the strong hyperbolicity of the model.

2.2.2.1 GLM Curl-Cleaning Approach

To restore the strong hyperbolicity and following the same strategy that can be found in [11, 16, 20, 29], we make use of the GLM curl-cleaning technique, where an evolution equation for a curl-cleaning field \(\psi ^k\) is added to the system (4). Using the abbreviation \(\delta _{12} = \frac{1}{2}(u_1^l)^2-\frac{1}{2}(u_2^l)^2 + h_1-h_2\) and denoting the curl-cleaning speed by \(a_{\varvec{\psi }}\), this equation is coupled with (4e) via a Maxwell-type sub-system as follows:

$$\left\{\begin{aligned} &\displaystyle {\frac{\partial w^k}{\partial t}+\frac{\partial \delta _{12}}{\partial x_{k}} + u^l\left( \frac{\partial w^k}{\partial x_{l}}-\frac{\partial w^l}{\partial x_{k}} \right) } \displaystyle {+ a_{\varvec{\psi }} \varepsilon _{klm} \frac{\partial \psi ^m}{\partial x_{l}}=0,} \\ &\displaystyle {\frac{\partial \psi ^k}{\partial t} + u^j\frac{\partial \psi ^k}{\partial x_{j}} -a_{\varvec{\psi }} \varepsilon _{klm}\frac{\partial w^m}{\partial x_{l}} = 0. } \end{aligned}\right.$$

Hence, the augmented system with GLM curl-cleaning reads

$$\begin{aligned}&\frac{\partial \alpha _{1}}{\partial t}+u^k \frac{\partial \alpha _{1}}{\partial x_{k}}=0, \end{aligned}$$
(12a)
$$\begin{aligned}&\frac{\partial \alpha _1\rho _1}{\partial t}+\frac{\partial (\alpha _1\rho _1 u_1^k)}{\partial x_{k}}=0, \end{aligned}$$
(12b)
$$\begin{aligned}&\frac{\partial \alpha _2\rho _2}{\partial t}+\frac{\partial (\alpha _2\rho _2 u_2^k)}{\partial x_{k}}=0, \end{aligned}$$
(12c)
$$\begin{aligned}&\frac{\partial \rho u^i}{\partial t}+ \frac{\partial (\alpha _1\rho _1 u_1^i u_1^k+ \alpha _2\rho _2 u_2^i u_2^k + p\delta _{ik} )}{\partial x_{k}}=0 , \end{aligned}$$
(12d)
$$\begin{aligned}&\frac{\partial w^k}{\partial t}+\frac{\partial \delta _{12}}{\partial x_{k}} + u^l\left( \frac{\partial w^k}{\partial x_{l}}-\frac{\partial w^l}{\partial x_{k}} \right) + a_{\varvec{\psi }} \varepsilon _{klm} \frac{\partial \psi ^m}{\partial x_{l}}=0, \end{aligned}$$
(12e)
$$\begin{aligned}&\frac{\partial \psi ^k}{\partial t} + u^j\frac{\partial \psi ^k}{\partial x_{j}} -a_{\varvec{\psi }} \varepsilon _{klm}\frac{\partial w^m}{\partial x_{l}} = 0, \end{aligned}$$
(12f)

where \(\varvec{\psi }=(\psi ^1,\psi ^2,\psi ^3)\) is the cleaning field, \(\varvec{\varepsilon }=\varepsilon _{klm}\) is the Levi-Civita tensor, and \(a_{\varvec{\psi }}\) is the curl-cleaning speed. Once the curl-cleaning field has been added, we can compute the eigenvalues and eigenvectors to check the hyperbolicity of the augmented GLM system. The matrix \(\textbf{C}\) in the x-direction can be written as

$$\begin{aligned} \textbf{C}(\textbf{V})=\left( \begin{array}{cccccccccccc} u^1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _1}{\alpha _1}\vartheta _2^1 &{} u^1_1 &{} 0 &{} \rho _1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _2}{\alpha _2}\vartheta _1^1 &{} 0 &{} u_2^1 &{} 0 &{} 0 &{} 0 &{} \rho _2 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \beta &{} \frac{a_1^2}{\rho _1} &{} 0 &{} u_1^1 &{} \vartheta _{22}^2 &{} \vartheta _{22}^3&{} 0 &{} \vartheta _{12}^2&{} \vartheta _{12}^3 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \xi _2 &{} 0 &{} 0 &{} -\vartheta _{12}^1 &{} 0 &{} 0 &{} 0 &{} -c_2 a_{\varvec{\psi }} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \xi _2 &{} 0 &{} 0 &{} -\vartheta _{12}^1 &{} 0 &{} c_2 a_{\varvec{\psi }} &{} 0 \\ \beta &{} 0 &{} \frac{a_2^2}{\rho _2} &{} 0 &{} -\vartheta _{12}^2 &{} -\vartheta _{12}^3 &{} u_2^1 &{} -\vartheta _{11}^2 &{} -\vartheta _{11}^3 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \vartheta _{12}^1 &{} 0 &{} 0 &{} \xi _1 &{} 0 &{} 0 &{} 0 &{} c_1 a_{\varvec{\psi }} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \vartheta _{12}^1 &{} 0 &{} 0 &{} \xi _1 &{} 0 &{} -c_1 a_{\varvec{\psi }} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} u^1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} a_{\varvec{\psi }} &{} 0 &{} 0 &{} -a_{\varvec{\psi }} &{} 0 &{} u^1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -a_{\varvec{\psi }} &{} 0 &{} 0 &{} a_{\varvec{\psi }} &{} 0 &{} 0 &{} 0 &{} u^1 \\ \end{array} \right) , \end{aligned}$$

where, as in the previous case, we make use of the auxiliary variables (11) to ease the notation of the matrix. In this case, it is easy to compute the 12 eigenvalues of the matrix \(\textbf{C}\) that are given by

$$\begin{aligned}&\lambda _1 = u^1_1-a_1, \quad \lambda _2 = u^1_1+a_1, \quad \lambda _{3} = u^1_2-a_2, \quad \lambda _{4} = u^1_2+a_2, \\&\lambda _{5-8} = u^1, \quad \lambda _{9-10} = u^1-a_{\varvec{\psi }}, \quad \lambda _{11-12} = u^1+a_{\varvec{\psi }} \end{aligned}$$

with \(a_j\) the sound speed of phase j, that is defined as \(a^2_j=\rho _j\left( \frac{\partial h_j}{\partial \rho _j}\right) , \, j=1,2\). Since the eigenvalues are real, to check if the system is weakly or strongly hyperbolic, it is necessary to compute the associated eigenvectors. Below, we will write the matrix that contains the right eigenvectors in columns. They are listed in the same order as the eigenvalues

$$\begin{aligned}{} & {} \textbf{R}_{\scriptscriptstyle {1-8}}=\left( \begin{array}{cccccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} {\frac{\alpha _1 \, \alpha _2 \,\vartheta _1^3}{\eta _2}} &{} {\frac{\alpha _1\, \alpha _2 \,\vartheta _1^2}{\eta _2}} &{} {-\frac{\alpha _1\, \alpha _2\, Z_{2}}{\eta _2\, \vartheta _1^1}} \\ {-\frac{\rho _1}{a_1}} &{} {\frac{\rho _1}{a_1}} &{} 0 &{} 0 &{} 0 &{} {-\frac{\varrho \, \vartheta _1^3}{\eta _2\,Z_{1}}} &{} {-\frac{\varrho \,\vartheta _1^2}{\eta _2\,Z_{1}}} &{} {\frac{\zeta _1\,\rho _1\, Z_{2}}{\eta _2\,\vartheta _1^1\,Z_{1}}} \\ 0 &{} 0 &{} {-\frac{\rho _2}{a_2}} &{} {\frac{\rho _2}{a_2}} &{} 0 &{} {\frac{\alpha _1\, \rho _2\, \vartheta _1^3}{\eta _2}} &{} {\frac{\alpha _1\, \rho _2\, \vartheta _1^2}{\eta _2}} &{} {\frac{\zeta _2\, \rho _2}{\eta _2\,\vartheta _1^1}}\\ 1 &{} 1 &{} 0 &{} 0 &{} 0 &{}{-\frac{\varepsilon \, \vartheta _2^1\, \vartheta _1^3}{\eta _2\,\,Z_{1}}} &{} {-\frac{ \varepsilon \, \vartheta _1^2 \vartheta _2^1}{\eta _2\,Z_{1}}} &{} {-\frac{c_2\,\eta _1 Z_{2}}{c_1\,\eta _2 Z_{1}}} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\{} & {} \textbf{R}_{\scriptscriptstyle {9-12}}=\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ -\frac{\rho _1 \tau _2^{+} \vartheta _2^2}{a_{\varvec{\psi }}\chi _2^{+}} &{} \frac{\rho _1 \tau _2^{+} \vartheta _2^3}{a_{\varvec{\psi }}\chi _2^{+}}&{} {\frac{\rho _1 \tau _2^{-} \vartheta _2^2}{a_{\varvec{\psi }}\chi _2^{-}}} &{} -\frac{\rho _1 \tau _2^{-} \vartheta _2^3}{a_{\varvec{\psi }}\chi _2^{-}} \\ \frac{\rho _2 \tau _2^{+} \vartheta _1^2}{a_{\varvec{\psi }}\chi _1^{-}} &{} -\frac{\rho _2 \tau _2^{+} \vartheta _1^3}{a_{\varvec{\psi }}\chi _1^{-}}&{} -\frac{\rho _2 \tau _2^{-} \vartheta _1^2}{a_{\varvec{\psi }}\chi _1^{+}} &{} \frac{\rho _2 \tau _2^{-} \vartheta _1^3}{a_{\varvec{\psi }}\chi _1^{+}} \\ \frac{\delta _2^{+} \tau _2^{+} \vartheta _2^2}{a_{\varvec{\psi }}\chi _2^{+}} &{} -\frac{\delta _2^{+} \tau _2^{+} \vartheta _2^3}{a_{\varvec{\psi }}\chi _2^{+}} &{} \frac{\delta _2^{-} \tau _2^{-} \vartheta _2^2}{a_{\varvec{\psi }}\chi _2^{-}} &{} -\frac{\delta _2^{-} \tau _2^{-} \vartheta _2^3}{a_{\varvec{\psi }}\chi _2^{-}} \\ \frac{\upsilon _1^{-}}{a_{\varvec{\psi }}} &{} 0 &{} -\frac{\upsilon _1^{+}}{a_{\varvec{\psi }}} &{} 0 \\ 0 &{} -\frac{\upsilon _1^{-}}{a_{\varvec{\psi }}} &{} 0 &{} \frac{\upsilon _1^{+}}{a_{\varvec{\psi }}} \\ \frac{\delta _1^{-} \tau _1^{-} \vartheta _1^2}{a_{\varvec{\psi }} \chi _1^{-}} &{} -\frac{\delta _1^{-} \tau _1^{-} \vartheta _1^3}{a_{\varvec{\psi }} \chi _1^{-}} &{} \frac{\delta _1^{+} \tau _1^{+} \vartheta _1^2}{a_{\varvec{\psi }} \chi _1^{+}} &{} -\frac{\delta _1^{+} \tau _1^{+} \vartheta _1^3}{a_{\varvec{\psi }} \chi _1^{+}} \\ -\frac{\upsilon _2^{+}}{a_{\varvec{\psi }}} &{} 0 &{} \frac{\upsilon _2^{-}}{a_{\varvec{\psi }}} &{} 0 \\ 0 &{} \frac{\upsilon _2^{+}}{a_{\varvec{\psi }}} &{} 0 &{} -\frac{\upsilon _2^{-}}{a_{\varvec{\psi }}} \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 1 \\ 1 &{} 0 &{} 1 &{} 0 \\ \end{array} \right) , \end{aligned}$$

where the auxiliary variables that have been used to write the 12 right eigenvectors more compactly are defined as

$$\left\{\begin{aligned}&Z_{1}= a_1^2-(\vartheta _{2}^1)^2, \!\! \quad Z_{2}=a_2^2-(\vartheta _{1}^1)^2, \!\! \quad \eta _1 = \alpha _2(a_1^2-\alpha _1\beta ), \!\! \quad \eta _2 = \alpha _1(a_2^2+\alpha _2\beta ), \\&\beta =\frac{p_1-p_2}{\rho }, \!\! \quad \vartheta _j^i=c_j w^i, \!\! \quad \vartheta _{jk}^i=c_j c_k w^i, \!\! \quad \xi _1 = u_2^1 + c_1 \vartheta _1^1, \!\! \quad \xi _2 = u_1^1 - c_2 \vartheta _2^1, \\&\delta _j^{\pm }=a_{\varvec{\psi }}\pm \vartheta _j^1, \quad \chi _1^{\pm }=(\delta _1^{\pm })^2-a_2^2, \quad \chi _2^{\pm }=(\delta _2^{\pm })^2-a_1^2, \\&\upsilon _1^{\pm }=c_2 \delta _1^{\pm }, \quad \upsilon _2^{\pm }=c_1 \delta _2^{\pm }, \quad \tau _1^{\pm }=\upsilon _1^{\pm }-c_1 a_{\varvec{\psi }}, \quad \tau _2^{\pm }=\upsilon _2^{\pm }-c_2 a_{\varvec{\psi }}, \\&\varrho = \alpha _2 \left( p_1+p_2(\gamma _2-1)-\rho _1 (\vartheta _2^1)^2\right) , \quad \varepsilon =\frac{\alpha _2}{\rho _1}\left( p_1(\gamma _1-1)-p_2(\gamma _2-1) \right) . \end{aligned}\right.$$

Using the GLM curl-cleaning technique, we obtain 12 real eigenvalues and the corresponding 12 linearly independent right eigenvectors, and hence, the augmented system with GLM curl-cleaning (12) is strongly hyperbolic.

2.2.2.2 Symmetrizing Godunov-Powell Terms

The second strategy used to recover the strong hyperbolicity of system (1) is based on the theory of SHTC systems and consists in adding terms that are proportional to the curl involution to the momentum equation (1d), so that the system has real eigenvalues and a complete set of linearly independent eigenvectors, see [16]. The modified system reads

Using (2), system (13) results in

As in the previous case, the eigenvalues and eigenvectors are computed to analyze the hyperbolicity of the system (14). The matrix \(\textbf{C}\) in the x-direction reads as

$$\begin{aligned} \textbf{C}(\textbf{V}) = \left( \begin{array}{ccccccccc} u^1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _1}{\alpha _1}\vartheta _2^1 &{} u^1_1 &{} 0 &{} \rho _1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{ \rho _2}{\alpha _2}\vartheta _1^1&{} 0 &{} u_2^1 &{} 0 &{} 0 &{} 0 &{} \rho _2 &{} 0 &{} 0 \\ \beta &{} \frac{a_1^2}{\rho _1} &{} 0 &{} u_1^1 &{} \vartheta _{2}^2 &{} \vartheta _{2}^3&{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} u^1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} u^1 &{} 0 &{} 0 &{} 0\\ \beta &{} 0 &{} \frac{a_2^2}{\rho _2} &{} 0 &{} 0 &{} 0 &{} u_2^1 &{} -\vartheta _{1}^2 &{} -\vartheta _{1}^3 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} u^1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} u^1 \\ \end{array} \right) . \end{aligned}$$

As previously, we have used the auxiliary variables (11) to lighten the matrix. In this case, the nine eigenvalues of the matrix \(\textbf{C}\) are given by

$$\begin{aligned}&\lambda _1 = u^1_1-a_1, \quad \lambda _2 = u^1_1+a_1, \quad \lambda _{3} = u^1_2-a_2, \quad \lambda _{4} = u^1_2+a_2, \quad \lambda _{5-9} = u^1 \end{aligned}$$

with \(a_j\) the sound speed of phase j, which is defined as \(a^2_j=\rho _j\left( \frac{\partial h_j}{\partial \rho _j}\right) , \, j=1,2\). Since the eigenvalues are all real, to check if the system is weakly or strongly hyperbolic, it is necessary to compute the associated eigenvectors. Below, we will write the matrix that contains the right eigenvectors in columns. They are listed in the same order as the eigenvalues

$$\begin{aligned} \textbf{R}=\left( \begin{array}{ccccccccc} 0 &{} 0 &{} 0 &{} 0 &{} \frac{\alpha _1\,\alpha _2\,\vartheta _1^3}{\eta _2} &{} \frac{\alpha _1\, \alpha _2\,\vartheta _1^2}{\eta _2} &{} -\frac{\alpha _1\,\alpha _2\, Z_{2}}{\eta _2\,\vartheta _1^1} &{} 0 &{} 0 \\ \frac{-\rho _1}{a_1} &{} \frac{\rho _1}{a_1} &{} 0 &{} 0 &{} -\frac{\zeta _1\,\rho _1\,\vartheta _1^3}{\eta _2 Z_{1}} &{} -\frac{\zeta _1\,\rho _1\, \vartheta _1^2}{\eta _2 Z_{1}} &{} \frac{\zeta _1\,\rho _1\,Z_{2}}{\eta _2\,\vartheta _1^1\,Z_{1}} &{} -\frac{\rho _1\, \vartheta _2^3}{Z_{1}} &{} -\frac{\rho _1\,\vartheta _2^2}{Z_{1}} \\ 0 &{} 0 &{} \frac{-\rho _2}{a_2} &{} \frac{\rho _2}{a_2} &{} \frac{\alpha _1\,\rho _2\,\vartheta _1^3}{\eta _2} &{} \frac{\alpha _1\, \rho _2\, \vartheta _1^2}{\eta _2} &{} \frac{\zeta _2\,\rho _2}{\eta _2\,\vartheta _1^1} &{} 0 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 &{} \frac{\eta _1\,\vartheta _2^1\,\vartheta _1^3}{\eta _2\,Z_{1}} &{} \frac{\eta _1\,\vartheta _2^1\,\vartheta _1^2}{\eta _2\,Z_{1}} &{} -\frac{c_2\,\eta _1\,Z_{2}}{c_1\,\eta _2\,Z_{1}} &{} \frac{\vartheta _2^1 \vartheta _2^3}{Z_{1}} &{} \frac{\vartheta _2^1\vartheta _2^2}{Z_{1}} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned}$$

where the auxiliary variables used to write the nine right eigenvectors more compactly are defined as

$$\begin{aligned}&Z_{1}= a_1^2-(\vartheta _{2}^1)^2, \quad Z_{2}=a_2^2-(\vartheta _{1}^1)^2, \quad \eta _1= \alpha _2(a_1^2-\alpha _1\beta ), \\&\eta _2 = \alpha _1(a_2^2+\alpha _2\beta ), \quad \zeta _1= \alpha _2\left( \alpha _1\beta -(\vartheta _2^1)^2\right) , \quad \zeta _2 = \alpha _1\left( \alpha _2\beta +(\vartheta _1^1)^2\right) . \end{aligned}$$

Since we have obtained nine real eigenvalues with a full set of linearly independent eigenvectors, the system (14) with the additional symmetrizing Godunov-Powell terms is strongly hyperbolic.

3 High-Order ADER-DG Finite-Element Scheme with a posteriori Subcell Finite-Volume Limiter

As described in Sect. 2 and Refs. [59, 62, 69], the system (4) is a hyperbolic system that can be compactly written as

$$\begin{aligned} \frac{\partial \textbf{Q}}{\partial t} + \nabla \cdot \textbf{F}(\textbf{Q}) + \textbf{B}_{}(\textbf{Q})\cdot \nabla \textbf{Q}= \textbf{S}(\textbf{Q}), \end{aligned}$$
(15)

where \(\textbf{Q}\) is the vector of conserved variables, \(\textbf{F}= (\textbf{f}, \textbf{g}, \textbf{h})\) is the flux tensor, \(\textbf{B}_{}(\textbf{Q})\cdot \nabla \textbf{Q}=\textbf{B}_{1}(\textbf{Q})\frac{\partial }{\partial x}\textbf{Q}+ \textbf{B}_{2}(\textbf{Q})\frac{\partial }{\partial y}\textbf{Q}+ \textbf{B}_{3}(\textbf{Q})\frac{\partial }{\partial z}\textbf{Q}\) are the non-conservative terms, and \(\textbf{S}\) is the vector of algebraic source terms. To solve the system (15), we will use high-order ADER-DG schemes with a posteriori subcell finite-volume limiter on uniform Cartesian meshes, see [24, 26, 27, 33, 34, 76] for further details. In this work, for the time-evolution, we propose to use a local space-time DG predictor, instead of using the Cauchy-Kovalevskaya procedure, following [27, 28]. The main reasons for this choice are the following: compared to the Cauchy-Kovalevskaya procedure, which is rather cumbersome, the local space-time DG predictor is much more general and simpler to implement for complex hyperbolic PDE systems as the ones studied in this paper. Furthermore, it allows also to deal with stiff source terms, like stiff velocity and pressure relaxation terms.

3.1 One-Step ADER-DG Schemes

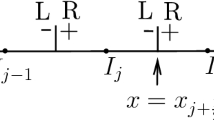
In the following, a description of the method is given for the two-dimensional (2D) case (\(d=2\)). The computational domain \(\varOmega = [-L_{x}/2,L_{x}/2]\times [-L_{y}/2,L_{y}/2]\) is discretized with a Cartesian grid composed of \(N_{x}\times N_{y}\) cells. These cells are given by \(\varOmega _i = [x_i-\frac{\Delta x}{2},x_i+\frac{\Delta x}{2}]\,\times\, [y_i-\frac{\Delta x}{2},y_i+\frac{\Delta y}{2}]\) with \((x_i,y_i)\) the barycenter of the cell \(\varOmega _i\), and \(\Delta x=\frac{L_x}{N_x}\), \(\Delta y=\frac{L_y}{N_y}\) the mesh spacing in the x- and y-directions. Let \(\varvec{u}_h(\textbf{x},t^n)\) be the discrete solution of (15) in each spatial control volume \(\varOmega _i\) at time \(t^n\), written in terms of tensor products of piecewise polynomials of degree N, and let \(V_h\) be the space of tensor products of piecewise polynomials of the degree up to N. Then, the discrete solution \(\varvec{u}_h\) can be written in terms of the basis functions, \(\varphi _l(x,y), \ l\in [1,(N+1)^d]\), in every cell \(\varOmega _i\) as

$$\begin{aligned} \varvec{u}_h(\textbf{x}, t^n) = \varphi _l(\textbf{x})\hat{\varvec{u}}_l^n,\quad \textbf{x}\in \varOmega _i, \end{aligned}$$
(16)

where \(\varphi _l=\varphi _l(\textbf{x})\) are the basis functions associated with \(V_h\). We take an orthogonal nodal basis \(\{\varphi _l\}_{l\in \{0,\cdots ,(N+1)^d\}}\), generated by the tensor product \(\{\varphi _{l_1} \varphi _{l_2} \varphi _{l_3} \}_{l_1,l_2,l_3\in \{0,\cdots, N\}},\) where \(\{\varphi _{l_l}\}_{l_l\in \{0,\cdots ,N\}}\) are the Lagrange interpolation polynomials going through the \(N+1\) Gauss-Legendre quadrature nodes. Multiplying (15) by a test function \(\varphi _l\in V_h\), and integrating the equation over the space-time control volume \(\varOmega _i\times [t^n,t^{n+1}]\), the weak formulation can be written as

$$\begin{aligned} \int _{t^n}^{t^{n+1}}\!\!\!\!\int _{\varOmega _i}\left( \frac{\partial \textbf{Q}}{\partial t} + \nabla \cdot \textbf{F}(\textbf{Q}) + \textbf{B}_{}(\textbf{Q})\cdot \nabla \textbf{Q}\right) \varphi _l\,\textrm{d}{\textbf{x}}\textrm{d}{t} = \int _{t^n}^{t^{n+1}}\!\!\!\!\int _{\varOmega _i} \textbf{S}(\textbf{Q})\varphi _l\,\textrm{d}{\textbf{x}}\textrm{d}{t}. \end{aligned}$$
(17)

To achieve high order in space and time, an ADER approach can be used. This methodology was put forward by Toro et al. for the first time in [72] for linear problems on Cartesian meshes, it can be implemented in both the finite volume and the DG finite-element framework and is uniformly and arbitrarily high-order accurate in both space and time. In this work, an alternative version of the ADER approach is considered, avoiding the use of the Cauchy-Kovalevskaya procedure using a local space-time DG predictor, which is based on a weak space-time formulation of the governing PDE (17).

Using (16) and integrating the term with the time derivative by parts in time and the divergence term by parts in space, then (17) results in

$$\begin{aligned}&\left( \int\nolimits _{\varOmega _i} \! \varphi _k \varphi _l \, \textrm{d}{\textbf{x}} \right) \left( \hat{\varvec{u}}_{l,i}^{n+1} - \hat{\varvec{u}}_{l,i}^{n} \, \right) + \int\nolimits_{t^n}^{t^{n+1}} \!\!\! \int \nolimits _{\partial \varOmega _i } \! \varphi _k \left( \mathcal {G}\left( \textbf{q}_h^-, \textbf{q}_h^+ \right) + \mathcal {D}\left( \textbf{q}_h^-,\textbf{q}_h^+ \right) \right) \cdot \textbf{n}\, \textrm{d}{S}\textrm{d}{t} \nonumber \\&-\int \nolimits _{t^n}^{t^{n+1}} \!\! \int \nolimits _{\varOmega _i } \!\! \nabla \varphi _k \cdot \textbf{F}(\textbf{q}_h) \,\textrm{d}{\textbf{x}}\textrm{d}{t} =\int \nolimits _{\varOmega _i} \varphi _k \textbf{S}(\textbf{q}_h) \,\textrm{d}{\textbf{x}}\textrm{d}{t}, \end{aligned}$$
(18)

where \(\textbf{n}\) is the outward unit normal vector at the cell boundary \(\partial \varOmega _i\), \(\textbf{q}_h\) is a local space-time predictor, which will be explained below, and \(\textbf{q}_h^+\) and \(\textbf{q}_h^-\) are the boundary-extrapolated values of the space-time predictor from within \(\varOmega _i\) and its neighbor \(\varOmega _j\). Usually, \(\textbf{q}_h\) presents jumps across the cell boundaries, which can be resolved by the solution of a generalized Riemann problem (see [40, 71] for more details). In (18), \(\mathcal {G}\) denotes the Riemann solver (numerical flux function), which depends on the left state \(\textbf{q}_h^{-}\) and the right state \(\textbf{q}_h^{+}\). In this case, this integral has been approximated using the Rusanov flux, see [64]

$$\begin{aligned} \mathcal {G}(\textbf{q}_h^-, \textbf{q}_h^+ ) \cdot \textbf{n}= \frac{1}{2} \left( \textbf{F}(\textbf{q}_h^+) + \textbf{F}(\textbf{q}_h^-) \right) \cdot \textbf{n}- \frac{1}{2} s_{\max } \,\textbf{I} \, \left( \textbf{q}_h^+ - \textbf{q}_h^- \right) , \end{aligned}$$
(19)

where \(s_{{\textrm{max}}} = \textrm{max}\left( \left| \lambda _k(\textbf{q}_h^+)\right| ,\left| \lambda _k(\textbf{q}_h^-) \right| \right)\) is the maximum wave speed at the interface. To deal with the jump terms in the non-conservative product, a path-conservative method is employed, following [13, 51]. In this setting, a straight-line segment path is chosen

$$\begin{aligned} \Psi (s, \textbf{q}_h^+, \textbf{q}_h^-) = \textbf{q}_h^-+s( \textbf{q}_h^+- \textbf{q}_h^+), \quad s\in [0,1], \end{aligned}$$

so that the non-conservative terms reduce to the following expression:

$$\begin{aligned} \mathcal {D}(\textbf{q}_h^{-},\textbf{q}_h^{+})\cdot \textbf{n}= \frac{1}{2}\widetilde{\textbf{B}_{}} \cdot (\textbf{q}_h^{+}-\textbf{q}_h^{-}) \quad \text {with} \quad \widetilde{\textbf{B}_{}} = \int _0^1 \textbf{B}_{}( \Psi (s, \textbf{q}_h^+, \textbf{q}_h^-)) \cdot \textbf{n}\ \textrm{d}{S}. \end{aligned}$$

3.2 Local Space-Time Predictor

In the following, we describe the local space-time predictor used to compute the coefficients \(\hat{\varvec{u}}^n_{l,i}\) in Eq. (18). We consider space-time basis functions \(\theta _l\), that are obtained as the tensor product \(\theta _l(\textbf{x},t)=\varphi _{k_0}(t)\varphi _{k_1}(\textbf{x})\), of the same previously introduced Lagrange interpolation polynomials, just that now the basis functions also depend on time. The predictor \(\textbf{q}_h\) is written in the form

$$\begin{aligned} \textbf{q}_h(\textbf{x},t) = \theta _l(\textbf{x},t) \hat{\textbf{q}}_{l,i} \end{aligned}$$
(20)

as a weak solution to (15). Then, using (20) in (15), multiplying by a space-time basis function \(\theta _l\) and integrating over \(\varOmega _i\times [t^n,t^{n+1}]\) yields

$$\begin{aligned} \int \nolimits _{t^n}^{t^{n+1}} \! \int \nolimits _{\varOmega _i}\theta _l\left( \varvec{U}_t + \nabla \cdot \textbf{F}(\varvec{U}) + \textbf{B}_{}(\varvec{U})\cdot \nabla \varvec{U}\right) \textrm{d}{\textbf{x}}\textrm{d}{t} = \int \nolimits _{t^n}^{t^{n+1}} \! \int \nolimits _{\varOmega _i}\theta _l \left( \textbf{S}(\varvec{U})\right) \textrm{d}{\textbf{x}}\textrm{d}{t}. \end{aligned}$$

Integrating by parts only the first term on the left-hand side and taking into account that at time \(t^n\), we start from the known state \(\varvec{u}_h^n\) allows us to write

$$\begin{aligned}&\int \nolimits _{\varOmega _i}\theta _l(\textbf{x},t^{n+1}) \textbf{q}_h(\textbf{x},t^{n+1}) \,\textrm{d}{\textbf{x}} -\int \nolimits _{\varOmega _i}\theta _l(\textbf{x},t^{n}) \varvec{u}_h(\textbf{x},t^{n}) \,\textrm{d}{\textbf{x}} -\int \nolimits _{t^n}^{t^{n+1}} \!\! \int \nolimits _{\varOmega _i}\frac{\partial \theta _l}{\partial t} \, \textbf{q}_h \,\textrm{d}{\textbf{x}}\textrm{d}{t} \nonumber \\ &+\int \nolimits _{t^n}^{t^{n+1}} \!\! \int \nolimits _{\varOmega _i}\theta _l\, \nabla \cdot \textbf{F}(\textbf{q}_h) \,\textrm{d}{\textbf{x}}\textrm{d}{t} +\int \nolimits _{t^n}^{t^{n+1}} \!\! \int \nolimits _{\varOmega _i^{\circ } } \theta _l\textbf{B}_{}(\textbf{q}_h ) \cdot \nabla \textbf{q}_h \,\textrm{d}{\textbf{x}}\textrm{d}{t} = \int \nolimits _{t^n}^{t^{n+1}} \!\! \int \nolimits _{\varOmega _i } \theta _l \textbf{S}(\textbf{q}_h) \,\textrm{d}{\textbf{x}}\textrm{d}{t} \end{aligned}$$
(21)

with \(\varOmega _i^{\circ }=\frac{\varOmega _i} {\partial \varOmega _i}\). Equation (21) is a system for the unknowns \(\hat{\textbf{q}}\) of the space-time predictor \(\textbf{q}_h(\textbf{x},t)\) and can be computed in terms of the spatial degrees of freedom \(\hat{\varvec{u}}_l^n\). It is solved by a fixed point iteration for which convergence was proven in [10]. Once the predictor is known, Eq. (18) allows to compute the polynomial coefficients \(\hat{\varvec{u}}^{n+1}\) in each cell using Gaussian quadrature for the remaining integrals.

3.3 A Posteriori Subcell Finite-Volume Limiter

Although the numerical method presented in the previous section is a high-order method, it is linear in the sense of Godunov, which means that spurious oscillations will appear in the presence of discontinuities or shock waves. To overcome this problem, we use the a posteriori subcell limiter for high-order fully discrete one-step ADER-DG schemes presented in [34, 76]. This subcell finite-volume limiter is based on the MOOD paradigm introduced in [17, 22, 23] for finite-volume schemes.

The scheme described in the previous section is run over the entire domain at each time step, and a so-called candidate solution \(\varvec{u}_h^*(\textbf{x},t^{n+1})\) is obtained. Then, one checks whether the candidate solution verifies some numerical and physical detection criteria (positivity of the densities \(\rho _1\) and \(\rho _2\), \(\alpha _1\) with values between 0 and 1) and whether the discrete maximum principle (DMP), [34], is verified. If a cell \(\varOmega _i\) violates any of the above criteria, that cell is flagged as a troubled cell and for the application of the subcell finite-volume limiter. The limiter is denoted as a posteriori, because it is applied after the candidate solution has been computed.

The limiter is applied in the following way: all cells \(\varOmega _i\) marked as troubled are subdivided into \((2N+1)^d\) subcells, which are denoted by \(\varOmega _{i,j}\) where \(\varOmega _i=\bigcup _j \varOmega _{i,j}\). The discrete solution at time \(t^n\) is given by the piecewise constant cell averages, denoted by \(\bar{\varvec{u}}^n_{i,j}\). They are obtained from the high-order DG polynomials \(\varvec{u}_h(\textbf{x},t^n)\) by averaging using the definition of the cell average

$$\begin{aligned} \bar{\varvec{u}}^n_{i,j} = \frac{1}{|\varOmega _{i,j}|} \int _{\varOmega _{i,j}} \varvec{u}_h(\textbf{x},t^n) \,\textrm{d}{\textbf{x}}. \end{aligned}$$
(22)

It is worth noting that subdividing a high-order DG element into \(2N+1\) finite-volume subcells per space dimension does not reduce the time step size of the overall scheme, since the CFL stability condition of explicit DG schemes scales with \(1/(2N+1)\) in one dimension, while the maximum Courant number of finite-volume methods is unity in one space dimension.

The cell averages (22) are evolved in time using either a second-order MUSCL-Hancock-type TVD finite-volume scheme with the minmod limiter, or by making use of a third-order ADER-WENO finite-volume scheme, see [34], which are also both predictor-corrector methods, and thus look almost identical to the ADER-DG scheme, except for the necessary nonlinear reconstruction step. Moreover, in this case, the test function is unity, which implies that the volume integral over the flux term disappears and the volumes computed over \(\varOmega _i\) are replaced by the volumes over the subcells \(\varOmega _{i,j}\), and hence

$$\begin{aligned}& \left| \varOmega _{i,j} \right| \left( \bar{\varvec{u}}^{n+1}_{i,j} - \bar{\varvec{u}}^{n}_{i,j} \right) + \int _{t^n}^{t^{n+1}} \! \! \int _{\partial \varOmega _{i,j}} \left( \mathcal {G}\left( \textbf{q}_h^-, \textbf{q}_h^+ \right) + \mathcal {D}\left( \textbf{q}_h^-, \textbf{q}_h^+ \right) \right) \cdot \textbf{n}\, \textrm{d}{S} \textrm{d}{t} \nonumber \\ &+ \int _{t^n}^{t^{n+1}} \! \! \int _{\varOmega _{i,j}^\circ } \left( \textbf{B}_{}(\textbf{q}_h) \cdot \nabla \textbf{q}_h \right) \textrm{d}{\textbf{x}} \textrm{d}{t} = \int _{t^n}^{t^{n+1}} \! \! \int _{\varOmega _{i,j}} \textbf{S}(\textbf{q}_h, \nabla \textbf{q}_h) \textrm{d}{\textbf{x}} \textrm{d}{t}\, . \end{aligned}$$
(23)

The limited DG polynomial \(\varvec{u}'_h\) at time \(t^{n+1}\) is then obtained by performing a constrained least-squares reconstruction and using the averages of all the subcells of \(\varOmega _i\) computed using (23). The reconstruction reads

$$\begin{aligned} \frac{1}{|\varOmega _{i,j}|} \int _{\varOmega _{i,j}} \varvec{u}'_h(\textbf{x},t^{n+1}) \textrm{d}{\textbf{x}} = \bar{\varvec{u}}^{n+1}_{i,j}, \quad \forall \, \varOmega _{i,j} \in \varOmega _i \end{aligned}$$

with the linear constraint

$$\begin{aligned} \int _{\varOmega _{i}} \varvec{u}'_h(\textbf{x},t^{n+1})\textrm{d}{\textbf{x}} = \displaystyle {\sum _{\varOmega _{i,j} \in \varOmega _i} |\varOmega _{i,j}| \bar{\varvec{u}}^{n+1}_{i,j}}. \end{aligned}$$
(24)

The constraint (24) means conservation of the solution within the element \(\varOmega _i\). In addition to the expansion coefficients \(\hat{\varvec{u}}_{i,l}^{n+1}\) of the limited DG polynomial, in all limited DG elements, we also keep in memory the averages of the finite-volume subcells \(\bar{\varvec{u}}^{n+1}_{i,j}\), as they serve as the initial condition for the finite-volume limiter of the subcell in case a cell is problematic also in the next time step, see [34]. More details about the a posteriori subcell finite-volume limiter can be found in [31, 34, 76].

4 Numerical Results

This section is devoted to showing some test cases to illustrate the high order of the accuracy of the proposed method, especially in the presence of steep gradients in the solution. First, some simulations are performed to show the experimental order of convergence (EOC) of the proposed ADER-DG method. Then, our scheme is used to solve some Riemann problems in one and two dimensions. Finally, a dambreak problem is simulated, and the results are compared with those obtained with a reduced BN model. Although the original system is only weakly hyperbolic, no stability problems have been found in the numerical simulations, contrary to what was reported in [15, 16, 21] for other weakly hyperbolic systems with curl involutions. In this section, some test cases are performed considering the original system (4), and some others, such as the convergence analysis and the dambreak, are solved using not only the original system but also the new GLM curl-cleaning technique and the symmetrizing Godunov-Powell terms to compare the solutions. Moreover, in all tests, the algebraic relaxation source terms have been neglected, and the gravity \(\varvec{g}\) is set to \(\varvec{0}\), except in the dambreak test case, where it is necessary to consider the gravity.

4.1 Accuracy Analysis

This section performs a numerical convergence analysis to show the EOC of the proposed ADER-DG method. To construct an exact solution, following [5, 30], an analytical, stationary, and rotationally symmetric solution of the system (4) is computed considering cylindrical coordinates (r, \(\theta,\) and z) with \((u^{r},u^{\theta }, u^{z})\) the velocity vector and \((w^{r},w^{\theta },w^{z})\) the relative velocity vector. The analytical solution is assumed to approach a constant state as the radial coordinate r tends to infinity to be compatible with periodic boundary conditions.

To obtain a steady analytical solution, we first write an equivalent PDE system in the radial direction. For this purpose, the pressure and the velocity relaxation are neglected, the gravity is set to zero, and system (4) is rewritten in cylindrical coordinates and assuming no variations in the \(z\)-direction (\(\frac{\partial} {\partial z}=0\)) and considering rotational symmetry (\(\frac{\partial} {\partial \theta} =0\)). The resulting system in radial direction reads

where the constraint \(\nabla \times \varvec{w}=0\) has been used in the last two equations. Since we are looking for a vortex-type solution, the radial velocities vanish, that is, we set \(u^{r}=u^{r}_1=u^{r}_2=w^{r}=0\). Also, we are interested in a stationary solution, hence \(\partial _t=0\). With these assumptions, the system (25) reduces to

$$\begin{aligned} \alpha _1\rho _1\frac{(u^{\theta }_1)^2}{ r}+\alpha _2\rho _2\frac{ (u^{\theta }_2)^2 }{ r}-\frac{\partial p}{\partial r}&=0,\end{aligned}$$
(26a)
$$\begin{aligned} \frac{\partial }{\partial r} \left( \frac{1}{2}(u^{\theta })^2-\frac{1}{2}(u^{\theta })^2 + h_1-h_2\right)&=0. \end{aligned}$$
(26b)

With some simple algebra in (26), we get

where k is a constant. Now, we prescribe radial profiles for \(\alpha _1\) and \(p_i\) as

$$\begin{aligned} \alpha _1 = \frac{1}{3}+\frac{{\rm{e}}^{-\frac{ r^2}{2}}}{2\sqrt{2\uppi }}, \qquad p_i = 1-\frac{{\rm{e}}^{1-r^2}}{4}, \end{aligned}$$

and then, the densities \(\rho _i\) and the velocities \(u^{\theta }_{i}\) result as

$$\begin{aligned} \rho _i = \left( 1 - \frac{{\rm{e}}^{1 - r^2}}{4} \right) ^{5/7}, \qquad u^{\theta }_{i} = 2^{3/14}\sqrt{ \frac{{\rm{e}}^{1 - r^2}r^2}{\left( 4 - {\rm{e}}^{1 - r^2}\right) ^{5/7}}}. \end{aligned}$$

With this, we have computed an exact stationary and rotationally symmetric solution of the PDE system (25) that approaches a constant state as \(r\rightarrow \infty\) to be compatible with periodic boundary conditions. Figure 1 shows the contours of the volume fraction function for our vortex-type solution together with the velocity but remains stationary due to its symmetry. Then, using the principle of the Galilean invariance, we can make the test unsteady if we add a uniform velocity field to this solution. After one advection period through a periodic computational domain, the exact solution will be given by the initial condition and we can perform the convergence test.

Fig. 1
figure 1

\(\alpha\) field for the stationary vortex-type solution at times \(t = 0,\,1\). The velocity streamlines are plotted to show that the solution is symmetric and is rotating over time

Full size image

To analyze the convergence order, we compute the solution with the proposed method, using different orders for the DG scheme, and compare it with the exact solution derived above. The computational domain is \(\varOmega =[-10,10]^2\) with the final simulation time \(t=1\) and periodic boundary conditions everywhere. Different polynomial approximation degrees have been considered for the DG scheme. The \(L^{2}\) errors and the corresponding numerical convergence rates for \(N=2,3,4,5\) are given in Table 1, showing the expected order of convergence.

Fig. 2
figure 2

Value of \(\alpha\) for the unsteady vortex at times \(t = 0,\,1,\,2,\,3,\,4,\,5\)

Full size image

For analyzing the convergence order using the unsteady solution, we make use of the principle of the Galilean invariance of Newtonian mechanics. We add a constant uniform velocity field \(\bar{u}_1=\bar{u}_2=4\) to both phases. The computational domain is the same as before \(\varOmega =[-10,10]\times [-10,10]\) with the final simulation time \(t=5\) and periodic boundary conditions everywhere. Figure 2 shows that this solution is symmetric and rotates over time, as the stationary one, but the vortex is transported with constant velocities \(\bar{u}_1=\bar{u}_2=4\). At time \(t=5\), after one advection period, the solution will be the initial one. The \(L^{2}\) errors and the corresponding convergence rates for the different degrees \(N=2,3,4,5\) are given in Table 2, finding the expected convergence order \(N+1\) of our high-order ADER-DG schemes.

Fig. 3
figure 3

Time evolution of the \(L^{1}\) (left) and \(L^{2}\) (right) norms of the curl errors

Full size image

Finally, we will perform a convergence analysis with the same unsteady solution used in the previous case, where we can compare the convergence order for the original system, as well as for the systems augmented with the GLM approach with the curl-cleaning speed \(a_{\varvec{\psi }}=1\) and with the Godunov-Powell terms. Table 3 shows the errors in the \(L^{2}\) norm and the convergence orders for \(N=3\). The difference among the errors for the three systems is almost negligible and the order of convergence is four, as expected.

For this test, we have also computed the \(L^{1}\) and \(L^{2}\) norms of the curl errors for different values of \(a_{\varvec{\psi }}\), to illustrate the time-evolution of these errors as a function of \(a_{\varvec{\psi }}\). As we can expected, the curl errors are decreasing when the GLM curl-cleaning speed \(a_{\varvec{\psi }}\) is increasing, as one can see in Fig. 3.

Table 1 Numerical convergence results for high-order DG schemes of polynomial approximation \(N=2,3,4,5\) with a uniform Cartesian mesh of \(N_x\times N_y\) elements. The \(L^{2}\) error norms and the corresponding orders of the convergence of the variables \(\alpha _1\), \(\rho _1\), \(\rho _2\), \(u_1\), and \(u_2\) are computed at time \(t=1\)
Full size table
Table 2 Numerical convergence rates for DG schemes of polynomial approximation \(N=2,3,4,5\) with a uniform Cartesian mesh of \(N_x\times N_y\) elements in the unsteady case. The \(L^{2}\) error norms and the convergence orders of the variables \(\alpha _1\), \(\rho _1\), \(\rho _2\), \(u_1\), and \(u_2\), are computed at time \(t=5\) with \(\bar{u}_1=\bar{u}_2=4\)
Full size table
Table 3 Numerical convergence rates for DG schemes with \(N=3\) using a uniform Cartesian mesh of \(N_x\times N_y\) elements in the unsteady case using the original system (4), the augmented system with the GLM approach (12), and the system with the Godunov-Powell terms (14). The \(L^{2}\) error norms and the convergence orders of the variables \(\alpha _1\), \(\rho _1\), \(\rho _2\), \(u_1\), and \(u_2\), are computed at time \(t=5\) with \(\bar{u}_1=\bar{u}_2=4\)
Full size table

4.2 The 1D Riemann Problem

This section is devoted to studying the behavior of the proposed methodology in the presence of shocks. First, we solve one of the 1D Riemann problems proposed in [69], where a shock in one phase appears inside a rarefaction of the other phase. This Riemann problem presents a discontinuity in \(x=0\) and has the left and right states shown in Table 4.

Table 4 Left and right states of the Riemann problem 1
Full size table

Since the problem that we want to reproduce is a 1D problem, \(u^2=u^3=0\) and \(w^2=w^3=0\). The computational domain is \(\varOmega = [-1,1]\) and has been discretized using a fourth-order ADER-DG scheme (\(N=3\)) with a posteriori subcell limiter on a mesh with 8 192 cells. The simulation is performed up to \(t=0.25\), and the CFL number is set to 0.25. Two ideal gases are considered for both phases with EOS (6), setting \(s_i=0\), \(\gamma _1=1.4\), and \(\gamma _2=2\), respectively. In Fig. 4, the numerical results are shown together with the reference solution computed with a second-order MUSCL-Hancock scheme based on the Rusanov flux as approximate Riemann solver and using a mesh spacing of \(\Delta x = 2\times 10^{-6}\) (see [69] for further details). We observe an excellent agreement between our numerical solution and the reference solution. Looking at the density and velocity of each phase, we see that as long as shock waves are absent, the rarefaction only affects the related phase, but that the interaction of the two rarefactions is observed in the mixing quantities. In addition, in the density of the first phase, we can see that to the right of the contact, a rarefaction begins (which does not affect the second phase) until the shock occurs. Once the shock appears inside the right rarefaction, the density jumps according to the jump conditions. Then, on the right, a plateau of the right state of the shock is observed inside the rarefaction, and then, the rarefaction continues again, see [69] for a detailed discussion of this peculiar shock-in-rarefaction phenomenon, which is a particular kind of nonlinear resonance, see [45]. The feature can best be appreciated inside the right rarefaction in the quantity w in the lower right panel of Fig. 4.

Fig. 4
figure 4

The 1D Riemann problem solved with a fourth-order ADER-DG scheme with the TVD subcell limiter on a Cartesian mesh with 8 192 cells at time \(t=0.25\). Top row: densities of each phase, \(\rho _1\) and \(\rho _2\). Second row: the mixture density \(\rho\) and \(\alpha\). Third row: the velocities \(u_1\) and \(u_2\). Bottom row: the mixture velocity \(u\) (left) and relative velocity \(w=u_1-u_2\) (right)

Full size image

4.3 The 2D Explosion Problems

In this section, we solve the system for multi-phase flows in two dimension in a circular computational domain with radius \(R=1\). The initial condition is given by

$$\begin{aligned} \textbf{Q}(\textbf{x},t) = \left\{ \begin{array}{ll} \textbf{Q}_{\rm{L}}, &{} \text{ if } |\textbf{x}|<0.5,\\ \textbf{Q}_{\rm{R}}, &{} \text{ otherwise, } \end{array} \right. \end{aligned}$$
(28)

where \(\textbf{Q}_{\rm{L}}\) and \(\textbf{Q}_{\rm{R}}\) are described in Table 5.

Table 5 Left and right states of the circular explosion problems
Full size table

As a reference solution, we will solve the following equivalent (non-conservative) PDE in radial direction with geometric reaction source terms:

where the parameter d is the number of spatial dimensions minus one. The 2D computations have been performed using a fourth-order (\(N=3\)) ADER-DG scheme with a posteriori subcell limiter. The computational domain is \(\varOmega =[-1,1]\times [-1,1]\) and has been discretized using a Cartesian mesh with \(512 \times 512\) elements. Following (28), the left state of the Riemann problem has been taken as the inner state and the right state of the same Riemann problem as the outer state. The reference solution has been computed by solving (29) with 128 000 cells using a second-order TVD finite-volume method with the Rusanov flux. The simulation is performed up to \(t=0.1\) with two ideal gases, so, for the two phases, the EOS is given by (6) with \(s_i=0\), \(\gamma _1=1.4\), and \(\gamma _2=2\), respectively.

Figures 5 and 6 show the numerical results of two circular explosion problems with the initial conditions of Table 5 and a final time of \(t=0.1\) for the first one and \(t=0.2\) for the second one. The numerical solution obtained with the ADER-DG method is then compared with the radial reference solution, showing excellent agreement. Moreover, Fig. 7 shows the limiter map of the second explosion problem. The values highlighted in blue are those DG elements where the limiter is not activated, and the red ones are the troubled zones where the a posteriori subcell finite-volume limiter is activated.

Fig. 5
figure 5

The 2D circular explosion problem for the initial condition CE1 in Table 5 solved on a Cartesian mesh at time \(t=0.1\), in comparison with the radial reference solution. Top row: densities of each phase, \(\rho _1\) and \(\rho _2\). Second row: the mixture density \(\rho\) and \(\alpha\). Third row: the velocities \(u_1\) and \(u_2\). Bottom row: the mixture velocity \(u\) (left) and relative velocity \(w=u_1-u_2\) (right)

Full size image
Fig. 6
figure 6

The 2D circular explosion problem for the initial condition CE2 in Table 5 solved on a Cartesian mesh at time \(t=0.2\), compared with the radial reference solution. Top row: densities of each phase, \(\rho _1\) and \(\rho _2\). Second row: the mixture density \(\rho\) and \(\alpha\). Third row: the velocities \(u_1\) and \(u_2\). Bottom row: the mixture velocity \(u\) (left) and relative velocity \(w=u_1-u_2\) (right)

Full size image
Fig. 7
figure 7

Left: the limiter map of the explosion problem in two dimensions. The values in red mean that the limiter is activated. Right: the 3D plot with the variable \(\rho _2\) in the \(z\)-axis

Full size image

4.4 Dambreak Problem

Finally, a 2D dambreak problem is solved using the barotropic two-phase model studied in this paper. In this case, the source term included in the momentum Eq. (4d) is non-zero, as a non-zero gravity source is considered, and hence, \(\varvec{g}=(0,-g,0)\) with \(g=9.81\). The computational domain is \(\varOmega =[0,4]\times [0,2]\), where the water domain is \(\varOmega _2=[0,2]\times [0,1]\) and the air domain is given by \(\varOmega _1=\varOmega \backslash \varOmega _2\).

The domain \(\varOmega\) has been discretized with a uniform Cartesian mesh with \(256\times128\) cells, using an ADER-DG scheme with \(N=3\) and a posteriori subcell finite-volume limiter. The simulation has been performed until a final time of \(t=0.4\), and a slip wall boundary condition is imposed on all boundaries. Following Sect. 2.1, an ideal gas is considered in \(\varOmega _1\), i.e., the EOS is given by (5) with parameters \(c_{01}=1\), \(\gamma _1 = 1.4\), \(\rho _{01}=1\), \(\alpha =\varepsilon\). The initial pressure profile is assumed hydrostatic, \(p=\rho _{01} g (y-2)\). The EOS for the liquid is a stiffened gas EOS given by (7), where \(c_{02}=20\), \(\gamma _2 = 2\), \(\rho _{02}=1\,000\), \(\alpha =1-\varepsilon\), and again a hydrostatic pressure profile \(p=\rho _{02} g (y-1)\) is imposed initially. The simulation was performed with \(\varepsilon =0\), i.e., initially, the phase volume fractions are really set to zero and unity, respectively. To obtain the value of the primitive variable \(\rho _k\), it is necessary to divide by \(\alpha _k\), and in this simulation, there exist areas with \(\alpha _k=0\), and it is necessary to apply a filter that avoids division by zero. In this paper, the density variables are filtered as follows:

$$\begin{aligned} \rho _k = \frac{\rho _k \alpha _k{^2} + \rho _{0k} \epsilon }{\alpha _k^2 + \epsilon }, \end{aligned}$$

see also [68], and the filter parameter is set \(\epsilon =10^{-12}\). The numerical results have been compared with the solution of the reduced barotropic BN model given in [25]. Figure 8 shows the values obtained at time \(t=0.4\) calculated with the reduced BN model in the upper plot, the solution calculated with the method proposed in this paper in the center, and a direct comparison of both models with the solution for the augmented model with the GLM approach and for the system with the Godunov-Powell terms, in the bottom plot, showing an excellent agreement among all the models. Similar results have also been recently obtained with a novel Arbitrary-Lagrangian-Eulerian hybrid finite-volume/finite-element method applied to the incompressible Navier-Stokes equations on moving unstructured meshes, see [12].

Fig. 8
figure 8

The dambreak problem at time \(t = 0.4\). Top: the reference solution, computed with a third-order ADER-WENO finite-volume scheme on a very fine uniform Cartesian grid, solving the inviscid and barotropic reduced BN model presented in [25]. Center: the numerical solution, computed using an ADER-DG scheme with a posteriori subcell limiter, to solve the barotropic SHTC model proposed in this work. Bottom: the comparison of the free-surface profile obtained for the reduced BN model, the original model solved in this paper, the augmented model with the GLM approach, and the model including the Godunov-Powell terms

Full size image

5 Conclusion

In this paper, the barotropic version of the conservative SHTC model for compressible two-fluid flows of Romenski et al. has been solved for the first time using high-order ADER-DG schemes in combination with a posteriori subcell finite-volume limiter. Since the model is only weakly hyperbolic in the general multidimensional case, two different methodologies have been presented to restore the strong hyperbolicity: (i) a GLM curl-cleaning approach; (ii) the addition of the Godunov-Powell terms to symmetrize the system. We obtain a full set of linearly independent eigenvectors with both methodologies, proving that strong hyperbolicity can indeed be restored.

A high-order ADER-DG finite-element scheme with a posteriori subcell finite-volume limiter has been used to deal with discontinuities and steep gradients in the solutions. To validate the model and the proposed method, a numerical convergence analysis has been carried out. For this purpose, we have constructed a new exact analytical and stationary equilibrium solution of the PDE system in cylindrical coordinates, and the high order of the method has been confirmed. A detailed comparison among the results obtained for the original system, for the augmented GLM curl-cleaning system, and for the Godunov-Powell-type system has been carried out, showing very similar results. Then, several Riemann problems in one and two dimensions have been simulated to show the behavior of the proposed methodology in the presence of shocks. First, a 1D Riemann problem where a shock in one phase appears inside the rarefaction of the other phase has been simulated. The results have been compared with those presented in [69], showing an excellent agreement. Then, two 2D explosion problems were solved. Thanks to the radial symmetry of the problem, the obtained results have been compared with an equivalent 1D reference solution, showing the accuracy of the proposed methodology even in the presence of sharp gradients in the solution. Finally, a dambreak test case has been considered, where the initial values of the volume fractions are set to \(\alpha _1=0\) and \(\alpha _2=1\). The numerical results obtained with the original system, with the augmented GLM system, and with the Godunov-Powell-type system are compared with those obtained for a reduced barotropic BN-type model, showing an excellent agreement between all the models. We can conclude that the results obtained with the original system, as well as those obtained with the GLM curl-cleaning approach and with the symmetrization of the system by adding the Godunov-Powell terms, are very similar at least for all the proposed tests and do not present evidence on which method is better for this type of model.

As future work, we plan to extend our methodology to compressible multi-phase flows with more than two phases and, in addition, to include also solids governed by the equations of nonlinear hyperelasticity, see, e.g., [32, 60, 61]. Furthermore, we will also apply exactly curl-free methods to the two-phase model discussed in this paper, such as the curl-free schemes recently forwarded in [6, 9, 15, 21].