High-Order Finite Element Methods for Interface Problems: Theory and Implementations

Abstract

We propose arbitrary order extended finite element (XFE) methods for solving both two and three dimensional elliptic interface problems. The meshes in our methods do not need to fit the interface and discontinuous Galerkin (DG) schemes are used in the vicinity of the interface to incorporate the transmission conditions between subdomains. Optimal error estimates in the piecewise H ¹-norm and in the L ²-norm are rigorously proved for the scheme. Two implementation aspects are addressed in this paper: (1) An optimal multigrid solver is introduced for the generated linear system, which converges uniformly with respect to the mesh size. (2) A high order algorithm is presented to compute the integral over elements intersecting the interface. Numerical experiments are reported to support the theoretical results.

1 Introduction

The interface problems which involve partial differential equations having discontinuous coefficients across certain interfaces are often encountered in fluid dynamics, electromagnetics and materials science. Because of the low global regularity and the irregular geometry of the interface, the standard numerical methods which are efficient for smooth solutions usually lead to loss in accuracy across the interface.

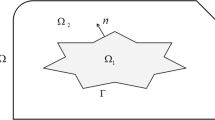
For arbitrarily shaped interface Γ, it is known that optimal or nearly optimal convergence rate can be recovered if body-fitted finite element meshes are used, see e.g. [6, 8, 21, 30]. Here, by “body-fitted meshes” we mean an element of the underlying mesh is required to intersect with the interface only through its boundaries (Fig. 1). Unfortunately, when the geometry is complex, this usually leads to a nontrivial interface meshing problem. Therefore, numerous modified finite difference methods based only on simple Cartesian grids have been proposed in the literature. We refer to the immersed boundary method [25], the immersed interface method [18, 19], the ghost fluid method [22], and the references therein. In the finite element setting, we refer to the work of the immersed finite element method [7, 11, 20], the multiscale finite element method [9], the penalty finite element method [1].

In the past decade, a combination of the extended finite element method (XFEM) with the Nitsche scheme has become a popular discretization method. As the first attempt, an unfitted finite element method was proposed in [13] which can be viewed as a linear and consistent modification of [1]. This approach has motivated a number of works, e.g., the unfitted finite element method [4, 5, 12], the Ghost penalty method [2, 3], the unfitted discontinuous Galerkin methods [23]. Although significant progresses in the error analyses of some methods have been made, the development of high-order accurate unfitted FEMs with rigorous error analysis is still challenging. We refer to the work of [14, 16, 17, 23, 28, 29] which claim high order approximations. In [23], an hp-unfitted discontinuous Galerkin method for Problem (1) was considered, and optimal h-convergence for arbitrary p was shown for the two-dimensional case in the energy norm and in the L ²-norm. With an extra flux penalty term applied on the interface, [29] gave better hp a priori error estimates in both two and three dimensions. In [16, 17], an isoparametric finite element method with a high order geometrical approximation of level set domains was presented. The analysis reveals optimal order error bounds with respect to h for the geometry approximation and for the finite element approximation. In [14, 28], various issues related to unfitted methods was addressed, including the dependence of error estimates on the diffusion coefficients, the condition number of the discrete system, and the choice of stabilization parameters.

Fig. 1

A body-fitted, shape regular mesh

The Nitsche-XFEM can be interpreted as applying interior penalty (IP) methods on the interface, and our method falls into this category. The major step in our variant is an appropriate choice of the mesh and geometry dependent weights in the average (see (6)), which lead to trace and inverse inequalities for possibly degenerated sub-elements (see (9)). We note that in our approach, the penalization is applied only to the jump of the solution values across the interface (compared with the bilinear form in [29]). The optimal h-convergence rate for arbitrary high-order discretization in the energy and L ₂-norm are proved regardless of the dimension. We refer to [14, 16, 17] for the similar estimates with respect to h and [29] for a refined version with respect to both h and p.

Efficient implementations of this method are then discussed in two aspects. We first consider an optimal multigrid solver for the generated linear system. We use the continuous FE space as a “background” subspace, with some smoothing operations added near the interface, to formulate a nested geometrical multigrid method. We prove the optimality of this special multiplicative multigrid method, which means the method converges uniformly with respect to the mesh size, and is independent of the location of the interface relative to the meshes. Since the assembling of the stiffness matrix will require integration over curved surfaces and volumes, we then implement a robust and arbitrarily high order numerical quadrature algorithm by transforming surface and volume integrals into multiple 1-D integrals. The code for the algorithm is freely available in the open source finite element toolbox Parallel Hierarchical Grid (PHG) [27]. We also refer to [24, 26] for different approaches to compute integrals on curved sub-elements and their curved boundaries.

The layout of this paper is as follows. In Sect. 2 we introduce the XFE spaces and reformulate the interface problem (1) in DG schemes. The H ¹- and L ²- error estimates of both schemes—which attain the optimal order of the convergence rate in respect to mesh size h—are given. In Sect. 3, we give an optimal multigrid method for the aforementioned DG-XFE schemes. Numerical examples for both two and three dimensions are reported in Sect. 4, to illustrate the high accuracy of the algorithm.

2 XFE and DG Schemes for Interface Problems

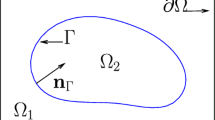
We consider the following elliptic interface problem for u: Let Ω = Ω₁ ∪ Γ∪ Ω₂ be a bounded and convex polygonal or polyhedral domain in $\mathbb {R}^d, d=2$ or 3, where Ω₁ and Ω₂ are two subdomains of Ω and are separated by a C ²-smooth interface Γ (see Fig. 2 for an illustration of a unit square that contains a circle as an interface),

$$\displaystyle \begin{aligned} \left\{ \begin{array}{rccl} -\nabla\cdot (\alpha(\mathbf { x }) \nabla u)&=&f, &\mbox{ in } \Omega_1\cup\Omega_2, \\ \left[\alpha(\mathbf { x }) \nabla u\right] &=& g_N, &\mbox{ on } \Gamma,\\ \left[u\right]&=&\boldsymbol{g_D}, &\mbox{ on } \Gamma,\\ u&=&0, &\mbox{ on } \partial\Omega. \end{array} \right. \end{aligned} $$

(1)

Here α(x) = α _i, i = 1, 2, is a piecewise constant function on the partition Ω₁ ∪ Ω₂.

Fig. 2

Domain Ω = Ω₁ ∪ Γ∪ Ω₂ with an unfitted mesh

Denote by $\{\mathcal {T}_h\}$, a family of conforming, quasi-uniform, and regular partitions of Ω into triangles and parallelograms/tetrahedrons and parallelepipeds. As K is of regular shape, there is a constant γ ₀ such that

$$\displaystyle \begin{aligned} h_K^d\le\gamma_0 |K|, \quad \forall K\in \mathcal{T}_h. \end{aligned} $$

(2)

We define the set of all elements intersected by Γ as $\mathcal {T}_h^\Gamma = \{K\in \mathcal {T}_h: |K\cap \Gamma | \neq 0\}$. Each $\mathcal {T}_h^\Gamma$ induces a partition of interface Γ, which we denote by $\mathcal {E}_h^\Gamma = \{e_K: e_K=K\cap \Gamma , K\in \mathcal {T}_h^\Gamma \}$. For any $K\in \mathcal {T}_h^\Gamma$, let K _i = K ∩ Ω_i denote the part of K in Ω_i and n _i be the unit outward normal vector on ∂K _i with i = 1, 2. As Γ is of class C ², it is easy to prove that (cf.[6, 32]) each interface segment/patch e _K is contained in a strip of width δ and satisfies

$$\displaystyle \begin{aligned} \delta\le \gamma_1 h_K^2~~~\mbox{and}~~~|\boldsymbol{n}_i(\mathbf { x })-\boldsymbol{n}_i(\mathbf { y })|\le \gamma_2 h_K,~\forall \mathbf { x },\mathbf { y }\in e_K. \end{aligned} $$

(3)

We define the weighted average {⋅} and the jump [⋅] on $e\in \mathcal {E}_h^\Gamma$ by

$$\displaystyle \begin{aligned} \{v\} &= \kappa_1 v_1 + \kappa_2 v_2, &[v] = v_1 \boldsymbol{n}_1 + v_2 \boldsymbol{n}_2,\quad \;\; {} \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} \{\boldsymbol{q}\} &= \kappa_1\boldsymbol{q}_1 + \kappa_2\boldsymbol{q}_2, & [\boldsymbol{q}] = \boldsymbol{q}_1\cdot \boldsymbol{n}_1 + \boldsymbol{q}_2\cdot \boldsymbol{n}_2. {} \end{aligned} $$

(5)

For the stability analysis of our schemes, we define (κ ₁, κ ₂) on each element as follows:

$$\displaystyle \begin{aligned} \kappa_i = \left\{ \begin{array}{cl} 0, &\mbox{ if } \frac{|K_i|}{|K|}<c_0 h_K, \\ 1, &\mbox{ if } \frac{|K_i|}{|K|}>1-c_0 h_K,\\ \frac{|K_i|}{|K|}, &\mbox{ otherwise }. \end{array} \right. \end{aligned} $$

(6)

Clearly, 0 ≤ κ _i ≤ 1 and κ ₁ + κ ₂ = 1 so that {⋅} is a convex combination along Γ. Roughly speaking, we adopt the weight $\kappa _i=\frac {|K_i|}{|K|}$ suggested in [13] for general sub-elements and we set κ _i = 0 for $|K_i|<c h_K^{d+1}$. Here, the user-defined constant c ₀ ≥ 2γ ₀ γ ₁ and γ ₀, γ ₁ are constants defined in (2) and (3), respectively. The dependence of c ₀ on these generic constants is elaborated in Lemma 1.

Let χ _i be the characteristic function on Ω_i with i = 1, 2. Given a mesh $\mathcal {T}_h$, let V _h be the continuous piecewise polynomial function space of degree p ≥ 1 on the mesh. Let $V_h^0:= V_h\cap H^1_0(\Omega )$, $V_h^1:= V_h^0\cdot \chi _1$ and $V_h^2 := V_h^0\cdot \chi _2$. We define the XFE space as $V_h^\Gamma = V_h^1 +V_h^2$.

Then, the DG-XFE method for the interface problem is: Find $u_h\in V_h^\Gamma$ such that

$$\displaystyle \begin{aligned} B_h(u_h,v_h) &= F_h(v_h), \quad \forall v_h\in V_h^\Gamma, \end{aligned} $$

(7)

where

$$\displaystyle \begin{aligned} B_h(w,v):=&\int_{\Omega_1\cup\Omega_2}\alpha(x) \nabla w \cdot \nabla v -\int_{\Gamma}\{\alpha(x)\nabla w\}\cdot [v]\\ &-\beta \int_{\Gamma}[w] \cdot \{\alpha(x)\nabla v\} +\sum_{K\in\mathcal{T}_h^\Gamma}\frac{\eta_{\beta}}{h_K}\int_{K\cap\Gamma}[w]\cdot [v],\\ F_h(v):=&\int_{\Omega} f\ v+\int_{\Gamma} g_N (\kappa_1v_2+\kappa_2v_1)\\ &-\beta\int_{\Gamma} \boldsymbol{g_D}\cdot \{\alpha(x)\nabla v\}+\sum_{K\in\mathcal{T}_h^\Gamma}\frac{\eta_\beta}{h_K}\int_{K\cap\Gamma}\boldsymbol{g_D}\cdot [v], \end{aligned} $$

For η _β sufficiently large, the norm corresponding to the bilinear form B _h(⋅, ⋅) is uniformly equivalent to $\|\cdot \|{ }_{B_h}$, which is defined by

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \|v\|{}^2_{B_h} = |v|{}^2_{1,\Omega_1\cup\Omega_2} + \sum_{K\in \mathcal{T}_h^\Gamma} \eta_\beta h_K^{-1}\|[v]\|{}^2_{L^2(e_K)}+ \sum_{K\in \mathcal{T}_h^\Gamma}\eta_\beta^{-1} h_K \|\{\alpha(x) \nabla v\}\|{}^2_{L^2(e_K)}. \end{array} \end{aligned} $$

(8)

The crucial component in regard to establishing this equivalence result and also the stability of bilinear forms is the control on the weighted normal derivatives, which is stated as a trace and inverse inequality in Lemma 1.

Lemma 1 ([28, 29])

Let γ ₀ and γ ₁ be constants defined in (2) and (3), respectively. If we choose c ₀ ≥ 2γ ₀ γ ₁ in the definition (6) of κ, there exists a positive constant h ₀ such that for all h ∈ (0, h ₀] and any interface segment/patch $e_K=K\cap \Gamma \in \mathcal {E}_h^\Gamma$ , the following estimates hold on both sub-elements of K:

$$\displaystyle \begin{aligned} \|\kappa_i^{1/2}v_i\|{}_{L^2(e_K)} \leq \frac{C}{h_K^{1/2}} \|v_i\|{}_{L^2(K_i)},~~~~v_i\in \mathcal{P}_p(K_i),~~ i=1,2. \end{aligned} $$

(9)

The coercivity and boundedness of B _h(⋅, ⋅) in its norm $\|\cdot \|{ }^2_{B_h}$ is then a direct consequence of the Cauchy–Schwarz inequality.

Lemma 2

Let V = H ²( Ω ₁ ∪ Ω ₂) and $V(h) = V_h^\Gamma + V$ , we have

$$\displaystyle \begin{aligned} B_h(w,v)\leq C_b \|w\|{}_{B_h}\,\|v\|{}_{B_h}, \quad \forall\, w,v \in V(h), \end{aligned} $$

(10)

and

$$\displaystyle \begin{aligned} B_h(v,v)\geq C_s\|v\|{}^2_{B_h}, \quad \forall\, v \in V_h^\Gamma, \end{aligned} $$

(11)

provided the penalty parameter η _β is chosen sufficiently large.

The XFE space has optimal approximation quality for piecewise smooth functions in H ^p( Ω₁ ∪ Ω₂). The following theorem is proved in [28] as an analogue of Cea’s lemma.

Theorem 1

Assume that the interface Γ is C ² smooth and that the solution of the elliptic interface problem (1) satisfies u ∈ H ^s( Ω ₁ ∪ Ω ₂), where s ≥ 2 is an integer. Let $\mu = \min \{p+1,s\}$ . The following error estimates hold for any h ∈ (0, h ₀]: If η _β is chosen sufficiently large (see (11)) and u _h is the solution to the first scheme of (7), then

$$\displaystyle \begin{aligned} \|u-u_h\|{}_{B_h}\lesssim h^{\mu-1} \|u\|{}_{H^s(\Omega_1\cup\Omega_2)},\quad \forall\,0<h\le h_0. \end{aligned} $$

(12)

The hidden constants in the above estimates are dependent on the angle condition of the mesh $\mathcal {T}_h$ , the degree of the polynomials, the parameter in the scheme, and α(x), but are independent of the location of the interface relative to the mesh. Here, the constant h ₀ is from Lemma 1.

3 An Optimal Multigrid Method for (7)

In this section, we propose a two-level geometric multigrid solver of the finite element problem (7). It is well known that the element K with a “small” cut (i.e. |K ∩ Ω_i|∕|K|≪ 1) would have adverse effect on the conditioning of the resulting stiffness matrices (see e.g. [3]). Our approach is based on the general theory of the successive subspace correction (SSC) method of solving on a linear vector space $\tilde V =\sum _{i=0}^J V_i$ with inner product (⋅, ⋅) the equation (Au, v) = (f, v), where $A:\tilde V\to \tilde V$ is a symmetric positive definite operator.

We apply SSC for a relatively simple case of two subspaces (i.e. J = 2), that is, $\tilde V=V_h^\Gamma =V_1\oplus V_2$, with $V_1=V_h^0$ and $V_2=\widetilde {V}_h^\Gamma$, where $\widetilde {V}_h^\Gamma \subset V_h^\Gamma$ is the space of nodal basis functions that vanish on $\widetilde {\mathcal {N}}_h:=\{x_j:~|\mathrm {supp}(\psi _j)\cap \Gamma | =0\}$. With a slight abuse of notation, the DG-XFE scheme induces a symmetric positive definite operator B _h for β = 1. Let $\tilde {B}_{h}$ and $\tilde {B}_h^\Gamma$ be the restrictions of B _h on $V_h^0$ and $\widetilde {V}_h^\Gamma$, respectively. Let $\tilde {R}_h:V_h^0\to V_h^0$ be approximately an inverse of $\tilde {B}_{h}$. We have this two-level successive subspace correction method (Algorithm 1). The similar idea has been employed in a special linear case in [33] and analyzed using the framework given in [31, 34].

Algorithm 1 The multigrid method for (7)

Implement this iterative procedure until converge:

• 1. do subspace correction on $V_h^0$ with an inexact solver $\tilde {R}_h$;

• 2. do subspace correction on $\widetilde {V}_h^\Gamma$ with an exact solver $(\tilde {B}_h^\Gamma )^{-1}$.

Obviously, Algorithm 1 defines an iterative method for solving B _h u _h = f _h. Denote by A _h the iterator of the method, then the error contract property is summarized as the following theorem.

Theorem 2 ([28])

Assume that $\|I-\tilde {R}_h\tilde {B}_{h}\|{ }_{\tilde {B}_{h}}\leqslant \rho <1$ . Then Algorithm 1 is uniformly convergent with respect to the mesh size with

$$\displaystyle \begin{aligned}\|I-A_hB_h\|{}_{B_h}^2\leqslant \frac{\Lambda}{1-\rho^2+\Lambda}, \end{aligned}$$

where Λ is a constant independent of h.

When $\mathcal {T}_h$ is a shape-regular grid with a geometrical multilevel structure, then a geometric multigrid process can be implemented on $V_h^0$, and the approximate inverse $\tilde {R}_h$ of $\tilde {B}_h$ can be chosen to be the iterator of V -cycle multigrid method.

4 Numerical Tests

In this section, we present some initial results to demonstrate the high-order accuracy and robustness of our method. A 2-D example was implemented in MATLAB. The numerical experiment for a 3-D case was carried out in the open source finite element toolbox PHG [27].

4.1 High-Order Numerical Quadratures on “cut” Elements

Assembling the local stiffness matrix and the corresponding RHS for $K\in \mathcal {T}_h^\Gamma$ requires integration over irregularly shaped manifolds:

$$\displaystyle \begin{aligned} I = \int _ { K \cap \Omega_i } u ( \mathbf { x } ) \mathrm { d } \mathbf { x } \quad \mbox{and}\quad I = \int _ { K \cap \Gamma } u ( \mathbf { x } ) \mathrm { d } \Gamma, \end{aligned} $$

(13)

where Γ is defined by the zero level set of a piecewise smooth function.

Our implementation of (13) relies on a general-purpose and arbitrarily high order numerical quadrature algorithm proposed in [10]. The basic idea is to choose a local coordinate system with three orthogonal directions, decompose integrals in (13) into multiple 1-D integrals along these directions, and use 1-D Gaussian quadratures to compute these integrals. For 1-D Gaussian quadratures to work, the local coordinate system should be suitably chosen according to properties of K and Γ to prevent essential singularities from appearing in the 1-D integrands, and the integration intervals are divided into subintervals at the non essential singularities of the integrands. We note that the proposed algorithm only requires finding roots of univariate nonlinear functions in given intervals and evaluating the integrand, the level set function, and the gradient of the level set function at given points. It can achieve arbitrarily high order by increasing the orders of Gaussian quadratures, and does not need extra a priori knowledge about the integrand and the level set function.

This algorithm has been implemented in the file src/quad-interface.c and include/phg/quad-interface.h in PHG [27]. Extensive h − and p −convergence tests have been performed in [10] and included in a sample code test/quad_test2.c.

4.2 2-D Numerical Examples

Let domain Ω be the unit square (0, 1)² and interface Γ be the zero level set of the function φ(x) = (x ₁ − 0.5)² + (x ₂ − 0.5)² − 1∕7. The subdomain Ω₁ is characterized by φ(x) < 0 and Ω₂ by φ(x) > 0. The domain Ω is partitioned into grids of squares with the same size h. The exact solution is chosen as

$$\displaystyle \begin{aligned} u(x_1,x_2)=\left\{\begin{array}{ll} 1/\alpha_1\exp(x_1x_2),& (x_1,x_2)\in\Omega_1,\\ 1/\alpha_2\sin{}(\pi x_1)\sin{}(\pi x_2),&(x_1,x_2)\in\Omega_2. \end{array}\right. \end{aligned} $$

The right-hand side can be computed accordingly.

We implement Algorithm 1, with V -cycle geometric multigrid based on the unfitted grid $\mathcal {T}_h$ playing as the coarse grid corrector. In each pre- and post-smoothing stage of V -cycle iterator, we perform Gauss-Seidel for two times. We record the numerical results in Table 1. In these examples, the initial guess is 0, and the stopping criterion is

$$\displaystyle \begin{aligned}\|f_h-B_hu_h^{(k)}\|{}_\infty/\|f_h-B_hu_h^{(0)}\|{}_\infty<10^{-10}.\end{aligned}$$

From Table 1, we can see that the multigrid method converges uniformly with respect to the mesh size, which confirms our theoretical results.

Table 1 Numerical performance of Algorithm 1 (2-D example)

4.3 3-D Numerical Examples

The settings of this numerical experiment are as follows. The domain Ω = (0, 1)³. The interfaces are two touched spheres of radius 0.1 centered at (0.4, 0.5, 0.5) and (0.6, 0.5, 0.5). The exact solution is given by

$$\displaystyle \begin{aligned} u(x_1, x_2, x_3) = \begin{cases} \exp(x_1+x_2+x_3), & (x_1, x_2, x_3)\in\Omega_1,\\ \sin{}(x_1)\sin{}(x_2)\sin{}(x_3), & (x_1, x_2, x_3)\in\Omega_2. \end{cases} \end{aligned}$$

The discontinuous coefficient function is defined such that α ₁ = 1 and α ₂ = 100.

A convergence study is performed on a series of meshes generated by uniform refinements of an initial mesh consisting of 6 congruent tetrahedra. Relative errors and convergence rates of numerical solutions for P _p elements for p = 1, 2, 3 and 4 are listed in Table 2, with the quadrature order q = 2p + 3. The convergence rates are optimal for both H ¹( Ω)-errors (order p) and L ²( Ω)-errors (order p + 1). For the time being, however, the design of multigrid solver for 3-D case is still on-going. The computations for P ₁, P ₂ and P ₃ elements were done using the 64-bit double precision and the linear systems were solved using MUMPS, but for P ₄ element, to eliminate influences of roundoff errors, the computations were done using the 80-bit extended double precision and the linear systems were solved using the GMRES method with MUMPS in double precision as its preconditioner. The performance of Algorithm 1 will be reported in a future work.

Table 2 Errors and convergence orders of the numerical solutions (3-D example)