Examining the normality assumption of a design-comparable effect size in single-case designs

Abstract

What Works Clearinghouse (WWC, 2022) recommends a design-comparable effect size (D-CES; i.e., g_AB) to gauge an intervention in single-case experimental design (SCED) studies, or to synthesize findings in meta-analysis. So far, no research has examined g_AB’s performance under non-normal distributions. This study expanded Pustejovsky et al. (2014) to investigate the impact of data distributions, number of cases (m), number of measurements (N), within-case reliability or intra-class correlation (ρ), ratio of variance components (λ), and autocorrelation (ϕ) on g_AB in multiple-baseline (MB) design. The performance of g_AB was assessed by relative bias (RB), relative bias of variance (RBV), MSE, and coverage rate of 95% CIs (CR). Findings revealed that g_AB was unbiased even under non-normal distributions. g_AB’s variance was generally overestimated, and its 95% CI was over-covered, especially when distributions were normal or nearly normal combined with small m and N. Large imprecision of g_AB occurred when m was small and ρ was large. According to the ANOVA results, data distributions contributed to approximately 49% of variance in RB and 25% of variance in both RBV and CR. m and ρ each contributed to 34% of variance in MSE. We recommend g_AB for MB studies and meta-analysis with N ≥ 16 and when either (1) data distributions are normal or nearly normal, m = 6, and ρ = 0.6 or 0.8, or (2) data distributions are mildly or moderately non-normal, m ≥ 4, and ρ = 0.2, 0.4, or 0.6. The paper concludes with a discussion of g_AB’s applicability and design-comparability, and sound reporting practices of ES indices.

Single-case experimental designs (SCEDs) are research designs that can be used to determine whether there exists a causal or functional relationship between the introduction of an intervention and changes in outcome behavior(s). SCED studies have been used to evaluate the effectiveness of interventions in psychology, education, speech pathology, medicine, sports and athletic performance, to name a few (Barker et al., 2011; Byiers et al., 2012; Franklin et al., 1996; Horner et al., 2005; Kunze et al., 2021; Morgan & Morgan, 2009; Vlaeyen et al., 2020). SCED typically employs a small number of cases who serve as their own controls. Among the variety of SCEDs, the multiple baseline (MB) design was by far the most popular design accounting for nearly 50% of published SCED studies (Hammond & Gast, 2010; Horner & Odom, 2014; Pustejovsky et al., 2019; Shadish & Sullivan, 2011; Smith, 2012; Tanious & Onghena, 2021). An MB design consists of one A phase and one B phase across multiple cases, multiple behaviors of one case, or multiple settings for the same behavior of a case. During the A phase, a case (or a behavior) is observed to be stabilized before an intervention is introduced to that case (or that behavior). An intervention in an MB design is successively administered to all cases (behaviors or settings) until all cases (all behaviors, or a behavior in all settings) are intervened to allow for an assessment of its effectiveness.

Advances in SCED methodology

Traditionally, systematic visual analysis of SCED data has been used to determine whether a behavioral change is due to the introduction of an intervention, but not chance fluctuations (Horner et al., 2005; Kazdin, 2011; Wolfe & McCammon, 2022). In recent years, advanced approaches have been applied to quantify intervention effects in SCED studies (Chen et al., 2019; Kazdin, 2019; Tanious & Manolov, 2022; WWC, 2022). Many scholarly journals published special issues to devote exclusively to these advanced approaches, such as Journal of School Psychology (2014, Volume 52, Issue 2), Remedial and Special Education (2017, Volume 38, Issue 6), Developmental Neurorehabilitation (2018, Volume 21, Issue 4), and Perspectives on Behavior Science (2022, Volume 45, Issue 1). The advanced approaches include (1) quantifying an intervention effect with standardized/unstandardized indices (e.g., Hedges et al., 2012, 2013; Moeyaert et al., 2013; Pustejovsky et al., 2014; Ugille et al., 2012, 2014) or with non-overlapping ESs (e.g., Michiels & Onghena, 2019; Parker & Vannest, 2009), (2) employing different methods to estimate an intervention effect (e.g., the method of moments by Hedges et al., 2012, 2013; the restricted maximum likelihood method by Pustejovsky et al., 2014; the Bayesian method by Natesan, 2019 or Natesan & Hedges, 2017), and (3) inferring an intervention effect based on a statistical model (e.g., hierarchical linear modeling by Pustejovsky et al., 2014) or a design (e.g., randomization tests by Michiels & Onghena, 2019, and Onghena, 2020). Among the advanced approaches, design-comparable ESs (D-CESs) were proposed as standardized indices to synthesize intervention effects across SCED and group studies, or over different outcome measures, based on a statistical model (Hedges et al., 2012, 2013; Pustejovsky et al., 2014; Shadish et al., 2014; Zelinsky & Shadish, 2018).

Version 5.0 of the What Works Clearinghouse Procedures and Standards Handbook (WWC, 2022) specifically recommends reporting D-CES indices, along with visual analysis, when assessing an intervention effect in SCED studies. Yet to the best of our knowledge, no published research has investigated D-CES’s statistical assumptions in SCED contexts. If statistical assumptions, such as normality, are not met or not robust, inferences derived from D-CES lack statistical validity. Furthermore, the small sample sizes and limited number of measurements used in most SCED studies render the normality assumption unlikely to be robust, if it is violated.

Small sample sizes and limited number of measurements are also a central concern when an effective intervention is to be generalized to another sample, setting, location, behavior, or measurement (Horner et al., 2005). That is, how does one know that an intervention is generalizable beyond the effect already documented in a SCED study? One way to address, or even enhance, the generalizability of an effect is to systematically replicate an intervention in different contexts using different participants, behaviors, and parallel measurements (Horner et al., 2005; Kazdin, 2011). Replication results are subsequently synthesized using meta-analysis methods (Becraft et al., 2020; Beretvas & Chung, 2008; Moeyaert et al., 2020; Onghena et al., 2018). To this end, methodologists have devised various approaches to perform SCED meta-analysis (Jamshidi et al., 2022; Vlaeyen et al., 2020). According to Becraft et al. (2020) and Moeyaert et al. (2021), there has been a dramatic increase from 1987 to 2019 in the number of scholarly publications on SCED intervention studies and their meta-analyses.

Definition of g _AB for SCED studies

One D-CES¹, namely g_AB, was proposed by Pustejovsky et al. (2014) to quantify intervention effects within and across primary SCED studies (Hedges et al., 2012, 2013; Pustejovsky et al., 2014; Shadish et al., 2014; WWC, 2022; Zelinsky & Shadish, 2018). A cursory search of the literature since 2014 has found g_AB reported in numerous primary studies or meta-analysis (Anaby et al., 2020; Grasley-Boy et al., 2021; Lee et al., 2022; Peltier et al., 2021; Peltier et al., 2020a, b; Rincón et al., 2021; Rivera Pérez et al., 2022; Romano & Windsor, 2020; Romano et al., 2021; Ruiz et al., 2018; Saul & Norbury, 2021; Teh et al., 2021; Thurmann-Moe et al., 2021). g_AB is the D-CES specifically recommended by the What Works Clearinghouse Procedures and Standards Handbook, Version 5.0 (WWC, 2022) for SCED studies.

g _AB is a sample estimator of the population standardized mean difference (δ_AB) between an A phase and a B phase, similar to Cohen’s d or Hedges’ g used in group studies (Pustejovsky et al., 2014; WWC, 2022). The δ_AB is defined according to Eq. 1:

$${\updelta}_{\textrm{A}\mathrm{B}}=\frac{\upmu_{\textrm{B}}-{\upmu}_{\textrm{A}}}{\sqrt{\upsigma^2+{\uptau}^2}},$$

(1)

where μ_A is the population mean of Phase A measurements, μ_B is the population mean of Phase B measurements, σ² is the variance of measurements within cases, and τ² is the variance of measurements across cases. Thus, (σ² + τ²) is the total variance of measurements within and across all cases.

Among the three MB design variations mentioned earlier, g_AB is suitable only for MB designs across three or more cases of the same behavior. It is a product of a bias correction factor [J(ν)] and the sample estimate of δ_AB (${\hat{\updelta}}_{\textrm{AB}}$), as in Eq. 2:

$${g}_{\textrm{AB}}=J\left(\upnu \right)\times {\hat{\updelta}}_{\textrm{AB}}.$$

(2)

Both J(ν) and ${\hat{\updelta}}_{\textrm{AB}}$ are estimated by the restricted maximum likelihood (REML) method (Pustejovsky et al., 2014) which we explain in the “Method” section. The performance of g_AB under normal and non-normal distributions is the focus of the present simulation study.

Five MB models formulated by Pustejovsky et al. (2014)

Pustejovsky et al. (2014) formulated five models for MB data. They are sequentially named MB1 to MB5 in this paper. All five models permit cases to vary in Phase A levels. They differ in how the intervention effect and the trends in A or B phase are modeled across cases. The five MB models are hierarchical linear models in which Level-1 parameters model the individual data and Level-2 parameters model how the Level-1 parameters vary across cases. Being the simplest and most restrictive model, MB1 assumes a fixed intervention effect for all cases with no trend in either A or B phase. MB1 is recommended by the What Works Clearinghouse Procedures and Standards Handbook, Version 5.0 (WWC, 2022) as a “starting point” (p. 182) for assessing an intervention effect.

MB2 to MB5 are more flexible and extensible than MB1, due to additional parameters and fewer restrictions (Pustejovsky et al., 2014). MB2 assumes a varying immediate effect due to intervention across cases, with no trend in either A or B phase. MB3 assumes a fixed intervention effect with a fixed linear trend in either A, B, or both phases. MB4 assumes a fixed intervention effect with a varying linear trend in the A phase and a fixed linear trend in the B phase. Being the most complex model, MB5 assumes a fixed intervention effect with a varying linear trend in both A and B phases. It is worth noting that MB2 is the only model among the five proposed that allows the immediate effect of intervention to vary across cases. Pustejovsky et al. (2014) conducted three simulation studies under MB1, MB2, and MB4 to provide empirical evidence to support the reporting of g_AB. Results from the three simulation studies are summarized next.

Three simulation studies of g _AB under MB1, MB2, and MB4

The first simulation study (Study 1) was conducted under MB1, Study 2 under MB2, and Study 3 under MB4. In all three studies, data were simulated from normal distributions. For Studies 1 and 2, four levels of number of cases (m) were used: 3, 4, 5, and 6. For Study 3, two additional levels were added to m: 3, 4, 5, 6, 9, and 12. The number of measurements (N) was either 8 or 16, the within-case reliability (ρ = the ratio of between-case variance to the total variance within and between cases) ranged from 0 to 0.8, and the first-order autocorrelation (ϕ) ranged from −0.7 to 0.7 in Studies 1 to 3. For Studies 2 and 3, the ratio of variance components (λ) was either 0.1 or 0.5. λ was defined in Study 2 as the variance of all cases’ level shifts between A and B phases as a fraction of the variance of all cases’ Phase A levels. In Study 3, λ was defined as the variance of all cases’ baseline slopes as a fraction of the variance of all cases’ Phase A levels. Four criteria were used in all three studies to assess the performance of g_AB: relative bias, relative bias of variance estimators, MSE, and coverage rate of the 95% CIs. The 95% CI was constructed using two methods: the symmetric and the noncentral t.

Results from Study 1 of Pustejovsky et al. (2014) showed that relative bias of g_AB under MB1 was small. At the smallest m = 3 and N = 8, the relative bias was no more than 4.3%, yet the relative bias of g_AB’s variance estimator was 16%. As both m and N increased, g_AB’s variance estimate was very close to the true variance. Between the two CI methods, the average coverage rate of the symmetric method was closer to the nominal level of 95% than the noncentral t method.

Results from Study 2 showed that g_AB’s average relative bias was small under MB2. Relative bias was generally greater when N = 8 than when N = 16. At the smallest m = 3 and N = 8, the relative bias was no more than 7.3%. For m = 4, the relative bias was always less than 4.9%. The relative bias decreased to no more than 2.9% when m ≥ 5. The variance of g_AB was overestimated. The relative bias in g_AB’s variance estimator was as large as 43% when m = 3 and N = 16. Even when m = 6 (the largest under MB2) and N =16, the relative bias was still 14%. The MSEs under MB2 ranged from 0.092 when m = 6 and N = 16, to 0.290 when m = 3 and N = 8. The MSEs generally increased as ρ, λ, and ϕ increased. Between the two CI methods, the symmetric method maintained an average coverage rate closer to 95% than the noncentral t method. Based on these results, Pustejovsky et al. (2014) recommended g_AB for meta-analysis with m ≥ 4 and the symmetric method for constructing CIs of g_AB under MB2.

Results from Study 3 revealed the same pattern under MB4 as under MB2, namely small relative bias. As with results of MB2, g_AB as a point estimator was suitable for studies with m ≥ 4. MSE obtained under MB4 was large, compared with those obtained under MB1, especially when m was small. Unlike results obtained under MB1 and MB2, g_AB’s variance was underestimated, except when m = 3 and N = 8. The variance’s underestimation was more pronounced when N = 16 than when N = 8. The average MSE of g_AB under MB4 ranged from 0.066 when m = 12 and N = 16, to 0.596 when m = 3 and N = 8. For a given m and N, MSE derived under MB4 were larger than those under MB1 or MB2, especially when m was small. MSEs generally increased as ρ, λ, and ϕ increased. The 95% CI based on the symmetric method approached the nominal level when m was large (i.e., ≥ 9). The CI based on the noncentral t method tended to substantially undercover the population δ_AB when m = 3, 4, 5, 6, or 9.

Based on Studies 1 to 3, Pustejovsky et al. (2014) concluded that the relative bias of g_AB was reasonably small, even with very few cases. Yet large sample sizes were needed in order to yield precise point estimates, reasonably accurate SE estimates and CIs under a complex model, namely MB4. Pustejovsky et al. (2014) further cautioned not to rely on model-based SE estimates in meta-analysis, because inaccurate SE estimates lead to inaccurate weights for primary studies and inaccurate estimates of between-study heterogeneity for meta-analysis.

The normality assumption of g _AB and the REML method

As previously mentioned, data in Studies 1 to 3 of Pustejovsky et al. (2014) were simulated only from normal distributions. Indeed, g_AB assumes that data within and across cases are normally distributed. Yet non-normal data are quite common in SCED studies (e.g., Au et al., 2017; Brosnan et al., 2018; Ferron et al., 2014; Joo, 2017; Stewart & Hall, 2017). Furthermore, due to asymptotic normality² of the REML method, voluminous data are needed in order to yield an acceptable g_AB for δ_AB. The ML method, of which the REML is a special case, is known to perform poorly when data are limited, even under normal conditions (Braunstein, 1992). Yet small sample sizes (or cases) and limited numbers of measurements are the norm rather than an exception in SCED studies. According to Shadish and Sullivan (2011), 73.5% of 809 SCED studies employed one to 13 participants with an average of 3.64 cases per study. Tanious and Onghena (2021) reported that the median sample size used in 210 MB studies was 4 with an interquartile range of 4. As for the number of measurements, Shadish and Sullivan (2011) reported that 90.6% of 809 SCED studies used 49 or fewer measurements with a median of 20 measurements. Pustejovsky et al.’s (2019) review of 303 SCED studies found a median of 7 measurements in initial baseline phases, with an interquartile range of 7.

Pustejovsky et al. (2014) did not investigate the performance of g_AB under non-normal conditions. Furthermore, sample sizes and the number of measurements used in their simulation studies were small for the REML method. It remains unknown whether g_AB performs satisfactorily under non-normal conditions with small samples and limited numbers of measurements (Maas & Hox, 2004; Man et al., 2022; Raudenbush & Bryk, 2002). To the best of our knowledge, no published study has systematically investigated the singular impact of non-normality, or the joint impact of non-normality with other data features (e.g., sample size, autocorrelation), on the performance of g_AB in primary SCED studies and their meta-analyses.

Aims of the present simulation

The present study aimed to fill the voids in the literature by investigating how distributions of data singularly and jointly impacted the performance of g_AB under MB2. We focused on MB2 because MB2 is more flexible, but less researched, than MB1. MB2 is also the only model among the five proposed by Pustejovsky et al. (2014) that allows the immediate effect of an intervention to vary across cases.

The singular and joint impacts of data distribution on g_AB were investigated by simulating data from normal and non-normal distributions, and by manipulating five data features (number of cases, number of measurements, autocorrelation, within-case reliability, and ratio of variance components). The five data features were also manipulated in Pustejovsky et al. (2014). The performance of g_AB was evaluated by the same four criteria as Pustejovsky et al. (2014): relative bias, relative bias of variance, MSE, and coverage rate. These four criteria have been routinely used to assess a statistic (e.g., g_AB) in primary studies (e.g., Algina et al., 2005; Hoogland & Boomsma, 1998), or for meta-analysis (e.g., American Psychological Association, 2020; Hoogland & Boomsma, 1998; Pustejovsky et al., 2014). Based on the evaluation of the four criteria, we identified conditions in which g_AB performed acceptably for primary MB studies and meta-analysis.

In sum, the present study aimed to answer two research questions under MB2:

• RQ1: What is the impact of data distribution, number of cases, number of measurements, within-case reliability, ratio of variance component, and autocorrelation on the performance of g_AB as measured by relative bias, relative bias of variance, MSE, and coverage rate?

• RQ2: What are the conditions in which g_AB performed acceptably for primary MB studies and meta-analysis?

Findings from the present study should provide empirical evidence to extend the recommendation made by the What Works Clearinghouse Procedures and Standards Handbook, Version 5.0 (WWC, 2022) to MB2. They should also inform practitioners and researchers about the suitability of g_AB for MB studies and their meta-analysis. To this end, we provide general recommendations on conditions under which it is appropriate to use g_AB to assess intervention effects. This paper concludes with a discussion of g_AB’s applicability in SCED contexts, its design-comparability across SCED and group studies, and sound reporting practices of ES indices including g_AB.

Method

In this section, we present MB2 and its assumptions first, followed by the definition of the population standardized mean difference (δ_AB) under MB2. Next, we describe the simulation design, justifications for the manipulated conditions, and an outline of seven steps for simulating and analyzing simulated data. Details of each step are provided following the outline.

MB2

As previously stated, MB2 assumes that cases vary in the average score of the A phase and also in the immediate intervention effect between A and B phases. Pustejovsky et al. (2014) referred to the average score of the A phase as Phase A level, and the immediate intervention effect as a level shift between A and B phases. MB2 also assumes that there is no linear trend in either A or B phase (Pustejovsky et al., 2014). Thus, for the jth measurement of the ith case, the score Y_ij is modeled by a within-case model according to Eq. 3:

$${Y}_{\textrm{ij}}={\upbeta}_{0\textrm{i}}+{\upbeta}_{1\textrm{i}}\times {D}_{\textrm{ij}}+{\varepsilon}_{\textrm{ij}},$$

(3)

where β_0i = Phase A level for Case i; β_1i = level shift for Case i = the immediate change in Case i’s measurement due to intervention; D_ij = a dummy variable that equals 0 (for Phase A measurements) or 1 (for Phase B measurements); ε_ij = Level-1 error; i = 1, 2, . . ., m; j = 1, 2, . . ., N; m = the number of cases; and N = the total number of measurements in A and B phases combined³.

Because MB2 assumes a varying Phase A level and a varying level shift between A and B phases across cases, β_0i and β_1i are further modeled by a between-case model according to Eqs. 4 and 5:

$${\upbeta}_{0\textrm{i}}={\upgamma}_{00}+{\upeta}_{0\textrm{i}},$$

(4)

$${\upbeta}_{1\textrm{i}}={\upgamma}_{10}+{\upeta}_{1\textrm{i}},$$

(5)

where γ₀₀ = the average Phase A level, γ₁₀ = the average level shift between A and B phases, and η_0i and η_1i are Level-2 errors.

Substituting Eq. 4 for β_0i and Eq. 5 for β_1i into Eq. 3, we obtain Eq. 6 of fixed and random effects for the distribution of Y_ij—the jth measurement of the ith case—under MB2:

$${\displaystyle \begin{array}{c}{Y}_{\textrm{ij}}={\upgamma}_{00}+{\upeta}_{0\textrm{i}}+\left({\upgamma}_{10}+{\upeta}_{1\textrm{i}}\right)\times {D}_{\textrm{ij}}+{\upvarepsilon}_{\textrm{ij}}\\ {}=\left[{\upgamma}_{00}+\left({\upgamma}_{10}\times {D}_{\textrm{ij}}\right)\right]+\left\{{\upeta}_{0\textrm{i}}+\left({\upeta}_{1\textrm{i}}\times {D}_{\textrm{ij}}\right)+{\upvarepsilon}_{\textrm{ij}}\right\}\\ {}=\left[\textrm{fixed}\ \textrm{effects}\right]+\left\{\textrm{random}\ \textrm{effects}\right\}.\end{array}}$$

(6)

Statistical and design assumptions for MB2 are stated in (a) to (f) below, according to Pustejovsky et al. (2014). The present study investigated normality assumptions stated in (a) and (d).

• (a) Within cases, ε_ijs are normally distributed with a mean of 0 and a variance of σ².

• (b) Within cases, ε_ijs are correlated with a first-order autocorrelation ϕ, or Cov (ε_ij, ε_ik) = ϕ^|k−j|σ².

• (c) Across cases, ε_ijs are homoscedastic and independently distributed, namely, Var(ε_ij) = Var(ε_hk) = σ² and Cov (ε_ij, ε_hk) = 0 for all i ≠ h.

• (d) (η_0i, η_1i) are multivariate normally distributed with mean (0, 0) and a covariance matrix T_2×2 = $\left[\begin{array}{cc}{\uptau}_0^2& {\uptau}_{10}\\ {}{\uptau}_{10}& {\uptau}_1^2\end{array}\right]$, where ${\uptau}_0^2$ is the variance of all cases’ Phase A levels, ${\uptau}_1^2$ is the variance of all cases’ level shifts between A and B phases, and τ₁₀ is the covariance between Phase A levels and level shifts⁴.

• (e) Level-1 errors (ε_ijs) are independent of Level-2 errors (η_0i and η_1i).

• (f) Measurements are equally spaced over time.

Definition of δ_AB

Under MB2, the population mean difference = (γ₀₀ + γ₁₀) – γ₀₀ = γ₁₀, and the total variance within and across cases = σ² + ${\uptau}_0^2$. Hence, δ_AB is defined by Eq. 7:

$${\updelta}_{\textrm{AB}}=\frac{\ {\upgamma}_{10}}{\sqrt{\upsigma^2+{\uptau}_0^2}}.$$

(7)

Equation 7 is identical to Eq. 1, except for the notation differences (Pustejovsky et al., 2014). Guided by Pustejovsky et al. (2014), we set⁵ γ₀₀ = 0, γ₁₀ = 1, and ${\upsigma}^2+{\uptau}_0^2$ = 1. Therefore, δ_AB = 1 for all simulated conditions in this study and also in Studies 1 to 3 of Pustejovsky et al. (2014).

Simulation design

The present study manipulated six factors according to Table 1. The first factor (Dist or distribution of data) was unique to the present study. The next four factors, namely, m, N, ρ, and λ were manipulated identically⁶ as in Study 2 of Pustejovsky et al. (2014). The sixth factor (ϕ) was manipulated slightly differently from Study 2 of Pustejovsky et al. (2014). Justifications for manipulated conditions are given in the next section. A total of 1792 conditions (= 4 × 4 × 2 × 4 × 2 × 7) were manipulated. Table 2 presents the start points for the intervention across cases. The start points were identical to those used in Study 2 of Pustejovsky et al. (2014).

Table 1 Simulation design of the present study

Table 2 Start points for intervention in N measurements

Justifications for manipulated conditions

The distribution of data was manipulated through the joint manipulation of Level-1 and Level-2 error distributions in Eq. 6. Four distributions—one normal and three non-normal—were simulated as the distributions of sums of Level-1 and Level-2 errors. Because of the large number of conditions (= 1792) investigated in this study, we did not simulate Level-1 and Level-2 errors separately from two different distributions (e.g., normal for Level-1 errors and non-normal for Level-2 errors). Each distribution was specified through the specification of its skewness and kurtosis (Joo & Ferron, 2019; Man et al., 2022; Owens & Farmer, 2013). For the normal distribution, we specified skewness = kurtosis = 0. For the nearly normal distribution, skewness = 0 and kurtosis = 0.35 were specified. For the mildly non-normal distribution, skewness = 1 and kurtosis = 0.35 were specified. For the moderately non-normal distribution, we specified skewness = 1 and kurtosis = 3. The four marginal distributions are shown in File 1⁷ at https://osf.io/hsvwu/.

We decided on these four distributions on the basis of empirical skewness and kurtosis of SCED data (Joo, 2017; Solomon, 2014) and conditions manipulated in Owens and Farmer (2013). Joo (2017) reported empirical skewness to range from −0.71 to 1.91 and empirical kurtosis from −1.07 to 3.01, based on 20 MB data sets published in the Journal of Applied Behavior Analysis. Solomon (2014) reported empirical skewness to range from 0.46 to 2.89 and empirical kurtosis from 0.49 to 1.57, based on 104 SCED studies of school-based interventions. Owens and Farmer (2013) investigated Level-2 normality assumption for MB data using multilevel modeling. They manipulated six Level-2 unimodal distributions ranging from normal (skewness = 0, kurtosis = 0), (0, −1), (0, 2), (0, 3.75), (1, 2), to most non-normal (1, 3.75). Of the six, four were symmetric and two were positively skewed. Of the four unimodal distributions manipulated in this study, two were symmetric and two were positively skewed. The three non-normal distributions of the present study were specified with skewness and kurtosis well within their respective empirical ranges reported in Joo (2017) and Solomon (2014). We confirmed that skewness and kurtosis of our simulated data matched closely with those specified in Table 1 (see File 2 at https://osf.io/hsvwu/).

Regarding m and N, Pustejovsky et al. (2014, supplemental materials⁸) justified their conditions by spreading the intervention start points as evenly as possible over measurements, while keeping at least three measurements in each phase. The within-case reliability ($\uprho ={\uptau}_0^2/\left({\upsigma}^2+{\uptau}_0^2\right)$, also called the intra-class correlation or ICC) was varied from 0.2 to 0.8 in increments of 0.2. A ρ of 0.2 represented a low between-case variance in levels (${\uptau}_0^2$) relative to the within-case variance (σ²), hence a low within-case reliability. A ρ of 0.8 represented a high between-case variance in levels relative to the within-case variance, hence a high within-case reliability. The ratio of variance components (λ = ${\uptau}_1^2$/${\uptau}_0^2$) was set to either 0.1 or 0.5. According to Pustejovsky et al. (2014, supplementary materials), a λ of 0.1 represented a moderate level of the between-case variation in level shifts, relative to the between-case variation in Phase A levels. A λ of 0.5 represented a high level of the between-case variation in level shifts, relative to the between-case variation in Phase A levels.

Because of the repeated observation of the same behavior in SCED studies, each case’s measurements are correlated. Such a correlation is quantified by the first-order autocorrelation (ϕ). Pustejovsky et al. (2014) manipulated the autocorrelation under MB2 to range from −0.7 to 0.7, in increments of 0.2. To ensure that our manipulation of autocorrelation was plausible for MB2 under non-normal distributions, we tested a range of autocorrelations based on empirical and simulation studies (Joo, 2017; Joo & Ferron, 2019; Solomon, 2014). We eventually decided on seven levels of ϕ: −0.4, −0.3, −0.1, 0, 0.1, 0.3, 0.4 for the present study (see File 3).

For each of the 1792 conditions, 20,000 replications were generated. We modified the R scdhlm package (Pustejovsky et al., 2021) for this simulation study. The modified R scdhlm package can be found in File 4 at https://osf.io/hsvwu/. File 4.1 is the superordinate R program to establish simulation conditions, execute File 4, and check convergence of each simulation. Under normal distributions, the modified R scdhlm package produced results comparable to those obtained from Study 2 of Pustejovsky et al. (2014) (see Appendix A).

The simulation and analysis procedures are outlined in seven steps. Details on each step are presented following the outline.

Outline of simulation and analysis procedures

• Step 1: Generate 20,000 random seeds which were used to create 20,000 replications for the 1792 conditions.

• Step 2: Given a random seed from Step 1, simulate a replication under a specific condition of MB2.

• Step 3: Use the REML method to compute g_AB based on data generated in Step 2.

• Step 4: Repeat Steps 2 and 3 until 20,000 replications and 20,000 g_ABs were obtained for each of the 1792 conditions.

• Step 5: Compute four criteria as indicators of the performance of g_AB.

• Step 6: Analyze the impact of the six factors on the four criteria.

• Step 7: Identify conditions in which g_AB performed acceptably for MB studies and meta-analysis.

Step 1: Generate 20,000 random seeds for the 1792 conditions

Before the simulation began, we assessed the adequacy of R = 20,000 replications used in Pustejovsky et al. (2014) by examining its Monte Carlo SE. A Monte Carlo SE provides an estimate of the empirical SE resulted from R replications. The Monte Carlo SE for the expected coverage rate of 95% CIs based on 20,000 replications was computed according to Eq. 8:

$$\kern0.5em \textrm{Monte}\ \textrm{Carlo}\ SE={\left[0.95\times \left(1-0.95\right)/\textrm{20,000}\right]}^{0.5}=0.00154,$$

(8)

where 0.95 = the expected coverage rate of 95% CIs. Such a Monte Carlo SE was deemed acceptable by Morris et al. (2019), who suggested keeping the Monte Carlo SE below 0.005. We therefore considered 20,000 replications adequate for the present study. And 20,000 random seeds were generated and used in each condition.

Step 2: Simulate a replication under a specific condition

Given Eq. 6 as the distribution of Y_ij and start points in Table 2, we generated data from one of the four distributions specified in Table 1. For N scores of a case, Eq. 6 can be expressed in matrix notations as Eq. 9:

$${\textbf{Y}}_{N\times 1}={\textbf{D}}_{N\times 2}\;{\boldsymbol{\upgamma}}_{2\times 1}+{\textbf{e}}_{N\times 1}.$$

(9)

The fixed effects in Eq. 6 are expressed as the product of the design matrix (D_N×2) and a fixed-effect vector (γ_2×1) in Eq. 9. The random effects in Eq. 6 are expressed as an error vector (e_N×1) in Eq. 9. The e_N×1 vector consists of Level-2 errors [η_0i + (η_1i × D_ij) in Eq. 6] and Level-1 errors (ε_ij in Eqs. 3 and 6).

As previously stated, sums of Level-1 and Level-2 errors followed a normal or non-normal distribution that was specified by its skewness and kurtosis. To generate random errors of e_N×1 from a multivariate normal distribution, we specified skewness = 0, kurtosis = 0, and a variance-covariance matrix of errors (Σ_N×N) in the mvrnonnorm function of the semTools package (Jorgensen et al., 2021). The Σ_N×N is written in matrix notation as Eq. 10:

$${\boldsymbol{\Sigma}}_{N\times N}={\textbf{DTD}}^{\textbf{T}}+\left(1\hbox{--} \uprho \right)\bullet \textbf{AR}\left(\textbf{1}\right),$$

(10)

where DTD^T = the variance-covariance matrix of Level-2 errors, (1 – ρ)∙AR(1) = the variance-covariance matrix of Level-1 errors, D = design matrix from Eq. 9, ${\textbf{T}}_{2\times 2}=\left[\begin{array}{cc}\rho & 0\\ {}0& \rho \times \lambda \end{array}\right]=\left[\begin{array}{cc}{\uptau}_0^2& 0\\ {}0& {\uptau}_1^2\end{array}\right]$ (see Footnote 4), and AR(1) is the matrix of first-order autocorrelations with 1s along the diagonal and ϕ^|k−j| off-diagonal. Once skewness, kurtosis, and Σ_N×N were specified, the mvrnonnorm function produced multivariate normal errors using the Vale and Maurelli method (Vale & Maurelli, 1983). Appendix B describes details in generating a replication of 3 (= m) cases from a normal distribution (Dist = normal) with 8 (= N) measurements, within-case reliability (ρ) = 0.2, ratio of variance components (λ) = 0.1, and first-order autocorrelation (ϕ) = −0.4.

Errors were similarly generated from the other three distributions by specifying their corresponding skewness and kurtosis, plus a Σ_N×N in the mvrnonnorm function (see File 4 at https://osf.io/hsvwu/). After data were generated for m cases, a replication was formed and a g_AB was computed.

Step 3: Use the REML method to compute g _AB

To explain the details of Step 3, we reformulate δ_AB in matrix notation. Next, we describe the estimation of δ_AB by g_AB and the estimation of the variance of g_AB.

Reformulating δ_AB in matrix notation

Using Pustejovsky et al.’s (2014) matrix notations, we define the vector of fixed effects of MB2 as γ_2×1 = (γ_00, γ₁₀)^T and the vector of variance components as ω_5×1 = (${\upsigma}^2,\upphi, {\uptau}_0^2,{\uptau}_1^2,{\uptau}_{10}$)^T. The ω_5×1 vector includes the within-case variance σ², the first-order autocorrelation ϕ, Level-2 variances ${\uptau}_0^2$ and ${\uptau}_1^2$, and the covariance τ₁₀ (see Footnote 4). With two constant vectors defined as p_2×1 = (0, 1)^T and r_5×1 = (1, 0, 1, 0, 0)^T, the δ_AB of Eq. 7 is reformulated as Eq. 11:

$${\updelta}_{\textrm{AB}}=\frac{{\textbf{p}}^{\textrm{T}}\boldsymbol{\upgamma}}{\sqrt{{\textbf{r}}^{\textrm{T}}\boldsymbol{\upomega}}}.$$

(11)

Estimating δ_AB by g _AB

g _AB is the product of the bias correction factor, J(ν), multiplied with the REML estimate of δ_AB (i.e., ${\hat{\updelta}}_{\textrm{AB}}$), as in Eq. 12:

$${g}_{\textrm{AB}}=J\left(\upnu \right)\times {\hat{\updelta}}_{\textrm{AB}},$$

(12)

where J(ν) = 1− 3/(4ν −1) and ν is determined from Eq. 13.

$$\nu =\frac{2{\left({\textbf{r}}^{\textrm{T}}\hat{\boldsymbol{\upomega}}\right)}^2}{{\textbf{r}}^{\textrm{T}}\textbf{C}\left(\hat{\boldsymbol{\upomega}}\right)\textbf{r}},$$

(13)

where $\textbf{C}\left(\hat{\boldsymbol{\upomega}}\right)$ is the estimated covariance matrix of $\hat{\boldsymbol{\upomega}}$, and $\hat{\boldsymbol{\upomega}}$ is the REML estimate of ω. When m and N both approach infinity, $\hat{\boldsymbol{\upomega}}$ approaches ω, $\textbf{C}\left(\hat{\boldsymbol{\upomega}}\right)$ approaches a null matrix, ν approaches infinity, and J(ν) approaches 1; hence, the need for bias correction diminishes.

By plugging γ’s REML estimate ($\hat{\boldsymbol{\upgamma}}$) and $\hat{\boldsymbol{\upomega}}$ into Eq. 11, we obtain ${\hat{\updelta}}_{\textrm{AB}}$ from Eq. 14:

$${\hat{\updelta}}_{\textrm{AB}}=\frac{{\textbf{p}}^{\textrm{T}}\hat{\boldsymbol{\upgamma}}}{\sqrt{{\textbf{r}}^{\textrm{T}}\hat{\boldsymbol{\upomega}}}}.$$

(14)

The REML algorithm estimated the random effects (i.e., ω) iteratively using a non-linear maximization approach. The algorithm stopped when it met a pre-specified convergence criterion (i.e., tolerance = 10^─6), or when it reached a pre-specified number of iterations (= 50). If the REML algorithm did not converge to the convergence criterion after 50 iterations, we re-simulated data (see File 4.1)⁹. After obtaining the estimated random effects ($\hat{\boldsymbol{\upomega}}$), the algorithm estimated fixed effects ($\hat{\boldsymbol{\upgamma}}$) using the generalized least squares estimator (Jiang, 2007).

Estimating the variance of g _AB

The variance of g_AB is estimated from Eq. 15 (Hedges, 2007; Pustejovsky et al., 2014):

$${V}_{{\textrm{g}}_{\textrm{AB}}}=J{\left(\nu \right)}^2\left[\frac{\nu {\kappa}^2}{\nu -2}+{g}_{\textrm{AB}}^2\times \left(\frac{\nu }{\nu -2}-\frac{1}{J{\left(\nu \right)}^2}\right)\right],$$

(15)

where J(ν) and g_AB are computed from Eqs. 12 and 14, ν by Eq. 13, and κ by Eq. 16.

$$\kappa =\sqrt{\frac{{\textbf{p}}^{\textbf{T}}\textbf{C}\left(\hat{\boldsymbol{\upgamma}}\right)\textbf{p}}{{\textbf{r}}^{\textrm{T}}\hat{\boldsymbol{\upomega}}}},$$

(16)

where $\textbf{C}\left(\hat{\boldsymbol{\upgamma}}\right)$ is the estimated covariance matrix of $\hat{\boldsymbol{\upgamma}}$.

Step 4: Repeat Steps 2 and 3 until 20,000 replications and 20,000 g _AB s are obtained

Steps 2 and 3 were repeated until all the data for the present study were generated. At the end of this step, we obtained 20,000 replications and 20,000 g_ABs in each of the 1792 conditions.

Step 5: Compute four criteria

We applied the same four criteria as those used in Pustejovsky et al. (2014) to assess the performance of g_AB. The four criteria were relative bias, relative bias of g_AB’s variance estimator, MSE, and coverage rate of symmetric 95% CI. They are abbreviated as RB, RBV, MSE, and CR respectively. Each criterion is defined below.

RB (relative bias)

The RB of g_AB was calculated according to Eq. 17:

$$RB=\frac{{\overline{g}}_{\textrm{AB}}-{\updelta}_{\textrm{AB}}}{\updelta_{\textrm{AB}}},$$

(17)

where ${\overline{g}}_{\textrm{AB}}$ was the mean of 20,000 g_ABs obtained in each condition. Because δ_AB = 1, bias and RB were the same. We refer to them both as RB. Based on Hoogland and Boomsma (1998), we interpreted |RB| < 5% as acceptable and |RB| ≥ 5% as unacceptable. In addition, RB < −5% was interpreted as unacceptable underestimate and RB > 5% as unacceptable overestimate.

RBV (relative bias of g _AB ’s variance estimator)

The RBV of g_AB was calculated according to Eq. 18¹⁰,

$$RBV=\frac{{\overline{V}}_{g_{\textrm{AB}}}-\textrm{Var}\left({g}_{\textrm{AB}}\right)}{\textrm{Var}\left({g}_{\textrm{AB}}\right)},$$

(18)

where ${\overline{V}}_{g_{\textrm{AB}}}$ was the mean of 20,000 ${V}_{g_{\textrm{AB}}}$s obtained under each condition with each ${V}_{g_{\textrm{AB}}}$computed from Eq. 15, and Var(g_AB) was the Monte Carlo variance of 20,000 g_ABs computed from Eq. 19,

$$\textrm{Var}\left({g}_{\textrm{AB}}\right)=\frac{\sum_1^{\textrm{20,000}}{\left({g}_{\textrm{AB}}-{\overline{g}}_{\textrm{AB}}\right)}^2}{\textrm{20,000}-1}.$$

(19)

The Monte Carlo variance, or Var(g_AB), was used in Eq. 18 as a proxy for the true variance of g_AB. Based on Hoogland and Boomsma (1998), we interpreted |RBV| < 21% as acceptable and |RBV| ≥ 21% as unacceptable¹¹. In addition, RBV < −21% was interpreted as unacceptable underestimate and RBV > 21% as unacceptable overestimate.

MSE (mean square error)

MSE measured the precision of g_AB as a point estimator. MSE is the sum of the squared bias plus variance of g_AB which we verified. MSE was calculated according to Eq. 20:

$$MSE=\frac{\sum_1^{\textrm{20,000}}{\left({g}_{\textrm{AB}}-{\updelta}_{\textrm{AB}}\right)}^2}{R},$$

(20)

where δ_AB = 1 and R = 20,000.

To assess the magnitude of MSE, we examined MSE’s distribution in terms of its mean, median, and maximum. As a point of comparison suggested by Pustejovsky et al. (2014), we compared MSE’s mean and median with estimated MSEs of Hedges’ g (Hedges, 1981) obtained from a balanced, two-group experiment with m × N participants when the population ES is 1. The estimated MSE of Hedges’ g with m_g participants in a balanced two-group experiment, when the population ES = 1, is given by Eq. 21:

$$MSE\ {\textrm{of}\ \textrm{Hedges}}^{'}\ g=\frac{m_{df}}{\left({m}_{df}-2\right)\times \left(\frac{m_g}{4}\right)}\times \left[1+\frac{m_g}{4}\right]+\left[1-\frac{2}{c\left({m}_{df}\right)}\right],$$

(21)

where m_df = m_g – 2, $c\ \left({m}_{df}\right)=\frac{\Gamma \left[\frac{m_{df}}{2}\right]}{\sqrt{\frac{m_{df}}{2}}\times \Gamma \left[\frac{m_{df}-1}{2}\right]}$, and Γ = gamma function.

For m = 3 and N = 8, the MSE of Hedges’ g is estimated to be 0.212 by setting m_g = 24 (= 3 × 8) into Eq. 21. Hence, 0.212 was used as a point of comparison when m = 3 and N = 8. Similarly, for m = 4 and N = 8, we specified m_g = 32 (= 4 × 8) to obtain a point of comparison = 0.154. For m = 5 and N = 8, the point of comparison = 0.121. For m = 6 and N = 8, the point of comparison = 0.099. For m = 3, 4, 5, 6 and N = 16, the points of comparison = 0.099, 0.073, 0.058, and 0.048, respectively. Additionally, we noted in Table S4 of Pustejovsky et al. (2014), supplemental materials) that maximum MSEs were approximately twice as large as the mean MSEs across levels of m and N under normal conditions. The overall maximum MSE (= 0.664) from Table S4 was approximately four times as large as the overall mean (= 0.167). Extremely large MSEs indicated imprecision. And conditions in which these large MSEs occurred needed to be identified. Hence, we decided to identify unacceptable MSEs as those greater than the 75th percentile of all MSEs.

CR (coverage rate of symmetric 95% CI)

Guided by Pustejovsky et al.’s (2014) findings that symmetric CIs of g_AB were closer to the nominal level of 95% than noncentral CIs, we constructed the symmetric 95% CI for δ_AB using Eq. 22:

$$\textrm{symmetric}\ 95\%\,\textrm{CI}\ \textrm{for}\ {\updelta}_{\textrm{AB}}={g}_{\textrm{AB}}\pm \sqrt{V_{{\textrm{g}}_{\textrm{AB}}}}\times {t}_{0.025,\upupsilon},$$

(22)

where t_0.025,υ is the critical value from the t distribution with df = υ (Eq. 13), and ${V}_{{\textrm{g}}_{\textrm{AB}}}$ is computed from Eq. 15. CR was defined as the percentage of the 95% CIs that covered δ_AB. We defined an acceptable CR to fall between 0.925 (lower bound) and 0.975 (upper bound), according to Algina et al. (2005). A CR outside the range of [0.925, 0.975] was deemed unacceptable. In addition, CR < 0.925 was interpreted as unacceptable under-coverage and CR > 0.975 as unacceptable over-coverage.

Step 6: Analyze the impact of the six factors on four criteria

The impact of the six factors on four criteria (RQ1) was analyzed by four ANOVAs and six plots depicting trends of acceptable and unacceptable criterion values. For each criterion, the ANOVA analyzed the six main effects of Dist, m, N, ρ, λ, and ϕ, plus five two-way interactions of Dist with m, N, ρ, λ, and ϕ, respectively. All effects were treated as fixed. Because each condition yielded one criterion value, the three-way and higher-order interactions were pooled to form the error term in ANOVAs¹². We defined effects with p-values < 0.05 and eta-squares > 5.9% as having a significant impact on a criterion. An eta-square > 5.9% was labeled by Cohen (1988) as a medium ES.

Step 7: Identify conditions acceptable for MB studies and meta-analysis

To identify conditions in which g_AB performed acceptably for MB studies and meta-analysis (RQ2), we applied acceptability standards to the four criteria in each condition. Conditions that yielded all acceptable criteria were identified as acceptable conditions (e.g., Algina et al., 2005; APA, 2020; Hoogland & Boomsma, 1998; Pustejovsky et al., 2014).

Results

Results pertaining to RQ1 are presented first. These include the ANOVA results of the four criteria (RB, RBV, MSE, and CR) and trends of acceptable and unacceptable criterion values. The ANOVA results are presented in the section titled “ANOVA results of the four criteria” and trends of criterion values are presented in the section titled “Trends of acceptable and unacceptable criterion values.” Results pertaining to RQ2 are presented in the section titled “Acceptable conditions.” We summarize all results in “Summary of findings.”

ANOVA results of the four criteria

The ANOVA results presented in Table 3 are eta-squares of the six main effects of Dist, m, N, ρ, λ, ϕ and the five two-way interactions of Dist with m, N, ρ, λ, and ϕ on the four criteria. Eta-squares of effects having a significant impact (p-values < 0.05 and eta-squares > 5.9%) are shown in bold. According to Table 3, RB’s variance was best explained by all effects with a total eta-square of 91.0%. This was followed by 89.7% of MSE’s variance and 83.1% of CR’s variance. RBV’s variance was least explained with an eta-square of 71.5%.

Table 3 Eta-squares (%) of effects on the performance of g_AB based on four criteria

The Dist factor had a significant impact on RB, RBV, and CR, accounting for most variance of RB (explaining 48.7% of its variance) and RBV (27.4%). Furthermore, Dist had the second greatest impact on CR (23.9%). The m factor had a significant impact on RBV, MSE, and CR with the greatest impact on MSE (34.4%) and the second greatest impact on RBV (22.2%). It is evident that Dist and m had greater impact on the four criteria than other factors. The N factor had a significant impact on RBV and CR with the greatest impact on CR (29.5%). The ρ factor had a significant impact on RB and MSE; its impact on MSE (33.9%) was the second greatest, only slightly smaller than the greatest impact by m (34.4%). The λ factor had a significant impact on RB and RBV. The ϕ factor had a significant impact on CR only.

Regarding two-way interactions of Dist with m, N, ρ, λ, and ϕ, Dist interacted with ρ in impacting RB significantly (8.2% of its variance). Dist did not interact with other factors in impacting RBV, MSE, or CR significantly.

Trends of acceptable and unacceptable criterion values

Based on the ANOVA results, we plot trends of acceptable and unacceptable criterion values as indicators of the performance of g_AB. Figures 1 and 2 plot trends of RB and RBV, respectively. Figures 3 and 4 plot trends of MSE. Figure 5 plots trends of CR for N = 8, whereas Fig. 6 plots trends of CR for N = 16.

Fig. 1

Effects of data distribution, within-case reliability (ρ), and ratio of variance components (λ) on RB (%). RBs inside the blue shaded area were acceptable; RBs outside the blue shaded area were unacceptable

Fig. 2

Effects of data distribution, number of cases (m), number of measurements (N), and ratio of variance components (λ) on RBV (%). RBVs inside the blue shaded areas were acceptable; RBVs outside the blue shaded areas were unacceptable.

Fig. 3

Effects of number of cases (m) and within-case reliability (ρ) on MSE by data distribution. MSEs inside the blue shaded area were acceptable; MSEs outside the blue shaded area were unacceptable

Fig. 4

Boxplots of MSEs for combinations of number of cases (m) and within-case reliability (ρ)

Fig. 5

Effects of data distribution, number of cases (m), and autocorrelation (ϕ) on CR when N = 8. CRs inside blue shaded areas were acceptable; CRs outside the blue shaded areas were unacceptable

Fig. 6

Effects of data distribution, number of cases (m), and autocorrelation (ϕ) on CR when N = 16. CRs inside blue shaded areas were acceptable; CRs outside the blue shaded areas were unacceptable

RB (relative bias)

According to Table 3, RB was significantly impacted by Dist, ρ, λ, and the interaction of Dist with ρ. Figure 1 plots RB by Dist, ρ, and λ. Acceptable RBs are inside blue shaded areas and unacceptable RBs are outside blue shaded areas, based on the cutoff for an unacceptable RB (|RB| ≥ 5%) established in the “Method” section.

According to Fig. 1, RBs were all acceptable when Dist was normal, nearly normal, or mildly non-normal. When Dist was moderately non-normal, RBs were acceptable when (1) ρ ≤ 0.4 and λ = 0.1, or (2) ρ ≤ 0.6 and λ = 0.5. Moreover, unacceptable RBs were all overestimates.

RB increased as ρ increased and Dist was mildly or moderately non-normal. Given a fixed Dist and ρ, RB was smaller when λ = 0.5 than when λ = 0.1.

RBV (relative bias of g _AB’s variance estimator)

According to Table 3, RBV was significantly impacted by Dist, m, N, and λ. Figure 2 plots RBV by Dist, m, N, and λ. Acceptable RBVs are inside blue shaded areas and unacceptable RBVs are outside blue shaded areas, based on the cutoff for an unacceptable RBV (|RBV| ≥ 21%) established in the “Method” section.

According to Fig. 2, when Dist was normal, RBVs were acceptable only when m = 6 and N = 16. When Dist was nearly normal, RBVs were acceptable when m = 6 and N = 16, or when m = 5, N = 16, and λ = 0.1. When Dist was mildly non-normal, RBVs were acceptable if (1) λ = 0.1, (2) m ≥ 5, N = 8, λ = 0.5, or (3) m ≥ 4, N = 16, and λ = 0.5. When Dist was moderately non-normal, RBVs were acceptable if (1) m ≥ 4, N = 8, and λ = 0.1, (2) m ≥ 5, N = 8, and λ = 0.5, (3) N = 16 and λ = 0.1, or (4) m ≥ 4, N = 16, and λ = 0.5. Moreover, unacceptable RBVs were all overestimates.

RBVs obtained from normal and nearly normal Dists were similar; they were noticeably larger than those obtained from mildly or moderately non-normal Dist. RBV decreased as m increased from 3 to 6, N increased from 8 to 16, or λ decreased from 0.5 to 0.1.

MSE (mean square error)

Table 4 presents means, medians, and maximums of g_AB’s MSE and points of comparison based on estimated MSEs of Hedges’ g. It was evident that means and medians of g_AB’s MSE were noticeably larger than MSEs of Hedges’ g. When N = 8, g_AB’s mean MSEs were approximately 1.5 times larger than MSEs of Hedges’ g. When N = 16, g_AB’s mean MSEs were approximately 2.5 times larger than MSEs of Hedges’ g. Similar to Pustejovsky et al.’s (2014) findings, extremely large MSEs were uncovered in this study. Maximum MSEs were approximately twice as large as mean MSEs across levels of m and N. The overall maximum MSE (= 0.808) was approximately four times as large as the overall mean (= 0.194). Thus, we decided that it was justified to use the 75th percentile (= 0.241) of all MSEs as a cutoff to identify unacceptable MSEs.

Table 4 Mean, median, and maximum MSEs of g_AB and estimated MSEs of Hedges’ g as points of comparison derived from Eq. 21

According to Table 3, MSE was significantly impacted by m and ρ. Figure 3 plots MSE by m, ρ, and Dist. Acceptable MSEs are inside the blue shaded areas and unacceptable MSEs are outside the blue shaded areas, based on the cutoff for an unacceptable MSE (MSE > 0.241).

According to Fig. 3, MSE decreased as m increased for a fixed ρ, regardless of data distribution. At a fixed m, MSE increased as ρ increased, again regardless of data distribution. When m = 6, all MSEs were acceptable. When m = 4 or 5, all MSEs were acceptable, except when ρ = 0.8 and Dist was mildly or moderately non-normal. When m = 3, MSEs were acceptable only when ρ = 0.2, or when ρ = 0.4 and Dist was normal or nearly normal.

Figure 4 presents boxplots of MSEs for each combination of m and ρ across levels of Dist, N, λ, and ϕ. Three reference lines are overlaid corresponding to the 95th percentile (= 0.401), 75th percentile (= 0.241), and median (= 0.170) of the 1792 MSEs, respectively. According to Fig. 4, when m = 3 (the smallest) and ρ = 0.8 (the largest), all MSEs were larger than 0.241 (= P₇₅). When m = 3 and ρ = 0.6, or when m = 4 and ρ = 0.8, more than 75% of MSEs were larger than 0.241 (= P₇₅). Under all other combinations of m and ρ, more than 50% MSEs were smaller than 0.241 (= P₇₅). The exact P₂₅, median, mean, P₇₅, and P₉₅ of each boxplot shown in Fig. 4 are presented in File 7.

CR (coverage rate of symmetric 95% CI)

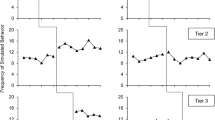
According to Table 3, CR was significantly impacted by Dist, m, N, and ϕ. Figure 5 plots CR by Dist, m, and ϕ for N = 8, whereas Fig. 6 plots CR by the same factors for N = 16. Acceptable CRs are inside the blue shaded areas and unacceptable CRs are outside the blue shaded areas, based on the cutoff for unacceptable CR (CR < 0.925 or > 0.975) established in the “Method” section.

When N = 8 and m = 5 or 6, CRs were mostly acceptable across the four Dists. As m decreased from 5, 4 to 3, CRs became increasingly unacceptable and overcovering, especially under normal and nearly normal distributions. When m = 3 or 4 under mildly and moderately non-normal Dists, CRs were mostly unacceptable when ϕ ≥ 0.

When N = 16, CRs were mostly acceptable across the four Dists. A few unacceptable overcovering CRs were found when (1) m = 3 or 4 and Dist was normal or nearly normal, or (2) m = 3, ϕ ≥ 0, and Dist was mildly or moderately non-normal. A few unacceptable undercovering CRs were identified when m = 5 or 6, ϕ ≤ −0.3, and Dist was moderately non-normal.

Acceptable conditions

To answer RQ2, we integrated findings across four criteria in Tables 5, 6, 7 and 8. Specifically, Tables 5 and 6 present acceptable conditions for λ = 0.1 and N = 8 or 16, respectively. Tables 7 and 8 present acceptable conditions for λ = 0.5 and N = 8 or 16, respectively. A circle (O) in Tables 5, 6, 7 and 8 indicates that g_AB performed acceptably on all four criteria in that condition; hence, g_AB was acceptable for MB studies and meta-analysis in that condition (e.g., Algina et al., 2005; APA, 2020; Hoogland & Boomsma, 1998; Pustejovsky et al., 2014). Actual values of the four criteria are shown in File 5 at https://osf.io/hsvwu/.

Table 5 Acceptable conditions when λ = 0.1 and N = 8 for MB studies and meta-analysis

Table 6 Acceptable conditions when λ = 0.1 and N = 16 for MB studies and meta-analysis

Table 7 Acceptable conditions when λ = 0.5 and N = 8 for MB studies and meta-analysis

Table 8 Acceptable conditions when λ = 0.5 and N = 16 for MB studies and meta-analysis

According to Tables 5, 6, 7 and 8, the number of acceptable conditions marked by O ranged from 55 (normal), 90 (nearly normal), 223 (moderately non-normal), to 233 (mildly non-normal). g_AB’s performance was acceptable in far more mildly or moderately non-normal conditions than normal or nearly normal conditions. At fixed λ and N, normal and nearly normal Dists yielded similar patterns, and mildly and moderately non-normal Dists yielded similar patterns.

The number of acceptable conditions increased as m or N increased. When m increased from 3, 4, 5 to 6, the number of acceptable conditions increased from 51, 113, 182, to 255, respectively. When N increased from 8 to 16, the number of acceptable conditions increased from 220 to 381.

In general, the number of acceptable conditions decreased as λ, ρ or ϕ increased. When λ increased from 0.1 to 0.5, the number of acceptable conditions decreased from 320 to 281. When ρ increased from 0.2, 0.4, 0.6 to 0.8, the number of acceptable conditions in general decreased from 172, 180, 157, to 92, respectively. When ϕ increased from −0.4, −0.3, −0.1, 0, 0.1, 0.3 to 0.4, the number of acceptable conditions gradually decreased from 110, 106, 87, 82, 81, 68, to 67, respectively.

According to Table 5, when λ = 0.1 and N = 8, most of the acceptable conditions were associated with (1) ρ = 0.2 or 0.4, m ≥ 4, and mildly or moderately non-normal Dist, (2) ρ = 0.6, m ≥ 5, and mildly non-normal Dist, or (3) ρ = 0.8, m = 6, and normal, nearly normal, or mildly non-normal Dist. According to Table 6, when λ = 0.1 and N = 16, most of the acceptable conditions were associated with (1) ρ = 0.2 or 0.4, and mildly or moderately non-normal Dist, (2) ρ = 0.6, m ≥ 4, and normal, nearly normal, or mildly non-normal Dist, or (3) ρ = 0.8, m ≥ 5, and normal or nearly normal Dist.

According to Table 7, when λ = 0.5 and N = 8, most of the acceptable conditions were associated with (1) ρ = 0.2, m ≥ 4, and moderately non-normal Dist, or (2) ρ = 0.4 or 0.6, m ≥ 5, and mildly or moderately non-normal Dist. According to Table 8, when λ = 0.5 and N = 16, most of the acceptable conditions were associated with (1) ρ = 0.2, and moderately non-normal Dist, (2) ρ = 0.2, m = 3 or 6, and mildly non-normal Dist, (3) ρ = 0.4 or 0.6 , m ≥ 4, and mildly or moderately non-normal Dist, (4) ρ = 0.4, 0.6, or 0.8, m = 6, and normal, nearly normal, or mildly non-normal Dist, or (5) ρ = 0.8, m = 5, and nearly normal Dist.

Summary of findings

Results presented above indicated that g_AB as a point estimator was fairly unbiased even under non-normal distributions. g_AB’s variance was generally overestimated and its 95% CI was over-covered, especially when data distribution was normal or nearly normal combined with m = 3 or 4, and N = 8. The imprecision of g_AB, as measured by MSE, was quite large when m = 3 or 4 and ρ = 0.6 or 0.8 across the four distributions.

Indeed, data distribution played a vital role in impacting g_AB’s performance for MB studies and meta-analysis. g_AB performed far better under mildly and moderately non-normal distributions than under normal and nearly normal distributions. This was because more RBVs were acceptable under mildly or moderately non-normal distribution than under normal or nearly normal distribution (see Fig. 2). Additionally, data distribution interacted with ρ in impacting the performance of g_AB significantly. Under normal or nearly normal distribution, g_AB performed more acceptably when ρ = 0.6 or 0.8 than when ρ = 0.2 or 0.4. Under mildly or moderately non-normal distribution, g_AB performed more acceptably when ρ = 0.2 or 0.4 than when ρ = 0.8. When ρ = 0.6 and λ = 0.5, g_AB performed equally acceptably under mildly and moderately distributions. When ρ = 0.6 and λ = 0.1, g_AB performed more acceptably under the mildly non-normal than under the moderately non-normal distribution. The negative impact of ρ on g_AB under any data distribution was mitigated by doubling N from 8 to 16 and/or by increasing m from 3 to 6.

Discussion

The What Works Clearinghouse Procedures and Standards Handbook, Version 5.0 (WWC, 2022) recommends g_AB as a D-CES (1) to gauge an intervention effect in SCED studies, and also (2) to synthesize findings from SCED and group studies in meta-analysis. As an estimator of its parameter δ_AB, g_AB’s interpretation is conditioned on its assumptions. Yet there have been no published studies that examined g_AB’s normality assumption. The present study aimed to investigate the impact of data distributions on the performance of g_AB by expanding Study 2 of Pustejovsky et al. (2014) to non-normal data. Our study applied the same REML method to compute g_AB and the same four criteria to evaluate the performance of g_AB, as Pustejovsky et al. (2014) did. The four criteria were: relative bias (RB), relative bias of g_AB’s variance estimator (RBV), mean square error (MSE), and coverage rate of symmetric 95% CI (CR). The present study differed from Pustejovsky et al. (2014) in two aspects. First, we analyzed converged results, whereas Pustejovsky et al. (2014) analyzed both converged and non-converged results. Second, we specified cutoffs for acceptable and unacceptable RB, RBV, MSE, and CR, whereas Pustejovsky et al. (2014) did not establish such standards.

Two research questions (RQ1 and RQ2) were raised concerning the impact of data distributions on the performance of g_AB. RQ1 explored the extent to which data distribution (Dist), the number of cases (m), the number of measurements (N), within-case reliability (ρ), ratio of variance components (λ), autocorrelation (ϕ) and the interactions of Dist with m, N, ρ, λ, and ϕ impacted each of the four criteria. Dist was manipulated in this study to range from normal, nearly normal, mildly non-normal to moderately non-normal. The other five factors (m, N, ρ, λ, and ϕ) were manipulated identically or similarly as in Pustejovsky et al. (2014). We answered RQ1 by analyzing the impact of the six main effects and five interactions on each criterion in an ANOVA framework (Table 3) and by plotting trends of acceptable and unacceptable RB (Fig. 1), RBV (Fig. 2), MSE (Figs. 3 and 4), and CR (Figs. 5 and 6).

We answered RQ2 by applying acceptability standards to all four criteria in each condition (Tables 5, 6, 7 and 8). The suitability of g_AB for MB studies and meta-analysis (RQ2) was answered by identifying conditions that yielded acceptable results on all four criteria. Our results indicated that g_AB as a point estimator was fairly unbiased even under non-normal distributions. Yet g_AB’s variance was generally overestimated, and its symmetric 95% CI was over-covered, especially when data distribution was normal or nearly normal combined with m = 3 or 4, and N = 8. The imprecision of g_AB, as measured by MSE, was a concern when m = 3 or 4 and ρ = 0.6 or 0.8, regardless of data distribution.

Under normal or nearly normal data distribution, bias in variance estimates of g_AB was mostly unacceptable. In contrast, more RBVs were acceptable under mildly or moderately non-normal distribution than under normal or nearly normal distribution. Consequently, g_AB was suitable for MB studies and meta-analysis in more conditions under mildly or moderately non-normal distribution than under normal or nearly normal distribution. It may seem counterintuitive as to why more RBVs were unacceptable under normal and nearly normal Dists than under mildly and moderately non-normal Dists. One explanation is given by Eq. 15 on the estimated variance of g_AB, or ${V}_{g_{\textrm{AB}}}$. Though Eq. 15 is derived under normality (Pustejovsky et al., 2014), its approximation to the true variance of g_AB is poor when m and N are small due to asymptotic normality of the REML method (see Footnote 2). Our results revealed that the largest m (= 6) and N (= 16) in this study were not large enough to yield acceptable estimates of the variance of g_AB under normal and nearly normal Dists¹³. Our results also showed that Eq. 15 yielded more biased estimates of g_AB’s variance under small m (= 3) and N (= 8) than under large m (= 6) and N (= 16). These findings are consistent with the mathematical derivation of Eq. 15 under the normality assumption. Given the substantial relative bias in g_AB’s variance estimator in the present study and in Pustejovsky et al. (2014), Eq. 15 needs to be improved in future research. We offer a few viable alternative methods under “Limitations and future research directions.”

Our results revealed a complex and joint impact of data distribution, along with number of cases, number of measurements, ratio of variance components, within-case reliability, and autocorrelation on the suitability of g_AB for MB studies and meta-analysis. According to the ANOVA results, data distribution contributed to approximately 49% of variance in RB and 25% of variance in both RBV and CR. Furthermore, data distribution interacted with within-case reliability in impacting 8% of variance in RB. Number of cases and within-case reliability each contributed to 34% of variance in MSE. Among the four criteria, RB was most accounted for (91%) and RBV was least accounted for (72%) by all effects combined.

Our findings showed that the performance of g_AB, as assessed by RB, MSE, RBV, and CR, depended on the distribution of data and five data features investigated in the present study. Of the six data features, the number of cases and measurements are within the control of a SCED researcher or interventionist, whereas data distribution, within-case reliability, ratio of variance components, and autocorrelation are not. In fact, our results demonstrated a mitigating effect of increased cases and measurements on the negative impact due to increased ratio of variance components, within-case reliability, and first-order autocorrelation on the performance of g_AB. The mitigating effect of increased m or N on g_AB was particularly evident for normal and nearly normal distributions.

Furthermore, large number of cases and measurements are required by the REML method to yield acceptable estimates of g_AB’s variance. Therefore, SCED researchers and interventionists should be encouraged to design a study with sufficiently large number of cases and measurements. In light of our findings, we offer general recommendations of g_AB for primary MB studies and meta-analysis. The preamble to our recommendations is that each SCED study, for which g_AB is applicable, had been well constructed, conducted, and documented (Chen et al., 2020; Kratochwill et al., 2013, 2021; Peng et al., 2013).

Our recommendations

We recommend g_AB for primary MB studies and meta-analysis when each study with at least 16 measurements, meets one of the following two conditions:

• (1) m = 6, the within-case reliability is 0.6 or 0.8, and the shape, skewness, and kurtosis of the data distribution are similar to the normal or nearly normal distribution investigated in this study;

• (2) m ≥ 4, the within-case reliability is 0.2, 0.4, or 0.6, and the shape, skewness, and kurtosis of the data distribution are similar to the mildly or moderately non-normal distribution investigated in this study.

The shape, skewness and kurtosis may be determined from raw data and compared to the four data distributions manipulated in the current study (see File 1 at https://osf.io/hsvwu/ for the four marginal distributions). Alternatively, the shape, skewness and kurtosis of empirical data distributions concerning a specific intervention or outcome measure may be conjectured from review studies, such as Joo (2017), Shadish et al. (2014), and Solomon (2014). Likewise, the within-case reliability of a study’s data may be computed from the ratio of the between-case variance in levels over the sum of the within-case variance plus the between-case variance in levels, and then compared to the four levels manipulated in the current study.

In empirical SCED studies, there may well be exceptions to the conditions recommended above when g_AB performs satisfactorily. When applied researchers find their data to not meet the recommended conditions, a cautionary note should be added for interpreting the magnitude of g_AB. Practitioners are advised to consider context effects of an intervention holistically when interpreting g_AB and its reasonableness.

Limitations and future research directions

As with any simulation study, findings and recommendations presented here are based on specific manipulations of the six factors investigated and acceptable standards established in the present study. Of the six factors, the number of cases (m), the within-case reliability (ρ), and the autocorrelation (ϕ) were well represented by levels commonly found in empirical MB studies. The number of measurements (N = 8 or 16) and the ratio of variance components (λ = 0.1 or 0.5) were represented by only two levels.

The manipulation of data distributions in the present simulation study ranged from normal to moderately non-normal. All four distributions were unimodal, either mesokurtic or leptokurtic. And the two non-normal distributions were both positively skewed. Future studies can examine performance of g_AB using discrete or count/frequency data with one or more modes, or different distributions at Level-1 and Level-2.

We fitted MB2 to normal and non-normal data. Hence, the impact of non-normality on g_AB has not been investigated under MB1, MB3, MB4, or MB5 (Pustejovsky et al., 2014). Simulation studies conducted under models other than MB2 should yield useful information to inform SCED researchers and interventionists about g_AB in broader contexts. Studies on the impact of model misspecification should facilitate our understanding of the application of g_AB.

Relative bias in g_AB’s variance estimator was substantial in the present study and in Pustejovsky et al. (2014). Such relative bias has impeded g_AB’s utility in meta-analysis. In the context of hierarchical modeling of SCED data, alternative methods, such as the Bayesian method (Baek et al., 2020; Joo & Ferron, 2019), have been proposed to improve the variance estimation of a random effect. However, biased variance estimation remains an unresolved issue in meta-analysis of SCED studies.

In sum, future studies should consider: (a) generating data from non-normal distributions not considered in the present study (e.g., platykurtic, discrete, count/frequency, bimodal/multimodal); (b) simulating data from different distributions for Level-1 and Level-2 errors separately; (c) increasing the number of cases > 6 and the number of measurements ≥ 20 to improve the convergence of REML estimates (see File 8 for non-convergence rates); (d) fitting a model different from MB2 to data; and (e) developing Bayesian or robust estimators of g_AB’s variance (e.g., Chen & Pustejovsky, 2022; Park & Beretvas, 2019; Tipton, 2015; Verbeke & Lesaffre, 1996; Yuan & Bentler, 2002), or applying the Box-Cox or square root transformation of g_AB’s variance (Man et al., 2022).

Concluding remarks

The g_AB statistic has been endorsed as a D-CES by the What Works Clearinghouse Procedures and Standards Handbook, Version 5.0 (WWC, 2022) to gauge an intervention effect in a SCED study and to synthesis findings from multiple SCED studies, or across SCED and group studies. Such an endorsement will surely increase the reporting of g_AB in published reports. Thus, it is crucial to examine the performance of g_AB under non-normal distributions with different data features in order to render appropriate reporting and interpretation of g_AB. Findings from our study highlight the importance of data distributions and features in determining the suitability of g_AB for primary MB studies and meta-analysis.

Based on g_AB’s definition and its REML estimation method, it is worth pointing out several issues associated with g_AB’s applicability in SCED contexts. First, g_AB is applicable to MB designs across three or more cases of the same behavior, as previously mentioned. g_AB is equally applicable to AB^k designs with at least three cases of the same behavior. Second, as a study-level ES index, g_AB does not permit the examination of factors that may vary between cases within a study, as in moderator analyses (Kratochwill et al., 2021). Third, g_AB’s computation and interpretation depend on a model. Such a model may be misspecified, or overly simplistic (Maggin et al., 2022; Valentine et al., 2016)¹⁴, and the model assumptions (e.g., normality, equally spaced measurements, no trend) may be untenable (Maggin et al., 2022) or non-robust. Fourth, its applicability beyond the “starting point,” or MB1, recommended by the What Works Clearinghouse Procedures and Standards Handbook, Version 5.0 (WWC, 2022) requires extensive research, especially under non-normal distributions with small number of cases and measurements.

In addition to issues discussed above, Kratochwill et al. (2021) raised concerns about the compatibility of constructs underlying outcomes measured in SCED and group studies. Such concerns cast doubt on the design-comparability of g_AB across SCED and group studies. Maggin et al. (2022) demonstrated several misleading conclusions based exclusively on ES indices. Thus, Maggin et al. (2022) emphasized the importance of conducting systematic visual analyses of single-case data in terms of level, trend, variability, immediacy of change, overlap, and consistency of data patterns both within and across phases.

Given the issues and concerns summarized above, we caution readers not to rely solely on the magnitude of a D-CES, such as g_AB, when determining an intervention’s effectiveness. Instead, a detailed description of an intervention study should be reviewed thoroughly when assessing an intervention. A study description should provide sufficient information regarding the definition of the construct being intervened, the construct validity of its measurements, the verification of the study’s design standards, the examination of the study’s operational issues, visual and quantitative demonstrations of the intervention’s effectiveness. As Chen et al. (2020), Kratochwill et al. (2021), and Wrigley and McCusker (2019) advocated, which we agree with, that it is more meaningful to ask, “For whom and under what conditions does an intervention work?” than to ask, “Does an intervention work?” A sound reporting of g_AB, or any ES index, should include (A) a thorough interpretation of the ES magnitude based on similar studies (i.e., construct and population of interest, treatment/intervention introduced, and measurements of outcomes), and (B) clinical or practical importance of the intervention effect.

The data and materials for the simulation study are available at https://osf.io/hsvwu/.

Appendices

Appendix A

In this Appendix, we compare our findings under normal distributions to those obtained from Study 2 of Pustejovsky et al. (2014) in terms of relative bias, relative bias of variance estimators, MSE, and CR.

In terms of g_AB’s relative bias, Pustejovsky et al. (2014) reported the average absolute relative bias of g_AB to be less than 7.3% when m = 3, less than 4.9% when m = 4, and less than 2.9% when m ≥ 5, across all combinations of parameters and N. In its supplementary materials, Pustejovsky et al. (2014) noted that relative bias was generally greater when N = 8 than when N = 16 (pp. 8–9). Relative bias decreased as m increased. We too observed these patterns in g_AB’s relative bias. The average absolute relative biases uncovered in our study were slightly higher than those cited above. The greatest absolute relative bias of g_AB was 10.8% when m = 3, 7.6% when m = 4, 5.5% when m = 5, and less than 4.4% when m = 6.

In terms of relative bias of g_AB’s variance estimator, Pustejovsky et al. (2014) reported substantial overestimation of variance when m was small, averaging 43% when m = 3 and N = 16. Even at the largest m = 6 and N = 16, the variance of g_AB was overestimated with an average relative bias of 14%. We too observed the persistent overestimation by g_AB’s variance estimator. The positive relative biases uncovered in our study were comparable to those cited above. When m = 3 and N = 16, the average relative bias was 48%. When m = 6 and N = 16, the average relative bias was 20%.

In terms of g_AB’s MSE as a criterion for its precision, Pustejovsky et al. (2014, supplementary materials) reported that MSE at N = 8 ranged from 0.290 (m = 3), 0.198 (m = 4), 0.149 (m = 5), to 0.120 (m = 6) across levels of the parameters (p. 9). At N = 16, MSE ranged from 0.221 (m = 3), 0.153 (m = 4), 0.116 (m = 5), to 0.092 (m = 6) also across levels of the parameters. Pustejovsky et al. (2014, supplementary materials) concluded that (1) g_AB was imprecise especially when m was small; (2) MSEs decreased as m or N increased; and (3) MSEs generally increased as ρ, λ, and ϕ increased (p. 9). We too uncovered patterns comparable to those cited above. Our MSEs at N = 8 ranged from 0.278 (m = 3), 0.191 (m = 4), 0.146 (m = 5), to 0.119 (m = 6). At N = 16, our MSEs ranged from 0.222 (m = 3), 0.156 (m = 4), 0.120 (m = 5), to 0.097 (m = 6).

In terms of CR, Pustejovsky et al. (2014) reported that the symmetric CI had greater than nominal coverage, ranging from 97.8% when m = 3 to 96.4% when m = 6, averaged across the parameter levels and N. When m = 6, CRs varied from 93.9% to 97.6% across levels of the manipulated factors. We too observed the g_AB’s CI to over-cover. The CRs in our study were comparable to those cited above. Our average CRs ranged from 97.3% when m = 3 to 96.6% when m = 6. When m = 6, CRs ranged from 95.0% to 98.0% across levels of the manipulated factors.

In summary, our results from the normal distribution agreed with Pustejovsky et al.’s (2014), obtained also under the normal distribution, in terms of g_AB’s overestimated variance, imprecision when m was small, and over-coverage of the symmetric 95% CI. As for g_AB’s small relative bias when m ≥ 4 claimed in Pustejovsky et al. (2014), the average absolute relative bias of g_AB in our study fell below 5% only when m = 6. Subtle differences in findings might be attributed to ways in which Pustejovsky et al. (2014) and this study dealt with non-converged results, and manipulated the autocorrelation (ϕ) slightly differently.

Appendix B

In this appendix, we explain (1) how a case was generated from a normal distribution and (2) how 3 (= m) cases were combined to form a replication. We use Pustejovsky et al.’s (2014) matrix notations to facilitate the explanation.

Generating a case

Under MB2, the distribution of the jth measurement of the ith case (Y_ij ) is given in Eq. 6 which is repeated here as Eq. B1:

$${\displaystyle \begin{array}{c}{Y}_{\textrm{ij}}={\upgamma}_{00}+{\upeta}_{0\textrm{i}}+\left({\upgamma}_{10}+{\upeta}_{1\textrm{i}}\right)\times {D}_{\textrm{ij}}+{\upvarepsilon}_{\textrm{ij}}\\ {}=\left[{\upgamma}_{00}+\left({\upgamma}_{10}\times {D}_{\textrm{ij}}\right)\right]+\left\{{\upeta}_{0\textrm{i}}+\left({\upeta}_{1\textrm{i}}\times {D}_{\textrm{ij}}\right)+{\upvarepsilon}_{\textrm{ij}}\right\}\\ {}=\left[\textrm{fixed}\ \textrm{effects}\right]+\left\{\textrm{random}\ \textrm{effects}\right\}.\end{array}}$$

(B1)

For N scores of a case, Eq. B1 can be expressed in matrix notations as Eq. B2 or 9:

$${\textbf{Y}}_{N\times 1}={\textbf{D}}_{N\times 2}\; {\boldsymbol{\upgamma}}_{2\times 1}+{\textbf{e}}_{N\times 1}.$$

(B2)

The fixed effects in Eq. B2 are expressed as the product of the design matrix (D_N×2) and a fixed-effect vector (γ_2×1). The random effects in Eq. B2 are expressed as a vector (e_N×1) that consists of Level-2 errors [η_0i + (η_1i × D_ij)] and Level-1 errors (ε_ij).

For illustration, let’s consider the first case from the condition of m = 3, N = 8, ρ = 0.2, λ = 0.1, and ϕ = −0.4. The D and γ matrices for this illustrated case are defined according to Eq. B3:

$${\textbf{D}}_{8\times 2}=\left[\begin{array}{cc}1& 0\\ {}1& 0\\ {}1& 0\\ {}1& 1\\ {}1& 1\\ {}1& 1\\ {}1& 1\\ {}1& 1\end{array}\right],\textrm{and}\ {\boldsymbol{\upgamma}}_{2\times 1}=\left[\begin{array}{c}0\\ {}1\end{array}\right],$$

(B3)

where the first column of D_8×2 is a vector of 1s, the second column of D_8×2 specifies that this case’s intervention starts on the fourth measurement (see Table 2), and γ_2×1 contains γ₀₀ and γ₁₀—the two parameters specified under MB2 (see “Definition of δ_AB”).

Errors in the error vector (e_8×1) were randomly generated from a distribution specified in Table 1, using the mvrnonnorm function in the semTools package (Jorgensen et al., 2021). If Dist = normal, random errors were generated from the normal distribution by specifying skewness = 0, kurtosis = 0, and a variance-covariance matrix of errors (Σ_8×8 from Eq. B6 below) in the mvrnonnorm function. With these specifications, the mvrnonnorm function produced multivariate normal errors using the Vale and Maurelli method (Vale & Maurelli, 1983). One such e_8×1 = (−0.54, 0.30, 0.14, 0.62, −0.07, 1.95, 1.33, 0.87)^T. Adding this e_8×1 to the product of D_8×2 and γ_2×1 matrices from Eq. B3, we obtained data for the illustrated case in Eq. B4:

$${\textbf{Y}}_{8\times 1}={\textbf{D}}_{8\times 2} \;{\boldsymbol{\upgamma}}_{2\times 1}+{\textbf{e}}_{8\times 1}=\left[\begin{array}{cc}1& 0\\ {}1& 0\\ {}1& 0\\ {}1& 1\\ {}1& 1\\ {}1& 1\\ {}1& 1\\ {}1& 1\end{array}\right] \left[\begin{array}{c}0\\ {}1\end{array}\right]+\left[\begin{array}{c}-0.54\\ {}\kern0.75em 0.30\\ {}\kern0.75em 0.14\\ {}\kern0.75em 0.62\\ {}-0.07\\ {}\kern0.75em 1.95\\ {}\kern0.75em 1.33\\ {}\kern0.75em 0.87\end{array}\right]=\left[\begin{array}{c}-0.54\\ {}\kern0.75em 0.30\\ {}\kern0.75em 0.14\\ {}\kern0.75em 1.62\\ {}\kern0.75em 0.93\\ {}\kern0.75em 2.95\\ {}\kern0.75em 2.33\\ {}\kern0.75em 1.87\end{array}\right].$$

(B4)

The variance-covariance matrix of errors (Σ) is written generally as Eq. B5:

$$\sum ={\textbf{DTD}}^{\textrm{T}}+\left(1-\uprho \right)\bullet \boldsymbol{AR}\left(\textbf{1}\right),$$

(B5)

where DTD^T = the variance-covariance matrix of Level-2 errors, (1 − ρ) ∙ AR(1) = the variance-covariance matrix of Level-1 errors, D = design matrix from Eq. B3, ${\textbf{T}}_{2\times 2}=\left[\begin{array}{cc}{\uptau}_0^2& 0\\ {}0& {\uptau}_1^2\end{array}\right]$ (see Footnote 4), and AR(1) is the matrix of first-order autocorrelations with 1s along the diagonal and ϕ^|k−j| off-diagonal.

For the illustrated case, ρ = 0.2 and λ = 0.1. Hence, ${\uptau}_0^2$ = 0.2 and ${\uptau}_1^2$ = 0.02 because (${\upsigma}^2+{\uptau}_0^2$) =1 (see “Definition of δ_AB”), ρ = ${\uptau}_0^2$/(${\upsigma}^2+{\uptau}_0^2$) = ${\uptau}_0^2$, and λ = ${\uptau}_1^2$/${\uptau}_0^2$. With ϕ = −0.4 and N = 8, the Σ_8×8 for the eight random errors was computed according to Eq. B6:

$${\displaystyle \begin{array}{c}{\boldsymbol{\Sigma}}_{\textbf{8}\times \textbf{8}}={\textbf{DTD}}^{\textrm{T}}+\left(1-\uprho \right)\bullet \boldsymbol{AR}\left(\textbf{1}\right)\\ {}=\left[\begin{array}{cc}1& 0\\ {}1& 0\\ {}1& 0\\ {}1& 1\\ {}1& 1\\ {}1& 1\\ {}1& 1\\ {}1& 1\end{array}\right] \left[\begin{array}{cc}0.2& 0\\ {}0& 0.02\end{array}\right] \left[\begin{array}{cccccccc}1& 1& 1& 1& 1& 1& 1& 1\\ {}0& 0& 0& 1& 1& 1& 1& 1\end{array}\right]+\\ {}\begin{array}{c}\left(1-0.2\right)\bullet \left[\begin{array}{cccccccc}1& -0.4& {\left(-0.4\right)}^2& {\left(-0.4\right)}^3& {\left(-0.4\right)}^4& {\left(-0.4\right)}^5& {\left(-0.4\right)}^6& {\left(-0.4\right)}^7\\ {}-0.4& 1& -0.4& {\left(-0.4\right)}^2& {\left(-0.4\right)}^3& {\left(-0.4\right)}^4& {\left(-0.4\right)}^5& {\left(-0.4\right)}^6\\ {}{\left(-0.4\right)}^2& -0.4& 1& -0.4& {\left(-0.4\right)}^2& {\left(-0.4\right)}^3& {\left(-0.4\right)}^4& {\left(-0.4\right)}^5\\ {}{\left(-0.4\right)}^3& {\left(-0.4\right)}^2& -0.4& 1& -0.4& {\left(-0.4\right)}^2& {\left(-0.4\right)}^3& {\left(-0.4\right)}^4\\ {}{\left(-0.4\right)}^4& {\left(-0.4\right)}^3& {\left(-0.4\right)}^2& -0.4& 1& -0.4& {\left(-0.4\right)}^2& {\left(-0.4\right)}^3\\ {}{\left(-0.4\right)}^5& {\left(-0.4\right)}^4& {\left(-0.4\right)}^3& {\left(-0.4\right)}^2& -0.4& 1& -0.4& {\left(-0.4\right)}^2\\ {}{\left(-0.4\right)}^6& {\left(-0.4\right)}^5& {\left(-0.4\right)}^4& {\left(-0.4\right)}^3& {\left(-0.4\right)}^2& -0.4& 1& -0.4\\ {}{\left(-0.4\right)}^7& {\left(-0.4\right)}^6& {\left(-0.4\right)}^5& {\left(-0.4\right)}^4& {\left(-0.4\right)}^3& {\left(-0.4\right)}^2& -0.4& 1\end{array}\right]\\ {}=\left[\begin{array}{cccccccc}1& -0.12& 0.33& 0.15& 0.22& 0.19& 0.20& 0.20\\ {}-0.12& 1& -0.12& 0.33& 0.15& 0.22& 0.19& 0.20\\ {}0.33& -0.12& 1& -0.12& 0.33& 0.15& 0.22& 0.19\\ {}0.15& 0.33& -0.12& 1.02& -0.10& 0.35& 0.17& 0.24\\ {}0.22& 0.15& 0.33& -0.10& 1.02& -0.10& 0.35& 0.17\\ {}0.19& 0.22& 0.15& 0.35& -0.10& 1.02& -0.10& 0.35\\ {}0.20& 0.19& 0.22& 0.17& 0.35& -0.10& 1.02& -0.10\\ {}0.20& 0.20& 0.19& 0.24& 0.17& 0.35& -0.10& 1.02\end{array}\right]\end{array}\end{array}}.$$

(B6)

The Σ_8×8 computed in Eq. B6 was input into the mvrnonnorm function, along with skewness = 0 and kurtosis = 0, to generate normally distributed errors shown in Eq. B4 above.

Generating m cases to form a replication

For a specific m in a replication, m cases were generated similarly as the illustrated case above. The design matrix D_N×2 of each case varied according to the start point specified in Table 2. After data were generated for m cases, a replication was formed and a g_AB was computed.