Change point detection is an old and important problem in time series analysis (Basseville & Nikiforov, 1993; Bhattacharya & Johnson, 1968; Kander & Zacks, 1966; Page, 1954). As indicated by its name, the goal of change point detection is to detect whether and when abrupt distributional changes take place in a time series, which is crucial in a diverse set of fields such as climate science, economy, medicine, etc. (see Chen & Gupta, 2012). Current applications in the field of behavioral sciences include detection of workload changes using heart rate variability (Hoover, Singh, Fishel-Brown, & Muth, 2011), capturing active state transition in fMRI activity (Lindquist, Waugh, & Wager, 2007) and revealing cardio-respiratory changes preceding the occurrence of panic attacks (Rosenfield, Zhou, Wilhelm, Conrad, Roth, & Meuret, 2010). Until recently, research on this topic focused almost exclusively on univariate time series, yielding approaches to detect changes in mean, and, in some cases, variance and/or autocorrelation.

With the advance of technology, more and more studies generate multivariate time series. For example, climate studies monitor several environmental factors such as temperature, precipitation and water discharges (Jarusikova, 1997). In neurophysiology (Terien, Germain, Marque, & Karlsson, 2013), analysis of biological functions entails following numerous physiological signals. Turning to examples from the behavioral sciences, in emotion psychology, experiential, behavioral, and physiological reactions to emotional stimuli are tracked across time (Christie & Friedman, 2004; Mauss, Levenson, McCarter, Wilhelm, & Gross, 2005), and in developmental psychology, performance on several Piagetian tasks (Piaget, 1972) is examined over time to assess how cognitive abilities of children develop (Amsel & Renninger, 1997; Klausmeier & Sipple, 1982; van der Maas & Molenaar, 1992).

Given multivariate data, change point detection involves more than changes in single variables because the system characteristics seldom react in an isolated way to change. Indeed, in many cases, theory prescribes that, next to the mean, also the correlation structure of (a subset of) the system characteristics alters when change occurs. In emotion psychology, researchers postulate that physiological, experiential, and behavioral reactions synchronize in emotion-inducing situations to enable the organism to quickly and efficiently cope with environmental threats or opportunities (Mauss et al., 2005). In developmental psychology, one conjectures that before a sudden developmental jump – the mastery of a specific ability - the correlation structure of a set of tasks changes (Amsel & Renninger, 1997; van der Maas & Molenaar, 1992). Outside psychology, one can think of the strengthened correlation between economic growth rates of countries implementing a common monetary policy (Crowley & Schultz, 2011), parts of the brain exhibiting excessive neuronal synchronization during a seizure (Terien et al., 2013), or climactic indices demonstrating higher correlations during cool seasons (Wright & Wallace, 1988). As a consequence, detecting correlation changes becomes an integral aspect of the change point analysis problem in the case of multivariate data (see Aue, Hӧrmann, Horváth, & Reimherr, 2009; Müller, Baier, Galka, Stephani, & Muhle, 2005; Terien, Marque, Germain, & Karlsson, 2009).

Recently, a number of non-parametric multivariate change point detection methods have been proposed that can be used to detect changes in both correlation structure and means: DeCon (Bulteel, Ceulemans, Thompson, Waugh, Gotlib, Tuerlinckx, & Kuppens, 2014), E-divisive (Matteson & James, 2014), Multirank (Lung-Yut-Fong, Lévy-Leduc, & Cappé, 2012), and KCP (Arlot, Celisse, & Harchaoui, 2012). However, we see two problems when an applied researcher wants to apply these methods. First, the methods are based on different statistical approaches: Robust methods for DeCon, rank information for Multirank, the kernel trick for KCP and Euclidean distances for E-divisive. This diversity makes it difficult for the applied researcher to appraise the methods. Second, because they are based on different statistical approaches, it is still unknown which of these four methods should be preferred in which circumstances. More specifically, a direct comparison between these methods for the detection of correlational changes is lacking (although Matteson & James, 2014, conducted a partial comparison).

Given these two problems, this paper fulfills two goals. The first goal is to introduce the basic principles behind each method and the corresponding algorithms in easy to follow steps to make them more accessible to readers. The second goal is to study the relative performance by means of extensive simulations. Note that we focus on non-parametric methods, given their wide applicability.

In the remainder of this paper, we first introduce each of the four methods, using an illustrative hypothetical example. Next, we apply the methods to two sets of simulated data based on Bulteel et al. (2014) and on Matteson and James (2014) and to an empirical data set on pilot reactions. In the final section, the results are discussed and future research directions are enumerated.

Method

Before discussing the four methods in detail, we introduce an illustrative hypothetical data set that will be used throughout this section. Let X = {X 1, X 2, …, X 50} denote the whole time series, composed of 50 time points at which three variables are measured. This time series is shown in Fig. 1. A change point occurs between the 25th and 26th time point, segmenting the time series into two phases of 25 subsequent time points. The 25 observations in Phase 1 are randomly sampled from a multivariate normal distribution with mean, \( {\boldsymbol{\mu}}_{1:25}=\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 2\hfill \\ {}\hfill 3\hfill \end{array}\right] \), and covariance matrix, \( {\varSigma}_{1:25}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right] \), implying that all variables are independent. In Phase 2, the observations are also drawn from a multivariate normal distribution but the means \( {\boldsymbol{\mu}}_{26:50}=\left[\begin{array}{c}\hfill 3\hfill \\ {}\hfill 6\hfill \\ {}\hfill 9\hfill \end{array}\right] \) are higher and the variables become strongly correlated, as indicated by the covariance matrix \( {\varSigma}_{1:25}=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0.9\hfill & \hfill 0.9\hfill \\ {}\hfill 0.9\hfill & \hfill 1\hfill & \hfill 0.9\hfill \\ {}\hfill 0.9\hfill & \hfill 0.9\hfill & \hfill 1\hfill \end{array}\right] \). It should be emphasized that the actual change occurs between the 25th and 26th time points. However, this true change point is unobserved. Hence, in the remainder of this paper, we will use the first observation after the change in distribution as the change point. Thus, for the hypothetical data, the change point is T = 26.

Fig. 1
figure 1

Illustrative hypothetical data set with three variables, 50 time points, and one change point between the 25th and 26th time point, segmenting the series into two phases. Phase 1 observations, X 1 : 25, were drawn from MVN \( \left(\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 2\hfill \\ {}\hfill 3\hfill \end{array}\right],\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]\right) \) and Phase 2 observations, X 26 : 50, were drawn from MVN \( \left(\left[\begin{array}{c}\hfill 3\hfill \\ {}\hfill 6\hfill \\ {}\hfill 9\hfill \end{array}\right],\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0.9\hfill & \hfill 0.9\hfill \\ {}\hfill 0.9\hfill & \hfill 1\hfill & \hfill 0.9\hfill \\ {}\hfill 0.9\hfill & \hfill 0.9\hfill & \hfill 1\hfill \end{array}\right]\right) \)

Full size image

DeCon

DeCon bases change point detection on outlier identification using robust statistics (Bulteel et al., 2014). The method slides a time window of size W across the time series by sequentially deleting the first time point in the window, and adding one new observation as the last time point. Per window, it is determined whether the last time point is an outlier with respect to the distribution of the other time points in the window. If the latter is the case for multiple consecutive windows, this signals that the observations that are added to the window might come from a different distribution, and, hence, that a change point occurred. Specifically, DeCon consists of the following four steps.

  1. 1.

    Apply Robust PCA in each time window and determine “outlyingness” of the last time point.

Per time window, DeCon computes a robust multivariate center, μ w , and a covariance matrix, Σ w , to determine the distribution of the regular observations (standardized per variable since we are interested in correlations rather than covariances), and generates an outlyingness measure for the last time point of the window. To this end, the robust principal components approach (ROBPCA) of Hubert et al. is used (for details, see Hubert, Rousseeuw & Vanden Branden, 2005). In this paper, we retained all principal components to avoid the issue of how to choose the optimal number of components.Footnote 1 Given that we used all components, the outlyingness measure is the so-called score distance, which equals the Mahalanobis distance between the last time point X last and the robust window-specific center μ w :

$$ S{D}_{last}=\sqrt{{\left({\boldsymbol{X}}_{last}-{\boldsymbol{\mu}}_w\right)}^T{\displaystyle {\sum}_w^{-1}\left({\boldsymbol{X}}_{last}-{\boldsymbol{\mu}}_w\right)}} $$
(1)

Note that the Mahalanobis distance differs from the Euclidean one, in that the covariance matrix of the variables under consideration is taken into account. If the data are normally distributed,Footnote 2 the squared Mahalanobis distances follow a χ 2 distribution with degrees of freedom equal to the number of variables. Thus, the last time point is classified as an outlier if the Mahalanobis distance exceeds the square root of the 97.5th quantile of this χ 2 distribution.

For analyzing our hypothetical data, the window size was set to W = 20. In general, this parameter should be chosen considering the minimum time period within which no change is expected to occur (for more considerations and detailed simulation results, see Bulteel et al., 2014). ROBPCA was applied to the first window, X 1 : 20, then to the second window, X 2 : 21, and so on, until the last window, X 31 : 50. Since the change point occurs at T = 26, chances are high that the last time point of the first time window that includes a new phase observation as its last time point, X 7 : 26 , has a large score distance. In general, this probability depends on how different the means and correlations are in the subsequent phases. For the time window, X 7 : 26 , where the robust center equals \( {\boldsymbol{\mu}}_{7:26}=\left[\begin{array}{c}\hfill 1.41\ \hfill \\ {}\hfill 1.89\ \hfill \\ {}\hfill 3.18\hfill \end{array}\right] \) and the robust covariance matrix is given by \( {\varSigma}_{7:26}=\left[\begin{array}{ccc}\hfill 0.29\hfill & \hfill -0.15\hfill & \hfill 0.11\hfill \\ {}\hfill -0.15\hfill & \hfill 0.62\hfill & \hfill 0.13\hfill \\ {}\hfill 0.11\hfill & \hfill 0.13\hfill & \hfill 0.57\hfill \end{array}\right] \), the last observation, \( {\boldsymbol{X}}_{26}=\left[\begin{array}{c}\hfill 1.08\ \hfill \\ {}\hfill 4.37\ \hfill \\ {}\hfill 7.36\hfill \end{array}\right] \), has a score distance equal to

$$ S{D}_{26}=\sqrt{{\left(\left[\begin{array}{c}\hfill 1.08\ \hfill \\ {}\hfill 4.37\ \hfill \\ {}\hfill 7.36\hfill \end{array}\right]-\left[\begin{array}{c}\hfill 1.41\ \hfill \\ {}\hfill 1.89\ \hfill \\ {}\hfill 3.18\hfill \end{array}\right]\right)}^T{\left[\begin{array}{ccc}\hfill 0.29\hfill & \hfill -0.15\hfill & \hfill 0.11\hfill \\ {}\hfill -0.15\hfill & \hfill 0.62\hfill & \hfill 0.13\hfill \\ {}\hfill 0.11\hfill & \hfill 0.13\hfill & \hfill 0.57\hfill \end{array}\right]}^{-1}\left(\left[\begin{array}{c}\hfill 1.08\ \hfill \\ {}\hfill 4.37\ \hfill \\ {}\hfill 7.36\hfill \end{array}\right]-\left[\begin{array}{c}\hfill 1.41\ \hfill \\ {}\hfill 1.89\ \hfill \\ {}\hfill 3.18\hfill \end{array}\right]\right)}=6.06. $$

For this example, the cut-off for the score distance is 3.06. Figure 2 (left panel) shows that the score distance of the last observation, X 26, indeed clearly exceeds the cut-off indicated by the red line.

Fig. 2
figure 2

ROBPCA outlier plot for window, X 7 : 26, and plot of the moving outlier sum generated by the forward procedure for the hypothetical data. The left panel shows that X 26 exceeds the score distance cut-off (indicated by the horizontal line), hence this observation is flagged as an outlier. The right panel reveals that the moving outlier sum reaches the moving sum cut-off at T = 21 when the sum is computed across observations, X 21, X 22, X 23, …, X 30. The vertical line indicates that the location of the change point is set at T = 26, since X 26 is the first outlier within these ten observations

Full size image
  1. 2.

    Track the moving sum of the outlyingness of ten subsequent last time points and declare a change point when this sum equals five at least.

The outlyingness of the last time point is a binary variable and thus a binary time series is created (with 1 indicating an outlier and 0 a regular observation). Although the outlyingness of the last time point of a window may correctly signal the presence of a change point, false negatives or false positives can of course occur. To mitigate their impact, the results of multiple windows are combined. Specifically, a moving sum of the outlyingness of the final time point of ten subsequent windows is computed. As soon as this sum equals at least five, the first outlying time point in the corresponding set of time points is declared as the change point. Note that the 5 out of 10 rule is recommended to balance Type 1 and Type 2 errors (see Bulteel et al., 2014). Going back to our example, Fig. 2 (right panel) shows the moving outlier sum for the whole sequence. The moving sum cut-off was reached for the first time when the moving sum included observations, X 21, X 22, X 23, …, X 30 . Out of these observations, the first outlying one was X 26. Thus, the change point is detected at time point T = 26.

When a change point occurs, it is quite likely that the moving outlier sum stays relatively high for a while, because the change in correlation structure and means will only start to influence the ROBPCA estimates if at least .25W time points within a window pertain to the next phase. This is because by default, the ROBPCA estimates are based on the 75 % least outlying cases only. Therefore, the minimum distance between subsequent change points equals .25W. In our hypothetical time series no further change points were detected.

  1. 3.

    Repeat steps 1 and 2 in the backward direction.

The original DeCon procedure executed steps 1 and 2 only. The simulations in the present paper revealed that this “forward procedure” (forward, because we slide the time window from the first to the last time point), works well for settings where the correlation decreases. Indeed, in these cases, the first time points in the moving window come from a more compact joint distribution (higher correlation), while later observations come from a more scattered joint distribution (low correlation). These later observations, thus, will generate larger score distances, and will be correctly flagged as outliers. However, when there is an increase in correlation across time, the time window moves from a phase with a lower correlation (Phase 1) to a phase with a higher one (Phase 2). If the means and variances remain the same, observations in Phase 2 will most likely have a small score distance, when compared to the distribution in Phase 1, because the distribution of Phase 2 will mostly overlap with that of Phase 1 (see Fig. 3). Since no outliers are detected, neither is the change point.

Fig. 3
figure 3

Overlapping phase distributions. Observations are bivariate normal with all means equal to zero and all variances equal to 1. Phase 1 observations are uncorrelated (ρ = 0.0) and Phase 2 observations are highly correlated (ρ = 0.9)

Full size image

This limitation of the forward DeCon procedure can be resolved by also performing a “backward search,” which boils down to reversing the time order (last time point of the sequence becomes the first one, etc.) and conducting steps 1 and 2 on this reversed sequence. Indeed, in the backward search, the increase in correlation becomes a drop in correlation, since the time points in Phase 2 constitute the standard against which observations in Phase 1 will be compared. Therefore, new observations are identified as outliers, and the change point can be detected. For the illustrative example, the change point was detected at T = 25. However, one should be aware that we are now working in the backward sense, implying that the detected change point actually is the last observation of a phase, rather than the first one of a new phase. Thus, to transform the backward estimate of the change point locations to the correct time order, we should add one to it. Thus, we obtain T = 26, which is indeed the correct change point.

  1. 4.

    Combine change points detected in the forward and the backward procedure.

Finally, the change points detected in the forward and backward procedure are pooled together. Of course, it will often happen that the forward and backward search will detect the same phase change, but yield slightly different estimates of the change point. In the simulations, change point estimates that are within a 10-time point distance will be pooled by computing their means. However, this maximum between distance for pooled change points may be adjusted by the user to a higher number when one deals with a much longer time series. Moreover, when the mean does not correspond to an exact time point in the series, we round the estimate to the next time point.

E-divisive

E-divisive detects change points by quantifying how different the characteristic functions of the distributions of subsequent segments of the time series are (Matteson & James, 2014). Indeed, given that characteristic functions uniquely describe a probability distribution (Gnedenko, 2005), changes in the characteristic function signal distributional change (Matteson & James, 2014). E-divisive performs the following segmentation steps.

  1. 1.

    Segment the time series into two phases for which the characteristic functions maximally differ.

To segment the time series into two phases for which the characteristic functions maximally differ, based on derivations from Szekely and Rizzo (2005), the following divergence measure of phases, X 1 : τ and X τ + 1 : n , is computed for different τ-values:

$$ \widehat{Q}\left(\tau \right)=\frac{\tau \left(n-\tau \right)}{n}\left[\frac{2}{\tau \left(n-\tau \right)}{\displaystyle \sum_{i=1}^{\tau }{\displaystyle \sum_{j=\tau +1}^n\parallel {X}_i-{X}_j\parallel }}-{\left(\begin{array}{c}\tau \\ {}2\end{array}\right)}^{-1}{\displaystyle \sum_{i=1}^{\tau -1}{\displaystyle \sum_{k=i+1}^{\tau}\parallel {X}_i-{X}_k\parallel }}-{\left(\begin{array}{c}n-\tau \\ {}2\end{array}\right)}^{-1}{\displaystyle \sum_{j=\tau +1}^{n-1}{\displaystyle \sum_{k=j+1}^n\parallel {X}_j-{X}_k\parallel }}\right], $$
(2)

where ‖ ⋅ ‖ denotes the Euclidean distance.Footnote 3 The left-most term within the square brackets expresses the average Euclidean distance of time points belonging to different phases, whereas the two right-most terms quantify the average within-phase distances, separately for Phase 1 and Phase 2. For instance, if we divide our illustrative time series into two candidate phases X 1 : 25 and X 26 : 50 by setting τ equal to 25, the corresponding divergence measure equals:

$$ \widehat{Q}\left(\tau \right)=\frac{25(25)}{50}\left[\mathrm{Dist}.\;\mathrm{Between}\kern0.3em {\boldsymbol{X}}_{1:25},{\boldsymbol{X}}_{26:50}-\mathrm{Dist}.\;\mathrm{Within}\kern0.3em {\boldsymbol{X}}_{1:25}-\mathrm{Dist}.\;\mathrm{Within}\kern0.3em {\boldsymbol{X}}_{26:50}\right]=136.42 $$

Indeed,

$$ \begin{array}{l}\mathrm{Dist}\kern0.3em .\kern0.3em \mathrm{Between}\kern0.3em {\boldsymbol{X}}_{1:25},{\boldsymbol{X}}_{26:50}=\frac{2}{25(25)}{\displaystyle \sum_{i=1}^{25}{\displaystyle \sum_{j=26}^{50}\left\Vert {X}_i-{X}_j\right\Vert }}\hfill \\ {}\kern16em =\frac{2}{25(25)}\left\{\sqrt{{\left(2.35-1.08\right)}^2+{\left(1.98-4.37\right)}^2+{\left(3.77-7.36\right)}^2}\right.\hfill \\ {}\kern16em +\sqrt{{\left(2.35-4.50\right)}^2+{\left(1.98-7.61\right)}^2+{\left(3.77-10.44\right)}^2}+\dots \hfill \\ {}\kern16em \left.+\sqrt{{\left(2.27-3.77\right)}^2+{\left(2.10-6.72\right)}^2+{\left(3.36-9.67\right)}^2}\right\}\hfill \\ {}\kern10.24em =15.28\hfill \end{array} $$
$$ \begin{array}{l}\mathrm{Dist}\kern0.3em .\mathrm{Within}\kern0.3em {\boldsymbol{X}}_{1:25}={\left(\begin{array}{c}\hfill 25\hfill \\ {}\hfill 2\hfill \end{array}\right)}^{-1}{\displaystyle \sum_{i=1}^{24}{\displaystyle \sum_{k=i+1}^{25}\left\Vert {\boldsymbol{X}}_i-{\boldsymbol{X}}_k\right\Vert }}\hfill \\ {}\kern3em ={\left(\begin{array}{c}\hfill 25\hfill \\ {}\hfill 2\hfill \end{array}\right)}^{-1}\left\{\sqrt{{\left(2.35-2.04\right)}^2+{\left(1.98-2.82\right)}^2+{\left(3.77-3.62\right)}^2}\right.\hfill \\ {}\kern3em +\sqrt{{\left(2.35-2.52\right)}^2+{\left(1.98-2.07\right)}^2+{\left(3.77-4.29\right)}^2+\dots}\hfill \\ {}\kern3.2em \left.+\sqrt{{\left(1.19-2.27\right)}^2+{\left(1.72-2.10\right)}^2+{\left(3.86-3.36\right)}^2}\right\}\hfill \\ {}\kern3em =1.90\hfill \end{array} $$
$$ \begin{array}{l}\mathrm{Dist}.\mathrm{Within}\kern0.3em {\boldsymbol{X}}_{26:50}={\left(\begin{array}{c}\hfill 25\hfill \\ {}\hfill 2\hfill \end{array}\right)}^{-1}{\displaystyle \sum_{j=26}^{49}{\displaystyle \sum_{k=j+1}^{50}\left\Vert {\boldsymbol{X}}_j-{\boldsymbol{X}}_k\right\Vert }}\hfill \\ {}\kern3em ={\left(\begin{array}{c}\hfill 25\hfill \\ {}\hfill 2\hfill \end{array}\right)}^{-1}\left\{\sqrt{{\left(1.08-4.50\right)}^2+{\left(4.37-7.61\right)}^2+{\left(7.36-10.44\right)}^2}\right.\hfill \\ {}\kern3em +\sqrt{{\left(1.08-2.01\right)}^2+{\left(4.37-5.26\right)}^2+{\left(7.36-7.88\right)}^2+\dots}\hfill \\ {}\kern3.2em \left.+\sqrt{{\left(2.37-3.77\right)}^2+{\left(6.19-6.72\right)}^2+{\left(9.41-9.67\right)}^2}\right\}\hfill \\ {}\kern3em =2.46\hfill \end{array} $$

The optimal estimate of the change point location can be derived by inspecting which τ-value maximizes \( \widehat{Q}. \) For our illustrative time series, Fig. 4 (first panel) shows the \( \widehat{Q} \)-values that are obtained when τ is varied from 1 to 50. As expected, \( \widehat{Q} \) is maximal for τ = 25, implying that the distribution changes after T = 25, generating a change point estimate at T = 26.

Fig. 4
figure 4

Optimization of the E-divisive, Multirank, and KCP segmentation statistics over all possible change point locations, τ ∈ 1 : n, for the hypothetical data. The first panel shows the maximization of the divergence measure, \( \widehat{Q} \), for E-divisive. The second panel displays the maximization of the homogeneity statistic, \( \widehat{T} \), for Multirank. The last panel exhibits the minimization of the variance-like criterion, \( \widehat{R} \), for KCP. For all three methods, the statistics were optimal when τ = 25, implying that a change point occurred at T = 26

Full size image
  1. 2.

    Determine if the change point is significant through a permutation test.

After estimating the change point location, its significance is tested by means of a permutation test on the maximal \( \widehat{Q} \)-value. This test is conducted by generating R permuted time series that are obtained by randomly changing the time order of the sequence. Step 1 is applied to each of these permuted sequences, yielding R new maximal \( \widehat{Q} \)-values. The p-value of the permutation test equals the percentage of permuted sequences that generated a larger maximal \( \widehat{Q} \)-value than the one obtained for the original sequence. For the illustrative data, the p-value for the maximal \( \widehat{Q} \) is 0.002, implying that the change point, T = 26, is considered significant (at a pre-specified significance level of 0.05).

  1. 3.

    Divide the sequence into separate phases according to the detected change point and look for further change points in each of them.

If the change point corresponding to the maximal \( \widehat{Q} \)-value obtained in Step 1 is found significant in Step 2, the sequence is divided into the corresponding phases. Steps 1 to 3 are then applied within each phase to detect additional change points, yielding a change point detection process that is hierarchically structured. Applying the procedure to the hypothetical data, the time series is split into two phases after the first change point was found significant in Step 2. The first phase, X 1 : 25, was further bisected, and the optimal change point estimate was T = 11. For the second phase, X 26 : 50, the optimal change point location was T = 41. The p-values were 0.668 and 0.268, respectively, for the first and second phases, implying non-significance of these additional change points. The phases were not further bisected and it was concluded that the time series contains one change point only.

Multirank

Multirank makes use of a homogeneity statistic, which is a multivariate extension of the Kruskal-Wallis test statistic (Lung-Yut-Fong, Lévy-Leduc, & Cappé, 2012). Hence, Multirank only takes the rank order of the scores per variable into account. The method consists of two steps.

  1. 1.

    Check whether the time series contains at least one significant change point.

Considering all possible τ-values, the sequence is divided into two phases X 1 : τ and X τ + 1 : n . For each τ-value, the dissimilarity of these phases is determined by computing the following homogeneity statistic

$$ \widehat{T}\left(\tau \right)=\frac{4}{n^2}\left[\left(\tau \right){\overline{\boldsymbol{R}}}_1^{\prime }{\widehat{\boldsymbol{\Sigma}}}^{-1}{\overline{\boldsymbol{R}}}_1+\left(n-\tau \right){\overline{\boldsymbol{R}}}_2^{\prime }{\widehat{\boldsymbol{\Sigma}}}^{-1}{\overline{\boldsymbol{R}}}_2\right] $$
(3)

where \( \widehat{\boldsymbol{\Sigma}} \) is the empirical covariance matrix of the rank orders of the scores, and \( {\overline{\boldsymbol{R}}}_k \) is a phase specific vector containing deviations of the observed mean phase ranks from the expected mean phase rank if the whole sequence is homogeneous. In case of homogeneity, the rank order of a score is completely random and, thus, the expected mean rank within a phase equals \( \frac{n+1}{2} \). However, if a change point segments the sequence into phases with different distributions, the rank orders would not be random anymore but dependent on the distributions. Consequently, the deviations of the mean phase ranks from the expected rank under homogeneity, and thus also \( \widehat{T}, \) would be large. Hence, to decide whether the time series contains at least one change point, the significance of the highest \( \widehat{T} \)–value is tested by computing the associated asymptotic p-value under the assumption of homogeneity. Details on this computation, which is based on Bessel functions of the first kind and the gamma function, can be found in Lung-Yut-Fong et al. (2012).

Figure 4 (second panel) displays the \( \widehat{T} \)-values that were obtained for our illustrative example using different τ-values, and indicates that τ = 25 yields the highest \( \widehat{T} \)-value. This implies a possible change point at the 26th observation. Specifically, the maximal homogeneity statistic equals 40.27, since

$$ {\overline{\boldsymbol{R}}}_1=\left[\begin{array}{c}\hfill \frac{R_1^{(1)}+{R}_2^{(1)}+{R}_3^{(1)}+\dots +{R}_{25}^{(1)}}{25}-\frac{n+1}{2}\hfill \\ {}\hfill \frac{R_1^{(2)}+{R}_2^{(2)}+{R}_3^{(2)}+\dots +{R}_{25}^{(2)}}{25} - \frac{n+1}{2}\hfill \\ {}\hfill \frac{R_1^{(3)}+{R}_2^{(3)}+{R}_3^{(3)}+\dots +{R}_{25}^{(3)}}{25} - \frac{n+1}{2}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \frac{31+26+33+\dots +30}{25}-25.5\hfill \\ {}\hfill \frac{14+22+15+\dots +16}{25}-25.5\hfill \\ {}\hfill \frac{19+16+24+\dots +15}{25}-25.5\hfill \end{array}\right]=\left[\begin{array}{c}\hfill -9.22\hfill \\ {}\hfill -12.30\hfill \\ {}\hfill -12.50\hfill \end{array}\right], $$
$$ {\overline{\boldsymbol{R}}}_2=\left[\begin{array}{c}\hfill \frac{R_{26}^{(1)}+{R}_{27}^{(1)}+{R}_{28}^{(1)}+\dots +{R}_{50}^{(1)}}{25} - \frac{n+1}{2}\hfill \\ {}\hfill \frac{R_{26}^{(2)}+{R}_{27}^{(2)}+{R}_{28}^{(2)}+\dots +{R}_{50}^{(2)}}{25} - \frac{n+1}{2}\hfill \\ {}\hfill \frac{R_{26}^{(3)}+{R}_{27}^{(3)}+{R}_{28}^{(3)}+\dots +{R}_{50}^{(3)}}{25} - \frac{n+1}{2}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \frac{12+49+25+\dots +50}{25}-25.5\hfill \\ {}\hfill \frac{29+49+31+\dots +40}{25}-25.5\hfill \\ {}\hfill \frac{29+48+31+\dots +41}{25}-25.5\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 9.22\hfill \\ {}\hfill 12.30\hfill \\ {}\hfill 12.50\hfill \end{array}\right] $$

and

$$ {\widehat{\varSigma}}^{-1}=\left[\begin{array}{ccc}\hfill 8.48\hfill & \hfill -0.83\hfill & \hfill -6.09\hfill \\ {}\hfill -0.83\hfill & \hfill 11.75\hfill & \hfill -9.45\hfill \\ {}\hfill -6.09\hfill & \hfill -9.45\hfill & \hfill 16.03\hfill \end{array}\right]. $$

In Step 1, \( {\overline{\boldsymbol{R}}}_2 \) is always equal to \( -{\overline{\boldsymbol{R}}}_1 \), since we are looking for one change point. When considering multiple change points, this property will of course not hold. The associated p-value for the maximal \( \widehat{T} \) is 1.38 × 10− 7, confirming that the change point, T = 26, is highly significant. Henceforward, we will denote the maximal \( \widehat{T} \) as \( {\widehat{T}}_{max} \).

  1. 2.

    Decide on the number of change points and on their location.

If the change point obtained in Step 1 is found to be significant, multiple change point detection is conducted by computing the generalized form of the homogeneity statistic in Eq. 3, where K denotes the number of change points, τ 0 = 0 and τ K + 1 = n:

$$ \widehat{T}\left({\tau}_1,{\tau}_2,\dots {\tau}_K\right)=\frac{4}{n^2}{\displaystyle \sum_{k=0}^K\left({\tau}_{k+1}-{\tau}_k\right){\overline{\boldsymbol{R}}}_k^{\prime }{\widehat{\boldsymbol{\Sigma}}}^{-1}{\overline{\boldsymbol{R}}}_k} $$
(4)

To determine the number of change points and their location, K is varied from 0 to K max. For each K-value, the phase boundaries, τ 1, τ 2, …, τ K , in Eq. 4 are varied and the homogeneity statistic, \( \widehat{T} \), for the resulting phases is computed. The change point locations that generate the maximal homogeneity statistic, \( {\widehat{T}}_{max} \) , are stored (see Table 1). Next, the \( {\widehat{T}}_{max} \) values are plotted against the number of change points K (see Fig. 5, left panel). To choose the optimal K, two linear regressions are performed for each K -one starting from 0 up to K and one on the points from K onwards. The total residual sum of squares of both regressionsFootnote 4 is then computed. The K-value associated with the lowest sum is retained as the optimal estimate of the number of change points. Based on Table 1, the K-value with the lowest total residual sum of squares is K = 1, revealing that our hypothetical data contain only one change point, located at T = 26. This is easily spotted as well in Fig. 5 (left panel), where K = 1 generated the best before and after regression fit as shown by the black lines.

Table 1 Maximal Multirank homogeneity statistic, \( {\widehat{\mathrm{T}}}_{\max } \), total residual sum of squares of the before and after K regressions and estimated change point locations for the hypothetical data
Full size table
Fig. 5
figure 5

MultiRank and KCP heuristic procedures for choosing the number of change points, K, for the hypothetical data. The left panel shows the \( {\widehat{T}}_{max} \) vs. K plot for Multirank, where the best before and after regression fit is generated when K is set to 1. The right panel displays the tuning of the penalty coefficient, C, for KCP, which generated K = 1 as the most stable K

Full size image

KCP

The Kernel Change Point (KCP) method proposed by Arlot et al. (2012) detects change points by evaluating how similar or dissimilar the scores at the observed time points are to each other. To this end, the observations are transformed to similarities by means of a kernel function (Shawe-Taylor & Christianini, 2004). In this paper, like Arlot et al. (2012), we used the Gaussian kernel, which is the most widely applied kernel in the literature (Sriperumbudur, Gretton, Fukumizu, Lanckriet, & Scholkopf, 2010).

  1. 1.

    Compute pairwise similarities using a Gaussian kernel function.

For each pair of observations, X i and X j , the pairwise similarity is computed using a Gaussian kernel function,

$$ k\left({\boldsymbol{X}}_i,\ {\boldsymbol{X}}_j\right)= \exp \left(\frac{-{\left\Vert {\boldsymbol{X}}_i-{\boldsymbol{X}}_j\right\Vert}^2}{2{h}^2}\right) $$

The similarities take on values close to 0 when X i and X j are distant and values close to 1 when X i and X j are similar. The bandwidth, h, is a smoothing parameter that indicates how strict one is when deciding if two observations are similar (see examples of usage in Hastie, Tibshirani, & Friedman, 2009). In this paper, we determined the bandwidth using the procedure of Arlot et al. (2012) which sampled 250 observations X i from the whole time series and set h to the median Euclidean distance among those 250 observations.

  1. 2.

    For different numbers of change points K, minimize the total intra-phase scatter to detect their location.

For varying numbers of change points, K = 0, …, K max , KCP minimizes the following criterion across all possible change point locations (τ 1, τ 2, …, τ K ):

$$ \widehat{R}\left({\tau}_1,{\tau}_2,\dots, {\tau}_K\right)=\frac{1}{n}{\displaystyle \sum_{k=0}^K{\widehat{V}}_k} $$

where \( {\widehat{V}}_k \) is the intra-phase scatter. \( {\widehat{V}}_k \) measures how homogeneous the corresponding phase is,

$$ {\widehat{V}}_k=\left({\tau}_k-{\tau}_{k-1}\right)-\frac{1}{\tau_k-{\tau}_{k-1}}{\displaystyle \sum_{i={\tau}_{k-1}+1}^{\tau_k}{\displaystyle \sum_{j={\tau}_{k-1}+1}^{\tau_k}k\left({\boldsymbol{X}}_i,{\boldsymbol{X}}_j\right)}} $$

Indeed, the more similar the observations in a segment, \( {\boldsymbol{X}}_{\tau_{k-1}+1} \): \( {\boldsymbol{X}}_{\tau_k} \), are, the larger the sum that is subtracted by the rightmost term of \( {\widehat{V}}_k \) and thus the smaller the intra-phase scatter. Moreover, the smaller are the \( {\widehat{V}}_k \)’s for all k, the smaller the criterion, \( \widehat{R} \), will be. For example, Fig. 4 (third panel) which shows the \( \widehat{R} \)-values obtained when looking for the optimal location of a single change point (τ = τ 1) in our illustrative time series, reveals that \( \widehat{R} \) is minimal for τ = 25, creating segments, X 1 : 25 and X 26 : 50 . Specifically, the intra-phase scatters for these two phases are

$$ {\widehat{V}}_1=25-\frac{1}{25}{\displaystyle \sum_{i=1}^{25}{\displaystyle \sum_{j=1}^{25}k\left({\boldsymbol{X}}_i,{\boldsymbol{X}}_j\right)}}=4.55 $$
$$ {\widehat{V}}_2=25-\frac{1}{25}{\displaystyle \sum_{i=26}^{50}{\displaystyle \sum_{j=26}^{50}k\left({\boldsymbol{X}}_i,{\boldsymbol{X}}_j\right)}}=7.00, $$

generating the minimal criterion value, \( \widehat{R}\left(\tau =25\right)=\frac{{\widehat{V}}_1+{\widehat{V}}_2}{n}=\frac{11.55}{50}=0.23 \). Henceforward, this minimal KCP criterion generated from the optimal change point locations will be denoted as \( {\widehat{R}}_{min} \). Applying the method for K = 0 to K max  = 5, yields the change points listed in Table 2.

Table 2 Minimal KCP criterion, \( {\widehat{\mathrm{R}}}_{\min }, \) and change point locations for different values of K for the hypothetical data
Full size table
  1. 3.

    Decide on the optimal number of change points.

After Step 2, what remains to be determined is the most appropriate number of change points, K. Since the \( {\widehat{R}}_{min} \)-values decrease with increasing K, Arlot et al. (2012) proposed to penalize the \( {\widehat{R}}_{min} \)-values for the additional complexity that is introduced by allowing for extra change points. Specifically, they select the number of change points which minimizes

$$ cri{t}_K={\widehat{R}}_{min}+pe{n}_K, $$
(5)

where \( pe{n}_K=C\frac{V_{max}\ \left(K+1\right)}{n}\left[1+ \log \left(\frac{n}{K+1}\right)\right] \). The constant, C, is a tuning parameter that controls the influence of the penalty term (see below). The remaining constant, v max , is determined by computing the trace of the estimated covariance matrix for the first 5 % time points as well as for the last 5 % time points, and choosing whichever is larger.

As can be expected, the value chosen for C, greatly influences the performance of the method, where a smaller C favors numerous change points, while a larger C causes undersegmentation. Whereas in previous simulations (Matteson & James, 2014) this tuning issue was dealt with by just setting a particular C value, without further motivation, we propose selecting C by plugging linearly increasing values starting from C = 1 into Eq. 5. When C = 1, the generated estimate for K is K max . If C is increased, the effect of the penalty term is strengthened and the generated estimate for K becomes smaller. Thus, the procedure terminates when C becomes so high that the associated estimate for K equals 0. Based on the theoretical motivations in Lavielle (2005), the K-value that is selected most often in this grid search is retained as the optimal number of change points. Figure 5 (right panel) shows the K-values that are selected across different C-values between 1 and 151.9 for our illustrative example. Since the mode of the selected K-values equals 1, as could be expected, we decided that the time series contains one change point. Note that in case only K max and 0 are selected in the grid search, it should be concluded that the time series contains no change points (see details in Lebarbier, 2005).

Software

For DeCon and for the tuning steps of the other methods, Matlab codes are available upon request from the first author of this paper. E-divisive can be applied using the ecp package in R. Multirank was programmed in Python, and the codes can be requested from the second author of the corresponding paper (Lung-Yut-Fong et al., 2012). For KCP, R codes are included in the supplementary files provided by Matteson and James (2014). The hypothetical data used for illustrating the methods was simulated with the “mvtnorm” R-package and can be obtained from the first author as well.

Simulation studies

Two simulation studies will be performed to compare the four methods, i.e., DeCon, E-divisive, Multirank and KCP, using the settings of Bulteel et al. (2014) and Matteson and James (2014). Neither of those earlier studies compared all four methods examined in this paper.

Simulation settings of Bulteel et al. (2014): Mean changes, correlation changes or both

The first simulation study is conducted to compare the performance of DeCon, E-divisive, MultiRank and KCP in detecting changes in mean, changes in correlation, or both. In particular, we used the simulation settings of Bulteel et al. (2014) to generate time series of 300 time points with 5 variables. Each time series consisted of two phases containing 150 time points each. The time series varied with respect to the following three factors, which were fully crossed with 1,000 replicates per cell of the design:

  1. 1.

    Change in mean between the two phases (three levels): There could be no change, an increase of 1 standard deviation for 3 variables, or an increase of 2 standard deviations for three variables (in the latter two levels, the mean of the other two variables remains the same).

  2. 2.

    Change in correlation structure between the two phases (two levels): The correlation structure of the variables is manipulated by generating true scores according to a principal component model. For settings with no correlation change, a 300×5 matrix was generated according to a model with 3 components. For settings with correlation change, two 150×5 matrices were generated, where the first one is based on three components and the second one on two components. The loadings on these components were sampled from a uniform distribution on the interval (-1,1). The component scores, on the other hand, were drawn from a standard normal distribution. Note that the loadings and the error values were rescaled to obtain data that contain 25 % noise.

  3. 3.

    Strength of autocorrelation within the phases (three levels): 0, .3 and .7.

    Each simulated time series was constructed by adding true scores and noise. The noise was sampled from a multivariate normal distribution having a zero vector as its mean vector and the identity matrix as its covariance matrix. Next, we imposed a lag-one autocorrelation on these noise scores by means of a recursive filter (Hamilton, 1994).

All four methods under study were then applied to these simulated data sets. The tuning parameters for each method are tabulated in Table 3. For E-divisive, default settings by Matteson and James (2014) were maintained imposing a maximum of ten phases and a minimum phase size of 30. Equivalently, for Multirank and KCP, K max Footnote 5 was set to 9. For DeCon, on the other hand, a window size of 75 was chosen to impose a minimum phase sizeFootnote 6 of .25WS ≈ 19.

Table 3 Tuning parameters for the four change point detection methods: first simulation study based on simulation settings of Bulteel et al. (2014)
Full size table

To quantify how well the four methods revealed the underlying phases, we computed the Rand Index (RI) between the recovered phases and the true phases. An RI value of 1 implies perfect recovery of the underlying phases, while 0 implies that recovered and underlying phases do not resemble one another (Rand, 1971). We also recorded the detected number of change points.

Results show that KCP outperforms the three other methods, exhibiting the highest RIs in almost all settings (Table 4). It also proved to be the most robust to the presence of autocorrelation, which leads to false detections for the other methods. All methods succeeded in detecting changes in mean, though DeCon performed worse for settings with a small mean change (1 standard deviation). Furthermore, change in correlation (without change in mean) proved to be harder to detect. Though KCP (RI≥ 0.94) and DeCon (RI≥0.87) still showed acceptable detection performance in these settings, performance of Multirank (RI≤0.61) and E-divisive (RI≤ 0.80) was inadequate. The RI-values for Multirank were close to 0.50, because the method either did not detect the change point and concludes that the time series contains only a single phase (no or weak autocorrelation) or yields too many change points (strong autocorrelation), rather than the correct two phases. Finally, for settings where both changes in mean and in correlation were introduced, all methods retrieved the change point in most cases. Note that a repeated measures ANOVA with method as within subjects factor and size of mean change, size of correlation change, and size of autocorrelation as between subjects factors, revealed that two effects had a generalized effect size (η 2 G ) larger than .13, indicating a medium effect size (Bakeman, 2005): size of mean change (η 2 G =.27) and its interaction with the method used (η 2 G =.18).

Table 4 Mean Rand indices and number of detected change points: first simulation study based on simulation settings of Bulteel et al. (2014) with one real change point
Full size table

Simulation settings of Matteson and James (2014): Correlation change and presence of noise variables

The first simulation study already showed that changes in correlation structure are more difficult to detect. To get further insight into the performance of the four methods in revealing correlation change, we ran a second studyFootnote 7 based on the simulation settings of Matteson and James (2014). An interesting feature of these settings is that they allow to investigate how performance is affected by the presence of noise variables. Noise variables are variables that do not change in means and correlations. Specifically, Matteson and James (2014) generated normally distributed time series that consist of three phases of equal length. In the first phase, the variables are uncorrelated. In the middle phase, they become strongly correlated, such that their pairwise correlations amount to 0.9. And in the final phase, the variables are uncorrelated again. Three factors were manipulated, with 1,000 replicates per possible combination:

  1. 1.

    Number of variables D (three levels): 2, 5, and 9.

  2. 2.

    Number of time points n (three levels): 300, 600, and 900.

  3. 3.

    Number of noise variables (two levels): 0 (i.e., all variables correlate in the middle phase) and number of variables minus two (only two variables become correlated in the middle phase).

When no noise variables are present, KCP is the best method in all conditions but one (two variables, 300 time points), with RI values larger than 0.97 (see Table 5). Multirank, on the other hand, consistently failed, being the worst method. Its RI values were close to 0.33, because no change points are detected, thus generating 1 phase only, instead of the three underlying phases. A repeated measures ANOVA, with method as within subjects factor and number of variables and number of time points as between subjects factors, revealed that RI was indeed clearly influenced by method (η 2 G =.87), as well as by its two-way interaction with number of variables (η 2 G =.34) and three-way interaction with number of variables and number of time points (η 2 G =.15); the main effect of number of variables (η 2 G =.29) was strong as well.

Table 5 Mean Rand indices and number of detected change points: second simulation study based on simulation settings of Matteson and James (2014) with two real change points
Full size table

When noise variables were present, DeCon was the clear winner, with RIs being consistently larger than 0.81. Moreover, its RI performance was not extremely affected by the number of noise variables or the number of time points, although both factors have an impact on the number of detected change points. All the other methods yielded inadequate RI values in all with noise settings and thus are severely affected by the presence of noise variables. In almost all settings (except for KCP on five variables and 900 time points), their RI values were close to 0.33, because no change point was detected for most data sets. Not surprisingly, the repeated measures ANOVA revealed that the main effect of method (η 2 G =.72) explained the bulk of the differences in the RIs for settings with noise.

In summary, the following conclusions can be drawn. First, KCP and Multirank seem to be reliable methods for detecting mean changes, whereas E-divisive and DeCon often yield false change points. Second, KCP and DeCon are the best methods for detecting correlation change, although KCP often fails if noise variables are present. DeCon is too sensitive however and frequently yields false positives. Thus, change points that are only found by DeCon should be approached cautiously: They can signal real correlation changes as well as false positives.

Illustrative application

Change point detection

We further assessed the performance of the methods by applying them to multivariate time series data obtained from a study on cardiorespiratory assessment of mental load in the field of aviation (Grassmann, Vlemincx, von Leupoldt, & Van den Bergh, in press). Male pilot applicants were subjected to four experimental periods: a resting baseline, a “vanilla” baseline, a highly demanding multiple task and a recovery period. During the resting baseline, participants were instructed to fix their eyes on a cross that was presented on the screen. In the vanilla baseline, they were asked to complete a minimally demanding vigilance task which was intended to reduce anticipatory arousal, hence improving the validity of baseline measures (see Jennings, Kamarck, Stewart, Eddy, & Johnson, 1992). In the multiple task period, participants had to perform three tasks simultaneously, tapping perceptual speed, spatial orientation and working memory (for a detailed description see Grassmann et al., in press). Finally, during the recovery period, participants watched a relaxing underwater movie. Each period lasted for 6 min, however the first and last 30 s were cut before data processing to procure stationary data, and to exclude artifacts that were occasionally caused by speech and movement during the periods of transition. Heart rate, respiration rate and partial pressure of end-tidal CO2 (petCO2) were monitored throughout the experiment.

Based on previous findings, the means of all three physiological variables were expected to change across the phases (e.g., Backs & Seljos, 1994; Brookings, Wilson, & Swain, 1996; Veltman & Gaillard, 1998; Wientjes, Grossman, & Gaillard, 1998). Heart rate, for instance, was hypothesized to decrease during the vanilla baseline and to increase during the multiple task while readjustments were expected for the recovery period (Jennings et al., 1992). Regarding correlation changes, we expect an increase in the correlation of cardiorespiratory variables in the vanilla baseline, as it requires focused attention and low cognitive activity (Wu & Lo, 2010). During the multiple task, where tasks are more highly demanding, a decrease in correlation could occur (Zhang, Yu, & Xie, 2010).

The study included 115 pilot applicants; however, for this paper, we analyzed data from a single randomly chosen pilot. The variables were initially measured in different frequencies. Cardiac data (sampled at 1,000 Hz) were processed beat-by-beat whereas respiratory data (sampled at 20 Hz) were processed breath-by-breath. For the present analyses, common time points were re-aligned by up-sampling the respiratory data (i.e., respiration rate and petCO2 values of one breath were assigned to each heart rate value that was initiated within the corresponding respiratory cycle). It is also important to note that variables were all scaled to have a variance of 1 as three methods, E-divisive, DeCon, and KCP, calculate distance measures which are influenced by the scale of the data. Where possible, methods were initialized in such a way that at maximum 20 phasesFootnote 8 would be discerned.

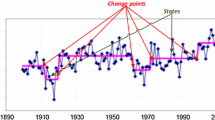
The change point detection results are displayed in Fig. 6. Employing DeCon, five change points were detected by the forward search (411, 568, 672, 889, 1,064), and three by the backward search (681, 901, 1,055). Given that the change point estimates from the backward search were considerably close to the last three change point estimates from the forward search, and given that the time series is quite long, we pooled these change points by computing their means. Thus, the final set of change points generated by DeCon is (411, 568, 676, 895, 1,060).

Fig. 6
figure 6

Change point selection output of the four methods for the cardio-respiratory data. The topmost panel displays the DeCon moving outlier sum from the forward and the backward procedure, implying five change points. The next panel exhibits the hierarchical change point detection process by E-divisive, generating ten change points. The lowest left panel shows the \( {\widehat{T}}_{max} \) vs K plot for Multirank, indicating two change points. The lowest right panel demonstrates the linear tuning of the penalty coefficient for KCP, suggesting using two change points

Full size image

E-divisive yields ten change points: 103, 191, 327, 418, 564, 674, 904, 1,054, 1,190, and 1,268, five of which are very close to the ones detected by DeCon. We initially attributed the five additional change points to Type 1 errors as E-divisive does not correct for multiple testing. However, changing the significance level did not dramatically change the results (nine change points for significance level = .01). Multirank and KCP both suggest that two change points might be present. Their change point estimates, 674 and 1,054 are identical, and were also obtained with DeCon and E-divisive. Examining Fig. 7, these two time points correspond to the boundaries of the Multiple task, confirming that the cardio respiratory measures from this specific pilot exhibited changes at the moment the highly demanding task was introduced as well as when the recovery period started. Given that in the simulations KCP and Multirank were reliable in detecting change points signaling changes in mean, whereas KCP and DeCon succeed rather well in revealing correlation change, we may say that the two common change points probably indicate changes in mean as well as changes in correlation.

Fig. 7
figure 7

Cardio-respiratory data and change points detected by the four methods. The experimental phases: resting baseline, vanilla baseline, multiple task, and recovery are indicated by the varying background shading

Full size image

Auxiliary analyses

To verify that both mean and correlation changed during the Multiple task (as hypothesized above on the basis of the simulation results), and to determine which variables specifically exhibited these changes, we conducted some auxiliary analyses. Focusing on mean changes, Mann-Whitney U tests revealed that the mean of all variables increased during the multiple task, and decreased again in the recovery period (see Fig. 8).

Fig. 8
figure 8

Mean changes for the two change points, indicated by the vertical lines, that were detected by all four methods. Levels of cardio-respiratory variables increased in the second phase, then decreased again

Full size image

In order to check for correlation changes during the multiple task, we utilized the test for the difference of two correlations based on the Fisher’s z-transformation of the sample correlation coefficients (Cohen, Cohen, West, & Aiken, 2003). On one hand, we concluded that heart rate and respiration rate became more negatively correlated during the multiple task, and correlated less during the recovery period. For petCO2, no significant correlation changes were found during the transition to the multiple task. However, during the transition to recovery, petCO2 significantly changed correlation with heart rate (negatively) and with respiration rate (positively).

Discussion and Conclusion

Change point detection in multivariate time series data presents a major data-analytical challenge because the variables involved can exhibit changes in means, in correlation, or in both (Terien et al., 2009). Detecting changes in correlation is crucial when one wants to understand the behavior of the system that is comprised of these variables. In this study, we compared the performance of four recently proposed non-parametric multivariate change point detection methods, focusing on changes in correlation.

In the first simulation study, Multirank and KCP, and to a somewhat lesser extent E-divisive, succeeded well in detecting mean changes. These results confirmed previous findings of Matteson and James (2014) regarding mean changes. DeCon, on the other hand, could only compete with these methods for large mean changes (Δ mean ≥ 2sd). Change in correlation without mean changes, proved to be harder to capture. For this specific setting, KCP and DeCon clearly outperformed E-divisive and Multirank. E-divisive missed to detect the change points in a considerable number of replicates, while Multirank failed in almost all cases. The second simulation study revealed that when the correlation change to be detected is sizeable (no noise settings), KCP performs the best. These results are somewhat different from those reported by Matteson and James (2014) which suggested that KCP performs poorly compared to E-divisive and Multirank for a relatively small sample size (n = 300). These differences are attributed to the additional tuning step of the penalty coefficient, C, that we implemented for KCP. In contrast, our Multirank results are worse than those of Matteson and James (2014), because we included the significance test for a single change point, which was proposed by the original authors but not implemented by Matteson and James (2014), leading to false positives. It is important to note that DeCon was clearly the best method in detecting changes in correlation for settings with only two variables, as well as settings in which the majority of the variables were noise variables (with noise settings). All other methods performed badly in these settings, failing to detect all change points.

Overall, we thus conclude that which methods perform well strongly depends on the specific data setting. Therefore, we recommend using multiple methods in order to be more sensitive to different types of changes. However, we see a major issue that needs to be tackled when applying multiple methods. For the simulation study, it was straightforward to know which methods produced correct detections and which ones generated false positives because we introduced the changes ourselves. When applying the methods to real data, such as in the application section, this is almost always not the case. The task of deciphering which change points are important then lies in the hands of the user. Based on our simulation results, we provide the following advice: For detecting mean changes, one should inspect the changes that are detected by both KCP and Multirank. For detecting correlation changes, change points yielded by both KCP and DeCon are probably trustworthy. Lastly, when numerous variables are monitored, without prior knowledge whether some of them are noise variables, change points unique to DeCon should be scrutinized as well as they may signal correlation change.

Aside from the simulation results, an overview of the similarities and differences between the four change point detection methods under study with respect to statistical method, segmentation strategy and number of change points heuristic used could help an applied researcher in deciding which method or set of methods is appropriate for the data at hand, and could yield interesting directions for future methodological research. Regarding the statistical method used, Multirank is based on a multivariate version of the Kruskal-Wallis test statistic, which looks at deviations from the overall median, thus it is mainly sensitive to changes in levels. DeCon looks at score distances computed using a robust center and covariances, thus it is expected to pick up not just changes in levels but also in correlations. E-divisive and KCP, on the other hand, are both based on Euclidean distances which can be influenced by changes in any moments of the distribution. This explains why these methods can capture both mean and correlation changes. An extra feature of the similarity measure in KCP, though, is that it uses a non-linear transformation of this distance through a Gaussian kernel, magnifying the differences. Therefore, it is not unexpected that KCP performs better than E-divisive when the change introduced in the simulations was purely correlational. Regarding segmentation strategy, KCP and Multirank optimize an overall homogeneity statistic to locate multiple change points simultaneously. E-divisive employs binary segmentation such that only one change point is estimated at a time, leaving previously found change points untouched. DeCon on the other hand does not look for the optimal location for a change point, but indicates for every time point whether or not it is likely that a change occurred (because the time point is outlying with respect to the previous ones). When deciding on the optimal number of change points, the number of change points obtained with DeCon can hardly be controlled; the method for instance cannot be used to retrieve the three most likely change points. E-divisive employs a permutation test which is embedded in the hierarchical segmentation, but this test disrupts the natural ordering of time points and is not corrected for family wise error rate. Both KCP and Multirank use a heuristic procedure which weighs both the minimization (maximization) of the distance measure and the number of change points. This weighting proved to be effective in avoiding false detections for KCP and Multirank. One could postulate that generalizing the E-divisive divergence measure to more than two groups might decrease false detections. A pruning step, in which all change points are re-examined and only the most evident ones are retained, could possibly improve the performance of DeCon.

Finally, a common limitation of all considered change point detection methods is that they neither indicate which type of change (mean/correlation/both) occurred nor which variables are involved. Regarding the type of change, the methods under study might even indicate changes in higher moments. This is the price to pay, of course, when applying non-parametric methods as the distance measures used can be caused by numerous types of changes in the joint distribution. In contrast, most parametric methods monitor specific parameters (Chen & Gupta, 2012). Thus, when a change is detected, one immediately knows which type of changes was exhibited. Regarding the variables involved, the four non-parametric methods are not able to pinpoint which channels demonstrate the changes and which ones did not. To address this limitation, one could implement auxiliary analyses as we did for the illustrative application. However, this is cumbersome, especially when there are numerous recovered phases. Future research may therefore aim to determine the type of change and the variables involved during change point detection.

In conclusion, KCP was generally the best method in detecting changes in mean, changes in correlation, or both, and can therefore be recommended. When the goal is capturing changes in mean, results can be confirmed by Multirank, as it detects this type of change with comparable reliability. When the focus is capturing changes in correlation, we recommend inspecting DeCon change points as well. Although in general, DeCon performed less reliably than KCP, the method is quite sensitive to correlation changes, especially when the multivariate time series contains multiple noise variables.