Redundant-signals effect

The redundant-signals task might be considered one of the most basic paradigms in research on cognitive architecture. In a typical redundant-signals experiment, participants receive stimuli from two different sources (hereafter, A and V, for auditory and visual stimuli, respectively; of course, the present results generalize to any combination of signals, within or across sensory modalities). The critical aspect is that the same speeded response is required for both A and V—for example, a simple manual response or a given choice. In a third condition, both stimuli are presented simultaneously (redundant signals, AV); in this condition, responses are often observed to be substantially faster than in the single-signal conditions A and V. At first glance, this redundancy gain, in itself, indicates some sort of integration of the information provided by the two signals. However, different models can account for the effect, including serial, parallel, and coactivation models of information processing (e.g., Miller, 1982; Schwarz, 1994; Townsend & Nozawa, 1997).

In the analysis of response times observed in a redundant-signals task, a general distinction is often made between separate activation and coactivation models. The information provided by the different sensory systems might be processed in separate pathways (separate-activation models; e.g., race model, serial self-terminating model), or it might be pooled into a common channel and processed as a combined entity (coactivation). The most important member of the class of separate-activation models is the so-called race model: The race model assumes that processing of a redundant AV stimulus occurs in separate channels; the overall processing time D AV is then determined by the faster of the two channels: D AV = min(D A, D V). If the processing-time distribution D A is invariant in A and AV, and D V is invariant in V and AV (context invariance; see, e.g., Luce, 1986, p. 130), the minimum rule yields, on average, faster processing of AV than of either A or V alone. The redundancy gain according to the race model has an upper limit, however. This upper limit is given by the well-known race model inequality (Miller, 1982),

$$ {F_{\text{AV}}}(t) \leqslant {F_{\text{A}}}(t) + {F_{\text{V}}}(t),\,{\text{for all}}\,t, $$
(1)

with F(t) = P{T ≤ t} denoting the probability for a response within t milliseconds, and T = D + M denoting the response time, which is usually decomposed into the processing time D and a context-invariant residual M (motor execution, finger movement etc.; see Luce, 1986, chap. 3). If Inequality (1) holds for all t, the response time distribution for AV is consistent with the race model prediction. Under the race model, the redundancy gain is maximal for F AV(t) = F A(t) + F V(t)—more precisely, F AV(t) = min[1, F A(t) + F V(t)], because the left side cannot exceed unity. This maximum is attained in some serial self-terminating models (Appx. B in Gondan, Götze & Greenlee, 2010) and in race models for which context invariance holds and the correlation of the channel-specific processing times D A, D V is maximally negative (rank correlation −1; see, e.g., Colonius, 1990; Townsend & Wenger, 2004).

Violation of Inequality (1) at any t (Fig. 1a) rules out the race model—and, more generally, the entire class of separate activation models (Miller, 1982). Since the race model inequality is based on both separate processing and context invariance, violation of the race model prediction rules out separate activation, or context invariance, or both. For example, race models with mutually facilitating channels have been shown to produce weak violations of the race model inequality (e.g., Mordkoff & Yantis, 1991; Townsend & Wenger, 2004). In most studies, however, a violation of Inequality (1) is interpreted as evidence for integrated processing of the redundant information.

Fig. 1
figure 1

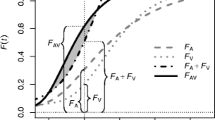
Tests of the race model. (a) The distribution function for AV is greater than the summed distributions for A and V, violating the race model inequality. The significance test is used to demonstrate that F AV(t) > F A(t) + F V(t), or, equivalently, that F AV(t) – F A(t) – F V(t) is significantly greater than zero, for some t. The direction of the significance test is illustrated by confidence-interval-like gray bars (CI). (b) Showing that the race model inequality holds: A significance test is used to demonstrate that violations are negligible—that is, significantly below the noninferiority margin (NI), F AV(t) – F A(t) – F V(t) < δ, for all t. (c) Numeric estimate for violation of the race model inequality predicted by the diffusion superposition model (Schwarz, 1994). This estimate can be used for the definition of a noninferiority margin (see the Discussion in the main text)

Full size image

The race model inequality can be generalized in a number of ways—for example, to stimuli presented with onset asynchrony (Miller, 1986), to experiments with catch trials (“kill-the-twin” correction; Eriksen, 1988; Gondan & Heckel, 2008), and to factorial manipulations within the two modalities (Theorem 1 in Townsend & Nozawa, 1995). Here, we focus on an issue related to statistical tests of Inequality (1), but the results hold for these generalizations as well.

As a motivating example, consider a prototypical scenario with two experimental conditions A and B. Theoretical considerations suggest that Inequality (1) is violated in Condition A, whereas it is expected to hold in Condition B (e.g., Feintuch & Cohen, 2002; Schröter, Frei, Ulrich, & Miller, 2009). Feintuch and Cohen presented two features of a redundant signal either in spatial correspondence (Condition A) or spatially separated (Condition B). In Condition A, the theory predicts coactivation of feature-specific response selectors, whereas in Condition B, redundancy gains were expected to be consistent with separate activation. In tests related to Condition A, the race model takes the role of the null hypothesis. Two types of tests have been developed for this situation, depending on whether Inequality (1) is tested in a single participant (Miller, 1986, pp. 336–337; Maris & Maris, 2003; Vorberg, 2008) or in a group (Gondan, 2010; Miller, 1982; Ulrich, Miller, & Schröter, 2007). We denote these tests as “standard tests” of the race model inequality. These tests demonstrate, at a controlled Type I error, that Inequality (1) is violated at some t. In contrast, for Condition B, the appropriate statistical test has to demonstrate that the observed results are consistent with Inequality (1),

$$ \begin{array}{*{20}{c}} {^{\text{coac}}{{\text{H}}_0}:{F_{\text{AV}}}(t) > {F_{\text{A}}}(t) + {F_{\text{V}}}(t),\,{\text{for some}}\;t,\,{\text{versus}}} \hfill \\ {^{\text{race}}{{\text{H}}_{{1}}}:{F_{\text{AV}}}(t) \leqslant {F_{\text{A}}}(t) + {F_{\text{V}}}(t),\,{\text{for all}}\;t.} \hfill \\ \end{array} $$
(2)

In the inequalities in (2), the race model prediction takes the role of the alternative hypothesis. It is well known that standard significance tests cannot be used to “prove” the null hypothesis. In other words, P values greater than 5% resulting from standard tests of the race model inequality (e.g., Gondan, 2010; Miller, 1986) do not demonstrate that F AV(t) ≤ F A(t) + F V(t) holds for all t.

Here, we describe a significance test that should be used when theoretical considerations predict that the race model inequality holds (i.e., Condition B). The proposed test controls the Type I error rate if the race model does not hold. In the alternative, the test is consistent—that is, the power increases with sample size when the race model holds. However, as null hypotheses with strict inequalities (2) are difficult to test within the classical null hypothesis testing framework, a so-called noninferiority margin needs to be introduced.

Noninferiority tests

Noninferiority tests are members of a more general class of equivalence tests. In applied disciplines, these tests are recommended if the study is designed to establish similarity between two groups or experimental conditions (see D’Agostino, Massaro, & Sullivan, 2003, for an overview). In psychology, only a few claims have been made in favor of equivalence tests—for example, to demonstrate that two therapeutic techniques have similar effects (e.g., Rogers, Howard, & Vessey, 1993; Seaman & Serlin, 1998; Tryon, 2001). For a noninferiority test, a margin δ > 0 is specified, which denotes a small effect in the wrong direction that one is willing to tolerate when deciding for the alternative hypothesis. The test is then used for demonstrating noninferiority; that is, the observed difference is significantly below this margin.

Freitag, Lange, and Munk (2006) proposed a nonparametric noninferiority test for comparison of two distributions: Denote the population distribution functions by G 1(t), G 2(t), with their respective sample distributions Ĝ 1(t), Ĝ 2(t). The test is used to demonstrate that G 1(t) stochastically dominates G 2(t)—that is, G 1(t) ≤ G 2(t), for all t. Restated in terms of a noninferiority test, G 1(t) < G 2(t) + δ, for all t. The vertical difference G 1(t) – G 2(t) should, thus, never reach or exceed δ,

$$ {G_{{1}}}(t)-{G_{{2}}}(t) < \delta, \,{\text{for all}}\;t. $$
(3)

An intuitive test for the above hypothesis can be constructed using point-wise one-sided confidence intervals for the difference of the sample distributions Ĝ 1(t) – Ĝ 2(t). If the upper 95% limit of this confidence interval does not include δ, for all t, violations of stochastic dominance are significantly below the noninferiority margin.

The point-wise approach is, of course, very conservative (see, e.g., Table 1 in Freitag et al., 2006). Bootstrapping can be used to improve the power of the test: If G 1(t) – G 2(t) is everywhere below δ, the maximum of this difference is below δ, as well:

$$ {\text{ma}}{{\text{x}}_t}\left[ {{G_{{1}}}(t)-{G_{{2}}}(t)} \right] < \delta . $$
Table 1 Simulated power for different sample sizes N and noninferiority margins δ
Full size table

This can be shown again statistically using a one-sided confidence interval for the maximum of the vertical distance between the two observed distributions, d max = max t [Ĝ 1(t) – Ĝ 2(t)]. The confidence interval for this maximum can be determined using so-called hybrid bootstrapping (Eq. 4 in Freitag et al., 2006). If the upper 95% limit of the confidence interval around d max is below δ, noninferiority is established over the entire range of t. Compared to the point-wise test in Inequality (3), the bootstrap distribution of d max preserves the positive correlation of consecutive values of Ĝ(t), which substantially increases statistical power (Table 1 in Freitag et al., 2006).

Application to the test of the race model inequality

In order to apply Freitag et al.’s (2006) test to data from a redundant-signals task, an appropriate noninferiority margin must be specified, say δ = 0.1. The hypotheses in (2) are then restated using the noninferiority margin:

$$ \begin{array}{*{20}{c}} {^{\text{coac}}{{\text{H}}_0}^{\delta }:{F_{\text{AV}}}(t) \geqslant {F_{\text{A}}}(t) + {F_{\text{V}}}(t) + \delta, {\text{for some}}\;t,{\text{versus}}} \hfill \\ {^{\text{race}}{{\text{H}}_{{1}}}^{\delta }:{F_{\text{AV}}}(t) < {F_{\text{A}}}(t) + {F_{\text{V}}}(t) + \delta, {\text{ for all}}\;t.} \hfill \\ \end{array} $$
(4)

In the reformulation of the problem in (4), the noninferiority margin is defined in probability units (“vertical” test; a horizontal test with the noninferiority margin defined on the milliseconds scale is outlined in Appx. A). If the violation of the race model inequality does not exceed δ, for all t, the null hypothesis in (4) is rejected (Fig. 1b).

Whereas F AV(t) never exceeds unity, the right-hand side must be transformed into a proper distribution function, F AV(t) ≤ min[1, F A(t) + F V(t)]. The shape of min[1, F A(t) + F V(t)] corresponds to the shape of the lower half of the 1 : 1 mixture of F A and F V (Maris & Maris, 2003). A one-tailed 1 – α confidence interval for the observed maximum violation of the race model inequality is then built using Freitag et al.’s (2006) algorithm. If the upper limit of the confidence interval is greater than δ, the coactivation H0 in (4) is retained—namely, that violations of the race model inequality are greater than or equal to δ. If the upper limit of the confidence interval is below δ, violations of the race model inequality are significantly below the noninferiority margin, which favors the race model H1 (Fig. 1b). The noninferiority test then demonstrates that for a given participant, the observed distribution on the left-hand side of the race model inequality does not substantially exceed the summed distributions of the right-hand side. For this decision, the Type I error is controlled.

Type I error and power

Assuming a specific distribution for the response times in conditions A and V, and assuming that the race model holds, simulations can be used to generate samples of a specific size. For a given noninferiority margin, it is then possible to estimate the power of the test—that is, the probability that the noninferiority test actually detects that the race model holds, at some prespecified significance level. This power estimate can be used for planning the number of trials required in an experiment. Rejection rates for different sample sizes and noninferiority margins are shown in Table 1 for three scenarios: In the first scenario (Table 1a), a race of stochastically independent (e.g., Eq. 1 in Miller, 1982) channels is assumed, with F AV(t) = F A(t) + F V(t) – F A(t)F V(t). Response times were generated for condition V67A measured in participant B.D. in Miller (1986). V67A means that AV stimuli were not presented synchronously, but with an onset asynchrony of 67 ms; in this condition, the response time distributions for A and V overlapped maximally. In the second scenario (Table 1b), a separate-activation model with maximum redundancy gain was chosen, F AV(t) = min[1, F A(t) + F V(t)]. Not surprisingly, the standard test of the race model inequality (Miller, 1986) rejects the race model in about 5% (i.e., α) of the simulations of Table 1b, mostly independent of the sample size. In contrast, the noninferiority test is consistent, with a positive relationship between power and sample size. However, especially for strict noninferiority margins, the power to detect that the race model inequality holds is rather low, with lowest power at the boundary of the maximally possible redundancy gain. Hence, if the experiment is designed to demonstrate that the race model inequality holds in a given experimental condition, 400 trials per condition or more should be considered (see, e.g., Miller, 1986).

In a third scenario, response times for the same conditions were generated assuming a coactivation model that assumes linear superposition of channel-specific diffusion processes (Schwarz, 1994). Using the parameters of Table 1 in Schwarz (1994, ρ DM = 0), the superposition model predicts a substantial violation of the race model inequality (see also Appx. A in Gondan et al., 2010). Table 1c shows that for this setting, the noninferiority keeps the nominal significance level, while the power of a standard test of the race model inequality (Miller, 1986) increases with sample size.

Discussion

Standard procedures for testing the race model use the race model prediction as the null hypothesis (Gondan, 2010; Maris & Maris, 2003; Miller, 1986; Ulrich et al., 2007; Vorberg, 2008). These tests control the Type I error if a theory predicts that the race model inequality is violated in a given experimental condition. In other experimental conditions, however, theoretical considerations might predict that the race model holds (e.g., Feintuch & Cohen, 2002; Schröter et al., 2009). Standard tests of the race model inequality would then be expected to yield a nonsignificant result. A nonsignificant violation of the race model prediction should, however, not be taken as support for the race model (e.g., Corballis, Hamm, Barnett, & Corballis, 2002; Feintuch & Cohen, 2002, Exp. 1; Grice, Canham, & Gwynne, 1984, Exp. 4). More generally, a nonsignificant test result should not be considered as evidence for the null hypothesis (Altman & Bland, 1995). Classical null hypothesis tests are consistent in the alternative hypothesis only (e.g., Rouder, Speckman, Sun, Morey, & Iverson, 2009): If the alternative hypothesis holds, the power to reject the null hypothesis increases with the precision of the measurement (e.g., sample size). Stated differently, standard tests of the race model inequality can be biased in favor of the race model by collecting small and noisy sets of data, thereby reducing the power of the test to detect violations of the race model prediction.

For such situations, we propose an alternative testing procedure in which the race model prediction takes the role of the alternative hypothesis. The test can be applied to data from single participants (for multiple participants, see Appx. B). For construction of the appropriate test, it was necessary to restate the nonstrict alternative hypothesis [Ineq. (2), raceH1] as its strict counterpart [Ineq. (3), raceH δ1 ], thereby introducing a noninferiority margin δ. It can then be tested whether violations of the race model inequality are significantly below the noninferiority margin. Powerful tests for noninferiority and stochastic dominance have been proposed by Freitag et al. (2006) and Davidson and Duclos (2009). The following technical aspect of these tests should be pointed out: In the classical comparison of two distributions (e.g., the one-tailed Kolmogorov–Smirnov test; see also the above references to standard tests of the race model inequality), the null hypothesis states that stochastic dominance holds, G 1(t) ≤ G 2(t) for all t. The alternative hypothesis assumes that stochastic dominance does not hold, G 1(t) > G 2(t) for some t. In contrast, in Freitag et al. and Davidson and Duclos, the alternative hypothesis establishes stochastic dominance—that is, G 1(t) < G 2(t) for all t. It is this important property that enables testing the race model prediction over its entire range, at a controlled Type I error probability. Such an alternative hypothesis is much more informative than the alternative hypothesis of the standard test of the race model, but comes at a cost: The new tests are rather conservative, and large samples are needed to obtain reasonable power.

In applied disciplines—in particular, biomedical research—the idea and the principle of equivalence testing and noninferiority testing is certainly not new (e.g., Blackwelder, 1982). Equivalence tests and noninferiority tests are now considered standard techniques for showing the similarity of two therapeutic arms (e.g., Allen & Seaman, 2006; Food and Drug Administration, 2001; Wellek, 2003; Westlake, 1988). For the assessment of formal models that are more complex than simple two-group comparisons, equivalence tests and noninferiority tests have only rarely been employed (for a forest growth model, see, e.g., Robinson & Froese, 2004). Rather, Bayesian model comparisons have been suggested for the choice between multiple model candidates (Gallistel, 2009; Wagenmakers, 2007; Wagenmakers, Lee, Lodewyckx, & Iverson, 2008). For the present application, in which only a single model prediction is under consideration, researchers are often satisfied to show that the results are consistent with the prediction, as reflected by a nonsignificant discrepancy measure—for example, a nonsignificant goodness-of-fit statistic, or P > .05 in the test of the race model inequality. In these situations, equivalence tests and noninferiority tests seem more appropriate, because they switch the roles of the null and the alternative hypotheses, and consistency of the theory and data is supported by statistical significance.

The new tests have a drawback, however: It is clear that the margin δ must be strictly positive—otherwise, data generated by a race model with F AV(t) = F A(t) + F V(t) would not belong to the alternative hypothesis in (4). As a consequence, the model prediction and observed data cannot be said to fit exactly anymore. Rather, close correspondence of the model and data is accepted. In the test outlined in (4), the race model is said to hold if deviations between the observed \( \widehat{F} \) AV(t) and \( \widehat{F} \) A(t) + \( \widehat{F} \) V(t) are significantly below the noninferiority margin. This conclusion should be given emphasis, because it might be considered one of the main limitations of the proposed new test: Whereas it would be desirable to have a test that indicates that the race model inequality “holds exactly,” the proposed test only states that violations of the model prediction are significantly below the tolerance defined by δ. Stated differently, and perhaps more optimistically, the noninferiority test takes into account that the predictions of abstract models and observed data can rarely be expected to fit exactly. Given a reasonable noninferiority margin, the test rather provides a means to determine if the model describes the data “well enough” (e.g., Serlin & Lapsley, 1993). The latter is again closely related to the definition of the noninferiority margin: If the experimenter desires to test the model prediction with high precision, a small margin is chosen, which in turn requires large samples (Table 1). If a more liberal margin is chosen, precision is lower, and the required sample size will decrease (in the extreme case, δ ≥ 1, noninferiority trivially holds).

Of course, the noninferiority margin should be defined before actually running the experiment. In applied disciplines, “biocreep” is avoided by choosing a noninferiority margin that reflects a therapeutically irrelevant effect in comparison to the best treatment available (D’Agostino et al., 2003). In contrast, in fundamental research, it would be difficult to justify a specific margin, and for a test of the race model inequality, any choice of δ will be somehow arbitrary.Footnote 1 A reasonable size for the noninferiority margin can be determined from parametric coactivation models—for example, the diffusion superposition model (Schwarz, 1994; Townsend & Wenger, 2004, Figs. 14 & 15). For example, with μ A = 1.34, σ A = 11.7, μ V = 0.53, σ V = 4.3, and a criterion fixed at 100 (Table 1 in Schwarz, 1994), the predicted detection times violate Inequality (1) by a maximum amount of 12% (Fig. 1c). This percentage might be too optimistic, because the observed response times include more than just stimulus detection (e.g., response execution, finger movement; see, e.g., the discussion in Schwarz, 1994). The violation predicted by specific coactivation models can, however, serve as a starting point for the definition of a realistic noninferiority margin for the experiment.

In our motivating example, coactivation was expected for Condition A, while separate activation was expected for Condition B. Thus, strictly speaking, both condition-specific predictions should be confirmed in order to support the theory. It is, of course, possible to directly compare the sizes of the violation observed in the two conditions (e.g., by a confidence interval approach; see Miller, 1986, p. 337, right column). Results would be considered consistent with the theory if the size of the race model violation observed in A were significantly higher than the size of the race model violation observed in B. Although this test does not demonstrate that the race model holds in Condition B, the violation observed in Condition A might serve to determine a reasonable limit for the noninferiority margin, as well. In any case, the specific choice of δ should be made transparent to the reader.

We have outlined a test that can be used if the race model is predicted to hold in a given experimental condition. Of course, the test cannot “confirm” the race model in a strict sense. In general, it is not possible to conclude that a given model is correct, just because a single prediction of the model holds in a given set of data. Another, completely different architecture might make the same prediction. More specifically, just because the race model inequality is not violated in a given set of response times, one cannot unambiguously conclude that participants actually processed the information in parallel (see, e.g., Table 1 in Ulrich & Miller, 1997). Our method, thus, cannot overcome the general limitations of abstract model testing, especially in one-way situations in which only a single model prediction is to be tested. However, we propose a valid statistical procedure to investigate whether this prediction of the model is met by the results. Although the decision of the test depends, by design, on the specific choice of the noninferiority margin, we think it is preferable to use an appropriate statistical test that adequately controls the Type I error and is consistent in the hypothesis of interest, instead of relying on the nonsignificant P value of an inappropriate test.