The use of mediation analysis in basic and applied research has been increasing (Baron & Kenny, 1986, has over 20,000 citations). In a mediation model, an independent variable (e.g., drug prevention intervention) is hypothesized to change a mediator (drug use norm among peers), which in turn changes an outcome (e.g., illicit drug use). Under certain assumptions, the mediated effect is the effect of the intervention on the outcome that is transmitted through the mediator. One important issue in mediation studies is to build confidence intervals (CIs) and test hypotheses regarding various effects (e.g., the mediated effect). There are several methods in the literature for computing CIs for the mediated effect. These methods can be roughly categorized into four groups: (1) the distribution of the product (e.g., MacKinnon, Fritz, Williams, & Lockwood, 2007; MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002), (2) the Monte Carlo method (MacKinnon, Lockwood, & Williams, 2004), (3) resampling methods (e.g., bootstrap resampling; MacKinnon et al., 2004), and (4) the asymptotic normal distribution method. Of these methods, the distribution of product has been shown to produce CIs with higher coverage rates, especially when the sample size is small (e.g., 50 or less; MacKinnon et al., 2002; Mackinnon et al., 2004). MacKinnon, Fritz, et al. adapted FORTRAN codeFootnote 1 to form a computer program, called PRODCLIN, that computes the CIs for mediated effects, using the results in Meeker and Escobar (1994). To the best of our knowledge, PRODCLIN is the only computer program that produces CIs on the basis of the distribution-of-the-product method.

However, the PRODCLIN program (MacKinnon, Fritz, et al., 2007) has some limitations. First, popular statistical software packages, such as SPSS, SAS, and R (R Development Core Team, 2010), cannot directly run the PRODCLIN program. Instead, these packages need to run PRODCLIN as an external program and then upload the results to their “native” environments. This process can be cumbersome for users not familiar with running an external program from another statistical package. Furthermore, the PRODCLIN program is limited in that it does not produce CIs for some mediated effects for certain values of means and standard errors. Finally, the algorithm implemented in PRODCLIN has some limitations in producing CIs for the product of coefficients that are correlated. Note that we fixed the issues in the algorithm implemented in the PRODCLIN program. The new version of the PRODCLIN program is implemented in the RMediation package.Footnote 2

The purpose of this study is to introduce an R (R Development Core Team, 2010) package called RMediation. The RMediation package provides a variety of methods for computing CIs, percentiles, and quantiles for the product of two normal random variables and the mediated effect. R is a freely available statistical software package that has become increasingly popular. R can be installed on various operating systems, such as different versions of MS Windows, Apple’s Mac OS X, and Linux-based systems such as Ubuntu. RMediation can readily be installed via the Internet onto any computer running the R software program. In addition, we conducted a small-scale simulation study that compared several methods of producing 95% CIs for mediated effects. These methods included the distribution-of-product method (MacKinnon et al., 2002), the Monte Carlo method (MacKinnon et al., 2004), the asymptotic normal distribution (AND) method, and three bootstrap methods: the percentile, bias-corrected bootstrap (BC), and accelerated bias-corrected bootstrap (BC a ).

The RMediation package employs three methods for producing CIs for the product of two normal random variables (e.g., mediated effects): (1) the distribution-of-product approach introduced by MacKinnon et al. (2002), (2) the Monte Carlo method, and (3) the AND method. The distribution-of-product method is implemented using two computer programs: PRODCLIN (MacKinnon, Fritz, et al., 2007), and R Distribution of Product (RDOP), which is an R program we wrote to implement the distribution-of-product method using the results in Meeker and Escobar (1994). A user can specify a significance level, the means and the standard errors for the random variables X and Y, and the correlation between the two variables. Furthermore, RMediation provides quantiles and percentiles for the distribution of the product of two normal random variables, using the distribution-of-product method and the Monte Carlo simulations. We present a method in RMediation for calculating the Monte Carlo error so that a user can modify the level of accuracy for the percentiles and quantiles.

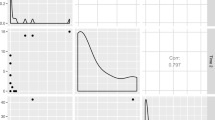
We also fixed the error that caused the PRODCLIN program to yield no results for the mediated effects with certain means and standard errors and for cases in which the two coefficients were correlated. The improvement was implemented in the algorithm generating the upper and lower confidence limits. Finally, RMediation produces a kernel density plot of the empirical distribution of the mediated effect and an overlaid plot of the associated CI with error bars (see Fig. 1). Such plots can help researchers visualize the uncertainty associated with the estimated mediated effect.

Fig. 1
figure 1

Kernel density plot of the distribution of the product of two normal variables (i.e., mediated effect) and the 90% CI with error bars for the mediated effect, with â = 0.295, \( \hat{b} = 1.673 \), SE(â) = 0.163, and \( SE(\hat{b}) = 0.695 \). LL lower limit, UL upper limit

Full size image

Single-mediator model

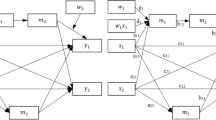
In single-level randomized controlled trials with two groups (e.g., intervention vs. control), a single-mediator model is defined as follows: An independent variable (e.g., X = 1, if a person participates in resistance skill program; otherwise, 0) is hypothesized to change a mediator (e.g., M = drug refusal skill) that, in turn, changes an outcome variable (e.g., Y = frequency of drug use). Three equationsFootnote 3 used to assess quantities in a single-mediator model are shown below (Baron & Kenny, 1986; MacKinnon, 2008):

$$ {Y_i} = {d_1} + c\;{X_i} + {\varepsilon_{{1i}}} $$
(1)
$$ {M_i} = {d_2} + a\;{X_i} + {\varepsilon_{{2i}}} $$
(2)
$$ {Y_i} = {d_3} + c \,\prime \;{X_i} + b\;{M_i} + {\varepsilon_{{3i}}}, $$
(3)

where Y i is the outcome variable measured on individual i, X i is an indicator variable that represents whether the i th person received the intervention (1 = program; 0 = control), and M i is the mediator. The coefficient c in Eq. 1 represents the total effect of the prevention program on drug use. The coefficient c′ in Eq. 3 represents the direct effect of the prevention program on drug use, controlling for the participants’ refusal skills. The direct effect captures the difference between treatment and control group adjusted for participants’ refusal skills and indicates the part of the program effect not accounted for by the mediator; the coefficient b describes the effect of refusal skills on drug use, controlling for the program effect; the coefficient a in Eq. 2 represents the degree to which the intervention increased refusal skills, relative to the control group. ε 1i , ε 2i , and ε 3i denote the residual terms; the coefficients d 1, d 2, and d 3 are the intercepts.

The magnitude of the effect of the prevention program on decreasing drug use mediated by the individuals’ refusal skills is represented by a b (MacKinnon & Dwyer, 1993). The total effect of the prevention program on decreasing drug use is \( c = a\;b + c \,\prime \)(Alwin & Hauser, 1975). A key interest in prevention studies is to test the mediated effect a b. A significant mediated effect provides evidence consistent with the theory: The preventive intervention changed the mediator, thereby altering the outcome.

The estimators of the parameters in Eqs. 1, 2 and 3 can be obtained using the least squares or the maximum likelihood method. The estimator of the mediated effect a b is shown by \( \hat{a}\;\hat{b} \), where “^” denotes the estimator of each respective parameter. Another estimator of the mediated effect is \( \hat{c} - \hat{c} \,\prime \). Under certain conditions, the following expression holds: \( \hat{a}\;\hat{b} = \hat{c} - {\hat{c}^{\prime }} \)(MacKinnon, Warsi, & Dwyer, 1995). It is assumed that the equations represent the true underlying mediation relations satisfying statistical and inferential assumptions (see MacKinnon, 2008, Chaps. 3 and 13 for more on these assumptions).

Hypothesis testing

Testing hypotheses in a single-mediator model has received extensive attention (MacKinnon et al., 2002). In classical statistics, researchers are often interested in testing whether a parameter or a function of parameters is significantly different from zero. Researchers have recently emphasized using CIs, as well as reporting p values for hypothesis testing (Harlow, Mulaik, & Steiger, 1997; Wilkinson & the Task Force on Statistical Inference, 1999). While classical hypothesis testing provides reject/not-reject decision for null hypothesis using test statistics, CIs also provide an interval estimate that represents uncertainty in estimating the quantities of interest in a single-mediator model. CIs can also be used in hypothesis testing. This section discusses three methods for building CIs for the mediated effect that were implemented in the RMediation package.

Distribution of the product

MacKinnon et al. (2002) proposed the distribution-of-product method for building a CI for the mediated effect. In addition, MacKinnon, Fritz, et al. (2007) introduced the PRODCLIN program, which produced CIs for the mediated effect on the basis of the distribution-of-product method, using the analytical method proposed by Meeker and Escobar (1994). This section describes a few methods for evaluating the cumulative distribution function (CDF) for the distribution of the product of two normal random variables, including the one used in the RMediation package and the PRODCLIN program.

First, let us define the CDF of the product of two normal random variables. Let variables X and Y have a bivariate normal distribution. Also, let μ X and μ Y be the means, σ X and σ Y be the standard deviations, and −1 < ρ < 1 be the correlation between X and Y. To simplify the derivation of the distribution of product XY, we make the variables scale free by dividing each variable by its respective standard deviation. That is,

$$ U = \frac{X} {{{{{\sigma }}_X}}}, \;{\hbox{and}}\; V = \frac{Y} {{{{{\sigma }}_Y}}}. $$

Let Z = U V. The relationship between the CDF of the product X Y and that of Z is as follows:

$$ Pr(XY \leqslant k) = Pr\left\{ {\frac{X}{{{{{\sigma }}_X}}}\frac{Y}{{{{{\sigma }}_Y}}} \leqslant \frac{k}{{{{{\sigma }}_X}\;{{{\sigma }}_Y}}}} \right\} = Pr(Z \leqslant z), $$

where \( z = k/({{{\sigma }}_X}{{{\sigma }}_Y}) \). Note that (U,V)T has a bivariate normal distribution:

$$ {\left( {\begin{array}{*{20}c} {U} \\ {V} \\ \end{array} } \right)} \sim BVN{\left( {{\left( {\begin{array}{*{20}c} {{\mu _{U} }} \\ {{\mu _{V} }} \\ \end{array} } \right)},{\left( {\begin{array}{*{20}l} {1 \hfill} & {\rho \hfill} \\ {\rho \hfill} & {1 \hfill} \\ \end{array} } \right)}} \right)} $$
(4)

where \( \mu _{U} = {\mu _{X} } \mathord{\left/ {\vphantom {{\mu _{X} } {\sigma _{X} }}} \right. \kern-\nulldelimiterspace} {\sigma _{X} }\,{\text{and}}\,\mu _{V} = {\mu _{Y} } \mathord{\left/ {\vphantom {{\mu _{Y} } {\sigma _{Y} }}} \right. \kern-\nulldelimiterspace} {\sigma _{Y} }\).

Now let F Z (q) be the CDF of Z. The CDF of Z is defined as follow:

$$ {F_Z} (q) = \int \int_A {{f_{{U,V}}} (u,\upsilon |{ {{μ}}, { Σ} )\,du\,d\upsilon }}$$
(5)

where \( A = \left\{ {\left( {u,\upsilon } \right) \in {\mathbb{R}^2}:u \times \upsilon \leqslant q} \right\} \), \( {f_{{U,V}}}(u,\upsilon |{{\mu }},\Sigma ) \) is the bivariate normal probability density function (PDF) for (U,V), and q∈ℝ is a quantile.

There are several methods for evaluating the distribution of the product in Eq. 5. Craig (1936) provided an analytical method for evaluating the CDF of the product of two normal random variables in Eq. 5. According to Craig, the mean and variance of Z are as follows:

$$ \matrix{ {{{{\mu }}_Z} = {{{\mu }}_U}\,{{{\mu }}_V} + {{\rho }}} \cr {{{\sigma }}_Z^2 = {{\mu }}_U^2 + \mu_V^2 + 2{{{\mu }}_U}\;{{{\mu }}_V}\;{{\rho }} + 1 + {{{\rho }}^2}} \cr }<!end array> $$
(6)

When either X or Y has a mean of zero, the distribution of Z is approximately proportional to the Bessel function of the second kind of zero order with a purely imaginary argument. The shape of the distribution is symmetric around the mean of zero. On the other hand, when neither X or Y has a mean of zero and X and Y are independent (ρ = 0), the mean and variance of Z are as follows:

$$ \matrix{ {{{{\mu }}_Z} = {{{\mu }}_U}\;{{{\mu }}_V}} \cr {{{\sigma }}_Z^2 = {{\mu }}_U^2 + {{\mu }}_V^2 + 1} \cr }<!end array> $$

In addition, Meeker, Cornwell, and Aroian (1981) provided a numerical algorithm for evaluating the CDF of Z. The numerical method directly evaluates the double integral in Eq. 5, using an adaptive Romberg integration method with an absolute error tolerance of 1.0E--10. Meeker et al. also provided tables of quantiles for the distribution of a standardized variable:

$$ W = \frac{{Z - {{{\mu }}_Z}}}{{{{{\sigma }}_Z}}}. $$

Finally, Meeker and Escobar (1994) provided a simpler method for evaluating the CDF in Eq. 5 (note that both RMediation and PRODCLIN employ this method). They simplified Eq. 5 as follows:

$$ {F_Z}(q) = \int_{{ - \infty }}^{\infty } {\phi \left( {u - {{{\mu }}_U}} \right)\Phi \left[ {{\hbox{sign}}(u)\frac{{q/u - {{{\mu }}_{{V|u}}}}}{{\sqrt {{1 - {{{\rho }}^2}}} }}du} \right]} $$
(7)

where φ and Ф are the PDF and CDF of the standard normal distribution, respectively. μ V | u is the conditional mean of V, which equals \( {{{\mu }}_V} + \rho \left( {u - {{{\mu }}_U}} \right) \). sign(.) is the sign function, and −1 < ρ <1.

Monte Carlo method

Another method for evaluating the CDF of a product of two normal variables in Eq. 5 is to use the Monte Carlo method. In this section, we also present a method for calculating the associated Monte Carlo error. Using the Monte Carlo method to evaluate the CDF of the product of two normal variables requires reformulating Eq. 5 as follows:

$$ \begin{array}{*{20}l} {{F_{Z} (q)} \hfill} & {{ = \iint_A {f_{{U,V}} {\left( {\left. {u,\,\upsilon } \right|{\mathbf{\mu }},\,\Sigma } \right)}\,du\,d\upsilon }} \hfill} \\ {{} \hfill} & {{ = \iint {I_{A} (u,\,\upsilon )f_{{U,\,V}} {\left( {\left. {u,\,\upsilon } \right|{\mathbf{\mu }},\,\Sigma } \right)}\,du\,d\upsilon ,}} \hfill} \\ \end{array} $$

where I A (u, v) is the indicator function defined as follows:

$$ {I_A}(u,\upsilon ) = \left\{ {\matrix{ 1 & {{\hbox{if}}\;(u,\upsilon ) \in A,} \cr 0 & {{\hbox{if}}\;(u,\upsilon )\not{ \in }A.} \cr }<!end array> } \right. $$

To illustrate, suppose that we simulate a random sample of (u 1, υ1),…,(u m, υm) from the bivariate normal distribution in Eq. 4. The Monte Carlo estimate of the percentile p for the quantile q is given by

$$ p = \frac{{\sum\nolimits_{{j = 1}}^m {{I_A}\left( {{u^j},{\upsilon^j}} \right)} }}{m}. $$

The associated Monte Carlo (simulation) error of the percentile estimate p is given by

$$ S{E_p} = \sqrt {{\frac{{{{\sum\nolimits_{{j = 1}}^m {\left( {{I_A}({u^j},{\upsilon^j}) - p} \right)} }^2}}}{{m(m - 1)}}}} . $$

Note that the Monte Carlo error depends on m, which is controlled by the user. As m becomes larger, the Monte Carlo error becomes smaller.

Asymptotic normal distribution method

Another approach to testing the mediated effect and producing CIs is to use the asymptotic properties of the ML estimator of a b and form a z test statistic. In this approach, \( z = (\hat{a}\;\hat{b})/SE(\hat{a}\;\hat{b})\dot{ \sim }N(0,1) \), where \( \dot{ \sim } \) means approximately and \( SE(\hat{a}\;\hat{b}) \) is the standard error of the estimator of ab. As the sample size increases, z converges in distribution to the standard normal distribution. There are various methods for calculating \( SE(\hat{a}\;\hat{b}) \) (MacKinnon, 2008). RMediation uses the variance of the product of two normal random variables presented in Eq. 6. For the mediated effect, because the covariance between â and \( \hat{b} \) is zero (Tofighi, MacKinnon, & Yoon, 2009), the standard error of the mediated effect is simplified as follows:

$$ SE(\hat{a}\hat{b}) = \sqrt {{{{(a\;SE(\hat{b}))}^2} + {{(b\;SE(\hat{a}))}^2} + SE{{(\hat{a})}^2}\;SE{{(\hat{b})}^2}}} . $$

The asymptotic 95% CI for the mediated effect is \( \hat{a}\;\hat{b}\pm 1.96 \times SE(\hat{a}\;\hat{b}) \).

RMediation package

The RMediation package provides functions for computing (1 -- )% CIs, percentiles, and quantiles for the distribution of the product of two normal random variables. To install the RMediation in R (R Development Core Team, 2010), one needs to be connected to the Internet. To install RMediation within R, use the following function: . The name of the package should be specified in quotation marks. Also note that the commands used in the R environment are called functions and are case sensitive. Each function (command) accepts arguments to be specified in parentheses after the name of the function. Arguments modify the behavior of a function. If there is more than one argument, the arguments need to be separated by commas. To assign a value to an argument, “=” is placed after the name of the argument and before the value.

To use RMediation, load the package into the R environment. To do that, use the R function . One of the arguments of the function is , whose value must be set to the name of the package to be loaded:

figure e

To illustrate, consider an example where the previous version of the PRODCLIN program did not yield the desired results. Suppose that we want to find a 90% CI for a mediated effect where â = 0.295, \( \hat{b} = 1.673 \), SE(â)=.163, and \( SE(\hat{b}) = 0.695 \). In RMediation, the function produces CIs for the product of two normal variables and mediated effects. The following command produces a 90% CI, using the new version of the PRODCLIN program:

figure g

The arguments and refer to the means for the first and second variables, respectively, which correspond to the estimates of a and b paths, respectively. The arguments and specify the standard deviations for the first and second variables, respectively, which correspond to the standard errors for the estimates for a and b paths, respectively. The argument specifies the correlation between two variables with the default value of 0. The argument is the significance level for the CI with the default value of .05. The argument takes on the values “” (default, the PRODCLIN program, MacKinnon, Fritz, et al., 2007), “” (the RDOP program), “” (the Monte Carlo approach), “” (the AND method), or “” (using all four methods). It is important to note that the values for the argument must be enclosed in single or double quotation marks.

In the example above, a user can also choose to not specify a value for the optional arguments and , because the default values for these arguments are “” and 0, respectively. The previous command can be shortened as follows:

figure x

On the other hand, if a user needs values other than the defaults for the optional arguments, the person needs to explicitly specify these arguments. Suppose that you want the 90% CI for the product of two normal random variables with the means equal to 0.2 and 0.4, standard deviations equal to 1 for both, and the correlation equal to .1, using all the available methods in the RMediation package. The specifications of arguments are as follows:

figure z

Another capability of the function is to produce a graph for the distribution of the product. The plot uses the kernel density method with a standard normal distribution as the kernel function to estimate the PDF of the product of two normal random variables.Footnote 4 To obtain a density plot, one needs to set the argument . At the same time, the argument in the function overlays the plot of (1-α)% CI with error bars on the density plot. The following command produces the density plot with an overlaid plot of the 90% CI, as shown in Fig. 1:

figure af

In addition, the RMediation package provides quantiles and percentiles of the distribution of the product of two normal random variables. The function computes the quantile for the distribution of product. The argument type in takes on the following values: “” (default, the PRODCLIN program; MacKinnon, Fritz, et al., 2007), “” (the RDOP program), “” (the Monte Carlo approach), and “” (using all three methods). To illustrate, suppose that we want to find quantiles for the probability p = .975 for the mediated effect, where â = 0.2, \( \hat{b} = 0.4 \), SE(â) = 1, and \( SE(\hat{b}) = 1 \). The following command produces the quantiles corresponding to p = .975, using all three methods with the associated numerical errors:

figure am

For example, the quantile for the probability p = .975 using both “” and “” is equal to 2.587.

The function produces percentiles for the distribution of the product in the RMediation package by specifying the argument to the following values: “” (default, the PRODCLIN program, MacKinnon, Fritz, et al., 2007),“” ( RDOP program), “” (the Monte Carlo approach), or “” (using all three methods). Let us find the percentile for the quantile q = 2.587 in the previous example:

figure av

As was expected, the percentile for q = 2.587 is equal to 0.975.

Simulation study

We conducted a simulation study to compare 95% CIs produced by the methods in the RMediation program with the CIs based on the three bootstraps methods in terms of the Type I error rates and the length of CIs. The simulation study followed a design similar to the one used by MacKinnon, Fritz, et al. (2007). Data for the single-mediator model were generated when a = 0 and b = 0, .14 (small), .39 (medium), and .59 (large). The value of c′ was fixed at zero. The sample size took on the values 50, 100, and 200.

Data generation was performed in R (R Development Core Team, 2010). Independent random data for X, εi2, and εi3 were generated from the standard normal distribution using the function in R . Values for M and Y were generated on the basis of the mediation model in Eqs. 2 and 3. Within each condition, 1,000 data sets were created. Each data set was analyzed using the model in Eqs. 2 and 3, and seven sets of 95% CIs were computed for each data set. The bootstrap methods used 1,000 bootstrap samples of each data set.

We used the standardized length of a CI, which is defined as d/SE, where d is the length of the CI and SE is the standard error for a particular method. Note that d for the AND CIs is constant and equals 3.920. For the PRODCLIN, RDOP, Monte Carlo, and AND methods, SE is computed using the formula in Eq. 6. For the bootstrap methods, SE is the standard error of a sample of 1,000 bootstrap mediated effect estimates. The results are shown in Table 1.

Table 1 Proportion coverage and standardized length for 95% CIs (a = c′ = 0)
Full size table

Note that the results for the PRODCLIN, RDOP , and Monte Carlo methods were similar, as were those for the BC and BC a bootstrap methods. To save space, we presented the results for only the PRODCLIN and BC bootstrap methods. As can be seen in Table 1, the AND method yielded the most conservative CIs across all conditions. For the conditions b = .14 (small), the Type I error rates of CIs for the PRODCLIN, the percentile bootstrap, and the BC bootstrap were below the nominal value of .05. For the conditions b = .39 (medium) and .59 (large), the PRODCLIN Type I error rates were closest to the nominal value of .05, followed by the percentile and then the BC bootstrap method. The BC (BC a ) had inflated Type I error rates above the nominal value of .05. As for the length of the CIs, the AND method had the shortest length, followed by PRODCLIN, the percentile bootstrap, and then the BC bootstrap method.

Conclusion

The present study provided a tutorial on how to use the RMediation package, using hypothetical numerical examples. The RMediation package provides functions to compute CIs, percentiles, and quantiles for the distribution of the product of two normal random variables based on the results of MacKinnon et al. (2002). In addition, the RMediation package produces a plot of the empirical distribution of the mediated effect and the overlaid plot of associated CI with error bars (see Fig. 1). These plots can help researchers visualize the uncertainty associated with the mediated effect. The RMediataion package can be used in any situation where aspects of the distribution of the product of two random variables is of interest, such as the distribution of interaction variables formed by the product of two main effect variables and the distribution of scales formed by the product of two individual scales.

Overall, we recommend the distribution-of-product method over the AND and the bootstrap methods, especially for smaller sample sizes (e.g., 50). The bootstrap methods are not recommended because the analytical solution for testing the mediated effect already exists and is implemented in the RMediation package. In addition, for sample sizes less than 100, the bootstrap methods may result in undercoverage (i.e., coverage less than 95%) for the CIs, since the confidence limits vary considerably across the bootstrap samples (Good, 2006, Chap. 2). The undercoverage of the bootstrap methods has been corroborated by our small-scale simulation study and is consistent with past research (MacKinnon et al., 2004).