Visual working memory facilitates the temporary maintenance of information over time for use in ongoing cognitive processes. The majority of working memory research has examined performance over short (~1 second) retention intervals. However, there is growing evidence that suggests that working memory performance declines after longer (~10 seconds) retention intervals (Donkin, Nosofsky, Gold, & Shiffrin, 2015; Rademaker, Park, Sack, & Tong, 2018; Zhang & Luck, 2009).Footnote 1 These studies have mostly focused on whether this decline in performance is due to changes in precision or due to the sudden loss of information over time. In the present work, however, we will focus on an orthogonal distinction that further characterizes how increasing retention intervals affect performance. Specifically, we will dissociate how attentional control and working memory capacity contribute to working memory performance over long retention intervals.

Previous work has investigated the intricate relationship between attention and working memory performance (Adam, Mance, Fukuda, & Vogel, 2015; Awh, Vogel, & Oh, 2006; De Fockert, Rees, Frith, & Lavie1, 2001; deBettencourt, Keene, Awh, & Vogel, 2019). This work has provided evidence that trial-by-trial variability in attention contributes to individual differences in working memory performance. One such study deployed a whole report procedure, in which participants reported the identity of each item from the memory display on every trial (Adam et al., 2015). They found that differences in visual working memory performance both across and within individuals over short retention intervals were well described by a combination of two separate parameters: Kmax, maximum working memory capacity, and a, a factor related to attentional control (Adam et al., 2015). Given that these two parameters, Kmax and a, explain performance variability at short retention intervals, in our study, we are interested in whether the decline in performance observed after long retention intervals is due to changes in Kmax, a, or some combination of these two parameters.

Another unresolved concern is that we do not know how long retention intervals act on multiple representations because previous research has utilized partial report tasks, in which a single item from the display is randomly chosen to be tested. In particular, there are two possible alternatives for performance declines at long retention intervals: (1) participants could drop all information from working memory (complete drop) or (2) participants could drop individual items (partial drop). Longer retention intervals could increase the probability that participants completely disengage from the task, causing participants to lose all information on a subset of trials. Previous research has found that information is lost suddenly and completely when participants have to maintain information for extended amounts of time (Zhang & Luck, 2009). This research investigated performance by probing one item at a time, so they could not draw conclusions about the maintenance of all items on a single trial. Nevertheless, their findings suggest that participants could suddenly and completely lose all information from working memory when they have to maintain information over longer (10 s) amounts of time. This hypothesis aligns with the complete drop model. Alternately, the efficiency of attentional control could decrease over time. This could cause a partial loss of information over long retention intervals. One task that is well suited to examine representations of multiple items on a single trial is a discrete whole report working memory task. This task requires participants to click among discrete colors to report the identity of each item in the display (Adam et al., 2015). Performance on discrete whole report tasks can range from getting no items correct, to getting all items correct, or anything in between. Across individuals, average discrete whole report performance is highly correlated with performance on traditional change detection tasks, where a single item is randomly probed (Adam et al., 2015). However, the discrete whole report task has substantial advantages because it measures memory for each item on a multi-item display. This allows us to assess whether changes in performance after long retention intervals are due to completely dropping all information from working memory or due to an increased likelihood of dropping individual items.

In the current study, we had participants perform a discrete whole report task while maintaining information over long (10 s) and short (1.5 s) retention intervals. To analyze the data, we designed a computational model that simultaneously solved for attentional control (a) and working memory capacity (Kmax) using grid search. By simultaneously fitting both of these parameters, we improved upon and extended previous research (Adam et al., 2015). We were interested in (1) characterizing how the distributions in the number of items remembered varied across short vs. long retention intervals, and (2) using these distributions to model how attention and working memory capacity were impacted by the length of the retention interval.

Experiment 1

In Experiment 1, we characterized trial-by-trial fluctuations in the number of items maintained over time, while distinguishing between effects on the maximum number of items that could be stored, and an attention parameter that quantifies the probability that participants would achieve that maximum. Participants performed a discrete whole-report task which probed memory for each item on every trial, following either short (1.5 s) or long (10 s) retention intervals. We had participants maintain information over short (1.5 s) and long retention intervals (10 s) in order to determine whether longer retention intervals lead to declines in maximum working memory capacity (Kmax), or the probability of achieving Kmax (a), which we will refer to as attentional control. Previous research has numerically solved for Kmax and a by running simulations (Adam et al., 2015). Here, we solved for these two parameters using a grid search. In addition, we examined whether failures to achieve maximum capacity were best characterized by a complete drop of all information from working memory, or a partial drop of some items while maintaining other items.

Methods

Participants

Twenty adults participated in Experiment 1 (eight male, 19–31 years, mean 23.25 years). Two additional participants were excluded for failing to complete the experiment in the allotted time (2 h), resulting in an insufficient number of trials per condition (< 180). The final sample size for both experiments was selected a priori based on previous discrete whole-report sample sizes (Adam, Vogel, & Awh, 2017). All participants in both experiments received payment (US $20, $10/h) or course credit (two credits, one credit/h). Additionally, all participants reported normal or corrected-to-normal visual acuity and color vision and provided informed consent to a protocol approved by the University of Chicago Institutional Review Board.

Stimuli

Participants encoded arrays of six differently colored squares (subtending approximately 1°×1°) on a gray background. Each square was one of nine possible colors without replacement (red, green, blue, yellow, magenta, cyan, white, black, orange). Therefore, each memory array consisted of six squares of six different colors. For the response screen, multicolored squares appeared that were a 3×3 grid of all nine colors. Participants were instructed to fixate on a black central dot (0.43°).

Apparatus

Stimuli were generated in MATLAB (The MathWorks, Natick, MA, USA) using the Psychophysics toolbox (Brainard, 1997). Participants were seated approximately 67 cm from a 24-inch LCD BenQ monitor. Squares could appear within approximately a 20°×20° area on the screen. To monitor compliance with the articulatory suppression instructions, audio was recorded through MATLAB with an Eberry microphone.

Procedure

Participants completed a discrete whole-report visual working memory task with articulatory suppression (Fig. 1a). Prior to the onset of the memory array, five randomly generated digits appeared above the fixation dot. Participants said the numbers out loud at least once before pressing spacebar to begin the trial and continued to repeat the numbers until the response screen appeared. Participants encoded memory arrays of six colored squares that appeared briefly (150 ms), and then maintained these squares over a blank retention interval. Critically, the retention interval was either short (1.5 s, 50% of trials) or long (10 s, 50% of trials). After the retention interval, a response screen appeared with multicolored squares at the location of each original square. To respond, participants selected the color of the original square at each location using the mouse. Participants were required to respond to all six items before the trial would proceed, and all squares remained on the screen until the participant finished responding. Participants completed a block of 60 trials and then took a 30-s break. Within each block, the retention interval length was held constant (short or long). In total, participants completed 360 trials.

Fig. 1
figure 1

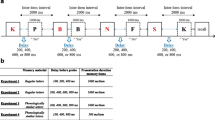
Task design and computational model. a Discrete whole-report working memory task for Experiment 1. At the start of each trial, five digits appeared on the screen. Participants said these numbers at least once before trial initiation and repeated them continuously until the response screen appeared. Participants initiated each trial by pressing spacebar, and then a memory array of six colored squares appeared briefly (150 ms). The critical manipulation was the length of the retention interval, either short (1.5 s) or long (10 s). At the end of the retention interval, a response screen appeared with multicolored squares at the location of each original square. Participants selected the color of each square using the mouse. Participants were required to respond to all six items before the trial would proceed, and the multicolored squares remained on the screen until the participant finished responding. b Both models assume that participants have a stable maximal capacity, plus guessing. These models assume that participants strategically guessed the colors of the items that they did not maintain in memory. If a participant remembers three items, for example, then they are able to narrow the possible colors of the remaining three items from 1/9 to 1/6 possible colors. If participants correctly guessed the colors of the items that they did not maintain in memory, then working memory performance on that trial could exceed working memory capacity (Kmax). c In the partial drop model, attentional control is distributed according to a beta-binomial function. d The partial drop model is unimodal. It reflects a partial loss of information, as participants can drop individual items, as opposed to the whole array. e In the complete drop model, attentional control is distributed according to a Bernoulli function. Attention to the array is therefore essentially all-or-none, as participants are either fully engaged and remember Kmax items, or they are fully disengaged and do not remember any of the items. f In the complete drop model, performance typically reflects a bimodal distribution. The distribution becomes unimodal if participants have extremely low working memory capacities

Full size image

Analysis

Working memory performance was quantified per trial as the number of items for which the correct color was selected, ranging from 0 (no items correct) to 6 (all items correct). Across trials, we calculated the mean number of correct responses.

Computational models

In order to describe performance, we applied a family of computational models that have two parameters, one for attentional control (a) and one for maximum working memory capacity (Kmax) (Fig. 1b–f). These models assume that performance can be described using (1) a stable maximal capacity (2) attentional control and (3) strategic guessing.

In these models, each participant has a stable maximal capacity. In line with work that suggests that participants remember entire objects (L), capacity is an integer value that can vary from one item to the maximum number of items in the display, with a step size of one (Kmax∈[1,2,3,4,5,6]). On any given trial (i), participants maintained some integer number of items (Ni) in memory, ranging from 0 to their maximal capacity (Ni∈[0,1, 2, … , Kmax]). To investigate whether an integer value was critical for these results, we re-ran the model using a smaller step size of (∆Kmax = 0.5) and found the same pattern of results.

We further assumed participants would strategically guess for the remaining items not maintained in memory. That is, for a given trial (i), participants maintained an integer number of items with the correct color in mind (Ni). For the remaining items (6−Ni), we used a binomial distribution to model strategic guessing from among the remaining colors (9−Ni).

These models also include a term for attentional control throughout the delay. Attentional control was operationalized as the probability of maintaining the maximum number of items (Kmax) for each trial.

In particular, this model distinguishes between working memory performance and working memory capacity. Maximal working memory capacity (Kmax) is the maximum amount of information that an individual can maintain in working memory at any one moment. Note that this operationalization of maximal working memory capacity is related to, but distinct from, traditional measures of average performance, i.e., K (Luck & Vogel, 2013; Cowan, 2010). On each trial, the number of correctly reported items can range from 0 to 6 items. Participants could correctly report more items than Kmax items if they correctly guess the color of any of the items that they did not maintain in working memory. They can report fewer items than their Kmax if they have low attention control (a) on that trial. We examined two conceptualizations of attentional control in the different models:

In the complete drop model, attentional control was effectively binary: participants either maintained their maximum number of items (Ni=Kmax), or they had no information at all (Ni=0). This model effectively reduces to a Bernoulli distribution over values zero and Kmax with the probability of Kmax being one minus the probability of potential failure.

In the partial drop model, the number of maintained items ranges over the integer numbers from 0 to Kmax. In this situation in statistics, we would typically apply the binomial distribution, which gives the probability distribution of zero to Kmax successes given a constant probability of success on each trial. However, we believe that the probability of success throughout an experiment is not constant. Prior evidence has shown that attentional control fluctuates over the course of an experiment and these attention fluctuations lead to fluctuations in working memory performance (deBettencourt et al., 2019). Therefore, we chose to use the beta-binomial distribution because this allowed the probability of success to also follow a probability distribution, rather than remain constant on each trial. For n trials, this beta-binomial distribution is characterized by a beta function, B(α, β), and a binomial coefficient \( \left(\frac{n}{Kmax}\right) \), with the following probability density function:

$$ P\left( Kmax|n,\alpha, \upbeta \right)=\frac{B\left(\ Kmax+\alpha, n- Kmax+\upbeta \right)\left(\frac{n}{Kmax}\right)}{B\left(\alpha, \upbeta \right)} $$

Model fitting

We computed the probability distributions for the complete and partial drop models over the 2D grid space of the free parameters for each model: Kmax∈[1,6] (with a step size of 1) and a∈[0,10] (with a step size of 0.01). The complete drop model had one free parameter, p, which represented the probability of disengagement. The partial drop model also had one free parameter, α, which represents the robustness of attentional control. Alpha determines the mean of the beta distribution for p by \( ean=\frac{\alpha }{\alpha +\upbeta} \) . For this model, we kept the β parameter equal to 1, so that the beta distribution was [α, 1] for each trial. We were interested in the mean of the distribution, so we fixed β equal to 1 and kept α free. By fixing β to 1, we assume that attentional control fluctuates quite a bit, especially when the success probability is intermediate. We then determined the best-fitting model to each individual participant’s performance distributions by calculating which combination of parameters produced the largest log likelihood (LL). We calculated LL separately for each participant and model. We then sum the LL for all participants for a given model (e.g., LLcomplete). To compare the complete and partial drop models, we used the Bayesian Information Criterion (BIC). We calculated the difference in BIC (∆BIC) values between the two models. In this calculation, the penalty term of the BIC drops out because both models have the same number of free parameters (i.e., 1). We used the following formula to calculate the difference in BIC values between the two models:

$$ \Delta BIC=-2\times \left({LL}_{complete}-{LL}_{partial}\right) $$

LLcomplete is the log-likelihood of the complete drop model, and LLpartial is the log-likelihood of the partial drop model. Positive values of ∆BIC indicate a better fit for the partial than the complete drop model.

To further investigate performance, we fit two combined partial drop models that aggregated across data from short and long retention intervals with three total parameters. Here, we manipulated which parameter (a or Kmax) was fixed or free to vary across long and short retention intervals. In the first model (“a-free model”), attentional control (a) was free to vary across retention intervals, while maximum working memory capacity (Kmax) was fixed. In the second model (“Kmax-free model”), maximum working memory capacity (Kmax) was free to vary across retention intervals, while attentional control (a) was fixed. We used the following formula to calculate the difference in BIC values between these two models:

$$ \Delta BIC=-2\times \left({LL}_{Kmax- free}-{LL}_{a- free}\right) $$

LLKmax − free is the log-likelihood of the Kmax-free model, and LLa − free is the log-likelihood of the a-free model. Positive values of ∆BIC indicate a better fit for the a-free than the Kmax-free model.

Statistics

Results are reported as the mean plus or minus the standard deviation, unless noted otherwise. Statistics in all experiments were computed using Student’s two-tailed paired t tests. Effect sizes are reported as Cohen’s d.

Results

Behavioral performance

Working memory performance (Fig. 2) was operationalized as the number of items correct per trial. Average working memory performance (n) was calculated for each individual across all trials. If participants had been randomly guessing, chance performance would equal the probability of getting any item correct (1 of 9) multiplied by the number of items (6, chance = 0.67). Working memory performance across both conditions was well above chance (n = 2.40 ± 0.85; t(19) = 10.00, p < 0.001).

Fig. 2
figure 2

Behavioral results and computational modeling fits for Experiment 1. a Working memory performance for short (green) vs. long (blue) retention intervals. Each dot represents the mean number correct in one condition for one participant. A line connects data from the same participant. The horizontal black line depicts the mean across participants. The black error bars reflect the standard error of the mean. The shaded area reflects the density across participants. b Histogram of the difference between the BIC values (∆BIC) in the complete and partial drop models for each participant. Positive values indicate a better fit for the partial drop model. The bars are centered within each bin (bin size = 10) for the short (green) and long (blue) retention intervals. c The green bars of the histogram depict the data from short retention interval trials. The height of each bar is the proportion of trials for each number of correct responses. Black error bars are the standard error of the mean across participants. The lines reflect the model fits using the best fitting parameters: complete drop model (purple) and partial drop model (red). Each model was fit independently for each participant, and error bars reflect the standard error of the mean of the best-fitting parameters across participants. d The data (blue bars) and best fitting models (purple and red lines) from long retention interval trials

Full size image

The critical question was how performance differed over time (long vs. short retention intervals; Fig. 2a). In line with prior work, we hypothesized that performance would decline following long retention intervals (Zhang & Luck, 2009). We calculated the average number of correctly remembered items separately for trials with long and short retention intervals (nlong = 2.15 ± 1.00, nshort = 2.66 ± 0.59). Indeed, participants remembered significantly fewer items after long vs. short retention intervals (t(19) = 4.35, p < 0.001, Cohen’s d = 0.62).

Computational modeling

We developed an analytical solution to two computational models that could describe performance distributions: complete and partial drop models. These models make distinct predictions about the distribution of the number of correct responses across trials. The complete drop model was “all-or-none,” such that participants either performed at their maximum capacity and remembered Kmax items, or they had no information about any of the items in the array, and, thus, maintained zero items. The partial drop model, on the other hand, assumed graded performance, such that participants could maintain anywhere from zero to Kmax items in working memory on any given trial. When Kmax is equal to 0 or 1, these models make similar predictions.

First, we determined whether the complete or partial drop model better explained our data. To do this, we compared the fits between the models using a goodness-of-fit measure, BIC. We took the difference between BIC values for the partial drop and the complete drop models, so positive ∆BIC values indicate that the data are better fit by the partial drop model, whereas negative ∆BIC values indicate better fit by the complete drop model. In this experiment, both models made reasonable fits to data (Fig. 2b, c). However, data from both short and long retention intervals (Fig. 2b, c) were better fit by the partial drop model (∆BIClong = 1042.86, ∆BICshort = 1298.73) than the complete drop model. For the short retention intervals, 19 out of 20 participants were better fit by the partial drop model and 1 out of 20 participants was better fit by the complete drop model. For long retention intervals, 15 out of 20 participants were better fit by the partial drop model, 3 out of 20 participants were better fit by the complete drop model, and 2 out of 20 participants were equally well fit by both models. This suggests that performance fluctuates along a continuum and these fluctuations affect the maintenance of individual items in an array.

Finally, the central question of interest was whether poorer performance following long retention intervals was best explained by a reduction in maximum working memory capacity or a reduction in the probability of achieving that maximum. The partial drop model showed that attentional control was reliably lower for long relative to short retention intervals (along = 1.28 ± 2.20, ashort = 2.44 ± 2.84; t(19) = 3.30, p = 0.004; Cohen’s d = 0.74). However, there was not a reliable difference in maximum capacity (Kmaxlong = 3.55 ± 0.55, Kmaxshort = 3.20 ± 0.36; t(19) = − 1.92, p = 0.07; Cohen’s d = − 0.43). These results suggest that the performance decrements after long retention intervals reflect an inability to maintain attentional control throughout the longer retention intervals, not a reduction in the maximum number of items that could be stored in working memory.

To more formally investigate how performance varied across long and short retention intervals, we fit two combined models. We alternated which parameter (a or Kmax) was free to vary across retention interval length. In the first model (a-free model), we allowed attentional control to vary across retention intervals while maximum working memory capacity was a fixed value for each individual (a-free, Kmax-fixed). In the second model (Kmax-free model), we allowed maximum working memory capacity to vary across retention intervals while attentional control was a fixed value for each individual (a-fixed, Kmax-free). We observed that the a-free model better fit the data (∆BIC = 17.15). This provides further evidence for the finding that attentional control (a) varied across short and long retention intervals, whereas maximum working memory capacity (Kmax) was stable.

Discussion

We developed a task that manipulated the length of the retention interval in a discrete whole-report working memory paradigm. Average performance declined after long vs. short retention intervals. We developed two models: the complete and the partial drop models, that both describe the number of items remembered as a result of some combination of attentional control and maximum working memory capacity. We found that the partial drop model better accounted for performance, which suggests that the amount of information in working memory across trials varied continuously. Additionally, the attentional control parameter reliably differed across retention intervals, such that it was lower after long retention intervals. However, the maximum working memory capacity parameter was equivalent for long and short retention intervals. Thus, decrements in performance after long retention intervals are due to a graded decline in sustaining attentional control, which leads to loss of individual items from working memory.

Experiment 2

In Experiment 2, we sought to replicate Experiment 1 and extend our understanding of the role of attentional control during working memory maintenance. We interpreted the findings from Experiment 1 as reflecting variations in sustained attentional control during retention of information in working memory. In Experiment 1, however, we manipulated retention interval length across blocks, so, the differences that we found in Experiment 1 could be due to differences in preparation. For example, if participants know that they are going to have to retain information over a very long retention interval, they could better prepare than if they did not know the duration of the upcoming retention interval. To further eliminate potential differences in preparation across blocks, we intermixed trials of short and long retention intervals within blocks.

Methods

Participants

Twenty adults participated in Experiment 2 (ten male, 18–33 years, mean 24.05 years). Four additional participants were eliminated for technical issues with the experimental display code and four additional participants were excluded from analyses for leaving the experiment early.

Stimuli and apparatus

Same as Experiment 1.

Procedure

Same as Experiment 1, except short and long retention intervals were randomly inter-mixed across trials within each block. Participants completed a block of 48 trials and then took a 30-s break. In total, participants completed 288 trials.

Analysis, computational modeling, and statistics

Same as Experiment 1.

Results

Behavioral performance

Just as in Experiment 1, working memory performance (Fig. 3) was operationalized as the number of items correct per trial, and average performance (n) was calculated for each individual across all trials. Working memory performance on the discrete whole-report task was significantly above chance (n = 1.88 ± 0.83; t(19) = 6.61, p < 0.001) suggesting that participants were not randomly guessing.

Fig. 3
figure 3

Behavioral results and computational modeling fits for Experiment 2. a Working memory performance for short (green) vs. long (blue) retention intervals. Each dot represents the mean number correct in one condition for one participant. A line connects data from the same participant. The horizontal black line depicts the mean across participants. The black error bars reflect the standard error of the mean. The shaded area reflects the density across participants. b Histogram of the difference between the BIC values (∆BIC) in the complete and partial drop models for each participant. Positive values indicate a better fit for the partial drop model. The bars are centered within each bin (bin size = 10) for the short (green) and long (blue) retention intervals. c The green bars of the histogram depict the data from short retention interval trials. The height of each bar is the proportion of trials for each number of correct responses. Black error bars are the standard error of the mean across participants. The lines reflect the model fits using the best fitting parameters: complete drop model (purple) and partial drop model (red). Each model was fit independently for each participant, and error bars reflect the standard error of the mean of the best-fitting parameters across participants. d Data (blue bars) and best-fitting models (purple and red lines) from long retention interval trials

Full size image

The critical question was whether working memory performance would again decline when the retention intervals were longer and whether this decline was due to changes in the attentional control parameter or due to changes in maximum capacity (Fig. 3a). We again observed worse performance after long retention intervals (nlong = 1.74 ± 0.91, nshort = 2.02 ± 0.75; t(19) = 3.73, p < 0.001, Cohen’s d = 0.34).

Computational modeling

We first compared our two computational models to determine whether the complete or partial drop model better explained our data. Once again, we found that both models made reasonable fits to the data (Fig. 2b, c). However, just as in Experiment 1, we found that data from both the short and long retention intervals were better fit by the partial drop model (∆BIClong = 590.38, ∆BICshort = 542.92) than the complete drop model. This finding reaffirms that performance across trials varies along a continuum and participants drop certain items from working memory while maintaining others over time. In fact, for the short retention interval trials, all participants were better fit by the partial drop model than the complete drop model. For the long retention interval trials, 17 out of 20 participants were better fit by the partial drop model, 2 out of 20 were better fit by the complete drop model, and 1 out of 20 participants were equally well fit by both models.

Next, we investigated the parameter fits for attentional control and maximum working memory capacity for the partial drop model. We again found that attentional control was reliably lower during long than short retention intervals (along = 0.73 ± 0.56, ashort = 1.15 ± 0.47; t(19) = 4.59, p < 0.001, Cohen’s d = 1.03). Additionally, there was not a reliable difference across retention intervals between maximum capacity (Kmaxlong = 3.00 ± 1.30, Kmaxshort = 2.95 ± 0.65; t(19) = − 0.24, p = 0.82; Cohen’s d = − 0.05).

Just as we did in Experiment 1, we additionally fit two combined models. One of these models (Kmax-free model) varied Kmax and kept a constant, while the other model (a-free model) varied a and kept Kmax constant. These models allowed us to account for behavior across short and long retention intervals at the same time. We found that the a-free model fit the data better than the Kmax-free model (∆BIC = 4.31). The comparison of these two models, once again, confirmed that maximum working memory capacity is stable across short and long retention intervals, whereas attentional control varies.

Discussion

In Experiment 2, we eliminated potential differences in preparation by randomly intermixing trials and, therefore, preventing participants from preparing for a certain length retention interval ahead of time. We replicated all of our findings from Experiment 1. Performance declined after long (vs. short) retention intervals. This decline in performance was graded, such that the amount of information in working memory across trials varied continuously. The maximum amount of information that could be maintained in working memory remained the same over both long and short retention intervals. However, the probability of maintaining this maximum amount of information in working memory declined for long compared to short retention intervals.

General discussion

Past work has shown that variability in attention and filtering at encoding is an important limiting factor for working memory performance (Adam et al., 2015; Fukuda & Vogel, 2011; Vogel, McCollough, & Machizawa, 2005). That said, the decline in working memory performance with longer retention intervals – for which encoding demands are perfectly matched – demonstrates that information is also lost even after successful encoding into working memory. Here, our main goals were to (1) characterize how the distributions of the number of items remembered varied across long and short retention intervals, and (2) use these distributions to characterize how the length of the retention interval impacts forgetting over time. Firstly, over two experiments, we observed that performance on a discrete whole-report task declined as retention interval increased (1.5 vs. 10 s). Secondly, we found evidence in favor of the partial drop model, in which information loss over time is best described as a probabilistic loss of individual items rather than a complete failure of storage during specific trials. We developed a refined computational model of working memory performance that simultaneously solves for attentional control (a) and a maximum capacity (Kmax) by using grid search. We observed that when participants had to maintain information for a longer amount of time, the maximum amount of information (Kmax) that they could store in working memory remained the same. However, the probability of sustaining attentional control (a) was lower after long compared to short retention intervals.

In both Experiments 1 and 2, an individual’s maximum working memory capacity (Kmax) was stable across short and long retention intervals. These results advocate for a perspective where maximal working memory capacity is relatively invariant across the population. Furthermore, there was relatively little range in maximal working memory capacity, suggesting that individuals differed not in the total maximum amount of information that they stored, but in the frequency with which they stored that information. An extension from these findings is that maximum working memory capacity might be an immutable variable, with little range across the population. However, one caveat to this interpretation is that we observed numerically lower values of maximal working memory capacity in Experiment 2, when retention interval length was inter-mixed. Therefore, there might be other factors, such as experimental design, which influence attentional control and/or maximum working memory capacity. Future work could address when and how maximum working memory capacity (Kmax) changes.

We found that performance decrements after long retention intervals were not driven by reductions in maximum capacity. However, precision of representations in working memory could still change over time, as has been previously suggested (Fougnie, 2008; Rademaker et al., 2018; Schneegans & Bays, 2018). Our task provides a coarse measure of individual working memory representations and, thus, we cannot draw strong conclusions about changes in precision. However, even if precision does change over time, it may not lead to an aggregate increase in forgetting rates at the level of individual items. Future work could investigate how working memory precision changes over time by using a whole report task where participants report the precise color of every representation on every trial (e.g., Adam et al., 2017).

In sum, with this series of experiments, we extend our understanding of the impact of retention interval length on working memory performance. Past work has tended to portray capacity limits in working memory as reflecting a “ceiling” on storage capacity, similar to the limited space inside a container. From that perspective, it is plausible that factors that impair working memory performance yield a reduction in the available space in working memory. By contrast, we highlight recent work that suggests that variations in working memory performance across individuals may be better understood in terms of the probability of achieving one’s maximum storage potential rather than in terms of differences in that potential (Adam et al., 2015). Likewise, we find that longer retention intervals reduce the probability of achieving one’s maximum storage capacity, instead of reducing that storage capacity. Thus, longer retention intervals do not reduce the maximum amount of information that can be stored in working memory, but they provide more opportunity to forget individual items through lapses of attentional control.