Abstract
In many everyday activities, individuals have a common interest in coordinating their actions. Orthodox game theory cannot explain such intuitively obvious forms of coordination as the selection of an outcome that is best for all in a common-interest game. Theories of team reasoning provide a convincing solution by proposing that people are sometimes motivated to maximize the collective payoff of a group and that they adopt a distinctive mode of reasoning from preferences to decisions. This also offers a compelling explanation of cooperation in social dilemmas. A review of team reasoning and related theories suggests how team reasoning could be incorporated into psychological theories of group identification and social value orientation theory to provide a deeper understanding of these phenomena.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Near the end of the 1960 movie Spartacus, directed by Stanley Kubrick, a Roman general addresses a group of slaves who have been captured after rising up in revolt, offering to spare them and return them to slavery if they identify their leader, Spartacus. To save his comrades, Spartacus (played by Kirk Douglas) rises to his feet and declares: “I am Spartacus.” Immediately and without any discussion among themselves, the other slaves stand up one by one, also claiming “I am Spartacus,” thereby preventing the Roman general from singling out their leader or anyone else for special punishment. This is a dramatic example of coordination, one of the most fundamental processes of social interaction, manifested whenever two or more individuals try to align their actions with one another in order to achieve a common goal.
Coordination is an elementary form of cooperation, relatively neglected by researchers, perhaps partly because it is so familiar and commonplace, but it is beginning to attract attention (e.g., Thomas, Scioli, Haque, & Pinker, 2014). Surprisingly, because it seems so simple and obvious, it turns out to be inexplicable by orthodox game theory, a highly developed theory designed precisely to explain interactive decision making. Coordination thus appears to be a classic example of the type of phenomenon referred to by Heider (1958), in which “the veil of obviousness that makes so many insights of intuitive psychology invisible to our scientific eye has to be pierced” (p. 7). In this article, we show how theories of team reasoning solve this problem convincingly and also provide a compelling explanation for cooperation in social dilemmas. We review the literature on team reasoning, including theoretical issues and experimental evidence, and, for the sake of balance and completeness, we discuss more briefly the principal competing theories of coordination and related theories of social psychology. We show how certain psychological theories could be strengthened significantly by incorporating team reasoning. Before going into details about these issues, it is necessary first to say something about game theory and why it fails to explain coordination.
Game theory
Although game-theoretic analyses of particular problems can be complicated and difficult to understand, the fundamental ideas of game theory are simple and straightforward. Any social interaction in which two or more decision makers choose between alternative ways of acting is a game in the technical sense, provided that the outcome depends on all their choices and they have consistent preferences among the possible outcomes. Virtually every interesting and important interpersonal, political, and economic interaction can therefore be modeled by a game, at least in principle. The conceptual apparatus of game theory, first expounded in detail by von Neumann and Morgenstern (1944), formalizes the decision makers (players), their ways of acting (strategies), and their preferences (payoffs), and makes two important assumptions. The first is a weak rationality assumption that players act in their own best interests (as they see them) in all circumstances that arise, given their preferences and their knowledge and beliefs at the time of acting. The second common knowledge assumption is that the specification of the game, including the players’ strategy sets and preferences, and the rationality of the players in the sense of the first assumption, are common knowledge in the game; this means that all players know these facts, all know that all know them, all know that all know that all know them, and so on. Common knowledge was a tacit assumption in game theory until it was explicitly introduced and named by Lewis (1969, pp. 52–69). From these primitive concepts and assumptions, the principal goal of the theory is simply to work out the logical implications that follow, seeking to determine how rational players will act in particular games or classes of games and hence what the outcomes will be.
Game theory spans disciplines across the behavioral and social sciences. Furthermore, according to at least one influential scientist, its extension into biology by Maynard Smith and Price (1973) was “one of the most important advances in evolutionary theory since Darwin” (Dawkins, 1976, p. 90). It is therefore remarkable that the theory fails completely in certain elementary cases, the most striking being strategic coordination. In particular, noncooperative game theory—the branch of the theory dealing with interactions in which the players cannot negotiate enforceable agreements among themselves—seems powerless to explain payoff dominance, a fundamental form of coordination.
Payoff dominance
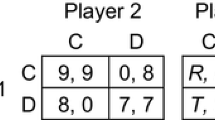
In their Nobel Prize winning work on equilibrium selection in noncooperative games, Harsanyi and Selten (1988, pp. 80–90, 355–359) discussed payoff dominance at length, especially in relation to Aumann’s (1987, p. 3) version of the Stag Hunt game, shown on the left in Fig. 1. Player 1 chooses between row C (cooperate) and row D (defect), Player 2 independently chooses between columns C and D, and the outcome of the game is one of the four cells where the chosen strategies intersect, with the payoffs to Players 1 and 2 shown in that order by convention. Aumann (1990) discussed this game again in a later publication, mentioning its name (as he had not done previously) but commenting in a footnote: “We have not succeeded in hunting this story down to its source” (p. 206). In fact, the game is named after a hypothetical strategic interaction suggested by the French philosopher Rousseau (1755, Part 2, paragraph 9) during a discussion of the early development of civil society. Rousseau imagined hunters who need to coordinate their actions (to choose C) to catch a stag (cerf), an endeavor that requires working together, but each is tempted to defect from the joint enterprise (to choose D) and go after a hare (lièvre), a smaller quarry that each could catch without the other’s help. In Aumann’s version of the game, the payoff for joint defection (7) is slightly less than the payoff for unilateral defection (8)—we might imagine that a hunter is slightly less likely to catch a hare if both hunters defect simultaneously, perhaps because both may chase after the same hare—but that payoff is less than the payoff for joint cooperation (9); and a unilateral C choice yields nothing (0).
On the right of Fig. 1 is a template commonly used to define any symmetric 2 × 2 game. According to the template, Aumann’s (1987, p. 3, 1990) Stag Hunt game is defined by the inequalities R > T > P > S. The version originally introduced into game theory and named by Lewis (1969, p. 7) had the implied payoff structure R > T = P > S, but the strategic properties of Aumann’s and Lewis’s versions are very similar.Footnote 1 Like any other game, the Stag Hunt game models a potentially unlimited range of social interactions (for a completely different scenario involving a butcher and a baker deciding whether to coordinate their actions and sell hot dogs, see Thomas et al., 2014). Some authorities, including Skyrms (2004), view the Stag Hunt game as the fundamental model of the evolution of social life.
In the Stag Hunt game (Fig. 1, left), the outcome (C, C) is a Nash equilibrium by virtue of the fact that the C strategies are best replies to each other. Neither player could get a better payoff by choosing differently against a co-player’s choice of C—against a C-chooser, a player receives 9 by choosing C but only 8 by choosing D—and it follows that neither player has a reason to regret choosing C if the co-player chooses it too. According to an important indirect argument that can be traced back to von Neumann and Morgenstern (1944, section 17.3.3, p. 148), in any game, a uniquely rational profile of strategies (one for each player) must necessarily be a Nash equilibrium. To see why this is so, note that the common knowledge assumption implies that, in any uniquely rational strategy profile, each player will be able to anticipate the co-player’s strategy, because each player knows that the co-player is rational and is therefore bound to choose the only available rational strategy; but if that strategy profile were not a Nash equilibrium, then at least one player would be choosing a strategy that is not a best reply, violating the rationality assumption; therefore, the strategy profile must be a Nash equilibrium.
In Aumann’s Stag Hunt game (Fig. 1), a complication arises from the fact that the outcome (D, D) is also a Nash equilibrium—against a D-chooser, a player receives 7 by choosing D but zero by choosing C. The asymmetric (C, D) and (D, C) outcomes are not Nash equilibria. It is tempting to think that rational players, who by definition seek to maximize their own payoffs, will coordinate by choosing C in this game simply because the (C, C) equilibrium is better for both than the (D, D) equilibrium—in game-theoretic terminology, because (C, C) is payoff dominant. In any game, an equilibrium, e, weakly payoff dominates another equilibrium, f, if every player receives at least as good a payoff in e as in f, and at least one player receives a better payoff; strong payoff dominance occurs when every player receives a strictly better payoff in e than in f. Economists and political scientists sometimes call payoff dominance Pareto dominance. In Aumann’s Stag Hunt game, remarkably, the fact that (C, C) is (strongly) payoff dominant does not provide the players with a reason, derivable from the standard assumptions, to choose their C strategies. The problem is that C is not an unconditionally best choice: It is best only if the co-player chooses C. In fact, against a D-chooser, the best reply is clearly D and not C. In other words, it is rational for a player to choose C if and only if there is a reason to expect the co-player to choose it, so the crucial question is whether a player has any reason to expect a co-player to choose C. The answer is clearly no, because the game is perfectly symmetric, and the co-player faces exactly the same dilemma.
The Hi-Lo game shown in Fig. 2 strips the payoff-dominance phenomenon bare and exposes the problem more starkly. Schelling (1960) introduced this game, calling it a “pure common-interest game” (p. 291), and Bacharach named it “Hi-Lo” in unpublished manuscripts and seminar presentations in the mid-1990s; the name probably first appeared in print in Bacharach and Stahl (2000). Using the template in Fig. 1 (right), the Hi-Lo game is defined by the inequalities and equalities R > P > S = T = 0. It is essentially a Stag Hunt game with the payoffs in the off-diagonal cells set to zero; (H, H) and (L, L) are Nash equilibria, and (H, H) is strongly payoff dominant over (L, L), as in the Stag Hunt game. Any 2 × 2 game that has positive payoffs (R, R) and (P, P) in the main diagonal and zero payoffs elsewhere is a Hi-Lo game, provided that R > P > 0.
Regarding the zeros, it is worth commenting that payoffs in game theory are assumed to be utilities, representing players’ preferences as determined or revealed by their own choices. Utilities are measured on interval scales that are unique up to a positive linear (affine) transformation and can differ between players; hence, adding a constant to all the payoffs in a game, or multiplying them all by a positive constant, leaves the strategic properties of a game intact. It follows that any set of payoffs that can be transformed into the specified pattern by positive linear transformations is also a Hi-Lo game.
In spite of its almost childlike simplicity, the Hi-Lo game models innumerable strategic interactions in everyday life, from two people deciding where to look for each other after being separated in a shopping mall (one location more convenient than another) to two car drivers deciding which side of a narrow road to move to when an ambulance needs to pass in an emergency (one side preferable in some way to the other). Colman, Pulford, and Lawrence (2014) offered the following illustrative scenario in which R = 2 and P = 1, as in Fig. 2:
Three children are trapped in a burning building, two of them in one room and the third in a second room some distance away. A neighbor breaks in and has just enough time to rescue either the two children in the first room or the single child in the second room, but the rescue can succeed only if another neighbor with a fire extinguisher, who has found a different point of entry, heads straight for the same room. If both go to the first room, then the two children in it will be rescued, and if both go to the second room, then the single child in that room will be rescued; but if each neighbor goes to a different room, then none of the children will be rescued. (p. 36)
Assuming that the neighbors prefer to save as many children as possible, and that each neighbor is aware of the other’s entry, the strategic structure of this burning building scenario matches the Hi-Lo game shown in Fig. 2, the first room corresponding to H and the second to L.
In Aumann’s Stag Hunt game, although the (C, C) equilibrium is payoff dominant, the (D, D) equilibrium is risk dominant in a sense defined mathematically by Harsanyi and Selten (1988, pp. 82–89), and risk dominance provides a positive reason for choosing D. Intuitively, it is obvious that D is much safer: a C choice risks a possible payoff of zero, whereas the worst possible payoff from a D choice is 7. In the Hi-Lo game, there is no complication arising from risk dominance, and H seems a “no-brainer” strategy choice. But careful analysis reveals once again that each player has a reason to choose H if and only if there is a reason to expect the co-player to choose it also, and there can be no such reason, because the co-player has a reason to choose H if and only if there is a reason to expect the first player to choose it. We are stuck in a vicious circle that provides neither player with any reason, based on the standard assumptions of game theory, to prefer H to L.
In spite of this vicious circle, the Hi-Lo game induces a powerful intuition in human decision makers that H is the rational choice, and experimental evidence confirms that virtually all players choose it (Bardsley, Mehta, Starmer, & Sugden, 2010). What accounts for this phenomenon? Classical game theory cannot explain it simply by pointing to the fact that (H, H) is payoff dominant. Harsanyi and Selten (1988), in order to achieve a “general theory of equilibrium selection in games” (pp. 357–359), therefore proposed adding a payoff-dominance principle to the standard rationality assumptions as an axiom. According to this principle, rational players choose payoff-dominant equilibria whenever they exist. Harsanyi and Selten acknowledged this to be an unsatisfactory and temporary work-around that provides no insight into the phenomenon it is designed to accommodate. Harsanyi (1995) abandoned it soon after, having been convinced by an argument put forward by Aumann (1990) that payoff-dominant Nash equilibria are not self-enforcing. In the Stag Hunt game, for example, “even the possibility of preplay communication will not enable the players to attain the payoff-dominant equilibrium—as long as the game is a noncooperative game without enforceable agreements” (Harsanyi, 1995, p. 94, footnote 3, italics in original).
Explaining coordination
Coordination has been a neglected aspect of interactive decision making, especially when viewed in relation to the vast amount of research attention that has been devoted to cooperation in the Prisoner’s Dilemma game and multiplayer social dilemmas, in which unilateral defection yields a higher payoff than joint cooperation (for reviews, see Balliet, Mulder, & Van Lange, 2011; Balliet & Van Lange, 2013; Ledyard, 1995). Thomas et al. (2014) call coordination mutualistic cooperation and cooperation of the social dilemma type altruistic cooperation. The problem of coordination is an interesting and arguably more basic phenomenon than altruistic cooperation: How do players coordinate on payoff-dominant outcomes, not only in games with multiple Nash equilibria but also more generally in common-interest games—games in which a single outcome payoff dominates all other outcomes, whether Nash equilibria or not? Leaving aside theories that involve alterations of the specification of the game, such as those that allow repetitions (e.g., Aumann & Sorin, 1989) or costless “cheap talk” between players (e.g., Anderlini, 1999; Farrell, 1988; Rabin, 1994), there are a couple of fallacies that need to be mentioned briefly before we turn to team reasoning.
Two common fallacies
The first is a fallacy that many people succumb to when they initially encounter the payoff-dominance problem. It is a belief that mere salience can explain coordination. A salient outcome is one that stands out from the others or that appears prominent or unique in some way, and it can serve as a focal point for coordination. Many decades ago, Schelling (1960) showed that people are remarkably adept at using salient focal points to solve problems of coordination, and there is no doubt that the (H, H) outcome in the Hi-Lo game, for example, is a focal point by virtue of the fact that it conspicuously offers higher payoffs than any other outcome. A focal point can provide a purchase for team reasoning but cannot explain coordination on its own. Gilbert (1989) presented a rigorous argument establishing that salience is not enough to provide a player with a reason for choosing a strategy. She showed that a player has no reason at all to choose a strategy associated with a salient focal point in the absence of an independent reason to expect the co-player to choose it. Furthermore, any attempt to derive, from the standard assumptions, a reason to expect a co-player to choose it generates a version of the vicious circle discussed above without leading to any conclusion, and this is now generally acknowledged by game theorists (e.g., Anderlini, 1999; Aumann & Sorin, 1989; Bacharach, 2006, Chapter 1; Bardsley et al., 2010; Janssen, 2001, 2006).
A second fallacy is the notion that if Player 1 (for example) has no reason to expect Player 2 to choose H or L in the Hi-Lo game, then Player 1 can use the principle of indifference (also called the principle of insufficient reason) and simply assume that Player 2 is equally likely to choose H or L. Under that assumption, Player 1’s expected payoff from choosing H is higher than from choosing L, because ½(2) + ½(0) = 1, whereas ½(0) + ½(1) = ½; therefore Player 1 will choose the payoff-maximizing strategy H. This argument is fallacious, because the problem is not one of individual decision making, where standard decision theory using simple expected utility maximization applies: Player 2 is not indifferent Nature but an intelligent player who can and will formulate and respond to expectations about Player 1’s intentions. If the argument from the principle of indifference were valid, then by the common knowledge assumption, Player 2 would anticipate Player 1’s choice of H and would choose a best reply to it, namely, H. But this means that Player 2 would choose H with certainty, and that contradicts the assumption on which Player 1’s argument for choosing H is based, namely that Player 2 is equally likely to choose H or L. This proves by reductio ad absurdum that the argument is invalid. The argument from the principle of indifference and closely related fallacies based on probabilities are discussed in greater depth by Colman, Pulford, and Lawrence (2014).
Team reasoning
According to theories of team reasoning, players solve coordination problems of the Hi-Lo or Stag Hunt type by adopting a distinctive mode of strategic reasoning from preferences to strategy choices. Standard game-theoretic reasoning amounts to asking What do I want? and, given my knowledge of the game and my expectations of what my co-player (s) will do, What should I do to achieve this? Team reasoning alters the unit of agency from the individual to the pair, or more generally to the group of players, by allowing each player to ask What do we want? and What should I do to play my part in achieving this? Team-reasoning players first search for an outcome that would be best for the pair or group of players; if such an outcome exists and is unique, they then identify and play their component strategies of the jointly optimal strategy profile, and if there is no uniquely best outcome for the group, then team reasoning may not be feasible. Within this theoretical framework, standard individual reasoning is merely a special case of team reasoning when the team has only one member (Bacharach, 1999; Gold & Sugden, 2007a, b).
The change of agency is both subtle and radical; it involves a concept of group agency in which rationality is transferred from individual players’ actions to the joint action of the group of players as a whole, although the decisions are ultimately taken by individuals. This notion is not entirely alien to psychology. Bandura (2000) has pointed out that, although social cognitive theory traditionally adopts an agentic perspective with its fundamental belief in personal efficacy, increasing social interdependence is creating an awareness of collective agency and beliefs in the power to produce effects through collective actions.
Team reasoning provides a solution to the problems of coordination and payoff dominance as follows. In Aumann’s Stag Hunt game (Fig. 1), a team-reasoning player notes that the (C, C) strategy profile is uniquely optimal for the player pair, because it offers the best possible payoff to both, and no other strategy profile yields either player a payoff as good as the payoff in (C, C). If both players adopt the team-reasoning mode, then both will select and play their C strategies. It is essentially the same in the Hi-Lo game shown in Fig. 2. The (H, H) strategy profile is uniquely optimal for the player pair, because it yields the best possible payoff to each player, therefore team-reasoning players select and play their H strategies. Team reasoning solves any common-interest game—any game with a single payoff-dominant outcome—in the same way.
Theories of team reasoning have been developed in some detail by Bacharach (1999, 2006) and Sugden (1993, 2003, 2015). Some of the ideas behind these theories can be traced back to Gilbert (1987, 1989, 1990); Hurley (1989, 1991); before them, Regan (1980); Gauthier (1975); and according to some authorities, originally, Hodgson (1967). Similar or at least closely related ideas have been suggested by Casajus (2001); Janssen (2001, 2006); Heath, Ho, and Berger (2006); Tuomela (2007, 2009); and Smerilli (2012).
Common knowledge of group identification
At first glance, team reasoning seems to make sense only if the co-player or all co-players are expected to adopt this mode of reasoning; for example, a player appears to have no reason to choose the C strategy in the Stag Hunt game (Fig. 1)—and the risk of a zero payoff provides a reason not to choose it—unless the co-player is expected to do likewise, and in the Hi-Lo game a player has no reason to choose or not to choose H in the absence of an expectation that the co-player will also choose H. It is only when both players identify with the group (in these cases, the dyad) that team reasoning seems workable. All theories of team reasoning involve assumptions about group identification by players, but Bacharach (1999) developed a theory of “unreliable team interaction” that allows the possibility of team reasoning in strategic interactions lacking common knowledge of group identification.
For Bacharach (1999, 2006), whether a player identifies with a particular group depends on how that player frames the decision problem. He defined a frame as the set of concepts that a player uses to conceptualize a problem, and in order to engage in team reasoning, a player’s frame must include the concept “we.” As already mentioned, the switch from individual to group identification has been extensively researched by social psychologists, who have discovered various factors that tend to increase or decrease it (Brewer, 2007; Brewer & Chen, 2007; Brewer & Gardner, 1996; Brewer & Kramer, 1986; Dawes, van de Kragt, & Orbell, 1988, 1990; Kramer & Brewer, 1984, 1986). Bacharach suggested that strong interdependence tends to induce or prime a “we” frame and that this is a necessary prerequisite for team reasoning.
Bacharach’s (1999) theory of reasoning in unreliable team interactions takes account of players’ expectations of group identification by their co-players. According to the theory, players who identify with the group and adopt the team-reasoning mode also know the probability that other players will do the same. His theory includes a parameter omega (0 ≤ ω ≤ 1), its value assumed to be common knowledge among those players who group identify, representing the probability that any individual player will adopt the “we” frame and identify with the group. Team reasoners maximize the expected collective payoff, taking into account the probability of group identification by the co-player(s); otherwise, if the value of ω is not high enough to make team reasoning yield a better expected payoff than individual reasoning, from the perspective of the team, then team reasoning leads to the same strategy choice that would arise from standard game-theoretic payoff maximization.
According to this theory, a player will sometimes adopt the team-reasoning mode even without assurance that the co-player(s) have identified with the group, that is, when ω < 1, and may thus end up receiving a worse individual payoff than expected. There are even extreme circumstances in which a player will adopt the team-reasoning mode despite a belief that the co-player(s) will certainly reason individually (ω = 0). Assuming once again that the collective payoff is the sum of individual payoffs, a case in point is the Prisoner’s Dilemma game shown in Fig. 3. In this game, whenever one player cooperates and the other defects, the collective payoff to the player pair (5) is greater than when both defect (2); therefore, even if ω = 0, a team-reasoning player will choose C, expecting a personal payoff of zero.
In Sugden’s (1993, 2003) theory, a player never deliberately pays a personal cost for team reasoning. For Sugden, individuals are motivated to adopt the team-reasoning mode only by a promise of a better outcome for everyone involved in the interaction, including themselves. It follows that, for Sugden, the collective utility function, or later the goal of achieving common interests (Sugden, 2015), can never make an individual player worse off, and in a Prisoner’s Dilemma, a player will never prefer an asymmetric outcome with a poor personal payoff to joint defection with a better personal payoff but a worse collective payoff.
According to widely accepted definitions in social psychology, cooperation is behavior that benefits two or more individuals including oneself, whereas altruism is behavior motivated exclusively to benefit one or more other individuals, and in evolutionary biology and economics, altruism is more explicitly paying a cost to provide a benefit to another individual or individuals (Clavien & Chapuisat, 2013). Coordination is clearly a form of cooperation—mutualistic cooperation, in the terminology of Thomas et al. (2014)—because it is motivated to benefit all individuals involved in an interaction.
Within this conceptual framework, Sugden’s (1993, 2003, 2015) approach to team reasoning is relevant to coordination, in contradistinction to Bacharach’s (1999, 2006), which includes a broader range of cooperative interactions, both mutualistic and altruistic. In Sugden’s theory, a player never cooperates in the Stag Hunt or Prisoner’s Dilemma game without having assurance that the co-player will also cooperate. Team reasoners pursue outcomes that are advantageous to all team members and, as a consequence, Sugden’s team reasoners, in contrast to Bacharach’s, do not knowingly expose themselves to the risk of receiving a sucker’s payoff. Sugden’s is a theory of mutually assured team reasoning in which a player will not risk team reasoning in the absence of assurance that the other team members will also team reason. In mutually assured team reasoning, players engage in team reasoning only if they have a reason or reasons to believe that the other player(s) identify with the group, endorse the idea of mutually assured team reasoning, and accept the idea that the goal is to maximize the collective payoff of the group or (in later writings) to achieve the group’s common interests.
Group identification
There is an influential stream of research in social psychology, arising from social identity theory, focusing on the closely related phenomenon of group identification and its effects on cooperation in social dilemmas (Brewer, 2007; Brewer & Chen, 2007; Brewer & Gardner, 1996; Brewer & Kramer, 1986; Dawes et al., 1988, 1990; Kramer & Brewer, 1984, 1986). This research has shown that mutually beneficial group identification can be increased substantially by the simple experimental manipulation of enhancing the salience of group identity—for example, by telling an all-female group that the research is designed to compare male and female behavior, thereby making their similarity salient.
Findings such as these are obviously relevant to understanding how individuals switch from individual to collective payoff maximization and team reasoning. For example, Hindriks (2012) argues that they contradict Bacharach’s (2006, p. 84) claim that strong interdependence is required for team reasoning. Bacharach suggested that team reasoning tends to occur in games that induce strong interdependence, a condition generally associated with games in which a Nash equilibrium is payoff dominated by a different outcome. But Bacharach (p. 86) acknowledged that games with this strong interdependence property do not invariably lead to team reasoning. In the Prisoner’s Dilemma game, for example, a player is likely to identify with the group (in this case, the pair) if the payoff-dominant joint cooperation (C, C) outcome appears salient, but may prefer to revert to individual reasoning and defect if the possibility of a double-cross by the co-player is salient. Smerilli (2012) developed this idea further by proposing an extension of the theory in which players use the “double-crossing intuition” as a basis for adjudicating between individual and team reasoning. Furthermore, experimental evidence has shown that perceived interdependence, as produced by a threat of negative outcomes from dissimilar-category others or a promise of positive outcomes from similar-category others, is a stronger driver of group identification than mere similarity or enhanced salience of group identity (Flippen, Hornstein, Siegal, & Weitzman, 1996; Henry, Arrow, & Carini, 1999). This is a rather different interpretation of interdependence from Bacharach’s strong interdependence, but the conclusion may apply also to strong interdependence, and the comparison would be well worth investigating experimentally.
Although they share many ideas and research questions, investigators based in behavioral game theory and social identity theory have rarely cited each other’s work, and their approaches are different in flavor. Nevertheless, incorporation of team reasoning into social identity theory could provide a deeper and more nuanced understanding of group identification. A synergistic mutual benefit would no doubt result from closer attention to each other’s work, or from collaborative research, but there is little sign of any such rapprochement at present. To borrow a powerful simile from Dummett (1994), the two streams of research “may be compared with the Rhine and the Danube, which rise quite close to one another and for a time pursue roughly parallel courses, only to diverge in utterly different directions and flow into different seas” (p. 25).
The team-reasoning theories of Bacharach (1999, 2006), Sugden (1993, 2003, 2015), and others differ in important ways, especially as regards the interpretation of the collective payoff function and what happens when common knowledge of group identification is lacking (Gold, 2012). Before discussing these issues, we first outline the implications of team reasoning for understanding cooperation in social dilemmas.
Team reasoning in social dilemmas
Although team reasoning was originally conceived to explain problems of coordination, it also provides a compelling explanation for a more familiar form of cooperation that occurs in social dilemmas. Figure 3 shows the Prisoner’s Dilemma game (T > R > P > S and 2R > S + T) with the now conventional payoff values popularized by Axelrod (1984). The game was discovered at the RAND Corporation, in California, in 1950, and was named by Tucker (1950/2001), after his well-known interpretation, in which two prisoners have to decide whether or not to confess to a joint crime in return for a lighter sentence. It models any binary-choice, dyadic interaction in which both players benefit by cooperating, but each is tempted to defect unilaterally to get the best possible payoff and relegate the co-player to the worst possible payoff. It has a unique Nash equilibrium at (D, D), and the D strategy is strongly dominant for both players in the sense that it yields a better payoff than C, irrespective of the co-player’s choice: 5 rather than 3 if the co-player cooperates, and 1 rather than zero if the co-player defects. (This is strategic dominance, not to be confused with payoff dominance.) Nevertheless, experimental studies have invariably revealed that human decision makers frequently cooperate, even when the game is played just once (Balliet & Van Lange, 2013; Ledyard, 1995; Roth, 1995; Van Lange, Joireman, Parks, & Van Dijk, 2013), and multiplayer social dilemmas also elicit frequent cooperation.
Team reasoning explains cooperation in social dilemmas very easily and, arguably, more persuasively than any other theory. Social dilemma researchers who are not conversant with game theory may believe that players cooperate simply because (C, C) yields a better payoff to each player than (D, D), but we have spelled out why this makes no sense as an explanation. The team reasoning explanation of cooperation is as follows. In Fig. 3, if a team-reasoning player interprets the collective payoff in the simplest and most intuitive way as simply the sum of payoffs to the two players, then it becomes obvious that the (C, C) strategy profile is uniquely optimal for the player pair, because 3 + 3 = 6 is a larger joint payoff than in any other outcome (we return to the issue of interpretation in the following subsection). If both players see this and also adopt the team-reasoning mode that we have described, then both will play C, their component strategies in this optimal profile.
Collective payoff function
Turning to areas of disagreement among team-reasoning researchers, the first step in team reasoning is to identify an outcome that is best for the group of players as a whole, and this is usually taken to imply that team-reasoning players seek to maximize a collective payoff function, but there is considerable debate and disagreement about the nature and relevance of this function.
The most intuitive interpretation of the collective payoff function is simply the sum (or, equivalently in game theory, the average) of the individual payoffs in each outcome of the game. This is in line with classical interpretations of utility in the writings of the pioneering utilitarian philosophers, building on what Bentham (1976/1977, p. 393) called his fundamental axiom: “the greatest happiness of the greatest number.” Early utilitarian philosophers suggested that what should be maximized is the sum of the individual utilities of everyone—this is called total utilitarianism or totalism. It is now widely accepted in moral philosophy that total utilitarianism generates a mere addition paradox and a repugnant conclusion (Parfit, 1984, Chapter 19). We need not go into those technical issues here; people who are not moral philosophers generally understand and accept the idea of interpersonal comparisons of utility (I enjoyed the concert twice as much as Jane did; This is going to hurt me as much as it hurts you), and the idea of summing or averaging two or more people’s utilities seems quite natural to some people, at least. Indeed, even von Neumann and Morgenstern (1944, Section 2.1.1) treated utility exactly like money: “unrestrictedly divisible and substitutable, freely transferable and identical, even in the quantitative sense, with whatever ‘satisfaction’ or ‘utility’ is desired by each participant” (p. 8), although they of all people knew that utilities are not really additive between people, because it was they who introduced the modern, formal theory of expected utility, with full axiomatic development in an appendix to the second edition of their book in 1947. According to the theory, a person’s utility is measured on an interval scale with an arbitrary zero point and unit of measurement for each individual.Footnote 2
Bacharach’s (1999) theory incorporates expected utility theory explicitly, but he acknowledged that the collective payoff function could be entirely different from the utilitarian function (Bacharach, 2006, p. 88). He believed the nature of the function to be an empirical question but that it must be Paretian in the sense that, if every individual receives as much utility in Outcome x as in Outcome y, and at least one individual receives more, then the collective payoff function must rank x above y. However, the Pareto criterion on its own does not fully specify a collective payoff function. It does not rank outcomes where the players’ interests must be traded off against each other. For example, it provides no ranking of the outcomes off the main diagonal in the Prisoner’s Dilemma game (Fig. 3) relative to the (C, C) outcome. In theory, a collective utility function could even allow the sacrifice of one player if it benefits the rest of the group. With this idea in mind, Bacharach (2006, p. 91, footnote 4) suggested that group identification could explain the existence of suicide bombers who are willing to sacrifice their lives for a cause.
Sugden (1993, 2003) rejected the idea of a collective payoff function as simply the sum or average of the individual payoffs in each outcome and, in later work, he rejected the relevance of a collective payoff function entirely, writing that “team members aim to achieve their common interests, not to maximise a common utility function” (Sugden, 2015, p. 156). In particular, Sugden assumed that individuals are motivated to engage in team reasoning only by the promise of better payoffs for themselves and other group members. In Sugden’s theory, players aim only to achieve team outcomes that give them more than their benchmark maximin payoffs—the highest payoffs that they can guarantee for themselves independently of the co-players’ strategy choices. This has the flavor of a bargaining or social contract theory. Indeed, Sugden (2015) mentioned Hobbes (1951/1961), comparing an individual’s maximin payoff to what that individual could get in a Hobbesian state of nature. A collective payoff function that simply maximizes the sum of the individual payoffs takes no account of whether some players reduce their individual payoffs by team reasoning, and therefore maximizing the sum of individual payoffs cannot function as a method of achieving common interests in Sugden’s theory (Gold, 2017).
Social value orientations
The psychological concept of social value orientation was introduced by Messick and McClintock (1968) and McClintock (1972) in recognition of the fact that several different social motives are possible in two-player social dilemmas: players may prefer to maximize their own individual payoffs (individualistic SVO), the collective payoffs of the player pair (cooperative SVO), the difference between own and co-player’s payoffs (competitive SVO), or the co-player’s payoffs (altruistic SVO). The default assumption in orthodox game theory, incorporated in the first assumption mentioned in the section on Game Theory, above, is that all players at all times are motivated by the individualistic SVO. However, reviews by Bogaert, Boone, and Declerck (2008) and Rusbult and Van Lange (2003) confirm the existence of much experimental evidence that people vary greatly in their predominant social motivations and the fact that SVO explains much of the variance in players’ choices in social dilemmas; in particular, people with the cooperative SVO make significantly more cooperative choices and expect more cooperation from their co-players than players with individualistic or competitive SVO. Merely noticing that the collective payoff is highest in (C, C) cannot, on its own, explain cooperation, for the same reason that it cannot explain a Hi choice in the Hi-Lo game discussed earlier, but the cooperative social value orientation (SVO) is nevertheless clearly relevant to the payoff dominance and coordination.
Most recent researchers have interpreted SVO as a trait or individual difference variable, measurable by questionnaires, that correlates significantly with personality descriptions given by friends and associates and predicts activities such as volunteering for charitable causes (Rusbult & Van Lange, 2003). However, Messick and McClintock (1968) originally conceived of SVO as an experimentally manipulable state variable—in their own experiment, they manipulated it by describing the co-player either as an “opponent” (to induce a competitive SVO) or a “partner” (to induce a cooperative SVO), and by displaying the players’ accumulated scores in different ways to draw attention to their own payoffs, joint payoffs, or relative payoffs. This suggests a feasible program of experimental research that could be designed to investigate SVO in relation to team reasoning. It seems likely that the stimulus conditions that tend to prime cooperative SVO in social dilemmas are also likely to prime team reasoning in coordination games. Incorporation of theoretical ideas and experimental findings from team reasoning would obviously strengthen and deepen SVO theory because the current theory cannot explain how or why cooperative SVO results in cooperative strategy choices in social dilemmas.
Experimental evidence for team reasoning
Mehta, Starmer, and Sugden (1994) reported the results of an experiment demonstrating that players in pure coordination games draw on shared concepts of salience to identify focal points that enable them to coordinate, but they did not discuss team reasoning as a mode of strategy selection in such games. The first published experiment explicitly designed to test team reasoning was reported by Colman, Pulford, and Rose (2008a), who presented subjects with five 3 × 3 common-interest games, each of which had a unique Nash equilibrium and a different outcome that was payoff dominant over all other outcomes, including the Nash equilibrium. In all five games, a majority of players chose strategies aligned with the payoff-dominant, collectively rational outcome in preference to individually rational strategies mandated by the Nash equilibria. This showed that, in these games, team reasoning predicted strategy choices more successfully than orthodox game theory did. Although these results are consistent with theories of team reasoning, they do not rule out other theories that explain the payoff-dominance phenomenon in different ways. Bardsley et al. (2010) reported two experiments specifically designed to distinguish between team reasoning and cognitive hierarchy theory (the main ideas of which are outlined in the section that follows). One of their experiments provided strong support for team reasoning, but the other supported cognitive hierarchy theory. Bardsley and Ule (2017) tested team reasoning experimentally against a theory according to which players choose best replies to co-players who choose randomly (a form of cognitive hierarchy theory), and the results were generally consistent with team reasoning.
Butler (2012) reported the results of two experiments designed to test Bacharach’s (1999, 2006) team-reasoning theory in particular. In the first experiment, he used 25 miscellaneous 2 × 2 games, including Stag Hunt, Prisoner’s Dilemma, Chicken, and Tender Trap games; and in the second, 20 Prisoner’s Dilemma games and 20 Chicken games. Although the results of both experiments were consistent with team reasoning, they did not support Bacharach’s mathematical model, according to which the proportion of team-reasoning strategy choices should be predicted by the value of the parameter ω, calculated by Butler for each game using an assumption of interpersonally additive payoffs.
Colman et al. (2014) reported the results of two experiments designed to test cognitive hierarchy theory, team reasoning, and strong Stackelberg reasoning, all of which provide putative explanations of coordination and are outlined in the subsection that follows, against one another. To get around the problem that these theories make identical predictions in common-interest games such as the Stag Hunt and Hi-Lo games, they used 3 × 3 and 4 × 4 experimental games, most of them asymmetric, all lacking payoff-dominant solutions, and each designed in such a way that the theories being tested make different predictions about the strategies that the players would choose. The two experiments yielded highly consistent results suggesting that cognitive hierarchy Level-1 reasoning, strong Stackelberg reasoning, and team reasoning each played a part in explaining strategy choices. Cognitive hierarchy Level-1 reasoning was most successful at predicting strategy choices, especially in 4 × 4 games, but strong Stackelberg reasoning was also successful in 3 × 3 games, and team reasoning, which imposes less of a cognitive burden on players than the other hypothesized reasoning processes, was successful in both 3 × 3 and 4 × 4 games.
Pulford, Colman, Lawrence, and Krockow (2017) tested six competing theories that can potentially explain cooperation in the Centipede game, a dynamic two-player game involving alternating cooperative or defecting choices. These researchers used four versions of the Centipede game with different payoff structures, plus a static (normal-form) version. The games were specially designed to test the theories against one another, each theory predicting a different pattern of behavior in the different versions of the game. The results decisively refuted four of the six theories that were tested. Only two theories, team reasoning and fuzzy-trace theory, successfully explained strategy choices across the different versions of this game.
Other explanations of coordination
As indicated earlier, theories of team reasoning are not the only explanations of coordination. For the sake of completeness, we sketch briefly in this section the principal alternatives, and we explain the fundamental ideas behind them in relation to the simplest Hi-Lo game shown in Fig. 2. What distinguishes team reasoning from most of the other theories is that it is a theory of rational choice, whereas the others, with the arguable exception of strong Stackelberg reasoning, are psychological explanations of nonrational behavior.
According to social projection theory (Acevedo & Krueger, 2005; Krueger, 2007; Krueger, DiDonato, & Freestone, 2012), most people expect others to behave as they do, and they therefore assume that, if they choose H (Fig. 2), then the co-player is also likely to choose H. It follows that a player expects to receive a payoff of 2 by choosing H and 1 by choosing L, and this provides a reason for choosing H. Al-Nowaihi and Dhami (2015) have recently developed a formal version of this theory. Social projection theory provides a psychological but not necessarily a rational mechanism for H choice. It is related to what economists and philosophers call evidential reasoning or magical thinking, which is generally regarded as irrational (Elster, 1989; Joyce, 1999; Lewis, 1981; Quattrone & Tversky, 1984).
Cognitive hierarchy and Level-k theories (Camerer, Ho, & Chong, 2004; Stahl & Wilson, 1994, 1995) are designed to model players who reason with varying levels of strategic depth. Level-0 players have no beliefs about their co-players and choose strategies either randomly, with uniform probability, or by using simple heuristics such as salience; Level-1 players maximize their own payoffs relative to a belief that their co-players are Level-0 players; Level-2 players maximize their own payoffs relative to a belief that their co-players are Level-1 players; and so on. Experiments have confirmed the findings of Camerer et al. that Level 1 is most common, followed by Level 2 (Bardsley et al., 2010; Colman et al., 2014). In the Hi-Lo game, a Level-1 player who assumes that the co-player is choosing between H and L randomly, with equal probability, chooses H, because that yields an expected payoff of 1, whereas choosing L yields ½—the same calculation as under the principle of indifference, mentioned earlier, but with a different idea behind it. Level-2 players choose H because they expect their co-players to choose H with certainty, and the same applies at higher levels.
Strong Stackelberg reasoning (Colman & Bacharach, 1997; Colman et al., 2014; Colman & Stirk, 1998; Pulford et al., 2014; Pulford et al., 2017) entails an assumption that players choose strategies as though their co-players could anticipate their choices. Thus, a Stackelberg reasoner chooses as though expecting a choice of H to be anticipated by the co-player, who would therefore choose H because it is the best reply, and an L choice to be met with an L choice by the co-player for the same reason. The Stackelberg reasoner gets a better payoff in the first case than the second and therefore chooses H. There is no necessary assumption that people who use strong Stackelberg reasoning actually believe that others can anticipate their choices, merely that they act as though this were the case. Strong Stackelberg reasoning is a straightforward generalization of a form of reasoning suggested by von Neumann and Morgenstern (1944, Sections 14.2 and 14.3) to explain rational strategy choices in strictly competitive games. It involves no magical thinking: players act as though their co-players could read their minds, without actually believing that they can, merely as a heuristic device to clarify the logic of the game. The reasoning described by von Neumann and Morgenstern is a special case of strong Stackelberg reasoning for strictly competitive games.
The theory of virtual bargaining (Misyak & Chater, 2014; Misyak, Melkonyan, Zeitoun, & Chater, 2014) proposes that individuals reason about problems of coordination by considering what strategies they would agree on if they could bargain or negotiate explicitly. In the Hi-Lo game and arguably also in the Stag Hunt game, it is obvious what bargain they would arrive at, hence communication is unnecessary and they choose the appropriate H or C strategies directly.
Where to from here? Interdisciplinary cross-fertilization
Team reasoning offers a persuasive solution to the ubiquitous problem of coordination in social interaction, and a growing body of experimental evidence reviewed in an earlier section suggests that it does indeed occur. The other prominent theories that we have outlined and discussed can also explain the phenomenon in principle, and there is evidence suggesting that they may also contribute to a full explanation, but team reasoning appears to have the strongest support across experiments. A full understanding of team reasoning requires further theoretical development and detailed experimental investigation of the stimulus conditions that prime it, and that is where psychologists could play a major role. The literature that we have reviewed suggests exciting possibilities for interdisciplinary integration that would help to advance both psychology (cognitive and social) and behavioral game theory.
Social psychologists working on group identification need to engage with the work of behavioral game theorists working on team reasoning, and vice versa. Psychologists Brewer and Chen (2007), in an excellent and otherwise comprehensive review of individualism and collectivism, did not even mention team reasoning, and it is quite rare for articles on team reasoning to make more than a passing reference to the burgeoning social psychological literature on group identification. It seems obvious that the two research traditions have a lot to learn from each other. If the manipulations reported by social psychologists as triggers of group identification (Brewer, 2007; Brewer & Chen, 2007; Brewer & Gardner, 1996; Brewer & Kramer, 1986; Dawes et al., 1988, 1990; Kramer & Brewer, 1984, 1986) have the same effect on team reasoning in games affording opportunities for coordination, then they will help to explain team reasoning directly, and the claim by Hindriks (2012) that strong interdependence is not a prerequisite for team reasoning will be vindicated. On the other hand, if strong interdependence can be shown experimentally to prime group identification, as hypothesized by Bacharach (2006, p. 84), then that would be an important addition, hitherto entirely neglected, to the social psychological theory of group identification. Incorporation of team reasoning into social identity theory could thus lead to a deeper understanding of group identification.
The other major opportunity for integration that emerges from our review relates to social value orientation (SVO), and the possibility of returning to the historical origins of this concept (McClintock, 1972; Messick & McClintock, 1968), when it was conceived primarily as a state variable, dependent on stimulus conditions, rather than a stable trait variable. Theories of team reasoning provide important insights into the stimulus conditions that lead to decision makers becoming motivated to maximize collective rather than individual payoffs. An SVO that is one of the most commonly observed is the cooperative SVO, according to which individuals are motivated to maximize the joint or collective payoff of the pair or group of players. An obvious lacuna in this theory, at least insofar as it purports to explain cooperation in social dilemmas, is that the cooperative motivation on its own does not amount to team reasoning, although it is a necessary step in the process of team reasoning. It therefore cannot explain cooperation fully, and incorporation of team reasoning into the theory of the cooperative SVO would obviously strengthen this theory significantly. In the Hi-Lo game, the payoff transformations associated with the cooperative or prosocial SVO merely results in another Hi-Lo game with larger payoffs (Colman, Pulford, & Rose, 2008b). Furthermore, any experimental findings on the stimulus conditions that prime the cooperative SVO, including those reported by Messick and McClintock all those years ago, are potentially relevant to our understanding of team reasoning and should be incorporated into behavioral game theory.
Concluding comments
Do people engage in team reasoning? It is difficult to argue that they do not, because they often say things that seem to imply that they do. People often claim to be performing some action “in the interests of the university,” “for the good of the department,” or “because it’s best for the family,” implying that they are pursuing group goals rather than individual self-interests, and there is no obvious reason to doubt that they mean what they say. Everyday experience suggests that it is not uncommon for people to set aside their individual self-interests and to act in what they judge to be best interests of groups to which they belong, including the religious, ethnic, and national groups that form part of their social identities. Although team reasoning is not the only explanation for such apparent manifestations of collective rationality, the experimental evidence suggests that team reasoning is at least one of the processes underlying them.
If team reasoning is indeed a common mode of choosing strategies in strategic interactions, then what is the nature of the collective payoff function that is implicitly being maximized when people adopt this mode of reasoning, if indeed that is what is happening? This is an open question, and there are sharp differences of opinion regarding the nature of this presumed function. At one extreme is the possibility that individuals maximize the objective payoffs of their co-players without any consideration of their own. This purely altruistic type of collective payoff function has been investigated theoretically, with interesting and unexpected results (Colman, Körner, Musy, & Tazdaït, 2011). At the other extreme is Sugden’s (1993, 2003, 2015) mutualistic assumption that individuals are motivated to engage in team reasoning only when they believe that they and all other group members will do likewise and that all will benefit from the resulting outcome. Concepts such as game harmony (Tan & Zizzo, 2008), indexed by product-moment correlation between the players’ payoffs in a two-player game, may help to explain when this is likely to occur. The nature of the collective payoff function is perhaps an empirical question that could be resolved by future experimental research.
Does team reasoning occur only when all members of a group feel sure that the others will also adopt the same approach? The theory developed by Bacharach (1999, 2006) does not restrict team reasoning to such situations of mutual assurance, but Sugden’s (1993, 2003, 2015) theory does: For Sugden, the motive for team reasoning is to achieve a better outcome for everyone, and players do not adopt this mode of reasoning without mutual assurance. This difference of opinion is difficult to resolve on purely theoretical grounds, although it is worth noting that Bacharach’s theory implies a more general conception of collective rationality and can, in principle at least, explain a wider range of instances of team reasoning. This difference may be an empirical question, or it may suggest the existence of different forms of team reasoning.
Team reasoning is a hard sell, especially in the United States and other fervently individualistic cultures. Cognitive and social psychology traditionally assumes an agentic view, according to which individuals are producers of experience and shapers of events, and human agency is conceived largely in terms of personal efficacy exercised individually (Bandura, 2000). But many human goals, from scheduling meetings and carrying large objects to agreeing international standards and coordinating military operations in theatres of war, are simply unattainable without coordination.
This article has drawn attention to exciting opportunities that appear to exist for incorporating team reasoning into social identity theory and also into the theory of cooperative social value orientation (SVO). Both theories could be significantly strengthened by such interdisciplinary cross-fertilization; furthermore, behavioral game theory could certainly benefit by incorporating some aspects of SVO theory, rather than assuming that decision makers are individualistically motivated in all circumstances. We agree with Thomas et al. (2014), who have argued that coordination or “mutualistic cooperation” deserves far more research attention than it has hitherto received:
Much has been learned about these domains of psychology from a focus on the problem of altruistic cooperation and the mechanisms of reciprocity. We hope that comparable insights are waiting to be discovered by psychologists as they investigate the problem of mutualistic cooperation. (p. 673)
Notes
Aumann’s Stag Hunt game is sometimes confused with the Assurance game, introduced by Sen (1969), in which R > P > T > S. Sen offered the following interpretation involving two people who face the choice of going to a lecture or staying at home: “Both regard being at the lecture together the best alternative; both, staying at home the next best; and the worst is for him or her to be at the . . . lecture without the other” (p. 4, footnote 5, italics in original).
Familiar interval scales are the Fahrenheit and Celsius scales of temperature. Suppose someone in New York, where Fahrenheit is commonly used, e-mails a relative in London, where the standard is Celsius, and says, “It’s quite warm here today: It’s 70 degrees,” and the relative replies, “We’re having a heatwave: It’s 30 degrees.” It would make no sense to say that the total temperature is 100 degrees, or that the average of the two temperatures is 50 degrees.
References
Acevedo, M., & Krueger, J. I. (2005). Evidential reasoning in the Prisoner’s Dilemma. American Journal of Psychology, 118, 431–457. Retrieved from http://www.jstor.org/stable/30039074
al-Nowaihi, A., & Dhami, S. (2015). Evidential equilibria: Heuristics and biases in static games of complete information. Games, 6(4), 637–676. https://doi.org/10.3390/g6040637
Anderlini, L. (1999). Communication, computability, and common interest games. Games and Economic Behavior, 27, 1–37. https://doi.org/10.1006/game.1998.0652
Aumann, R. J. (1987). Correlated equilibrium as an expression of Bayesian rationality. Econometrica, 55, 1–18. https://doi.org/10.2307/1911154
Aumann, R. J. (1990). Nash equilibria are not self-enforcing. In J. J. Gabszewicz, J. F. Richard, & L. A. Wolsey (Eds.), Economic decision making: Games econometrics and optimization: Contributions in honour of Jacques H. Drèze (pp. 201–206). Amsterdam, Netherlands: North Holland.
Aumann, R. J., & Sorin, S. (1989). Cooperation and bounded recall. Games and Economic Behavior, 1, 5–39. https://doi.org/10.1016/0899-8256(89)90003-1
Axelrod, R. (1984). The evolution of cooperation. New York, NY: Basic Books.
Bacharach, M. (1999). Interactive team reasoning: A contribution to the theory of co-operation. Research in Economics, 53, 117–147. https://doi.org/10.1006/reec.1999.0188
Bacharach, M., (2006). Beyond individual choice: Teams and frames in game theory (N. Gold, & R. Sugden, Eds.). Princeton, NJ: Princeton University Press.
Bacharach, M., & Stahl, D. O. (2000). Variable-frame level-n theory. Games and Economic Behavior, 32, 220–246. https://doi.org/10.1006/game.2000.0796
Balliet, D., Mulder, L. B., & Van Lange, P. A. M. (2011). Reward, punishment, and cooperation: A meta-analysis. Psychological Bulletin 137, 594–615. https://doi.org/10.1037/a0023489
Balliet, D., & Van Lange, P. A. M. (2013). Trust, conflict, and cooperation: A meta-analysis. Psychological Bulletin, 139(5), 1090–1112. https://doi.org/10.1037/a0030939
Bandura, A. (2000). Exercise of human agency through collective efficacy. Current Directions in Psychological Science, 9, 75–78. https://doi.org/10.1111/1467-8721.00064
Bardsley, N., Mehta, J., Starmer, C., & Sugden, R. (2010). Explaining focal points: Cognitive hierarchy theory versus team reasoning. Economic Journal, 120, 40–79. https://doi.org/10.1111/j.1468-0297.2009.02304.x
Bardsley N., & Ule, A. (2017). Focal points revisited: Team reasoning, the principle of insufficient reason and cognitive hierarchy theory. Journal of Economic Behavior & Organization, 133, 74–876. https://doi.org/10.1016/j.jebo.2016.10.004
Bentham, J. (1977). A fragment on government. In J. H. Burns & H. L. A. Hart (Eds.), The collected works of Jeremy Bentham: A comment on the commentaries and a fragment on government. Oxford, UK: Oxford University Press. (Original work published 1776)
Bogaert, S., Boone, C., & Declerck, C. (2008). Social value orientation and cooperation in social dilemmas: A review and conceptual model. British Journal of Social Psychology 47(3), 453–480. https://doi.org/10.1348/014466607X244970
Brewer, M. B. (2007). The importance of being we: Human nature and intergroup relations. American Psychologist, 62, 728–738. https://doi.org/10.1037/0003-066X.62.8.728
Brewer, M. B., & Chen, Y. R. (2007). Where (who) are collectives in collectivism? Toward conceptual clarification of individualism and collectivism. Psychological Review, 114, 133–151. https://doi.org/10.1037/0033-295X.114.1.133
Brewer, M. B., & Gardner, W. (1996). Who is this “we”? Levels of collective identity and self representations. Journal of Personality and Social Psychology, 71, 83–93. https://doi.org/10.1037/0022-3514.71.1.83
Brewer, M. B., & Kramer, R. M. (1986). Choice behavior in social dilemmas: Effects of social identity, group size, and decision framing. Journal of Personality and Social Psychology, 50, 543–549. https://doi.org/10.1037/0022-3514.50.3.543
Butler, D. J. (2012). A choice for “me” or for “us”? Using we-reasoning to predict cooperation and coordination in games. Theory and Decision, 73, 53–76. https://doi.org/10.1007/s11238-011-9270-7
Camerer, C. F., Ho, T.-H, & Chong, J.-K. (2004). A cognitive hierarchy model of games. Quarterly Journal of Economics, 119, 861–898. https://doi.org/10.1162/0033553041502225
Casajus, A. (2001). Focal points in framed games: Breaking the symmetry. Berlin, Germany: Springer-Verlag.
Clavien, C., & Chapuisat, M. (2013). Altruism across disciplines: One word, multiple meanings. Biology and Philosophy, 28, 125–140. https://doi.org/10.1007/s10539-012-9317-3
Colman, A. M., & Bacharach, M. (1997). Payoff dominance and the Stackelberg heuristic. Theory and Decision, 43, 1–19. https://doi.org/10.1023/A:1004911723951
Colman, A. M., Körner, T. W., Musy, O., & Tazdaït, T. (2011). Mutual support in games: Some properties of Berge equilibria. Journal of Mathematical Psychology, 55, 166–175. https://doi.org/10.1016/j.jmp.2011.02.001
Colman, A. M., Pulford, B. D., & Lawrence, C. L. (2014). Explaining strategic coordination: Cognitive hierarchy theory, strong Stackelberg reasoning, and team reasoning. Decision, 1, 35–58. https://doi.org/10.1037/dec0000001
Colman, A. M., Pulford, B. D., & Rose, J. (2008a). Collective rationality in interactive decisions: Evidence for team reasoning. Acta Psychologica, 128, 387–397. https://doi.org/10.1016/j.actpsy.2007.08.003
Colman, A. M., Pulford, B. D., & Rose, J. (2008b). Team reasoning and collective rationality: Piercing the veil of obviousness. Acta Psychologica, 128, 409–412. https://doi.org/10.1016/j.actpsy.2008.04.001
Colman, A. M., & Stirk, J. A. (1998). Stackelberg reasoning in mixed-motive games: An experimental investigation. Journal of Economic Psychology, 19, 279–293. https://doi.org/10.1016/S0167-4870(98)00008-7
Dawes, R. M., van de Kragt, J. C., & Orbell, J. M. (1988). Not me or thee but we: The importance of group identity in eliciting cooperation in dilemma situations: Experimental manipulations. Acta Psychologica, 68, 83–97. https://doi.org/10.1016/0001-6918(88)90047-9
Dawes, R. M., van de Kragt, J. C., & Orbell, J. M. (1990). Cooperation for the benefit of us: Not me, or my conscience. In J. J. Mansbridge (Ed.), Beyond self-interest (pp. 97–110). Chicago, IL: University of Chicago Press.
Dawkins, R. (1976). The selfish gene. Oxford, UK: Oxford University Press.
Dummett, M. (1994). Origins of analytic philosophy. Cambridge, MA: Harvard University Press.
Elster, J. (1989). The cement of society: A survey of social order. Cambridge, UK: Cambridge University Press.
Farrell, J. (1988). Communication, coordination and Nash equilibrium. Economics Letters, 27, 209–214. https://doi.org/10.1016/0165-1765(88)90172-3
Flippen, A. R., Hornstein, H. A., Siegal, W. E., & Weitzman, E. A. (1996). A comparison of similarity and interdependence as triggers for in-group formation. Personality and Social Psychology Bulletin, 22, 882–893. https://doi.org/10.1177/0146167296229003
Gauthier, D. (1975). Coordination as a principle of rational action among 2 or more individuals. Dialogue, 14, 195–221. https://doi.org/10.1017/S0012217300043365
Gilbert, M. (1987). Modelling collective belief. Synthese, 73, 185–204. https://doi.org/10.1007/BF00485446
Gilbert, M. (1989). Rationality and salience. Philosophical Studies, 57, 61–77. https://doi.org/10.1007/BF00355662
Gilbert, M. (1990). Rationality, coordination and convention. Synthese 84, 1–21. https://doi.org/10.1007/BF00485004
Gold, N. (2012). Team reasoning, framing and cooperation. In S. Okasha & K. Binmore (Eds.), Evolution and rationality: Decisions, co-operation and strategic behaviour (pp. 185–212). Cambridge, UK: Cambridge University Press.
Gold, N. (2017). Team reasoning: Controversies and open research questions. In K. Ludwig & M. Jankovic (Eds.), Handbook of collective intentionality (pp. 221–232). New York, NY: Routledge.
Gold, N., & Sugden, R. (2007a). Collective intentions and team agency. Journal of Philosophy, 104, 109–137. https://doi.org/10.5840/jphil2007104328
Gold, N., & Sugden, R. (2007b). Theories of team agency. In F. Peter & H. B. Schmid (Eds.), Rationality and commitment (pp. 280–312). Oxford, UK: Oxford University Press.
Harsanyi, J. C. (1995). A new theory of equilibrium selection for games with complete information. Games and Economic Behavior, 8, 91–122. https://doi.org/10.1016/S0899-8256(05)80018-1
Harsanyi, J. C., & Selten, R. (1988). A general theory of equilibrium selection in games. Cambridge, MA: MIT Press.
Heath, C., Ho, B., & Berger, J. (2006). Focal points in coordinated divergence. Journal of Economic Psychology, 27, 635–647. https://doi.org/10.1016/j.joep.2006.04.004
Heider, F. (1958). The psychology of interpersonal relations. Hillsdale, NJ: Erlbaum.
Henry, K. B., Arrow, H., & Carini, B. (1999). A tripartite model of group identification: Theory and measurement. Small Group Research, 30(5), 558–581. https://doi.org/10.1177/104649649903000504
Hindriks, F. (2012). Team reasoning and group identification. Rationality and Society, 24(2), 198–220. https://doi.org/10.1177/1043463111429274
Hobbes, T. (1961). Leviathan. London: Macmillan. (Original work published 1651)
Hodgson, D. (1967). Consequences of utilitarianism. Oxford, UK: Clarendon Press.
Hurley, S. (1989). Natural reasons. Oxford, UK: Oxford University Press.
Hurley, S. (1991). Newcomb’s problem, prisoners’ dilemma, and collective action. Synthese, 86, 173–196. https://doi.org/10.1007/BF00485806
Janssen, M. C. W. (2001). Rationalising focal points. Theory and Decision, 50, 119–148. https://doi.org/10.1023/A:1010349014718
Janssen, M. C. W. (2006). On the strategic use of focal points in bargaining situations. Journal of Economic Psychology, 27, 622–634. https://doi.org/10.1016/j.joep.2006.04.006
Joyce, J. M. (1999). The foundations of causal decision theory. Cambridge, UK: Cambridge University Press.
Kramer, R. M., & Brewer, M. B. (1984). Effects of group identity on resource use in a simulated commons dilemma. Journal of Personality and Social Psychology, 46, 1044–1057. https://doi.org/10.1037/0022-3514.46.5.1044
Kramer, R. M., & Brewer, M. B. (1986). Choice behavior in social dilemmas: Effects of social identity, group-size, and decision framing. Journal of Personality and Social Psychology, 50, 543–549. https://doi.org/10.1037/0022-3514.50.3.543
Krueger, J. I. (2007). From social projection to social behavior. European Review of Social Psychology, 18, 1–35. https://doi.org/10.1080/10463280701284645
Krueger, J. I., DiDonato, T. E., & Freestone, D. (2012). Social projection can solve social dilemmas. Psychological Inquiry, 23, 1–27. https://doi.org/10.1080/1047840X.2012.641167
Ledyard, J. O. (1995). Public goods: A survey of experimental research. In A. E. Roth & J. H. Kagel (Eds.), The handbook of experimental economics (Vol. 1, pp. 111–194). Princeton, NJ: Princeton University Press.
Lewis, D. K. (1969). Convention: A philosophical study. Cambridge, MA: Harvard University Press.
Lewis, D. K. (1981). Causal decision theory. Australasian Journal of Philosophy, 59(1), 5–30. https://doi.org/10.1080/00048408112340011
Maynard Smith, J., & Price, G. R. (1973). The logic of animal conflict. Nature, 246(5427), 15–18. https://doi.org/10.1038/246015a0
McClintock, C. G. (1972). Social motivation: A set of propositions. Behavioral Science, 17(5), 438–454. https://doi.org/10.1002/bs.3830170505
Mehta, J., Starmer, C., & Sugden, R. (1994). The nature of salience: An experimental investigation of pure coordination games. American Economic Review, 84(3), 658–673. Retrieved from http://EconPapers.repec.org/RePEc:aea:aecrev:v:84:y:1994:i:3:p:658-73
Messick, D. M., & McClintock, C. G. (1968). Motivational bases of choice in experimental games. Journal of Experimental Social Psychology 4(1), 1–25. https://doi.org/10.1016/0022-1031(68)90046-2
Misyak, J. B., & Chater, N. (2014). Virtual bargaining: A theory of social decision-making. Philosophical Transactions of the Royal Society, B: Biological Sciences, 369, 20130487. https://doi.org/10.1098/rstb.2013.0487
Misyak, J. B., Melkonyan, T., Zeitoun, H., & Chater, N. (2014). Unwritten rules: Virtual bargaining underpins social interaction, culture, and society. Trends in Cognitive Sciences, 18, 512–519. https://doi.org/10.1016/j.tics.2014.05.010
Parfit, D. (1984). Reasons and persons. Oxford, UK: Oxford University Press.
Pulford, B. D., Colman, A. M., & Lawrence, C. L. (2014). Strong Stackelberg reasoning in symmetric games: An experimental replication and extension. PeerJ, 2, e263, 1–30. https://doi.org/10.7717/peerj.263
Pulford, B. D., Colman, A. M., Lawrence, C. L., & Krockow, E. M. (2017). Reasons for cooperating in repeated interactions: Social value orientations, fuzzy traces, reciprocity, and activity bias. Decision 4(2), 102–122. https://doi.org/10.1037/dec0000057
Quattrone, G. A., & Tversky, A. (1984). Causal versus diagnostic contingencies: On self-deception and on the voter’s illusion. Journal of Personality and Social Psychology, 46(2), 237–248. https://doi.org/10.1037/0022-3514.46.2.237
Rabin, M. (1994). A model of pre-game communication. Journal of Economic Theory, 63, 370–391. https://doi.org/10.1006/jeth.1994.1047
Regan, D. T. (1980). Utilitarianism and co-operation. Oxford, UK: Clarendon Press.
Roth, A. E. (1995). Introduction to experimental economics. In J. Kagel & A. E. Roth (Eds.), Handbook of experimental economics (pp. 3–109). Princeton, NJ: Princeton University Press.
Rousseau, J.-J. (1755). Discours sur l’origine et les fondements de l’inégalité parmi les hommes [Discourse on the origin and the foundations of inequality among men]. In J.-J. Rousseau (Ed.), Oeuvres Complètes (Vol. 3, pp. 109–223). Paris, France: Edition Pléiade.
Rusbult, C. E., & Van Lange, P. A. M. (2003). Independence, interaction, and relationships. Annual Review of Psychology, 54(1), 351–375. https://doi.org/10.1146/annurev.psych.54.101601.145059
Schelling, T. C. (1960). The strategy of conflict. Cambridge, MA: Harvard University Press.
Sen, A. K. (1969). A game-theoretic analysis of theories of collectivism in allocation. In T. Majumdar (Ed.), Growth and choice: Essays in honour of U. N. Ghosal (pp. 1–17). Calcutta, India: Oxford University Press.
Skyrms, B. (2004). The Stag Hunt and the evolution of social structure. Cambridge, UK: Cambridge University Press.
Smerilli, A. (2012). We-thinking and vacillation between frames: Filling a gap in Bacharach’s theory. Theory and Decision, 73, 539–560. https://doi.org/10.1007/s11238-012-9294-7
Stahl, D. O., & Wilson, P. W. (1994). Experimental evidence on players’ models of other players. Journal of Economic Behavior & Organization, 25, 309–327. https://doi.org/10.1016/0167-2681(94)90103-1
Stahl, D. O., & Wilson, P. W. (1995). On players’ models of other players: Theory and experimental evidence. Games and Economic Behavior, 10, 218–254. https://doi.org/10.1006/game.1995.1031
Sugden, R. (1993). Thinking as a team: Towards an explanation of nonselfish behavior. Social Philosophy and Policy, 10, 69–89. https://doi.org/10.1017/S0265052500004027
Sugden, R. (2003). The logic of team reasoning. Philosophical Explorations, 6(3), 165–181. https://doi.org/10.1080/10002003098538748
Sugden, R. (2015). Team reasoning and intentional cooperation for mutual benefit. Journal of Social Ontology, 1, 143–166. https://doi.org/10.1515/jso-2014-0006
Tan, J. H. W., & Zizzo, D. J. (2008). Groups, cooperation and conflict in games. The Journal of Socio-Economics, 37, 1–17. https://doi.org/10.1016/j.socec.2006.12.023
Thomas, K. A., De Scioli, P., Haque, O. S., & Pinker, S. (2014). The psychology of coordination and common knowledge. Journal of Personality and Social Psychology, 107, 657–676. https://doi.org/10.1037/a0037037
Tucker, A. (2001). A two-person dilemma (Unpublished notes, Stanford University). Reprinted in E. Rasmussen (Ed.), Readings in games and information (pp. 7–8). Malden, MA: Blackwell. (Original work published 1950)
Tuomela, R. (2007). The philosophy of sociality: The shared point of view. Oxford, UK: Oxford University Press.
Tuomela, R. (2009). Beyond individual choice: Teams and frames in game theory. Economics and Philosophy, 25, 125–133. https://doi.org/10.1017/S0266267108002356
Van Lange, P. A. M., Joireman, J. Parks, C., & Van Dijk, E. (2013). The psychology of social dilemmas: A review. Organizational Behavior and Human Decision Processes 120(2), 125–141. https://doi.org/10.1016/j.obhdp.2012.11.003
von Neumann, J., & Morgenstern, O. (1944). Theory of games and economic behavior. Princeton, NJ: Princeton University Press.
Acknowledgements
Preparation of this article was supported by an award to the first author from the Leicester Judgment and Decision Making Endowment Fund (Grant RM43G0176) and to the second author by funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement 283849.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Colman, A.M., Gold, N. Team reasoning: Solving the puzzle of coordination. Psychon Bull Rev 25, 1770–1783 (2018). https://doi.org/10.3758/s13423-017-1399-0
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13423-017-1399-0