Abstract
Knowing which properties of visual displays facilitate statistical reasoning bears practical and theoretical implications. Therefore, we studied the effect of one property of visual diplays – iconicity (i.e., the resemblance of a visual sign to its referent) – on Bayesian reasoning. Two main accounts of statistical reasoning predict different effect of iconicity on Bayesian reasoning. The ecological-rationality account predicts a positive iconicity effect, because more highly iconic signs resemble more individuated objects, which tap better into an evolutionary-designed frequency-coding mechanism that, in turn, facilitates Bayesian reasoning. The nested-sets account predicts a null iconicity effect, because iconicity does not affect the salience of a nested-sets structure—the factor facilitating Bayesian reasoning processed by a general reasoning mechanism. In two well-powered experiments (N = 577), we found no support for a positive iconicity effect across different iconicity levels that were manipulated in different visual displays (meta-analytical overall effect: log OR = −0.13, 95 % CI [−0.53, 0.28]). A Bayes factor analysis provided strong evidence in favor of the null hypothesis—the null iconicity effect. Thus, these findings corroborate the nested-sets rather than the ecological-rationality account of statistical reasoning.
Similar content being viewed by others
Research has firmly established that people struggle with statistical reasoning, but has also identified some methods of improvement (e.g., Cosmides & Tooby, 1996; Gigerenzer & Hoffrage, 1995; Girotto & Gonzalez, 2001). In Bayesian reasoning, for example, presenting statistical information in a nested-sets structure leads to more Bayesian inferences than in a normalized structure (e.g., “4 out of 6 chances” vs. “67 % chance”; Sloman, Over, Slovak, & Stibel, 2003). Visual displays accompanying a Bayesian task represent another source of improvement (Brase, 2009; Cosmides & Tooby, 1996; Sedlmeier, 1999; Sloman et al., 2003; Yamagishi, 2003). Indeed, visual displays accompanying problems with normalized structures benefit participants unambiguously (Sedlmeier, 1999; Sloman et al., 2003). However, the evidence is more mixed for problems entailing nested-sets structures—whereas visual displays did not improve Bayesian performance in tasks involving natural frequencies (Cosmides & Tooby, 1996) or nested-sets probabilities (Sloman et al., 2003), they did benefit performance in tasks featuring a chances format (Brase, 2009).
Since the authors used different visual displays, such contradictory evidence raise a question as to what specifically in visuals promoted the improved statistical performance. A better understanding of the underlying mechanisms would enable the design of more effective visual displays; it would also inform a theoretical debate between the two accounts of Bayesian reasoning: the ecological-rationality account and the nested-sets account. According to some proponents of the ecological-rationality account, visuals facilitate performance to the extent they mimic the natural occurrence of statistical information—the individuated objects with a natural-sampling structure—because these tap into an evolutionary designed frequency-coding mechanism (Brase, 2009; Cosmides & Tooby, 1996). In contrast, according to some proponents of the nested-sets account, visuals facilitate performance to the extent they make the relationships between the sets, the nested-sets structure, more “visible” to participants (Barbey & Sloman, 2007; Sloman et al., 2003; Tversky & Kahneman, 1983). When the statistical format already highlights the nested-sets structure, the presence of a visual is redundant and does not promote Bayesian reasoning.
Thus, two separate properties of visuals were proposed to enable the facilitation: (1) the iconicity of the visual elementsFootnote 1 (i.e., the extent to which the signs resemble the represented objects), and (2) the depiction of the nested-sets/natural-sampling structure (i.e., the specific partitioned structure of the statistical information). Although the effect of the partitioned information structure is a common ground for both accounts, the effect of iconicity is not. The ecological-rationality account predicts a positive iconicity effect on statistical reasoning (iconicity-effect hypothesis), because the higher in iconicity the representations are, the more easily they should elicit frequency representations, which tap into “intuitive cognitive mechanisms for tracking frequencies of real-world objects, events or locations” (Brase, 2009, p. 372). Therefore, increasing the iconicity of displays should increase performance with less-individuated objects such as chances. For instance, chances represented by icon arrays (i.e., pictographs,Footnote 2 high-iconic representations) led to superior performance relative to chances represented by dots in Venn diagrams (or, rather, Euler circlesFootnote 3; low-iconic representations): “Adding dots to Venn circles . . . does not appear to be sufficient to generate facilitation similar to that found with iconic representations” (Brase, 2009, p. 379). In contrast, the nested-sets account predicts a null iconicity effect on statistical reasoning (null-iconicity hypothesis), because high-iconic representations entail the same nested-sets structure as do low-iconic representations, which is the only factor responsible for facilitation and is processed by a general reasoning mechanism (Sloman et al., 2003).
Previous research has addressed the effects of iconicity and nested-sets components by showing differences in the magnitudes of the effects for various visual displays deemed to represent these properties (see Brase, 2009; Sedlmeier, 1999; Sloman et al., 2003; Yamagishi, 2003). Most recently, Brase found that normative performance in a Bayesian task with chances accompanied by an Euler circles diagram (either empty or with dots) was lower than when chances were accompanied by pictographs, and he attributed this effect to—what we will label here as—iconicity. Thus, prior research has estimated the iconicity effect from comparisons between different types of visual displays (e.g., Euler circles and pictographs). Different displays may represent not only different levels of iconicity, but different visual patterns not related to iconicity, different wordings connecting the tasks with the displays, or different previous states of knowledge of the displays. Indeed, from a graph-processing point of view, such differences as mentioned above could affect reasoning performance because of their effect on the basic graph comprehension processes not related to iconicity (such as encoding the visual patterns of the displays, translating the patterns into conceptual relations, or identifying referents of the relations; see Carpenter & Shah, 1998). For example, in visuals accompanying a Bayesian task, dots in Euler circles could be interpreted as having an illustrative meaning (e.g., to represent “shading” denoting a category), whereas icons in pictographs could be interpreted as having a literal meaning (e.g., to represent corresponding numbers in a task)—not because of different levels of iconicity, but because of different previous experiences with the visuals. Such a visual pattern would translate into a conceptually different relationship between the task and the visual, which could affect the performance. In summary, we do not know whether the “iconicity effect” observed in previous studies occurred due to iconicity or to other factors.
Present research
In this article, we aim to estimate the effect of iconicity on Bayesian reasoning without the confounding variables mentioned above. We adopted the paradigm that Gaissmaier et al. (2012) had used to study the comprehension of health-related statistics, in which the authors manipulated the iconicity of visual elements representing the objects (e.g., women represented as icons or photographs) within one visual display rather than between types of visual displays. Similarly, we disentangled the effect of iconicity from other possible facilitating variables that are inherent to visual displays by manipulating the iconicity of the visual elements within the same types of visual displays. In Experiment 1, we investigated the effect of an orthogonal manipulation of iconicity (iconicity low [dots] vs. high [icons]) and visual displays (Euler circles and pictographs) on Bayesian reasoning with chances. In Experiment 2, we tested the effect of Euler circles with three levels of iconicity (i.e., dots, icons, and 3-D plastic figurines) on Bayesian reasoning with chances, using a verbally concealed nested-sets structure. We hypothesized that a positive iconicity effect would support the ecological-rationality account, whereas a null iconicity effect would support the nested-sets account.
Experiment 1
Method
Participants and design
We assumed an iconicity effect similar to the one in Brase’s (2009, Exp. 3) study: a 24.0 % difference (23.6 % correct answers across two low-iconicity levels, subtracted from 47.6 % correct answers across two high-iconicity levels) and α = .05, 1 – β = .80, and a two-sided test (Cohen, 1988). Therefore, we planned to recruit 62 participants per experimental condition (i.e., in total 310 participants, adjusted then for the assumption that 20 % would fail to pass an instructional manipulation check; Oppenheimer, Meyvis, & Davidenko, 2009).
Consequently, 372 Amazon Mechanical Turk users participated in this experiment. We excluded 54 (four because of a duplicated entry, and 50 others because they failed to pass the instructional manipulation check) and analyzed the data from the remaining 318 participants (184 males, 134 females; age range 18–72 years, M = 32.8, SD = 11.9). In a between-subjects design, the participants were randomly allocated to one of the five conditions: four experimental conditions, manipulated in a 2 (iconicity: dots vs. icons) × 2 (visual displays: Euler circles vs. pictographs) design, and one control condition (no pictorial representation).
Materials and procedure
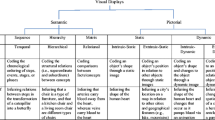
Participants in the experimental conditions solved a Bayesian problem, the Disease X problem (as had been used in Brase, 2009; see Table 1, panel A), which was accompanied by one of the four visual displays depicted in Fig. 1a: Euler circles with dots, Euler circles with icons, a pictograph with dots, or a pictograph with icons. Participants in the control condition solved the same Bayesian problem, but with no visual aids. Afterward, all participants were asked to answer an unexpected recognition task (a paradigm employed in Mani & Johnson-Laird, 1982). It consisted of eight statements describing a mental model of the problem (the Bayesian Reasoning Understanding Scale; see Table 1, panel B) that measured the participants’ understanding of the problem. On the basis of an item discrimination analysis (item-total correlations), we combined six items into an index ranging from 0 (no understanding) to 6 (complete understanding) (Cronbach’s α = .72, M = 4.9, SD = 1.5). Finally, participants answered the question of whether they had previous experience with Bayesian tasksFootnote 4 and some sociodemographic questions.
Visual displays used in (a) Experiment 1 (upper panel) and (b) Experiment 2 (lower panel). Panel A. In Experiment 1, the figures were preceded by the following text: “The picture below summarizes the above information, and is provided for you to use in the process of answering the following item. 100 chances are represented by the 100 dots [figures] printed below. Dots [Figures] that are in a dark-grey circle (darkened) represent those chances with the infection. Dots [Figures] that are in a light-grey circle are those chances which have a positive reaction to the test.” The text without italics, brackets, and parentheses represents the exact wording for the Euler circles in the low-iconicity condition. The squared brackets indicate alterations in the wording for the high-iconicity conditions. The parentheses indicate an alteration in the wording for the pictograph conditions. Panel B. In Experiment 2, the figures were preceded by the following text: “Dots [icons, 3-D plastic figurines] in the picture below represent the information from the task above and correspond with the numerical values, which the task contains.” The text without brackets represents the exact wording for the Euler circles in the low-iconicity condition. The squared brackets indicate alterations in the wording for the medium- and high-iconicity conditions. Please note that participants saw real 3-D figurines placed in the circles drawn on a sheet of paper in high level iconicity condition; the picture above depicts only a schematic representation of this condition
Results and discussion
The overall proportion of correct Bayesian answers was relatively high and varied just minimally and nonsignificantly as a function of the manipulations (Table 2, upper panel): The visual displays provided no additional benefit, as compared with the control group, and most importantly, iconicity did not influence the Bayesian performance. Additionally, the different visual displays (Euler circles or pictographs) did not influence Bayesian performance (respectively, 37.9 % vs. 38.3 %), χ 2(1) < 0.01, p = 1.000, φ < .01. A two-way analysis of variance (ANOVA) with iconicity and types of visual displays as independent variables and the Bayesian Reasoning Understanding Scale score as a dependent variable yielded similarly nonsignificant results (all effects: Fs < 1 and η p 2s < .01).
Nevertheless, not rejecting the null hypothesis does not logically entail accepting the null hypothesis (Albert, 2009; Rouder, Speckman, Sun, Morey, & Iverson, 2009). Therefore, we quantified the evidence to support the null or the alternative hypothesis by computing a Bayes factor for the focal effect of iconicity on (a) the proportion of correct answers and (b) the extent of Bayesian reasoning understanding. A Bayes factor analysis for the proportion of correct answers yielded substantial evidence to support the null iconicity effect (BF01 = 2.91, assuming a uniform distribution of priors; see Albert, 2009): The data were almost three times more likely under H0 than H1. A Bayes factor analysis for the extent of Bayesian reasoning understandingFootnote 5 yielded strong evidence to support the null iconicity effect (BF01 = 10.18, assuming equal priors for both hypotheses; Rouder et al., 2009): The data were approximately 10 times more likely under H0 than H1.
Taken together, our findings indicate that the level of iconicity of the visual displays did not play a role in facilitating Bayesian reasoning. This result is not consistent with the ecological-rationality account, which assumes that high-iconic representations facilitate Bayesian reasoning because they better tap into cognitive mechanisms for tracking frequencies (Brase, 2009). The null iconicity effect supports the nested-sets account, which does not assume that the iconicity of visuals is the driving force of the facilitation (Sloman et al., 2003).
We should, nevertheless, consider alternative explanations for the null iconicity effect before drawing strong theoretical conclusions. First, the lack of facilitation found here for the visual displays, in contrast to Brase (2009), might have hindered the effect of iconicity on reasoning. Second, the lack of an iconicity effect might have been related to the task’s administration: We presented the visuals through a computer screen and not in a paper-and-pencil format (as had Brase, 2009). It is possible that high-iconic visuals may only encourage more interactivity, which has been shown to facilitate reasoning, than low-iconic visuals when they are presented in a paper-and-pencil format (e.g., Vallée-Tourangeau & Krüsi Penney, 2005). For example, high-iconic displays could trigger more spontaneous notes or drawings that would help people realize the nested-sets structure of the display. Finally, the null iconicity effect may have been due to a weak iconicity manipulation. To test these possibilities, we designed the second experiment, in which we (1) modified the wording of the Disease X text problem to decrease the salience of the nested-sets structure, and therefore decrease the overall performance (this should maximizes chances to detect a beneficial effect of visual displays); (2) presented the Bayesian problem in a paper-and-pencil form, to enable interactivity; and (3) devised an additional manipulation of a high-iconic visual featuring concrete physical stimuli (i.e., 3-D plastic figurines), as had been suggested in Brase (2009).
Experiment 2
Method
Participants and design
A total of 259 social science undergraduates (62 males, 197 females; age range 19–28 years, M = 21.2, SD = 1.3; one person failed to report age) of Comenius University in Slovakia participated in this experiment. In a between-subjects design, the participants were randomly allocated to one of the four conditions: three experimental conditions (iconicity: dots, icons, or 3-D plastic figurines; see Fig. 1, panel B) and one control condition (no visual aid).
Materials and procedure
Participants solved the modified version of the Disease X problem (see Table 1, panel C) accompanied by a visual display (i.e., Euler circles) with one of the three different levels of iconicity, or by no visual display (a control condition). We modified the Disease X task so as to decrease the verbal transparency of the nested-sets structure by using conditional expressions instead of set reference wordings and by using the singular term for “chances” (i.e., “chance”). In addition, we used only Euler circles, since they had shown performance similar to that with pictographs in Experiment 1. We also minimized the amount of textual information describing the visual elements by introducing short descriptive labels instead (consequently, we removed the redundant shading). Finally, given the similar data patterns between the proportion of correct Bayesian answers and the score in the Bayesian Reasoning Understanding Scale, we only measured the former not the latter. As in Experiment 1, participants answered some sociodemographic questions.
Results and discussion
The proportions of correct Bayesian answers as a function of manipulation are depicted in the lower panel of Table 2. The performance in the control condition was low; thus, our intention to create a difficult version of the task was successful. The visual displays significantly facilitated performance (visual-display effect); nevertheless, the degree of iconicity of the visual displays did not influence the proportions of correct answers. To test the null iconicity effect further, we quantified the evidence, using a Bayes factor analysis for the three levels of iconicity on the proportions of correct answers (Albert, 2009). The analysis yielded strong evidence to support the independence model (i.e., the null iconicity effect), BF01 = 13.16 (assuming a uniform distribution of priors), which means that the data were roughly 13 times more likely under H0 than under H1.
The participants in Experiment 2 performed noticeably worse than those in Experiment 1, probably due to the harder task with the verbally concealed nested-sets structure (although featuring the same format of the statistical information). Visual displays, regardless of their iconicity, compensated somewhat for the performance discrepancy. Therefore, the visual facilitation occurred here, most likely, due to appreciation of the nested-sets structure depicted in the visual displays, which increased the very low absolute performance (observed in the control group). The parsimony of such an explanation makes the changes introduced in the visual materials used in Experiment 2 (e.g., the inclusion of descriptive labels) less likely to be responsible for the facilitation. These changes are also unlikely to be responsible for the null iconicity effect, since the null effect occurred with visuals not featuring these changes in Experiment 1. Thus, the present results replicated the null iconicity effect and substantiated its robustness: The effect was independent of visual facilitation or interaction with the materials.
However, we must account for one additional concern about the null results of iconicity—a lack of precision in the estimation. A small-scale meta-analysis provided an effective tool to increase statistical precision to detect a smaller iconicity effect than was assumed in our power analysis (Cumming, 2012). We synthesized the following four comparisons using the R package metafor (Viechtbauer, 2010): from Experiment 1, (1) dots versus icons in Euler circles and (2) dots versus icons in pictographs, and from Experiment 2, (3) dots versus icons and (4) dots versus figurines. Due to the lack of evidence on heterogeneity between the comparisons [Q(3) = 1.01, p = .800], we fitted a fixed-effect model. The overall effect was slightly negative and approaching zero, log OR = −0.13, 95 % CI [−0.53, 0.28], z = −0.61, p = .543 (Fig. 2). Thus, the null iconicity effect does not appear to be due to an imprecise estimation of a population effect (Cumming, 2012).
Meta-analytical effect of low- versus high-iconic visual displays on Bayesian reasoning, depicted in a forest plot (a fixed-effect model). Source, the individual comparisons (the low-iconicity group in Exp. 2 was randomly split into two subgroups); Weight, weighting of the comparisons; Effect Size [95 % CI], log odds ratio and its 95 % confidence interval; FE Model for All Comparisons, the overall fixed effect. Technical Note: We randomly split the “dots” group of Experiment 2 into two subsets to avoid the problem of group repetition in the “multiarm” Experiment 2 (see Higgins & Green, 2008); The number of correct answers out of the total answers was n1 = 7 out of 33 for the first subset and n2 = 9 out of 34 for the second subset
General discussion
In two well-powered experiments, we found that iconicity did not play a role in facilitating Bayesian reasoning with chances. A measurable effect of iconicity did not occur either in a factorial experiment featuring two iconicity levels in Euler circles and pictographs (Exp. 1) or in an experiment featuring three iconicity levels in Euler circles (Exp. 2); the data meta-analysis suggests that the iconicity effect did not occur due to a lack of precision. We quantified this evidence using a Bayes factor analysis and found reasonably strong support for the null-iconicity-effect hypothesis. Our results diverge from those demonstrating the effect of iconicity on Bayesian reasoning, featuring the identified confounders (e.g., Brase, 2009), but converge with results demonstrating the null iconicity effect in other reasoning domains, avoiding the identified confounders (e.g., Gaissmaier et al., 2012).
Overall, these findings contribute to the theoretical debate on the underlying mechanism of partitive formats facilitations in Bayesian reasoning. First of all, the two theoretical accounts of the facilitative effect in Bayesian reasoning predict different effects of iconicity in a chances format (Brase, 2009; Sloman et al., 2003). The null iconicity effect demonstrates that gradations of visual iconicity (i.e., processing chances by using less or more individuated objects) failed to benefit statistical reasoning. Therefore, the processing of natural frequencies seems not to be guided by a specialized cognitive mechanism (Cosmides & Tooby, 1996), but rather by a more general reasoning mechanism (Sloman et al., 2003). Furthermore, if the low-iconic material (i.e., dots) already tapped into the specialized frequency mechanism then doubts about its evolutionary roots remain: Less than a half of the participants benefited from such activation. An explanation more consistent with our data suggests that dots as well as icons encourage the representation of chances as instances of categories (thus promoting an outside view), which reveals the set structure of the problem (Sloman et al., 2003).
Moreover, although the nested-sets structure was not directly manipulated here, the visual representations only facilitated performance when the nested-sets structure of the problem was verbally concealed (Exp. 2). This further supports the nested-sets rather than the ecological-rationality account, since the former posits that the facilitative power of visuals would rely on a clear depiction of the nested-sets structure only. Our results thus complement findings supporting the existence of a general reasoning mechanism responsible for processing frequencies or probabilities with a partitioned structure (e.g., Barbey & Sloman, 2007; Lesage, Navarrete, & De Neys, 2013; Sirota & Juanchich, 2011; Sirota et al., 2013). Indeed, if we clearly depict sets or, in more general terms, logical relations (see Over, 2007), the level of iconicity of the set representation should not affect reasoning performance. Finally, the absence of facilitation by visual displays that we found in Experiment 1 and its presence with increased verbal task difficulty in Experiment 2 indicate that the nested-sets structure had to be adequately communicated in order to trigger a nested-sets mental representation. Thus, future research should elaborate in more detail the cognitive processes involved in solving Bayesian tasks (see Sirota et al., 2013).
Some methodological limitations of our present findings should be addressed in future research. For example, future studies should include a manipulation check to ensure a successful manipulation of iconicity. For the purpose of our studies, this limitation had only a narrow impact on our conclusions, because we used stimuli very similar—in terms of iconicity—to those used in previous research in which a positive iconicity effect had allegedly been observed (e.g., Brase, 2009). Moreover, our findings fit with those of Gaissmaier et al. (2012), who used even more highly iconic signs than we did, such as actual photographs of people, but did not find any iconicity effects on statistical information processing. Future research should investigate the effects of other variables associated with visuals, such as attractiveness or prior knowledge of the visuals; these may co-occur with iconicity and represent different mechanisms through which iconicity can influence performance.
Despite these limitations, the null iconicity effect remains a robust effect, as estimated by a meta-analysis of the data of two well-powered experiments, and thus is unlikely to be a statistical artifact. On the contrary, using Bayesian inference, strong evidence supports the null iconicity effect. Naturally, more replication studies should firmly establish the null effect and extend it to other types of statistical reasoning. We would also call for more evidence before formulating any practical guidelines for the communication of health, climate, or other publicly relevant risks (see also Sirota & Juanchich, 2012). So far, the current evidence suggests that visual displays can sometimes be unnecessary, and sometimes efficient, in communicating information requiring statistical reasoning. Nevertheless, such beneficial effects do not hinge on the iconicity of the visuals.
Conclusion
We found that visual displays improved Bayesian reasoning as compared with a text-task condition, but only when the nested-sets structure was not verbally salient. The iconicity of visuals did not generate any facilitation: schematic, low-iconic visual displays appear to aid statistical Bayesian reasoning as well as high-iconic visual displays. Therefore, our findings do not support the ecological-rationality account, which predicts a positive effect of iconicity on performance, but do support the nested-sets account, according to which iconicity plays a negligible role in Bayesian reasoning.
Notes
From a semiotic perspective, we can conceptualize iconicity in two ways (see Morris & Hamilton, 1965): (1) iconicity for all, including arbitrary, signs (the definition used in Gaissmaier et al., 2012) or (2) iconicity of visual signs only (used here, because it enabled us to distinguish the similarity of the visual elements in the displays from their respective organizations).
To avoid equivocal labels, we will refer to the types of visual displays here as “pictographs,” and to the specific elements of pictographs featuring human-like figures as “icons.”
As was noted by a reviewer, a more appropriate label for the “Venn diagrams” used here and in Brase (2009) would be “Euler circle diagrams,” a term that we will use in the rest of this article.
Previous experience affected Bayesian performance but not the focal effects, and therefore we kept the participants with previous knowledge in the subsequent analyses.
The difference between the low- and high-iconic elements in Bayesian reasoning understanding was not significant (respectively, n 1 = 127, M 1 = 4.84, SD 1 = 1.51; n 2 = 133, M 2 = 4.82, SD 2 = 1.48), t(258) = 0.124, p = .902.
References
Albert, J. (2009). Bayesian computations with R (2nd ed.). New York: Springer.
Barbey, A. K., & Sloman, S. A. (2007). Base-rate respect: From ecological rationality to dual processes. Behavioral and Brain Sciences, 30, 241–297. doi:10.1017/S0140525X07001653
Brase, G. L. (2009). Pictorial representations in statistical reasoning. Applied Cognitive Psychology, 23, 369–381. doi:10.1002/acp.1460
Carpenter, P. A., & Shah, P. (1998). A model of the perceptual and conceptual processes in graph comprehension. Journal of Experimental Psychology: Applied, 4, 75–100. doi:10.1037/1076-898X.4.2.75
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale: Erlbaum.
Cosmides, L., & Tooby, J. (1996). Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition, 58, 1–73. doi:10.1016/0010-0277(95)00664-8
Cumming, G. (2012). Understanding the new statistics: effect sizes, confidence intervals, and meta-analysis. New York: Routledge.
Gaissmaier, W., Wegwarth, O., Skopec, D., Muller, A. S., Broschinski, S., & Politi, M. C. (2012). Numbers can be worth a thousand pictures: Individual differences in understanding graphical and numerical representations of health-related information. Health Psychology, 31, 286–296. doi:10.1037/a0024850
Gigerenzer, G., & Hoffrage, U. (1995). How to improve Bayesian reasoning without instruction: Frequency formats. Psychological Review, 102, 684–704. doi:10.1037/0033-295X.102.4.684
Girotto, V., & Gonzalez, M. (2001). Solving probabilistic and statistical problems: A matter of information structure and question form. Cognition, 78, 247–276. doi:10.1016/S0010-0277(00)00133-5
Higgins, J. P. T., & Green, S. (Eds.). (2008). Cochrane handbook for systematic reviews of interventions. Chichester: Wiley-Blackwell.
Lesage, E., Navarrete, G., & De Neys, W. (2013). Evolutionary modules and Bayesian facilitation: The role of general cognitive resources. Thinking and Reasoning, 19, 27–53. doi:10.1080/13546783.2012.713177
Mani, K., & Johnson-Laird, P. N. (1982). The mental representation of spatial descriptions. Memory & Cognition, 10, 181–187. doi:10.3758/BF03209220
Morris, C., & Hamilton, D. J. (1965). Aesthetics, signs, and icons. Philosophy and Phenomenological Research, 25, 356–364.
Oppenheimer, D. M., Meyvis, T., & Davidenko, N. (2009). Instructional manipulation checks: Detecting satisficing to increase statistical power. Journal of Experimental Social Psychology, 45, 867–872. doi:10.1016/j.jesp.2009.03.009
Over, D. (2007). The logic of natural sampling. Behavioral and Brain Sciences, 30, 277–277. doi:10.1017/S0140525X07001859
Rouder, J. N., Speckman, P. L., Sun, D., Morey, R. D., & Iverson, G. (2009). Bayesian t tests for accepting and rejecting the null hypothesis. Psychonomic Bulletin & Review, 16, 225–237. doi:10.3758/PBR.16.2.225
Sedlmeier, P. (1999). Improving statistical reasoning: Theoretical models and practical implications. Mahwah: Erlbaum.
Sirota, M., & Juanchich, M. (2011). Role of numeracy and cognitive reflection in Bayesian reasoning with natural frequencies. Studia Psychologica, 53, 151–161.
Sirota, M., & Juanchich, M. (2012). Risk communication on shaky ground. Science, 338, 1286–1287. doi:10.1126/science.338.6112.1286
Sirota, M., Juanchich, M., & Hagmayer, Y. (2013). Ecological rationality or nested sets? Individual differences in cognitive processing predict Bayesian reasoning. Psychonomic Bulletin & Review. Advance online publication.. doi:10.3758/s13423-013-0464-6
Sloman, S. A., Over, D., Slovak, L., & Stibel, J. M. (2003). Frequency illusions and other fallacies. Organizational Behavior and Human Decision Processes, 91, 296–309. doi:10.1016/S0749-5978(03)00021-9
Tversky, A., & Kahneman, D. (1983). Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment. Psychological Review, 90, 293–315. doi:10.1037/0033-295X.90.4.293
Vallée-Tourangeau, F., & Krüsi Penney, A. (2005). The impact of external representation in a rule discovery task. European Journal of Cognitive Psychology, 17, 820–834. doi:10.1080/09541440440000249
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36, 1–48.
Yamagishi, K. (2003). Facilitating normative judgments of conditional probability: Frequency or nested sets? Experimental Psychology, 50, 97–106. doi:10.1027/1618-3169.50.2.97
Author note
We thank Cathleen Moore and three anonymous reviewers for their helpful comments on an earlier version of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sirota, M., Kostovičová, L. & Juanchich, M. The effect of iconicity of visual displays on statistical reasoning: evidence in favor of the null hypothesis. Psychon Bull Rev 21, 961–968 (2014). https://doi.org/10.3758/s13423-013-0555-4
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13423-013-0555-4