1 Introduction

Thin shells are extensively used in naval architecture and ocean engineering, as well as in civil, mechanical, and aeronautical engineering. Open circular cylindrical shells (OCCSs) are often used as structural components of pressure vessels, roof structures, open space buildings, and marine structures. It is of great significance for engineers to be familiar with the vibration behaviors of such shell structures in practical design.

Many pioneering scholars have developed numerous approximate analytical models for thin shells. Most thin shell theories developed before 1973 were formulated by Leissa (1973). In subsequent decades many studies of the vibration of OCCSs have been carried out. Early research mainly used numerical approaches such as the Rayleigh-Ritz method (Sewall, 1967; Leissa and Narita, 1984), the finite element method (FEM) (Cantin and Clough, 1968; Lakis and Selmane, 2000), and the finite strip method (Cheung et al., 1989). Exact solutions for determining the natural frequencies of OCCSs were presented in (Suzuki and Leissa, 1986; Lim and Liew, 1995; Yu et al., 1995; Price et al., 1998; Ye et al., 2014a). A wave propagation approach is introduced by Zhang et al. (2001) to carry out frequency analysis of cylindrical panels. Free vibration analyses of stiffened cylindrical shallow shells are presented in (Mecitoglu and Dokmeci, 1992; Nayak and Bandyopadhyay, 2002; Zhang and Xiang, 2006). Vibration behaviors of anisotropic OCCSs are analyzed by Selmane and Lakis (1997a; 1997b) and Toorani and Lakis (2001). Recently, much attention has been paid to vibration analysis of laminated, composite or functionally graded OCCSs (Qatu, 2002; Singh and Shen, 2005; Qatu et al., 2010; Su et al., 2014; Ye et al., 2014b).

As far we are aware, research on the vibration analysis of plate-shell coupled structures is rare, especially any using analytical methods. From the literature, it appears that the accuracy of approximate methods is lower than that of analytical methods. The available analytical methods are sometimes too targeted for shell structures to be consistent with exact solutions of other structural components, such as beams and plates. The method of reverberation-ray matrix (MRRM) is suitable for determining the natural frequencies and steady-state response of multi-span structures and space frame structures with complex geometry. MRRM was first proposed by Howard and Pao (1998) and Pao et al. (1999) to analyze wave propagation in planar trusses. Subsequently, Pao and his associates extended the method to study waves propagating in multilayered media (Pao et al., 2000; Su et al., 2002; Guo and Chen, 2008; Tian and Xie, 2009). Much attention was paid to applications of MRRM for dynamic analysis of frames and beams (Tian et al., 2003; Chen et al., 2005; Liu et al., 2006; Yu, 2007a; 2007b; Guo et al., 2008; Jiang et al., 2011; Qiao and Chen, 2011; Miao et al., 2013; Guo and Fang, 2014). MRRM is also employed to analyze unidirectional wave propagation through plates (Li et al., 2005; Liu and Xie, 2005; Liu et al., 2010; 2011a; Zhu et al., 2011; 2012; Li et al., 2012, Yu et al., 2012) and closed shells (Tian and Su, 2000; Liu et al., 2011b; 2013). Recently, MRRM has been directed towards the study of functionally graded or laminated structures (Zhou et al., 2009; Li et al., 2012; Liu et al., 2013; Miao et al., 2013; 2015). It is aimed to obtain a unidirectional traveling wave form solution for OCCSs, which is of good consistency with the solutions for beams and plates presented in (Yu, 2007a; 2007b; Jiang, 2011; Liu et al., 2010; 2011a). Therefore, the formulation presented in this paper should prove to be fundamental for vibration analysis of ring-stiffened OCCSs and plate-shell coupled structures.

This paper extends MRRM to the dynamic analysis of OCCSs. Based on the Donnell-Mushtari-Vlasov (DMV) thin shell theory, the free vibration equation of the OCCS with either two simply supported straight edges or two simply supported curved edges is solved to obtain an analytical solution of the traveling wave form along the simply supported edges and the modal wave form along the remaining two edges. With these solutions expressed in matrix form, the scattering matrix, phase matrix, and permutation matrix as well as the reverberation-ray matrix of the OCCS are derived. Then, the equation of natural frequencies of the OCCS is obtained and subsequently solved by the golden section search algorithm (Press et al., 1992; Vajda, 2007). Finally, the method presented in this paper is validated by comparing the calculation results with those obtained by FEM and the method of Leissa (1973). In addition, the effects of shell length, shell radius, shell thickness, and the included angle as well as the classical boundary conditions such as simply supported edge (SSE), clamped edge (CE), and free edge (FE) for the remaining two edges on the natural frequencies are investigated.

2 Formulation

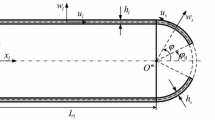
Consider an isotropic OCCS with length L, included angle θ0, uniform thickness h, middle surface radius R, Young’s modulus E, Poisson’s ratio μ, and mass density ρ shown in Fig. 1. The axial, circumferential, and radial displacements of the middle surface of the OCCS with reference to the coordinate system are denoted as u(x, θ, t), v(x, θ, t), and w(x, θ, t), respectively. Either the two straight edges or the two curved edges of the shell are assumed to be simply supported in the following discussion. The problem at hand is to determine the natural frequencies of the OCCS.

Fig. 1
figure 1

Geometry and coordinate system for an OCCS

Full size image

To begin with, the expressions of the force and moment resultants in terms of the displacement components and the governing equations based on the DMV thin shell theory are introduced. Subsequently, with the employment of a Fourier transform, an analytical solution of the traveling wave form along the simply supported edges and the modal wave form along the remaining two edges is obtained in the frequency domain. Then, the solutions of the displacements and the force and moment resultants are expressed in matrix form. Finally, the equation of natural frequencies of the OCCS with various classical boundary conditions is obtained by MRRM and solved by the golden section search algorithm. The above-mentioned formulation is presented in detail as follows.

2.1 Force and moment resultants in the shell

The force and moment resultants in an OCCS, shown in Fig. 2, are expressed in terms of the displacements u, v, and w as follows (Leissa, 1973):

$${N_{xx}} = C\left({{{\partial u} \over {\partial x}} + {\mu \over R}{{\partial v} \over {\partial \theta }} + {\mu \over R}w} \right), $$
(1)
$${N_{\theta \theta }} = C\left({{1 \over R}{{\partial v} \over {\partial \theta }} + \mu {{\partial u} \over {\partial x}} + {w \over R}} \right), $$
(2)
$${N_{x\theta }} = {N_{\theta x}} = C{{1 - \mu } \over 2}\left({{1 \over R}{{\partial u} \over {\partial \theta }} + {{\partial v} \over {\partial x}}} \right), $$
(3)
$${M_{xx}} = - D\left({{{{\partial ^2}w} \over {\partial {x^2}}} + {\mu \over {{R^2}}}{{{\partial ^2}w} \over {\partial {\theta ^2}}}} \right), $$
(4)
$${M_{\theta \theta }} = - D\left({{1 \over {{R^2}}}{{{\partial ^2}w} \over {\partial {\theta ^2}}} + \mu {{{\partial ^2}w} \over {\partial {x^2}}}} \right), $$
(5)
$${M_{x\theta }} = {M_{\theta x}} = - D{{1 - \mu } \over R}{{{\partial ^2}w} \over {\partial x\partial \theta }}, $$
(6)
$$\begin{array}{*{20}c} {{Q_{xz}} = {{\partial {M_{xx}}} \over {\partial x}} + {1 \over R}{{\partial {M_{\theta x}}} \over {\partial \theta }}\quad \quad \quad \quad \quad }\\ { = - D\left({{{{\partial ^3}w} \over {\partial {x^3}}} + {1 \over {{R^2}}}{{{\partial ^3}w} \over {\partial x\partial {\theta ^2}}}} \right),} \end{array} $$
(7)
$$\begin{array}{*{20}c} {{Q_{\theta z}} = {{\partial {M_{x\theta }}} \over {\partial x}} + {1 \over R}{{\partial {M_{\theta \theta }}} \over {\partial \theta }}\quad \quad \quad \quad \quad \;\;}\\ { = - D\left({{1 \over {{R^3}}}{{{\partial ^3}w} \over {\partial {\theta ^3}}} + {1 \over R}{{{\partial ^3}w} \over {\partial {x^2}\partial \theta }}} \right),} \end{array} $$
(8)
$$\begin{array}{*{20}c} {{F_{x\theta }} = {N_{x\theta }} + {{{M_{x\theta }}} \over R}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;}\\ { = {{1 - \mu } \over 2}D\left({{{12} \over {{h^2}}}{1 \over R}{{\partial u} \over {\partial \theta }} + {{12} \over {{h^2}}}{{\partial v} \over {\partial x}} - {2 \over {{R^2}}}{{{\partial ^2}w} \over {\partial x\partial \theta }}} \right),} \end{array} $$
(9)
$${F_{\theta x}} = {N_{\theta x}} = C{{1 - \mu } \over 2}\left({{1 \over R}{{\partial u} \over {\partial \theta }} + {{\partial v} \over {\partial x}}} \right), $$
(10)
$$\begin{array}{*{20}c} {{V_{xz}} = {Q_{xz}} + {1 \over R}{{\partial {M_{x\theta }}} \over {\partial \theta }}\quad \quad \quad \quad \quad \quad }\\ { = - D\left({{{{\partial ^3}w} \over {\partial {x^3}}} + {{2 - \mu } \over {{R^2}}}{{{\partial ^3}w} \over {\partial x\partial {\theta ^2}}}} \right),} \end{array} $$
(11)
$$\begin{array}{*{20}c} {{V_{\theta z}} = {Q_{\theta z}} + {{\partial {M_{\theta x}}} \over {\partial x}}\quad \quad \quad \quad \quad \quad \quad \quad \;\;}\\ { = - D\left({{1 \over {{R^3}}}{{{\partial ^3}w} \over {\partial {\theta ^3}}} + {{2 - \mu } \over R}{{{\partial ^3}w} \over {\partial {x^2}\partial \theta }}} \right),} \end{array} $$
(12)

where u, v, and w denote the displacement components in the axial (x), circumferential (θ), and radial (z) directions, respectively. C=Eh/(1−μ2) and D =Eh3/[12(1−μ2)] represent the middle surface stiffness and the bending stiffness of the shell. N xx and N θθ denote the in-plane normal forces, N xθ and N θx , the in-plane shear forces, M xx and M θθ , the bending moments, M xθ and M θx , the torsional moments, and Q xz and Q θz , the out-of-plane shear forces acting on the cross-sections perpendicular to the axial and circumferential directions. F xθ and Fθx indicate the in-plane shear force resultants, and V xz and V θz , the out-of-plane shear force resultants acting on the cross-sections perpendicular to the axial and circumferential directions.

Fig. 2
figure 2

Force and moment resultants in a shell

Full size image

2.2 Governing differential equations

The governing differential equations for free vibration of an OCCS based on the DMV thin shell theory can be written as (Leissa, 1973)

$$\begin{array}{*{20}c} {{{{\partial ^2}u} \over {\partial {x^2}}} + {{1 - \mu } \over {2{R^2}}}{{{\partial ^2}u} \over {\partial {\theta ^2}}} + {{1 + \mu } \over {2R}}{{{\partial ^2}v} \over {\partial x\partial \theta }} + {\mu \over R}{{\partial w} \over {\partial x}}}\\ { - {{(1 - {\mu ^2})\rho } \over E}{{{\partial ^2}u} \over {\partial {t^2}}} = 0,\quad \quad \quad \quad } \end{array} $$
(13)
$$\begin{array}{*{20}c} {{{1 - \mu } \over 2}{{{\partial ^2}v} \over {\partial {x^2}}} + {1 \over {{R^2}}}{{{\partial ^2}v} \over {\partial {\theta ^2}}} + {{1 + \mu } \over {2R}}{{{\partial ^2}u} \over {\partial x\partial \theta }}}\\ { + {1 \over {{R^2}}}{{\partial w} \over {\partial \theta }} - {{(1 - {\mu ^2})\rho } \over E}{{{\partial ^2}v} \over {\partial {t^2}}} = 0,} \end{array} $$
(14)
$$\begin{array}{*{20}c} {{R^2}\lambda \left({{{{\partial ^4}w} \over {\partial {x^4}}} + {1 \over {{R^4}}}{{{\partial ^4}w} \over {\partial {\theta ^4}}} + {2 \over {{R^2}}}{{{\partial ^4}w} \over {\partial {x^2}\partial {\theta ^2}}}} \right)\quad \quad \quad \quad \quad \quad }\\ { + \left({{w \over {{R^2}}} + {\mu \over R}{{\partial u} \over {\partial x}} + {1 \over {{R^2}}}{{\partial v} \over {\partial \theta }}} \right) + {{(1 - {\mu ^2})\rho } \over E}{{{\partial ^2}w} \over {\partial {t^2}}} = 0,} \end{array} $$
(15)

where λ=h2/(12R2) is a dimensionless parameter, which is related to the ratio of shell thickness to radius.

The Fourier transform of an arbitrary physical quantity X(t) is defined by

$$\tilde X(\omega) = \int\nolimits_{ - \infty }^{ + \infty } {X(t){{\rm {e}}^{ - {\rm {i}}\omega t}}} {\rm {d}}t, $$
(16)

where ω is the circular frequency, and a tilde over a symbol represents the corresponding quantity expressed in the frequency domain. The inverse Fourier transform is given by

$$X(t) = {1 \over {2\pi }}\int\nolimits_{ - \infty }^{ + \infty } {\tilde X(\omega)} {{\rm {e}}^{{\rm {i}}\omega t}}{\rm {d}}\omega {.} $$
(17)

Taking the Fourier transforms of Eqs. (13)–(15) and eliminating the other two displacement components from the Fourier transforms of Eqs. (13)–(15), three independent equations of motion respectively in terms of and are obtained as follows:

$$\left({{L_1}{L_2}{L_3}{L_4} + {1 \over {{R^4}\lambda }}{{1 - \mu } \over {1 + \mu }}{L_5}{L_6}} \right){{\partial \tilde u} \over {\partial x}} = 0, $$
(18)
$$\left({{L_1}{L_2}{L_3}{L_4} + {1 \over {{R^4}\lambda }}{{1 - \mu } \over {1 + \mu }}{L_5}{L_6}} \right){{\partial \tilde v} \over {R\partial \theta }} = 0, $$
(19)
$$\left({{L_1}{L_2}{L_3}{L_4} + {1 \over {{R^4}\lambda }}{{1 - \mu } \over {1 + \mu }}{L_5}{L_6}} \right){1 \over R}{{{\partial ^2}\tilde w} \over {\partial x\partial \theta }} = 0, $$
(20)

where \(\tilde u, \; \tilde v\) and \(\tilde w\) denote the axial, circumferential, and radial displacement components expressed in the frequency domain. \(\gamma = {\{ [{R^2}k_L^2 - (1 - \mu)/(1 + \mu)]/(\lambda {R^4})\} ^{1/4}}\) is a parameter of the same dimension with the wave number. L j (j=1, 2, …, 6) are linear differential operators defined as follows:

$${L_1} = {{{\partial ^2}} \over {\partial {x^2}}} + {1 \over {{R^2}}}{{{\partial ^2}} \over {\partial {\theta ^2}}} + {\gamma ^2}, $$
(21)
$${L_2} = {{{\partial ^2}} \over {\partial {x^2}}} + {1 \over {{R^2}}}{{{\partial ^2}} \over {\partial {\theta ^2}}} - {\gamma ^2}, $$
(22)
$${L_3} = {{{\partial ^2}} \over {\partial {x^2}}} + {1 \over {{R^2}}}{{{\partial ^2}} \over {\partial {\theta ^2}}} + k_L^2, $$
(23)
$${L_4} = {{{\partial ^2}} \over {\partial {x^2}}} + {1 \over {{R^2}}}{{{\partial ^2}} \over {\partial {\theta ^2}}} + {2 \over {1 - \mu }}k_L^2, $$
(24)
$${L_5} = \mu {{{\partial ^2}} \over {\partial {x^2}}} - {1 \over {{R^2}}}{{{\partial ^2}} \over {\partial {\theta ^2}}} + {{2\mu } \over {1 - \mu }}k_L^2, $$
(25)
$${L_6} = (2 + \mu){{{\partial ^2}} \over {\partial {x^2}}} + {1 \over {{R^2}}}{{{\partial ^2}} \over {\partial {\theta ^2}}} + {2 \over {1 - \mu }}k_L^2, $$
(26)

where kL=ω[(1−μ2)ρ/E]1/2.

It can be observed from Eqs. (18)–(20) that, the differences among the linear differential operators operating on the axial, circumferential, and radial displacement components lie in the parts outside the braces, which represent zero wave number solutions, or in other words, the rigid-body motions. As normal in free vibration analysis, the zero wave number solutions will be neglected throughout this paper.

2.3 Solutions for OCCS with simply supported curved edges

As the two curved edges of the OCCS are assumed to be simply supported, the boundary conditions at x=0 and x=L are given by (Leissa, 1973)

$$v = 0,\;\;w = 0,\;\;{N_{xx}} = 0,\;\;{M_{xx}} = 0,\;\;\;\;x = 0,L{.} $$
(27)

According to the boundary conditions defined by Eq. (27), the axial, circumferential, and radial displacements of the OCCS can be written as

$$\tilde u(x,\theta) = \sum\limits_{m = 1}^\infty {U(\theta)\cos \left({{k_x}x} \right)},$$
(28)
$$\tilde v(x,\theta) = \sum\limits_{m = 1}^\infty {V(\theta)\sin \left({{k_x}x} \right)},$$
(29)
$$\tilde w(x,\theta) = \sum\limits_{m = 1}^\infty {W(\theta)\sin \left({{k_x}x} \right)},$$
(30)

where kx=mπ/L denotes the wave number in the axial direction, m is the axial mode number, and L represents the length of the OCCS.

Assuming that the axial, circumferential, and radial displacement components can be expressed by exponential functions of the circumferential variable θ, a common circumferential wave number equation for the axial, circumferential, and radial displacements of the OCCS is obtained as

$$\begin{array}{*{20}c} {\left({k_\theta ^2 + {R^2}k_x^2 - {R^2}{\gamma ^2}} \right)\left({k_\theta ^2 + {R^2}k_x^2 + {R^2}{\gamma ^2}} \right)\quad \quad \quad }\\ { \times \left({k_\theta ^2 + {R^2}k_x^2 - {R^2}k_L^2} \right)\left({k_\theta ^2 + {R^2}k_x^2 - {2 \over {1 - \mu }}{R^2}k_L^2} \right)}\\ { - {1 \over \lambda }{{1 - \mu } \over {1 + \mu }}\left({k_\theta ^2 - \mu {R^2}k_x^2 + {{2\mu } \over {1 - \mu }}{R^2}k_L^2} \right)\quad \quad \quad \quad }\\ { \times \left[ {k_\theta ^2 + (2 + \mu){R^2}k_x^2 - {2 \over {1 - \mu }}{R^2}k_L^2} \right] = 0{.}\quad \quad \quad \;\;} \end{array} $$
(31)

By solving Eq. (31), eight circumferential wave numbers are obtained:

$${k_\theta } = \pm {k_{\theta 1}},\;\; \pm {k_{\theta 2}},\;\; \pm {k_{\theta 3}},\;\; \pm {k_{\theta 4}}{.} $$
(32)

Therefore, the solutions of the equations of motion of the OCCS with two simply supported curved edges are expressed as

$$\tilde u(x,\theta) = \sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {{\alpha _j}\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \cos \left({{k_x}x} \right)},$$
(33)
$$\tilde v(x,\theta) = \sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {{\beta _j}\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \sin \left({{k_x}x} \right)},$$
(34)
$$\tilde w(x,\theta) = \sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \sin \left({{k_x}x} \right)},$$
(35)

where a j and d j (j=1, 2, 3, 4) are amplitudes of the axial and circumferential waves. α j and β j (j=1, 2, 3, 4) are ratios of the amplitudes of the axial and circumferential waves to the amplitude of the radial wave. The expressions of α j and β j are defined as follows:

$${\alpha _j} = {{ - R{k_x}\left({k_{\theta j}^2 - \mu {R^2}k_x^2 + {{2\mu {R^2}k_L^2} \over {1 - \mu }}} \right)} \over {\left({k_{\theta j}^2 + {R^2}k_x^2 - {R^2}k_L^2} \right)\left({k_{\theta j}^2 + {R^2}k_x^2 - {{2{R^2}k_L^2} \over {1 - \mu }}} \right)}}, $$
(36)
$${\beta _j} = {{{\rm{i}}{k_{\theta j}}\left({k_{\theta j}^2 + (2 + \mu){R^2}k_x^2 - {{2{R^2}k_L^2} \over {1 - \mu }}} \right)} \over {\left({k_{\theta j}^2 + {R^2}k_x^2 - {R^2}k_L^2} \right)\left({k_{\theta j}^2 + {R^2}k_x^2 - {{2{R^2}k_L^2} \over {1 - \mu }}} \right)}}{.} $$
(37)

The rotation of the normal to the middle surface of the OCCS about the axial direction is defined as

$${\phi _\theta } = {v \over R} - {{\partial w} \over {R\partial \theta }}{.} $$
(38)

Substituting Eqs. (34) and (35) into the Fourier transform of Eq. (38) yields the frequency domain expression of the rotation as

$${\tilde \phi _\theta } = \sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {{{{\beta _j} - {\rm{i}}{k_{\theta j}}} \over R}\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \sin \left({{k_x}x} \right)} {.} $$
(39)

Substitution of Eqs. (33)–(35) into the Fourier transforms of Eqs. (2), (5), (10), and (12) yields the frequency domain expressions of the force and moment resultants of the OCCS:

$$\begin{array}{*{20}c} {{{\tilde N}_{\theta \theta }} = {C \over R}\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {\left[ {\left({1 - \mu R{k_x}{\alpha _j} + {\beta _j}{\rm{i}}{k_{\theta j}}} \right)} \right.} } \quad \quad \;\;}\\ {\left. { \cdot \left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \right]\sin \left({{k_x}x} \right),} \end{array}$$
(40)
$$\begin{array}{*{20}c} {{{\tilde M}_{\theta \theta }} = {D \over {{R^2}}}\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {\left[ {\left({k_{\theta j}^2 + \mu {R^2}k_x^2} \right)} \right.} } \quad \quad \quad \quad \quad }\\ {\left. { \cdot \left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \right]\sin \left({{k_x}x} \right),} \end{array} $$
(41)
$$\begin{array}{*{20}c} {{{\tilde F}_{\theta x}} = {{1 - \mu } \over 2}{C \over R}\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {\left[ {\left({{\alpha _j}{\rm{i}}{k_{\theta j}} + {\beta _j}R{k_x}} \right)} \right.} } \quad }\\ {\left. { \cdot \left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \right]\cos \left({{k_x}x} \right),} \end{array} $$
(42)
$$\begin{array}{*{20}c} {{{\tilde V}_{\theta z}} = {D \over {{R^3}}}\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^4 {\left\{ {\left[ {(2 - \mu){R^2}k_x^2{\rm{i}}{k_{\theta j}} + {\rm i}k_{\theta j}^3} \right]} \right.} } }\\ {\left. { \cdot \left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{\theta j}}\theta }} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{\theta j}}\theta }}} \right)} \right\}\sin \left({{k_x}x} \right){.}} \end{array} $$
(43)

2.4 Solutions for OCCS with simply supported straight edges

Since the derivation for solutions of the OCCS with simply supported straight edges is independent of the derivation for the OCCS with simply supported curved edges and the two derivation procedures are quite similar to each other, the symbols used in this subsection will be very similar and frequently the same as those used in the preceding subsection. In addition, the derivation presented in this subsection will be greatly simplified and only the differences between the two derivation procedures will be pointed out.

As the two straight edges of the OCCS are assumed to be simply supported, the boundary conditions at θ=0 and θ=θ0 are given by (Leissa, 1973)

$$u = 0,\;\;w = 0,\;\;{N_{\theta \theta }} = 0,\;\;{M_{\theta \theta }} = 0{.} $$
(44)

According to the boundary conditions defined by Eq. (44), the axial, circumferential, and radial displacements of the OCCS can be written as

$$\tilde u(x,\theta) = \sum\limits_{n = 1}^\infty {U(x)\sin \left({{k_\theta }\theta } \right)},$$
(45)
$$\tilde v(x,\theta) = \sum\limits_{n = 1}^\infty {V(x)\cos \left({{k_\theta }\theta } \right)},$$
(46)
$$\tilde w(x,\theta) = \sum\limits_{n = 1}^\infty {W(x)\sin \left({{k_\theta }\theta } \right)},$$
(47)

where kθ=nπ/θ0 denotes the wave number in the circumferential direction, and n is the circumferential mode number.

Assuming that the axial, circumferential, and radial displacements can be expressed by exponential functions of the axial variable x, a common axial wave number equation of the axial, circumferential, and radial displacements of the OCCS can be obtained as

$$\begin{array}{*{20}c} {\left({k_x^2 + {1 \over {{R^2}}}k_\theta ^2 - {\gamma ^2}} \right)\left({k_x^2 + {1 \over {{R^2}}}k_\theta ^2 + {\gamma ^2}} \right)\quad \;\;}\\ { \times \left({k_x^2 + {1 \over {{R^2}}}k_\theta ^2 - k_L^2} \right)\left({k_x^2 + {1 \over {{R^2}}}k_\theta ^2 - {{2k_L^2} \over {1 - \mu }}} \right)}\\ { + {{\mu (1 - \mu)(2 + \mu)} \over {1 + \mu }}{1 \over {{R^4}\lambda }}\left({k_x^2 - {1 \over {\mu {R^2}}}k_\theta ^2 - {{2k_L^2} \over {1 - \mu }}} \right)\quad \quad \quad }\\ { \times \left({k_x^2 + {1 \over {2 + \mu }}{1 \over {{R^2}}}k_\theta ^2 - {{2k_L^2} \over {(1 - \mu)(2 + \mu)}}} \right) = 0{.}\quad \quad \quad \quad \;} \end{array} $$
(48)

By solving Eq. (48), eight axial wave numbers are obtained as follows:

$${k_x} = \pm {k_{x1}},\;\; \pm {k_{x2}},\;\; \pm {k_{x3}},\;\; \pm {k_{x4}}{.} $$
(49)

Therefore, for the boundary conditions defined by Eq. (44), the solutions of Eqs. (18)–(20) are written as

$$\tilde u(x,\theta) = \sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {{{\alpha}_j^ \prime }\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \sin \left({{k_\theta }\theta } \right)},$$
(50)
$$\tilde v(x,\theta) = \sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {{{\beta}_j^ \prime }\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \cos \left({{k_\theta }\theta } \right)},$$
(51)
$$\tilde w(x,\theta) = \sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \sin \left({{k_\theta }\theta } \right)},$$
(52)

where α′ j and β′ j (j=1, 2, 3, 4) are ratios of the amplitudes of the axial and circumferential waves to the amplitude of the radial wave. The expressions of α′ j and β′ j are defined as follows:

$${\alpha_j^\prime } = {{{\rm {i}}R{k_{xj}}\left({\mu {R^2}k_{xj}^2 - k_\theta ^2 - {{2\mu {R^2}k_L^2} \over {1 - \mu }}} \right)} \over {\left({{R^2}k_{xj}^2 + k_\theta ^2 - {R^2}k_L^2} \right)\left({{R^2}k_{xj}^2 + k_\theta ^2 - {{2{R^2}k_L^2} \over {1 - \mu }}} \right)}}, $$
(53)
$${\beta _j^\prime } = {{{k_\theta }\left({(2 + \mu){R^2}k_{xj}^2 + k_\theta ^2 - {{2{R^2}k_L^2} \over {1 - \mu }}} \right)} \over {\left({{R^2}k_{xj}^2 + k_\theta ^2 - {R^2}k_L^2} \right)\left({{R^2}k_{xj}^2 + k_\theta ^2 - {{2{R^2}k_L^2} \over {1 - \mu }}} \right)}}{.} $$
(54)

The rotation of the normal to the middle surface about the circumferential direction is defined as

$${\phi _x} = - \partial w/\partial x{.} $$
(55)

Substituting Eq. (52) into the Fourier transform of Eq. (55) yields the frequency domain expression of the rotation as

$${\tilde \phi _x} = \sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 { - {\rm{i}}{k_{xj}}\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \sin \left({{k_\theta }\theta } \right)} {.} $$
(56)

Substituting Eqs. (50)–(52) into the Fourier transforms of Eqs. (1), (4), (9), and (11) yields the frequency domain expressions of the force and moment resultants of the OCCS:

$$\begin{array}{*{20}c} {{{\tilde N}_{xx}} = C\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {\left[ {\left({{\mu \over R} + {\rm{i}}{k_{xj}}{{\alpha}_j^\prime } - {{\mu {k_\theta }{{\beta}_j}^\prime } \over R}} \right)\quad \quad \;} \right.} } }\\ {\left. { \cdot \left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} + {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \right]\sin \left({{k_\theta }\theta } \right),} \end{array} $$
(57)
$$\begin{array}{*{20}c} {{{\tilde M}_{xx}} = D\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {\left[ {\left({k_{xj}^2 + \mu {{k_\theta ^2} \over {{R^2}}}} \right)} \right.} \quad \quad \quad \quad \quad \;\;} }\\ {\left. { \cdot \left({{a_j}{{\rm{e}}^{{\rm{i}}{k_{xj}}x}} + {d_j}{{\rm{e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \right]\sin \left({{k_\theta }\theta } \right),} \end{array}$$
(58)
$$\begin{array}{*{20}c} {{{\tilde F}_{x\theta }} = 6D\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {\left[ {\left({{{{{\alpha }_j^\prime }{k_\theta }} \over {R{h^2}}} + {{{\rm{i}}{k_{xj}}{{\beta}_j^\prime }} \over {{h^2}}} - {{{\rm{i}}{k_{xj}}{k_\theta }} \over {6{R^2}}}} \right)\quad \quad \quad \;} \right.} } }\\ {\left. { \cdot (1 - \mu)\left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \right]\cos \left({{k_\theta }\theta } \right),} \end{array} $$
(59)
$$\begin{array}{*{20}c} {{{\tilde V}_{xz}} = D\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^4 {\left\{ {\left[ {(2 - \mu){\rm{i}}{k_{xj}}{{k_\theta ^2} \over {{R^2}}} + {\rm {i}}k_{xj}^3} \right]} \right.} } \quad \;}\\ {\left. { \cdot \left({{a_j}{{\rm {e}}^{{\rm{i}}{k_{xj}}x}} - {d_j}{{\rm {e}}^{ - {\rm{i}}{k_{xj}}x}}} \right)} \right\}\sin \left({{k_\theta }\theta } \right){.}} \end{array} $$
(60)

2.5 Solutions expressed in matrix form

2.5.1 Simply supported curved edges

For an arbitrary axial mode number m, Eqs. (33)–(35) and (39) can be expressed in matrix form as

$${W_{\rm {d}}} = {H_{\rm {m}}}(x)W_{\rm {d}}^\ast,$$
(61)

where Wd denotes the displacement vector of the OCCS, Hm(x) indicates the axial mode matrix, and Wd* represents the wave vector of the circumferential displacement. They are presented in detail as follows:

$${W_{\rm {d}}} = {\left[ {\tilde u}\quad {\tilde v}\quad {\tilde w}\quad {{{\tilde \phi }_\theta }}\right]^{\rm{T}}},$$
(62)
$${H_{\rm {m}}}(x) = {\rm{diag}}\left({\cos ({k_x}x)\;\;{\sin}({k_x}x)\;\;{\sin}({k_x}x)\;\;{\sin}({k_x}x)} \right), $$
(63)
$$W_{\rm{d}}^\ast = {A_{\rm{d}}}{P_{\rm{h}}}(\theta)a + {D_{\rm{d}}}{P_{\rm{h}}}(- \theta)d, $$
(64)

where Ph(θ) denotes the phase matrix, Ad and Dd are coefficient matrices of fourth-order, a and d are amplitude vectors of the arriving wave and the departing wave corresponding to the displacements of the OCCS, which can be given by

$${P_{\rm{h}}}(\theta) = {\rm{diag}}\left({{{\rm{e}}^{{\rm{i}}{k_{\theta 1}}\theta }}}\quad{{{\rm{e}}^{{\rm{i}}{k_{\theta 2}}\theta }}}\quad{{{\rm{e}}^{{\rm{i}}{k_{\theta 3}}\theta }}}\quad{{{\rm{e}}^{{\rm{i}}{k_{\theta 4}}\theta }}} \right), $$
(65)
$$a = {\left[ {{a_1}}\quad{{a_2}}\quad{{a_3}}\quad{{a_4}}\right]^{\rm{T}}}, $$
(66)
$$d = {\left[ {{d_1}}\quad{{d_2}}\quad{{d_3}}\quad{{d_4}} \right]^{\rm{T}}}, $$
(67)
$$\left\{ {\begin{array}{*{20}c} {{A_{\rm {d}}}(1,j) = {D_{\rm {d}}}(1,j) = {\alpha _j},\quad \quad \quad \quad \quad \;\;}\\ {{A_{\rm {d}}}(2,j) = - {D_{\rm {d}}}(2,j) = {\beta _j},\quad \quad \quad \quad \;\;}\\ {{A_{\rm {d}}}(3,j) = {D_{\rm {d}}}(3,j) = 1,\quad \quad \quad \quad \quad \quad }\\ {{A_{\rm {d}}}(4,j) = - {D_{\rm {d}}}(4,j) = \left({{\beta _j} - {\rm{i}}{k_{\theta j}}} \right)/R,} \end{array}} \right. $$
(68)

where j=1, 2, 3, 4.

Meanwhile, Eqs. (40)–(43) can be expressed in matrix form as

$${W_{\rm{f}}} = {H_{\rm{m}}}(x)W_{\rm{f}}^\ast,$$
(69)

where Hm(x) is defined in Eq. (63). Wf denotes the force vector of the shell, and Wf* represents the wave vector of the circumferential force and moment resultants. Then, we can obtain:

$${W_{\rm{f}}} = {\left[ {{{\tilde F}_{\theta x}}}\quad{{{\tilde N}_{\theta \theta }}}\quad{{{\tilde V}_{\theta z}}}\quad{{{\tilde M}_{\theta \theta }}} \right]^{\rm{T}}}, $$
(70)
$$W_{\rm{f}}^\ast = {A_{\rm{f}}}{P_{\rm{h}}}(\theta)a + {D_{\rm{f}}}{P_{\rm{h}}}(- \theta)d, $$
(71)

in which the physical significances and expressions of Ph(θ), a, and d are the same as those presented in Eq. (64). However, Af and Df are coefficient matrices of the arriving wave and the departing wave corresponding to the force and moment resultants of the OCCS. They are presented as

$$\begin{array}{*{20}c} {{A_{\rm{f}}}(1,j) = - {D_{\rm{f}}}(1,j) = {{(1 - \mu)C} \over {2R}}\left({{\alpha _j}{\rm{i}}{k_{\theta j}} + {\beta _j}R{k_x}} \right),}\\ {{A_{\rm{f}}}(2,j) = {D_{\rm{f}}}(2,j) = {C \over R}\left({ - \mu R{k_x}{\alpha _j} + {\beta _j}{\rm{i}}{k_{\theta j}} + 1} \right),\;\;}\\ {{A_{\rm{f}}}(3,j) = - {D_{\rm{f}}}(3,j) = {D \over {{R^3}}}\left[ {(2 - \mu){R^2}k_x^2{\rm{i}}{k_{\theta j}} + {\rm{i}}k_{\theta j}^3} \right],}\\ {{A_{\rm{f}}}(4,j) = {D_{\rm{f}}}(4,j) = {D \over {{R^2}}}\left({k_{\theta j}^2 + \mu {R^2}k_x^2} \right),\quad \quad \quad \quad \;\;} \end{array} $$
(72)

where j=1, 2, 3, 4.

2.5.2 Simply supported straight edges

For an arbitrary circumferential mode number n, Eqs. (50)–(52) and (56) can be written in the same matrix form as Eq. (61) only if the element \({\tilde \phi _\theta}\) in Wd is replaced by \({\tilde \phi _x}\), the axial mode matrix Hm(x) and the phase matrix Ph(θ) are replaced by the circumferential mode matrix Hn(θ) and the phase matrix Ph(x) defined as follows:

$${H_{\rm{n}}}(\theta) = {\rm{diag}}\left({{\rm{sin}}({k_\theta }\theta)\;\;{\rm{cos}}({k_\theta }\theta)\;\;{\rm{sin}}({k_\theta }\theta)\;\;{\rm{sin}}({k_\theta }\theta)} \right), $$
(73)
$${P_{\rm{h}}}(x) = {\rm{diag}}\left({{{\rm{e}}^{{\rm{i}}{k_{x1}}x}}}\quad{{{\rm{e}}^{{\rm{i}}{k_{x2}}x}}}\quad{{{\rm{e}}^{{\rm{i}}{k_{x3}}x}}}\quad{{{\rm{e}}^{{\rm{i}}{k_{x4}}x}}} \right){.} $$
(74)

The elements of the coefficient matrices Ad and Dd are replaced by

$$\left\{ {\begin{array}{*{20}c} {{A_{\rm{d}}}(1,j) = - {D_{\rm{d}}}(1,j) = {\alpha _j},\;\;}\\ {{A_{\rm{d}}}(2,j) = {D_{\rm{d}}}(2,j) = {\beta _j},\;\;\;}\\ {{A_{\rm{d}}}(3,j) = {D_{\rm{d}}}(3,j) = 1,\quad \;\;}\\ {{A_{\rm{d}}}(4,j) = - {D_{\rm{d}}}(4,j) = {\rm{i}}{k_{xj}},} \end{array}} \right. $$
(75)

where j=1, 2, 3, 4.

Eqs. (57)–(60) can be written in the same matrix form as Eq. (69) only if the axial mode matrix Hm(x) and the phase matrix Ph(θ) are replaced by the circumferential mode matrix Hn(θ) and the phase matrix Ph(x), and the force vector Wf turns to be

$${W_{\rm{f}}} = {\left[ {{{\tilde F}_{x\theta }}}\quad{{{\tilde N}_{xx}}}\quad{{{\tilde V}_{xz}}}\quad{{{\tilde M}_{xx}}} \right]^{\rm{T}}}{.} $$
(76)

The elements of the coefficient matrices Af and Df are replaced by

$$\begin{array}{*{20}c} {{A_{\rm{f}}}(1,j) = {D_{\rm{f}}}(1,j) = C\left({{\rm{i}}{k_{xj}}{\alpha _j} + {{\mu - \mu {k_\theta }{\beta _j}} \over R}} \right),\quad }\\ {{A_{\rm{f}}}(2,j) = - {D_{\rm{f}}}(2,j)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {\quad \quad \quad = 6(1 - \mu)D\left({{{{\alpha _j}{k_\theta } + {\rm{i}}R{k_{xj}}{\beta _j}} \over {R{h^2}}} - {{{\rm{i}}{k_{xj}}{k_\theta }} \over {6{R^2}}}} \right),}\\ {{A_{\rm{f}}}(3,j) = - {D_{\rm{f}}}(3,j) = D\left[ {(2 - \mu){{{\rm{i}}{k_{xj}}k_\theta ^2} \over {{R^2}}} + {\rm{i}}k_{xj}^3} \right],}\\ {{A_{\rm{f}}}(4,j) = {D_{\rm{f}}}(4,j) = D\left({k_{xj}^2 + \mu {{k_\theta ^2} \over {{R^2}}}} \right),\quad \quad \quad \quad \;\;} \end{array} $$
(77)

where j=1, 2, 3, 4.

2.6 Equations of natural frequencies

Taking advantage of the unidirectional traveling wave solutions of the OCCS with simply supported curved edges and simply supported straight edges which are respectively obtained in Subsections 2.3 and 2.4, the MRRM is introduced to derive the equation of natural frequencies of the OCCS. Since the scattering matrix is related to boundary conditions of the remaining two edges, it will be discussed in the first step. Then, the phase matrix and permutation matrix, which are independent of the boundary conditions, are obtained. Finally, the reverberation matrix and the equation for natural frequencies of the OCCS are derived. The formulations mentioned above are presented in detail in the following discussion.

Since the derivation procedures of the scattering matrix, phase matrix, and permutation matrix for the OCCS with simply supported curved edges and simply supported straight edges are very similar to each other, the one for simply supported curved edges will be taken as an example and the other will be omitted. Note that the only difference between the two derivation procedures is that the one for simply supported curved edges takes advantage of the solutions obtained in Section 2.3 while the other one employs the solutions obtained in Section 2.4.

2.6.1 Scattering matrix for various classical boundary conditions

With regard to an OCCS with simply supported curved edges and simply supported straight edges, the boundary conditions and the dual local coordinate systems of the OCCS are shown in Fig. 3. The scattering matrix corresponding to various classical boundary conditions, including simply supported edges, free edges, and clamped edges, of the remaining two edges are derived in the following discussion.

  1. 1.

    Simply supported edge

    Assuming that the OCCS is simply supported at Node Line 1, the boundary conditions are defined in the local coordinate (oxθz)12 as

    $${u^{12}} = 0,\;\;{w^{12}} = 0,\;\;N_{\theta \theta }^{12} = 0,\;\;M_{\theta \theta }^{12} = 0{.} $$
    (78)

    Substitution of Eqs. (33), (35), (40), and (41) into the Fourier transform of Eq. (78) yields

    $$\sum\limits_{j = 1}^4 {{\alpha _j}a_j^{12} + {\alpha _j}d_j^{12}} = 0, $$
    (79)
    $$\sum\limits_{j = 1}^4 {a_j^{12} + d_j^{12}} = 0, $$
    (80)
    $$\begin{array}{*{20}c} {\sum\limits_{j = 1}^4 {\left[ {\left({ - \mu R{k_x}{\alpha _j} + {\beta _j}{\rm{i}}{k_{\theta j}} + 1} \right)a_j^{12}} \right.} \quad \quad \quad \;\;}\\ {\left. { + \left({ - \mu R{k_x}{\alpha _j} + {\beta _j}{\rm{i}}{k_{\theta j}} + 1} \right)d_j^{12}} \right] = 0,} \end{array} $$
    (81)
    $$\sum\limits_{j = 1}^4 {\left[ {\left({k_{\theta j}^2 + \mu {R^2}k_x^2} \right)a_j^{12} + \left({k_{\theta j}^2 + \mu {R^2}k_x^2} \right)d_j^{12}} \right]} = 0{.} $$
    (82)

    Eqs. (79)–(82) can be presented in matrix form as

    $${d^1} = {S^1}{a^1}, $$
    (83)

    where d1=d12=[d112 d212 d312 d412]T and a1=a12=[a112 a212 a312 a412]T are amplitude vectors of the departing wave and the arriving wave, and S1=−I4 is defined as the scattering matrix at Node Line 1, in which I4 is a unit matrix of fourth-order.

  2. 2.

    Free edge

    Assuming that the edge of the OCCS at Node Line 1 is free, the boundary conditions are defined in the local coordinate (oxθz)12 as

    $$N_{\theta \theta }^{12} = 0,\;\;F_{\theta x}^{12} = 0,\;\;V_{\theta z}^{12} = 0,\;\;M_{\theta \theta }^{12} = 0.$$
    (84)

    Substitution of Eq. (69) into the Fourier transform of Eq. (84) yields

    $$W_{\rm{f}}^{\ast 12} = {A_{\rm{f}}}{P_{\rm{h}}}(0){a^{12}} + {D_{\rm{f}}}{P_{\rm{h}}}(0){d^{12}} = 0.$$
    (85)

    Since the phase matrix turns into a unit matrix at the origin of the local coordinate, which is obvious from its definition, Eq. (85) can be presented in the same form as Eq. (83) with the scattering matrix replaced by S1=−Df−1Af.

  3. 3.

    Clamped edge

    Assuming that the edge of the OCCS at Node Line 1 is clamped, the boundary conditions are defined in the local coordinate (oxθz)12 as

    $${u^{12}} = 0,\;\;{v^{12}} = 0,\;\;{w^{12}} = 0,\;\;\phi _\theta ^{12} = 0{.} $$
    (86)
Fig. 3
figure 3

Boundary conditions and dual local coordinate system of the shell

(a) Simply supported curved edges; (b) Simply supported straight edges

Full size image

Substituting Eq. (61) into the Fourier transform of Eq. (86) yields

$$W_{\rm{d}}^{\ast 12} = {A_{\rm{d}}}{P_{\rm{h}}}(0){a^{12}} + {D_{\rm{d}}}{P_{\rm{h}}}(0){d^{12}} = 0{.} $$
(87)

In a same manner, Eq. (87) can be presented in the same form as Eq. (83) with the scattering matrix replaced by S1=−Dd−1Ad.

Similarly, the scattering relation for the OCCS at Node Line 2 is presented as

$${d^2} = {S^2}{a^2}, $$
(88)

where d2=d21=[d121 d221 d321 d421]T and a2=a21=[a121 a221 a321 a421]T are amplitude vectors of the departing wave and the arriving wave at Node Line 2. In the same manner as the scattering matrix for Node Line 1 is derived, the scattering matrix at Node Line 2 can be obtained as S2=−I4 for a simply supported edge, S2=−Df−1Af for a free edge, and S2=−Dd−1Ad for a clamped edge.

Assembling both of the local scattering equations at Node Line 1 and Node Line 2 by stacking d1 and d2, a1 and a2 into two column vectors d and a, the global scattering equation is obtained:

$$d = Sa, $$
(89)

where d=[(d1)T (d2)T]T and a=[(a1)T (a2)T]T are global amplitude vectors of the departing wave and the arriving wave, and S=diag(S1 S2) is the global scattering matrix.

2.6.2 Phase and permutation matrices

The phase relations of harmonic waves in the dual coordinate system of MRRM provide additional equations for solving the unknown amplitude vectors. Note that the departing wave from Node Line 1 is exactly the arriving wave to Node Line 2, and vice versa. Therefore, the amplitudes of the departing wave and the arriving wave differ with each other by a phase factor.

With the employment of the solutions of the OCCS with simply supported curved edges, the relations between the amplitudes of the departing wave and the arriving wave are presented as

$$\left\{ \begin{array}{*{20}c} a_1^{12} = - {{\rm{e}}^{ - {\rm{i}}{k_{\theta 1}}{\theta _0}}}d_1^{21},\;\;a_2^{12} = - {{\rm {e}}^{ - {\rm{i}}{k_{\theta 2}}{\theta _0}}}d_2^{21},\\ a_3^{12} = - {{\rm{e}}^{ - {\rm{i}}{k_{\theta 3}}{\theta _0}}}d_3^{21},\;\;a_4^{12} = - {{\rm{e}}^{ - {\rm{i}}{k_{\theta 4}}{\theta _0}}}d_4^{21},\end{array} \right. $$
(90)
$$\left\{ \begin{array}{*{20}c} a_1^{21} = - {{\rm{e}}^{ - {\rm{i}}{k_{\theta 1}}{\theta _0}}}d_1^{12},\;\;a_2^{21} = - {{\rm {e}}^{ - {\rm{i}}{k_{\theta 2}}{\theta _0}}}d_2^{12},\\ a_3^{21} = - {{\rm{e}}^{ - {\rm{i}}{k_{\theta 3}}{\theta _0}}}d_3^{12},\;\;a_4^{21} = - {{\rm{e}}^{ - {\rm{i}}{k_{\theta 4}}{\theta _0}}}d_4^{12},\end{array} \right. $$
(91)

which are rewritten in matrix form as

$${a^1} = - {P_{\rm{h}}}(- {\theta _0}){d^2}, $$
(92)
$${a^2} = - {P_{\rm{h}}}(- {\theta _0}){d^1}{.} $$
(93)

Assembling both the local phase equations defined by Eqs. (92) and (93) results in the global phase equation

$$a = P{d\ast }, $$
(94)

where a is defined in Eq. (89). However, d*=[(d2)T (d1)T]T is a rearranged global amplitude vector of the departing wave, and P=−diag(Ph(−θ0) Ph(−θ0)) is the global phase matrix.

A comparison of the global amplitude vectors of the departing waves d and d* indicates that the two amplitude vectors contain the same scalar state variables arranged in different sequential orders. The relation between d and d* is

$${d\ast} = Ud, $$
(95)

where U=[04 I4; I4 04] is the permutation matrix from d to d*, in which 04 and I4 are respectively the zero matrix and the unit matrix of fourth-order.

2.6.3 Equation for natural frequencies

Substitution of Eqs. (94) and (95) into Eq. (89) yields

$$(I - R)d = 0, $$
(96)

where R=SPU is defined as the reverberation-ray matrix.

To obtain a nontrivial solution of the global amplitude vector of the departing wave d, the determinant of (I−R) must be zero:

$$\det (I - R) = 0, $$
(97)

which is the equation of natural frequencies of the OCCS.

2.7 Searching algorithm for natural frequencies

As the equation of natural frequencies of the OCCS is obtained, the problem at hand is to solve the equation for the natural frequencies. It is obvious that the left hand side of Eq. (97) represents a function of frequency, and the natural frequencies are zero points of the function. Unfortunately, for most values of the frequency, the left hand side of Eq. (97) are complex numbers. Therefore, finding the zero points of the function needs to search the common zero points of the real part and the imaginary part of the function. A good idea is to search the zero points or the minimal values of the absolute value of the function. This simple approach is adopted in this paper and the golden section search algorithm (GSSA) (Press et al., 1992; Vajda, 2007) is introduced to determine the natural frequencies of the OCCS. The procedure for determining natural frequencies of the OCCS, which is shown in Fig. 4, is presented in detail as follows.

Fig. 4
figure 4

Calculation procedure for natural frequencies of the OCCS (Guo, 2008)

Full size image

Firstly, for a trial value of frequency ω1 and a given frequency step Δω, choose both of the endpoints of the interval (ω1, ω1+Δω) and the points with the distance of golden ratio of the interval length from the endpoints as observation frequencies and calculate the absolute values of the determinant of (I−R) for the observation frequencies.

Secondly, compare the absolute values of the determinant for the two frequencies at the left hand side and for the two frequencies at the right hand side of the interval to determine whether there is a zero point or minimal value in the interval. If the answer is yes, the golden section search algorithm is employed to find the zero point or minimal value; if not, the trial frequency will increase by a frequency step, and the above-mentioned process will be repeated until the answer becomes yes.

Thirdly, calculate the absolute value of the determinant for the minimal value obtained in the preceding step to check whether the calculation result is less than the predefined tolerance. If the answer is no, the minimal value will be ignored and the trial frequency will increase by a frequency step, and the above-mentioned process will be repeated until the answer becomes yes. While if the answer is yes, the minimal value is one of the natural frequencies and then the trial frequency will increase by a frequency step, and the above-mentioned process will be repeated to find the next natural frequency. The procedure will be terminated when enough natural frequencies are obtained.

2.8 Mode shapes for the OCCS

Substituting one of the natural frequencies determined in the preceding subsection into Eq. (96), the global amplitude vector of the departing wave d is obtained. By normalization, the global amplitude vector of the departing wave is determinate. Subsequently, by substituting the global amplitude vector of the departing wave into Eqs. (94) and (95), the global amplitude vector of the arriving wave a is determined.

Finally, substituting the global amplitude vector of the departing wave and the arriving wave into the expressions of the displacement components of the OCCS, the mode shape corresponding to the natural frequency is obtained.

3 Results and discussion

The MRRM and the golden section search algorithm are applied in this section to obtain the exact natural frequencies for the OCCS. To begin with, the natural frequencies for the OCCS with all four edges simply supported are calculated and compared with the results obtained by FEM and the method of Leissa. Then, natural frequencies for the OCCS of different length, radius, thickness, and included angle are obtained and the effects of these parameters on the natural frequencies are analyzed. Finally, natural frequencies for the OCCS with different boundary conditions are calculated and the effects of boundary conditions on the natural frequencies are also analyzed.

3.1 Verification of the method

The basic parameters of the OCCS are defined in Table 1. For such an OCCS with all four edges simply supported, a comparison study, with the calculation results shown in Table 2, is carried out by the MRRM presented in this paper, FEM, and the method of Leissa. In addition, some mode shapes obtained by FEM and MRRM are presented in Fig. 5.

Fig. 5
figure 5

Comparison of some selected mode shapes calculated by FEM and MRRM

(a) FEM, (m, n)=(1, 1); (b) FEM, (m, n)=(3, 2); (c) FEM, (m, n)=(5, 2); (d) FEM, (m, n)=(8, 3); (e) MRRM, (m, n)=(1, 1); (f) MRRM, (m, n)=(3, 2); (g) MRRM, (m, n)=(5, 2); (h) MRRM, (m, n)=(8, 3)

Full size image
Table 1 Basic parameters of the OCCS
Full size table
Table 2 Comparison of natural frequencies obtained by FEM, Leissa’s method (LM), and MRRM
Full size table

The results by FEM in Table 2 and Fig. 5 are obtained with the common program software ANSYS, in which the geometry and material properties of the open circular cylindrical shell are defined according to Table 1 and a 250×66 finite element mesh (element edge length 0.04 m) of SHELL181 elements is used during the calculation.

The integer numbers m and n in Table 2 denote the half-wave numbers of the vibration mode in the axial and circumferential directions. MRRM1 and MRRM2 represent the results calculated by MRRM with the solutions for simply supported curved edges derived in Section 2.3 and with the solutions for simply supported straight edges derived in Section 2.4.

It is observed from Table 2 that an excellent agreement is achieved between the results obtained by MRRM based on both of the two solutions and the results obtained by the method of Leissa. Therefore, the comparison study confirms the validity of MRRM for vibration analysis of OCCSs. The results obtained by FEM are quite close to those obtained by MRRM.

Fig. 5 shows that the mode shapes obtained by FEM and MRRM are almost the same as each other, which further indicates that MRRM is suitable for free vibration analysis of OCCSs.

Table 2 also shows that the natural frequencies of the OCCS increase with the increase of the axial mode number. However, as the circumferential mode number increases, the natural frequencies of the OCCS firstly decrease to a minimal value at a certain mode number, for example n=2 for m=1, 2, n=3 for m=3–6, and n=4 for m=7–10, and then gradually increase all the way up. Table 2 also shows that the natural frequencies of the OCCS increase with the increase of the circumferential mode number more rapidly than they do with the increase of the axial mode number.

3.2 Effect of shell length on natural frequencies

The effect of shell length on natural frequencies of the OCCS with all four edges simply supported is investigated in this subsection. The shell length is set to be 6 m, 8 m, 10 m, and 12 m, respectively. The other parameters of the OCCS are defined in Table 1. The comparison results are presented in Table 3, in which all the natural frequencies are normalized by the results presented in Table 2. Since all the normalized natural frequencies corresponding to shell length of 10 m turn out to be unit one, they are omitted in this table. The same manner is used for Table 4–8, and it will not be mentioned in the next subsections.

Table 3 Effect of shell length on the normalized natural frequencies
Full size table
Table 4 Effect of shell radius on the normalized natural frequencies
Full size table
Table 5 Effect of shell thickness on the normalized natural frequencies
Full size table
Table 6 Effect of included angle on the normalized natural frequencies
Full size table
Table 7 Effect of boundary conditions (BCs) on normalized natural frequencies of the OCCS with simply supported curved edges
Full size table
Table 8 Effect of boundary conditions (BCs) on normalized natural frequencies of the OCCS with simply supported straight edges
Full size table

Table 3 shows that, for an arbitrary pair of mode numbers, the natural frequencies of the OCCS decrease with the increase of the shell length.

For an arbitrary axial mode number, the difference of natural frequencies corresponding to different shell lengths decreases with the increase of the circumferential mode number. However, for an arbitrary circumferential mode number, the difference of natural frequencies corresponding to different shell lengths increases with the increase of the axial mode number, which indicates that the effect of shell length on natural frequencies of the OCCS increases with axial mode number while it decreases with the circumferential mode number.

3.3 Effect of shell radius on natural frequencies

The effects of shell radius on natural frequencies of the OCCS with all four edges simply supported are investigated in this subsection. The shell radii are taken as 3 m, 4 m, 5 m, and 6 m. The other parameters of the OCCS are defined in Table 1. The calculation results are presented in Table 4.

It can be found from Table 4 that, for most but not all of the mode numbers (except for (m, n)=(1–5, 1) and (4–9, 2)), the natural frequencies of the OCCS decrease with the increase of the shell radius. The effect of shell radius on natural frequencies of the OCCS decreases with axial mode number while it increases with circumferential mode number.

3.4 Effect of shell thickness on natural frequencies

Table 5 presents the natural frequencies of the OCCS with all four edges simply supported as the shell thickness varies from 4 mm, by every 2 mm, to 10 mm. The rest parameters of the OCCS are defined in Table 1. The calculation results are presented in Table 5.

It is observed from Table 5 that the natural frequencies of the OCCS increase with the increase of the shell thickness for all mode numbers. The effect of shell thickness on natural frequencies of the OCCS decreases with axial mode number while it increases with the circumferential mode number.

For small circumferential mode numbers n=1 and 2, the natural frequencies corresponding to different shell thickness are very close to each other. However, for large circumferential mode numbers n≥7, the natural frequencies vary linearly with the shell thickness.

3.5 Effect of included angle on natural frequencies

The effect of the included angle on the natural frequencies of the OCCS with all four edges simply supported is investigated in this subsection. The included angles are taken as 10°, 20°, 30°, and 40°. The other parameters of the OCCSs are defined in Table 1. The calculation results are presented in Table 6.

Table 6 shows that the included angle exerts a significant influence on the natural frequencies of the OCCS. For most but not all mode numbers, the natural frequencies of the OCCS decrease as the included angle increases.

For mode numbers n≤4, the natural frequencies of the OCCS vary complicatedly with the included angle. Specifically, for n=1, the natural frequencies of the OCCS increase with increase of the included angle with an exception for m=1. While for mode numbers of (m, n)=(1, 1), (3–5, 2), and (8–10, 3), the highest and the lowest natural frequencies are corresponding to the included angles of 10° and 20°. For mode numbers of (m, n)=(2, 2), (4–7, 3), and (7–10, 4), the highest and the lowest natural frequencies are corresponding to the included angles of 10° and 30°. For mode numbers of (m, n)=(6–10, 2), the highest and the lowest natural frequencies are corresponding to the included angles of 40° and 20°.

3.6 Effect of boundary conditions on natural frequencies

Based on the solutions derived in Sections 2.3 and 2.4, the MRRM is employed to calculate the natural frequencies of the OCCS with the two curved edges or the two straight edges simply supported, and the two remaining edges supported by an arbitrary combination of SSE, CE, and FE, such as SSE-SSE, SSE-CE, SSE-FE, CE-CE, CE-FE, and FE-FE. However, for simplicity, cases of the two remaining edges with the same boundary conditions are chosen as calculation examples to investigate the effect of the boundary conditions on the natural frequencies. The basic parameters are defined in Table 1. The boundary conditions of the two remaining edges SSE-SSE, CE-CE, and FE-FE are respectively denoted as SSEs, CEs, and FEs in the following discussion.

The effects of boundary conditions on natural frequencies of the shell with simply supported curved edges and simply supported straight edges are respectively presented in Tables 7 and 8. In addition, some mode shapes obtained by MRRM are presented in Fig. 6.

Fig. 6
figure 6

Mode shapes obtained by MRRM for different boundary conditions

(a) SSE-CE-SSE-CE; (b) SSE-FE-SSE-FE; (c) CE-SSE-CE-SSE; (d) FE-SSE-FE-SSE

Full size image

It can be observed from Table 7 that, as the two curved edges are simply supported, the natural frequencies corresponding to the three kinds of boundary conditions of the remaining two edges decrease in the order of CEs, SSEs, and FEs for most but not all mode numbers. For mode numbers (m, n)=(1–10, 1) and (5–10, 2), the natural frequencies of the OCCS with the two remaining edges supported by SSEs, CEs, and FEs decrease in sequence.

Table 8 shows that, as the two straight edges are simply supported, the boundary conditions of the remaining two edges have little effect on the natural frequencies of the OCCS. For circumferential mode numbers no more than 5, the natural frequencies with the two remaining edges supported by CEs, SSEs, and FEs decrease in sequence. However, as the circumferential mode number becomes larger than 5, the natural frequencies of the remaining two edges decrease in the order of FEs, CEs, and SSEs.

4 Conclusions

This paper presents analytical solutions and exact natural frequencies for the OCCS with either the two curved edges or the two straight edges simply supported. Based on the DMV thin shell theory, the solutions of the unidirectional traveling wave form for the OCCS with two opposite simply supported edges are obtained. Subsequently, MRRM is applied to derive the equation of natural frequencies of the OCCS, and the golden section search algorithm is employed to obtain the exact natural frequencies. Then, the proposed procedure is verified by the comparison of the present results with those obtained by FEM and MRRM. Finally, the effects of shell length, shell radius, shell thickness, included angle, and the boundary conditions on natural frequencies of the OCCS are investigated. It can be concluded as follows:

  1. 1.

    MRRM is validated and of high precision for vibration analysis of OCCSs.

  2. 2.

    The natural frequencies of the OCCS decrease with the increase of the shell length.

  3. 3.

    The natural frequencies of the OCCS decrease with the increase of the shell radius for most mode numbers.

  4. 4.

    The natural frequencies of the OCCS increase with the increase of the shell thickness. The natural frequencies corresponding to different shell thickness are very close to each other for mode numbers n=1 and 2, while they vary linearly with the shell thickness for mode numbers n≥7.

  5. 5.

    The natural frequencies of the OCCS decrease rapidly as the included angle increases for most mode numbers.

  6. 6.

    As the two curved edges are simply supported, the natural frequencies corresponding to the three kinds of boundary conditions of the remaining two edges decrease in the order of CEs, SSEs, and FEs for most of the mode numbers.

  7. 7.

    As the two straight edges are simply supported, the boundary conditions of the remaining two edges have little effect on the natural frequencies of the OCCS.

Finally, the exact natural frequencies of the OCCS for various parameters and different boundary conditions are presented in tabular form for easy reference as benchmark values for researchers to verify their numerical methods and for convenient consulting for engineers in practical design.