1 Introduction

As a buckling-restrained brace (BRB) possesses adequate hysteretic performance and its core can yield both under tension and compression loads without overall buckling, it has been widely applied in building structures (Black et al., 2004; Qiang, 2005; Tremblay et al., 2006; Di Sarno and Manfredi, 2010; 2012; Di Sarno et al., 2013). A BRB core member is used to carry the entire axial force. Because of the large slenderness ratio of the core member, it is easy to buckle. Accordingly, an external restraining member is applied to provide lateral support and prevent the core member from lateral deformation. There are two kinds of connection types between the BRB and frame, namely a fixed or pinned connection. Compared with a fixed BRB (Iwata and Murai, 2006; Tsai and Hsiao, 2008; Chou and Chen, 2010), a pinned BRB (Fahnestock et al., 2007; Wigle and Fahnestock, 2010; Zhao et al., 2012b) can only withstand axial forces and its end rotation is not restrained by the frame, which usually leads to BRB overall buckling failure. Accordingly, this study will focus on the strength design method of pinned BRBs.

When designing a BRB, to prevent the core from failure at its two ends, it is usually reinforced before it extends out of the external restraining member (Chen et al., 2001; Qiang, 2005; Iwata and Murai, 2006). For a pinned BRB, its global lateral deflection as well as the flexural deformation of the extended core usually appears under axial load. There exist three distinct failure modes of a BRB in such situations: (1) The core bending failure around the extended core due to its insufficient bearing capacity (Zhao et al., 2011); (2) Overall buckling failure due to insufficient bending stiffness of external restraining member (Ju et al., 2009; Zhao et al., 2012a); (3) Local failure of external restraining member at its ends due to immense contact force with the core or serious stiffness weakening. These failure modes are mainly related to a series of design parameters of a BRB, including the gap between the core and the external restraining member, overall initial imperfection of axis of the BRB, and the rigidity and material strength in external restraining member. This study mainly focuses on the first two failure modes. In addition, when a BRB is subjected to cyclic load, fatigue failure of the core may also occur (Usami et al., 2011; Wang et al., 2012). But if the elasticity of the external member can be guaranteed in its design, the fatigue failure will only be related to the material characteristics of the core. This mechanism is not discussed in this study.

By investigating a BRBs inherent mechanical behavior, it is found that the core contact force acting on the external member is the key factor affecting the BRB failure modes. The core contact force directly affects the working conditions of the extended core and external restraining member. Accordingly, prior to utilizing the design method of the pinned BRBs, it is necessary to determine the contact force distribution mode between the core and the external member. If the assumed contact force distribution is not compliant with the actual distribution mode, the obtained maximum bending moment acting on the extended core and external member and the contact forces acting on the end of external member will not be accurate.

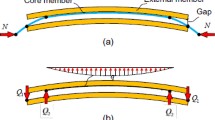
The core contact force distribution is closely related to the core deformation mode. For pinned BRBs with a single flat-plate core, the core may deform according to two distinct deformation modes, namely, the single-wave overall deformation (Fig. 1a) and the multi-wave deformation associated with a single-wave overall deformation (Fig. 1b). For the secondary deformation mode, namely the multi-wave deformation associated with a single-wave overall deformation, of the core, it appears that the stress state of the external restraining member is the superposition of the core multi-wave deformation and the single-wave overall deformation. At the mid-span of the BRB, the moment of the external restraining member caused by the core multi-wave deformation equals zero because the pushing forces of the core outwards are self-balanced (Fig. 1d). Therefore, the maximum moment of the external restraining member at the mid-span happens only when the core behaves as a single-wave deformation. Based on this, only the influence of the core single wave overall deformation is considered in this paper.

Fig. 1
figure 1

Deformation mode of BRB and corresponding force state of external member

(a) Core single-wave overall deformation; (b) Force analysis on external member when BRB has single-wave overall deformation; (c) Core multi-wave buckling together with large lateral displacement deformation; (d) Force analysis on external member when BRB has multi-wave deformation associated with a single-wave overall deformation N is the axial force acting on the core member, q is the distribution load acting on the core contact region, Q1 is the concentrated contact force between the core and the external restraining member ends when BRB has single-wave overall deformation, Q2 is the concentrated contact force between the core and the external restraining member when BRB has single-wave overall deformation, and Fl1 is the mid-span core contact force when BRB has multi-wave buckling deformation

Full size image

2 Previous research on contact force distribution mode

Few studies are concerned with the contact force distribution mode between the core and the external restraining member; and studies on the design method considering the influences of extended core in a pinned BRB are even fewer. In some research the assumptions used for the contact force distribution mode are inadequate. Usami and Kaneko (2001) put forward the continuous beam model with variable rigidity for the pinned BRBs with an H-shaped core member, and assumed that the extended core and the external restraining member met the deformation compatibility conditions at the external member end (Fig. 2). However, as there was a gap between the actual core and the external member, when the BRB end rotates, the strengthened core region (SCR) and external restraining member would be faced with the two-point contact condition (Fig. 3). In such a case, the boundary conditions of extended core and external member at points c, d would be discontinuous and their lateral displacement and rotation were different, which magnifies the bending moment of the extended core and the overall stress state of the external member. Accordingly, the results obtained by using such a method were inaccurate.

Fig. 2
figure 2

Continuous beam model with variable rigidity

Full size image
Fig. 3
figure 3

Real force state of BRB

Full size image

Guo and Jiang (2010) supposed that the lateral deformation of the core and the external restraining member are similar, therefore the contact force between the core and the external member follows a sinusoidal geometric distribution mode. The influence of gap between the core and the external member was ignored, which led to inaccuracy when calculating the contact force distribution.

Zhao et al. (2011) assumed that two-point contact was formed between the core and the external member end, and simplified the core yield region contact force distribution to the uniform distribution mode. Considering the contact force at the core end and mid-span as well as the deformation compatibility relationship at some contact points, the maximum bending moment of the extended core and external member were obtained. Finally, design criteria for predicting the limit strength of the extended core and external member were established according to the yield criterion of the cross-sectional edge stresses. The method is adequately applicable. However, the influences of geometric imperfection of the core and the external member as well as the gap when selecting the initial working state are not accounted for. Besides, the plasticity influence of the extended core is not mentioned and the assumption of the contact force distribution form of the core yield region needs to be revised.

Wang et al. (2013) proposed a simplified calculation model for the pinned BRBs to investigate the influence of BRB end detail construction on the BRB’s overall performance. A double iterative algorithm was used to consider the influence of end additional eccentricity ea on the performance of the extended core. In spite of the lucid concept of the simplified model, and the consideration of factors like the extended core and external member rigidity, gap and initial imperfection, the check of the extended core must be carried out by the finite element (FE) analysis, and it is unable to offer analytic expressions; on this account, it is not recommended as a design proposal in engineering application.

Based on the research results stated above, this study takes the pinned BRBs with extended core as a research object and investigates the force state of the pinned BRBs when the core behaves as a single-wave overall deformation. Under the assumption of the core contact force distribution mode, the core contact force and the bending moment distribution of external member are deduced. Finally, according to the stress characteristics of the pinned BRBs, the design criteria for the external restraining member and the extended strengthened core region (ESCR) are established. In the theoretical derivation of the design method, the influence of some parameters is considered, including the external member rigidity, strength and initial geometrical imperfection, the gap, the rigidity reduction of restrained strengthened core region (RSCR), and the change of contact position.

3 Stress state of the pinned BRBs with core single-wave overall deformation

The core single-wave overall deformation of a pinned BRB is analysed in this section. The initial geometrical configuration of the BRB is taken as its initial state when the external restraining member starts to provide lateral support to the core member. Based on the assumption of core contact force distribution, the equilibrium equations of ESCR and RSCR are established. By employing the deformation compatibility relationship between the core and the external member at some specific contact points, the maximum bending moment acting on the extended core, the contact force distribution and the bending moment distribution acting on the external member are obtained, so as to lay a foundation for developing design criteria of the external member and the SCR. There follows a discussion on the simplified analytical model, initial state, equilibrium equation, deformation compatibility, and bending moment effect.

3.1 Simplified analytical model

The following assumptions are made for the simplified analytical model:

  1. 1.

    The initial geometric imperfection of the core and the external member follow a sinusoidal distributed geometric pattern, and the geometric state when the two-point-contact just starts to be formed at the end of the core and the external member is defined as the initial state of the pinned BRBs.

  2. 2.

    Two-point-contact occurs at the ends of the core and the external restraining member. The deformation mode of the core contact region and the external member is identical in the core contact region, and a sinusoidal distributed contact force in this region is specified. Nagao and Takahashi (1991), Inoue and Sawaisumi (1992), and Zhao et al. (2011) found that the core yield region possessing single-wave overall deformation and their contact forces appearing as a sinusoidal or uniformly distributed pattern would be the worst for BRB overall performance. It is also confirmed from FE numerical results that the contact force distribution in the core yield region is very complicated; however, it is more likely to follow a sinusoidal pattern.

  3. 3.

    Core deformation is assumed to be a single-wave, and the bending moment acting on the core contact region is zero.

The simplified analysis model of a pinned BRB is shown in Fig. 4. As a pinned connector of the BRB has enough flexural rigidity, it can be simplified and considered as a rigid body. Given that the external member and core member often have initial geometrical imperfections (δ0, δ1) because of construction and manufacture error, the influence of the initial geometrical imperfections should be taken into account (Fig. 5a).

Fig. 4
figure 4

Simplified analytical model of a pinned BRB

LBRB is the distance between two pinned connectors of BRB, L0 is the length of a pinned connector, Lc10 and Lc20 are the RSCR lengths with uniform section and variable section when BRB is in the initial state, respectively, Lc0 is the total length of the RSCR when BRB is in the initial state, Lp0 is the length of the ESCR when BRB is in the initial state, Ly0 is the length of the core flat-plate when BRB is in the initial state, Lcm and Lem are the lengths of the core member and external restraining member, respectively, L1 and L2 are the horizontal distances between the contact points d and e and the pinned connector, respectively, Lpc is the length of SCR with uniform section, g is the gap between the core and the external member, EbIb is the flexural rigidity of the external restraining member, EpIp is the flexural rigidity of the ESCR, b0 and t0 are respectively the height and thickness of wing-plate of the SCR; hc and tc respectively represent the width and thickness of the core member, and Ip and Ip0 respectively are the moments of inertia of the ESCR and core member

Full size image
Fig. 5
figure 5

Changing process of stress state of a pinned BRB

(a) Original state of BRB with imperfections; (b) Initial state; (c) Working state Lp is the length of the ESCR, Lc is the horizontal distance between two contact points of the core member end, Ly is the horizontal distance between two inner contact points in the middle of core member, and L3 is the horizontal distance between the contact point d and the core member end

Full size image

3.2 Initial state

The core of a pinned BRB often has a large slenderness ratio, and accordingly its lateral deflection occurs when subjected to axial compression. In such a case, the core will push one side of the external restraining member and cause rigid body movement. After the core contacts the end of the external member, it will formally enter the working state (Fig. 5b). Accordingly, the state can be taken as the initial state of the BRB and the corresponding core deformation is the initial geometrical configuration of the BRB. As the BRB enters the initial state at the beginning of loading, the geometrical dimensions of the BRB can be assumed as unchanged.

It is assumed that the external restraining member and the core member have a sinusoidal initial imperfection distribution with amplitudes of δ0 and δ1, respectively. In such a case, when the BRB is in the initial state, the core deformation is sinusoidal. Let the core deformation amplitude be δ2, then the core deformation y0(x) when the BRB is in the initial state can be obtained:

$$\matrix{{{y_0}(x) = {\delta _2}{\rm{sin}}\left({{{x - {L_0}} \over {{L_{{\rm{BRB}}}} - 2{L_0}}}{\rm{\pi }}} \right) + {y_0}({L_0}),} \hfill \cr {\quad \quad {L_0} \leq x \leq {L_{{\rm{BRB}}}} - {L_0},} \hfill \cr }$$
(1)

where LBRB represents the distance between two pinned connectors of BRB; L0 represents the length of a pinned connector; and δ2 represents the deformation amplitude of the core in the initial state, which can be calculated by Eq. (5).

Fig. 5b shows that, at position x=L2, the core contacts the end of external restraining member and the core deformation should meet the following boundary conditions:

$${\left. {{y_0}(x)} \right\vert_{x = {L_{{\rm{BRB}}}}/2}} - {\left. {{y_0}(x)} \right\vert_{x = {L_2}}} = {\delta _0} + 2g,$$
(2)
$${\left. {{y_0}(x)} \right\vert_{x = {L_0}}} = {L_0}{\left. {{{y^{\prime}}_0}(x)} \right\vert_{x = {L_0}}},$$
(3)

where g represents the lateral gap between the core and the external member.

Thus, the BRB initial geometrical configuration y0(x) can be expressed as

$$\matrix{{{y_0}(x) = {\delta _2}\sin ({m_0}x - {m_0}{L_0}) + {m_0}{L_0}{\delta _2},} \hfill \cr {\quad \quad \quad {L_0} \leq x \leq {L_{{\rm{BRB}}}} - {L_0},} \hfill \cr }$$
(4)

where m0=π/(LBRB−2L0), and

$${\delta _2} = {{{\delta _0} + 2g} \over {1 - \sin ({m_0}{L_{{\rm{p}}0}})}},$$
(5)

where Lp0 denotes the length of the ESCR when the BRB is in the initial state, as shown in Fig. 5b.

3.3 Equilibrium equation

For the pinned BRBs in the working state (Fig. 5c), differential equations of equilibrium are established for the ESCR and RSCR, which are given by

$$\matrix{{{\eta _1}{E_{\rm{p}}}{I_{\rm{p}}}[{y_1}(x) - {y_0}(x)]^{\prime\prime} + N{y_1}(x) = 0,} \hfill \cr {\quad \quad \quad \;{L_0} \leq x \leq {L_2},} \hfill \cr }$$
(6)
$$\matrix{{{{\bar \mu }_0}{\eta _1}{E_{\rm{p}}}{I_{\rm{p}}}[{y_2}(x) - {y_0}(x)]^{\prime\prime} + [N{y_2}(x) - {Q_1}(x - {L_2})] = 0,} \hfill \cr {\quad \quad \quad \quad \quad \quad \;{L_2} \leq x \leq {L_1},} \hfill \cr }$$
(7)

where EpIp is the elastic flexural rigidity of the ESCR. Considering that the RSCR is a beam-column with a variable cruciform section, its flexural rigidity is replaced with a constant equivalent stiffness. The simply supported beam-column with equivalent stiffness should possess the same rotation at the beam-column end with the RSCR subjected to end moment (Fig. 6). Through simplification, the RSCR equivalent flexural rigidity can be obtained. η1 represents the RSCR rigidity reduction coefficient. Considering the plasticity influence of the RSCR, its value is related to the core axial strain. From the FE analysis discussed in part II (Jiang et al., 2015), when the core axial strain is 1%, η1 takes 4/9; when the core axial strain is 2%, η1 takes 1/4; when the core axial strain is 3%, η1 takes 4/25. represents the RSCR equivalent flexural rigidity coefficient, which is calculated by

$${\bar \mu _0} = {{L_{{\rm{c}}0}^3} \over {{\mu _1}L_{{\rm{c}}20}^3 + L_{{\rm{c}}0}^3}},$$
(8)
$${\mu _1} = {{7b_0^3{t_0} + 9b_0^2{t_0}{t_{\rm{c}}} + 3{b_0}{t_0}t_{\rm{c}}^2} \over {b_0^3{t_0} + 3b_0^2{t_0}{t_{\rm{c}}} + 3{b_0}{t_0}t_{\rm{c}}^2 + {h_{\rm{c}}}t_{\rm{c}}^3}},$$
(9)

where Lc20 and Lc0 respectively represent the length of RSCR with variable section length and the total length of the RSCR when a pinned BRB is in the initial state, μ1 is a dimensionless coefficient, b0 and t0 respectively represent the height and thickness of wing-plate of the SCR, and hc and tc respectively represent the width and thickness of the core member, as shown in Fig. 4 and Fig. 6.

Fig. 6
figure 6

Uniformly sectional equivalence of RSCR

(a) Variable cross section model; (b) Equivalent model 1; (c) Equivalent model 2

Full size image

From the force analysis of the SCR (Fig. 7), it is found that the end contact force Q1 is

$${Q_1} = {{N{\delta _{{\rm{cd}}}} + {M_{{\rm{ec}}}}} \over {{L_{\rm{c}}}}},$$
(10)

where N is the axial force acting on the core member, Mec is the bending moment applied at the end of the core contact region (x=L2) of the ESCR, and δcd is the vertical distance between two contact points c and d, which are shown in Fig. 7. Lc represents the horizontal distance between two contact points c and d of the core member end.

Fig. 7
figure 7

Force analysis of SCR

Full size image

After performing deformation and force analysis with the extended core and the external member as free bodies, the following four boundary conditions can be obtained:

$${y_1}(x){\vert_{x = {L_0}}} = y_1^{\prime}(x){\vert_{x = {L_0}}}{L_0},$$
(11)
$${y_1}(x){\vert_{x = {L_2}}} = {y_2}(x){\vert_{x = {L_2}}},$$
(12)
$$y_1^{\prime}(x){\vert_{x = {L_2}}} = y_2^{\prime}(x){\vert_{x = {L_2}}},$$
(13)
$${E_{\rm{p}}}{I_{\rm{p}}}y_2^{\prime\prime}(x){\vert_{x = {L_1}}} - {E_{\rm{p}}}{I_{\rm{p}}}y_0^{\prime\prime}(x){\vert_{x = {L_1}}} = 0.$$
(14)

Substituting Eqs. (6) and (7) into the above boundary conditions, the expression of the deformation function y1(x) of the extended core can be obtained:

$$\matrix{{{y_1}(x) = {{{m_0}{L_0}\sin (kx)} \over {({k^2} - m_0^2)[k{L_0}\cos (k{L_0}) - \sin (k{L_0})]}}m_0^2{\delta _2}} \hfill \cr {\quad \quad \quad - {{\sin [{m_0}(x - {L_0})]} \over {{k^2} - m_0^2}}m_0^2{\delta _2}} \hfill \cr {\quad \quad \quad + {{k{L_0}\cos [k(x - {L_0})] + \sin [k(x - {L_0})]} \over {k{L_0}\cos (k{L_0}) - \sin (k{L_0})}}{c_1},} \hfill \cr }$$
(15)

where \(k = \sqrt {N/({\eta _1}{E_{\rm{p}}}{I_{\rm{p}}})}\) and c1 represents the undetermined coefficient in the deformation function y1(x), which can be found from the boundary conditions Eqs. (12), (13), and (16). k1, k2 are dimensionless coefficients, which can be found from Eq. (17); A0, A1, A2, Y1, and Y2 are calculation coefficients, which can be found from Eq. (18); \({\mu _0} = 1/{\bar \mu _0}\).

$${c_1} = {k_1}{\delta _2} + {k_2}{Q_1}/(kN),$$
(16)
$${k_1} = {{m_0^2} \over {{A_0}{Y_1}{Y_2}}}{A_2},\;{k_2} = {{{A_1}\sin (k{L_{\rm{c}}}\sqrt {{\mu _0}})} \over {{A_0}}},$$
(17)
$$\matrix{{{A_0} = \sqrt {{\mu _0}} \cos (k{L_{\rm{c}}}\sqrt {{\mu _0}})[\sin (k{L_{\rm{p}}}) + k{L_0}\cos (k{L_{\rm{p}}})]} \hfill \cr {\quad \quad + \sin (k{L_{\rm{c}}}\sqrt {{\mu _0}})[\cos (k{L_{\rm{p}}}) - k{L_0}\sin (k{L_{\rm{p}}})],} \hfill \cr {{A_1} = k{L_0}\cos (k{L_0}) - \sin (k{L_0}),} \hfill \cr {{A_2} = {\rm{(}}{\mu _0} - 1{\rm{)}}k{A_1}{A_{21}} + {Y_1}{A_1}{A_{22}} - {m_0}{L_0}{Y_2}{A_{23}},} \hfill \cr {{Y_1} = {k^2} - m_0^2,\;{Y_2} = {\mu _0}{k^2} - m_0^2,} \hfill \cr {{A_{21}} = k\sqrt {{\mu _0}} \sin ({m_0}{L_{\rm{p}}})\cos (k{L_{\rm{c}}}\sqrt {{\mu _0}})} \hfill \cr {\quad \quad + {m_0}\cos ({m_0}{L_{\rm{p}}})\sin (k{L_{\rm{c}}}\sqrt {{\mu _0}}),} \hfill \cr {{A_{22}} = \sqrt {{\mu _0}} \sin ({m_0}{L_3}),} \hfill \cr {{A_{23}} = \sqrt {{\mu _0}} \cos (k{L_{\rm{c}}}\sqrt {{\mu _0}})\sin (k{L_{\rm{2}}}) + \sin (k{L_{\rm{c}}}\sqrt {{\mu _0}})\cos (k{L_{\rm{2}}}),} \hfill \cr }$$
(18)

where Lp represents the length of ESCR subjected to given flexural moment (Fig. 7); L1, L2 respectively represent the distances between the contact points d, c and the pinned connector; L3 represents the distance between the contact point d and the core member end (Fig. 7).

After obtaining the deformation y1(x) of the extended core, the bending moment Mec at the contact position between the ESCR and the external restraining member can be determined by

$$\matrix{{{M_{{\rm{ec}}}} = {{\left. {N{y_1}(x)} \right\vert}_{x = {L_2}}} = ({m_1}{\delta _2} + {m_2}{c_1})N} \hfill \cr {\quad \;\;\; = ({m_1} + {m_2}{k_1})N{\delta _2} + {m_2}{k_2}{Q_1}/k,} \hfill \cr }$$
(19)
$$\matrix{{{m_1} = {{m_0^3{L_0}\sin (k{L_2}) - {A_1}m_0^2\sin ({m_0}{L_{\rm{p}}})} \over {{Y_1}{A_1}}},} \hfill \cr {{m_2} = {{k{L_0}\cos (k{L_{\rm{p}}}) + \sin (k{L_{\rm{p}}})} \over {{A_1}}},} \hfill \cr }$$
(20)

where m1, m2 are dimensionless coefficients.

In addition, the rotation θec at a pinned connector (x=L0) can be easily obtained. Its expression is shown in Eq. (21), and its physical meaning is shown in Fig. 7, where r1, r2 are coefficients.

$$\matrix{{{\theta _{{\rm{ec}}}} = {{\left. {{{y^{\prime}}_1}(x)} \right\vert}_{x = {L_0}}} = {r_1}{\delta _2} + {r_2}{c_1}} \hfill \cr {\quad \; = ({r_1} + {r_2}{k_1}){\delta _2} + {r_2}{k_2}{Q_1}/(kN),} \hfill \cr }$$
(21)
$${r_1} = {{m_0^3\sin (k{L_0})} \over {{Y_1}{A_1}}},\;\;{r_2} = {k \over {{A_1}}},$$
(22)

where the contact force Q1, bending moment Mec, and deformation δcd are three unknown quantities, and the equations related to these quantities established are only Eqs. (10) and (19). Accordingly, other equations should be built by using the deformation compatibility relationship between the core and the external restraining member.

3.4 Deformation compatibility and bending moment effect

The force analysis is carried out with respect to the core contact region and the external restraining member in the working state (Fig. 8). The deformation compatibility relationship of the core and the external member between points c, d and points d, e are elucidated by this figure.

Fig. 8
figure 8

Force analysis on the core contact region (a) and external restraining member (b)

Full size image

The core contact region and the external restraining member are taken as free bodies, as shown in Figs. 8a and 8b. It is supposed that the contact force distribution is sinusoidal and the mid-span contact force distribution intensity is q0. After performing force analysis on the core contact region, the distribution load q acting on the core contact region can be obtained:

$$q = {q_0}\sin \left({{{\rm{\pi }} \over {L_{\rm{y}}^{}}}u} \right) = {{{{\rm{\pi }}^2}N{\delta _{{\rm{de}}}}} \over {L_{\rm{y}}^2}}\sin \left({{{\rm{\pi }} \over {L_{\rm{y}}^{}}}u} \right),$$
(23)

where Ly represents the horizontal distance between two contact points in the middle of the core member; δde represents the vertical distance between points d and e on the core contact region, which can be obtained by the bending deformation analysis of the external restraining member. It is mainly related to the external restraining member initial imperfection amplitude δ0, bending moment Q1Lc, and the sinusoidal distribution contact force q. δde can be given by

$${\delta _{{\rm{de}}}} = {\delta _{{\rm{de0}}}}{\rm{ + }}{{{Q_{\rm{1}}}{L_{\rm{c}}}L_{\rm{y}}^2} \over {8{E_{\rm{b}}}{I_{\rm{b}}}}} + {{{q_0}L_{\rm{y}}^4} \over {{{\rm{\pi }}^4}{E_{\rm{b}}}{I_{\rm{b}}}}},$$
(24)

where EbIb is the flexural rigidity of the external restraining member, and δde0 is the vertical distance between points d and e when the BRB is in its initial state.

Let the length of external restraining member equal Lem, then the expression of the external restraining member deformation function y3(v) in the initial state can be obtained:

$${y_3}(v) = {\delta _0}{\rm{sin}}\left({{{\rm{\pi }} \over {{L_{{\rm{em}}}}}}v} \right).$$
(25)

Let x1=1−sin(πLc/Lem), then another expression of the vertical distance δde0 between points d and e can be given as

$${\delta _{{\rm{de}}0}} = {x_1}{\delta _0} = [1 - \sin ({\rm{\pi }}{L_{\rm{c}}}/{L_{{\rm{em}}}})]{\delta _0}.$$
(26)

By substituting Eq. (24) into Eq. (23), the equation of the distribution force intensity q0 can be written as

$${q_0} = {{{{{{\rm{\pi }}^2}N} \over {L_{\rm{y}}^2}}\left({{{{Q_{\rm{1}}}{L_{\rm{c}}}L_{\rm{y}}^2} \over {8{E_{\rm{b}}}{I_{\rm{b}}}}} + {x_1}{\delta _0}} \right)} \mathord{\left/{\vphantom {{{{{{\rm{\pi }}^2}N} \over {L_{\rm{y}}^2}}\left({{{{Q_{\rm{1}}}{L_{\rm{c}}}L_{\rm{y}}^2} \over {8{E_{\rm{b}}}{I_{\rm{b}}}}} + {x_1}{\delta _0}} \right)} {\left({1 - {{NL_{\rm{y}}^2} \over {{{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}}}}} \right)}}} \right.\kern-\nulldelimiterspace} {\left({1 - {{NL_{\rm{y}}^2} \over {{{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}}}}} \right)}}.$$
(27)

Similarly, the vertical distance δcd between points c and d in the center of SCR can be obtained by deformation analysis of the external restraining member:

$$\matrix{{{\delta _{{\rm{cd}}}} = 2g - \nu {\varepsilon _{\rm{c}}}{t_{\rm{c}}} + {\delta _0}{\rm{sin}}\left({{\pi \over {{L_{{\rm{em}}}}}}{L_{\rm{c}}}} \right)} \hfill \cr {\quad + {{{q_0}L_{\rm{y}}^3{L_{\rm{c}}}} \over {{{\rm{\pi }}^3}{E_{\rm{b}}}{I_{\rm{b}}}}} + {{{Q_{\rm{1}}}L_{\rm{c}}^2L_{\rm{y}}^{}} \over {2{E_{\rm{b}}}{I_{\rm{b}}}}} + {{{Q_{\rm{1}}}L_{\rm{c}}^3} \over {3{E_{\rm{b}}}{I_{\rm{b}}}}},} \hfill \cr }$$
(28)

where the first three terms refer to the gap, Poisson effect, and the influence of the external restraining member initial geometrical imperfection. The fourth term is caused by the sinusoidal distribution contact force q, and last two terms denote the contribution of the end contact force Q1. v and εc respectively represent the steel Poisson’s ratio and the core axial compressive strain.

By substituting Eq. (27) into Eq. (28), δcd is obtained, then substitute δcd into Eq. (10), the contact force of SCR at point c can be expressed by

$$\matrix{{{Q_{\rm{1}}} = {w_1}N + {w_2}{M_{{\rm{ec}}}}/{L_{\rm{c}}},} \hfill \cr {{w_1} = \{ [({{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}} - NL_{\rm{y}}^2)(2g - \nu {\varepsilon _{\rm{c}}}{t_{\rm{c}}} + {\delta _0}\sin ({\rm{\pi }}{L_{\rm{c}}}/{L_{{\rm{em}}}}))} \hfill \cr {\;\;\;\;\;\; + {\rm{\pi }}{x_1}{\delta _0}{L_{\rm{c}}}{L_{\rm{y}}}N]24{E_{\rm{b}}}{I_{\rm{b}}}\}/\{ {L_{\rm{c}}}[24{{\rm{\pi }}^2}E_{\rm{b}}^2I_{\rm{b}}^2} \hfill \cr {\;\;\;\;\;\; - 4{E_{\rm{b}}}{I_{\rm{b}}}N(2{{\rm{\pi }}^2}L_{\rm{c}}^2 + 3{{\rm{\pi }}^2}{L_{\rm{c}}}{L_{\rm{y}}} + 6L_{\rm{y}}^2)} \hfill \cr {\;\;\;\;\; + {L_{\rm{c}}}L_{\rm{y}}^2{N^2}(8{L_{\rm{c}}} + (12 - 3{\rm{\pi }}){L_{\rm{y}}})]\},} \hfill \cr }$$
(29)
$$\matrix{{{w_2} = [({{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}} - NL_{\rm{y}}^2)24{E_{\rm{b}}}{I_{\rm{b}}}]/\{ [24{{\rm{\pi }}^2}E_{\rm{b}}^2I_{\rm{b}}^2} \hfill \cr {\;\;\;\;\;\; - 4{E_{\rm{b}}}{I_{\rm{b}}}N(2{{\rm{\pi }}^2}L_{\rm{c}}^2 + 3{\pi ^2}{L_{\rm{c}}}{L_{\rm{y}}} + 6L_{\rm{y}}^2)} \hfill \cr {\;\;\;\;\;\; + {L_{\rm{c}}}L_{\rm{y}}^2{N^2}(8{L_{\rm{c}}} + (12 - 3{\rm{\pi }}){L_{\rm{y}}})]\},} \hfill \cr }$$
(30)

where w1 and w2 represent dimensionless calculation coefficients.

By Eq. (29) and Eq. (19), the expressions of bending moment Mec which acts on the ESCR end, and the end contact force Q1 between ESCR and external restraining member can be given by Eq. (31) and Eq. (32).

$${M_{{\rm{ec}}}} = {c_{\rm{2}}}N{L_{\rm{c}}},$$
(31)
$${Q_1} = ({w_1} + {c_{\rm{2}}}{w_2})N,$$
(32)
$${c_2} = {{({m_1} + {m_2}{k_1})k{\delta _2} + {m_2}{k_2}{w_1}} \over {k{L_{\rm{c}}} - {m_2}{k_2}{w_2}}}.$$
(33)

By substituting Eq. (29) into Eq. (21), the expression of the BRB end rotation θec can be obtained:

$${\theta _{{\rm{ec}}}} = ({r_1} + {r_2}{k_1}){\delta _2} + {r_2}{k_2}({w_1} + {c_{\rm{2}}}{w_2})/k.$$
(34)

As the contact force Q1 and the sinusoidal distribution force q of the core contact region are known, according to the equilibrium equation, the expression of the contact force Q2 (Fig. 5c) can be obtained, which is given by Eq. (35). After performing force analysis on the external restraining member, the bending moment distribution of the external member within the core contact region can be obtained:

$$\matrix{{{Q_2} = {Q_1} - {1 \over 2}\int_0^{{L_{\rm{y}}}} q {\rm{d}}u} \hfill \cr {\;\;\;\; = {{{Q_1} - {{{\rm{\pi }}N} \over {{L_{\rm{y}}}}}\left({{{{Q_1}{L_{\rm{c}}}L_{\rm{y}}^2} \over {8{E_{\rm{b}}}{I_{\rm{b}}}}} + {x_1}{\delta _0}} \right)} \mathord{\left/{\vphantom {{{Q_1} - {{{\rm{\pi }}N} \over {{L_{\rm{y}}}}}\left({{{{Q_1}{L_{\rm{c}}}L_{\rm{y}}^2} \over {8{E_{\rm{b}}}{I_{\rm{b}}}}} + {x_1}{\delta _0}} \right)} {\left({1 - {{NL_{\rm{y}}^2} \over {{{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}}}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left({1 - {{NL_{\rm{y}}^2} \over {{{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}}}}} \right)}},} \hfill \cr }$$
(35)
$${M_{{\rm{em}}}}(u) = {Q_1}{L_{\rm{c}}} + {{L_{\rm{y}}^2} \over {{\pi ^2}}}{q_0}{\rm{sin}}\left({{\pi \over {{L_{\rm{y}}}}}u} \right),\;\;\;0 \leq u \leq {L_{\rm{y}}},$$
(36)

where u represents the horizontal distance between a certain point on the external restraining member and point d (Fig. 8). At the mid-span, namely u=Ly/2, the bending moment of the external member is the maximum, which is given by

$${M_{{\rm{em,}}\max }} = {Q_{\rm{1}}}{L_{\rm{c}}} + {{L_{\rm{y}}^2} \over {{\pi ^2}}}{q_0}.$$
(37)

Note that Lp, Lc, and Ly will change with the increase of core axial strain, which can be respectively calculated by

$${L_{\rm{p}}} = {L_{{\rm{p}}0}} - {\Delta _{{\rm{BRB}}}}/2,$$
(38)
$${L_{\rm{c}}} = {L_{{\rm{c}}10}} + {\Delta _{{\rm{BRB}}}}/2 + {\eta _2}{L_{{\rm{c}}20}},$$
(39)
$${L_{\rm{y}}} = {L_{{\rm{em}}}} - 2{L_{\rm{c}}},$$
(40)

where η2 represents the correction coefficient of the contact position variation at the variable cruciform region of the RSCR, which is obtained by FE numerical analysis. When the core axial strain is 1%, η2 takes 1.0; when the core axial strain is 2%, η2 takes 0.9; when the core axial strain is 3%, η2 takes 0.8.

When the core yields, the relation between the core axial force N and the core axial strain εc is shown in Eq. (41). Considering the effect of axial force, some part of the variable cruciform region of the RSCR will also enter plasticity (Fig. 9). Through simple derivation, the expression of core axial displacement ΔBRB corresponding to axial force N can be obtained, as shown in Eq. (42). Relevant parameters can be calculated from Eq. (43).

$$N = w{N_{\rm{y}}} = [1 + \alpha ({\varepsilon _{\rm{c}}}/{\varepsilon _{\rm{y}}} - 1)]{N_{\rm{y}}},$$
(41)
$$\matrix{{{\Delta _{{\rm{BRB}}}} = {N \over {{E_{\rm{c}}}{A_{\rm{p}}}}} \cdot 2{L_{{\rm{pc}}}} + {N \over {{E_{\rm{c}}}{A_{{\rm{c}}2}}}} \cdot 2{l_{{\rm{c}}2}}} \hfill \cr {\;\;\;\;\;\;\;\; + \left[ {{N \over {\alpha {E_{\rm{c}}}{A_{{\rm{c}}1}}}} + (1 - 1/\alpha){\varepsilon _{\rm{y}}}} \right] \cdot 2{l_{{\rm{c}}1}} + {\varepsilon _{\rm{c}}}{L_{{\rm{y}}0}},} \hfill \cr }$$
(42)
$$\matrix{{{A_{{\rm{c}}0}} = {N \over {{f_{{\rm{cy}}}}}},\;{A_{{\rm{c}}1}} = {{{A_{{\rm{c}}0}}{\rm{ + }}{A_{\rm{c}}}} \over 2},\;{A_{{\rm{c}}2}} = {{{A_{{\rm{c}}0}}{\rm{ + }}{A_{\rm{p}}}} \over 2},} \hfill \cr {{l_{{\rm{c}}1}} = {{{A_{{\rm{c}}0}} - {A_{\rm{c}}}} \over {{A_{\rm{p}}} - {A_{\rm{c}}}}}{L_{{\rm{c}}20}},\;{l_{{\rm{c}}2}} = {L_{{\rm{c}}20}} - {l_{{\rm{c}}1}},} \hfill \cr }$$
(43)

where w is the core strength improvement coefficient in the plasticity stage; α is the ratio between the tangent modulus and elastic modulus of the core member in its plasticity stage; εy represents the yield strain of the core member; Ny is the core yield load; fcy is the core yield strength; Ec is the elastic modulus of the core member; Ac and Ap respectively represent the section areas of the core flat-plate and the uniform section strengthened region; Ac0 represents the critical area of the core plasticity section, which is the dividing plane of core plasticity and elasticity portion; Ac1 and Ac2 respectively represent the equivalent section areas of the plasticity region and the elastic region of the variable cruciform region of the RSCR; lc1 and lc2 respectively represent the length of the plasticity region and the elastic region of the core member variable cruciform region; Lpc is the length of the uniform section SCR; Ly0 denotes the length of the core flat-plate when the BRB is in the initial state.

Fig. 9
figure 9

Relationship between core axial displacement and force

(a) Original status; (b) Working status

Full size image

4 Design method of the pinned external integrated BRBs

It is confirmed that only the external restraining member with both sufficient rigidity and strength can guarantee the core member reaching the full sectional yielding without global buckling. Currently, the design method of the BRB can be classified into two categories: one is based on the rigidity standards of the external restraining member, namely the restraining ratio expressed by Eq. (45), and the other is based on the moment-bearing capacity of the external restraining member. This study will further explore the design method of the pinned BRBs which combines both the rigidity and the strength of external restraining member.

In addition, the SCR should also have sufficient strength under combined axial force and moment so as to avoid the bending failure at the core end. Its strength design method is also discussed.

4.1 Design criteria for the external restraining member

As the external restraining member only offers lateral support to the core member, it is a flexural member. Accordingly, the sectional bending capacity of the external member can be considered as a control of the BRB restraining ratio in its design method. For the pinned BRBs, it should be ensured that:

$${M_{{\rm{em}},\max }} \leq {M_{{\rm{em}},{\rm{u}}}},$$
(44)

where Mem,max is the maximum bending moment of the external member, which can be calculated by Eq. (37); Mem,u is the bending capacity of the external restraining member. If the external member is made from all-steel as some kind of integrated restraining member, then Mem,u=Wem fey, where Wem is the elastic modulus of the section in the external restraining member to the outer fiber in the bending direction, and fey is the yield stress of the external member steel.

The defined design parameter is the restraining ratio ξ (Black et al., 2004; Guo et al., 2010), given by Eq. (45). It is only related to the BRB geometrical parameters and the yield stress of the core material.

$$\xi = ({{\rm{\pi }}^2}{E_{\rm{b}}}{I_{\rm{b}}})/(L_{{\rm{BRB}}}^2{N_y}),$$
(45)

where Ny represents the core member yield load.

After some manipulation of Eq. (44), the minimal value of the BRB restraining ratio [ξ] can be obtained:

$$\xi \geq [\xi ] = {{wL_{\rm{y}}^2[{W_{{\rm{em}}}}{f_{{\rm{ey}}}} + ({\pi ^2}/8 - 1){Q_1}{L_{\rm{c}}}]} \over {L_{{\rm{BRB}}}^2({W_{{\rm{em}}}}{f_{{\rm{ey}}}} - w{N_{\rm{y}}}{x_1}{\delta _0} - {Q_1}{L_{\rm{c}}})}}.$$
(46)

Note that as this study mainly focuses on the external integrated BRB, the external restraining member flexural rigidity is clear. However, for the external assembled BRB, as the external members are bundled by scattered bolts, the external member rigidity will inevitably be reduced. The determination of the rigidity reduction coefficient of the external member will be a focus in the assembled BRB, and is not included in this study.

4.2 Design recommendations for the SCR

Since the ESCR behaves as a typical beam-column, its limit strength is considered as a full sectional yielding and is expressed as an interaction between axial force N and bending moment Mec. For the ESCR with cruciform section, its interaction equation is complicated. For convenience, the approximation equation (Chen, 2005) is applied:

$${(N/{N_{{\rm{p,ec}}}})^2} + {M_{{\rm{ec}}}}/{M_{{\rm{p,ec}}}} < 1.0,$$
(47)

where N refers to the core axial force which is calculated by Eq. (41); Np,ec is the fully sectional yield force of ESCR; Mec is the maximum bending moment of the ESCR, which can be calculated by Eq. (31); Mp,ec represents the fully sectional plasticity bending moment of the ESCR.

5 Conclusions

Taking a pinned BRB with extended core as a research object, this paper presents a theoretical derivation for its design method. Firstly, considering the core single-wave overall deformation mode, the equilibrium equations are established for the ESCR and the RSCR based on the assumed core contact force distribution modes. In addition, by employing the deformation compatibility relationship at some specific contact points, the maximum bending moment acting on the extended core (Eq. (31)), and the core contact force distribution (Eqs. (32) and (35)) as well as the bending moment distribution acting on the external restraining member (Eq. (36)) are also obtained. In the theoretical derivation, the following factors are considered: the initial geometrical imperfection of the external member, the gap between the core and the external member, the rigidity reduction of the RSCR, and the change of contact position.

Lastly, based on the stress characteristics of the external restraining member and the SCR, their design criteria denoted by Eqs. (46) and (47) are established. The theoretical derivation reliability is verified by finite element numerical analysis in another study as Part II (Jiang et al., 2015).